Chroma Enhancement in CIELAB Color Space Using a Lookup Table

Abstract

In this study, we present a method of chroma enhancement in the CIELAB color space and compare it with that in the RGB color space. Color image enhancement using the CIELAB color space has the disadvantage that the color gamut problem occurs because the conversion to the RGB color space is necessary to display the image. However, since the CIELAB color space is based on human visual perception, the quality of the resulting images is expected to be higher than that of the RGB color space. In the method using the CIELAB color space, we introduce a lookup table to reduce the calculation costs. Experiments comparing image enhancement results obtained from two color spaces are performed using several digital images.

1. Introduction

Color digital images have been used in various situations in daily life due to the development of digital devices and Internet technologies. Therefore, it is necessary to improve the quality of these color digital images depending on their application [1,2].

The choice of color space when performing color image enhancement is an important factor that influences the quality of the resulting images [3]. The RGB color space is a typical color space for digital image processing. An arbitrary color in the RGB color space is represented by the ratio of the three primary colors of R (red), G (green), and B (blue). Meanwhile, the three attributes of color (i.e., hue, chroma, and lightness) are more useful when specifying a certain color based on human sensitivities than the RGB components [4]. These three attributes of color can also be geometrically defined in the RGB color space. Naik et al. clarified the conditions for preserving the hue in the RGB color space and demonstrated the method of image enhancement with its conditions [5]. Furthermore, several image enhancement methods have been proposed with reference to Naik’s method [6,7,8,9,10,11,12,13]. These methods make it possible to suppress hue distortion when image enhancement is applied in the RGB color space. Color image enhancement in the RGB color space has the advantage of not causing the color gamut problem, because the conversion to other color spaces is unnecessary. Furthermore, the relationship between hue, chroma, and lightness is easy to formulate, and the algorithm for color image enhancement can be expressed simply. However, since these attributes defined in the RGB color space are not based on human visual perception as in uniform color spaces, the quality of the resulting images may not be sufficient.

When focusing on human visual perception, the color spaces that can directly represent colors by using hue, chroma, and lightness, such as the HSI [14,15,16,17,18] and CIELAB [19,20,21,22,23,24,25] color spaces, are more useful than the RGB color space. Previously, we proposed an image enhancement method in the CIELAB color space, which is one of the uniform color spaces. In our previous method [22], a color gamut adjustment is applied to address the problem that may occur when inversely converting processed color components in the CIELAB color space to the RGB color space. However, in this method, there is a problem in that the calculation cost is high because it is necessary to solve the third-order polynomial for the pixels outside the color gamut. In this study, we introduce a lookup table that stores the maximum chroma values at sample points of hue and lightness. Finally, we compare the results obtained from the methods using the RGB and CIELAB color spaces.

The remainder of this paper is organized as follows: Section 2 and Section 3 explain the chroma enhancement methods in the RGB and CIELAB color spaces, respectively. In Section 4, a lookup table introduced in a method using CIELAB color space is described. Section 5 provides the experimental results of applying the proposed chroma enhancement methods to several digital images. Section 6 presents the conclusions of our study.

2. Chroma Enhancement in RGB Color Space

The RGB color space is usually used to represent color digital images acquired by various digital devices. In this section, we describe a method to enhance the chroma while preserving the hue and lightness in the RGB color space.

2.1. Equal Hue and Equal Lightness in RGB Color Space

In this study, sRGB is assumed as the RGB color space. Let $I(i,j)$ be the input digital image at the pixel $(i,j)$. $I(i,j)$ have the three RGB components $\left(I_r(i,j),I_g(i,j),I_b(i,j)\right)$. Here, each RGB component is assumed to be normalized to the interval $[0,1]$. For simplicity of notation, we omit $(i,j)$ after this.

Let J be the RGB color components after applying color image enhancement to I. When J have the same hue as I, they are obtained as follows [5]:

$$\begin{array}{c}\hfill J=\alpha I+\beta e,\end{array}$$

(1)

where $e=(1,1,1)$. Equation (1) is the plane equation passing through $(0,0,0),(1,1,1),$ and I with the parameters $\alpha$ and $\beta$. The lightness of I is given by the inner product of I and $V=(V_r,V_g,V_b)$:

$$\begin{array}{c}\hfill V·I=l.\end{array}$$

(2)

In our previous method [11], we employed $V=e/3$. In this study, to correspond to the lightness defined in the CIELAB color space, let V be (0.2126, 0.7152, 0.0722), where $V·e=1$.

Here, the lightness is kept at l before and after color image enhancement. That is,

$$\begin{array}{c}\hfill V·J=l.\end{array}$$

(3)

By calculating the inner products of both sides of Equation (1) and V, and substituting Equations (2) and (3) for the calculation result, we get

$$\begin{array}{c}\hfill \beta =l-\alpha l.\end{array}$$

(4)

Hence, by substituting Equation (4) for Equation (1), we get

$$\begin{array}{c}\hfill J=\alpha \left(I-le\right)+le.\end{array}$$

(5)

The chroma enhancement is executed by selecting the appropriate RGB color components on the straight line J (Figure 1).

2.2. Chroma in RGB Color Space

In the HSI color space with a cylindrical coordinate system (Figure 2), the hue, H, and the chroma, S, are obtained as follows [26]:

$$\begin{array}{ccc}\hfill H\left(I\right)& =& arctan\left(\frac{\sqrt{3}(I_g-I_b)}{2I_r-I_g-I_b}\right),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill S\left(I\right)& =& \sqrt{\frac{{(I_r-I_g)}^2+{(I_g-I_b)}^2+{(I_b-I_r)}^2}{3}}.\hfill \end{array}$$

(7)

From Equations (5) and (6), $H\left(I\right)$ = $H\left(J\right)$. This indicates that the hue is preserved after the chroma enhancement.

In addition, S($I$) can be rewritten as

$$\begin{array}{c}\hfill S\left(I\right)=∥I-\left(I·\frac{e}{\parallel e\parallel }\right)\frac{e}{\parallel e\parallel }∥,\end{array}$$

(8)

where $\parallel ·\parallel$ indicates the Euclidean distance. Equation (8) represents the distance between I and the achromatic axis, e, as shown in Figure 1. That is, the chroma of a color in the RGB color space increases as the color moves away from the achromatic axis, e. Thus, from Equation (5), the chroma of J becomes larger than that of I as $\alpha$ increases from 1.

Figure 2. HSI color space with cylindrical coordinate system.

Figure 2. HSI color space with cylindrical coordinate system.

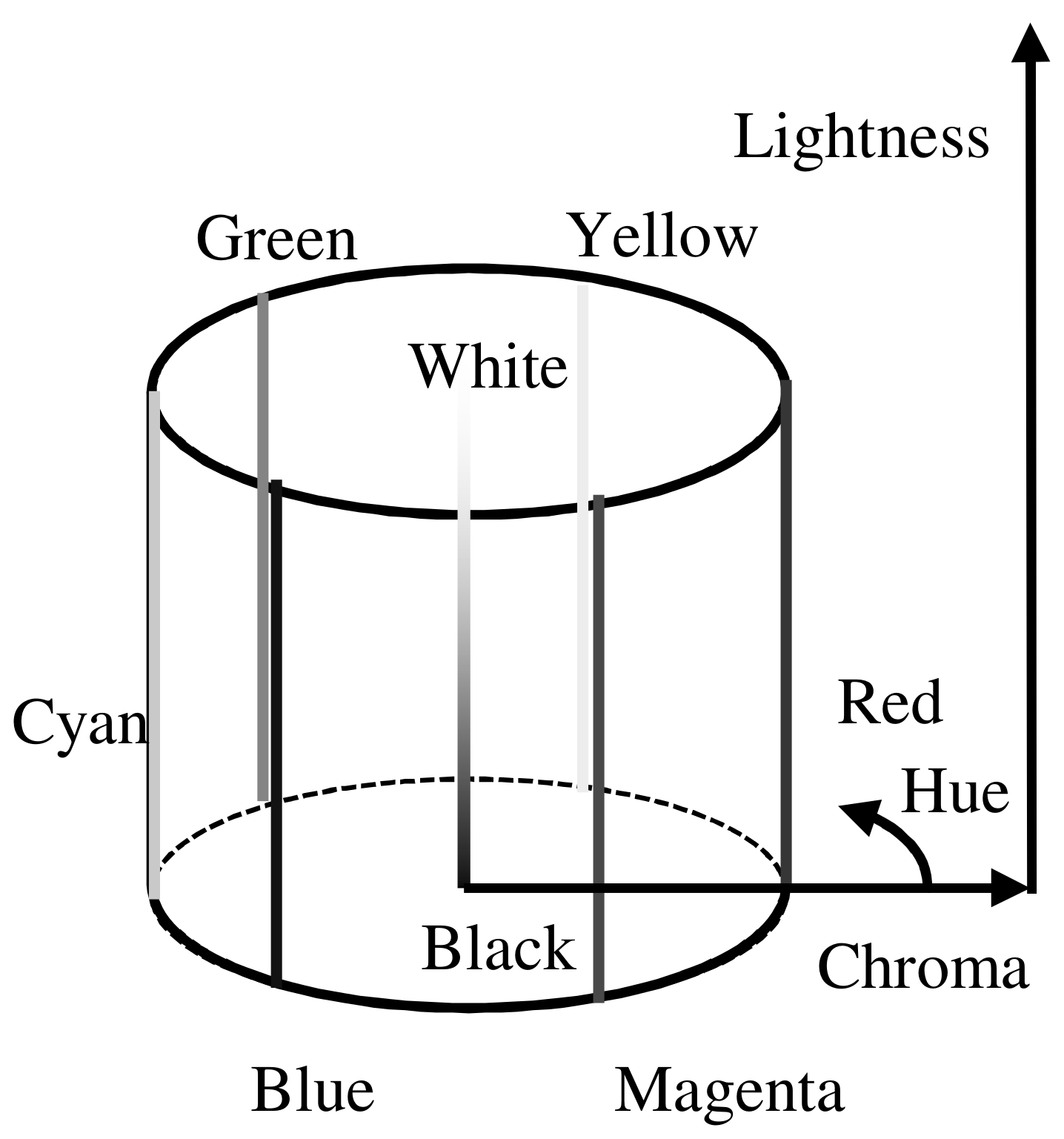
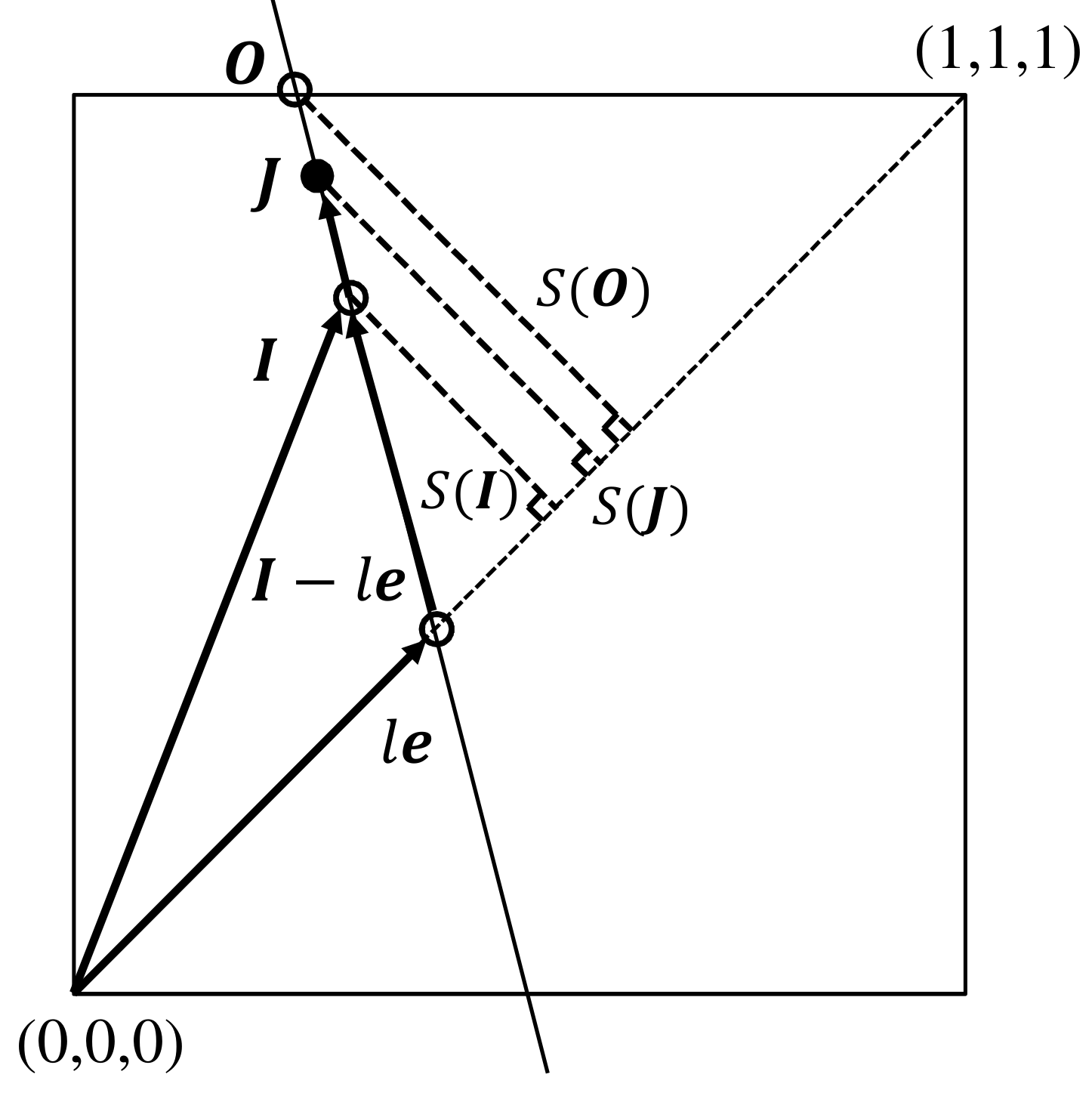
2.3. Chroma Enhancement Method

Let O be the intersection point between the straight line, J, and the boundary surface of the RGB color space. O has the maximum chroma among the colors that are of equal hue and equal lightness with the input color, I. The enhanced color is decided by using the distance, $D_{\gamma }$, as follows:

$$\begin{array}{c}\hfill J=D_{\gamma }\left(O-le\right)+le.\end{array}$$

(9)

Here, $D_{\gamma }$ is obtained as

$$\begin{array}{c}\hfill D_{\gamma }={\left(\frac{∥I-le∥}{∥O-le∥)}\right)}^{1/\gamma },\end{array}$$

(10)

where $\gamma$ is the parameter that determines the degree of the chroma enhancement. J coincides with I when $\gamma =1$ and coincides with O having the maximum chroma when $\gamma \to \infty$ owing to $D_{\gamma }\to 1$. Hence, by setting the parameter $\gamma$ to a value larger than 1, we get a color with a chroma larger than that of the input color, I.

3. Chroma Enhancement in CIELAB Color Space

The definitions of hue, chroma, and, lightness in the RGB color space may not exactly match human visual perception because it is not a uniform color space. In this section, we present a method to enhance the chroma while preserving the hue and lightness in the CIELAB color space, which is one of the uniform color spaces.

Let $F_E^{\prime }$ be the input value of a nonlinear RGB component. E takes any one of r, g, and b, which indicate the red, green, and blue components, respectively. The nonlinear RGB component $F_E^{\prime }$ is converted to the linear RGB component $F_E$ as follows [27]:

$$\begin{array}{ccc}\hfill F_E& =& \left\{\begin{array}{cc}{F}_E^{\prime }/12.92\hfill & F_E^{\prime }\le 0.03928\hfill \\ {\displaystyle {\left(\frac{F_E^{\prime }+0.055}{1.055}\right)}^{2.4}}\hfill & \mathrm{otherwise}\hfill \end{array}\right..\hfill \end{array}$$

(11)

The RGB color components, $(F_r,F_g,F_b)$, are first converted to the CIEXYZ color components, $(X,Y,Z)$, by the following linear transformation:

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}\hfill 0.4124& \hfill 0.3576& \hfill 0.1805\\ \hfill 0.2126& \hfill 0.7152& \hfill 0.0722\\ \hfill 0.0193& \hfill 0.1192& \hfill 0.9505\end{array}\right]\left[\begin{array}{c}{F}_r\\ F_g\\ F_b\end{array}\right].$$

(12)

Next, $(X,Y,Z)$ are converted to the CIELAB color components, $(L^{*},a^{*},b^{*})$, by the following nonlinear transformation [28]:

$$\begin{array}{ccc}\hfill L^{*}& =& 116f(Y/Y_n)-16,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill a^{*}& =& 500\left(f(X/X_n)-f(Y/Y_n)\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill b^{*}& =& 200\left(f(Y/Y_n)-f(Z/Z_n)\right),\hfill \end{array}$$

(15)

where the function, f, is defined by

$$\begin{array}{c}\hfill f\left(x\right)=\left\{\begin{array}{cc}{x}^{1/3}\hfill & x>0.008856\hfill \\ 7.787x+16/116\hfill & otherwise\hfill \end{array}\right..\end{array}$$

(16)

Here, $L^{*}$ is the lightness, and $a^{*}$ and $b^{*}$ represent the chromaticity indices of redness, greenness and yellowness, and blueness. $X_n,Y_n,$ and $Z_n$ are the CIEXYZ values for the reference white of the illuminant CIE D65 and are 0.9505, 1.000, and 1.089, respectively. Note that $0\le X/X_n$, $Y/Y_n$, and $Z/Z_n\le 1$ and $0\le L^{*}\le 100$. The chroma, $C^{*}$, and the hue, h, in the CIELAB color space are obtained by $C^{*}=\sqrt{{\left(a^{*}\right)}^2+{\left(b^{*}\right)}^2}$ and $h=arctan(b^{*}/a^{*})$, respectively. Here, $C^{*}\ge 0$ and $0\le h<360$. In this study, let $h=0$ in the case of $C^{*}<0.1$ because h becomes very sensitive to the change in $a^{*}$ or $b^{*}$ when $C^{*}$ is very small.

The chroma enhancement is conducted in the CIELAB color space while preserving the hue. The enhanced chroma, $C_e^{*}$, is obtained by

$$\begin{array}{c}\hfill C_e^{*}=\sqrt{{\left(k{a}^{*}\right)}^2+{\left(k{b}^{*}\right)}^2}=k{C}^{*},\end{array}$$

(17)

where k is the parameter that determines the degree of the chroma enhancement. When applying the chroma enhancement by Equation (17), the hue, h, is preserved regardless of the value of k owing to $h=arctan(k{b}^{*}/k{a}^{*})=arctan(b^{*}/a^{*})$. When the lightness is not changed before and after image enhancement, the CIELAB color components after the chroma enhancement are given by $(L^{*},k{a}^{*},k{b}^{*})$. The final RGB color components, $(G_r,G_g,G_b)$, are obtained by converting $(L^{*},k{a}^{*},k{b}^{*})$ to the RGB color space. However, it is unknown whether $(G_r,G_g,G_b)$ is within the color gamut of the RGB color space. Therefore, it is necessary to address the color gamut problem.

4. Color Gamut Adjustment after Chroma Enhancement Using Lookup Table

When image enhancement is conducted in the CIELAB color space, some pixels of the enhanced image may not be correctly converted into the RGB color space. In this section, as a solution to this problem, we propose a method of color gamut adjustment using a lookup table.

4.1. Relationship among Hue, Chroma, and Lightness

In our previous method [22], to handle the color gamut problem, Equations (14) and (15) are reformulated using variables related to hue, chroma, and lightness as follows:

$$\begin{array}{ccc}\hfill f(X/X_n)& =& \frac{\mathrm{sgn}\left(a^{*}\right)C^{*}}{500\sqrt{1+H^2}}+f(Y/Y_n),\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill f(Z/Z_n)& =& \frac{-\mathrm{sgn}\left(b^{*}\right)C^{*}}{200\sqrt{1+(1/H^2)}}+f(Y/Y_n),\hfill \end{array}$$

(19)

where $H=b^{*}/a^{*}$ and $\mathrm{sgn}(·)$ is the sign function defined as follows:

$$\begin{array}{c}\hfill \mathrm{sgn}\left(x\right)=\left\{\begin{array}{cc}\hfill 1& x>0\hfill \\ \hfill 0& x=0\hfill \\ \hfill -1& x<0\hfill \end{array}\right..\end{array}$$

(20)

$f(X/X_n)$ and $f(Z/Z_n)$ are the equations of straight lines with $C^{*}$ as a variable when H and $f(Y/Y_n)$, which are related to the hue and lightness, are fixed. Therefore, the color gamut problem is solved by finding the maximum value of $C^{*}$ at arbitrary hue and lightness.

4.2. Preparation of Lookup Table

We proposed a color gamut adjustment method that obtains the maximum chroma values while preserving the lightness and hue according to the range of Y. However, our previous method has a problem in that the calculation cost is high because it is necessary to solve the third-order polynomial for the pixels outside the color gamut.

Therefore, we introduced a lookup table to reduce the calculation cost. The lookup table stores the maximum chroma values at the sampled Y and h. The procedure of making the lookup table is as follows: First, Y and h are sampled at 100 points from 0.005 to 0.995 with a step of 0.01 and at 360 points from 0.5 to 359.5 with a step of 1, respectively. Next, the maximum chroma values are calculated at these 36,000 points of $(Y,h)$ using our previous method. Let $t(m,n)$ be the element of the lookup table, where $m=\{1,2,\cdots ,100\}$ and $n=\{1,2,\cdots ,360\}$. $t(m,n)$ stores the maximum chroma value at the point, ($Y=0.005+0.01(m-1)$, $h=0.5+(n-1)$). Figure 3 shows the lookup table obtained by the above procedure. This indicates the maximum chroma for a given hue and lightness.

4.3. Determination Method for Maximum Chroma Value Using Lookup Table

The approximate maximum chroma value of an arbitrary point, $(Y,h)$, can be obtained by the lookup table. Y and h are first converted to the integers as follows:

$$\begin{array}{ccc}\hfill iY& =& \mathrm{round}\left(100Y\right),\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill ih& =& \mathrm{round}\left(h\right),\hfill \end{array}$$

(22)

where $\mathrm{round}(·)$ is the function that rounds to the nearest integer.

The point $(Y,h)$ is located inside the quadrangle with four vertices, namely, $(iY,ih)$, $(iY+1,ih)$, $(iY,ih+1)$, and $(iY+1,ih+1)$, as shown in Figure 4. Therefore, in the proposed method, the maximum chroma value of the point, $(Y,h)$, is assigned the minimum value among the four elements of the lookup table on the above points as follows:

$$\begin{array}{c}\hfill C_{\mathrm{LT}}^{*}=\mathrm{MIN}\left(t(iY,ih),t(iY+1,ih),t(iY,ih+1),t(iY+1,ih+1)\right),\end{array}$$

(23)

where $\mathrm{MIN}(·)$ is the function that finds the minimum value in any given data. However, $C_{\mathrm{LT}}^{*}$ is set to 0 when $iY=0$ and $iY=100$, corresponding to black and white. In addition, when $ih=0$ and $ih=360$, the following formula is used

$$\begin{array}{c}\hfill C_{\mathrm{LT}}^{*}=\mathrm{MIN}\left(t(iY,1),t(iY+1,1),t(iY,360),t(iY+1,360)\right).\end{array}$$

(24)

4.4. RGB Components after Color Gamut Adjustment

The approximate maximum chroma $C_{\mathrm{LT}}^{*}$ of the color gamut that is determined by h and Y is extracted from the lookup table by the procedure in Section 4.3. Substituting $C_{\mathrm{LT}}^{*}$ for Equations (18) and (19), we get

$$\begin{array}{ccc}\hfill f(X^{\prime }/X_n)& =& \frac{\mathrm{sgn}\left(a^{*}\right)C_{\mathrm{LT}}^{*}}{500\sqrt{1+H^2}}+f(Y/Y_n),\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill f(Z^{\prime }/Z_n)& =& \frac{-\mathrm{sgn}\left(b^{*}\right)C_{\mathrm{LT}}^{*}}{200\sqrt{1+(1/H^2)}}+f(Y/Y_n),\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill f(Y/Y_n)& =& \frac{L^{*}+16}{116}.\hfill \end{array}$$

(27)

Figure 5 shows $f(X^{\prime }/X_n)$ and $f(Z^{\prime }/Z_n)$ at ($Y=0.005+0.01(20-1)$, $h=0.5+(30-1)$). By applying the inverse function of $f\left(\alpha \right)$ to the above equations, we get

$$\begin{array}{ccc}\hfill X^{\prime }& =& X_n{f}^{-1}\left(f(X^{\prime }/X_n)\right),\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill Z^{\prime }& =& Z_n{f}^{-1}\left(f(Z^{\prime }/Z_n)\right),\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill Y& =& Y_n{f}^{-1}\left(f(Y/Y_n)\right).\hfill \end{array}$$

(30)

Here, $f^{-1}\left(\alpha \right)$ is defined as follows:

$$\begin{array}{c}\hfill f^{-1}\left(x\right)=\left\{\begin{array}{cc}{x}^3\hfill & x>0.20689\hfill \\ {\displaystyle \frac{x-16/116}{7.787}}\hfill & otherwise\hfill \end{array}\right..\end{array}$$

(31)

$(G_r,G_g,G_b)$ are obtained by converting ($X^{\prime }$, Y, $Z^{\prime }$) to the RGB color space by using the inverse of the matrix used in Equation (12):

$$\left[\begin{array}{c}{G}_r\\ G_g\\ G_b\end{array}\right]=\left[\begin{array}{ccc}\hfill 3.2410& \hfill -1.5374& \hfill -0.4986\\ \hfill -0.9692& \hfill 1.8760& \hfill 0.0416\\ \hfill 0.0556& \hfill -0.2040& \hfill 1.0570\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y\\ Z^{\prime }\end{array}\right].$$

(32)

Finally, the nonlinear RGB component $G_E^{\prime }$ of the output image is obtained as

$$\begin{array}{c}\hfill G_E^{\prime }=\left\{\begin{array}{cc}12.92G_E\hfill & G_E\le 0.0304\hfill \\ 1.055G_E^{(1.0/2.4)}-0.055\hfill & \mathrm{otherwise}\hfill \end{array}\right..\end{array}$$

(33)

Figure 5. $f(X/X_n)$ and $f(Z/Z_n)$ plotted as a function of $C^{*}$ at ($Y=0.005+0.01(20-1)$, $h=0.5+(30-1)$). In this case, $C_{\mathrm{LT}}^{*}$ is 89.941.

Figure 5. $f(X/X_n)$ and $f(Z/Z_n)$ plotted as a function of $C^{*}$ at ($Y=0.005+0.01(20-1)$, $h=0.5+(30-1)$). In this case, $C_{\mathrm{LT}}^{*}$ is 89.941.

5. Experiments

5.1. Chroma Enhancement

To illustrate the effectiveness of the proposed method, experiments are conducted using seven digital images: Pepper, Mandrill, Sailboat, Airplane, Balloon, Earth, and Lenna [29]. These are 24-bit color images of 256 × 256 pixels in size.

Figure A1 shows the experimental results of seven digital images. We can see that the large red bell peppers in Figure A1d1,e1 are deeper red than that in Figure A1b1. In addition, the blue part of the mandrill’s face in Figure A1d2,e2, the trunks and branches of the trees in Figure A1d3,e3, the clouds in Figure A1d4,e4, and the Earth in Figure A1d6,e6 are not over-enhanced compared to those in Figure A1b2–b4,b6.

To evaluate the quality of enhanced images from a perceptual point of view objectively, the difference related to hue between the enhanced and original images is calculated as follows [30]:

$$\begin{array}{c}\hfill |\Delta h^{*}|=2\sqrt{C_e^{*}{C}_o^{*}}sin\left(\frac{|h_e-h_o|}{2}\right),\end{array}$$

(34)

where $h_e$ and $h_o$ are the hues of the corresponding pixels in the enhanced and original images, respectively. Similarly, $C_e^{*}$ and $C_o^{*}$ refer to the chromas. $\left|·\right|$ is the absolute value. In addition, the differences, $\Delta L^{*}=L_e^{*}-L_o^{*}$ and $\Delta C^{*}=C_e^{*}-C_o^{*}$, related to lightness and chroma are calculated to confirm the degree of image enhancement. Here, $L_e^{*}$ and $L_o^{*}$ refer to the lightnesses in the same meaning as above.

Table A1. Averages and standard deviations of $|\Delta h^{*}|$, $\Delta L^{*}$, and $\Delta C^{*}$ in Figure A1.

	$|\mathit{\Delta }{\mathit{h}}^{*}|$		$\mathit{\Delta }{\mathit{L}}^{*}$		$\mathit{\Delta }{\mathit{C}}^{*}$
	ave	std	ave	std	ave	std
(b1)	3.836	2.142	0.000	0.000	33.040	14.823
(c1)	12.645	9.664	7.953	8.203	46.223	13.035
(d1)	0.224	0.699	0.029	0.171	23.940	16.369
(e1)	0.016	0.150	0.031	0.227	22.802	16.691
(b2)	1.349	1.210	0.000	0.000	32.049	17.907
(c2)	6.763	7.433	0.950	3.491	35.602	15.934
(d2)	0.017	0.129	0.003	0.026	28.585	14.542
(e2)	0.009	0.100	0.003	0.021	27.829	14.601
(b3)	2.350	2.724	0.000	0.000	36.777	10.661
(c3)	5.869	6.632	6.946	8.626	43.621	14.031
(d3)	0.163	0.502	0.002	0.003	29.880	12.455
(e3)	0.036	0.212	0.003	0.010	28.774	13.066
(b4)	0.421	0.836	0.000	0.000	24.535	10.445
(c4)	0.913	2.524	0.845	4.031	24.933	24.783
(d4)	0.003	0.020	0.004	0.009	21.153	19.274
(e4)	0.003	0.002	0.004	0.003	20.450	18.558
(b5)	0.856	0.951	0.000	0.000	33.384	14.116
(c5)	2.559	6.620	0.514	1.378	40.062	18.335
(d5)	0.003	0.016	0.002	0.003	36.953	17.623
(e5)	0.002	0.008	0.002	0.003	36.611	17.439
(b6)	1.058	0.681	0.000	0.000	34.598	14.955
(c6)	1.907	1.264	8.704	14.991	72.097	14.419
(d6)	0.003	0.001	0.003	0.002	49.015	25.670
(e6)	0.004	0.001	0.003	0.002	46.926	25.850
(b7)	0.513	0.347	0.000	0.000	19.756	13.775
(c7)	10.679	6.936	4.055	14.988	54.951	9.873
(d7)	0.005	0.003	0.000	0.002	26.863	13.405
(e7)	0.003	0.001	0.000	0.001	25.313	13.703

shows the averages and standard deviations of $|\Delta h^{*}|$, $\Delta L^{*}$, and $\Delta C^{*}$ over all pixels in Figure A1. From the results of $|\Delta h^{*}|$, we can see that $|\Delta h^{*}|$ and $\Delta C^{*}$ of the proposed method (e1–e7) are not so different from that of our previous method (d1–d7). In addition, the limitation of our previous method is trying to approximate Equation (16) by $f\left(x\right)=x^{1/3}$ when applying color gamut adjustment. Therefore, when the lightness is very low, it becomes an approximate solution [22]. Since the present method using the lookup table selects the minimum chroma value among the four surrounding elements, the resulting color is highly likely to exist within the color gamut, and then it is thought that $|\Delta h^{*}|$ becomes smaller than that of our previous method. That is, the lookup table can achieve the image enhancement without significantly deteriorating the quality.

5.2. Combination of Lightness and Chroma Enhancement

The advantage of using the CIELAB color space compared to the RGB color space is that the chroma and lightness components are completely independent. The proposed lookup table can also be applied when both the lightness and chroma are enhanced. Here, the lightness is enhanced as follows:

$$\begin{array}{c}\hfill L_e^{*}=100{\left(\frac{L_o^{*}}{100}\right)}^{1/p},\end{array}$$

(35)

where p is the parameter that determines the degree of lightness enhancement.

The proposed method is compared with the method of Ref. [5] using histogram equalization, the method of Ref. [7] using the parameters $(l,r,\lambda )$ = ($exp(-9/2)$, $exp(-9/2)$, $1/2$) [31], and the RGB chroma enhancement in Section 2, in which histogram equalization is applied to the lightness.

Figure A2 show the experimental results of four digital images. These are 24-bit color images of 960 × 1280 pixels, 1478 × 1108 pixels and 1280 × 622 pixels, 623 × 1280 pixels in size, respectively. We can see that Figure A2e1–e4 are more naturally enhanced in comparison to Figure A2b1,c1,d1,b2,c2,d2 and Figure A2b3,c3,d3,b4,c4,d4. Especially, the colors of the cat and various objects in Figure A2e4 are well reproduced.

Table A2. Averages and standard deviations of $|\Delta h^{*}|$, $\Delta L^{*}$, and $\Delta C^{*}$ in Figure A2.

	$|\mathit{\Delta }{\mathit{h}}^{*}|$		$\mathit{\Delta }{\mathit{L}}^{*}$		$\mathit{\Delta }{\mathit{C}}^{*}$
	ave	std	ave	std	ave	std
(b1)	0.991	1.140	1.990	6.494	24.768	17.487
(c1)	0.024	0.070	2.720	6.483	−1.247	2.203
(d1)	0.169	0.626	4.842	5.171	3.603	5.657
(e1)	0.841	2.081	11.429	2.931	24.765	16.642
(f1)	0.007	0.064	11.296	2.309	22.811	14.573
(b2)	1.967	1.231	2.273	8.386	33.528	17.005
(c2)	0.131	0.174	3.970	8.482	−5.353	4.661
(d2)	0.154	0.458	3.755	3.947	3.650	3.324
(e2)	4.241	5.695	12.212	4.610	46.189	20.786
(f2)	0.005	0.038	11.609	3.903	38.464	19.173
(b3)	0.717	0.693	−14.627	19.233	14.353	13.810
(c3)	0.003	0.006	−14.054	18.193	−4.951	5.504
(d3)	0.065	0.135	−3.700	3.629	1.301	1.067
(e3)	13.015	5.495	7.550	2.904	31.514	5.773
(f3)	0.002	0.004	8.653	1.536	20.922	11.502
(b4)	0.114	0.258	44.572	29.079	5.865	10.769
(c4)	0.095	0.257	44.666	29.078	−4.196	6.154
(d4)	0.043	0.531	2.923	4.038	0.680	2.680
(e4)	2.505	5.296	5.317	6.734	21.035	25.491
(f4)	0.007	0.094	5.429	5.989	14.285	18.111

shows the averages and standard deviations of $|\Delta h^{*}|$, $\Delta L^{*}$, and $\Delta C^{*}$ over all pixels in Figure A2. We can see that $|\Delta h^{*}|$ of the proposed method (e1–e4) provides better results than those of the other methods (b1–b4, c1–c4, and d1–d4).

5.3. Computational Load

Our previous method is computationally expensive. In contrast, the computational costs of the proposed method are low because it uses the lookup table. The flow of the proposed method is as follows:

Step 1. 

Input image is converted to the CIELAB color space.

Step 2. 

Image enhancement is executed by either Equations (17) or (35), or both.

Step 3. 

Enhanced image is converted to the RGB color space.

Step 4. 

If the pixels in the enhanced image are outside the color gamut of the RGB color space, the color gamut adjustment is executed by the lookup table.

The execution times required to obtain Figure A1e1–e7 and Figure A2e1–e4 using CPU Intel(R) Core(TM) i5-5200U, RAM 8GB, MATLAB R2020a are 0.33 s, 0.33 s, 0.32 s, 0.31 s, 0.31 s, 0.32 s, 0.33 s and 3.78 s, 4.98 s, 2.58 s, 2.05 s, respectively.

6. Conclusions

In this study, we proposed a method of chroma enhancement in the CIELAB color space, which incorporates a lookup table and compared it with that in the RGB color space. The lookup table was implemented to solve the color gamut problem that occurs when inversely converting the CIELAB color space to the RGB color space at low computational costs. The experimental results showed that the proposed method using the CIELAB color space provides better results than that of the RGB color space, especially when performing both the lightness and chroma enhancement.

However, since the methods using the RGB color space does not require the color space conversion, the formulation for image enhancement can be easily realized in comparison to those using the HSI or the CIELAB color space. Furthermore, the color gamut problem does not occur when image enhancement is performed in the RGB color space.

Therefore, the proposed method needs to be further improved its performance. The CIELAB color space is not a complete uniform color space. This limits the performance of the proposed method. Hence, it is expected to extend the proposed method by considering better uniform color spaces that accurately simulate human vision such as DIN99d [32] and CAM02-UCS [33].

Future works are needed to confirm the validity of the images resulting from the proposed method via psychometric assessment and to further improve the quality of enhanced images by refining the accuracy of the maximum chroma assignment by the lookup table [34].