Abstract
Growing demands for energy are motivating researchers to conduct in-depth analysis of positive displacement machines such as oil-injected screw compressors which are frequently used in industrial applications like refrigeration, oil and gas and air compression. The performance of these machines is strongly dependent on the oil injection. Optimisation of oil has a great energy saving potential by both increasing efficiency and reducing other impacts on the environment. Therefore, a three-dimensional, transient computational fluid dynamics study of oil injection in a twin-screw compressor is conducted in this research. This study explores pseudo single-fluid multiphase (SFM) models of VOF (Volume of Fluid) and a mixture for their capability to predict the performance of the oil-injected twin screw compressor and compare this with the experimental values. SCORGTM (Screw Compressor Rotor Grid Generator) is used to generate numerical grids for unstructured solver Fluent with the special interface developed to facilitate user defined nodal displacement (UDND). The performance predictions with both VOF and mixture models provide accurate values for power consumption and flow rates with low deviation between computational fluid dynamics (CFD) and the experiment at 6000 RPM and 7.0 bar discharge pressure. In addition, the study reflects on differences in predicting oil distribution with VOF, mixture and Eulerian-Eulerian two-fluid models. Overall, this study provides an insight into multiphase flow-modelling techniques available for oil-injected twin-screw compressors comprehensively accounting for the details of oil distribution in the compression chamber and integral compressor performance.
1. Introduction
Twin-screw compressors have been widely used in compression processes due to their advantages such as compact structure, stable operation and high efficiency. They are used in a number of industries such as oil and gas, refrigeration, processing or mining. In many cases, twin-screw compressors have replaced reciprocating compressors [1]. The market for compressors is projected to grow at a compound annual growth rate (CAGR) of 6.62% from 2016–2021, to reach a market size of USD 11.01 billion by 2021 [2]. With this growing pace, more and more researchers and engineers are interested in looking for ways to improve efficiency and reduce the carbon footprint [3].
Oil-injected compressors are popular compared to oil-free compressors as achieving high-pressure ratios within single stage with reduced mechanical elements is possible. Oil is injected for cooling, sealing gaps and lubricating rotors. Excessive amount of oil can lead to frictional and momentum losses [4]. In early years of screw machines, analytical modelling was used to understand the effect of oil injection. In 1986, Singh and Bowman [5] developed a mathematical model to evaluate the effect of oil droplet size. They reported that with 10 times reduction in oil droplet size, specific power could be reduced by 7%. A parametric study on oil injection variants conducted by Stosic et al. [6] concluded that oil mass flow and oil port position had more significant effect on integral performance. These key analytical studies had promised improvements in performance which lead to further experimental research. Peng et al. [7] studied the effect of oil to gas mass ratio at varying rotational speeds and de Paepa et al. [8] studied the effect of cooling effectiveness. Further to this, authors have carried out elaborate experiments to understand the effect of oil flow on compressor performance at varying shaft speeds and discharge pressures [9]. Study has strongly indicated that, for lower discharge pressures (6.5 bar and 8.5 bar), power consumption increased with the increase in oil flow. Meanwhile, at higher discharge pressures (10.5 bar and 12.5 bar) the power consumption decreased with the increase in the oil flow. Hence, an optimal quantity of oil exists for a compressor running at a certain design or operating condition.
There is a growing interest in visualising distribution of oil in the compression chamber because experimental investigations of two-phase flows in a compressor are often difficult and cumbersome. Physical or optical access to measure the chamber pressures or temperatures is limited, which makes it hard to determine internal flow characteristics of the oil phase. Hence, computational fluid dynamics (CFD) provides an excellent insight to visualise flow pattern and oil distribution within compression chamber.
Very little work was done on CFD before the break of 20th Century as reliable grids were not available for complex deforming domains of twin-screw machines. Kovacevic [10,11,12] made a breakthrough in CFD modelling of screw machines by developing a methodology to produce block-structured grids for deforming domains and this was further developed to form single domain-type mesh. This had resulted in better solution accuracy for single phase flow of air in oil free compressor [13,14]. Rane et al. [15] conducted analysis with non-homogenous Eulerian-Eulerian approach which showed distribution of oil as it was expected based on experience. The difference in power predictions were noticed as the mechanical losses were estimated. The highest deviations in power from experimental data around 10% was noticed at 8.0 bar discharge pressure and 6000 RPM. At the same time, the flow predictions were only 2% different.
Further to this, authors conducted investigation using CFD solver Ansys CFX to compare the inhomogeneous Euler-Euler approach, and homogeneous model. The homogeneous approach resulted in lower flow and power predictions than the Eulerian-Eulerian model [16]. However, the calculation time of the homogeneous model was shorter than non-homogeneous model. The only available SFM model which represents homogeneous approach in CFX is comparable to VOF (Volume of Fluid) modelling. However, it is known that the fluid-fluid interphase is better resolved in ANSYS Fluent where additional interface reconstruction algorithms are used when compared to CFX within the VOF approach [17]. This encouraged authors to explore Fluent as a solver which is known for resolving sharper interphase well and reducing smearing problems for fluids with high-density ratios compared to CFX. In Fluent, the interface between two phases is reconstructed for every time step based on calculated volume fraction distributions.
Another solver used for a case study of oil-injected twin-screw compressors is Pumplinx which has only one multiphase flow model available VOF [18]. As presented in this case study, the mass imbalance for both air and oil is as low as 1%, although integral parameters are not compared with experimental data. Another study looks at oil droplet trajectories in terms of diameter size (0.5 μm, 5.0 μm and 50.0 μm), simulation is conducted for a static mesh for single screw compressor domain in Star CCM+ [19]. Although this modelling gives an indication of distributed oil droplets, the effects of rotation or compression cycle are neglected and the results do not always look as expected. Eulerian-Eulerian modelling with Fluent has been explored by Papes et al., but the simulation results have not been validated experimentally nor mass balance was shown [20]. Therefore, further exploration is required with SFM models to obtain a stable and reliable approach towards modelling of oil injection within twin-screw compressors.
In the light of above considerations, SFM models of VOF and mixture are explored in Fluent to check for their stability, calculation speed and more importantly performance predictions. For achieving solution, SCORGTM is used with UDND to transition the nodes for each time step. Successful running of UDND code in parallel framework is used for the case of oil-injected compressor operating at discharge pressure of 7.0 bar with the male rotor shaft speed of 6000 RPM.
Research questions investigated in this paper are,
- How is Fluent solver customised to solve for oil-injected twin screw compressor?
- Are pseudo-SFM models capable of predicting integral performance comparable to experimental data?
- How is the oil distributed within the compression chamber for various multiphase flow models and what is its effect on integral performance?
2. Multiphase Flow Modelling
Two-phase flow includes all complexities of single-phase flow such as non-linearities, transition to turbulence and instabilities, and additional multiphase characteristics such as motion and deformation of the interface, non-equilibrium effects and momentum interaction between phases. Oil is initially injected as a continuous fluid which is dispersed due to the shear of the incoming rotor lobe leading to the formation of droplets. Smaller droplets leave the compression chamber faster while others coalescence to form the oil lubrication film on the rotors and casing. It would be difficult to capture all these flow regimes that occur in twin-screw machines within one multiphase scheme.
Key challenges faced for modelling of oil-injected flows in a screw compressor are,
- i.
- Binary fluids with high-density ratios
Air and oil exist with the density ratio of magnitude of approximately 900. Challenges here are attributed largely to the difference in material properties between phases, which can lead to formation of high interfacial forces [21]. Numerical simulations with high density ratios tend to have sharp discontinuities across the interface resulting in instability. Various interpolation schemes are available in Fluent for advection of volume fraction. These are geometric construction, donor-acceptor and compressive scheme. Out of these, a compressive discretisation scheme is useful for blending sudden jump in material properties [17]. Therefore, this scheme is chosen in this study.
- ii.
- Compressible fluids
Interpolation schemes for volume fraction advection applied to the interphase cells can sometimes result in smearing of density. This smeared density if not treated carefully can affect Pressure-velocity coupling equations as pressure is a function of density. As a result, unphysical pressures can occur in the solution leading to instability for iterative solution of continuity equation. This instability is cautiously controlled by under-relaxation factor of 0.01 for current case.
- iii.
- Mesh quality
Poor mesh quality can lead to problems in resolving higher volume fraction gradients. Higher aspect ratio, orthogonality and a sudden change in cell sizes can affect conservativeness of pressure-velocity-density balancing and result in abrupt changes in physical properties. This in turn can lead to localised and unphysical increase in pressure and temperature. However, for this study, good-quality mesh was obtained with aspect ratio- 326, expansion factor- 96 and orthogonal angle- 6.9.
Two key approaches are available in Fluent for modeling multiphase flows known as the separated and dispersed techniques multiphase models (Figure 1). The dispersed model assumes that the complete volume of the second phase is dispersed in droplets of a certain diameter size. The VOF model is representative of the separated approach whereas Eulerian-Eulerian, mixture and particle tracking models are representatives of dispersed models. A full Eulerian-Eulerian approach is computationally expensive and complicated compared to VOF or Mixture models. The other models such as Eulerian-Lagrangian or particle tracking models are suitable for dilute particle loading of oil volume fraction <12%. Such model will track the droplet within a Lagrangian frame. The presence of oil within compressor at the tips and sealing line is more than 12%, therefore the Lagrangian technique is considered as not suitable for modelling this case.
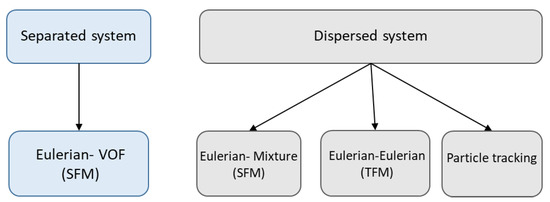
Figure 1.
Multiphase flow models within Fluent.
More details about the mentioned multiphase models are given in Section 2.1.
2.1. Governing Equations
The governing equations of the mathematical model describing Eulerian-Eulerian, VOF and mixture models in the section below are adopted from the Fluent theory guide [22].
2.1.1. Eulerian-Eulerian Model
This model in Fluent is known as a TFM (Two Fluid Model). The number of conservation equations depends on the number of phases. In this case, there are two phases, air and oil which have separate governing equations. The model describes multiphase flow as interpenetrating continua incorporating the concept of phasic volume fraction (αq). Volume fraction here represents the space occupied by each phase.
Volume of phase q, Vq is defined as,
Continuity equation:
Momentum equation:
Transient and convection terms are located on the left-hand side of the equation. Terms on the right-hand side are pressure gradient, stress strain, gravity, interaction between phases, mass transfer, external body, lift and mass forces.
Interphase momentum transfer Rpq can be written as,
In the above set of equations, ρ is density, v is velocity, p is pressure, is shear stress, g is gravity, is mass flow rate, F is drag force, α is volume fraction, is drag coefficient, Re is Reynolds number, S is source term, dp is diameter of the droplet, µ is viscosity and τ is particle relaxation time. Subscripts p and q indicate first and second phase, respectively.
The interphase momentum transfer term (Rpq) is dependent on the velocity of each phase, phase volume fraction, phase densities and droplet diameter.
Energy equation:
Here, h, T and δ denote static enthalpy, temperature and thermal conductivity of the phase q. Sq describes external heat sources (momentum, continuity etc.). Qpq is the interface heat transfer which is a heat transfer coefficient between the phases, interface area and temperature difference.
2.1.2. VOF Model
The VOF model consist of a single set of governing equations. In this model, the phases of gas and oil are treated as immiscible and not interpenetrating. Variables fields and properties in each equation are shared by both phases and are represented by the volume-averaged values (example shown for density in Equation (10)). Variable/property in any given cell is either a pure representative of one of the phases or mixture of both the phases that is represented as an interface.
k represents number of phases.
Continuity:
Momentum:
Unlike Eulerian-Eulerian model, the VOF model does not account for the interphase momentum transfer within momentum equation.
Energy:
An essential part of VOF model is the interface reconstruction scheme, which attempts to explicitly approximate the location of the interface within a computational cell, based on the volume fraction of the current and surrounding cells. The compressive scheme is based on the algebraic formulation, which is known for its application when the viscosity ratio between two phases is high thus ensuring smoothness of the interface [23]. This interface-capturing technique is used in this study.
2.1.3. Mixture Model
Both mixture and VOF models are single phase models. However, the mixture model differs from the VOF model by,
- Including the additional term for the interphase momentum transfer in the momentum Equation (16).
- Treating the phases to be interpenetrating continua similar to the Eulerian-Eulerian model.
Continuity:
Momentum:
The velocity of only one phase is solved. For the second phase, the directional velocity ( is used which depends on the slip velocity () and the concentration of the second phase (). The slip velocity depends on the particle relaxation time (τp), phase and mixture densities, droplet diameters (dp) and drag forces (fdrag). In the equations above, the annotation subscript ‘m’ stands for mixture and is the secondary-phase particle’s acceleration. Slip velocity between the phases is obtained according to Algebraic slip model or Manninen et al. model [24].
The energy equation for the mixture model is the same as in the VOF model (Equation (13)).
2.2. Comparison of Computational Multiphase Flow Models
Which multiphase flow model will be used depends on the dominant flow regime and average cell or grid size. In a twin-screw compressor, oil can exist in the form of film as well as droplets which should ideally be treated with different multiphase models. Therefore, available multiphase models are explored in this study.
VOF model better resolves average oil droplet size larger than the average cell size in a mesh. Whereas the mixture and Eulerian-Eulerian models are suitable for resolving droplets with size smaller than average cell size (Figure 2). Using the VOF model based on the cell volume fraction and the interface-tracking algorithm, the free surface is obtained. Mixture properties are applied to the cells with partial volume fraction. On the other hand, for the mixture/Eulerian-Eulerian model phase properties are averaged based on volume fraction in a discrete domain and no free surface is obtained.
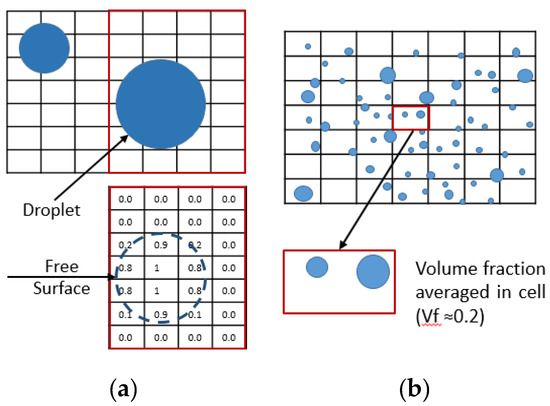
Figure 2.
(a), Droplets bigger than grid scale-VOF model; (b), droplets smaller than grid scale-mixture or Eulerian-Eulerian model.
Differences between the multiphase models described above are summarised in Table 1. The VOF model is generally used for the cases where large deforming interfaces are of interest. Both mixture and Eulerian-Eulerian models are suitable where the interphase forces are of importance. Furthermore, the Eulerian-Eulerian model is suitable when the lift forces are of importance in the flow. The Eulerian-Eulerian model is good fit when the flow regime is unknown and the Mixture model in many cases can be a good replacement for the full Eulerian-Eulerian model as it is computationally cheaper.

Table 1.
Parameters considered within multiphase flow models.
3. Case Study
In this case study, the performance of oil-injected air twin-screw compressor was obtained with Fluent using different multiphase modelling techniques. This compressor has a radial suction port and an axial discharge port with an oil injection port on the female side of the rotor. The lobe combination is 4–5 with ‘N’ profile. The compressor operates at 6000 RPM and discharge pressure of 7.0 bar. The rotor center distance is 67.5 mm, the outer diameter of the male rotor is 98.8 mm and the outer diameter of the female rotor is 77.8 mm. The length of the rotors is 153.1 mm with the male rotor wrap angle of 306.6° and volume index of 4.6.
Test measurements for the compressor performance were carried out at City University of London’s oil-injected test rig (ISO 1217:2009—Displacement Compressor-acceptance testing). Discharge pressure is controlled via the check valve; the flow is measured using an orifice plate in the discharge line, a speed encoder on the male rotor shaft, and a torque meter installed between the transmission system and the compressor.
Figure 3 shows the compressor in the test rig. Measurement data acquisition is carried out using CompactRIO. At least 15 readings were taken at the operating condition of 6000 RPM and 7.0 bar, which was later averaged in order to obtain the performance values. Considering the instrumentation error and dependent variables of the integral values of flow rate and power, the measured error propagation for the flow rate and power was estimate to be 4.7% and 2.7%, respectively [9].

Figure 3.
Compressor in a test rig.
3.1. Grids
A single-domain mesh was used for calculating performance prediction in this case. The technique used to generate the single domain rotor mesh is based on the algebraic background blocking technique as described in [13]. Figure 4a shows the rotor grid in one transverse cross section. Figure 4b shows the mesh of the complete fluid volume with rotors represented by the first layer of numerical cells on the rotor surface. The nominal interlobe, radial and axial leakage gaps are 50 µm. Oil injection port diameter is 5 mm.
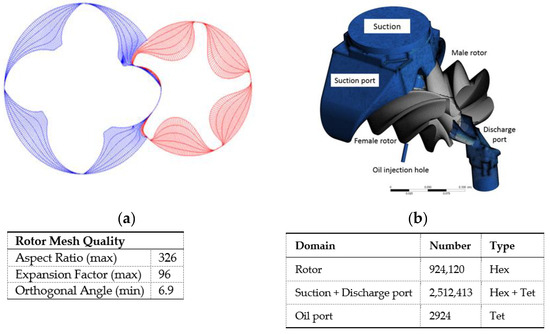
Figure 4.
(a) Circumferential: 60, Radial: 5, Angular: 90 and Interlobe: 77, grid distribution on rotor with divisions and (b), Numerical grid of flow domain.
3.2. Interface with Fluent
User-defined functions (UDF) are written and compiled in ‘C’ programing language. Their function is to link meshes generated in SCORGTM and the Fluent parallel multiprocessor calculation framework. This is based on the integration for sliding vane machines developed by authors [25], and has been extended to the parallel framework for twin-screw machines [26,27,28].
With some unstructured cell-centered solvers like Fluent, the node numbers need to be updated each time the new mesh is loaded in the solver. Figure 5 shows the mesh generated from SCORGTM for 4–5 lobe combination compressor. This mesh is loaded into Fluent as a customised grid. Mismatch in the cell node numbers occur between the imported mesh and the existing definition in Fluent. Therefore, the node mapping procedure needs to be performed in order to align the nomenclature of nodes. Node mapping is computationally intensive. Since majority of simulations are performed with parallel solver, it is advantageous to perform the node mapping also in the parallel framework using this tailor made UDF. Without parallelisation of node mapping, it is possible that the node numbers would be repeated which can result in error and mismatch of nodal information.
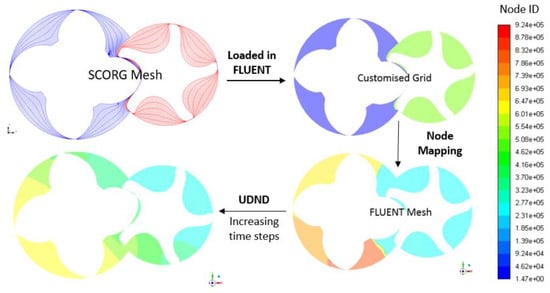
Figure 5.
Node number mismatching between mesh loaded in Fluent and customised grid generated by SCORG.
After the node mapping code is executed, the node numbers are aligned between SCORG mesh and mesh in Fluent. Files generated from SCORG contain x, y, z coordinates of each node. With marching time steps, x, y, z positions of the node positions are updated in Fluent mesh resulting in the correct transition of nodes with time. This technique ensures that the cell connectivity and conservation of intrinsic quantities are preserved.
3.3. Numerical Set-Up
Air is simulated as an ideal gas and the injected oil is treated as an incompressible fluid. The properties of these fluids are described in Table 2. Oil is injected at 65 °C and with pressure of 7.0 bar. Compressor suction or inlet is at atmospheric pressure and 293K while the discharge or outlet is at 7.0 bar.

Table 2.
Phase properties.
Table 3 shows the numerical setup with both VOF and mixture models in Fluent. For first 270 time steps of the simulation, solver relaxation for continuity equation is set as 0.005 and this is gradually increased to 0.01. To ensure convergence of the case, the cyclic repeatability of the chamber pressure, suction and discharge flow rates were observed for every male rotor rotation at various points. The solution is regarded converged if these values are repeated over three consecutive interlobe rotations.

Table 3.
Numerical setup with Fluent.
As mentioned in Section 2.1.3, the Mixture model drag forces are required to account for slip between the phases. Drag forces depend on the droplet diameter and drag coefficient (CD). Droplet diameter (dp) is assumed to be of 50 µm.
Drag coefficient in the mixture model is calculated based on the model of Bannari et al. (Equation (20)) [29]. Here, Reynolds number (Re) depends both on laminar () and turbulent viscosity of the fluid. ρ and v are density and viscosity of fluid in the region.
For stability reasons and better initialisation of the case, both discharge pressure and oil injection pressures are gradually increased until the full values are reached. The discharge pressure and oil injection pressure are ramped up across 270 time steps. The case was solved for 990 time steps observing cyclic repetitions in the pressure and flow rates.
4. Results and Discussions
Using developed interface with Fluent and the numerical setup explained in Section 3, this oil-injected compressor is calculated with VOF and the mixture models. The 3D analysis provides pressure, oil and temperature distribution within the compression chamber. Integral parameter prediction for both models are assessed and compared with the test data.
4.1. Pressure Distribution
Figure 6 shows variation of pressure in the compression chamber as function of the angle of the male rotor rotation. Oil is injected at 67°. At 7.0 bar pressure and 6000 RPM, the peak pressure reaches around 9.0 bar just before the discharge port opens at 260°. Once the port is open, pressure drops in the discharge port to the outlet pressure of 7.0 bar. Some pulsations are noticed which are similar for both of the models. The mixture model achieves slightly higher peak pressure, 0.08 bar higher than the VOF model. This difference is very small compared to the order of magnitude of the peak pressure.
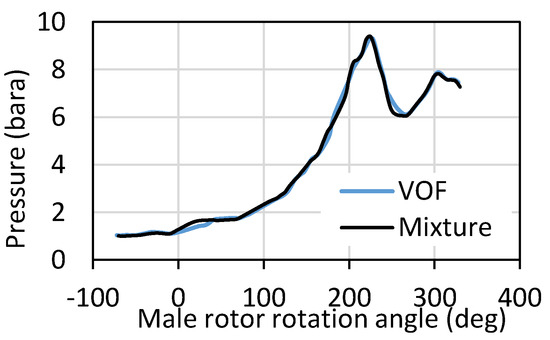
Figure 6.
Variation in pressure with male rotor angle.
The distribution of pressure on rotors as well as on the port surfaces and the oil iso-volume fraction of 0.035 is shown in Figure 7 for both models. The pressure distribution on surfaces is similar to both models. From the same figure, the distribution of oil is different for VOF and mixture models which is further discussed in the next section.
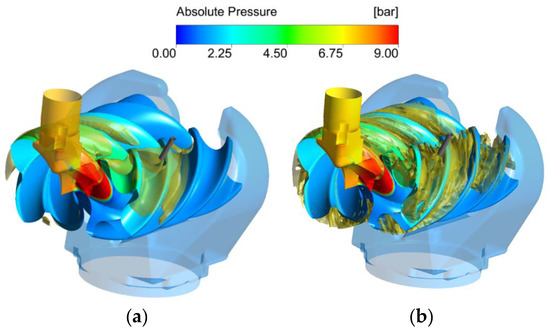
Figure 7.
Domains coloured by pressure with oil volume fraction iso-surface of 0.035 for (a), VOF model and (b), Mixture model.
4.2. Oil Distribution
To clearly distinguish between the oil distribution in VOF and mixture models, the rotor surface is coloured uniformly with the iso-surface of oil volume fraction 0.035 coloured in yellow (Figure 8). In addition, Figure 9 shows the variation of the mass flow of injected oil in the compression chamber with the male rotor angle. The amount of oil injected is very similar for both models. However, the distribution of oil within the compression chamber is different for two models. With the VOF model, distribution of oil volume fraction is changing smoothly from one to another region and the oil volume fraction near the suction port is lower than 0.035.

Figure 8.
Oil volume fraction iso-surface of 0.035 for (a), VOF model and (b), mixture model.
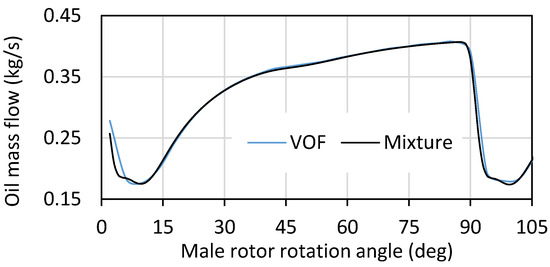
Figure 9.
Oil injection mass flow according to male rotor rotation angle.
Oil distribution study is further focused on the oil volume fraction distribution on the male rotor surface. Figure 10 shows the distribution of oil on the surface obtained from the mixture and VOF models as well as the Eulerian–Eulerian model. The Eulerian–Eulerian model has not been used for comparison of integral values because this model was previously solved with CFX with the same geometry and similar boundary conditions. The difference was in the male rotor shaft speed of 6572 RPM. The Eulerian-Eulerian model could not be solved with Fluent due to stability reasons which will be further investigated in the separate research work. The slight variation in the male rotor speed between CFX and Fluent will quantitively effect the amount of oil, but it will not affect significantly oil distribution characteristics with various multiphase flow model pattern. Therefore, it is reasonable to assume that this approach will still give good qualitative comparison of different multiphase models.
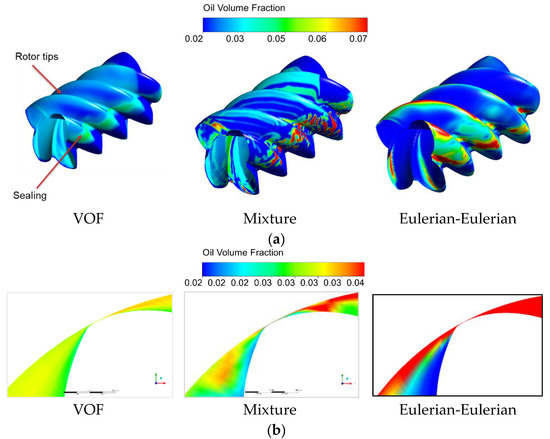
Figure 10.
(a), Male rotor surface coloured by oil volume fraction and (b), rotor tips coloured by oil volume fraction.
Figure 10 shows the comparison of oil distribution with three different multiphase models. The VOF model shows smooth transition in oil concentration on the rotor surface as it treats both phases as non-interpenetrating continua (Section 2.2). Relatively higher oil volume fraction is observed at rotor tips and along the sealing line. With the mixture model, strips of oil volume fraction are observed on the rotor tips and higher oil volume fraction of pitted oil are appearing along the sealing line. Clearly, with the mixture model, higher volume fraction of oil is observed at the sealing line than in the VOF model but the distribution is not smooth and continuous. This is because the phases are interpenetrating; in addition, the oil phase experiences slip, which is highly dependent on drag forces. However, with Eulerian-Eulerian model, substantially higher content of oil is observed on the rotor tips with the clear gradient surrounding the tip region. The Eulerian-Eulerian solves velocities of each phase individually and couples them through the interphase momentum transfer term (Equation (4)). In this way, it is expected that the Eulerian-Eulerian model represents the oil distribution better than the mixture model where slip is more of an empirical term, or VOF with no consideration of slip or drag at all.
Comparing this case with the water flow (in air) over the stepped spill ways taken from literature [30]. With three different multiphase models, a similar distribution of second phase is observed, as shown in Figure 11.VOF has a clear interface with none of the two phases mixing with each other, the mixture model is able to predict mixing of two phases, and lastly the Eulerian-Eulerian model better resolves for velocities leading to saturation of water on steps. When compared with experiments, it was reported that the Eulerian-Eulerian model best matched experimental visualisation, the mixture model showing most of the flow features and VOF being least comparable to experimental visualisation.
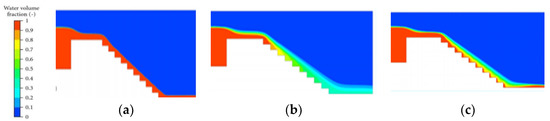
Figure 11.
(a) VOF, (b) Mixture, (c) Eulerian-Eulerian. Water volume fraction over stepped spillways [30].
4.3. Temperature Distribution
With built-in Vi of 4.6, the adiabatic discharge temperature of air without oil will be around 420 K. Injecting oil cools the gas substantially. Figure 12 shows variation in the discharge temperature with both VOF and mixture models. Similar prediction of the discharge temperature is observed for both models. Therefore, Figure 13 shows similar temperature distribution on the rotor and discharge port surfaces.
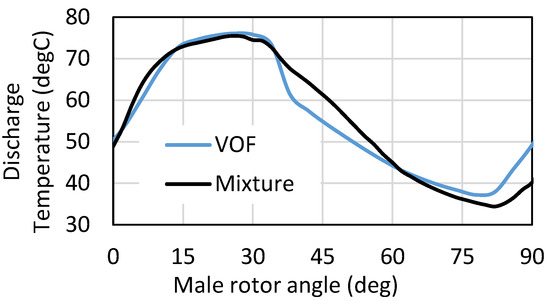
Figure 12.
Variation of discharge temperature with male rotor angle
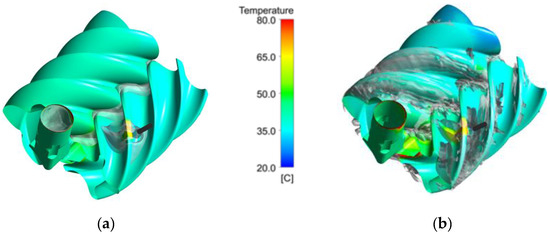
Figure 13.
(a) VOF, (b) Mixture. Temperature distribution on rotor surfaces with oil iso-surface of volume fraction 0.05.
Both VOF and mixture models are single phase models where cell temperatures are based on the phase volume fraction averaged in a cell, similar to other properties like density and viscosity. Distribution of the oil volume fraction based on the phase velocities plays a role in energy distribution. From one region to another, the change in oil volume fraction and temperature are observed with both investigated models. The effects of oil on the temperature field are higher in the mixture model than in VOF.
4.4. Overall Performance with Measurements
Table 4 shows comparison of calculated flow rate and power with the experimentally obtained data along with the mass imbalance error. Both models are capable of predicting overall values of flow and power close to measured data with a good mass balance.

Table 4.
Integral performance results with various models.
Performance of a helical screw compressor is influenced by the internal gas leakage. Typical leakages are through the axial, radial and interlobe gaps. According to the leakage areas, radial leakage will be higher compared to other forms of leakages. Therefore, Figure 14 shows velocity vectors through the radial gaps. Overall, growth in the magnitude of velocity vectors increase consecutively from one pressure chamber to another depending on the difference in pressure ratios between the chambers. Oil has an important tendency to seal leakage gaps. Higher oil volume fraction is observed in the rotor tips with the mixture model compared to VOF. This oil seals the radial leakage gaps. Hence, relatively higher radial leakages velocities are observed with VOF compared to the mixture model. Due to these effects, flow predictions with the mixture model are as close as 0.88% and with VOF model the difference is 3.46% when compared to experimental value.
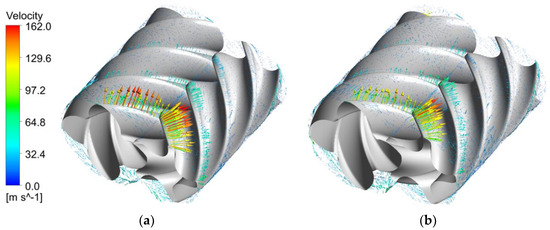
Figure 14.
(a) VOF, (b) Mixture. Velocity vectors at radial leakages with VOF and mixture model.
Overall, power is slightly better predicted at 4.55% error percentage with the mixture model than VOF at 5.68% (Table 4). Using a chamber model from SCORG at the same operating conditions, it was noticed that indicated power is 83% of total power. This estimate is applied for comparison with the experiment.
Also, it can be noticed that the percentage of mass imbalance is higher with VOF model at 9.54% leading to higher error in flow prediction at 3.46%.
Lastly, it is witnessed that SFM models take less clock time per timestep when compared with the Eulerian–Eulerian model solved in CFX (Table 5). The mixture model takes slightly longer compared to VOF as it solves additional terms related to slip and drag forces. However, there is further scope for improving the solver time. A concluding remark is that SFM models are computationally economical.

Table 5.
Comparison of calculation time per time step.
5. Conclusions
A typical oil-injected twin-screw compressor was modelled in Fluent using the numerical mesh generated by SCORGTM and newly developed interface which used the UDND technique. The interface was integrated in the UDF code in a parallel framework to transition the mesh with the marching time steps. The achieved set-up is used to solve for a test case with rotor shaft speed of 6000 RPM and 7.0 bar pressure with mixture and VOF models.
Key conclusions from this study are:
- Both mixture and VOF models are capable of predicting overall performance of the flow and power close to measured values. The mixture model predicts flow with 0.9% and power with 4.5% error compared with measured values. The VOF model predicts flow with 3.5% and power with 5.7% error compared with measured values.
- Pseudo single-phase models are computationally economical, and on average a 22% improvement in time was observed with pseudo-single fluid models compared to the Eulerian–Eulerian TFM model.
- This study shows a good comparison of oil distribution within the compression chamber, which differs between mixture and VOF models. With the VOF model, smooth distribution of oil volume fraction was observed due to the air and oil phases being treated as non-interpenetrating. With the mixture model, the distribution of oil phase was different since the phases are penetrating and the slip between phases is included. However, the Eulerian–Eulerian model which was originally solved in CFX still shows distribution closer to expected reality.
- With the mixture model there is flexibility and opportunity for further improvements in terms of customised empirical model for interphase drag and slip forces which can lead to more realistic oil distribution. The mixture model can be a good replacement for the full Eulerian–Eulerian models as it is computationally more efficient, but further investigation into better interphase modelling forces will be required.
Author Contributions
Conceptualization, N.B., A.K. and S.R.; methodology, N.B. and A.K.; software, N.B. and S.R.; writing—original draft preparation, N.B.; writing—review and editing, A.K., S.R.; supervision, A.K.; project administration, A.K.; funding acquisition, A.K.
Funding
This research was funded by the Centre for Compressor Technology at City, University of London.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stosic, N.; Smith, I.; Kovacevic, A.; Mujic, E. Three Decades of Modern Practice in Screw Compressors. In Proceedings of the International Compressor Engineering Conference, Purdue, IN, USA, 12–15 July 2010. [Google Scholar]
- Wood, L. Screw Compressor Market 2017—Global Forecast to 2021. Research and Markets. Available online: https://www.globenewswire.com/news-release/2017/01/26/911099/0/en/Global-Screw-Compressor-Market-2017-2021-Atlas-Copco-Ingersoll-Rand-GE-Oil-Gas-Gardner-Denver-and-Siemens-Lead-the-11-Billion-Market.html (accessed on 26 January 2017).
- Abdan, S.; Basha, N.; Kovacevic, A.; Stosic, N.; Birari, A.; Asati, N. Development and Design of Energy Efficient Oil-Flooded Screw Compressors. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 604. [Google Scholar]
- Deipenwisch, R.; Kauder, K. Oil as a design parameter in screw-type compressors: Oil distribution and power losses caused by oil in the working chamber of a screw-type compressor. In Proceedings of the International Conference on Compressor and their Systems, London, UK, 13–15 September 1999; pp. 49–58. [Google Scholar]
- Singh, P.; Bowman, J. Heat Transfer in Oil-Flooded Screw Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 4–7 August 1986; pp. 135–153. [Google Scholar]
- Stošic, N.; Milutinović, L.; Hanjalić, K.; Kovačević, A. Investigation of the influence of oil injection upon the screw compressor working process. Int. J. Refrig. 1992, 15, 206–220. [Google Scholar] [CrossRef]
- Peng, X.; Xing, Z.; Cui, T.; Shu, P. Experimental Study of Oil Injection and Its Effect On Performance of Twin Screw Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- De Paepe, M.; Bogaert, W.; Mertens, D. Cooling of oil injected screw compressors by oil atomisation. Appl. Therm. Eng. 2005, 25, 2764–2779. [Google Scholar] [CrossRef]
- Basha, N.; Kovacevic, A.; Stosic, N.; Smith, I. Effect of oil-injection on twin screw compressor performance. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Kovacevic, A. Three-Dimensional Numerical Analysis for Flow Prediction in Positive Displacement Screw Machines. Ph.D. Thesis, City University London, Lodon, UK, 2002. [Google Scholar]
- Kovacevic, A. Boundary adaptation in grid generation for CFD analysis of screw compressors. Int. J. Numer. Methods Eng. 2005, 64, 401–426. [Google Scholar] [CrossRef]
- Kovacevic, A.; Stosic, N.; Smith, I. Screw Compressors: Three Dimensional Computational Fluid Dynamics and Solid Fluid Interaction; Springer: Berlin, Germany, 2005. [Google Scholar]
- Kovacevic, A.; Rane, S.; Stosic, N.; Jiang, Y.; Furmanczyk, M.; Lowry, S. Influence of approaches in CFD Solvers on Performance Prediction in Screw Compressors. In Proceedings of the International Compressor Engineering Conference, Purdue, IN, USA, 14–17 July 2014. [Google Scholar]
- Kovacevic, A.; Rane, S. Algebraic generation of single domain computational grid for twin screw machines Part II—Validation. Adv. Eng. Softw. 2017, 109, 31–43. [Google Scholar] [CrossRef]
- Rane, S.; Kovacevic, A.; Stosic, N. CFD Analysis of Oil Flooded Twin Screw Compressors. In Proceedings of the 23rd International Compressor Engineering Conference, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Basha, N.; Rane, S.; Kovacevic, A. Multiphase Flow Analysis in Oil-injected Twin Screw Compressor. In Proceedings of the 3rd International Conference on Multiphase Flow and Heat Transfer, Budapest, Hungary, 12–14 April 2018. [Google Scholar]
- Yeoh, G.H.; Barber, T. Assessment of interface capturing methods in Computational Fluid Dynamics (CFD) codes—A case study. J. Comput. Multiph. Flows 2009, 1, 201–215. [Google Scholar] [CrossRef]
- Ding, H.; Jiang, Y. CFD simulation of a screw compressor with oil injection. In Proceedings of the 10th International Conference on Compressors and their Systems, London, UK, 11–13 September 2017. [Google Scholar]
- Randi, S.; Suman, A.; Casari, N.; Pinelli, M.; Ziviani, D. Numerical analysis of oil injection effects in a single screw expander. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018. [Google Scholar]
- Papes, I.; Degroote, J.; Vierendeels, J. 3D CFD Analysis of an Oil Injected Twin Screw Expander. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition IMECE2013, Fairfield, CT, USA, 15–21 November 2014. [Google Scholar]
- Manik, J.; Dalal, A.; Natarajan, G. International Journal of Multiphase Flow A generic algorithm for three-dimensional multiphase flows on unstructured meshes. Int. J. Multiph. Flow 2018, 106, 228–242. [Google Scholar] [CrossRef]
- Fluent, A. ANSYS Fluent 12.0 User’s Guide; Ansys Inc.: Pittsburgh, PA, USA, 2009; Volume 15317, pp. 1–2498. [Google Scholar]
- Ubbink, O.; Issa, R.I. A Method for Capturing Sharp Fluid Interfaces on Arbitrary Meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- Kallio, S.; Akademi, A. On the Mixture Model for Multiphase Flow; VTT: Espoo, Finland, 1996; Volume 288. [Google Scholar]
- Bianchi, G.; Rane, S.; Kovacevic, A.; Cipollone, R. Deforming grid generation for numerical simulations of fluid dynamics in sliding vane rotary machines. Adv. Eng. Softw. 2017, 112, 180–191. [Google Scholar] [CrossRef]
- Basha, N.; Kovacevic, A.; Rane, S. User defined nodal displacement of numerical mesh for analysis of screw machines in FLUENT. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 604. [Google Scholar]
- Lu, Y.; Kovacevic, A.; Basha, N.; Read, M. CFD Analysis of Twin Screw Vacuum Pump. In Proceedings of the 9th International Conference on Compressor and Refrigeration, Xi′an, China, 10–12 July 2019. [Google Scholar]
- Lu, Y.; Kovacevic, A.; Read, M.; Basha, N. Numerical Study of Customised Mesh for Twin Screw Vacuum Pumps. Designs 2019, 3, 52. [Google Scholar] [CrossRef]
- Bannari, R.; Kerdouss, F.; Selma, B.; Bannari, A.; Proulx, P. Three-dimensional mathematical modelling of dispersed two-phase flow using class method of population balance in bubble columns. Comput. Chem. Eng. 2008, 32, 3224–3237. [Google Scholar] [CrossRef]
- Van Alwon, J.; Borman, D.; Sleigh, A.; Kapur, N.I.K. Experimental and numerical modelling of aerated flows over stepped spillways. In Proceedings of the IAHR 2017 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).