Abstract
A detailed study of the fluid flow and thermodynamic processes in positive displacement machines requires 3D CFD modeling in order to capture their real geometry, including leakage gaps. However, limitations in the conventional computational grids, used in commercial software packages, exclude their use for classical twin screw machines. The screw compressor rotor grid generator (SCORG) is a customized grid generation tool developed to overcome these limitations. This paper shows how it can be further extended to include non-conventional rotor designs, such as those with variable lead or profile variation and even internally geared machines with conical rotors. Other arrangements possible with this improvement include multiple gate rotors to increase volumetric displacement or dual lead, high wrap angle rotors for very high-pressure differences and vacuum applications. A case study of a water-injected twin screw compressor is included to demonstrate its use for both detailed flow analysis and design.
1. Introduction
Twin screw compressors are widely used in industry and their principle of operation is based on the volume changes between a pair of meshing rotors and their surrounding casing. These are shown in Figure 1, with the casing removed. As they rotate, opening of the space between the rotor lobes and the suction port, located in the casing, allows gas to flow into the passages formed between them until the trapped volume is a maximum. Further rotation leads to cut off the chamber from the suction port and progressive reduction in the trapped volume thus compressing the gas. The compression process continues until the required pressure is reached when the opposite ends of the passages are exposed to the discharge port through which the gas flows out of the compression chamber at approximately constant pressure. The asymmetric flow of the gas through the passages leads to axial and bending forces on the rotors and to contact forces between the rotor lobes.
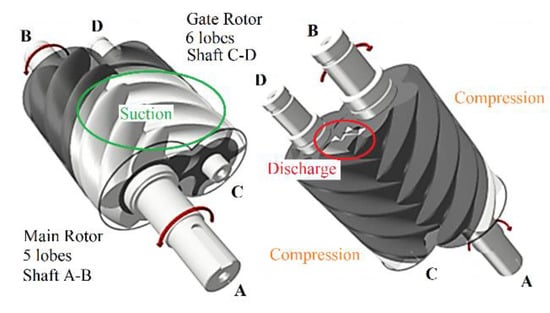
Figure 1.
Conventional twin screw rotors with a 5–6 profile.
Apart from conventional designs, based on constant rotor diameter, pitch and profile shape, there are some possible alternatives [1], based on the same operating principle but with variations in the rotor geometry, as indicated in Figure 2. The need to reduce energy losses, and for higher gas pressure differences in compact machines, has led to the investigation of what improvements, if any, are possible by their use and hence the need for 3 dimensional analytical tools to predict their flow characteristics and performance.
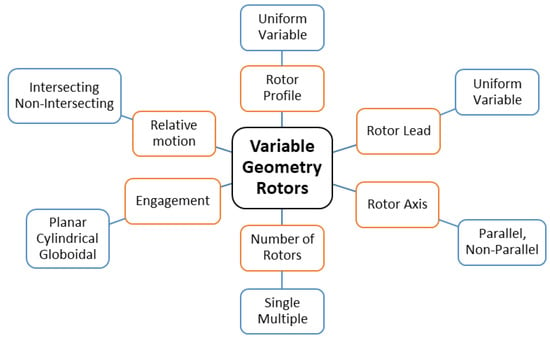
Figure 2.
A representation of possibilities for rotary screw machine geometries [1].
Although a patent for screw compressor rotors with a continuously variable lead for the lobes of the male and gate rotors was issued as long ago as 1969 [2], as shown in Figure 3a they are still at the research stage. It was then shown that for the same rotor lengths, diameter, wrap angles and lobe profiles, variable pitch rotors can be designed to provide higher pressure ratios and larger discharge port opening areas, thus reducing the exit throttling losses. These advantages can be better appreciated if the rotor diameters are made to vary from suction to the discharge. An alternative of a rotors with parallel axes but variable profile is shown in Figure 3b. As the rotors of a screw machine turn during operation, the fluid volume in between them is deformed (compressed or expanded, depending or the direction of rotation) and the CFD grid which represents the fluid volume also needs to deform. Without capturing this deformation, it is not possible to determine the correct three- dimensional fluid flow characteristics inside the working chamber. A breakthrough was achieved in 1999 by Kovačević et al. [3,4] with the use of an analytical rack generation method, proposed by Stošić [5], and applied to generate an algebraic, adaptive, block structured, deforming grid for twin screw rotors. This methodology of deforming grid generation was implemented in the customized grid generation tool called SCORG [1,3,4,6].
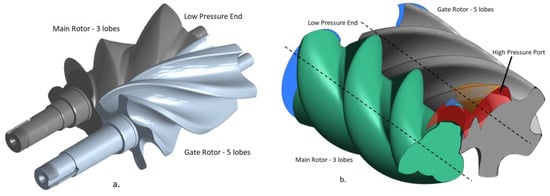
Figure 3.
Non-conventional variable geometry twin screw rotors with a N 3–5 profile: (a) variable lead, (b) variable rotor profile [1,7].
Since then, there have been several studies that reported on the CFD analysis of twin screw machines. The use of this method for screw compressor applications is justified by its ease of use and its speed. The analysis of the working chamber is transient in nature and requires a grid representing every time step rotor position and domain deformation (arbitrary Lagrangian–Eulerian, ALE, solver formulation [1]). In this respect, algebraic methods can be used to recalculate the grid quickly. SCORG has been written in FORTRAN with a C# front-end application [6]. In his thesis, Kovačević [3] presented the grid generation aspects in detail. Several CFD simulations of twin screw machines to predict flow, heat transfer, fluid-structure interaction, etc. have been reported in [3,4,6,7]. Sauls and Branch [8] used the results from CFD calculations to develop an improved one-dimensional thermodynamic model for refrigerant screw compressors, by extracting calibration coefficients that influence the pressure variation during the discharge process. Mujić [9] presented an optimization of the discharge port area based on flow behavior in the discharge chamber. The CFD model was used for relative comparison of port geometry modifications and their influence on predicted pressure pulsations to judge the sound spectrum and noise level from the compressor. These noise levels predicted by CFD solutions have been used for designing discharge ports with reduced noise levels. In his thesis, Mujić [9] presented a 3D CFD coupled model in which the boundary conditions for the discharge port were obtained as time-varying data from 1D thermodynamic chamber models. The procedure was implemented for Star CCM+ solver. It was found that the results predicted by the coupled model for sound pressure levels were closer to the full 3D CFD models and were also in close agreement with the experimental measurements. Such an approach simplified the numerical analysis and also provided faster results from the CFD models. Riemslagh et al. [10] were the first to implement a grid generation algorithm for block structured mesh, from the solution of the Laplace equation, for twin screw compressors and pumps using differential methods. The use of differential methods requires the partial differential equations (PDE) to be solved for every rotor position and then the grid generation has to be repeated from the equipotential and gradient lines. In his thesis, Vande Voorde [11] presented the principles of solving the initial Laplace equation and then using it to construct a block structured deforming mesh. Based on this grid generation, flow in a double tooth compressor and a twin screw compressor was analysed and the results were compared with experimental data over a range of discharge pressures and rotor speeds. A detailed comparison of the algebraic and differential methods has been presented by Rane and Kovačević [1,12]. In [13] these techniques, implemented in SCORG, have been validated for a dry air twin screw compressor at various operating conditions and with various types of computational grids.
In the case of non-conventional screw machines, Schulze-Beckinghausen et al. [14] have recently presented a thermodynamic chamber model and compared the results of the variable lead compressor performance with constant lead rotors. Their model predicted higher compression with rotors of varying pitch. The volumetric efficiency showed an improvement compared to constant lead rotors, but the indicated power was high due to non-optimal internal pressure rise, which increased the specific power. Utri and Brümmer [15] presented a thermodynamic comparison of screw expanders with constant and variable pitch in an ORC system. Instead of a continuous lead variation, they considered a stepped variation which gives a larger port area for the high-pressure filling part of the cycle. The overall wrap angle on the rotors was maintained equal to 245°. A multi-chamber thermodynamic model was then used to evaluate and compare the performance of different configurations. Rotors with variable rotor pitch showed an increase of up to 5% in effective power output. Kauder and Fost [16] and Fost [17] evaluated options for modifying screw rotors to improve the filling process in screw expanders and proposed a few non-conventional concepts such as conical rotors and rotors with inlet discs, each with a different pitch. Conical rotors had a variable rotor profile similar to the rotors in Figure 3b and showed an improvement in chamber filling mainly influenced by a reduction in pressure loss at the inlet. For the same built-in volume index, = 5, the maximum inlet area showed an increase from 540 to 1080 mm2. All these studies were done with the intention of predicting the performance and characteristics of screw machines at the design stage and optimizing the geometry and control parameters for a given application and operating condition. The use of Computational Fluid Dynamics for screw machine design is to be encouraged as it would provide better insight into the internal flow dynamics as a result of the vast improvements in computational technology and the availability of more accurate calculation methods. A CFD model of compressors with such non-conventional rotor shapes, was studied by the authors in [1,7,18]. In this paper, recent advances in the implementation of a differential grid [19,20], in the SCORG grid generator is demonstrated, using a PDE solution of the Poisson’s form. The quality of the numerical cells and their distribution is greatly improved by this differential method making the grid suitable for multiphase models such as oil injected screw compressors [21,22], (Video S2). A special procedure has been introduced that completely smooths the transition of the partitioning rack curve between the two rotors thus improving the grid node movement and the robustness of the CFD solver [20]. Further, applications of the SCORG tool are shown for a variety of screw machines such as variable geometry rotors with lead or profile variation, internally geared conical screw machines, multiple gate rotors and dual lead, high wrap angle rotors. A case study of a water-injected twin screw compressor [23] has been presented to demonstrate the use of the developed grid generation tools in analysis and design.
2. SCORG—Customized Rotor CFD Grid Generation
An analytical grid generation of the screw machine working domain is explained in Kovačević et al. [3,4]. It includes separating domains of the screw rotors with a rack curve [5] and forming independent flow domains around each of the rotors. After the grid points are distributed on boundaries, an initial grid is obtained by trans-finite interpolation (TFI). Recently, in order to achieve a conformal single domain mesh, Rane and Kovacevic [12,13] introduced a new approach to background blocking. In this procedure, the outer boundary in each background block (Figure 4a), a coarse analytically generated mesh, is defined as a combination of the rack segment and the casing circle segment. The rack segment stretches between the bottom and top cusp points and is closed by the casing. The distribution obtained on the outer boundaries of the two blocks is used to constrain the distribution on rotor profile as shown in Figure 4a.
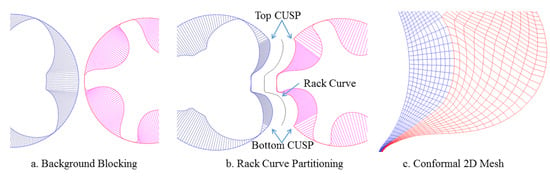
Figure 4.
Background blocking used in SCORG for differential mesh.
The rack curve used to partition the two rotor domains, and the boundary distribution so obtained, is shown in Figure 4b. This is employed to generate a 2D mesh using TFI. The blocking approach then allows both a conformal and a non-conformal boundary map to produce a fully hexahedral 3D grid. The nodes on the rack segment between the main and the gate rotor grids together with a conformal boundary map are shown in Figure 4c. The 3D mesh generated from such 2D cross sections allows the rotor domains of the male and female rotors to be combined into a single rotor mesh. This avoids inaccuracies and instabilities that may arise due to the interface mismatch in a non-conformal boundary map. The resultant grids are recommended for oil injected multiphase flow modelling and have been described in more detail by Rane and Kovacevic in [20,22] (Video S2). However, even with this approach, during operation, as the rotors revolve, the rack curve comes to a position when it changes with a relatively large deformation between two consecutive steps. The algebraic method results in this transition as a step change at certain positions. One of the objectives of the elliptic PDE mesh generation implemented in SCORG was to improve the time transition of the partitioning rack curve between the two rotor domains.
Techniques based on solutions of Partial Differential Equations (PDE) to define coordinate transformation are widely used in grid generation. The idea of using an elliptic PDE, like the Laplace or Poisson equations, is based on the work of Crowley and Winslow, and is described in detail by Knupp and Steinberg [19]. Elliptic PDE’s have certain beneficial properties in their solution that make them preferable for body fitted curvilinear grids. These are that they are less prone to folding of the mesh lines, and they introduce inherent smoothness so that the discontinuities over the boundaries are not propagated into the interior of the domains and the physical boundaries can be used exactly as boundary conditions in the computational space. However, numerical grid generation is computationally expensive without an initial grid. If an initial grid based on algebraic method could be used, the required time for the solution of PDE’s is significantly reduced. This treatment requires the solution of the coupled PDE equations in which schemes like Tri-diagonal Matrix Algorithm can be used for the solution [19]. The boundary conditions are specified as grid coordinates at computational boundaries. This means that for the generation of a grid in the twin screw rotor domain the coordinates of the boundary nodes need to be used as the boundary condition. At this stage the initial grid generated by the TFI is used for both initial and boundary conditions. An O grid topology produced by TFI, shown in Figure 5b, has been used by the differential solver with successive-over-relaxation procedures as described by Knupp and Steinberg [19]. In addition, convenient input parameters are used to control the intensity of smoothing and inflation layer formation by the elliptic solver. The final O grids generated separately for the two rotors by the differential solver are merged to produce a single domain mesh for the two rotors, as shown in Figure 5d. The PDE solver is also used in the interlobe area bounded by the cusp radial nodes (Figure 4b) to convert the rack curve into a smooth transitioning curve across the specified number of angular positions of the rotor. This is obtained over a four-step procedure to gradually change the partition between the two O grids into a smooth one as shown in Figure 5a–d.
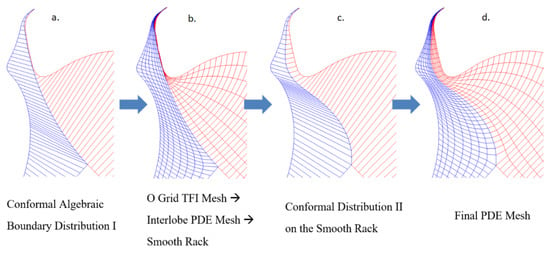
Figure 5.
Four-step procedure for improving time transition of the rack curve.
The smooth rack obtained by this procedure is supplied back to a second stage of boundary distribution calculation resulting in a new conformal distribution. This conformal distribution is further used as a boundary condition for final differential mesh generation. As a result, a significant improvement in the mesh quality is achieved. Figure 6 shows the comparison of the cell orthogonal quality between the algebraic meshes and the elliptic meshes. Figure 6a–d are algebraic meshes and Figure 6e–h are elliptic meshes in the respective rotor positions. The algebraic method results in the transition of the rack curve as a step change at certain positions as shown in Figure 6b,c.
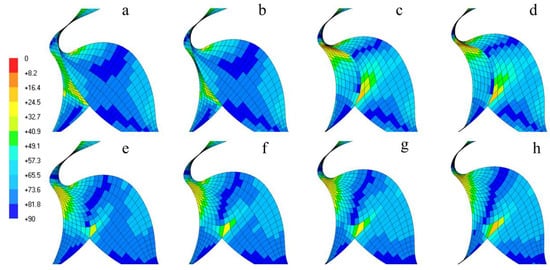
Figure 6.
Comparison of cell orthogonal quality between algebraic (a–d) and elliptic (e–h) meshing.
The values for the minimum orthogonal angle of the algebraic meshes in Figure 6 (top) drop to about 8 degrees after the rack curve transitions from position b to c. The majority of cells are in the range 40–60 degrees orthogonality. Low orthogonality values are also noticed in position d. However, in the case of elliptic meshing, the overall orthogonality has greatly improved so that the minimum orthogonal angle is 25 degrees. Most of the cells are in the range 75–90 degrees orthogonality. There is one cell at the bottom cusp which shows low orthogonality of about 15 degrees in both sets of meshes, which is the consequence of the discontinuity at the cusp point and cannot be avoided. However, the overall mesh quality is greatly improved. With these techniques, a good quality quadrilateral cell structure can be constructed in the 2D cross sections of the rotor. Data from the 2D cross sections is then combined to construct the full 3D grid representing the main and gate rotor positions, and a set of such 3D grids needs to be generated with successive increments in the rotor position and provided to the flow solver during numerical analysis [1].
2.1. Conventional Twin Screw Machine
Figure 7 shows the computational grid of a conventional twin screw machine. This example is that of a water-injected twin screw compressor [23]. The case study analysis is presented in Section 3. SCORG generates a set of 2D cross sections with quadrilateral cells, as seen in one rotor profile position in Figure 7. These sets of 2D sections are then assembled as 3D rotor domain grids, as seen in Figure 7, for one rotor position. Several such 3D rotor node positions are produced by SCORG and supplied to the flow solver during computations. A priori generation of 3D grid data for all the cyclically repeating rotor positions ensures that the solver will function robustly (without failing due to cell degeneration) during the simulation.
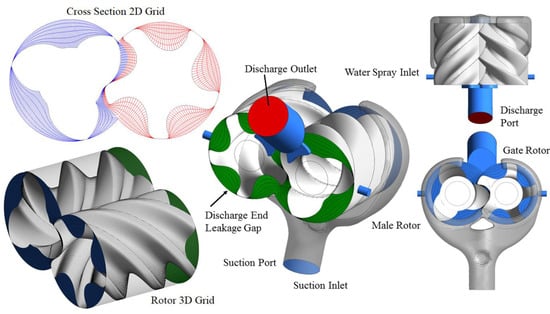
Figure 7.
Flow domain and rotor grid of a water-injected twin screw compressor [23].
A choice of hexahedral structure allows for ease of re-use of the database, and at the same time ALE formulations in the solver can be utilized that only demand accurate node positions with time in order to capture grid deformation. Decomposition of the working chamber consists of splitting the flow region into three main blocks as shown in Figure 7. This gives the flexibility to treat mesh generation in these blocks independently, in the choice of the grid generation methods. In a single domain mesh, both the rotors are contained in one deforming grid block thereby eliminating the non-conformal interface between the rotors. The deforming rotor grid has non-conformal interfaces with static ports and the water injection port.
2.2. Variable Lead Twin Screw Machine
Figure 3a shows the gearing of twin screw rotors with a variable helix lead. SCORG can be used to generate the deforming rotor domain grid for such variable lead rotors [1,7]. A pitch variation function is specified for the rotors and used to derive a relation between the fixed angular increments from one section to the other, and the required variable axial displacements (Δz), for each cross section of the rotor. Thus, the grid vertex data generated for one interlobe are reused but positioned in the axial direction with variable Δz such that the pitch variation function gets applied. An example rotor and the pitch function are shown in Figure 8, where the suction side pitch is 130 mm and the discharge side pitch is 40 mm.
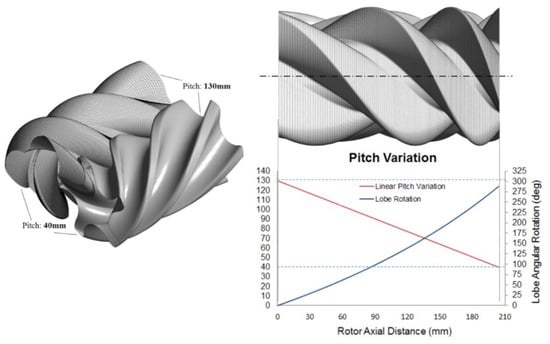
In [1], a comparative study was presented between uniform pitch (85 mm) with built in volume index of 1.8 and 2.2, and those with a variable pitch with > 1.8 is shown in Figure 8. A wrap angle of 285° was maintained for both the rotors, as shown in Figure 8. The analysis showed that by varying the rotor lead continuously from the suction to the discharge ends, it is possible to achieve a steeper internal pressure build up. Varying the rotor lead also allows a larger discharge port area, thereby reducing throttling losses, and an increase in volumetric efficiency by reducing the sealing line length in the high pressure zone. Uniform rotors show the highest volumetric efficiency at 2.0 bar. But with = 2.2 the efficiency was lower than that of the variable pitch rotors due to a comparable internal pressure rise and a comparatively shorter sealing line length. The variable lead rotors were found to improve by 2.2% at 2.0 bar and by 2.0% at 3.0 bar discharge pressure.
2.3. Variable Profile Twin Screw Machine
The SCORG grid generation algorithm was extended to variable profile rotors in [1]. The functionality also allows a covariation of rotor lead as well as rotor profile. An example of uniform lead and variable profile rotor is shown in Figure 3b and the grid generated by SCORG is shown in Figure 9. In this algorithm, additional computational effort is required to calculate the 2D grid data in every cross section as compared to that of a uniform pitch rotor grid generation calculation. The assembly of the grid from a 2D to a 3D structure was completely redesigned in order to provide flexibility to generate grids for variable geometry rotors. The inputs for the geometry of the rotors can be provided as a set of profile coordinate files for the main and gate rotors in each cross section. These data points can be extracted from CAD models. In the case of profiles such as the ‘N’ profile which are defined by a generating rack, a set of rack coordinate files for each of the rotor cross section could be used. A comparative study between uniform profile and variable profile rotors has been presented in [1]. In the case of the variable profile, the addendum on the suction end of the rotors was 33mm while on the discharge side it was reduced to 21mm. The addendum on the uniform profile rotors had a constant value 28.848mm. Due to variation of the addendum, the outer diameter of the male rotor changes while the inner diameter remains constant and vice versa for the female rotor, as shown in Figure 9. The volumetric displacement of these rotors was smaller than that of the uniform profile rotors. Analysis of the variable profile rotors showed a steeper internal pressure rise but there was no reduction of the sealing line length and blow-hole area for the same size of rotors. The increase in root diameter of the female rotors with variable profile certainly helps in producing stiffer rotors for high pressure applications. There was not much gain in at 3.0bar with the variable profile rotors due to there being no significant reduction in the sealing line length.

Figure 9.
Variable profile screw rotor grid with 3/5 ‘N’ profile [1,7].
A 1.2% reduction in was observed at 2.0 bar due to the smaller capacity of the machine and the higher internal pressure rise resulting in over-compression. The uniform rotors show the highest adiabatic efficiency () at 2.0 bar. However, with = 2.2 their was lower than that of the variable geometry rotors. At 3.0 bar, the uniform rotors have a reduced adiabatic efficiency, but this is still 0.7% higher than that of the variable geometry rotors. Both the variable pitch and the variable profile rotors show an increment in adiabatic efficiency due to a balanced internal pressure rise. The improvement was found to be 2.8% at 2.0 bar and 1.0% at 3.0 bar with the variable lead rotors and 1.1% at both pressures with the variable profile rotors.
2.4. Tri-Rotor Screw Machine
As the pressure difference between suction and discharge increases in screw compressors, the rotor root diameter has to be increased, in order to be able to endure the bending loads and avoid rotor damage due to bending. Also, the number of rotor lobes has to be increased. Consequently, there is a decrease in the volumetric displacement achievable with rotors of a given outer diameter. One of the methods of achieving higher volumetric displacement is by running two or more compressors in parallel. Another approach is to utilize a single male rotor and multiple female rotors to effectively increase the number of compression chambers and boost the flow rate. One arrangement for two female rotors is shown in Figure 10, which is similar to that patented by Nilsson [24]. The suction and discharge in this configuration happen on both axial ends of the male rotor and this can help in reducing the radial load on it. The design of the ports is challenging because the end plates have to accommodate heavy bearings. This increases the chances of having the full pressure difference across a leakage path, increasing the effective leakage as compared to a twin screw arrangement. Such a possibility, and also the port design, can be investigated in detail by CFD analysis and the required multi-gate rotor grid can be generated using SCORG.

Figure 10.
Tri-rotor screw compressor grid with 4/5 ‘N’ profile (Video S3).
2.5. Internally Geared Twin Screw Machine
Another example of grid generation with a uniform pitch and a variable section is in the design of an internally geared twin screw machine. A 3/4 lobe combination compressor with cycloidal profiles can be generated using SCORG as shown in Figure 11. The rotor diameter changes along the length with a helical spiral of constant pitch. In comparison to a classical twin screw compressor, there are two screw rotors but the gate rotor is an internally lobed helical spiral rotor driven by the inner main screw rotor which is externally lobed. The compression chamber is formed in the volume trapped between the inner and the outer rotors. The reduction of volume occurs because of the progressive reduction of the rotor diameter due to scaling of the profile along the spiral. This in turn causes internal compression and increase in pressure. In operation, the outer rotor is positioned on a central axis while the inner rotor rotates about an eccentric axis with varying centre distance from the suction to the discharge ends. Both axes are stationary in space.
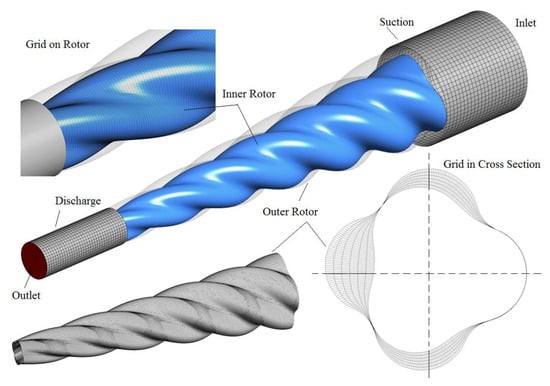
Figure 11.
Grid of the working chamber of conical internally geared screw rotors ([1], Video S4).
2.6. Dual Lead Twin Screw Machine
In liquid pumping application with a very high pressure difference between suction and discharge, or in vacuum pumps, a conventional screw rotor has a very high wrap angle of the order of 1080º. In comparison, a twin screw compressor has a wrap angle in the range of 250°–310°. The large wrap angle severely reduces the volumetric capacity of such pump rotors. One of the means of increasing displacement is to use a dual lead rotor as shown in Figure 12. SCORG can generate a rotor grid for such high wrap angle rotors and can construct dual/multiple lead sections.
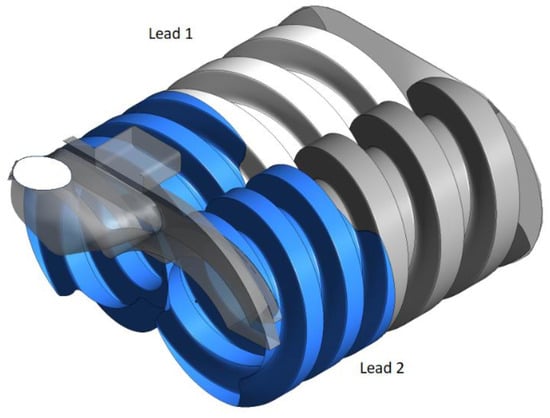
Figure 12.
Grid of the working chamber of dual lead, high wrap angle, screw pump rotors.
3. Application of SCORG Grid for Analysis of Water-Injected Twin Screw Compressor
There are industrial processes requiring clean compressed air where oil contamination is not acceptable such as in food and pharmacy plants. In the absence of oil in the compression chamber, leakage and thermal deformation significantly limit the delivery pressures that can be achieved in one compression stage. Accordingly, multistage compression with intercooling has been employed which adds immensely to the cost of the compressor plant. Injection of liquid water into twin screw air compressors has been pursued for a long time to gain thermodynamic benefits over dry air compression. When water is used in small quantities during the compression process, internal cooling and sealing can be achieved while a condenser fitted downstream of the compressor can strain the water out of the delivered high pressure air. In such a system or when there are no condensers employed it is desirable to inject an optimum quantity of water into the compression chamber to gain evaporative cooling. Recent studies have shown that using CFD models for dry air and oil injected air compressors achieved a good agreement with measurements, in the prediction of performance parameters [22]. In these simulations, Eulerian-Eulerian multiphase modelling has been applied. Implementation of the same model for water injected compressors presents an additional challenge in that the liquid water injected into the compression chamber changes phase and evaporates depending on local saturation and thermodynamic conditions [23]. Water also forms a liquid film on the rotor and housing and thereby influences thermal changes. The objective of the present analysis was to estimate the temperature distribution inside the compressor, identify non-uniformity and provide data to estimate thermal deformation due to high temperatures. A CFD model was used to calculate four different operating conditions with gradually increasing water content. The analysis indicates that with an increased amount of water injection into the compression chamber it is possible to control the gas discharge temperature within the limit of 200℃ to ensure the safe operation of the bearings and seals.
3.1. CFD Model and Operating Conditions
A detailed description of typical CFD modeling for twin screw compressors is presented in Rane [1,12,13]. The whole working domain of the compressor was split into four main sub-domains, namely the rotor domain, the suction port, the discharge end leakage gap and the discharge port. All the sub-domains were connected in the solver by non-conformal interfaces. The grid for the rotor domain was generated using SCORG while grids for all stationary domains were obtained using ANSYS meshing. The ANSYS CFX solver was used in this study. Inhomogeneous formulation treats momentum transport for each phase separately and can account for high slip conditions. Evaporation of the water-liquid phase is defined as per Equation (1) and the saturation temperature is specified with latent heat in Equation (2) corresponding to 11.0 bar delivery pressure. An empirical form of the Lee model [23] has been used in the present study. It is assumed that during the entire compression process from suction pressure to discharge pressure, secondary phase water-liquid changes phase to water-vapour only when its temperature exceeds the saturation temperature at a discharge pressure corresponding to . Such high temperatures can occur inside the compression chamber due to the heat addition of compression and reheating of the leakage gas. Possible internal over-compression is another contributor. Another crude assumption is that the phase change is unidirectional i.e., only evaporation occurs and no condensation. It is anticipated that condensation if it has to occur will happen in the discharge pipes and not in the compression chamber where continuous heat addition occurs. As the discharge piping is not a part of the computational domain, condensation can be ignored. Once the water-liquid is evaporated it is artificially removed from the domain. The entire enthalpy of evaporation is extracted from the primary phase air resulting in its cooling. In empirical form the evaporation mass transfer rate for water-liquid phase is
If (Evaporation)
Such that,
The enthalpy source in energy equation applied for air phase is defined as
where is the latent heat due to evaporation at discharge pressure. Such an empirical model also enables the use of constant thermodynamic properties for the water-liquid in the calculations. Four cases were calculated in this study. The corresponding operating conditions are as shown in Table 1.

Table 1.
Evaluated CFD cases and resultant discharge temperatures at 11.0 bar.
The fluid properties are defined in Table 2 with air as the primary phase and water-liquid as the secondary phase. Pressure boundary conditions were specified at the suction and discharge. Solver parameters were set at higher stability conditions. The SST k-Omega turbulence model was applied. Results from CFD analysis are presented in this section. They reflect a state when full 11.0 bar discharge pressure has been reached in the discharge port and 1–2 cycles of calculation were continued at these operating conditions. The cycle averaged temperature data were collected during the simulation.

Table 2.
Fluid properties.
3.2. Internal Compression Chamber Pressure
Figure 13 shows the rise of pressure in the compression chamber with main rotor rotation for Case1 at 6000 rpm and 0.018 kg/s water mass flow rate condition. Both air and water are at the same pressure inside the chamber. Because of the high under-compression which can be observed by the steep pressure rise at 350° rotor angle, a strong pressure pulse is generated in the discharge port.
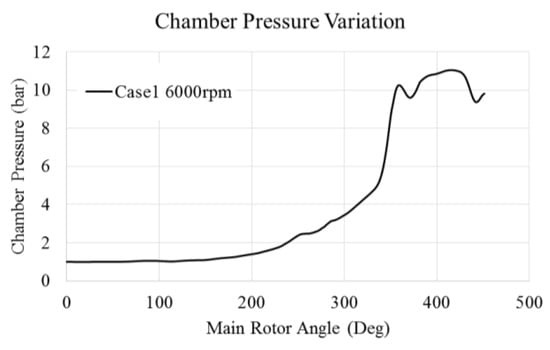
Figure 13.
Internal chamber pressure variation during a compression cycle.
The indicated power at 6000 rpm was 21.0 kW and at 4500 rpm it was 15.0 kW. The average torque on the main rotor was close to 30.0 Nm while that on the gate rotor was close to 3.69 Nm. The direction of gate rotor torque was opposite to that of the main rotor. All four cases were calculated at 11.0 bar discharge pressure and the resultant rotor torque was in a similar range in all cases.
3.3. Gas Temperature Distribution
If water was not injected into the compressor, the air temperature would have exceeded 380 °C at 11.0 bar discharge pressure. In the analysed cases, water was injected at 10 °C. Table 1 presents the average air temperature at discharge in the four cases. It can be observed that for a low water mass flow rate of 0.009 kg/s the cooling effect was stronger in Case 2 at 4500 rpm compared to Case 1 at 6000 rpm, which had twice the water mass flow compared to Case 2.
A water mass of 0.009 kg/s was determined so as to achieve saturated air at the exit with power dissipation of approximately 30 kW. But these estimates did not account for transient effects. The CFD calculation therefore resulted in higher than saturation exit temperatures. Additionally, leakage of gas during compression adds to the accumulation of energy in the compression chamber which further raises the gas temperature. Cases 2 and 4 were designed so that the mass flow rate of water is 5 and 10 times that of the saturation mass of Case 2, respectively, with the aim of achieving a discharge temperature lower than 200 ℃. The limit of 200 ℃ is due to the maximum temperature that the compressor bearings and housing can withstand during operation. It can be observed from Table 1 that the temperature of 205 ℃ is achieved at 4500 rpm and 187 ℃ is achieved at 6000 rpm with increased mass flow of water. Figure 14 presents the distribution of air temperature inside the compressor. An iso-surface generated with a water-liquid volume fraction of 0.01% is also shown in the figure. The air temperature in the suction port is lower on the gate rotor side, but on the main rotor side it is higher. This indicates that the leakage is higher from the tip of the main rotor than that from the gate rotor and also that the cooling is more effective on the gate rotor side than on the main rotor side for the same mass of injected water. The temperature on the gate rotor is higher than on the main rotor close to the discharge port. Water-liquid is observed in the region where the air temperature is below the saturation temperature at 11.0 bar. An evaporation effect is visible in the compression chamber opened to the discharge port and also in the discharge port, i.e., no liquid water is present there. In comparison to Case 2, Case3 resulted in about 50 ℃ lower cycle averaged temperature.
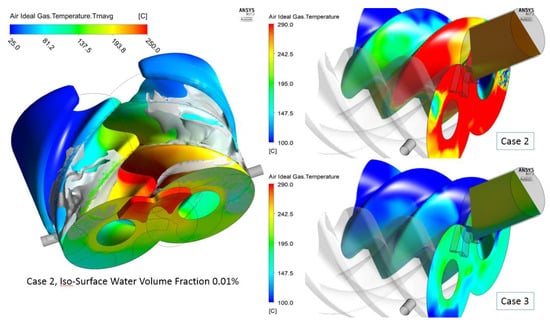
Figure 14.
Iso-surface of liquid water and cycle averaged air temperature distribution.
3.4. Evaporation Effect
Representation of water-vapour formation and cooling of the air is shown in Figure 15. The air temperature distribution on the main rotor surface, in the end leakage and in a plane through the discharge port is shown in Figure 15a. The region where liquid water is getting converted to vapour is shown in Figure 15b. The distribution of liquid water on the main rotor surface is shown in Figure 15c and the removal of energy by the latent heat, removed from air the in regions where evaporation is active is shown in Figure 15d.
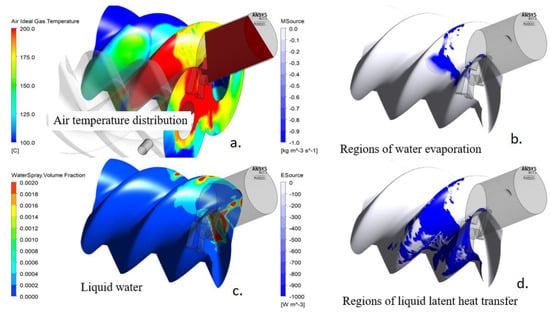
Figure 15.
Visualization of Case 2: (a) air temperature distribution; (b) regions of water evaporation; (c) liquid water distribution; and (d), regions of liquid latent heat transfer.
The air temperature and presence of liquid water can be correlated to the regions of vapour formation and heat extraction in this figure. Due to the very low mass of water (0.009 Kg/s) in Case 2, the local air temperature reaches up to about 290 ℃. In Case 3 which had a 5 times higher mass injection than in Case 2 the peak air temperature dropped to below 200 ℃ as shown in Figure 14.
4. Discussion
Rotary screw machines in their current form have been in operation for a long time and the basic design has not changed. Classical twin screw and single screw rotor arrangements have been successfully used as compressors, pumps and expanders. With ever-increasing demands for higher efficiency, operating pressure ratio and reliability, designers are constantly exploring non-conventional rotary arrangements. 3D CFD models are being used more and more to improve rotary machine design by optimizing the rotors, ports and the interaction of flow within the working chambers but the use of 3D CFD for exploring non-conventional design space has been mainly constrained by the non-availability of computational mesh generation tools.
The test case of a water-injected twin screw compressor is an example of multi-phase flow consisting of two fluids, air and water. A single domain structured numerical mesh of the flow domain was generated using the recently developed boundary blocking, analytical grid generation, and elliptical smoothing of SCORG. Analysis of the test cases indicated the following design performance:
- Results show higher cooling at 4500 rpm than at 6000 rpm for the same water mass flow rate. The total mass of water injected and its residence time in the compression chamber is higher at lower speed resulting in greater heat transfer and cooling. At 4500 rpm the compression power is lower than at 6000 rpm. Therefore the same mass of water will provide higher cooling at lower speeds.
- When water mass required just for saturation is injected, the exit temperature exceeds 300 ℃. By injecting with a five times higher water mass flow rate, a cycle average temperature close to 200 ℃ could be achieved.
- In this compressor design, the water cooling effect was higher on the Gate rotor side due to early injection. Accordingly, an increase in the water injection on the main rotor side can help to achieve better temperature uniformity.
- Tip leakage was higher on the main rotor side and this resulted in non-uniform temperature of the housing.
The test case demonstrated that the analysis of a physical mechanism such as water injection in the compression chamber and evaporation during the compression cycle is still at a primitive level where simplification of the evaporation mechanism was required to avoid excessively high computational resource and facilitate numerical stability of the flow solver. This implies the need to further develop numerical models and flow solvers to be suitable for the design and analysis of rotary screw machines.
5. Conclusions
It is anticipated that more customized grid generation tools such as SCORG will need to be developed as further positive displacement screw machine designs are explored and their computational models are needed. In this paper, SCORG, a customized grid generation tool that has a framework developed for classical twin screw machines has been presented as applied to a variety of screw machines. It was possible to extend the grid generation to a variety of variable geometry rotors such as rotor lead variation or rotor profile variation. Similarly, a completely non-conventional internally geared conical screw machine could be analysed. Other arrangements include multiple gate rotors intended to increase volumetric displacement or dual lead high wrap angle rotors intended for very high-pressure differences. The availability of a computational grid for such screw rotors now makes it possible to evaluate the flow and thermal field in the working chambers of these machines. Additional 3D CFD methods that can provide robust grid re-meshing algorithms, or meshless methods, that can be used for flow computation in the complex deforming domains of these machines will also need to be evolved.
Supplementary Materials
The following are available online at https://www.mdpi.com/2411-9660/3/2/30/s1, Video S1: Variable lead rotors; Video S2: CFD simulation of oil injected twin screw compressor; Video S3: Tri-rotor screw machine; Video S4: SCORG grid for internal screw rotors.
Author Contributions
Conceptualization, S.R., A.K., and N.S.; Methodology, S.R., A.K., and N.S.; Investigation, S.R., A.K., and N.S.; Writing—original draft preparation, S.R.; Writing—review and editing, A.K., and N.S.; Supervision, N.S.; Project administration, S.R. and A.K.
Funding
This research was funded by the Centre for Compressor Technology, City, University of London.
Acknowledgments
Authors would like to thank Ian K Smith, Center for Compressor Technology, City, University of London for supporting the research, and Graham Stupple and Andreas Korner from Jäcklin GmbH for water-injected screw compressor technical inputs.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| ALE | Arbitrary Lagrangian–Eulerian |
| CFD | Computational fluid dynamics |
| PDE | Partial differential equations |
| TFI | Trans-finite interpolation |
| Latent heat | |
| Water temperature | |
| Water density | |
| Volumetric efficiency | |
| Saturation temperature at vapor partial pressure | |
| Evaporation enthalpy source | |
| Evaporation mass source | |
| Solver time step size | |
| Lee–Mass transfer coefficient | |
| Empirical mass transfer coefficient | |
| Vapor partial pressure | |
| Water volume fraction | |
| Adiabatic efficiency | |
| SCORG | Screw compressor rotor grid generator |
References
- Rane, S. Grid Generation and CFD Analysis of Variable Geometry Screw Machines. Ph.D. Thesis, University of London, London, UK, 2015. [Google Scholar]
- Gardner, J.W. Variable Lead Compressor. U.S. Patent No 3,424,373, 28 January 1969. [Google Scholar]
- Kovačević, A. Three-Dimensional Numerical Analysis for Flow Prediction in Positive Displacement Screw Machines. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Kovačević, A. Boundary Adaptation in Grid Generation for CFD Analysis of Screw Compressors. Int. J. Numer. Methods Eng. 2005, 64, 401–426. [Google Scholar] [CrossRef]
- Stošić, N.; Smith, I.K.; Kovačević, A. Screw Compressors: Mathematical Modeling and Performance Calculation, Monograph; Springer: Berlin, Gernmany, 2005; ISBN 3-540-24275-9. [Google Scholar]
- Kovačević, A.; Stošić, N.; Smith, I.K. Screw Compressors—Three Dimensional Computational Fluid dynamics and Solid Fluid Interaction; Springer: Berlin/Heidelberg, Gernmay; New York, NY, USA, 2007; ISBN 3-540-36302-5. [Google Scholar]
- Rane, S.; Kovačević, A.; Stošić, N.; Kethidi, M. Deforming grid generation and CFD analysis of variable geometry screw compressors. Comput. Fluids 2014, 99, 124–141. [Google Scholar] [CrossRef]
- Sauls, J.; Branch, S. Use of CFD to develop improved one-dimensional thermodynamic analysis of refrigerant screw compressors. In 8th International Conference on Compressors and Their Systems; IOP Publishing: Bristol, UK, 2013; p. 591. [Google Scholar]
- Mujic, E. A Numerical and Experimental Investigation of Pulsation Induced Noise in Screw Compressors. Ph.D. Thesis, University of London, London, UK, 2008. [Google Scholar]
- Riemslagh, K.; Vierendeels, J.; Dick, E. An arbitrary Lagrangian-Eulerian finite-volume method for the simulation of rotary displacement pump flow. Appl. Numer. Math. 2000, 32, 419–433. [Google Scholar] [CrossRef]
- Voorde Vande, J.; Vierendeels, J. A grid manipulation algorithm for ALE calculations in screw compressors. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar] [CrossRef]
- Rane, S.; Kovačević, A. Algebraic generation of single domain computational grid for twin screw machines. Part I. Implementation. Adv. Eng. Softw. 2017, 107, 38–50. [Google Scholar] [CrossRef]
- Kovačević, A.; Rane, S. Algebraic generation of single domain computational grid for twin screw machines Part II—Validation. Adv. Eng. Softw. 2017, 107, 31–43. [Google Scholar] [CrossRef]
- Schulze-Beckinghausen, P.; Hauser, J.; Beinert, M.; Herlemann, S. Advanced analysis of twin screw compressors with variable rotor pitch using one-dimensional thermodynamic simulation. In Proceedings of the 9th International Conference on Screw Compressor, Dortmund, Germany, 23–24 September 2014; Volume 2228, pp. 237–248. [Google Scholar]
- Utri, M.; Brümmer, A. A comparative examination of the potential of screw expanders with variable rotor pitch. In Proceedings of the 9th International Conference on Screw Compressor, Dortmund, Germany, 23–24 September 2014; Volume 2228, pp. 249–266. [Google Scholar]
- Kauder, K.; Fost, C. Investigations about the Improvement of the Filling Process of a Screw-Type Engine, Part III; VDI-Berichte Report; TU Dortmund: Dortmund, Germany, 23–24 September 2002. [Google Scholar]
- Fost, C. Geometrical Variations at the Inlet of Screw–Type Engines. In Proceedings of the International Screw Compressor Conference, Dortmund, Germany, 25–26 September 2006. [Google Scholar]
- Rane, S.; Kovačević, A.; Stošić, N.; Kethidi, M. Grid Deformation Strategies for CFD Analysis of Screw Compressors. Int. J. Refrig. 2013, 36, 1883–1893. [Google Scholar] [CrossRef]
- Knupp, P.; Steinberg, S. The Fundamentals of Grid Generation; CRC Press: Boca Raton, FL, USA, 2002; ISBN 9780849389870. [Google Scholar]
- Rane, S.; Kovačević, A. Application of numerical grid generation for improved CFD analysis of multiphase screw machines. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 232. [Google Scholar] [CrossRef]
- Crowe, T.C. Multiphase Flow Handbook; CRC Press, Taylor and Francis: Boca Raton, FL, USA, 2006; ISBN 0-8493-1280-9. [Google Scholar]
- Rane, S.; Kovačević, A.; Stošić, N. CFD Analysis of Oil Flooded Twin Screw Compressors. In Proceedings of the 23rd International Compressor Engineering Conference at Purdue 2016, West Lafayette, IN, USA, 11–14 July 2016; p. 2392. [Google Scholar]
- Rane, S.; Kovačević, A.; Stošić, N.; Stupple, G. On Numerical Investigation of Water Injection to Screw Compressors. In ASME 2018 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 6A, p. V06AT08A031. [Google Scholar] [CrossRef]
- Nilsson, H.R. Rotary Multiple Helical Rotor Machine. U.S. Patent No 2,481,527, 13 September 1949. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).