Stuck on a Plateau? A Model-Based Approach to Fundamental Issues in Visual Temporal-Order Judgments
Abstract
1. Introduction
2. Material and Methods
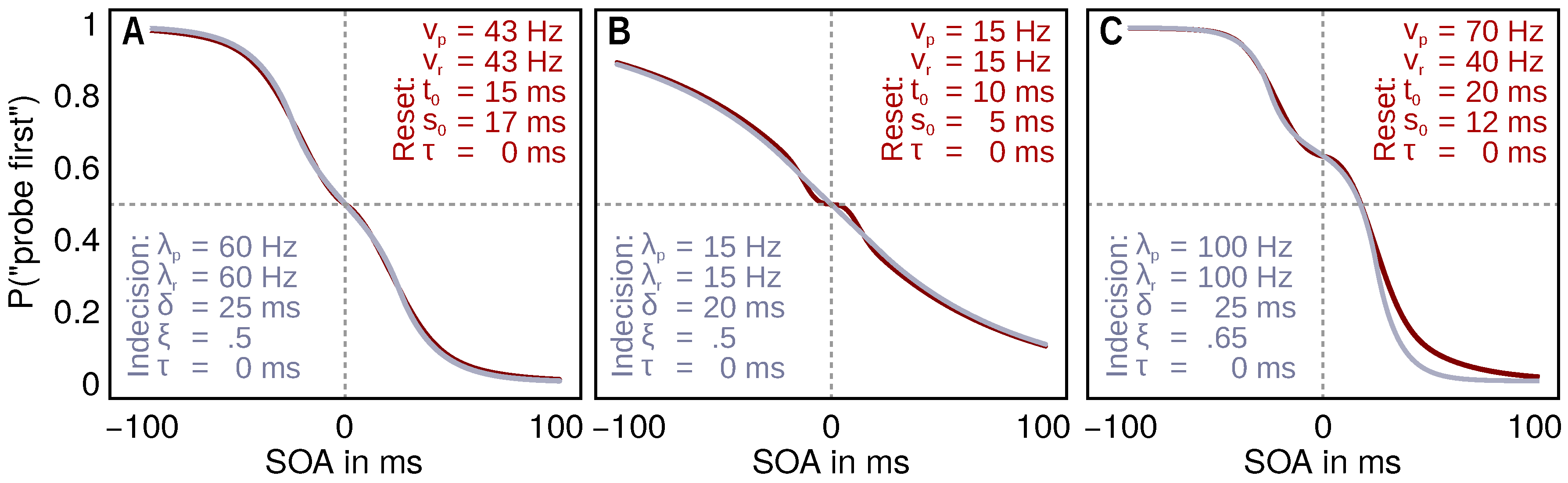
2.1. Exponential Race Models of Temporal-Order Judgments
2.2. Cause of a Plateau: Range of Indecision
2.3. Cause of a Plateau: Encoding Reset
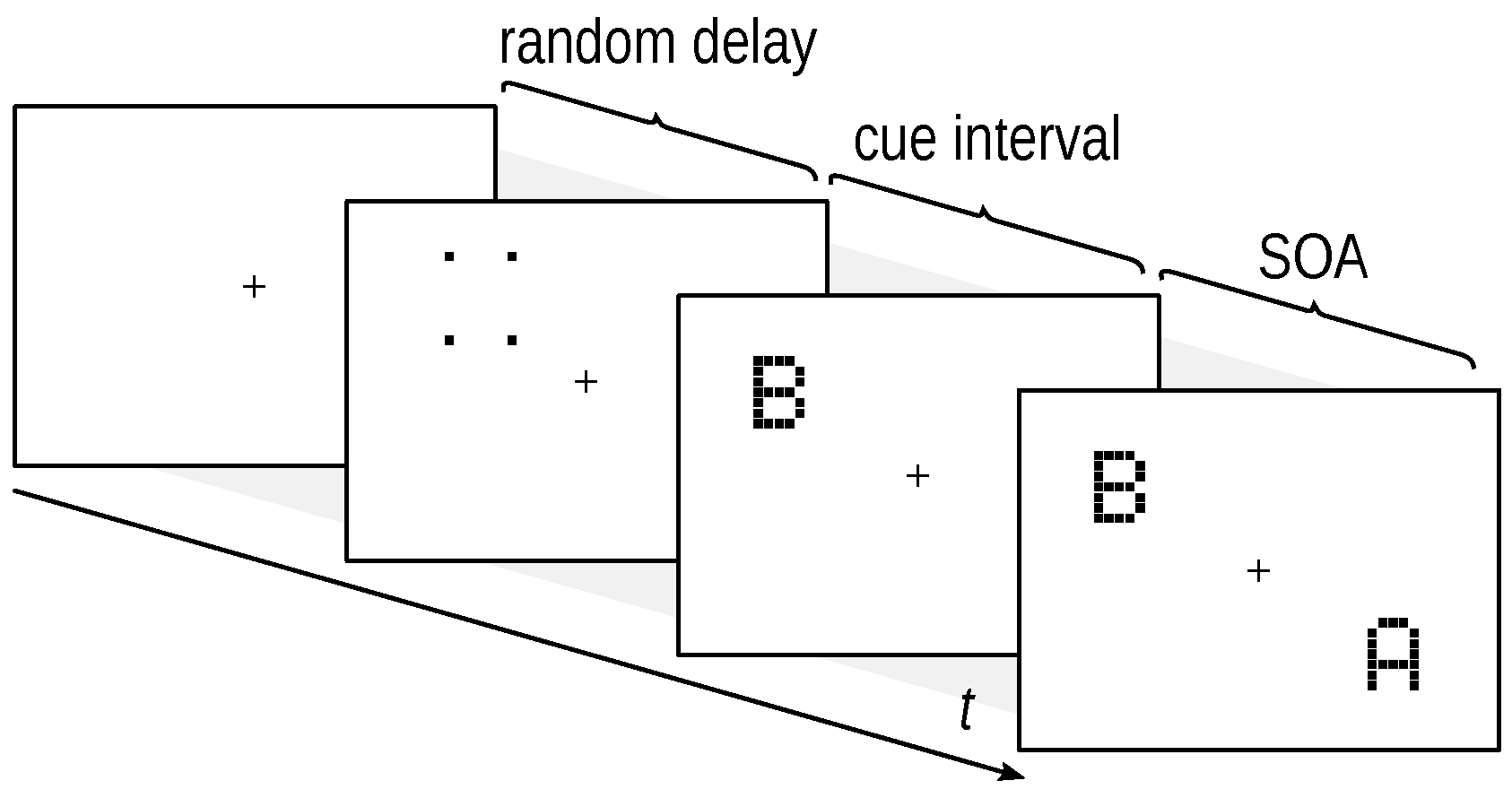
2.4. General Experimental Procedure
2.4.1. Stimuli
2.4.2. Procedure
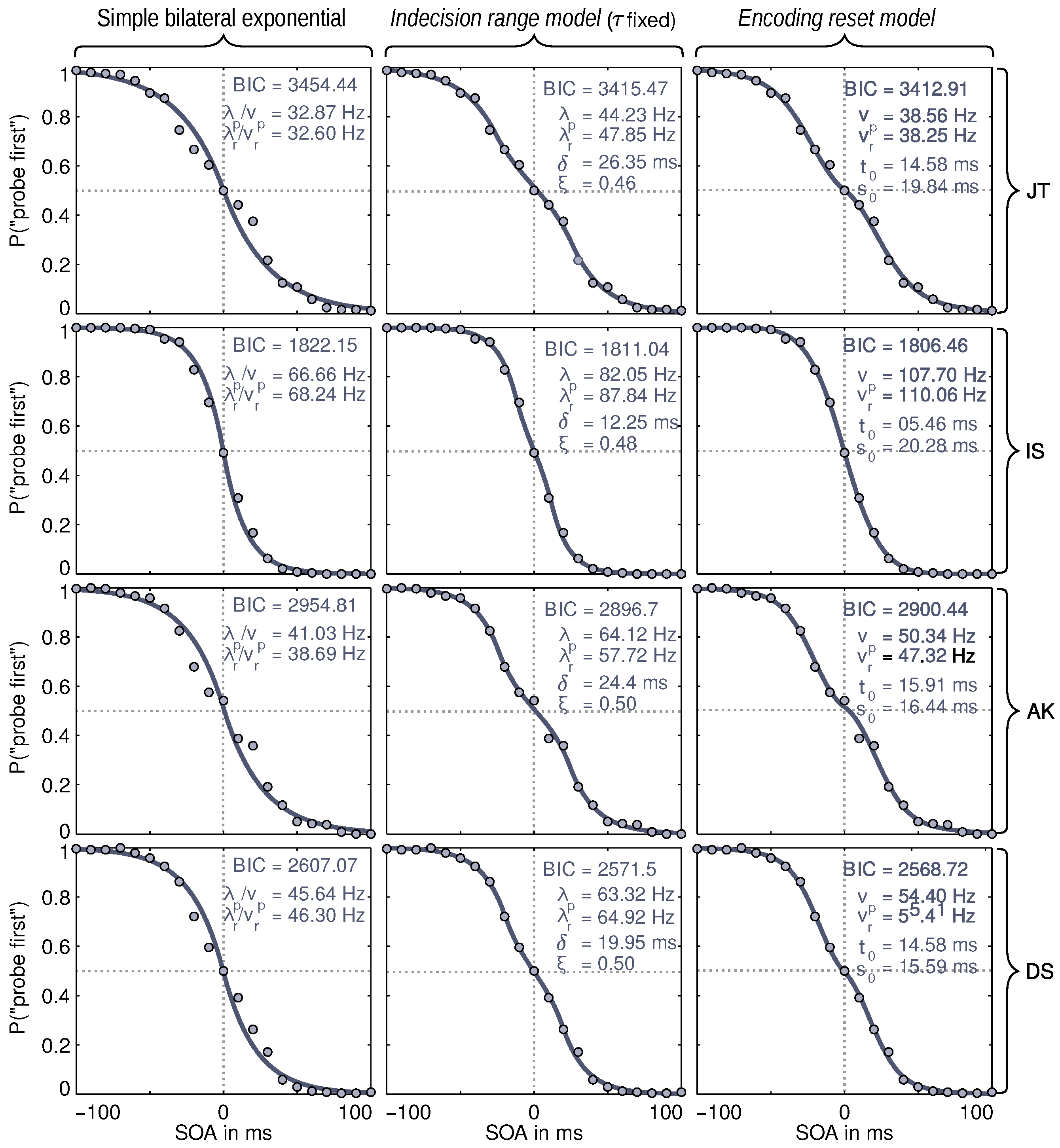
2.5. Experiment 1: Basic TOJs
2.6. Participants
2.7. Stimuli and Procedure
2.8. Results
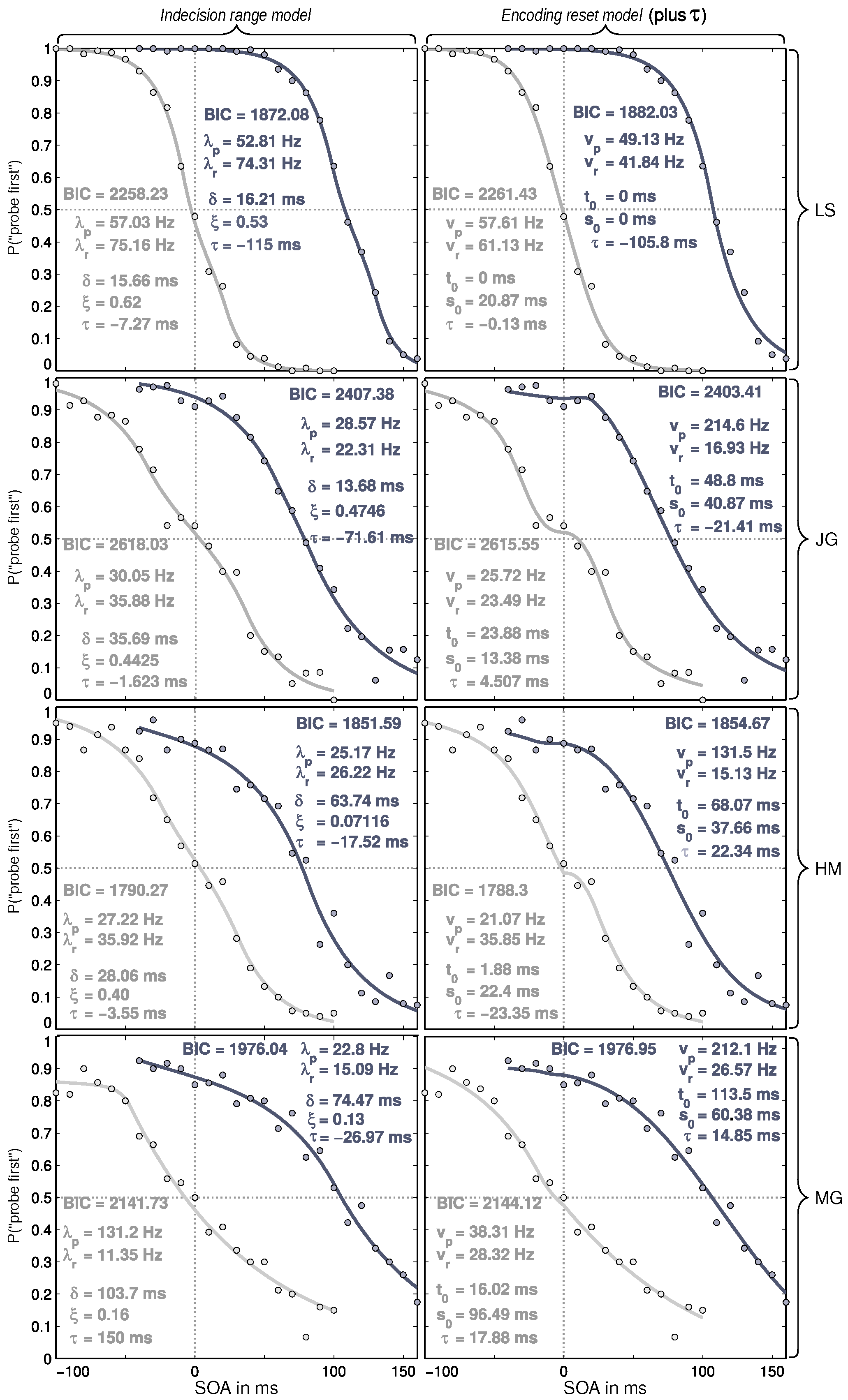
3. Experiment 2: TOJs with Exogenous Attention Manipulation
3.1. Participants
3.2. Stimuli
3.3. Procedure
3.4. Results
4. Discussion
5. Conclusions
Ethics Statement
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BIC | Bayes information criterion |
| cm | centimeter |
| Hz | Hertz |
| ms | milliseconds |
| SOA | Stimulus onset asynchrony |
| TOJ | Temporal-order judgment |
| TVA | Theory of visual attention |
References
- Sternberg, S.; Knoll, R.L. The perception of temporal order: Fundamental issues and a general model. In Attention and Performance IV; Academic Press: New York, NY, USA, 1973; pp. 629–685. [Google Scholar]
- Ulrich, R. Threshold models of temporal-order judgments evaluated by a ternary response task. Percept. Psychophys. 1987, 42, 224–239. [Google Scholar] [CrossRef] [PubMed]
- Guilford, P.J. Psychometric Methods, 2nd ed.; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Finney, D.J. Probit Analysis; Cambridge University Press: Cambridge, UK, 1971. [Google Scholar]
- Neumann, O.; Scharlau, I. Experiments on the Fehrer–Raab effect and the ‘Weather Station Model’ of visual backward masking. Psychol. Res. 2007, 71, 667–677. [Google Scholar] [CrossRef] [PubMed]
- Allan, L.G. Temporal order psychometric functions based on confidence-rating data. Atten. Percept. Psychophys. 1975, 18, 369–372. [Google Scholar] [CrossRef]
- Allan, L.G.; Kristofferson, A.B. Psychophysical theories of duration discrimination. Percept. Psychophys. 1974, 16, 26–34. [Google Scholar] [CrossRef]
- Gibson, B.S.; Egeth, H. Inhibition and disinhibition of return: Evidence from temporal order judgments. Percept. Psychophys. 1994, 56, 669–680. [Google Scholar] [CrossRef] [PubMed]
- Shore, D.I.; Spence, C.; Klein, R.M. Visual prior entry. Psychol. Sci. 2001, 12, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Stelmach, L.B.; Herdmann, C.M. Directed attention and perception of temporal order. J. Exp. Psychol. Hum. Percept. Perform. 1991, 17, 539–550. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, S.; Knoll, R.L.; Gates, B.A. Prior entry reexamined: Effect of attentional bias on order perception. Presented at the Annual Meeting of the Psychonomic Society, St. Louis, MO, USA, 10 November 1971. [Google Scholar]
- Zackon, D.H.; Casson, E.J.; Zafar, A.; Stelmach, L.B.; Racette, L. The temporal order judgment paradigm: Subcorticalattentional contribution under exogenous and endogenouscueing conditions. Neuropsychologia 1999, 37, 511–520. [Google Scholar] [CrossRef]
- Alcalá-Quintana, R.; García-Pérez, M.A. Fitting model-based psychometric functions to simultaneity and temporal-order judgment data: MATLAB and R routines. Behav. Res. Methods 2013, 45, 972–998. [Google Scholar] [CrossRef] [PubMed]
- Schneider, K.A.; Bavelier, D. Components of visual prior entry. Cognit. Psychol. 2003, 47, 333–366. [Google Scholar] [CrossRef]
- Tünnermann, J.; Krüger, A.; Scharlau, I. Measuring attention and visual processing speed by model-based analysis of temporal-order judgments. J. Vis. Exp. 2017, 119, e54856. [Google Scholar] [CrossRef] [PubMed]
- Tünnermann, J.; Petersen, A.; Scharlau, I. Does attention speed up processing? Decreases and increases of processing rates in visual prior entry. J. Vis. 2015, 15, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Tünnermann, J.; Scharlau, I. Peripheral visual cues: Their fate in processing and effects on attention and temporal-order perception. Front. Psychol. 2016, 7, 1442. [Google Scholar] [CrossRef] [PubMed]
- Tünnermann, J. On the Origin of Visual Temporal-Order Perception by Means of Attentional Selection. Ph.D. Thesis, Paderborn University, Paderborn, Germany, 2016. [Google Scholar]
- Krüger, A.; Tünnermann, J.; Scharlau, I. Fast and conspicuous? Quantifying salience with the theory of visual attention. Adv. Cognit. Psychol. 2016, 12, 20–38. [Google Scholar] [CrossRef] [PubMed]
- Krüger, A.; Tünnermann, J.; Scharlau, I. Measuring and modeling salience with the theory of visual attention. Atten. Percept. Psychophys. 2017, 79, 1593–1614. [Google Scholar] [CrossRef] [PubMed]
- Tünnermann, J.; Scharlau, I. Poking left to be right? A model-based analysis of temporal order judged by mice. Adv. Cognit. Psychol. 2018, 12, 39–50. [Google Scholar] [CrossRef]
- Bundesen, C. A theory of visual attention. Psychol. Rev. 1990, 97, 523–547. [Google Scholar] [CrossRef] [PubMed]
- Bundesen, C.; Habekost, T. Principles of Visual Attention: Linking Mind and Brain; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Taagepera, R. Making Social Sciences More Scientific: The Need for Predictive Models; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- García-Pérez, M.A.; Alcalá-Quintana, R. Response errors explain the failure of independent-channels models of perception of temporal order. Front. Psychol. 2012, 3, 94. [Google Scholar] [CrossRef] [PubMed]
- Shibuya, H.; Bundesen, C. Visual selection from multielement displays: Measuring and modeling effects of exposure duration. J. Exp. Psychol. Hum. Percept. Perform. 1988, 14, 591–600. [Google Scholar] [CrossRef] [PubMed]
- Luce, R.D. The choice axiom after twenty years. J. Math. Psychol. 1977, 15, 215–233. [Google Scholar] [CrossRef]
- Weiß, K.; Scharlau, I. Simultaneity and temporal order perception: Different sides of the same coin? Evidence from a visual prior-entry study. Q. J. Exp. Psychol. 2011, 64, 394–416. [Google Scholar] [CrossRef] [PubMed]
- Dyrholm, M.; Kyllingsbæk, S.; Espeseth, T.; Bundesen, C. Generalizing parametric models by introducing trial-by-trial parameter variability: The case of TVA. J. Math. Psychol. 2011, 55, 416–429. [Google Scholar] [CrossRef]
- Tünnermann, J. Interactive Demonstration of Plateau-Generating Mechanisms in Temporal-Order Judgments (TOJs). Code Ocean Capsule. 2018. Available online: https://codeocean.com/2018/06/03/interactive-demonstration-of-plateau-generating-mechanisms-in-temporal-order-judgments-lpar-tojs-rpar/interface (accessed on 6 July 2018).
- Schwarz, G. Estimating the dimension of a model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Scharlau, I.; Ansorge, U.; Horstmann, G. Latency facilitation in temporal-order judgments: Time course of facilitation as a function of judgment type. Acta Psychol. 2006, 122, 129–159. [Google Scholar] [CrossRef] [PubMed]
- Spence, C.; Parise, C. Prior-entry: A review. Conscious. Cognit. 2010, 19, 364–379. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tünnermann, J.; Scharlau, I. Stuck on a Plateau? A Model-Based Approach to Fundamental Issues in Visual Temporal-Order Judgments. Vision 2018, 2, 29. https://doi.org/10.3390/vision2030029
Tünnermann J, Scharlau I. Stuck on a Plateau? A Model-Based Approach to Fundamental Issues in Visual Temporal-Order Judgments. Vision. 2018; 2(3):29. https://doi.org/10.3390/vision2030029
Chicago/Turabian StyleTünnermann, Jan, and Ingrid Scharlau. 2018. "Stuck on a Plateau? A Model-Based Approach to Fundamental Issues in Visual Temporal-Order Judgments" Vision 2, no. 3: 29. https://doi.org/10.3390/vision2030029
APA StyleTünnermann, J., & Scharlau, I. (2018). Stuck on a Plateau? A Model-Based Approach to Fundamental Issues in Visual Temporal-Order Judgments. Vision, 2(3), 29. https://doi.org/10.3390/vision2030029



