Greater Neuromuscular and Perceptual Fatigue after Low versus High Loads in the Bench Press: A Preliminary Study Applying Frequentist and Bayesian Group Analyses with Subject-by-Subject Case Series Reports
Abstract
1. Introduction
2. Methods
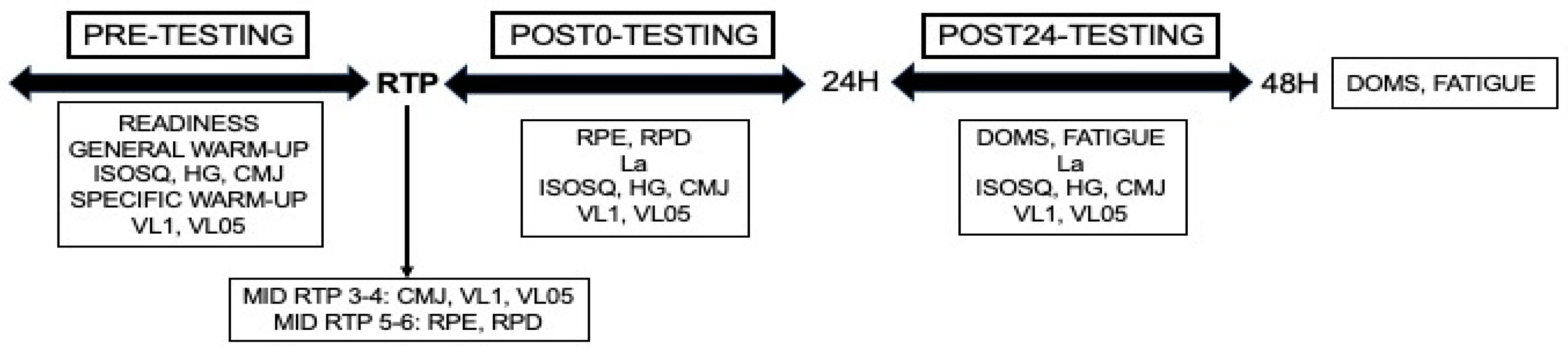
2.1. Experimental Design
- (a)
- RTP1: 3 sets to failure (TF); 50%RM; 3 min inter-set rest.
- (b)
- RTP2: 3 TF sets; 85%RM; 3 min inter-set rest.
- (c)
- RTP3: 6 sets with half-RTP1 mean set repetitions; 50%RM; 3 min inter-set rest.
- (d)
- RTP4: 6 sets with half-RTP2 mean set repetitions; 85%RM; 3 min inter-set rest.
- (e)
- RTP5: 1 cluster set (2 + 2 +…) equalizing RTP1 total repetitions; 50%RM; 30 s intra-set rest.
- (f)
- RTP6: 1 cluster set (1 + 1 +…) equalizing RTP1 total repetitions; 85%RM; 30 s intra-set rest.
2.2. Participants
2.3. Familiarization Sessions
2.4. One Repetition Maximum and Load–Velocity Relationship
2.5. Resistance Training Protocols
2.6. Neuromuscular Measures
2.6.1. Countermovement Jump
2.6.2. Velocity Loss during Sets and against 1 m/s and 0.5 m/s Loads
2.6.3. Blood Lactate
2.7. Subjective Measures of Fatigue
2.7.1. Rate of Perceived Effort and Discomfort
2.7.2. Delayed-Onset Muscle Soreness and Perceived Fatigue
2.8. Time under Tension (TUT) and Force/Impulse Estimation
2.9. Effort Index
2.10. Statistical Analysis
2.11. Sample Size Justification
3. Results
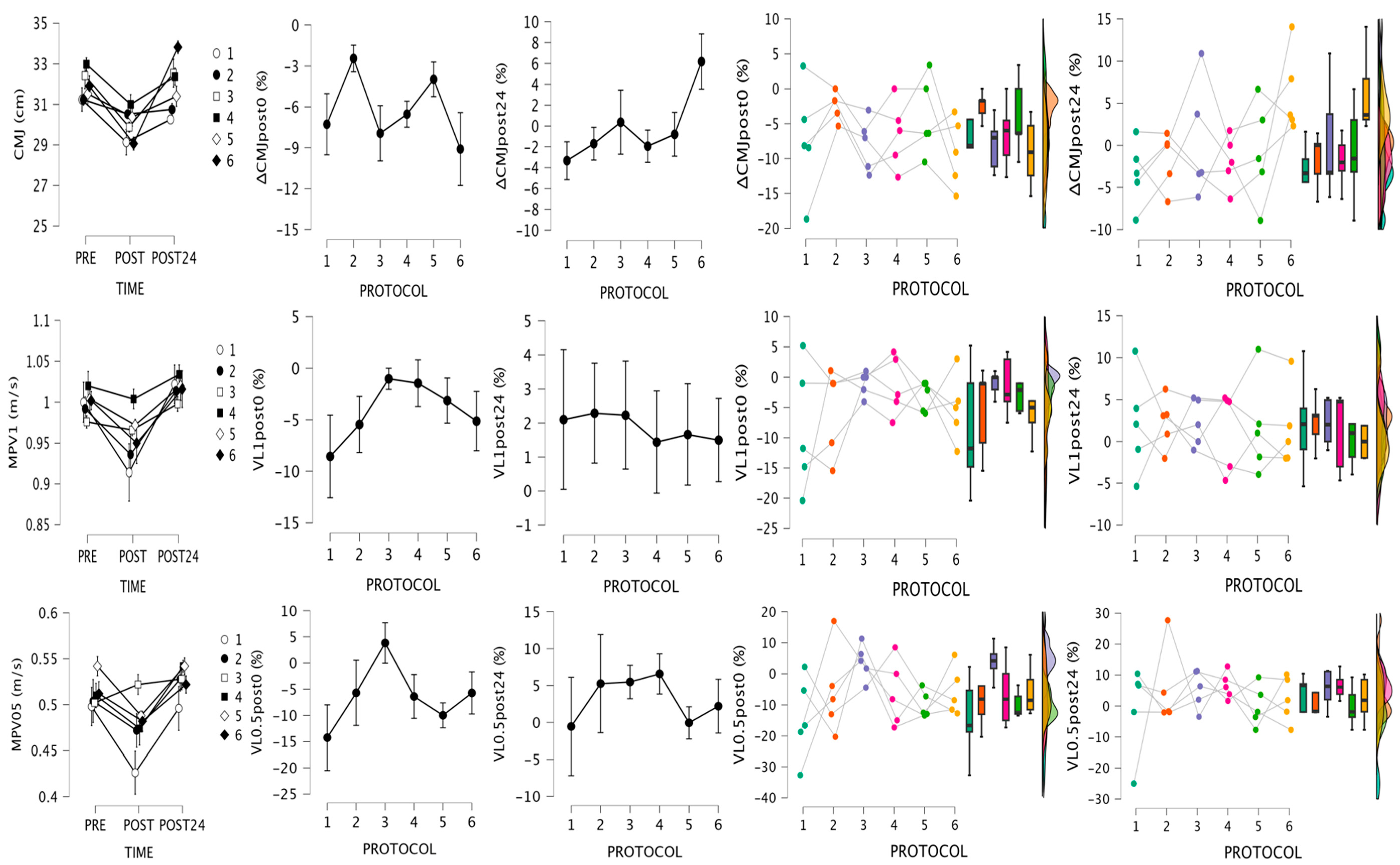
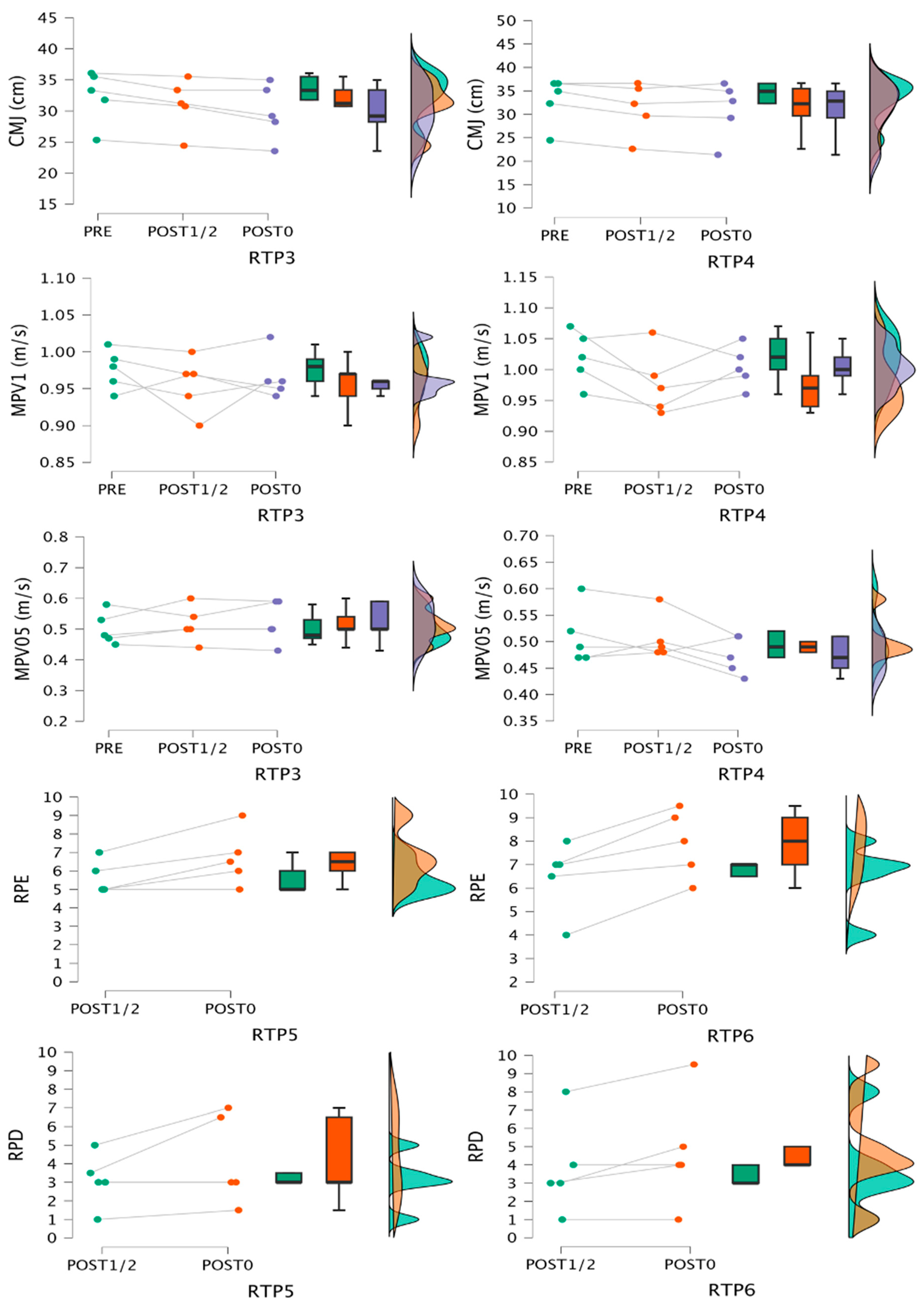
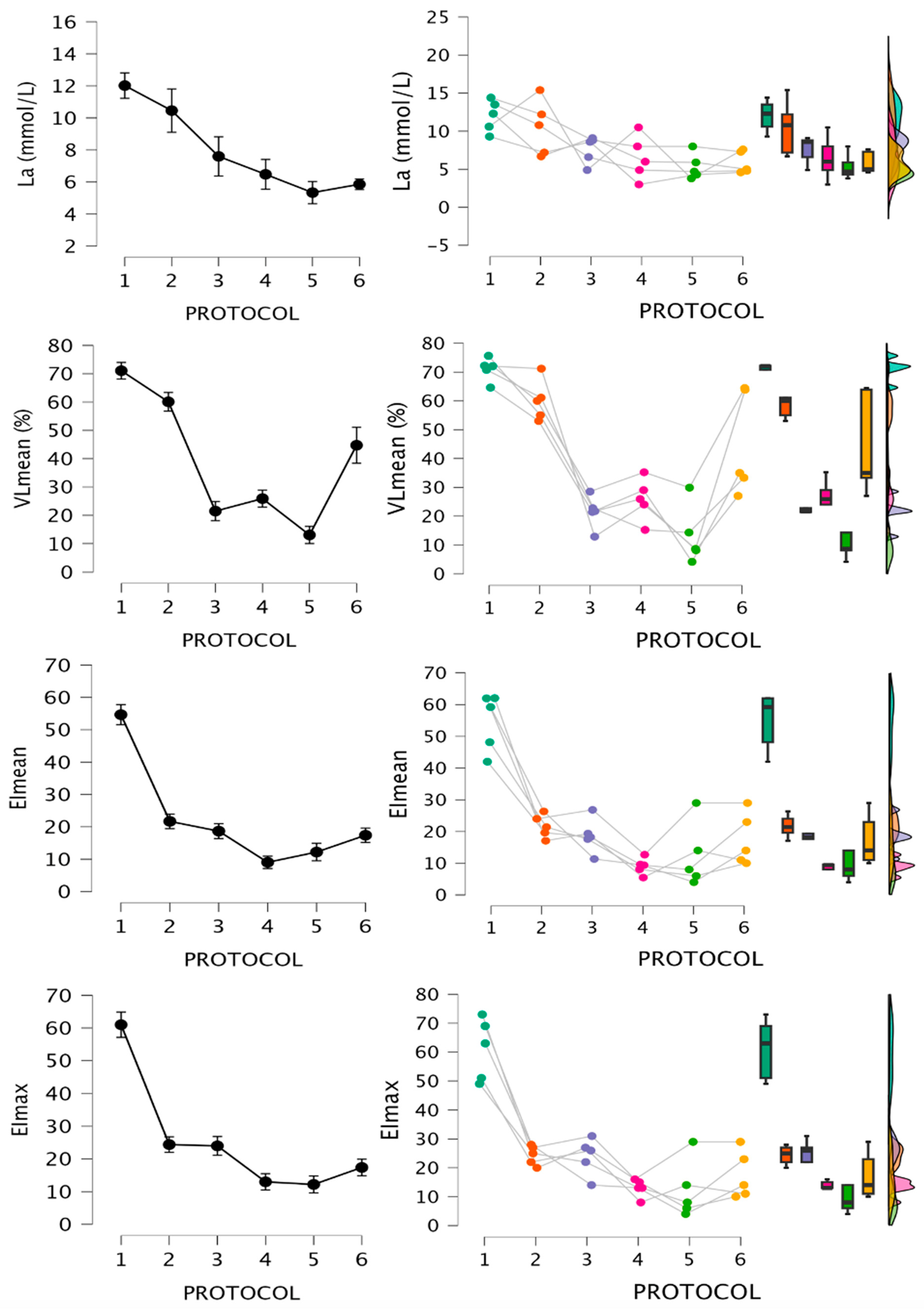
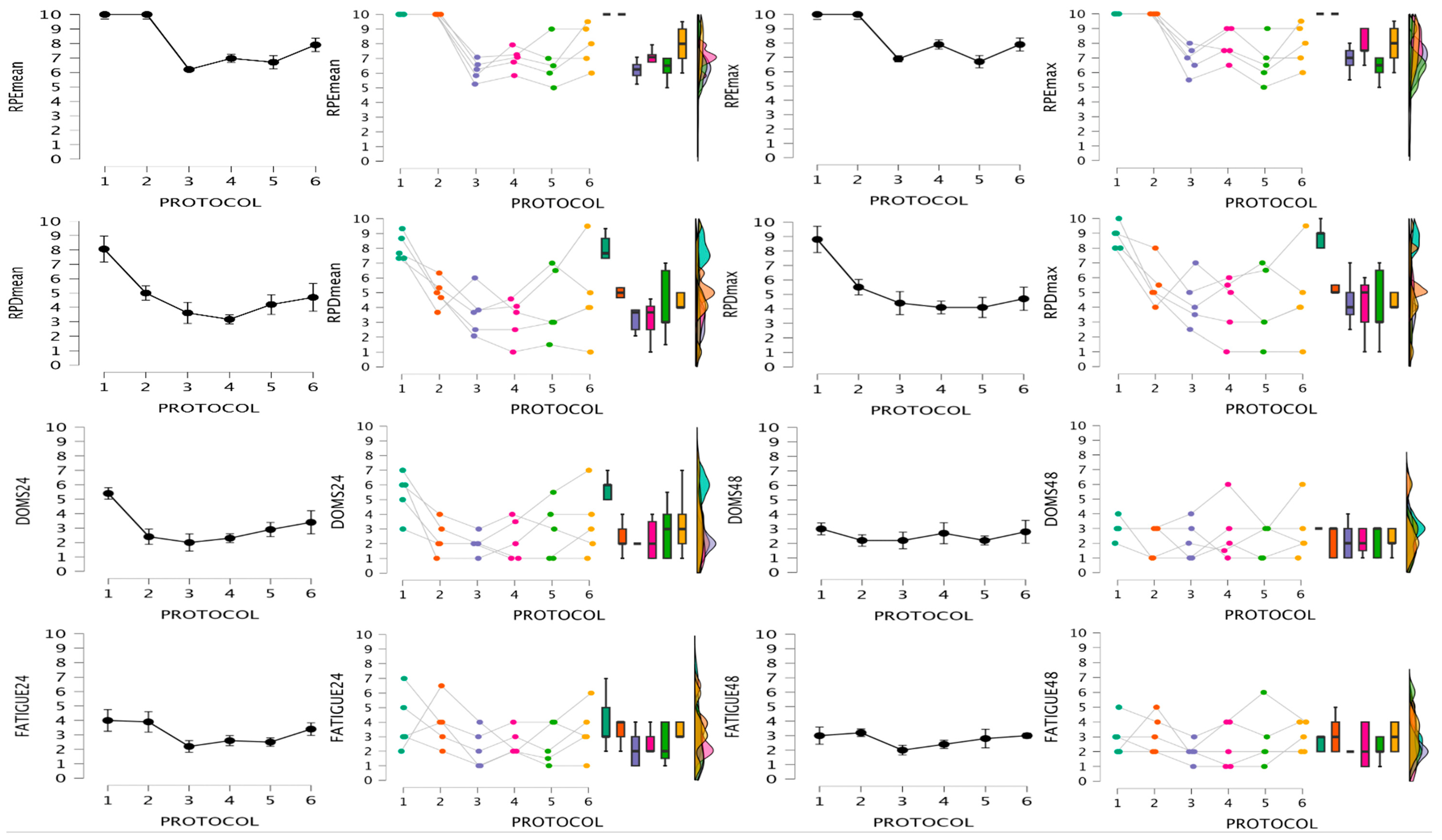
3.1. Within-Protocol Comparisons
3.2. Between-Protocol Comparisons
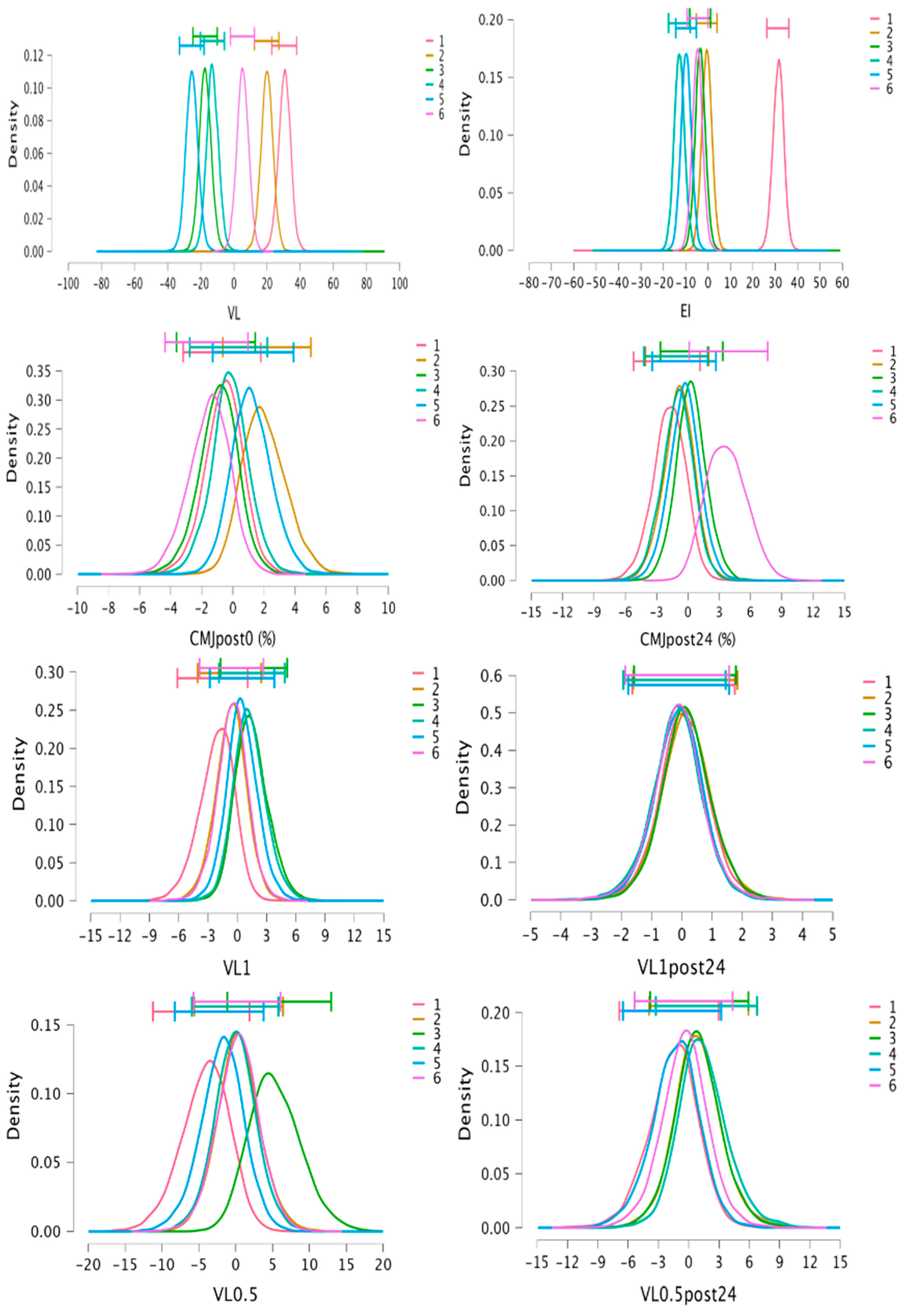
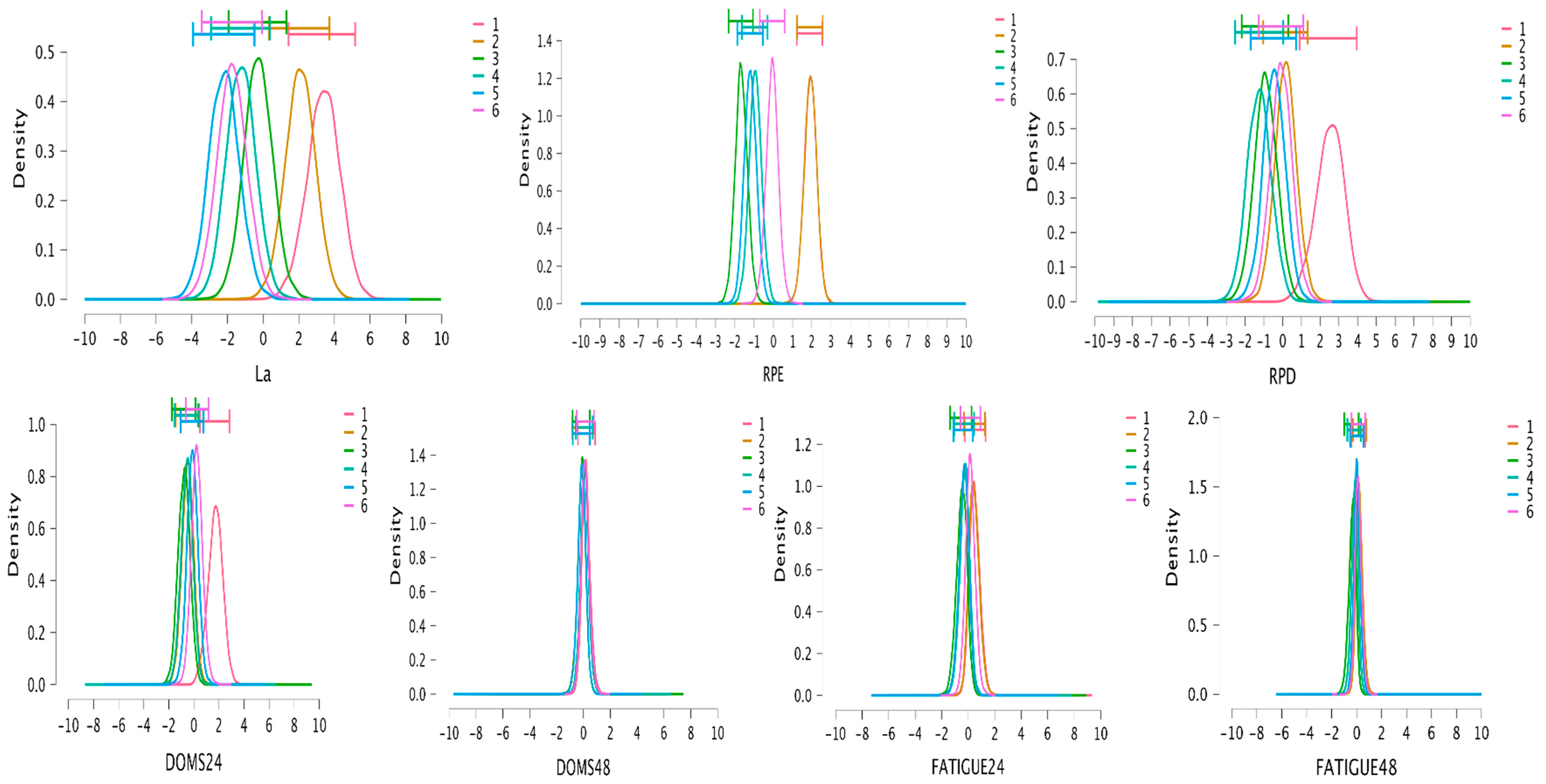
3.3. Bayesian Analysis
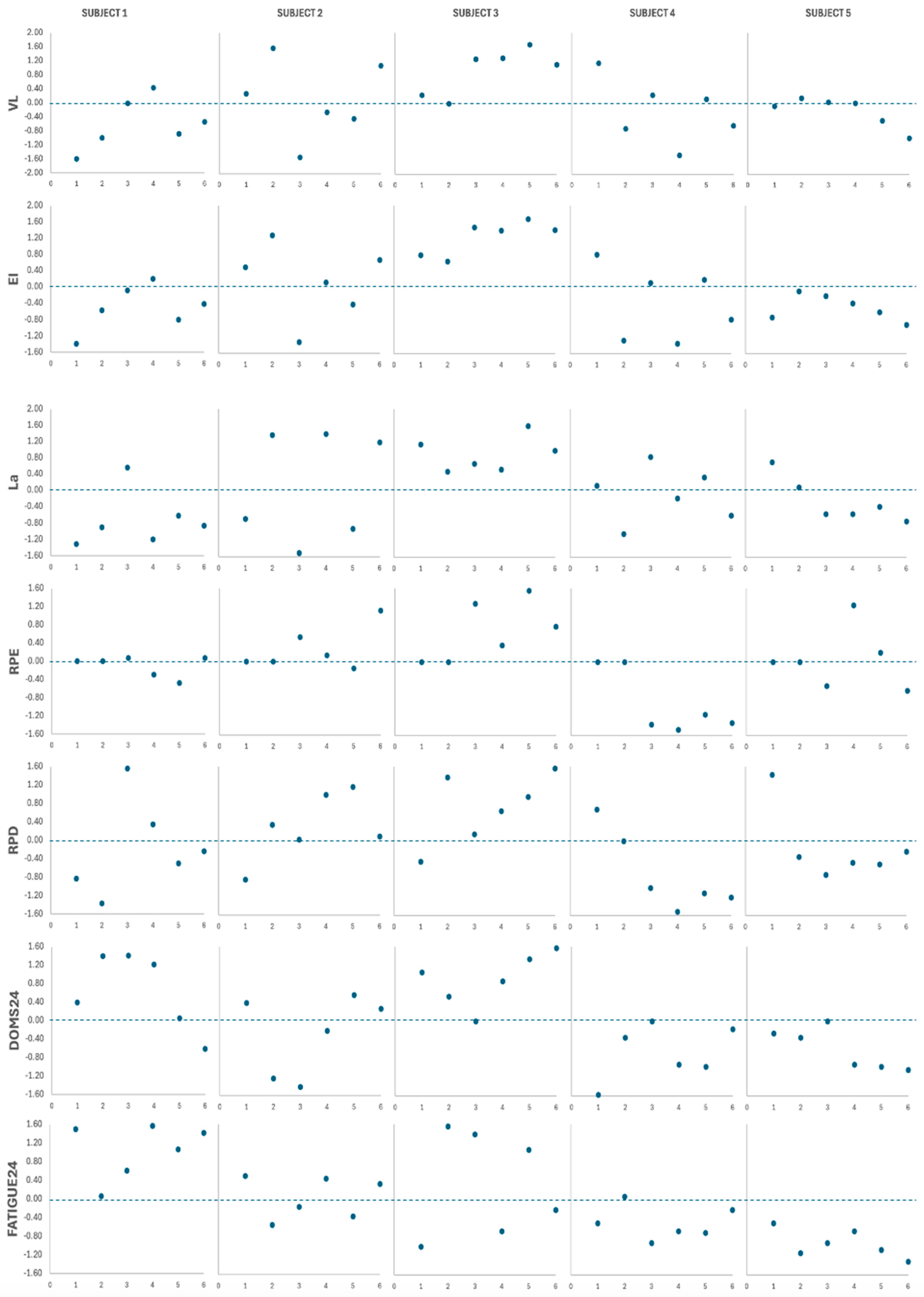
3.4. Subject-by-Subject Analysis
4. Discussion
Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Furrer, R.; Hawley, J.A.; Handschin, C. The molecular athlete: Exercise physiology from mechanisms to medals. Physiol. Rev. 2023, 103, 1693–1787. [Google Scholar] [CrossRef] [PubMed]
- Lauersen, J.B.; Bertelsen, D.M.; Andersen, L.B. The effectiveness of exercise interventions to prevent sports injuries: A systematic review and meta-analysis of randomised controlled trials. Br. J. Sports Med. 2014, 48, 871–877. [Google Scholar] [CrossRef] [PubMed]
- Mcleod, J.C.; Currier, B.S.; Lowisz, C.V.; Phillips, S.M. The influence of resistance exercise training prescription variables on skeletal muscle mass, strength, and physical function in healthy adults: An umbrella review. J. Sport Health Sci. 2023; advance online publication. [Google Scholar]
- Jukic, I.; Castilla, A.P.; Ramos, A.G.; Van Hooren, B.; McGuigan, M.R.; Helms, E.R. The acute and chronic effects of implementing velocity loss thresholds during resistance training: A systematic review, meta-analysis, and critical evaluation of the literature. Sports Med. 2023, 53, 177–214. [Google Scholar] [CrossRef] [PubMed]
- Jukic, I.; Van Hooren, B.; Ramos, A.G.; Helms, E.R.; McGuigan, M.R.; Tufano, J.J. The effects of set structure manipulation on chronic adaptations to resistance training: A systematic review and meta-analysis. Sports Med. 2021, 51, 1061–1086. [Google Scholar] [CrossRef] [PubMed]
- Grgic, J.; Schoenfeld, B.J.; Orazem, J.; Sabol, F. Effects of resistance training performed to repetition failure or non-failure on muscular strength and hypertrophy: A systematic review and meta-analysis. J. Sport Health Sci. 2022, 11, 202–211. [Google Scholar] [CrossRef]
- Behm, D.G.; Sale, D.G. Intended rather than actual movement velocity determines velocity-specific training response. J. Appl. Physiol. 1993, 74, 359–368. [Google Scholar] [CrossRef]
- Potvin, J.R.; Fuglevand, A.J. A motor unit-based model of muscle fatigue. PLoS Comput. Biol. 2017, 13, e1005581. [Google Scholar] [CrossRef]
- Rodríguez-Rosell, D.; Yáñez-García, J.M.; Mora-Custodio, R.; Torres-Torrelo, J.; Ribas-Serna, J.; González-Badillo, J.J. Role of the effort index in predicting neuromuscular fatigue during resistance exercises. J. Strength Cond. Res. 2020; advance online publication. [Google Scholar] [CrossRef]
- Sánchez-Medina, L.; González-Badillo, J.J. Velocity loss as an indicator of neuromuscular fatigue during resistance training. Med. Sci. Sports Exerc. 2011, 43, 1725–1734. [Google Scholar] [CrossRef]
- Enoka, R.M.; Almuklass, A.M.; Alenazy, M.; Alvarez, E.; Duchateau, J. Distinguishing between fatigue and fatigability in multiple sclerosis. Neurorehabil. Neural Repair 2021, 35, 960–973. [Google Scholar] [CrossRef]
- Enoka, R.M.; Duchateau, J. Translating fatigue to human performance. Med. Sci. Sports Exerc. 2016, 48, 2228–2238. [Google Scholar] [CrossRef]
- Farrow, J.; Steele, J.; Behm, D.G.; Skivington, M.; Fisher, J.P. Lighter-load exercise produces greater acute- and prolonged-fatigue in exercised and non-exercised limbs. Res. Q. Exerc. Sport. 2021, 92, 369–379. [Google Scholar] [CrossRef] [PubMed]
- Stuart, C.; Steele, J.; Gentil, P.; Giessing, J.; Fisher, J.P. Fatigue and perceptual responses of heavier- and lighter-load isolated lumbar extension resistance exercise in males and females. PeerJ 2018, 6, e4523. [Google Scholar] [CrossRef] [PubMed]
- Helms, E.R.; Kwan, K.; Sousa, C.A.; Cronin, J.B.; Storey, A.G.; Zourdos, M.C. Methods for regulating and monitoring resistance training. J. Hum. Kinet. 2020, 74, 23–42. [Google Scholar] [CrossRef]
- Larsen, S.; Kristiansen, E.; Van den Tillaar, R. Effects of subjective and objective autoregulation methods for intensity and volume on enhancing maximal strength during resistance-training interventions: A systematic review. PeerJ 2021, 9, e10663. [Google Scholar] [CrossRef]
- Varela-Olalla, D.; Romero-Caballero, A.; Del Campo-Vecino, J.; Balsalobre-Fernández, C. A cluster set protocol in the half squat exercise reduces mechanical fatigue and lactate concentrations in comparison with a traditional set configuration. Sports 2020, 8, 45. [Google Scholar] [CrossRef]
- Pérez-Castilla, A.; Piepoli, A.; Delgado-García, G.; Garrido-Blanca, G.; García-Ramos, A. Reliability and concurrent validity of seven commercially available devices for the assessment of movement velocity at different intensities during the bench press. J. Strength Cond. Res. 2019, 33, 1258–1265. [Google Scholar] [CrossRef] [PubMed]
- Balsalobre-Fernández, C.; Glaister, M.; Lockey, R.A. The validity and reliability of an iPhone app for measuring vertical jump performance. J. Sports Sci. 2015, 33, 1574–1579. [Google Scholar] [CrossRef]
- Tomczak, M.; Tomczak, E. The need to report effect size estimates revisited. An overview of some recommended measures of effect size. Trends Sport Sci. 2014, 1, 19–25. [Google Scholar]
- García-Ramos, A.; González-Hernández, J.M.; Baños-Pelegrín, E.; Castaño-Zambudio, A.; Capelo-Ramírez, F.; Boullosa, D.; Haff, G.G.; Jiménez-Reyes, P. Mechanical and metabolic responses to traditional and cluster set configurations in the bench press exercise. J. Strength Cond. Res. 2020, 34, 663–670. [Google Scholar] [CrossRef]
- González-Hernández, J.M.; García-Ramos, A.; Castaño-Zambudio, A.; Capelo-Ramírez, F.; Marquez, G.; Boullosa, D.; Jiménez-Reyes, P. Mechanical, metabolic, and perceptual acute responses to different set configurations in full squat. J. Strength Cond. Res. 2020, 34, 1581–1590. [Google Scholar] [CrossRef]
- Mora-Custodio, R.; Rodríguez-Rosell, D.; Yáñez-García, J.M.; Sánchez-Moreno, M.; Pareja-Blanco, F.; González-Badillo, J.J. Effect of different inter-repetition rest intervals across four load intensities on velocity loss and blood lactate concentration during full squat exercise. J. Sports Sci. 2018, 36, 2856–2864. [Google Scholar] [CrossRef] [PubMed]
- Tufano, J.J.; Conlon, J.A.; Nimphius, S.; Brown, L.E.; Seitz, L.B.; Williamson, B.D.; Haff, G.G. Maintenance of velocity and power with cluster sets during high-volume back squats. Int. J. Sports Physiol. Perform. 2016, 11, 885–892. [Google Scholar] [CrossRef] [PubMed]
- Jukic, I.; Ramos, A.G.; Helms, E.R.; McGuigan, M.R.; Tufano, J.J. Acute effects of cluster and rest redistribution set structures on mechanical, metabolic, and perceptual fatigue during and after resistance training: A systematic review and meta-analsis. Sports Med. 2020, 50, 2209–2236. [Google Scholar] [CrossRef] [PubMed]
- Goss-Sampson, M.A.; Van Doorn, J.; Wagenmakers, E.J. Bayesian Inference in JASP: A Guide for Students; JASP: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Kruschke, J.K.; Liddell, T.M. The Bayesian New Statistics: Hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon. Bull. Rev. 2018, 25, 178–206. [Google Scholar] [CrossRef]
- Quintana, D.S.; Williams, D.R. Bayesian alternatives for common null-hypothesis significance tests in psychiatry: A non-technical guide using JASP. BMC Psychiatry 2018, 18, 178. [Google Scholar] [CrossRef]
- Van den Bergh, D.; Wagenmakers, E.-J.; Aust, F. Bayesian repeated-measures analysis of variance: An updated methodology implemented in JASP. Adv. Meth. Pract. Psychol. Sci. 2023, 6. [Google Scholar] [CrossRef]
- Van den Bergh, D.; Van Doorn, J.; Marsman, M.; Draws, T.; Van Kesteren, E.; Derks, K.; Wagenmakers, E. A tutorial on conducting and interpreting a Bayesian ANOVA in JASP. L’Année Psychol. 2020, 120, 73–96. [Google Scholar] [CrossRef]
- Ward, P.; Coutts, A.J.; Pruna, R.; McCall, A. Putting the “I” back in team. Int. J. Sports Physiol. Perform. 2018, 13, 1107–1111. [Google Scholar] [CrossRef]
- Dooley, L.M. Case study research and theory building. Adv. Dev. Hum. Resour. 2002, 4, 335–354. [Google Scholar] [CrossRef]
- Packer, C.D.; Katz, R.B.; Iacopetti, C.L.; Krimmel, J.D.; Singh, M.K. A case suspended in time: The educational value of case reports. Acad. Med. 2017, 92, 152–156. [Google Scholar] [CrossRef]
- Sayre, J.W.; Toklu, H.Z.; Ye, F.; Mazza, J.; Yale, S. Case reports, case series—From clinical practice to evidence-based medicine in graduate medical education. Cureus. 2017, 9, e1546. [Google Scholar] [CrossRef] [PubMed]
- Muñoz de la Cruz, V.; Agudo-Ortega, A.; Sorgente, V.; Turner, A.P.; González-Ravé, J.M. The effectiveness of adjusting resistance training loads through velocity-based techniques in experienced sprinters: A case series study. Front. Physiol. 2023, 14, 1241459. [Google Scholar] [CrossRef]
- Brown, N.; Bubeck, D.; Haeufle, D.F.B.; Weickenmeier, J.; Kuhl, E.; Alt, W.; Schmitt, S. Weekly time course of neuro-muscular adaptation to intensive strength training. Front. Physiol. 2017, 8, 329. [Google Scholar] [CrossRef] [PubMed]
- Iglesias-Soler, E.; Carballeira, E.; Sánchez-Otero, T.; Mayo, X.; Jiménez, A.; Chapman, M.L. Acute effects of distribution of rest between repetitions. Int. J. Sports Med. 2012, 33, 351–358. [Google Scholar] [CrossRef]
- Gorostiaga, E.M.; Navarro-Amézqueta, I.; Calbet, J.A.; Hellsten, Y.; Cusso, R.; Guerrero, M.; Granados, C.; González-Izal, M.; Ibañez, J.; Izquierdo, M. Energy metabolism during repeated sets of leg press exercise leading to failure or not. PLoS ONE 2012, 7, e40621. [Google Scholar] [CrossRef]
- Gorostiaga, E.M.; Navarro-Amézqueta, I.; Cusso, R.; Hellsten, Y.; Calbet, J.A.; Guerrero, M.; Granados, C.; González-Izal, M.; Ibáñez, J.; Izquierdo, M. Anaerobic energy expenditure and mechanical efficiency during exhaustive leg press exercise. PLoS ONE 2010, 5, e13486. [Google Scholar] [CrossRef]
- Zając, A.; Chalimoniuk, M.; Maszczyk, A.; Gołaś, A.; Lngfort, J. Central and peripheral fatigue during resistance exercise—A critical review. J. Hum. Kinet. 2015, 49, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Hureau, T.J.; Broxterman, R.M.; Weavil, J.C.; Lewis, M.T.; Layec, G.; Amann, M. On the role of skeletal muscle acidosis and inorganic phosphates as determinants of central and peripheral fatigue: A 31P-MRS study. J. Physiol. 2022, 600, 3069–3081. [Google Scholar] [CrossRef]
- Siegler, J.C.; Marshall, P. The effect of metabolic alkalosis on central and peripheral mechanisms associated with exercise-induced muscle fatigue in humans. Exp. Physiol. 2015, 100, 519–530. [Google Scholar] [CrossRef]
- Sundberg, C.W.; Hunter, S.K.; Trappe, S.W.; Smith, C.S.; Fitts, R.H. Effects of elevated H+ and Pi on the contractile mechanics of skeletal muscle fibres from young and old men: Implications for muscle fatigue in humans. J. Physiol. 2018, 596, 3993–4015. [Google Scholar] [CrossRef]
- Allen, D.G.; Lamb, G.D.; Westerblad, H. Skeletal muscle fatigue: Cellular mechanisms. Physiol. Rev. 2008, 88, 287–332. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, D.G.; Lamb, G.D.; Stephenson, G.M. Events of the excitation-contraction-relaxation (E-C-R) cycle in fast- and slow-twitch mammalian muscle fibres relevant to muscle fatigue. Acta Physiol. Scand. 1998, 162, 229–245. [Google Scholar] [CrossRef] [PubMed]
- Raastad, T.; Owe, S.G.; Paulsen, G.; Enns, D.; Overgaard, K.; Crameri, R.; Kiil, S.; Belcastro, A.; Bergersen, L.; Hallén, J. Changes in calpain activity, muscle structure, and function after eccentric exercise. Med. Sci. Sports Exerc. 2010, 42, 86–95. [Google Scholar] [CrossRef] [PubMed]
- Hody, S.; Croisier, J.L.; Bury, T.; Rogister, B.; Leprince, P. Eccentric muscle contractions: Risks and benefits. Front. Physiol. 2019, 10, 536. [Google Scholar] [CrossRef]
- Owens, D.J.; Twist, C.; Cobley, J.N.; Howatson, G.; Close, G.L. Exercise-induced muscle damage: What is it, what causes it and what are the nutritional solutions? Eur. J. Sport Sci. 2019, 19, 71–85. [Google Scholar] [CrossRef]
- de Morree, H.M.; Klein, C.; Marcora, S.M. Perception of effort reflects central motor command during movement execution. Psychophysiology 2012, 49, 1242–1253. [Google Scholar] [CrossRef]
- Halperin, I.; Vigotsky, A.D. A Conceptual framework of effort and perception of effort. Preprints 2023. [Google Scholar] [CrossRef]
- Marcora, S. Perception of effort during exercise is independent of afferent feedback from skeletal muscles, heart, and lungs. J. Appl. Physiol. 2009, 106, 2060–2062. [Google Scholar] [CrossRef]
- Lopes, T.R.; Pereira, H.M.; Silva, B.M. Perceived exertion: Revisiting the history and updating the neurophysiology and the practical applications. Int. J. Environ. Res. Public Health 2022, 19, 14439. [Google Scholar] [CrossRef]
- Greenhouse-Tucknott, A.; Wrightson, J.G.; Raynsford, M.; Harrison, N.A.; Dekerle, J. Interactions between perceptions of fatigue, effort, and affect decrease knee extensor endurance performance following upper body motor activity, independent of changes in neuromuscular function. Psychophysiology 2020, 57, e13602. [Google Scholar] [CrossRef]
- Norbury, R.; Smith, S.A.; Burnley, M.; Judge, M.; Mauger, A.R. The effect of elevated muscle pain on neuromuscular fatigue during exercise. Eur. J. Appl. Physiol. 2022, 122, 113–126. [Google Scholar] [CrossRef] [PubMed]
| Variable | RTP 1 | RTP 2 | RTP 3 | RTP 4 | RTP 5 | RTP 6 |
|---|---|---|---|---|---|---|
| Total KG | 2540.5 ± 636.2 2212.5 (1950.0–3230.0) 2,4 | 1172.0 ± 289.3 1187.5 (850.0–1472.5) 1,3,5 | 2562.0 ± 543.9 2400.0 (1980.0–3135.0) 2,4 | 1179.0 ± 278.1 1215.0 (810.0–1440.0) 1,3,5 | 2740.0 ± 778.2 2400.0 (2080.0–3740.0) 2,4,6 | 1248.0 ± 324.2 1282.5 (877.5–1662.5) 5 |
| Total repetitions | 62.40 ± 6.88 65.00 (52.00–68.00) 2,4,6 | 17.20 ± 2.49 18.00 (13.00—19.00) 1,3,5 | 62.40 ± 5.37 66.00. (54.00–66.00) 2,4,6 | 16.80 ± 2.68 18.00 (12.00–18.00) 1,3,5 | 62.40 ± 6.69 64.00 (52.00–68.00) 2,4,6 | 17.20 ± 2.49 18.00 (13.00–19.00) 1,3,5 |
| MPVmean (m/s) | 0.53 ± 0.09 0.56 (0.43–0.62) 2 | 0.25 ± 0.02 0.26 (0.22–0.27) 1,3,5 | 0.76 ± 0.04 0.74 (0.71–0.81) 2,6 | 0.30 ± 0.03 0.29 (0.27–0.34) 5 | 0.80 ± 0.08 0.84 (0.66–0.87) 2,4,6 | 0.27 ± 0.05 0.27 (0.22–0.34) 3,5 |
| MPVbest (m/s) | 0.84 ± 0.11 0.85 (0.72–0.98) 4,6 | 0.40 ± 0.04 0.40 (0.33–0.45) 5 | 0.91 ± 0.04 0.90 (0.87–0.97) 4,6 | 0.39 ± 0.03 0.39 (0.34–0.42) 1,3,5 | 0.91 ± 0.10 0.95 (0.73–0.98) 2,4,6 | 0.38 ± 0.05 0.37 (0.33–0.45) 1,3,5 |
| meanMPVbest (m/s) | 0.77 ± 0.09 0.82 (0.65–0.86) | 0.36 ± 0.03 0.37 (0.31–0.40) 3,5 | 0.87 ± 0.05 0. 85 (0.81–0.94) 2,4,6 | 0.35 ± 0.03 0.36 (0.31–0.39) 3,5 | 0.91 ± 0.10 0.95 (0.73–0.98) 2,4,6 | 0.38 ± 0.05 0.37 (0.33–0.45) 3,5 |
| MPVlast (m/s) | 0.22 ± 0.05 0.22 (0.16–0.30) 5 | 0.13 ± 0.03 0.14 (0.10–0.17) 3,5 | 0.65 ± 0.07 0.63 (0.59–0.77) 2 | 0.22 ± 0.04 0.20 (0.17–0.28) 5 | 0.79 ± 0.11 0.84 (0.67–0.91) 1,2,4,6 | 0.21 ± 0.06 0.22 (0.13–0.27) 5 |
| meanMPVlast (m/s) | 0.22 ± 0.02 0.23 (0.20–0.24) 5 | 0.14 ± 0.02 0.14 (0.11–0.17) 3,5 | 0.68 ± 0.05 0.67 (0.63–0.76) 2 | 0.26 ± 0.04 0.24 (0.23–0.30) | 0.79 ± 0.11 0.84 (0.67–0.91) 1,2,6 | 0.21 ± 0.06 0.22 (0.13–0.27) 5 |
| Fset (N) | 8841.0 ± 2219.3 7830.0 (6644.0–11,385.0) 4,5,6 | 3884.6 ± 959.6 3940.0 (2824.0–4880.0) 6 | 4740.2 ± 1016.6 4477.0 (3645.0–5840.0) 5,6 | 1966.6 ± 463.3 2121.0 (1356.0–2412.0) 1 | 976.0 ± 180.6 910.0 (749.0–1196.0) 1,3 | 717.4 ± 115.7 672.0 (579.0–874.0) 1,2,3 |
| IMPset (N*s) | 7515.0 ± 1924.3 6789.0 (5816.0–10,203.0) 5,6 | 6872.4 ± 1614.7 6871.0 (4595.0–8536.0) 5,6 | 2771.2 ± 547.8 2602.0 (2164.0–3394.0) 5 | 2902.6 ± 721.3 3280.0 (1838.0–3599.0) 5 | 547.8 ± 137.0 506.0 (382.0–730.0) 1,2,3 | 1220.4 ± 329.6 1247.0 (746.0–1672.0) 1,2 |
| Fsession (N) | 26,522.4 ± 6658.3 23,489.0 (19,931.0–34,155.0) | 11,653.8 ± 2878.7 11,821.0 (8471.0–14,640.0) 3,5 | 28,441.2 ± 6098.2 26,865.0 (21,872.0–35,039.0) 2,4,6 | 11,798.2 ± 2780.3 12,124.0 (8135.0–14,470.0) 3 | 30,707.0 ± 8094.0 27,117.0 (23,665.0–40,668.0) 2 | 12,438.4 ± 3221.9 12,767.0 (8712.0–16,614.0) 3 |
| IMPsession (N*s) | 22,544.4 ± 5772.6 20,366.0 (1747.0–30,608.0) 3 | 20,617.2 ± 4843.8 20,613.0 (13,786.0–25,608.0) | 16,627.8 ± 3284.7 15,615.0 (12,987.0–20,362.0) 1 | 17,415.2 ± 4327.9 19,683.0 (11,027.0–21,593.0) | 17,356.2 ± 5781.0 15,198.0 (12,105.0–24,998.0) | 21,084.4 ± 6816.6 22,262.0 (12,712.0–30,138.0) |
| TUTmean (s) | 17.88 ± 3.62 17.56 (13.85–22.14) 4,5,6 | 10.10 ± 1.01 10.71 (8.81–11.04) 5,6 | 6.09 ± 0.45 6.29 (5.44–6.53) 5 | 4.15 ± 0.85 4.51 (2.71–4.87) 1 | 1.11 ± 0.08 1.12 (1.02–1.22) 1,2,3 | 1.69 ± 0.33 1.74 (1.29–2.11) 1,2 |
| TUTtotal (s) | 53.63 ± 10.85 52.69 (41.54–66.42) 2,4,6 | 30.31 ± 3.03 32.12 (26.43–33.13) 1 | 36.55 ± 2.72 37.71 (32.64–39.19) 4 | 24.88 ± 5.09 27.05 (16.27–29.22) 1,3,5 | 34.89 ± 5.59 33.63 (27.69–41.80) 4 | 28.98 ± 6.58 27.53 (21.97–38.04) 1 |
| BP | ||||||
|---|---|---|---|---|---|---|
| Within-Protocol Comparisons | ||||||
| RTP1 | RTP2 | RTP3 | RTP4 | RTP5 | RTP6 | |
| CMJ (cm) Pre–Post1/2 | n.a | n.a | 1.00 [1.00–1.00] | 0.87 [0.34–0.98] | n.a | n.a |
| CMJ (cm) Pre–Post0 | 0.87 [0.34–0.98] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.80 [0.03–0.97] | 1.00 [1.00–1.00] |
| CMJ (cm) Post1/2–Post0 | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.33 [(−0.55)–0.87] | n.a | n.a | |
| CMJ (cm) Pre–Post24 | 0.73 [(−0.03)–0.96] | 0.40 [(−0.57)–0.91] | 0.20 [(−0.65)–0.83] | 0.60 [(−0.36)–0.94] | 0.07 [(−0.72)–0.78] | −1.00 [(−1.00)–(−1.00)] |
| CMJ (cm) Post0–Post24 | −0.80 [(−0.97)–(−0.03)] | −0.33 [(−0.87)–0.55)] | −1.00 [(−1.00)–(−1.00)] | −0.73 [(−0.96)–0.03)] | −0.73 [(−0.96)–0.03] | −1.00 [(−1.00)–(−1.00)] |
| MPV1 (m/s) Pre–Post1/2 | n.a | n.a | 0.47 [(−0.43)–0.90] | −0.87 [(−0.98)–(−0.34)] | n.a | n.a |
| MPV1 (m/s) Pre–Post0 | 0.73 [(−0.03)–0.96] | 0.87 [0.34–0.98] | 0.67 [(−0.40)–0.97] | 0.33 [(−0.55)–0.87] | 1.00 [1.00–1.00] | 0.87 [0.34–0.98] |
| MPV1 (m/s) Post1/2–Post0 | n.a | n.a | −0.20 [(−0.83)–0.65] | −0.60 [(−0.93)–0.27] | n.a | n.a |
| MPV1 (m/s) Pre–Post24 | −0.33 [(−0.87)–0.55] | −0.73 [(−0.96)–0.03] | −0.80 [(−0.98)–(−0.03)] | −0.40 [(−0.88)–0.50] | −0.13 [(−0.80)–0.68] | −0.20 [(−0.86)–0.70] |
| MPV1 (m/s) Post0–Post24 | −0.87 [(−0.98)–(−0.34)] | −0.87 [(−0.98)–(−0.34)] | −1.00 [(−1.00)–(−1.00)] | −1.00 [(−1.00)–(−1.00)] | −1.00 [(−1.00)–(−1.00)] | −0.67 [(−0.94)–0.16] |
| MPV05 (m/s) Pre–Post1/2 | n.a | n.a | −0.33 [(−0.87)–0.55] | 0.20 [(−0.70)–0.86] | n.a | n.a |
| MPV05 (m/s) Pre–Post0 | 0.87 [0.34–0.98] | 0.47 [(−0.43)–0.90] | −0.67 [(−0.95)–0.16] | 0.60 [(−0.36)–0.94] | 1.00 [1.00–1.00] | 0.73 [(−0.03)–0.96] |
| MPV05 (m/s) Post1/2–Post0 | n.a | n.a | 0.00 [(−0.84)–0.84] | 0.80 [0.13–0.97] | n.a | n.a |
| MPV05 (m/s) Pre–Post24 | −0.20 [(−0.83)–0.65] | −0.20 [(−0.83)–0.65] | −0.73 [(−0.96)–0.03] | −1.00 [(−1.00)–(−1.00)] | 0.07 [(−0.72)–0.78] | −0.33 [(−0.87)–0.55] |
| MPV05 (m/s) Post0–Post24 | −0.73 [(−0.96)–0.03] | −1.00 [(−1.00)–(−1.00)] | 0.00 [(−0.84)–0.84] | −1.00 [(−1.00)–(−1.00)] | −1.00 [(−1.00)–(−1.00)] | −1.00 [(−1.00)–(−1.00)] |
| Between-Protocol Comparisons | ||||||
| RTP | CMJpost0 (%) | CMJpost24 (%) | VL1post0 (%) | VL1post24 (%) | VL05post0 (%) | VL05post24 (%) |
| 1 vs. 2 | −0.73 [(−0.96)–0.03] | −0.33 [(−0.87)–0.55] | −0.07 [(−0.78)–0.72] | −0.07 [(−0.78)–0.72] | −0.33 [(−0.87)–0.55] | 0.33 [(−0.55)–0.87] |
| 1 vs. 3 | 0.20 [(−0.65)–0.83] | −0.20 [(−0.83)–0.65] | −0.73 [(−0.96)–0.03] | −0.33 [(−0.87)–0.55] | −0.87 [(−0.98)–0.34] | −0.73 [(−0.96)–0.03] |
| 1 vs. 4 | −0.07 [(−0.78)–0.72] | −0.33 [(−0.87)–0.55] | −0.60 [(−0.93)–0.27] | 0.20 [(−0.65)–0.83] | −0.47 [(−0.90)–0.43] | −0.33 [(−0.87)–0.55] |
| 1 vs. 5 | −0.60 [(−0.93)–0.27] | −0.47 [(−0.90)–0.43] | −0.47 [(−0.90)–0.43] | 0.07 [(−0.72)–0.78] | −0.47 [(−0.90)–0.43] | 0.20 [(−0.65)–0.83] |
| 1 vs. 6 | 0.07 [(−0.72)–0.78] | −1.00 [(−1.00)–(−1.00)] | −0.20 [(−0.83)–0.65] | 0.07 [(−0.72)–0.78] | −0.47 [(−0.90)–0.43] | −0.20 [(−0.83)–0.65] |
| 2 vs. 3 | 1.00 [1.00–1.00] * | −0.33 [(−0.87)–0.55] | −0.60 [(−0.93)–0.27] | 0.20 [(−0.65)–0.83] | −0.47 [(−0.90)–0.43] | −0.33 [(−0.87)–0.55] |
| 2 vs. 4 | 1.00 [1.00–1.00] | 0.00 [(−0.79)–0.79] | −0.33 [(−0.87)–0.55] | 0.07 [(−0.72)–0.78] | 0.07 [(−0.72)–0.78] | −0.33 [(−0.87)–0.55] |
| 2 vs. 5 | 0.40 [(−0.57)–0.91] | −0.20 [(−0.83)–0.65] | −0.33 [(−0.87)–0.55] | 0.07 [(−0.72)–0.78] | 0.20 [(−0.65)–0.83] | 0.33 [(−0.55)–0.87] |
| 2 vs. 6 | 0.87 [0.34–0.98] | −1.00 [(−1.00)–(−1.00)] | −0.07 [(−0.78)–0.72] | 0.20 [(−0.65)–0.83] | −0.07 [(−0.78)–0.72] | 0.07 [(−0.72)–0.78] |
| 3 vs. 4 | −0.47 [(−0.90)–0.43] | 0.33 [(−0.55)–0.87] | 0.07 [(−0.72)–0.78] | 0.47 [(−0.43)–0.90] | 0.60 [(−0.27)–0.93] | −0.07 [(−0.78)–0.72] |
| 3 vs. 5 | −0.87 [(−0.98)–0.34] | 0.07 [(−0.72)–0.78] | 0.60 [(−0.27)–0.93] | 0.20 [(−0.65)–0.83] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] |
| 3 vs. 6 | 0.20 [(−0.65)–0.83] | −0.47 [(−0.90)–0.43] | 0.60 [(−0.27)–0.93] | 0.07 [(−0.72)–0.78] | 0.87 [0.34–0.98] | 0.33 [(−0.55)–0.87] |
| 4 vs. 5 | −0.80 [(−0.97)–0.03] | −0.33 [(−0.87)–0.55] | 0.33 [(−0.55)–0.87] | 0.07 [(−0.72)–0.78] | 0.47 [(−0.43)–0.90] | 0.60 [(−0.27)–0.93] |
| 4 vs. 6 | 0.47 [(−0.43)–0.90] | −1.00 [(−1.00)–(−1.00)] * | 0.33 [(−0.55)–0.87] | 0.07 [(−0.72)–0.78] | −0.20 [(−0.83)–0.65] | 0.60 [(−0.27)–0.93] |
| 5 vs. 6 | 0.60 [(−0.27)–0.93] | −0.87 [(−0.98)–0.34] | 0.33 [(−0.55)–0.87] | 0.33 [(−0.55)–0.87] | −0.33 [(−0.87)–0.55] | 0.00 [(−0.75)–0.75] |
| VLmean | EImean | EImax | La | |
|---|---|---|---|---|
| χ2 | 23.51 | 17.87 | 18.85 | 19.20 |
| p | <0.001 | 0.003 | 0.002 | 0.002 |
| W | 0.94 | 0.72 | 0.75 | 0.77 |
| Conover’s T-Statistic ES [95%CI] | ||||
| 1 vs. 2 | 0.96 | 1.44 | 1.60 | 0.80 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.47 [−0.43–0.90] | |
| 1 vs. 3 | 3.19 * | 1.76 | 1.28 | 1.44 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 1 vs. 4 | 2.55 * | 3.52 * | 3.36 | 2.45 * |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 1 vs. 5 | 3.83 * | 3.12 * | 3.28 * | 3.28 * |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 1 vs. 6 | 1.43 | 2.16 * | 2.48 * | 3.04 * |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 2 vs. 3 | 2.23 * | 0.32 | 0.32 | 0.64 |
| 1.00 [1.00–1.00] | 0.33 [−0.55–0.87] | −0.20 [−0.83–0.65] | 0.60 [−0.27–0.93] | |
| 2 vs. 4 | 1.59 | 2.08 | 1.76 | 1.68 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 2 vs. 5 | 2.87 * | 1.68 | 1.68 | 2.48 * |
| 1.00 [1.00–1.00] | 0.73 [(−0.03)–0.96] | 0.87 [0.34–0.98] | 1.00 [1.00–1.00] | |
| 2 vs. 6 | 0.48 | 0.72 | 0.88 | 2.24 * |
| 0.87 [0.34–0.98] | 0.73 [−0.03–0.96] | 0.87 [0.34–0.98] | 1.00 [1.00–1.00] | |
| 3 vs. 4 | 0.64 | 1.76 | 2.08 | 1.04 |
| −0.60 [−0.93–0.27] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.40 [−0.50–0.88] | |
| 3 vs. 5 | 0.64 | 1.36 | 2.00 | 1.84 |
| 0.87 [0.34–0.98] | 0.87 [0.34–0.98] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |
| 3 vs. 6 | 1.75 | 0.40 | 1.20 | 1.60 |
| −1.00 [−1.00–(−1.00)] | 0.20 [−0.65–0.83] | 0.60 [−0.27–0.93] | 0.60 [−0.27–0.93] | |
| 4 vs. 5 | 1.28 | 0.40 | 0.08 | 0.80 |
| 1.00 [1.00–1.00] | −0.20 [−0.83–0.65] | 0.07 [−0.72–0.78] | 0.40 [−0.57–0.91] | |
| 4 vs. 6 | 1.12 | 1.36 | 0.88 | 0.56 |
| −1.00 [−1.00–(−1.00)] | −1.00 [−1.00–(−1.00)] | −0.60 [−0.93–0.27] | 0.47 [−0.43–0.90] | |
| 5 vs. 6 | 2.39 * | 0.96 | 0.80 | 0.24 |
| −1.00 [−1.00–(−1.00)] | −0.80 [−0.97–(−0.03)] | −0.80 [−0.97–(−0.03)] | −0.07 [−0.78–0.72] | |
| RPEmean | RPEmax | RPDmean | RPDmax | DOMS24 | DOMS48 | FATIGUE24 | FATIGUE48 | |
|---|---|---|---|---|---|---|---|---|
| χ2 | 21.96 | 21.67 | 13.28 | 11.73 | 10.93 | 3.13 | 9.75 | 8.98 |
| p | <0.001 | <0.001 | 0.02 | 0.04 | 0.05 | 0.68 | 0.08 | 0.11 |
| W | 0.88 | 0.87 | 0.53 | 0.47 | 0.44 | 0.13 | 0.39 | 0.36 |
| Conover’s T-Statistic ES [95%CI] | ||||||||
| 1 vs. 2 | 0.00 | 0.00 | 1.53 | 1.47 | 2.16 * | 1.42 | 0.17 | 0.28 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.13 [−0.68–0.80] | 0.00 [−0.84–0.84] | |||
| 1 vs. 3 | 3.18 * | 2.91 * | 2.66 * | 2.45 * | 2.66 * | 1.16 | 2.34 * | 2.34 * |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.70 [−0.20–0.96] | 0.73 [−0.03–0.96] | 1.00 [1.00–1.00] | |||
| 1 vs. 4 | 2.04 * | 1.91 * | 3.14 * | 2.61 * | 2.50 * | 0.80 | 1.42 | 1.78 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.00 [−0.84–0.84] | 1.00 [1.00–1.00] | 0.40 [−0.50–0.88] | |||
| 1 vs. 5 | 3.02 * | 3.24 * | 2.09 * | 2.69 * | 2.41 * | 1.42 | 1.84 | 1.22 |
| 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | 0.67 [−0.16–0.94] | 0.20 [−0.70–0.86] | |||
| 1 vs. 6 | 1.55 | 1.91 | 1.69 | 2.04 | 1.75 | 10.7 | 0.75 | 0.56 |
| 0.87 [0.34–0.98] | 0.87 [0.34–0.98] | 1.00 [1.00–1.00] | 0.33 [−0.55–0.87] | 0.60 [−0.36–0.94] | 0.00 [−0.84–0.84] | |||
| 2 vs. 3 | 3.18 * | 2.91 * | 1.13 | 0.98 | 0.50 | 0.27 | 2.17 * | 2.06 |
| 0.60 [−0.27–0.93] | 0.40 [−0.50–0.88] | 1.00 [1.00–1.00] | 0.00 [−0.84–0.84] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |||
| 2 vs. 4 | 2.04 | 1.91 | 1.61 | 1.14 | 0.33 | 0.62 | 1.25 | 1.50 |
| 1.00 [1.00–1.00] | 0.80 [0.03–0.97] | 0.20 [−0.70–0.86] | −0.40 [−0.91–0.57] | 1.00 [1.00–1.00] | 1.00 [1.00–1.00] | |||
| 2 vs. 5 | 3.02 * | 3.24 * | 0.56 | 1.22 | 0.25 | 0.00 | 1.67 | 0.94 |
| 0.40 [−0.50–0.88] | 0.67 [−0.16–0.94] | −0.20 [−0.83–0.65] | 0.00 [−0.90–0.90] | 1.00 [1.00–1.00] | 0.50 [−0.59–0.94] | |||
| 2 vs. 6 | 1.55 | 1.91 | 0.16 | 0.57 | 0.42 | 0.36 | 0.58 | 0.28 |
| 0.27 [−0.60–0.84] | 0.40 [−0.57–0.91] | −0.40 [−0.88–0.50] | −0.40 [−0.91–0.57] | 0.20 [−0.65–0.83] | 1.00 [1.00–1.00] | |||
| 3 vs. 4 | 1.14 | 1.00 | 0.48 | 0.16 | 0.17 | 0.36 | 0.92 | 0.56 |
| −1.00 [−1.00–(−1.00)] | −0.87 [−0.98–(−0.34)] | 0.40 [−0.50–0.88] | 0.27 [−0.60–0.85] | −0.33 [−0.87–0.55] | −0.33 [−0.87–0.55] | −0.33 [−0.87–0.55] | −0.50 [−0.94–0.59] | |
| 3 vs. 5 | 0.16 | 0.33 | 0.56 | 0.25 | 0.25 | 0.27 | 0.50 | 1.12 |
| −0.20 [−0.83–0.65] | 0.30 [−0.64–0.88] | −0.20 [−0.83–0.65] | 0.13 [−0.68–0.80] | −0.40 [−0.91–0.57] | 0.00 [−0.80–0.80] | −1.00 [−1.00–(−1.00)] | −0.50 [−0.94–0.59] | |
| 3 vs. 6 | 1.63 | 1.00 | 0.97 | 0.41 | 0.92 | 0.09 | 1.59 | 1.78 |
| −1.00 [−1.00–(−1.00)] | −1.00 [−1.00–(−1.00)] | −0.33 [−0.87–0.55] | −0.07 [−0.78–0.72] | −0.47 [−0.90–0.43] | −0.10 [−0.83–0.75] | −0.80 [−0.97–(−0.03)] | −1.00 [−1.00–(−1.00)] | |
| 4 vs. 5 | 0.98 | 1.33 | 1.05 | 0.08 | 0.08 | 0.62 | 0.42 | 0.56 |
| 0.33 [−0.55–0.87] | 1.00 [1.00–1.00] | −0.60 [−0.93–0.27] | 0.00 [−0.84–0.84] | −0.67 [−0.97–0.40] | 0.33 [−0.70–0.92] | 0.20 [−0.70–0.86] | −0.50 [−0.94–0.59] | |
| 4 vs. 6 | 0.49 | 0.00 | 1.45 | 0.57 | 0.75 | 0.27 | 0.67 | 1.22 |
| −0.73 [−0.96–0.03] | 0.00 [−0.79–0.79] | −1.00 [−1.00–(−1.00)] | −0.30 [−0.88–0.64] | −0.60 [−0.94–0.36] | −0.13 [−0.80–0.68] | −0.67 [−0.94–0.16] | −1.00 [−1.00–(−1.00)] | |
| 5 vs. 6 | 1.47 | 1.33 | 0.40 | 0.65 | 0.67 | 0.36 | 1.09 | 0.65 |
| −1.00 [−1.00–(−1.00)] | −1.00 [−1.00–(−1.00)] | −0.33 [−0.87–0.55] | −0.40 [−0.91–0.57] | −0.67 [−0.97–0.40] | −0.50 [−0.94–0.59] | −0.80 [−0.97–(−0.03)] | −0.17 [−0.88–0.78] | |
| Variable | 1 vs. 2 | 1 vs. 3 | 1 vs. 4 | 1 vs. 5 | 1 vs. 6 | 2 vs. 3 | 2 vs. 4 | 2 vs. 5 | 2 vs. 6 | 3 vs. 4 | 3 vs. 5 | 3 vs. 6 | 4 vs. 5 | 4 vs. 6 | 5 vs. 6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VL | Post | 0.96 | 61.94 | 15.17 | 43.52 | 0.85 | 6.67 | 7.21 | 9.60 | 0.42 | 0.20 | 0.49 | 0.54 | 0.67 | 0.52 | 1.98 |
| BF10 | 3.68 | 238.29 | 58.38 | 167.41 | 3.28 | 25.67 | 27.73 | 36.92 | 1.61 | 0.76 | 1.89 | 2.07 | 2.56 | 1.99 | 7.61 | |
| %Er | <0.001 | <0.001 | <0.001 | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.01 | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |
| EI | Post | 8.76 | 9.18 | 18.73 | 30.88 | 13.68 | 0.14 | 17.41 | 0.35 | 0.23 | 1.59 | 0.37 | 0.11 | 0.13 | 0.68 | 0.23 |
| BF10 | 33.37 | 35.33 | 72.07 | 118.79 | 52.62 | 0.55 | 66.99 | 1.35 | 0.90 | 6.10 | 1.44 | 0.42 | 0.51 | 2.61 | 0.89 | |
| %Er | 0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.007 | <0.001 | 0.02 | 0.01 | <0.001 | 0.03 | 0.002 | 0.005 | <0.001 | 0.01 | |
| La | Post | 0.14 | 1.29 | 1.20 | 19.19 | 3.71 | 0.18 | 1.77 | 0.58 | 1.41 | 0.12 | 0.91 | 0.20 | 0.13 | 0.14 | 0.12 |
| BF10 | 0.54 | 4.97 | 4.63 | 73.84 | 14.29 | 0.68 | 6.80 | 2.24 | 5.42 | 0.46 | 3.50 | 0.77 | 0.51 | 0.53 | 0.46 | |
| %Er | 0.007 | 0.002 | 0.003 | 0.001 | <0.001 | 0.01 | <0.001 | <0.001 | 0.002 | 0.003 | <0.001 | 0.01 | 0.005 | 0.006 | 0.003 | |
| CMJ post0 | Post | 0.27 | 0.11 | 0.11 | 0.22 | 0.11 | 0.77 | 0.56 | 0.13 | 0.67 | 0.12 | 0.35 | 0.11 | 0.25 | 0.14 | 0.23 |
| BF10 | 1.04 | 0.40 | 0.44 | 0.86 | 0.44 | 2.97 | 2.13 | 0.51 | 2.52 | 0.46 | 1.34 | 0.42 | 0.98 | 0.53 | 0.87 | |
| %Er | 0.02 | 0.001 | 0.002 | 0.01 | 0.002 | <0.001 | <0.001 | 0.005 | <0.001 | 0.003 | 0.02 | 0.002 | 0.02 | 0.006 | 0.01 | |
| VL1 | Post | 0.12 | 0.28 | 0.26 | 0.16 | 0.12 | 0.20 | 0.14 | 0.12 | 0.10 | 0.11 | 0.21 | 0.20 | 0.12 | 0.14 | 0.12 |
| BF10 | 0.47 | 1.07 | 1.00 | 0.63 | 0.45 | 0.77 | 0.56 | 0.47 | 0.40 | 0.41 | 0.81 | 0.75 | 0.46 | 0.54 | 0.46 | |
| %Er | 0.004 | 0.02 | 0.02 | 0.009 | 0.003 | 0.01 | 0.007 | 0.003 | 0.001 | 0.002 | 0.01 | 0.01 | 0.003 | 0.007 | 0.003 | |
| VL0.5 | Post | 0.13 | 0.49 | 0.18 | 0.14 | 0.14 | 0.18 | 0.10 | 0.12 | 0.10 | 0.20 | 2.01 | 0.40 | 0.13 | 0.10 | 0.14 |
| BF10 | 0.51 | 1.89 | 0.69 | 0.55 | 0.55 | 0.69 | 0.40 | 0.45 | 0.40 | 0.77 | 7.72 | 1.55 | 0.48 | 0.40 | 0.54 | |
| %Er | 0.005 | 0.001 | 0.01 | 0.007 | 0.007 | 0.01 | 0.001 | 0.003 | 0.001 | 0.01 | <0.001 | <0.001 | 0.004 | 0.001 | 0.006 | |
| RPE | Post | n.a | 26.07 | 10.63 | 2.23 | 0.82 | 26.07 | 10.63 | 2.23 | 0.82 | 0.40 | 0.16 | 1.84 | 0.12 | 0.23 | 0.33 |
| BF10 | n.a | 100.29 | 40.90 | 8.58 | 3.16 | 100.29 | 40.90 | 8.58 | 3.16 | 1.52 | 0.63 | 7.08 | 0.44 | 0.88 | 1.29 | |
| %Er | n.a | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.03 | 0.009 | 0.005 | 0.003 | 0.01 | 0.02 | |
| RPD | Post | 2.32 | 1.59 | 2.25 | 0.61 | 0.35 | 0.21 | 0.53 | 0.14 | 0.11 | 0.13 | 0.12 | 0.13 | 0.25 | 0.22 | 0.12 |
| BF10 | 8.91 | 6.11 | 8.65 | 2.33 | 1.35 | 0.80 | 2.04 | 0.55 | 0.41 | 0.51 | 0.44 | 0.51 | 0.98 | 0.85 | 0.46 | |
| %Er | <0.001 | <0.001 | <0.001 | <0.001 | 0.02 | 0.01 | <0.001 | 0.007 | 0.002 | 0.005 | 0.003 | 0.005 | 0.02 | 0.01 | 0.003 | |
| DOMS post24 | Post | 1.50 | 1.77 | 5.02 | 3.02 | 0.38 | 0.24 | 0.11 | 0.12 | 0.14 | 0.12 | 0.14 | 0.17 | 0.15 | 0.17 | 0.14 |
| BF10 | 5.76 | 6.82 | 19.33 | 11.60 | 1.48 | 0.92 | 0.41 | 0.45 | 0.53 | 0.45 | 0.55 | 0.66 | 0.58 | 0.64 | 0.55 | |
| %Er | 0.01 | <0.001 | 0.004 | 0.001 | 0.03 | 0.01 | 0.002 | 0.003 | 0.006 | 0.003 | 0.007 | 0.01 | 0.008 | 0.01 | 0.007 | |
| FATIGE post24 | Post | 0.10 | 0.27 | 0.56 | 0.24 | 0.17 | 1.22 | 0.21 | 0.63 | 0.12 | 0.12 | 0.22 | 0.24 | 0.11 | 0.24 | 0.22 |
| BF10 | 0.40 | 1.02 | 2.17 | 0.92 | 0.65 | 4.70 | 0.81 | 2.41 | 0.45 | 0.47 | 0.83 | 0.92 | 0.40 | 0.92 | 0.83 | |
| %Er | 0.001 | 0.02 | <0.001 | 0.01 | 0.01 | 0.003 | 0.01 | <0.001 | 0.003 | 0.004 | 0.01 | 0.01 | 0.001 | 0.01 | 0.01 | |
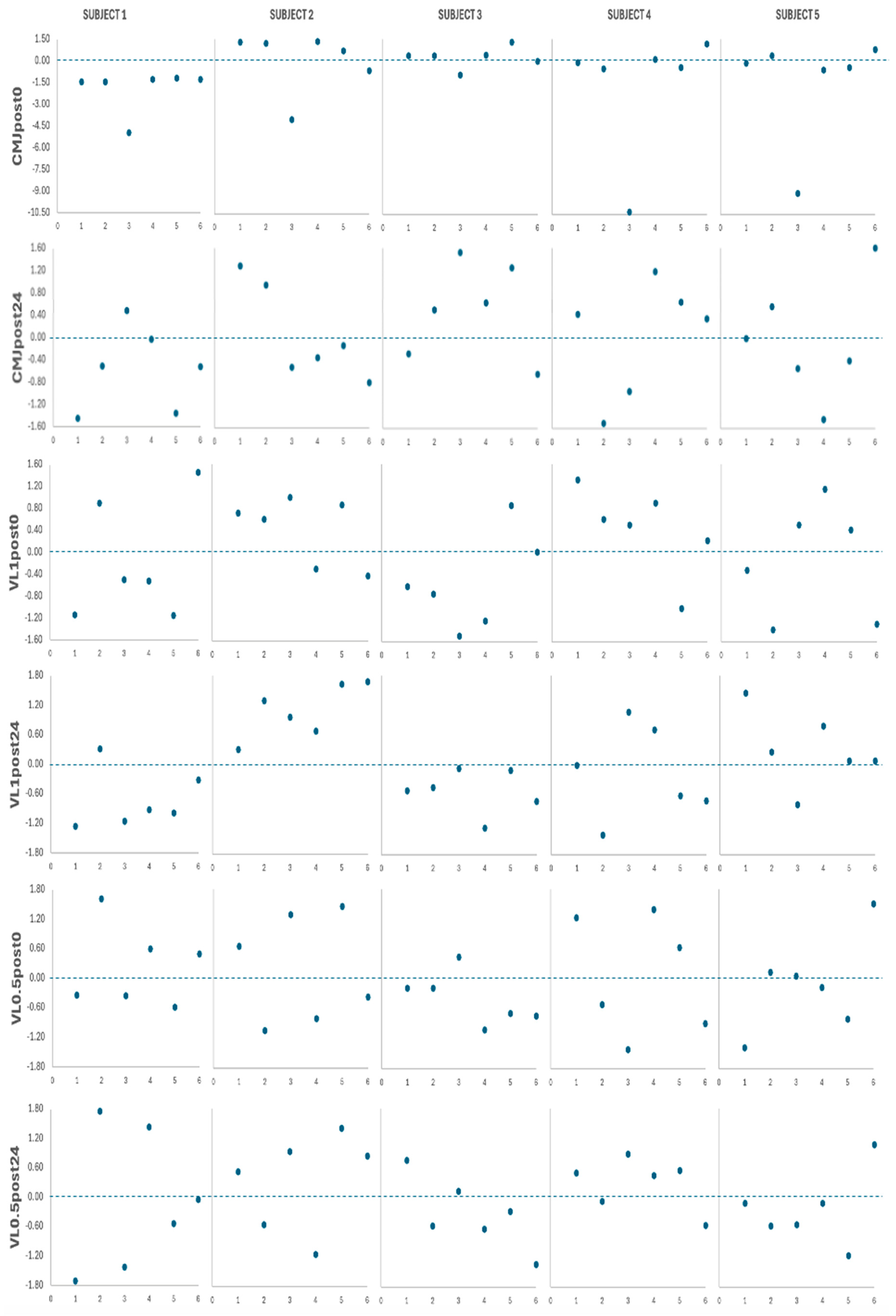
| Case | Report Summary |
|---|---|
| Subject 1 | Lower overall VL and EI, especially after TF protocols Lower overall La responses Greater overall non-local fatigue in CMJ test Greater overall impairments against 1 m/s load at post0 and post24 Greater overall impairments against 0.5 m/s load at post24 Higher overall DOMS and perceived-fatigue perceptual responses |
| Subject 2 | Greater VL and EI with high loads after TF and cluster protocols Higher La responses after high-load protocols Lower overall impairments against 1 m/s load at post0 and post24 Greater impairments against 0.5 m/s load with high loads respective to low loads |
| Subject 3 | Highest overall VL and EI Highest overall La responses Greater overall impairments against 1 m/s load at post0 (except for cluster protocols) and post24 Greater overall impairments against 0.5 m/s load at post0 and post24 Highest overall RPE and RPD responses Higher overall DOMS and perceived-fatigue perceptual responses |
| Subject 4 | Lower VL and EI with high loads Lower La responses with high loads Lower overall impairments against 1 m/s load at post0 Lower overall impairments against 0.5 m/s load at post24 Lowest overall RPE and RPD responses Lower overall DOMS and perceived-fatigue responses |
| Subject 5 | Greater VL and EI with cluster respective to straight set protocols Lower overall La responses Lower overall RPD responses Lower overall DOMS and perceived-fatigue responses |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varela-Olalla, D.; Del Campo-Vecino, J.; Balsalobre-Fernández, C. Greater Neuromuscular and Perceptual Fatigue after Low versus High Loads in the Bench Press: A Preliminary Study Applying Frequentist and Bayesian Group Analyses with Subject-by-Subject Case Series Reports. J. Funct. Morphol. Kinesiol. 2024, 9, 186. https://doi.org/10.3390/jfmk9040186
Varela-Olalla D, Del Campo-Vecino J, Balsalobre-Fernández C. Greater Neuromuscular and Perceptual Fatigue after Low versus High Loads in the Bench Press: A Preliminary Study Applying Frequentist and Bayesian Group Analyses with Subject-by-Subject Case Series Reports. Journal of Functional Morphology and Kinesiology. 2024; 9(4):186. https://doi.org/10.3390/jfmk9040186
Chicago/Turabian StyleVarela-Olalla, Daniel, Juan Del Campo-Vecino, and Carlos Balsalobre-Fernández. 2024. "Greater Neuromuscular and Perceptual Fatigue after Low versus High Loads in the Bench Press: A Preliminary Study Applying Frequentist and Bayesian Group Analyses with Subject-by-Subject Case Series Reports" Journal of Functional Morphology and Kinesiology 9, no. 4: 186. https://doi.org/10.3390/jfmk9040186
APA StyleVarela-Olalla, D., Del Campo-Vecino, J., & Balsalobre-Fernández, C. (2024). Greater Neuromuscular and Perceptual Fatigue after Low versus High Loads in the Bench Press: A Preliminary Study Applying Frequentist and Bayesian Group Analyses with Subject-by-Subject Case Series Reports. Journal of Functional Morphology and Kinesiology, 9(4), 186. https://doi.org/10.3390/jfmk9040186







