The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
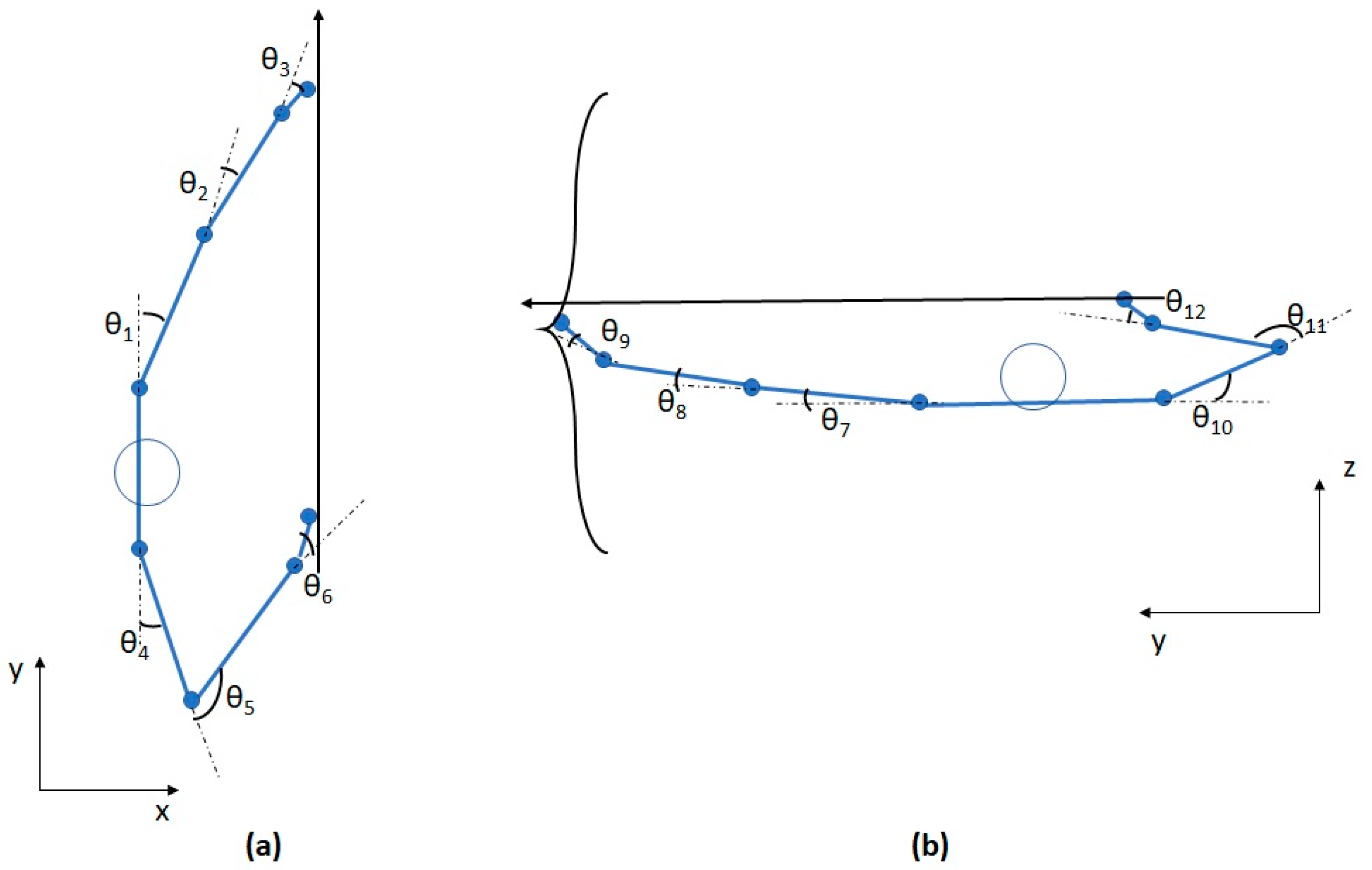
2.2. Task and Measurements
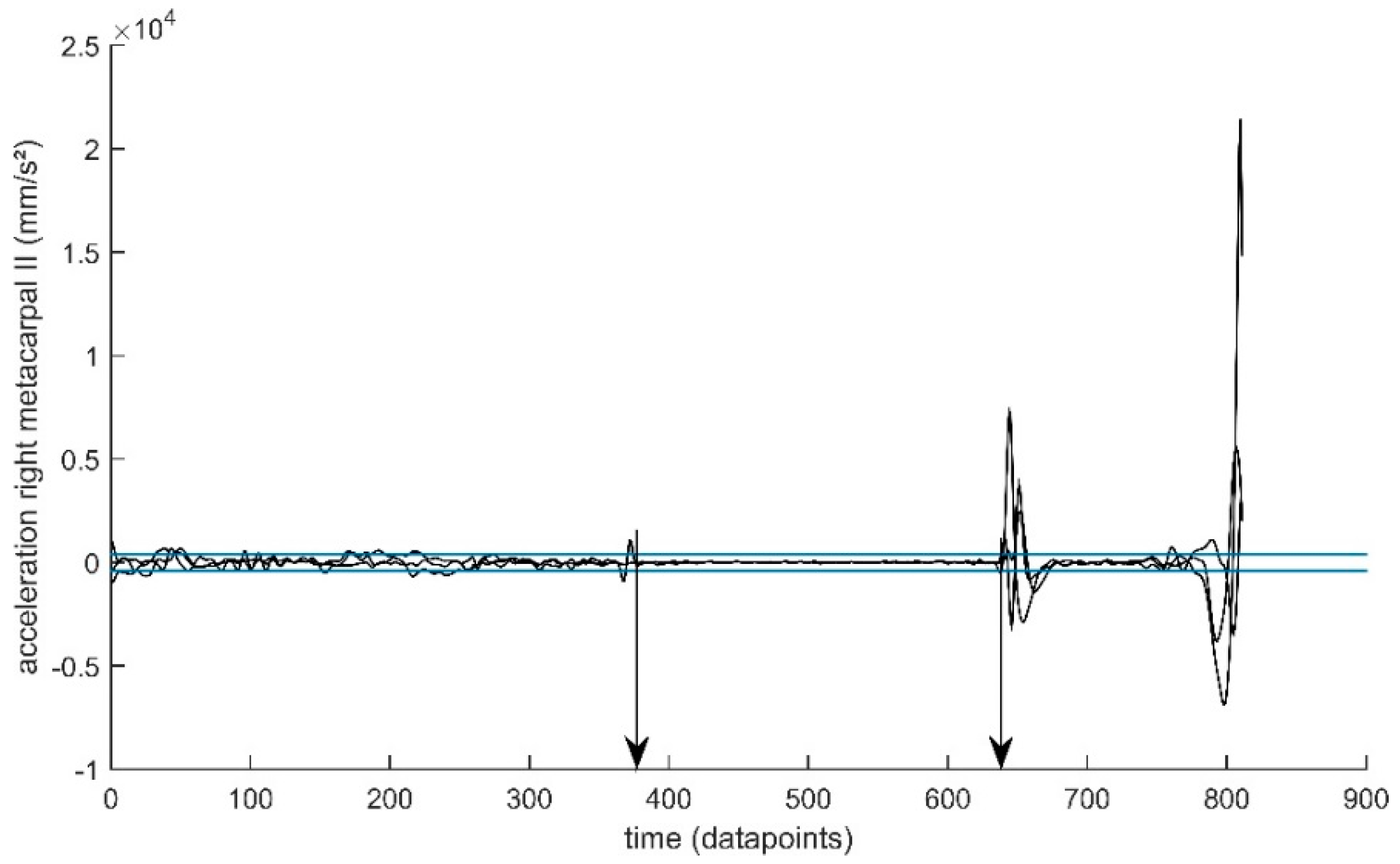
2.3. Data Pre-Processing
2.4. Uncontrolled Manifold (UCM) Analysis
2.5. Statistical Analysis
3. Results
3.1. Shooting Accuracy
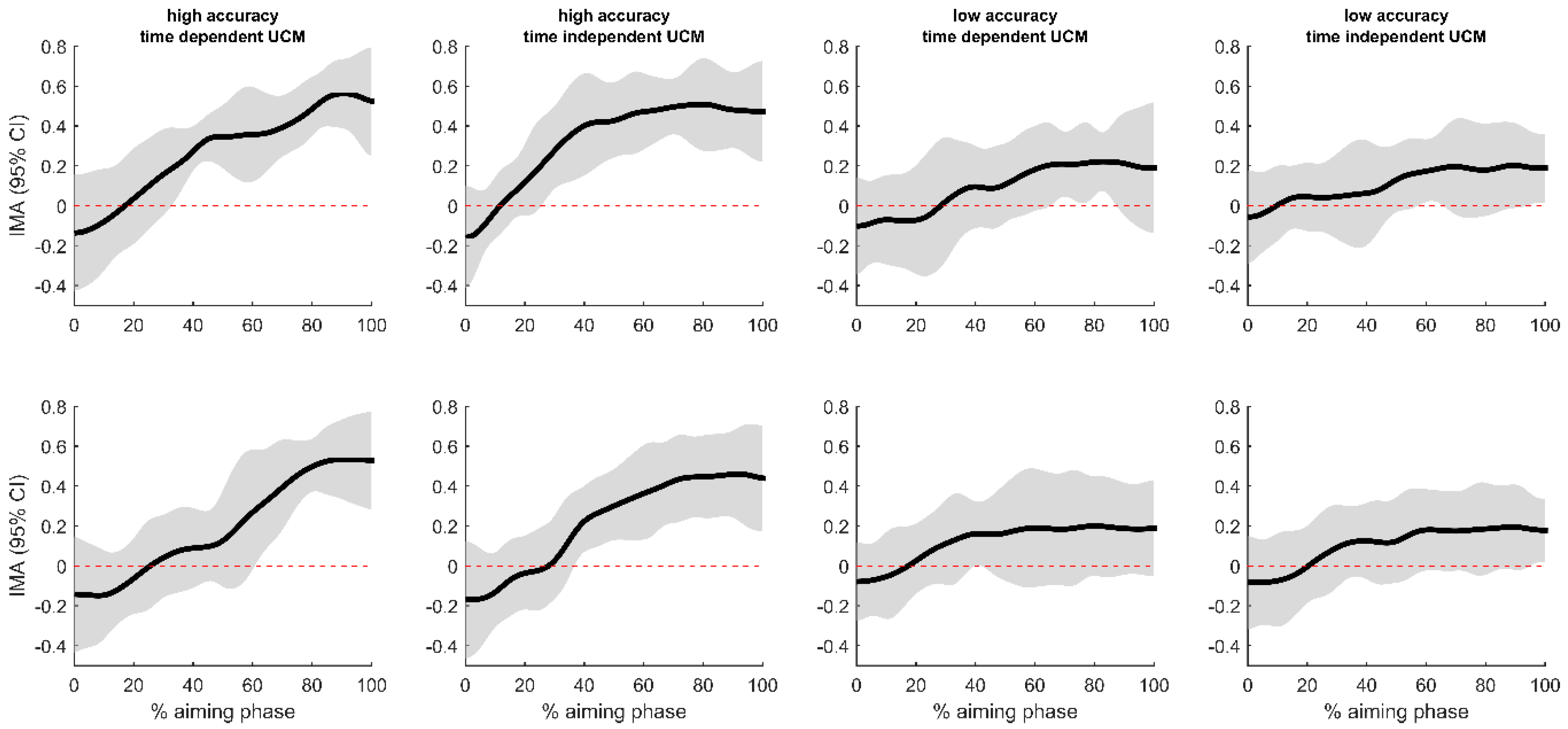
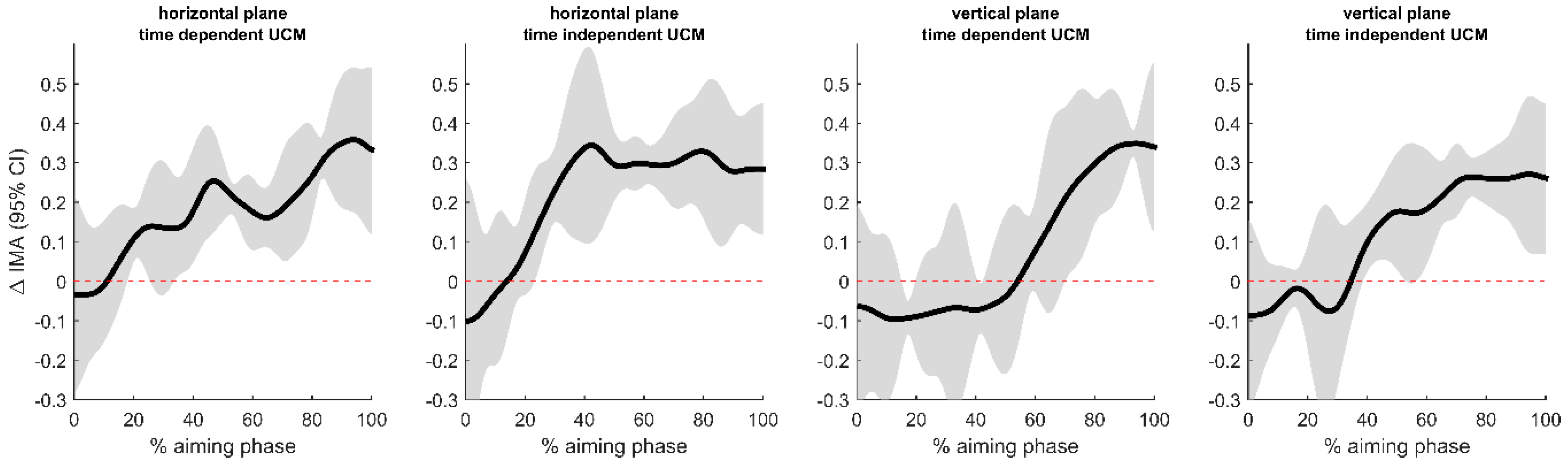
3.2. Uncontrolled Manifold Analysis
4. Discussion
4.1. Postural Control and Accuracy
4.2. On the Nature of Stabilizing Kinematic Synergies in Archery
4.3. Study Limitations and Further Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ertan, H.; Soylu, A.R.; Korkusuz, F. Quantification the relationship between FITA scores and EMG skill indexes in archery. J. Electromyogr. Kinesiol. 2005, 15, 222–227. [Google Scholar] [CrossRef] [PubMed]
- Ertan, H. Muscular activation patterns of the bow arm in recurve archery. J. Sci. Med. Sport 2009, 12, 357–360. [Google Scholar] [CrossRef] [PubMed]
- Soylu, A.R.; Ertan, H.; Korkusuz, F. Archery performance level and repeatability of event-related EMG. Hum. Mov. Sci. 2006, 25, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Ertan, H.; Kentel, B.; Tümer, S.T.; Korkusuz, F. Activation patterns in forearm muscles during archery shooting. Hum. Mov. Sci. 2003, 22, 37–45. [Google Scholar] [CrossRef]
- Keast, D.; Elliott, B. Fine body movements and the cardiac cycle in archery. J. Sports Sci. 1990, 8, 203–213. [Google Scholar] [CrossRef] [PubMed]
- Callaway, A.J.; Wiedlack, J.; Heller, M. Identification of temporal factors related to shot performance for indoor recurve archery. J. Sport Sci. 2016. [Google Scholar] [CrossRef] [PubMed]
- Nabavinik, M.; Abaszadeh, A.; Mehranmanesh, M.; Rosenbaum, D.A. Especial skills in experienced archers. J. Mot. Behav. 2018, 50, 249–253. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.N.; Azhar, A.H. Postural sway and shooting accuracy of skilled recurve archers. Mov. Health Exerc. 2012, 1, 49–60. [Google Scholar] [CrossRef]
- Spratford, W.; Campbell, R. Postural stability, clicker reaction time and bow draw force predict performance in elite recurve archery. Eur. J. Sport Sci. 2017, 17, 539–545. [Google Scholar] [CrossRef] [PubMed]
- Tinazci, C. Shooting dynamics in archery: A multidimensional analysis from drawing to releasing in male archers. Procedia Eng. 2011, 13, 290–296. [Google Scholar] [CrossRef]
- Stuart, J.; Atha, J. Postural consistency in skilled archers. J. Sports Sci. 1990, 8, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Scholz, J.P.; Schöner, G. The uncontrolled manifold concept: Identifying control variables for a functional task. Exp. Brain Res. 1999, 126, 289–306. [Google Scholar] [CrossRef] [PubMed]
- Latash, M.L. Motor synergies and the equilibrium-point hypothesis. Mot. Control 2010, 14, 294–322. [Google Scholar] [CrossRef]
- Feldman, A.G.; Levin, M.F. The Equilibrium-Point Hypothesis—Past, Present and Future. In Progress in Motor Control; Sternad, D., Ed.; Springer: Berlin, Germany, 2016; pp. 699–725. ISBN 978-3-319-47312-3. [Google Scholar]
- Feldman, A.G. Space and time in the context of equilibrium-point theory. Wiley Interdiscip. Rev. Cogn. Sci. 2011, 2, 287–304. [Google Scholar] [CrossRef] [PubMed]
- Latash, M.L. Abundant Degrees of Freedom Are Not a Problem. Kinesiol. Rev. 2018, 7. [Google Scholar] [CrossRef]
- Latash, M.L.; Scholz, J.P.; Schöner, G. Towards a new theory of motor synergies. Mot. Control 2007, 11, 276–308. [Google Scholar] [CrossRef]
- Scholz, J.P.; Schoner, G.; Latash, M.L. Identifying the control structure of multijoint coordination during pistol shooting. Exp. Brain Res. 2000, 135, 382–404. [Google Scholar] [CrossRef] [PubMed]
- Balasubramaniam, R.; Riley, M.; Turvey, M.T. Specificity of postural sway to the demands of a precision task. Gait Posture 2000, 11, 12–24. [Google Scholar] [CrossRef]
- Yen, J.T.; Chang, Y.-H. Rate-dependent control strategies stabilize limb forces during human locomotion. J. R. Soc. Interface 2010, 7, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Y.; Scholz, J.P. The effect of workspace on the use of motor abundance. Mot. Control 2005, 9, 75–100. [Google Scholar] [CrossRef]
- Pataky, T.C. Generalized n-dimensional biomechanical field analysis using statistical parametric mapping. J. Biomech. 2010, 43, 1976–1982. [Google Scholar] [CrossRef] [PubMed]
- Pataky, T.C. One-dimensional statistical parametric mapping in Python. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Latash, M.L. Stages in learning motor synergies: A view based on the equilibrium-point hypothesis. Hum. Mov. Sci. 2010, 29, 642–654. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Kim, Y.-T.; Song, H.-J.; Lee, H.J.; Lee, J.; Jung, T.-D.; Lee, G.; Kwon, E.; Kim, J.G.; Chang, Y. Stronger activation and deactivation in archery experts for differential cognitive strategy in visuospatial working memory processing. Behav. Brain Res. 2012, 229, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, H.M.; Kim, W.J.; Park, H.J.; Kim, S.W.; Moon, D.H.; Woo, M.; Tennant, L.K. Neural correlates of pre-performance routines in expert and novice archers. Neurosci. Lett. 2008, 445, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Chang, Y.; Kim, J.; Ryu, K.; Lee, E.; Woo, M.; Janelle, C.M. An fMRI study of differences in brain activity among elite, expert and novice archers at the moment of optimal timing. Cogn. Behav. Neurol. 2014, 27, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-H.; Latash, M.L. The effects of practice on coordination. Exerc. Sport Sci. Rev. 2014, 42, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Schöllhorn, W.I.; Beckmann, H.; Davids, K. Exploiting system fluctuations. Differential training in physical prevention and rehabilitation programs for health and exercise. Med. Kaunas 2010, 46, 365–373. [Google Scholar] [CrossRef]
| Score 6 | Score 7 | Score 8 | Score 9 | Score 10 | Mean ± SD | Total Score | |
|---|---|---|---|---|---|---|---|
| S1 | 2 | 6 | 6 | 66 | 10 | 8.84 ± 0.79 | 796 |
| S2 | 0 | 5 | 17 | 65 | 3 | 8.73 ± 0.61 | 786 |
| S3 | 0 | 3 | 9 | 72 | 6 | 8.90 ± 0.54 | 801 |
| S4 | 0 | 0 | 10 | 75 | 5 | 8.94 ± 0.41 | 805 |
| S5 | 1 | 7 | 39 | 30 | 13 | 8.52 ± 0.88 | 767 |
| S6 | 1 | 14 | 45 | 24 | 6 | 8.22 ± 0.83 | 740 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrien, B.; Witterzeel, E.; Baeyens, J.-P. The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy. J. Funct. Morphol. Kinesiol. 2018, 3, 48. https://doi.org/10.3390/jfmk3030048
Serrien B, Witterzeel E, Baeyens J-P. The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy. Journal of Functional Morphology and Kinesiology. 2018; 3(3):48. https://doi.org/10.3390/jfmk3030048
Chicago/Turabian StyleSerrien, Ben, Elout Witterzeel, and Jean-Pierre Baeyens. 2018. "The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy" Journal of Functional Morphology and Kinesiology 3, no. 3: 48. https://doi.org/10.3390/jfmk3030048
APA StyleSerrien, B., Witterzeel, E., & Baeyens, J.-P. (2018). The Uncontrolled Manifold Concept Reveals That the Structure of Postural Control in Recurve Archery Shooting Is Related to Accuracy. Journal of Functional Morphology and Kinesiology, 3(3), 48. https://doi.org/10.3390/jfmk3030048





