Review: Deep Learning-Based Survival Analysis of Omics and Clinicopathological Data
Abstract
1. Introduction
2. The Cox Model
3. Rationale behind Survival Algorithms with an NN Component
- (I)
- Shattering benchmarks with neural networks seems to be doable due to the following considerations:
- (a)
- (b)
- CoxPH relies on parametric assumptions that do not always hold [15].
- (c)
- (II)
- (III)
- To ensure a wide applicability under all sorts of restrictions and special conditions as in the statistical survival analysis, the following hold:
- (IV)
- Provide interpretability, which is a must in biomedical research, on a modest scale to integrate the a posteriori analysis specific to bioinformatics (such as GSEA, heatmaps, and so on) [11]. More importantly, there is a body of research aiming at the creation of principally new explanatory frameworks such as revealing latent explanatory features to uncover higher-order biological themes [13,14], and benefiting from the pathway models in terms of the reproducibility of biomarkers [18], etc.
- (V)
4. Examples of Deep Survival Architectures
- Redrawn the architectures in a graphically uniform way;
- Excluded dubious conclusions (e.g., when a published comment exists about low-data quality;
- When comparing the performance metrics, we kept practically meaningful differences only, e.g., C-index of 0.62 is as good as 0.615;
- Highlighted the parts of the algorithms in color that represent a trait transferable between architectures (as detailed in Section 5).
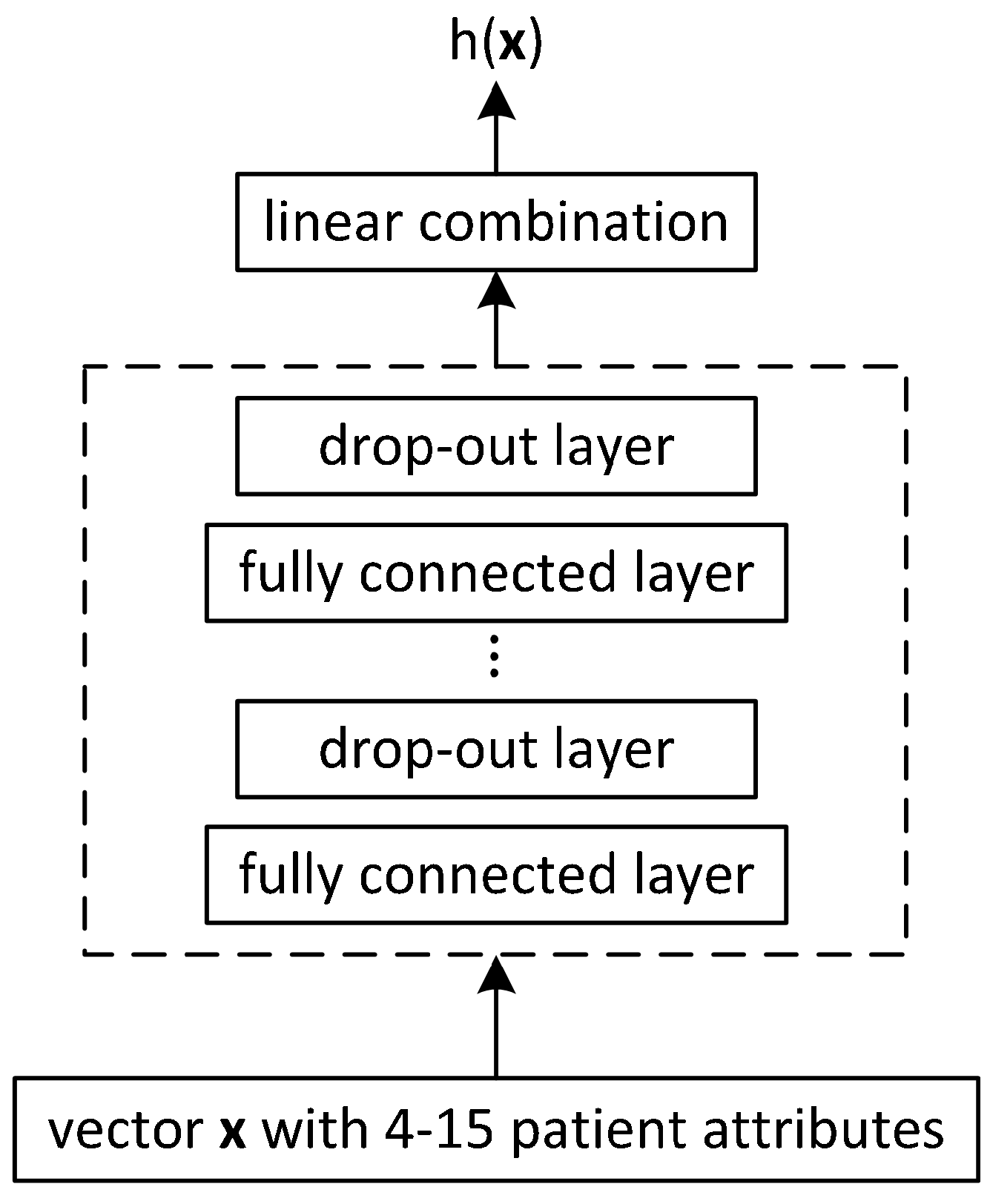
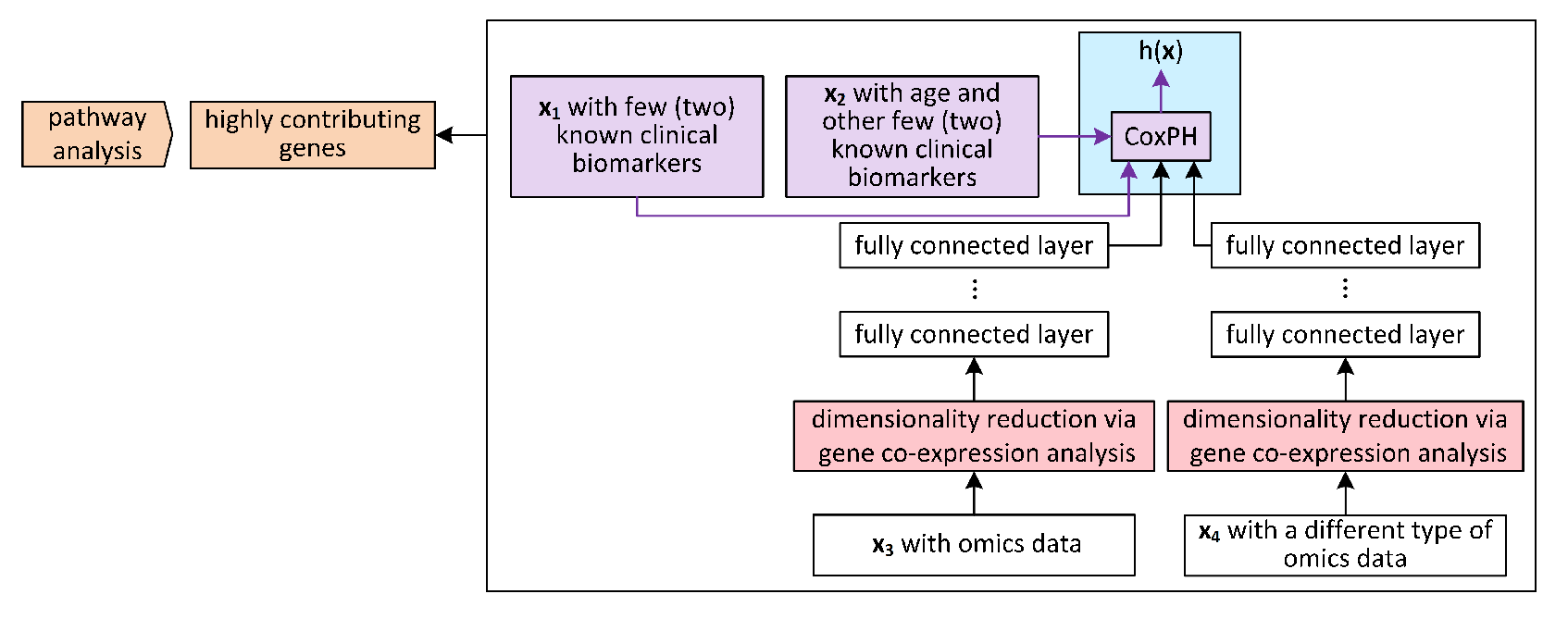
4.1. Architectures for Problems with Few Clinicopathological Variables Tested on Large Datasets
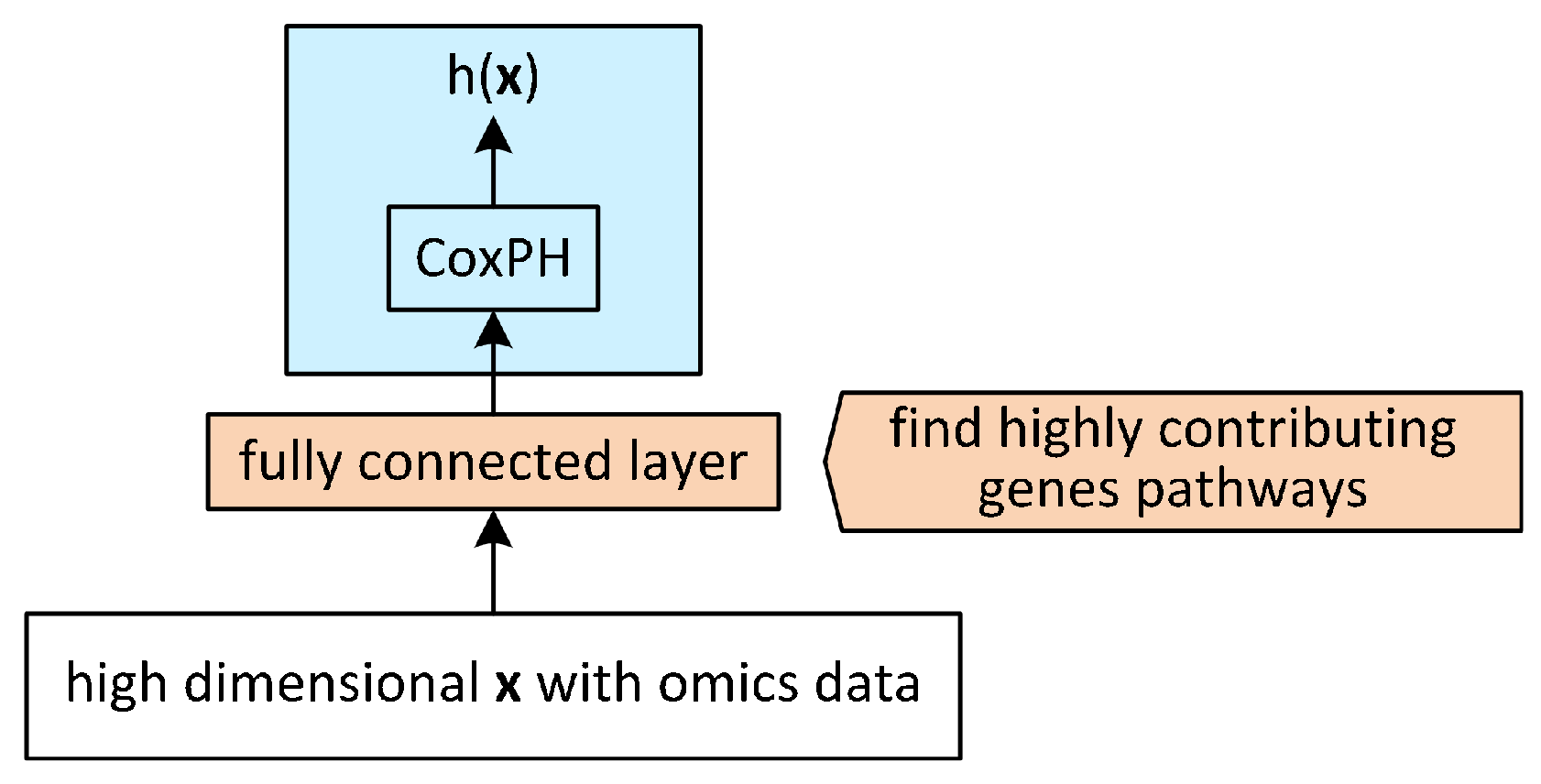
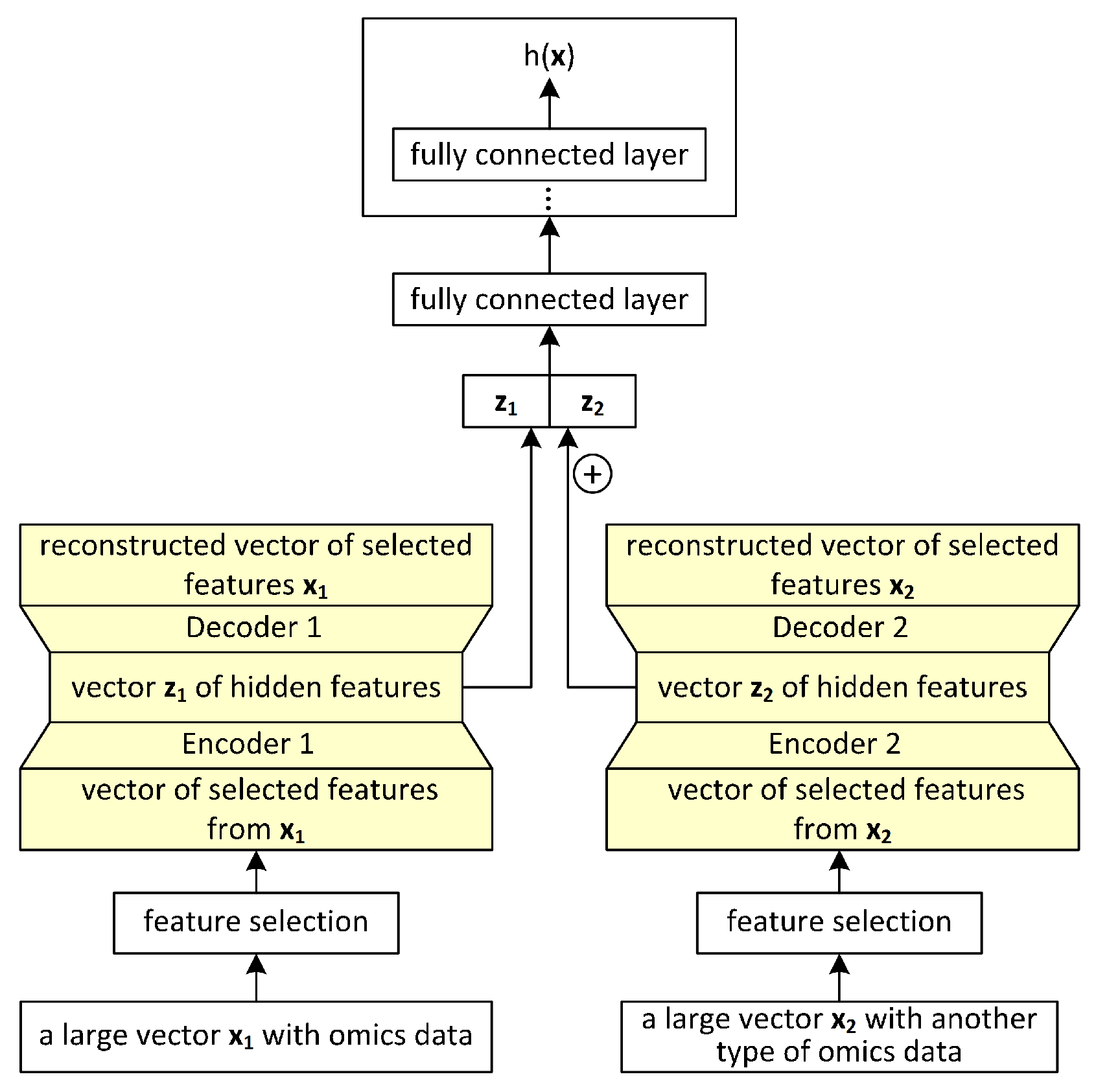
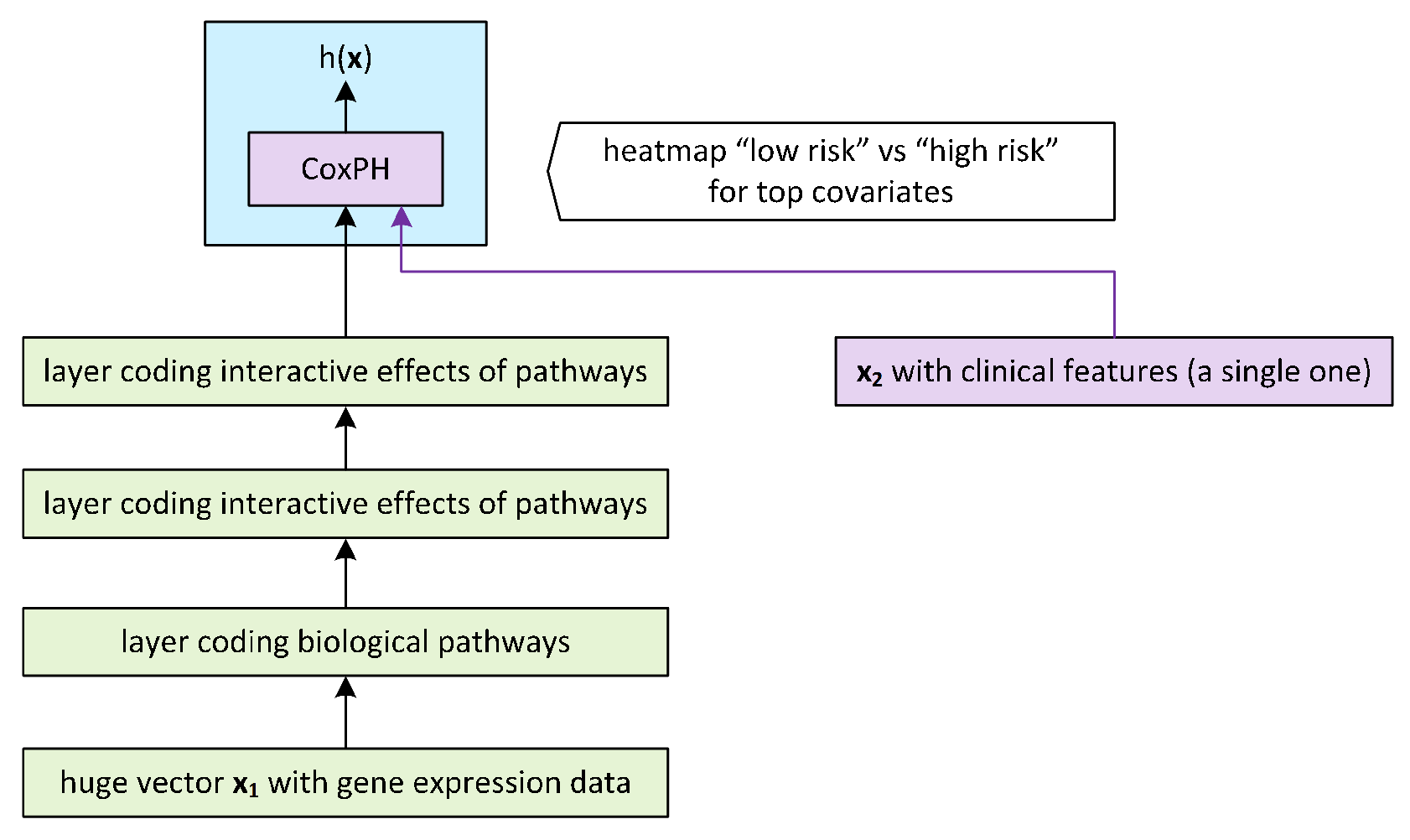
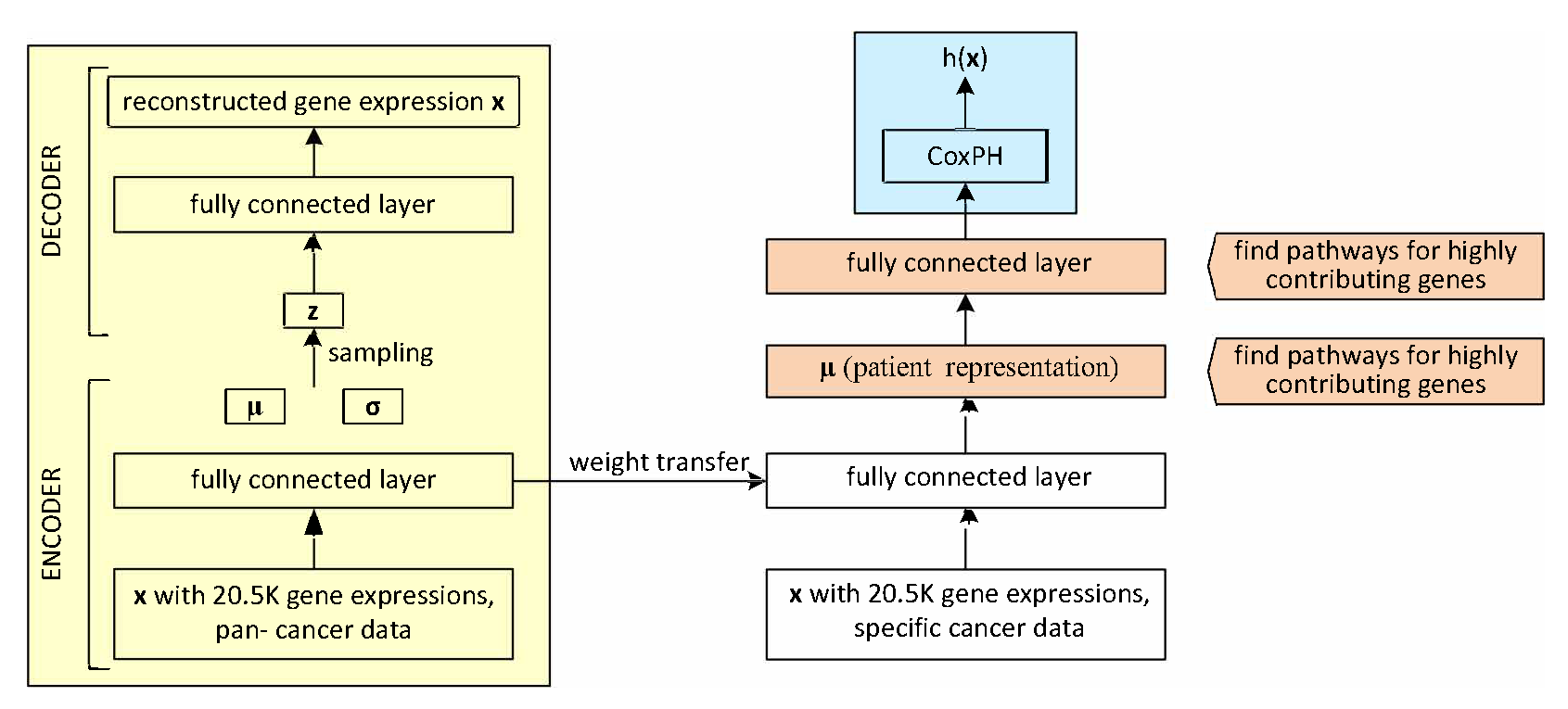
4.2. Architectures for the Output of Omics Platforms
4.3. Performance Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, Y.C.; Salleb-Aouissi, A.; Hooven, T.A. Interpretable prediction of necrotizing enterocolitis from machine learning analysis of premature infant stool microbiota. BCM Bipoinformatics 2022, 23, 104. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Chapter 9 for Survival Analysis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Faraggi, D.; Simon, R. A neural network for survival data. Stat. Med. 1995, 14, 72–73. [Google Scholar] [CrossRef]
- Wiegrebe, S.; Kopper, P.; Sonabend, R.; Bender, A. Deep learning for survival analysis: A review. Aritificial Intell. Rev. 2024, 57, 65. [Google Scholar] [CrossRef]
- Sidorova, J.; Lozano, J.J. Need for Quality Auditing for Screening Computational Methods in Clinical Data Analysis, Including Revise PRISMA Protocols for Cross-Disciplinary Literature Reviews. In Proceedings of the International Conference on Advanced Research in Technologies, Information, Innovation and Sustainability, Madrid, Spain, 18–20 October 2023; Springer: Cham, Switzerland, 2023; pp. 133–142. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An introduction to Statistical Learning; Chapter 11 for Survival Analysis and Censored Data; Springer: New York, NY, USA, 2021. [Google Scholar]
- Kalbfleish, J.D.; Schaubel, D.E. Fifty years of the Cox Model. Annu. Rev. Stat. Appl. 2024, 10, 1–23. [Google Scholar] [CrossRef]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalised treatment recommender system using a Cox proportinal hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef]
- Sidorova, J.; Lozano, J.J. Commentary on “A systematic review on machine learning and deep learning techniques in cancer survival prediction”. Prog. Biophys. Mol. Biol. 2023, 174, 62–71. [Google Scholar]
- Zhou, H.; Wang, H.; Wang, S.; Zou, Y. SurvMetrics: An R package for predictive evaluation metrics in survival analysis. R J. 2022, 14, 252–263. [Google Scholar] [CrossRef]
- Huang, Z.; Zhan, X.; Xiang, S.; Johnson, T.S.; Helm, B.; Yu, C.Y.; Zhang, J.; Salama, P.; Rizkalla, M.; Han, Z.; et al. SALMON: Survival Analysis Learning with Multi-Omics Neural Networks on Breast Cancer. Front. Genet. 2019, 10, 166. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Choe, J.; Lee, I.; Kang, J. Improved survival analysis by learning shared genomic information from pan-cancer data. Bioinformatics 2020, 36, i389–i398. [Google Scholar] [CrossRef]
- Ching, T.; Zhu, X.; Garmire, L.X. Cox-nnet: An artificial neural network method for prognosis prediction of high-thoughput omics data. PLoS Comput. Biol. 2018, 14, e1006076. [Google Scholar] [CrossRef]
- Yang, C.H.; Moi, S.H.; Ou-Yang, F.; Chuang, L.Y.; Hou, M.F.; Lin, Y.D. Identifying risk stratification associated with a cancer for overall survival by deep-learning based CoxPH. IEEE Access 2019, 7, 67708–67717. [Google Scholar] [CrossRef]
- Lee, C.; Zame, W.; Yoon, J.; Van Der Schaar, M. DeepHit: A Deep Learning Approach to Survival Analysis with Competing Risks. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; AAAI Press: Palo Alto, CA, USA, 2018. [Google Scholar]
- Kvamme, H.; Borgan, Ø.; Scheel, I. Time-to-event prediction with neural network and Cox regression. J. Mach. Learn. Res. 2019, 20, 1–30. [Google Scholar]
- Yousefi, S.; Amrollahi, F.; Amgad, M.; Dong, C.; Lewis, J.E.; Song, C.; Gutman, D.A.; Halani, S.H.; Velazquez Vega, J.E.; Brat, D.J.; et al. Predicting clinical outcomes from large scale cancer genomic profiles with deep survival models. Sci. Rep. 2017, 7, 11707. [Google Scholar] [CrossRef]
- Hao, J.; Kim, Y.; Mallavarapu, T.; Oh, J.H.; Kang, M. Cox-PASNet: Pathway-based sparse deep neural network for survival analysis. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 3–6 December 2018; pp. 381–386. [Google Scholar]
- Tong, L.; Mitchel, J.; Chatlin, K.; Wang, M.D. Deep learning based feature-level integration of multi-omics data for breast cancer patients survival analysis. BCM Med. Inform. Decis. Mak. 2020, 20, 225. [Google Scholar] [CrossRef]
- Knaus, W.A.; Harrell, F.E.; Lynn, J.; Goldman, L.; Phillips, R.S.; Connors, A.F.; Dawson, N.V.; Fulkerson, W.J.; Califf, R.M.; Desbiens, N.; et al. The SUPPORT prognostic model: Objective estimates of survival for seriously ill hospitalized adults. Ann. Intern. Med. 1995, 122, 191–203. [Google Scholar] [CrossRef]
- Sahu, A.; Wang, X.; Munson, P.; Klomp, J.P.; Wang, X.; Gu, S.S.; Han, Y.; Qian, G.; Nicol, P.; Zeng, Z.; et al. Discovery of targets for immune-metabolic antitumor drugs identifies estrogen-related receptor alpha. Cancer Discov. 2008, 13, 672–701. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.X.; Cao, X.; Qiang, M.Y.; Liang, C.X.; Ke, L.R.; Cai, Z.C.; Huang, Y.Y.; Zhan, Z.J.; Zhou, J.Y.; et al. Widely targeted quantitative lipidomics and prognostic model reveal plasma lipid predictors for nasopharingal carcinoma. Lipids Health Dis. 2023, 22, 81. [Google Scholar] [CrossRef]
- Luo, L.; Tan, Y.; Zhao, S.; Yang, M.; Che, Y.; Li, K.; Liu, J.; Luo, H.; Jiang, W.; Li, Y.; et al. The potential of high-order features of routine blood test in predicting prognosis of non-small cell lung cancer. BCM Cancer 2023, 23, 496. [Google Scholar] [CrossRef]
- Thernau, T.M.; Grambsch, P.M. Modeling Survival Data: Extending the Cox Model; Version 2.38; Springer: New York, NY, USA, 2000; ISBN 0-387-98784-3. [Google Scholar]
- Sonabend, R.; Király, F.J.; Bender, A.; Bischl, B.; Lang, M. mlr3proba: An R package for machine learning in survival analysis. Bioinformatics 2021, 37, 2789–2791. [Google Scholar] [CrossRef]
- Schulze, J.B.; Durante, L.; Günther, M.P.; Götz, A.; Curioni-Fontecedro, A.; Opitz, I.; von Känel, R.; Euler, S. Clinically Significant Distress and Physical Problems Detected on a Distress Thermometer are Associated with Survival Among Lung Cancer Patients. J. Acad. Consult. Liaison Psychiatry 2023, 64.2, 128–135. [Google Scholar] [CrossRef]
- SEER Cause—Specific Death Classification. Available online: https://seer.cancer.gov/causespecific/ (accessed on 1 April 2024).
- Yang, F.O.; Hsu, N.C.; Moi, S.H.; Lu, Y.C.; Hsieh, C.M.; Chang, K.J.; Chen, D.R.; Tu, C.W.; Wang, H.C.; Hou, M.F. Efficacy and toxicity of pegylated liposomal doxorubicin-based chemotheraphy in early-stage breast cancer: A multicenter retrspective case-control study. Asia Pac. J. Clin. Oncol. 2018, 14, 198–203. [Google Scholar] [CrossRef] [PubMed]
- Grossman, R.L.; Heath, A.P.; Ferretti, V.; Varmus, H.E.; Lowy, D.R.; Kibbe, W.A.; Staudt, L.M. Toward a shared vision for cancer genomic data. N. Engl. J. Med. 2016, 375, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Jain, S.; Kim, H.; Bar-Joseph, Z. Using neural networks for reducing the dimensions of single-cell RNA-Seq data. Nucleic Acids Res. 2017, 45, e156. [Google Scholar] [CrossRef]
- Hou, Z.; Leng, J.; Yu, J.; Xia, Z.; Wu, L.Y. PathExpSurv: Pathway expansion for explainable survival analysis and disease gene discovery. Bioinformatics 2023, 24, 434. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Zeng, W.; Liu, X. A gene signature of survival prediction for kidney renal cell carcinoma by multi-omic data analysis. Int. J. Mol. Sci. 2019, 20, 5720. [Google Scholar] [CrossRef] [PubMed]
- Alinia, S.; Asghari-Jafarabadi, M.; Mahmoudi, L.; Norouzi, S.; Safari, M.; Roshanaei, G. Survival predicion and prognostic factors in colorectal cancer after curative surgery: Insights from cox regression and neural networks. Sci. Rep. 2023, 13, 15675. [Google Scholar] [CrossRef]
- Wysocka, M.; Wysocki, O.; Zufferey, M.; Landers, D.; Freitas, A. A systematic review of biologically-informed deep models for cancer: Fundamental trends for encoding and interpreting oncology data. BCM Bipoinformatics 2023, 24, 198. [Google Scholar] [CrossRef]




| Algorithm | Common Databases | C-Index | Performance Comparison |
|---|---|---|---|
| DeepSurv [8] | SUPPORT, METABRIC, Rot&GBSD | 0.62, 0.65, 0.68 | CPH (=0.58) < DeepSurv; CPH (=0.63) < DeepSurv; CPH (=0.65) < DeepSurv. |
| Cox-CC-Time [16] | SUPPORT, METABRIC, Rot&GBSD | 0.62, 0.66, 0.67 1 | CPH (=0.6) < DeepSurv < CoxTime (=0.63) < DeepHit; CPH (=0.63) < DeepSurv < CoxTime(=0.66) < DeepHit; CPH (=0.67) < DeepSurv < CoxTime (=0.68). |
| DeepHit [15] | METABRIC | 0.69 | CPH (=0.65) = DeepSurv < DeepHit. |
| Algorithm | Common Databases | C-Index | Performance Comparison |
|---|---|---|---|
| Cox-nnet [13] | 10 datasets from TCGA, those with at least 50 deaths, gene expression | On 4 out of 10 databases CoxPH (0.67) < Cox-nnet, while for the overall comparison the improvement with Cox-nnet is small (<0.02) yet statistically significant. | |
| Concatenation autoencoders [19] | Breast cancer data (BRCA) from TCGA, modalities: gene expression, miRNA, DNA methylation, and copy number variations | 0.64 | Concatenation autoencoders ≈ Cox-nnet (slightly) < CoxPH (if taken to be 0.675 as reported by [13]) |
| SALMON [11] | BRCA from TCGA with five omics data types incl. gene expression, miRNA, DNA methylation, and copy number variations | Median concordance index of 0.72 | CoxPH (0.65) < Cox-nnet < SALMON |
| VAE-Cox [12] | Same data as in [13] | 0.65 | VAE-Cox (0.66) is slightly < Cox-nnet |
| Cox-PASNet [18] | GBM from TCGA, gene expression | 0.64 | CoxPH (glmnet) < SurvivalNet 1 < Cox-nnet < Cox-PASNet (0.65), the order as reported in [18]. |
| SurvivalNet [17] | GBM, BRCA, KIPAN from TCGA with different set of features: (1) 17K gene expression features, and (2) the set including 3–400 clinicopathological attributes, mutations, gene- and chromosome arm-level copy number variations, and protein expression. | >0.8 | On GBM, PASNet < SurvivalNet (>0.8), the order as reported in [17]. On BRCA, SurvivalNet < Cox-nnet (0.67) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorova, J.; Lozano, J.J. Review: Deep Learning-Based Survival Analysis of Omics and Clinicopathological Data. Inventions 2024, 9, 59. https://doi.org/10.3390/inventions9030059
Sidorova J, Lozano JJ. Review: Deep Learning-Based Survival Analysis of Omics and Clinicopathological Data. Inventions. 2024; 9(3):59. https://doi.org/10.3390/inventions9030059
Chicago/Turabian StyleSidorova, Julia, and Juan Jose Lozano. 2024. "Review: Deep Learning-Based Survival Analysis of Omics and Clinicopathological Data" Inventions 9, no. 3: 59. https://doi.org/10.3390/inventions9030059
APA StyleSidorova, J., & Lozano, J. J. (2024). Review: Deep Learning-Based Survival Analysis of Omics and Clinicopathological Data. Inventions, 9(3), 59. https://doi.org/10.3390/inventions9030059





