IIR Shelving Filter, Support Vector Machine and k-Nearest Neighbors Algorithm Application for Voltage Transients and Short-Duration RMS Variations Analysis
Abstract
1. Introduction
- Input data stage. It is obvious that the quality of machine learning is directly related to input data which is closely related to algorithms used and tasks undertaken. However, discussion on these aspects is skipped in [1]: in our opinion, one of the reasons (for that skipping) can be the deficiency of PQ monitoring systems at that time [2]. In this paper, initial data gathering is described in Section 2.1.
- Feature extraction stage. The following taxonomy of the techniques is given in [1]: Fourier transform, Kalman filter, wavelet transform, S-transform, Hilbert–Huang transform, Gabor transform, and miscellaneous or less often used (e.g., time–frequency representation, Teager energy operator, etc.). A result of classification highly depends on both the features selection strategy and their extraction accuracy.
- Classification stage. The following tools are highlighted in [1]: artificial neutral network, support vector machine, fuzzy expert system, and miscellaneous (e.g., k-nearest neighbors).
- Feature selection and parameter optimization stage. In this stage, the redundant features with low recognition rate are discarded. The following tools for selection of the best suitable feature subset are highlighted in [1]: genetic algorithms, particle swarm optimization, and ant colony optimization.
- Decision stage. Discussion on this topic is also skipped in [1]: in our opinion, one of the reasons can be that a practical significance of many research studies (algorithms) is insufficient and more comprehensive investigations (technical progress) are required for their commercialization and application in electric power systems.
2. Materials and Methods
2.1. Database
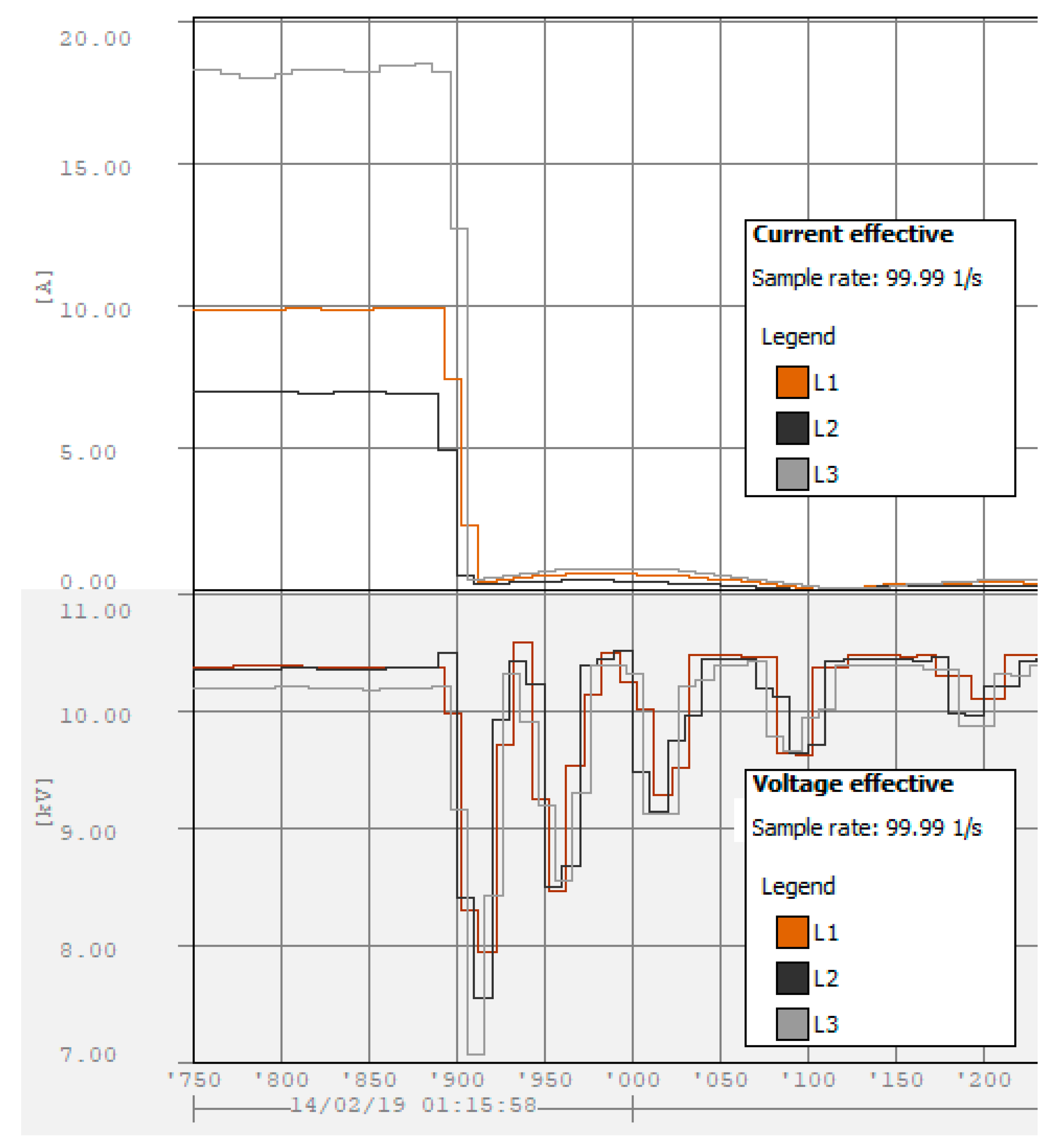
2.1.1. Commutation Transients
2.1.2. Atmospheric Transients
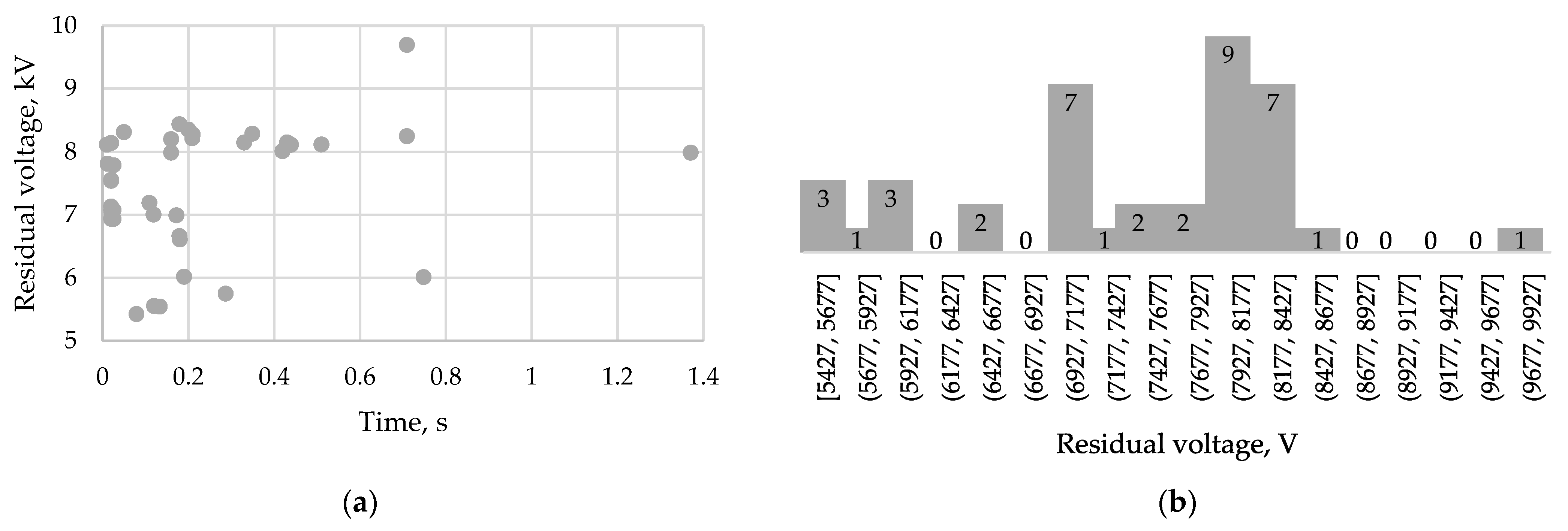
- According to the calculations given in [42] (pp. 268–269), when the striking distance was 30 m, a 30 kA impulse induced an approximately 195 kV voltage peak, when 100 m—approximately 50 kV, and when 300 m—approximately 20 kV. The duration of these impulses is longer than 6 μs (see Section 4.1 for more details and discussion about the duration of transients). It was assumed that the height of the line (above ground) is 5 m (this assumption is not realistic), the steepness of the impulse is 20 kA/μs (see Equation (10)), the rise time of the impulse is 1.5 μs, and the speed of the return stroke is equal to 0.1 of the speed of light.
- In [45], when the striking distance was 1.16 m, 10 kA impulse induced 50 kV voltage, but the predicted result from theoretical simulation was 28 kV. The length of the single-phase overhead power line is 200 m, and the height is 10 m. The durations of induced impulses are up to 10–20 μs.
- In [46], when the striking distance was 50 m, the 12 kA impulse induced 52–80 kV voltages at various points of the single-phase overhead power line whose length is 1 km and height is 10 m. The duration of the induced impulse is up to 10 μs.
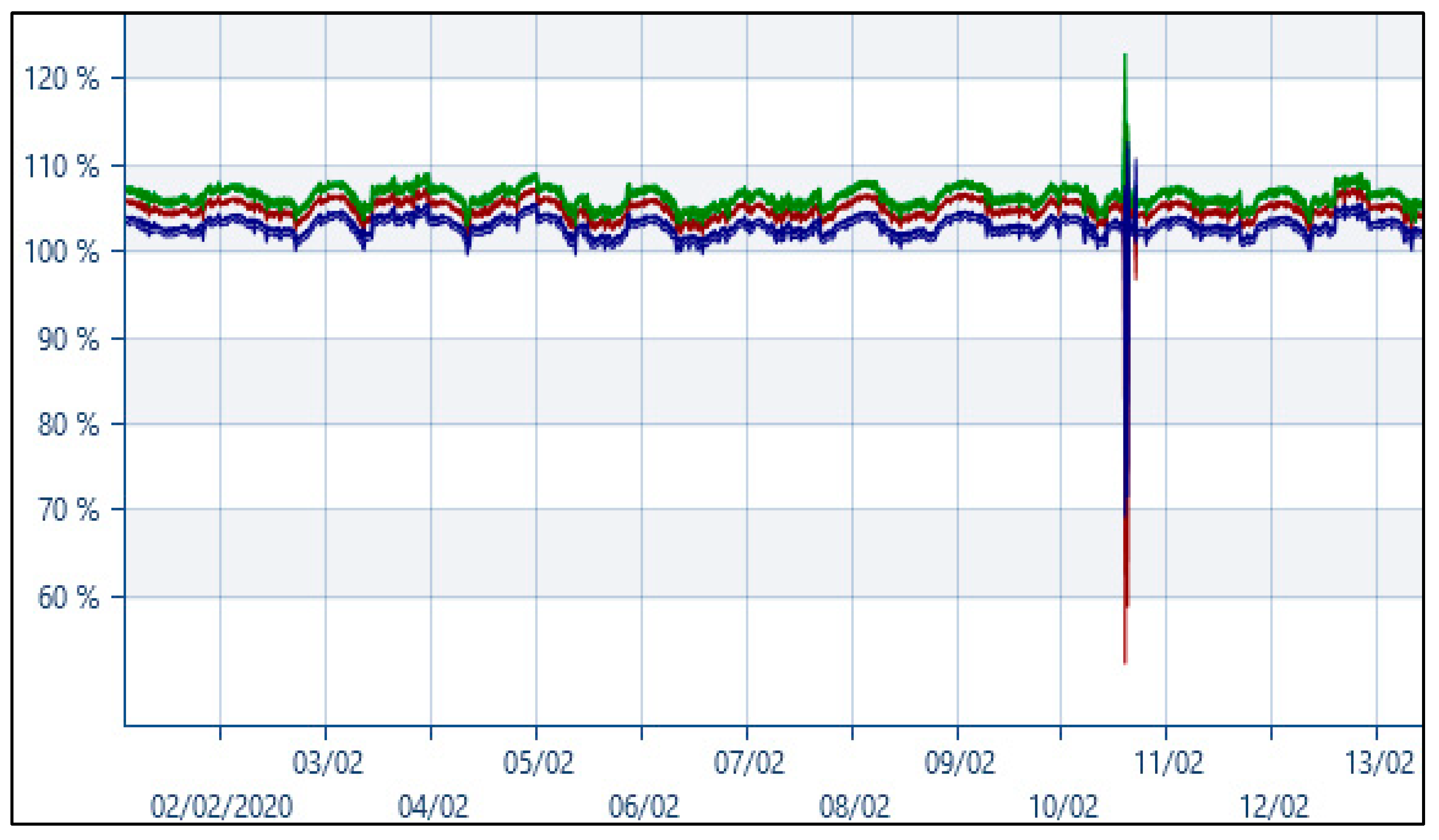
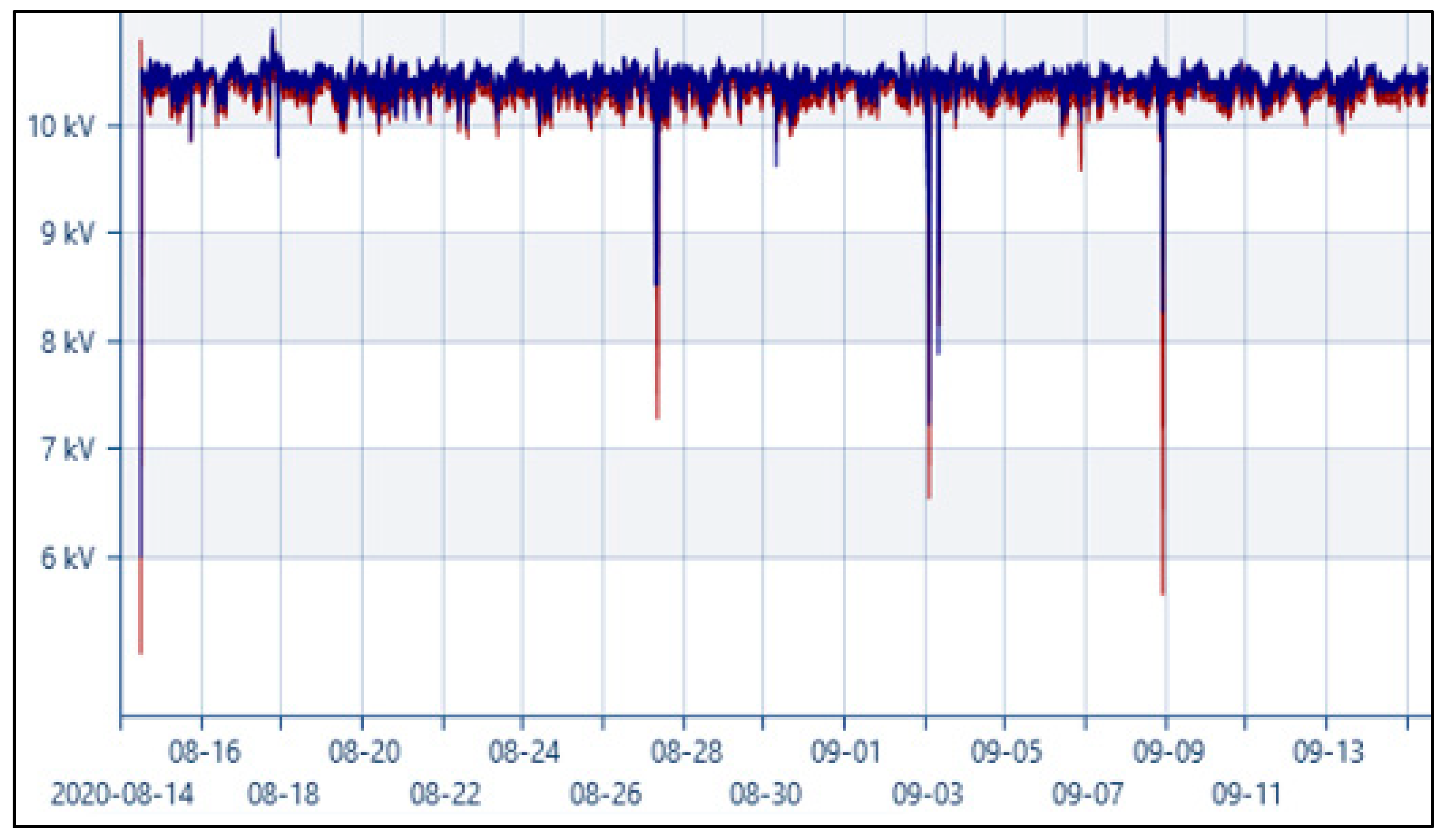
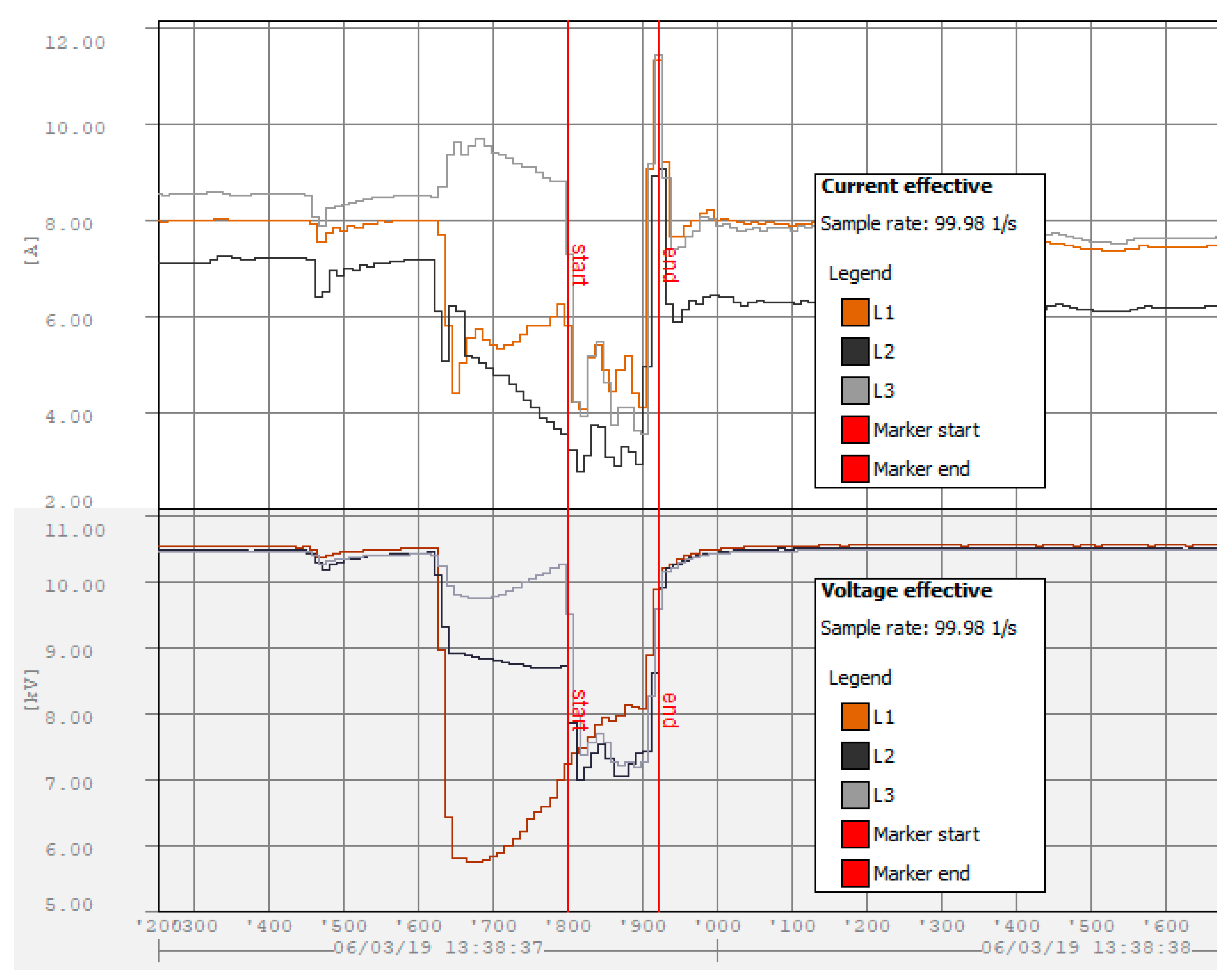
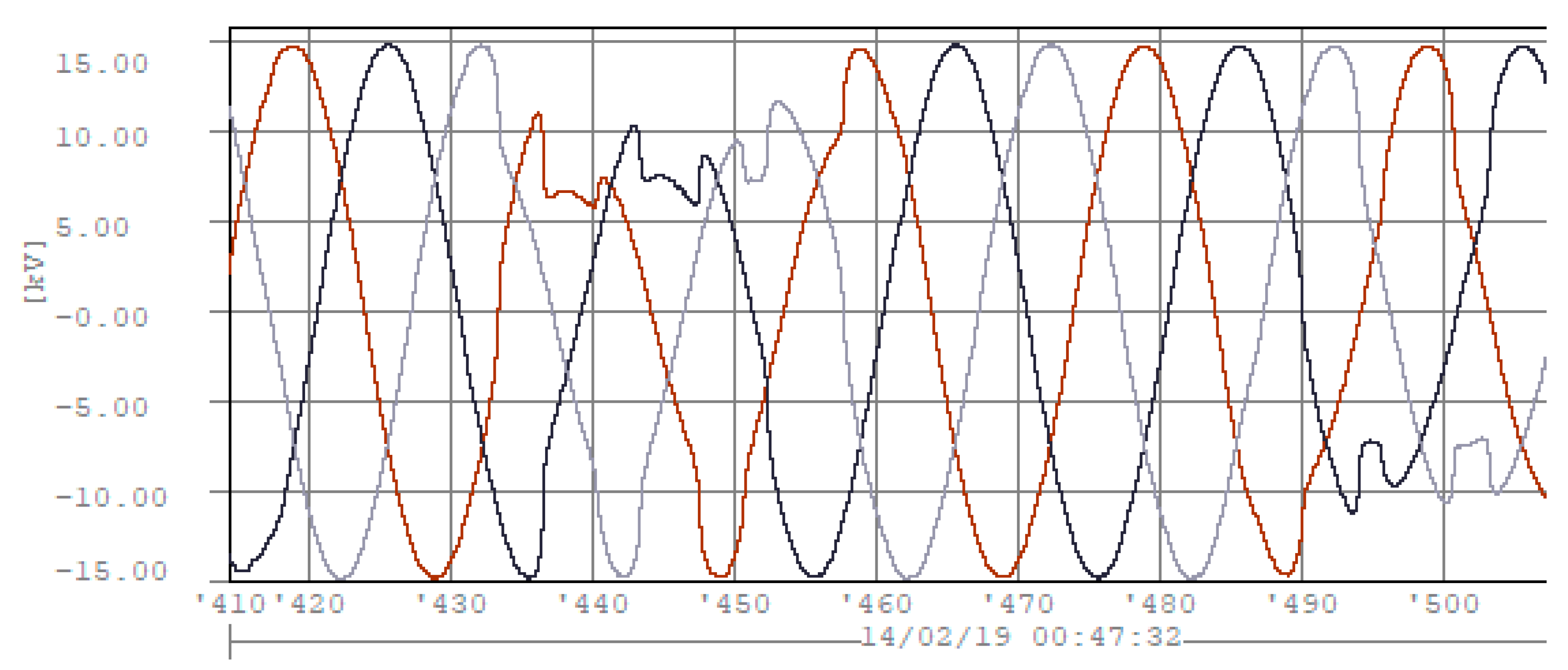
2.1.3. Short-Duration RMS Variations: PQ Monitoring Campaign
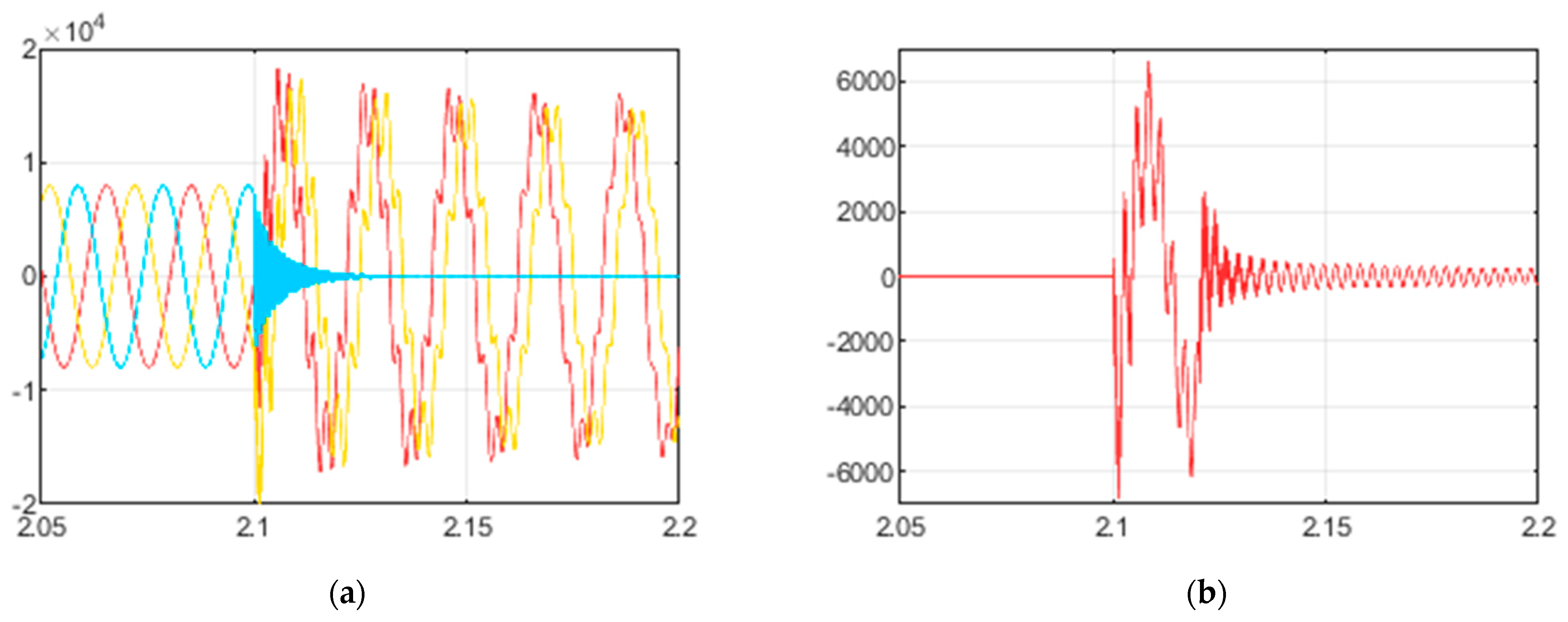
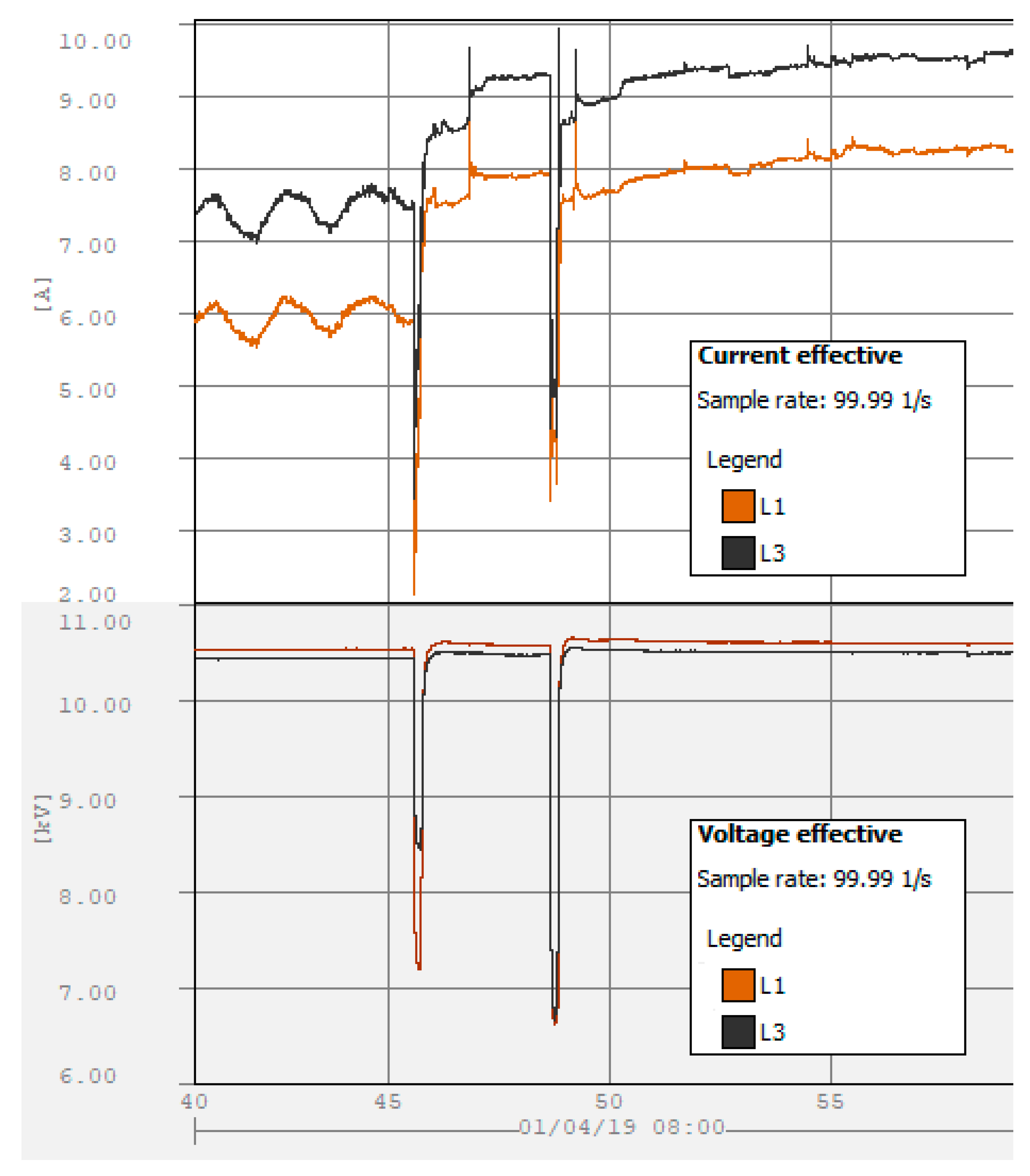
2.1.4. Voltage Sags Caused by Electric Motor Starting
- One figure is given in IEEE Std 1159-2019 (p. 22): the minimal residual voltage is 0.8 p.u., and the voltage sag duration is approximately 2 s. The motor type is not specified, but it is mentioned that a motor is large.
- In [14] that investigates an induction motor fed by a current controlled pulse width modulation inverter, the minimal residual voltage and duration of the simulated voltage sag is 0.88 p.u. and 0.8 s.
- In [49] (investigates an induction squirrel-cage motor), the minimal residual voltage and duration of voltage sags are as follows: (1) 0.35 p.u. and 307 ms (simulated) or 327 ms (measured) with the capacitor bank switching; (2) 0.25 p.u. and 710 ms without the capacitor bank switching. The simulation results coincide with the experimental results. It should be noticed that the applied AC motor starting method (as well as others, for example, reactor starting, autotransformer starting, Y-Δ transform, etc.) limits both inrush current and voltage sag.
- In [50] that investigates water pumps driven by the induction motors, the minimal residual voltage and duration of both simulated voltage sags are 0.85–0.87 p.u. and 0.05 s.
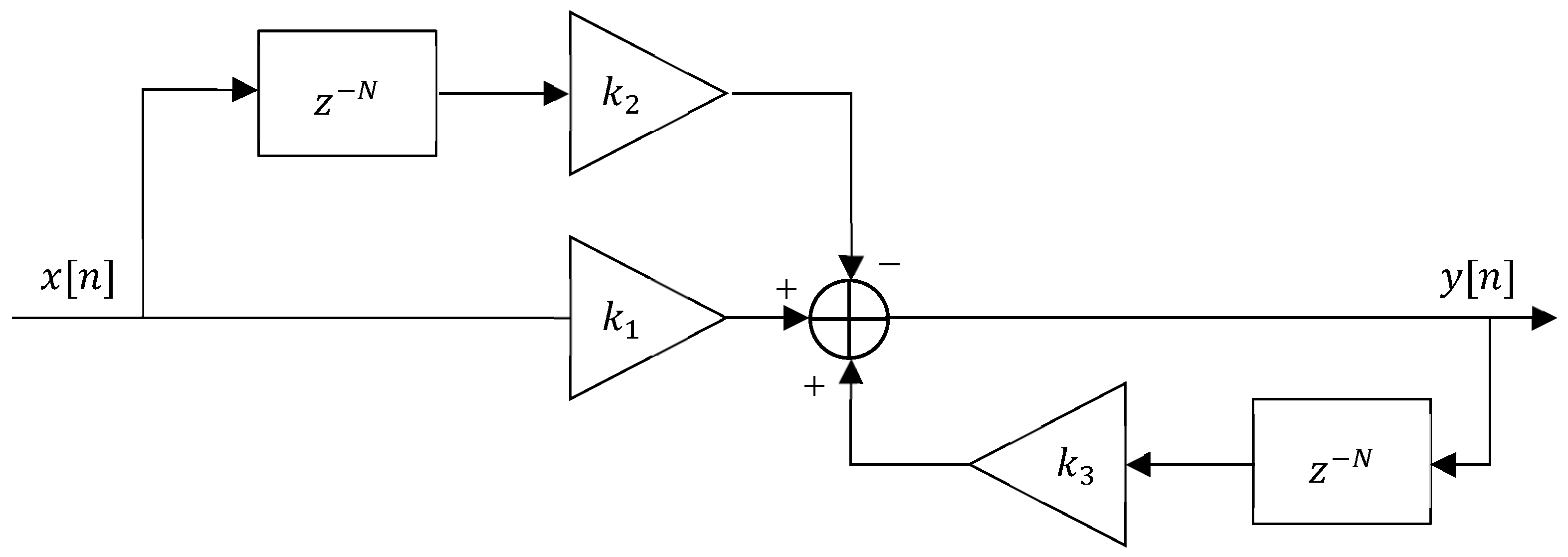
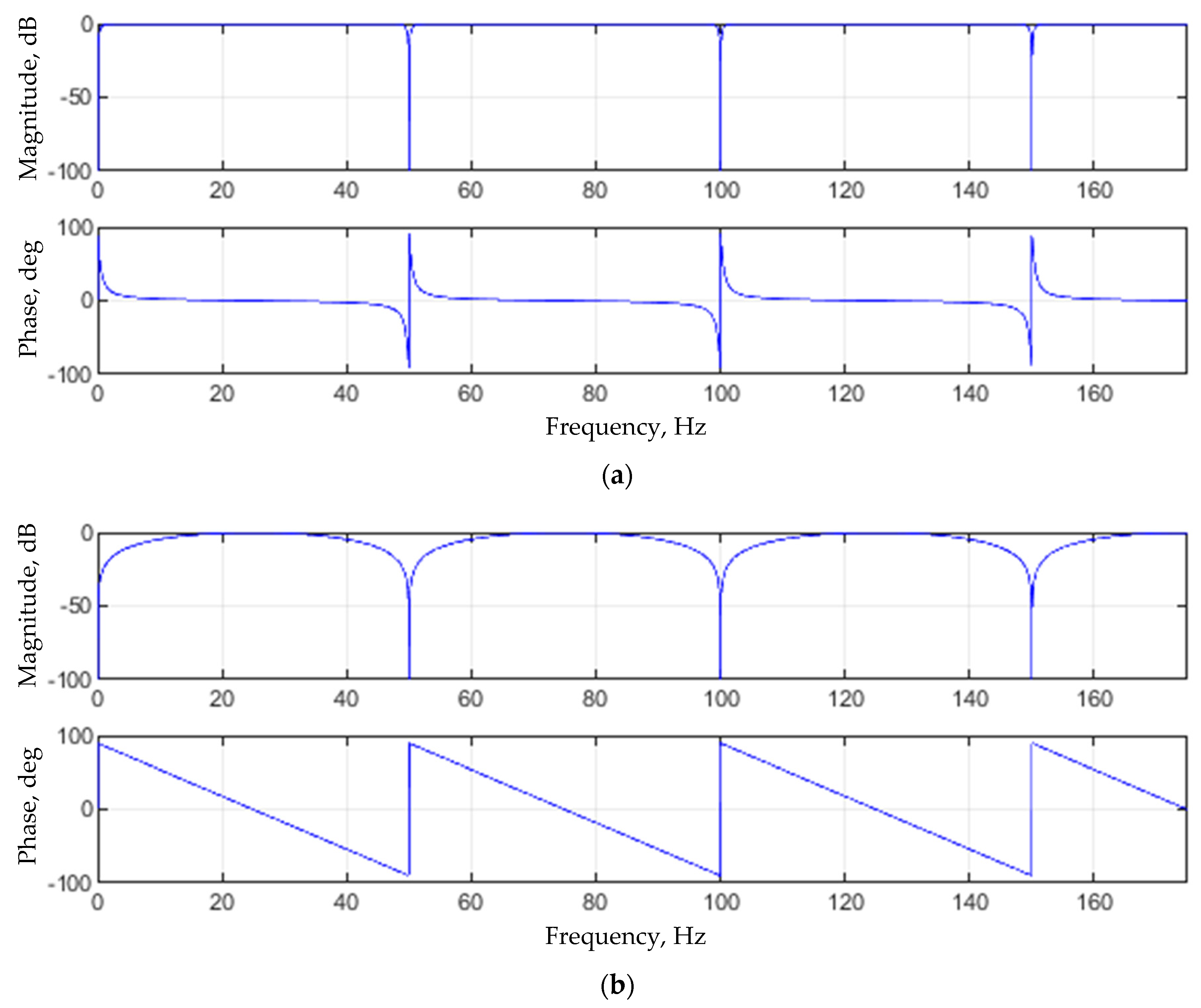
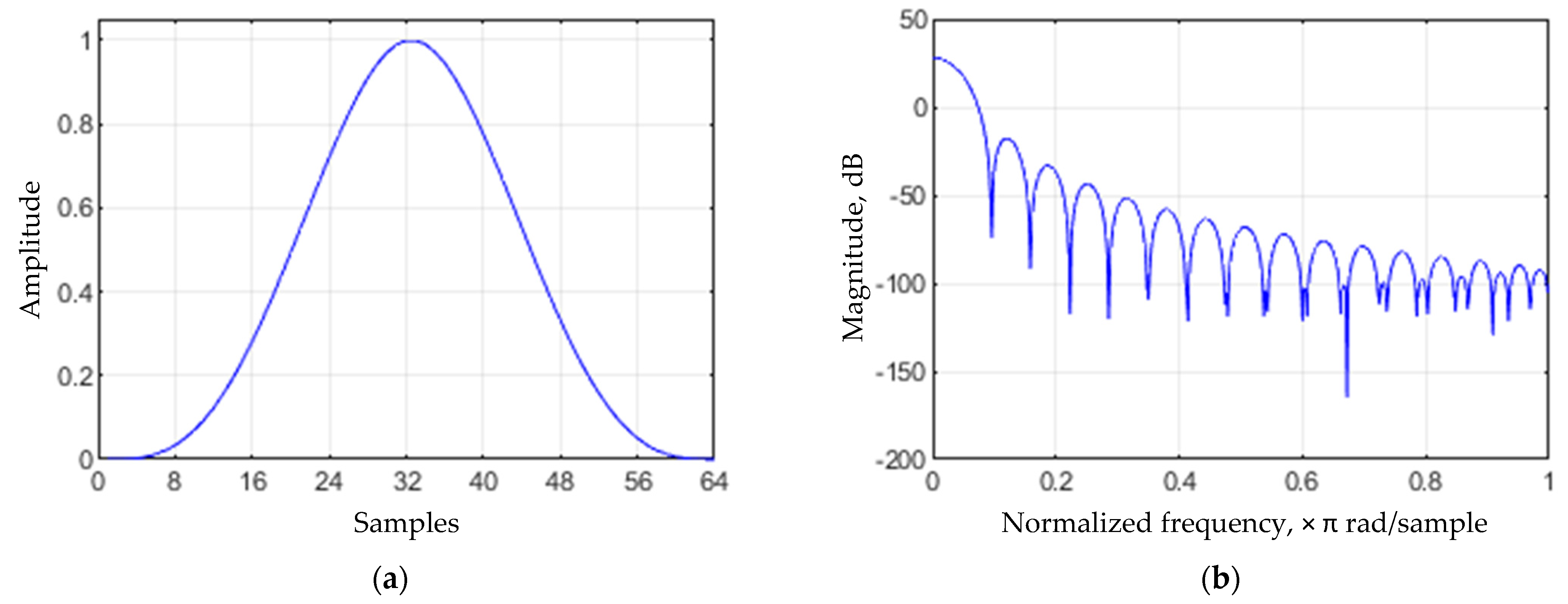
2.2. Shelving Filter
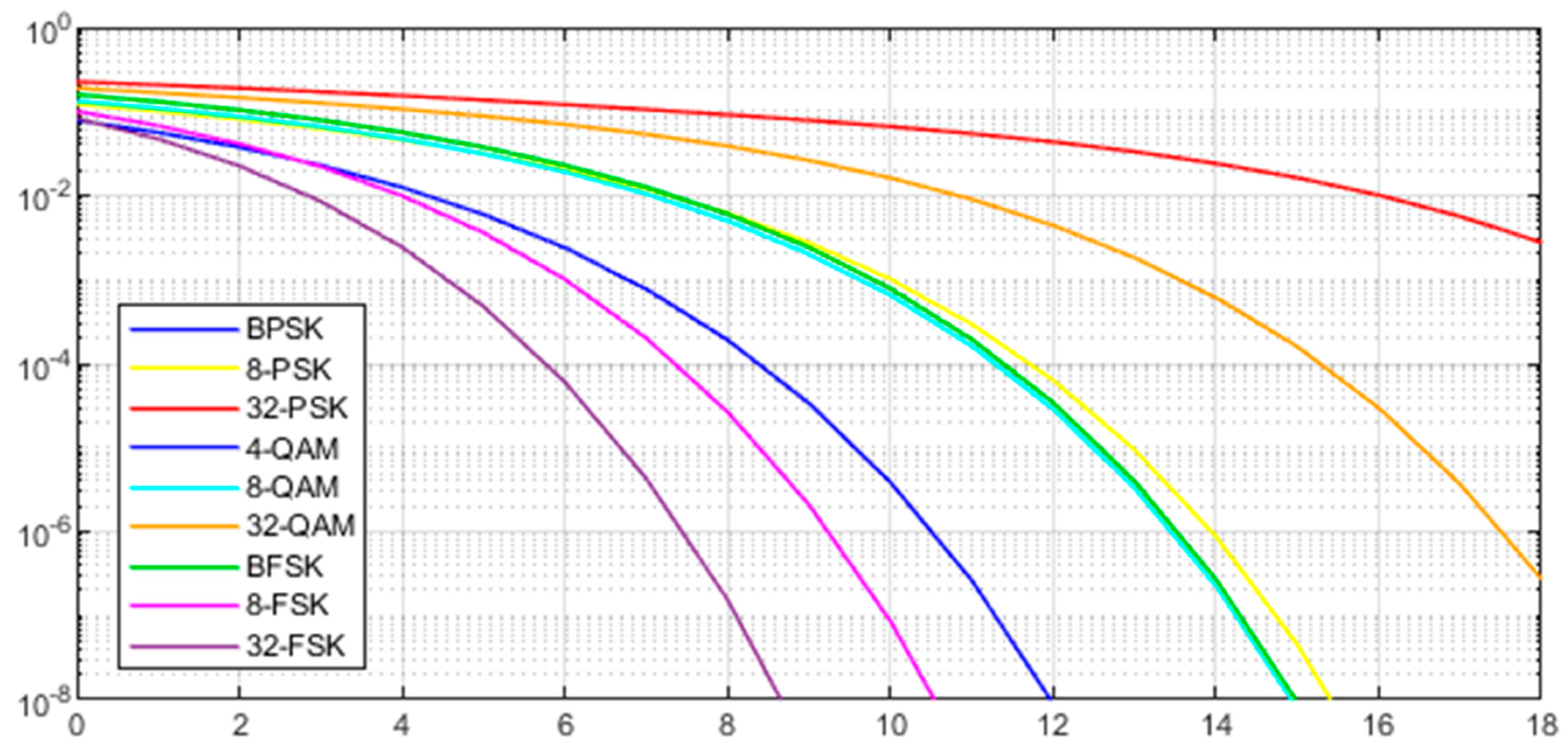
2.3. Fundamental Theory of SVM
2.4. Fundamental Theory of KNN
2.5. Additional Methods
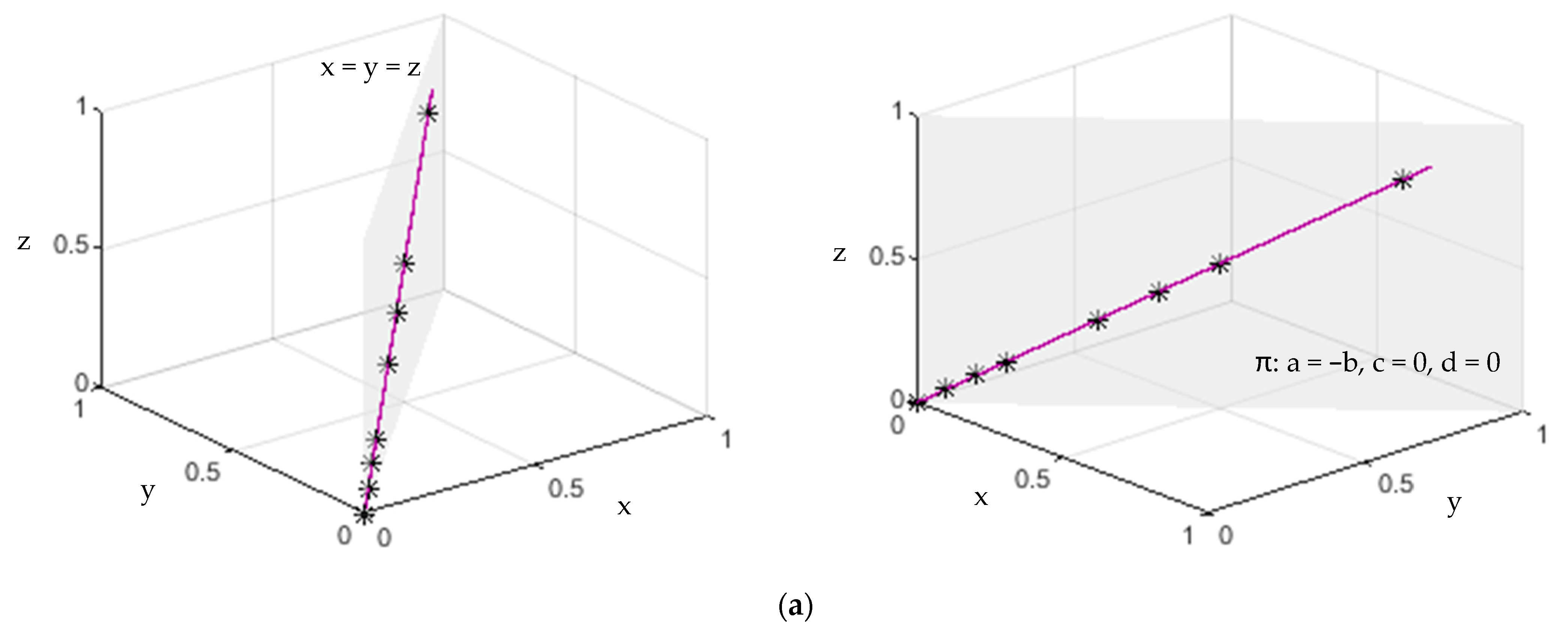
2.5.1. Geometric Analysis
2.5.2. Clarke Transformation
3. Results
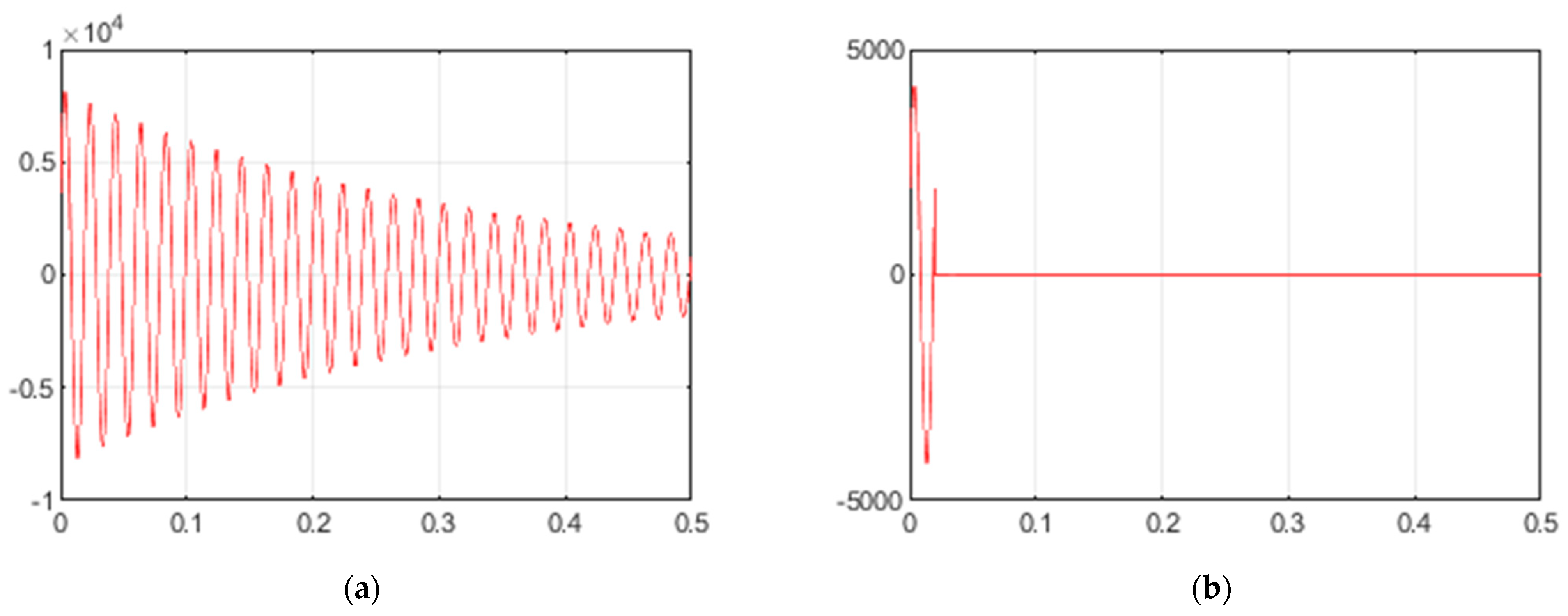
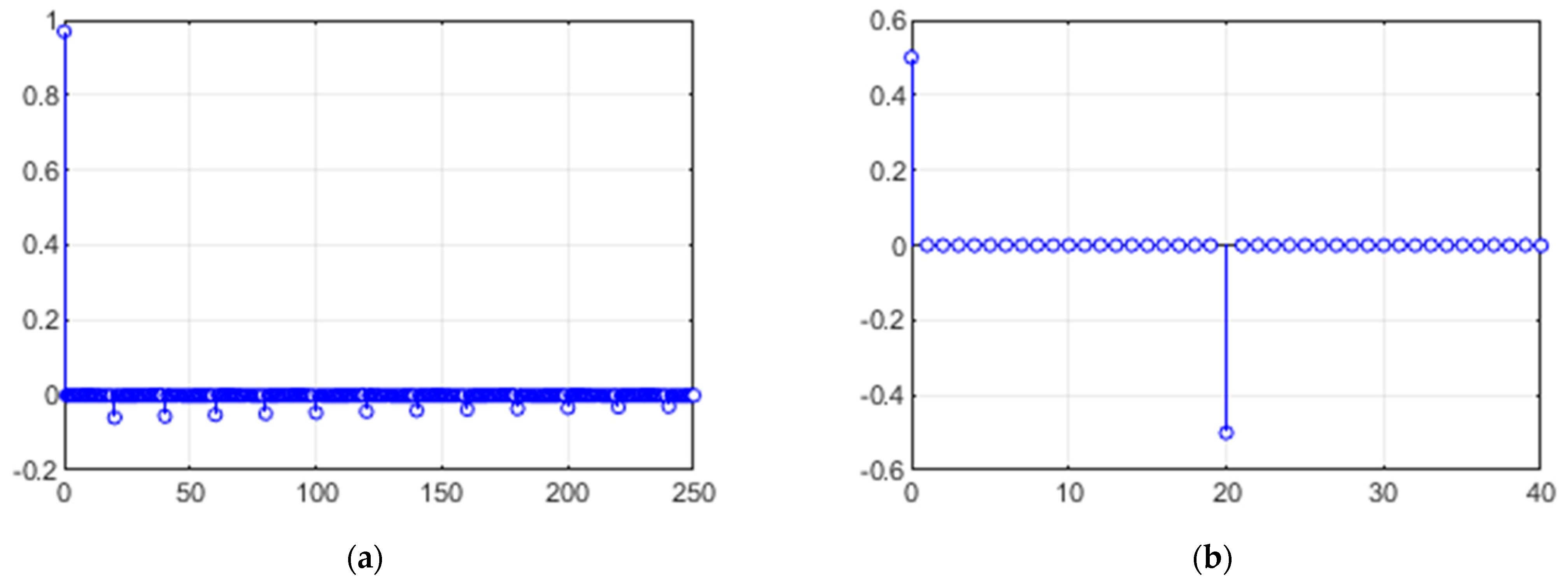
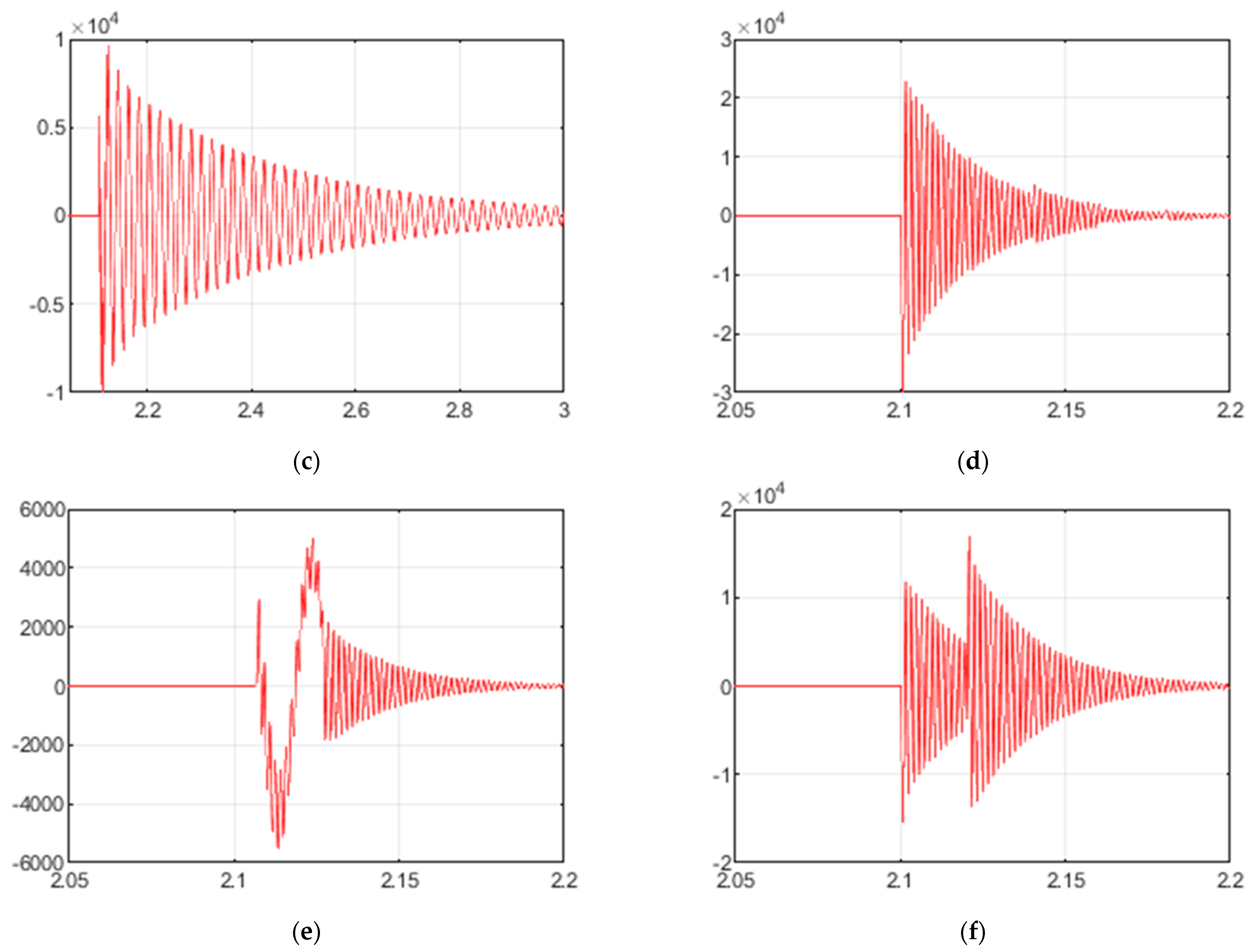
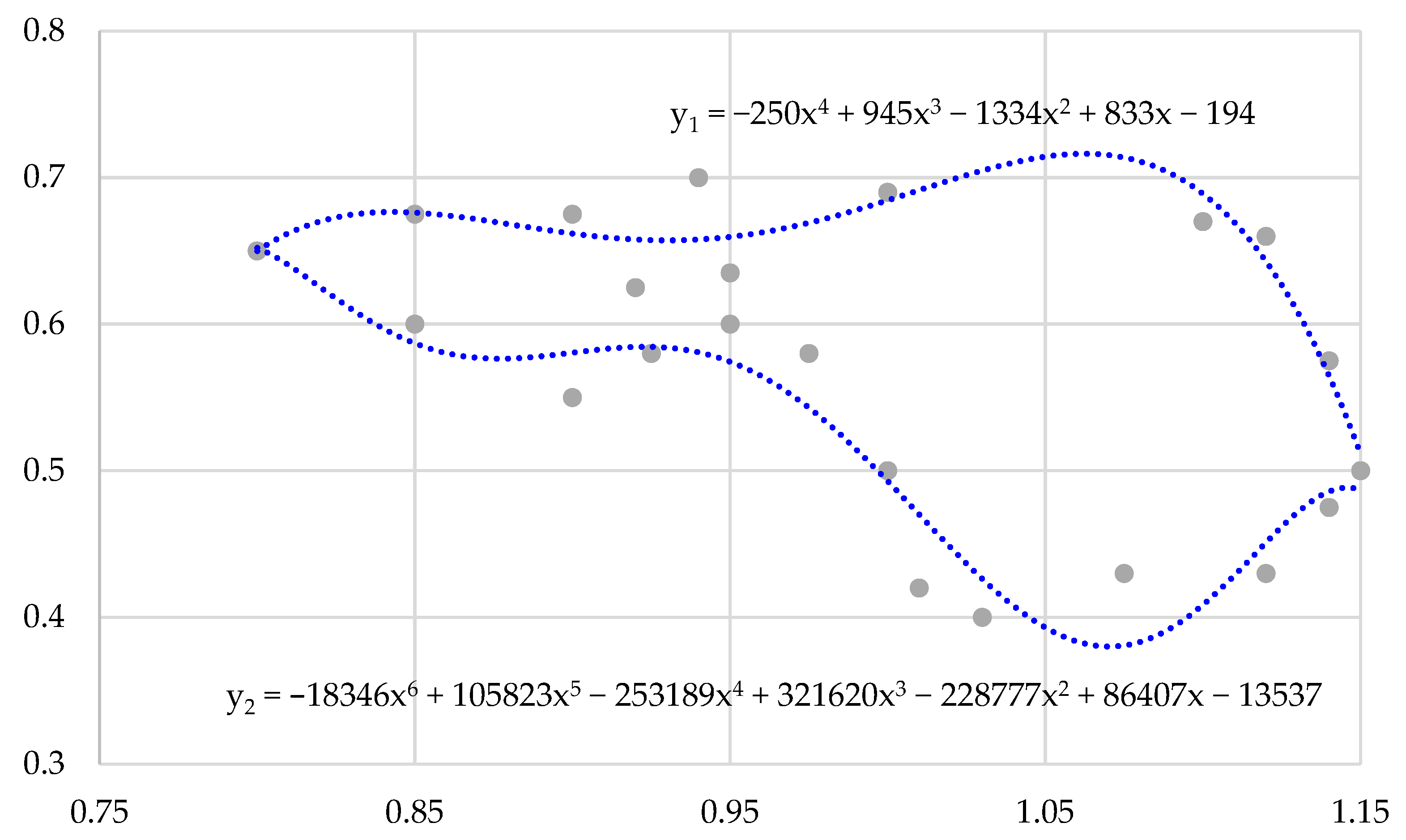
3.1. Shelving Filter
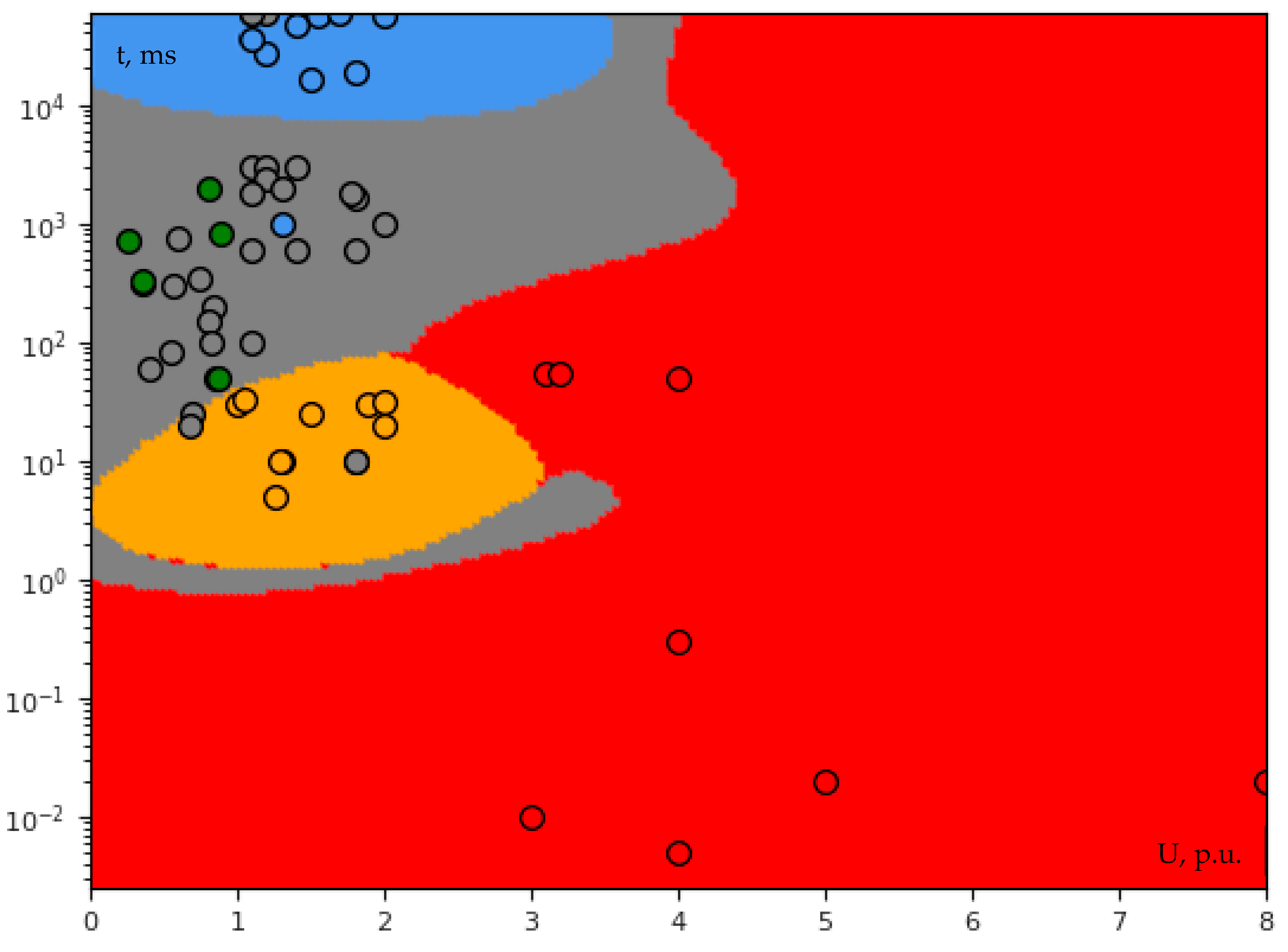
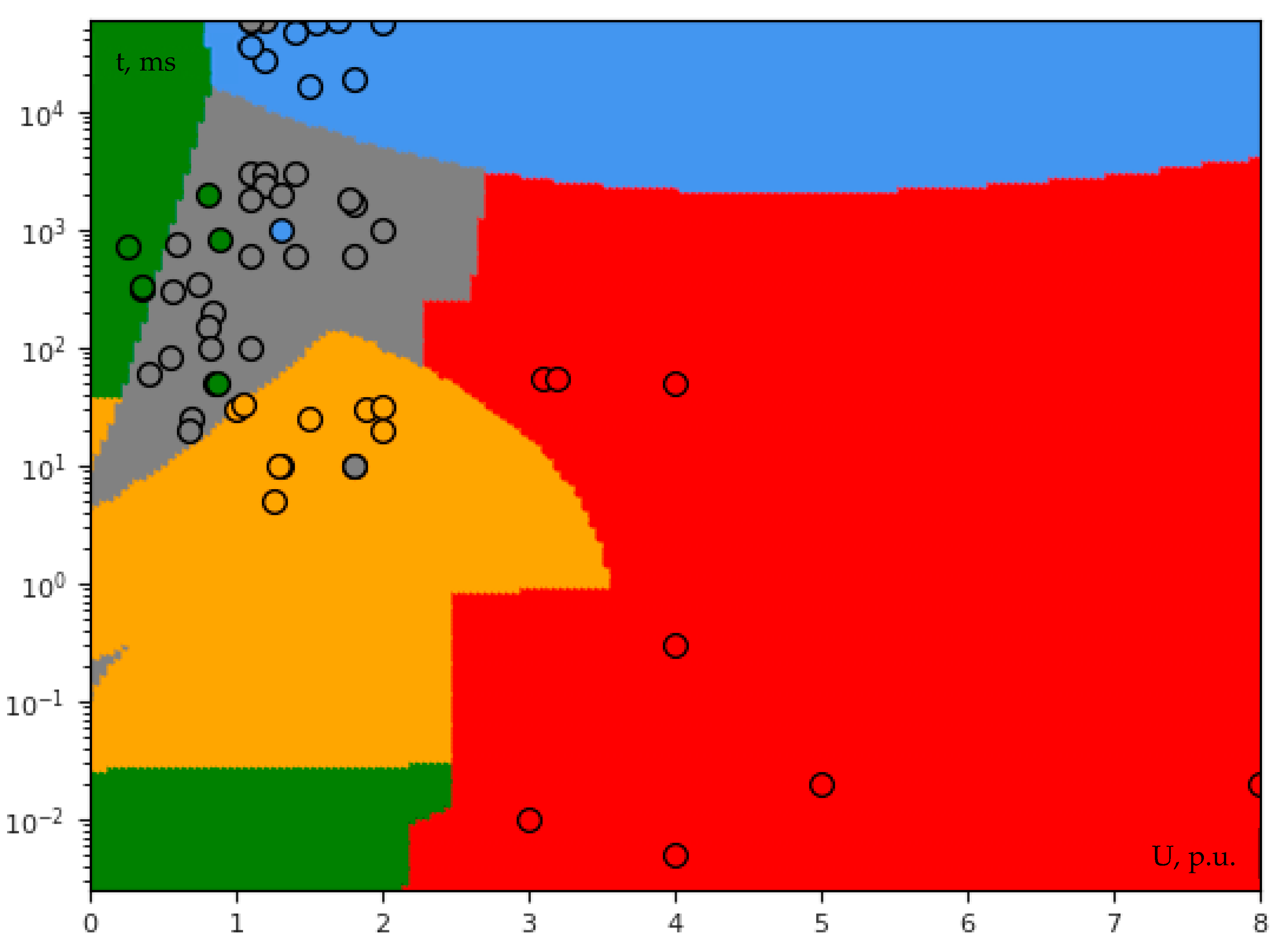
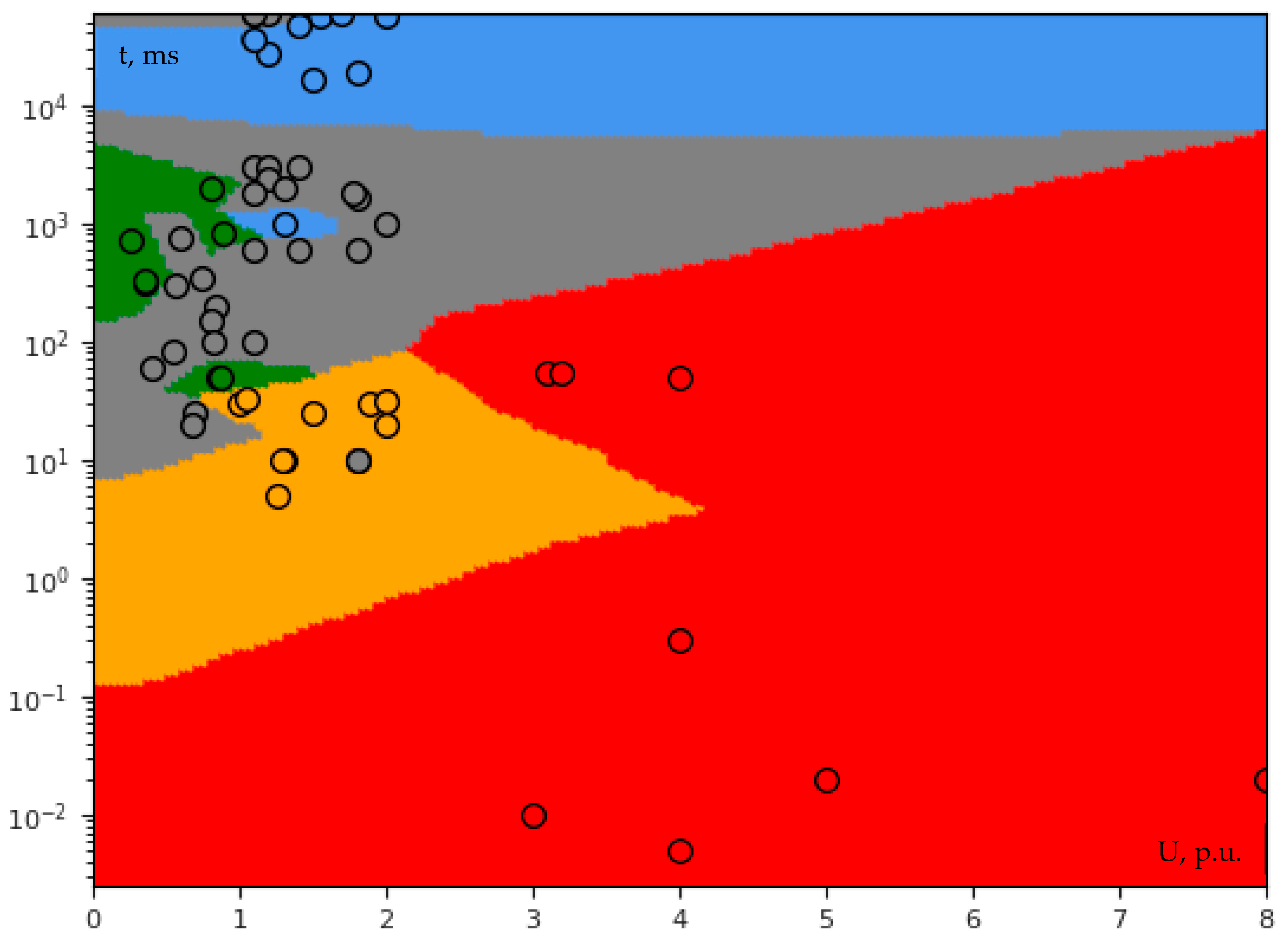
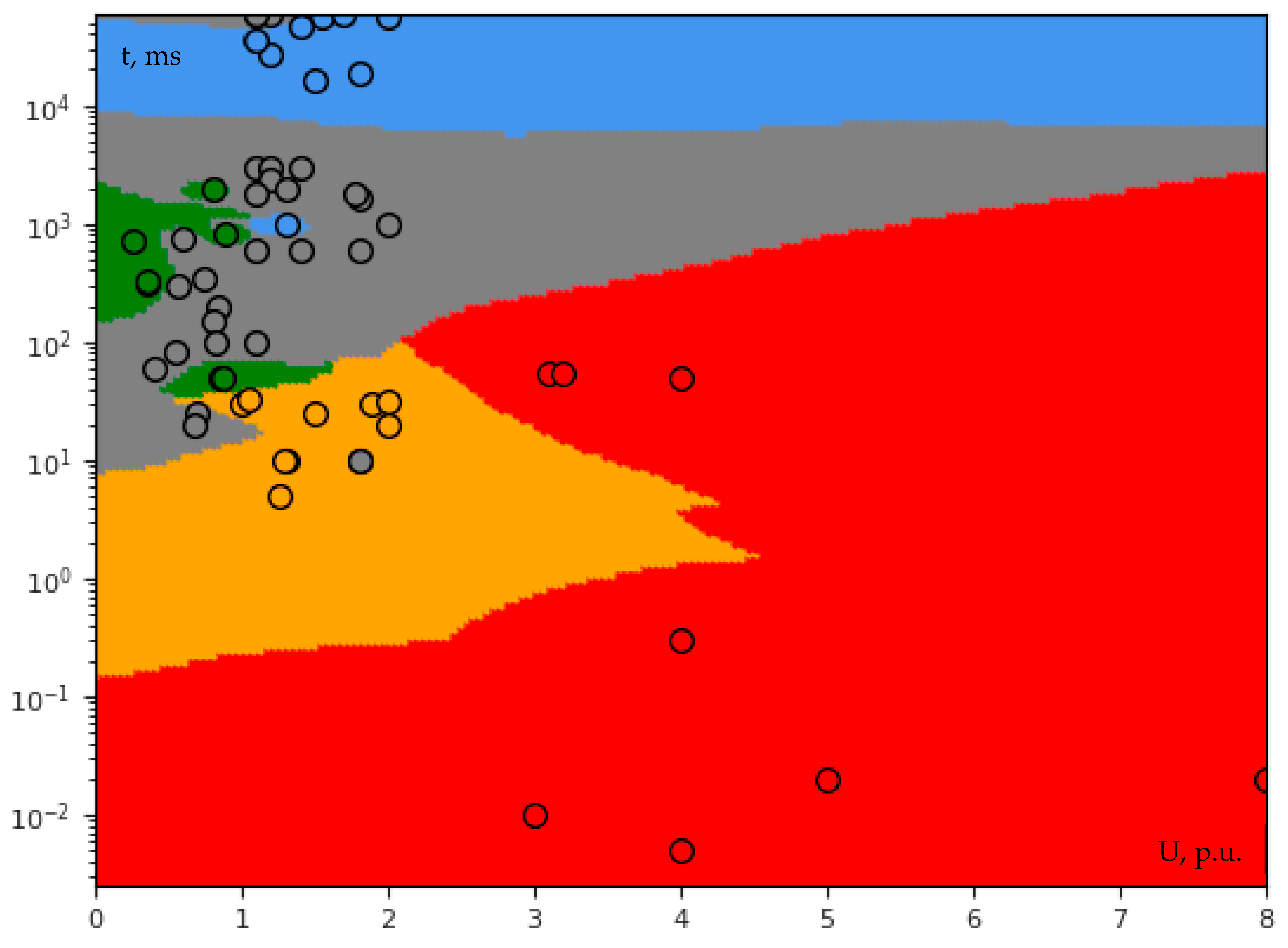
3.2. Classification
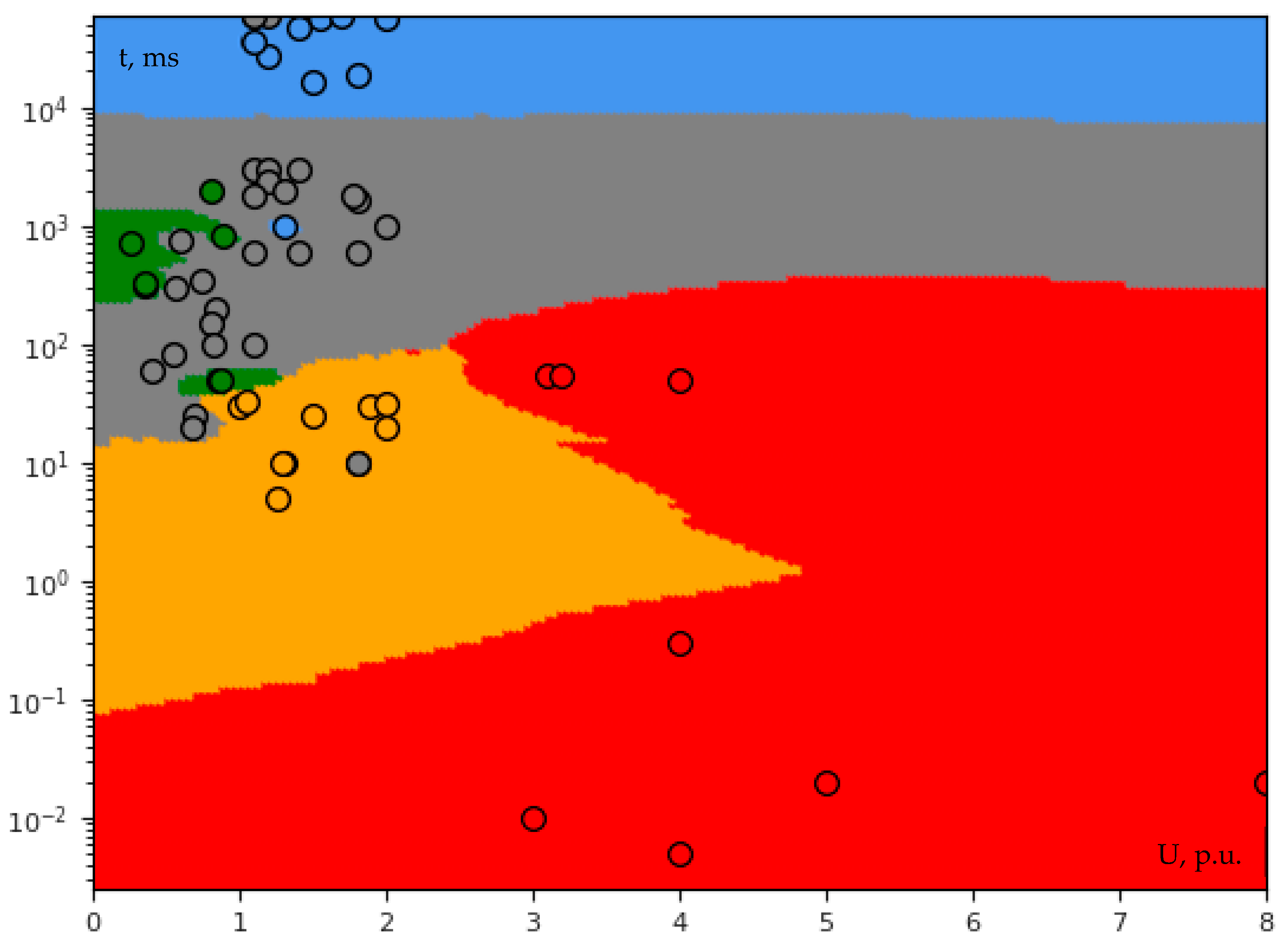
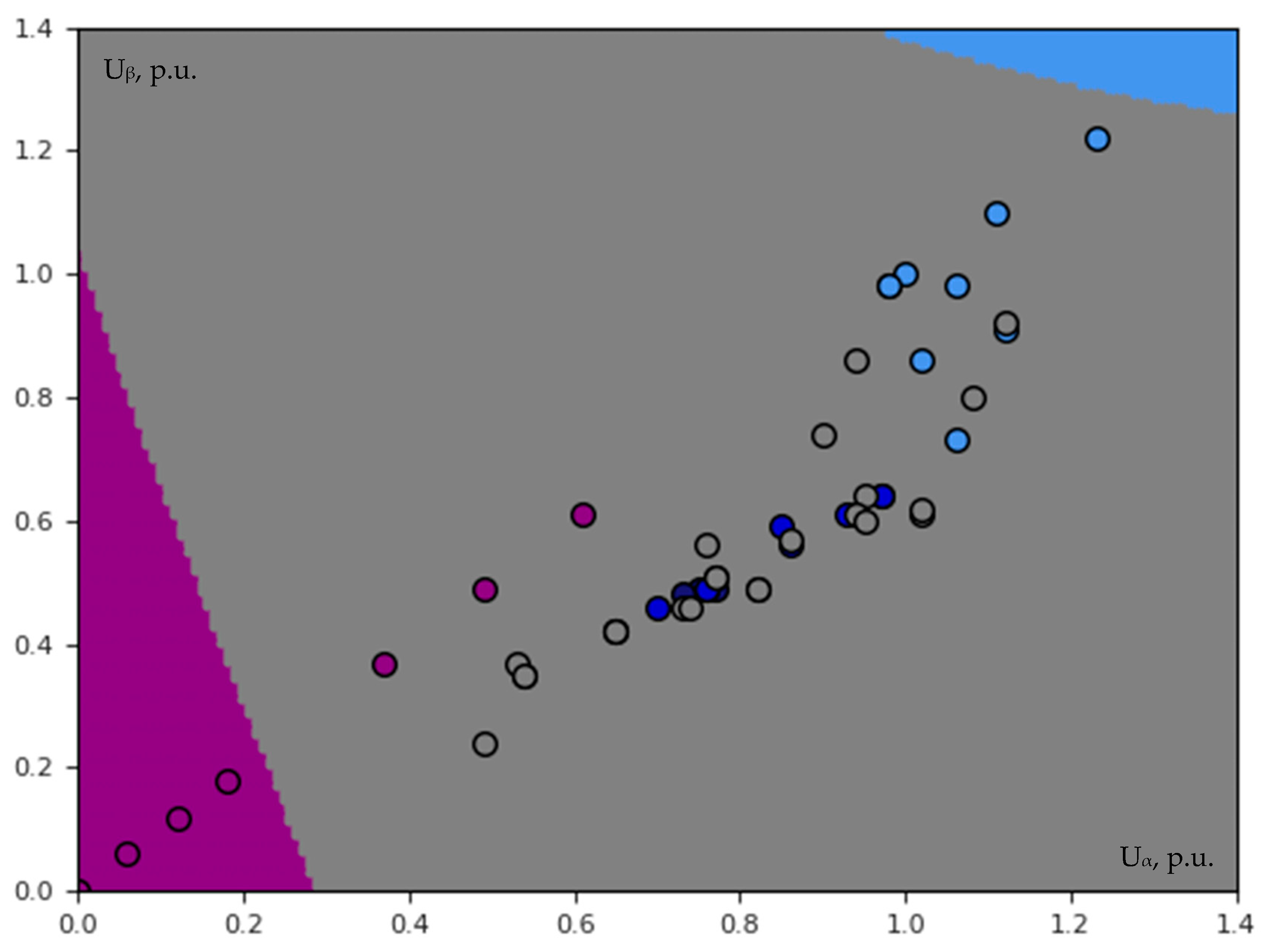
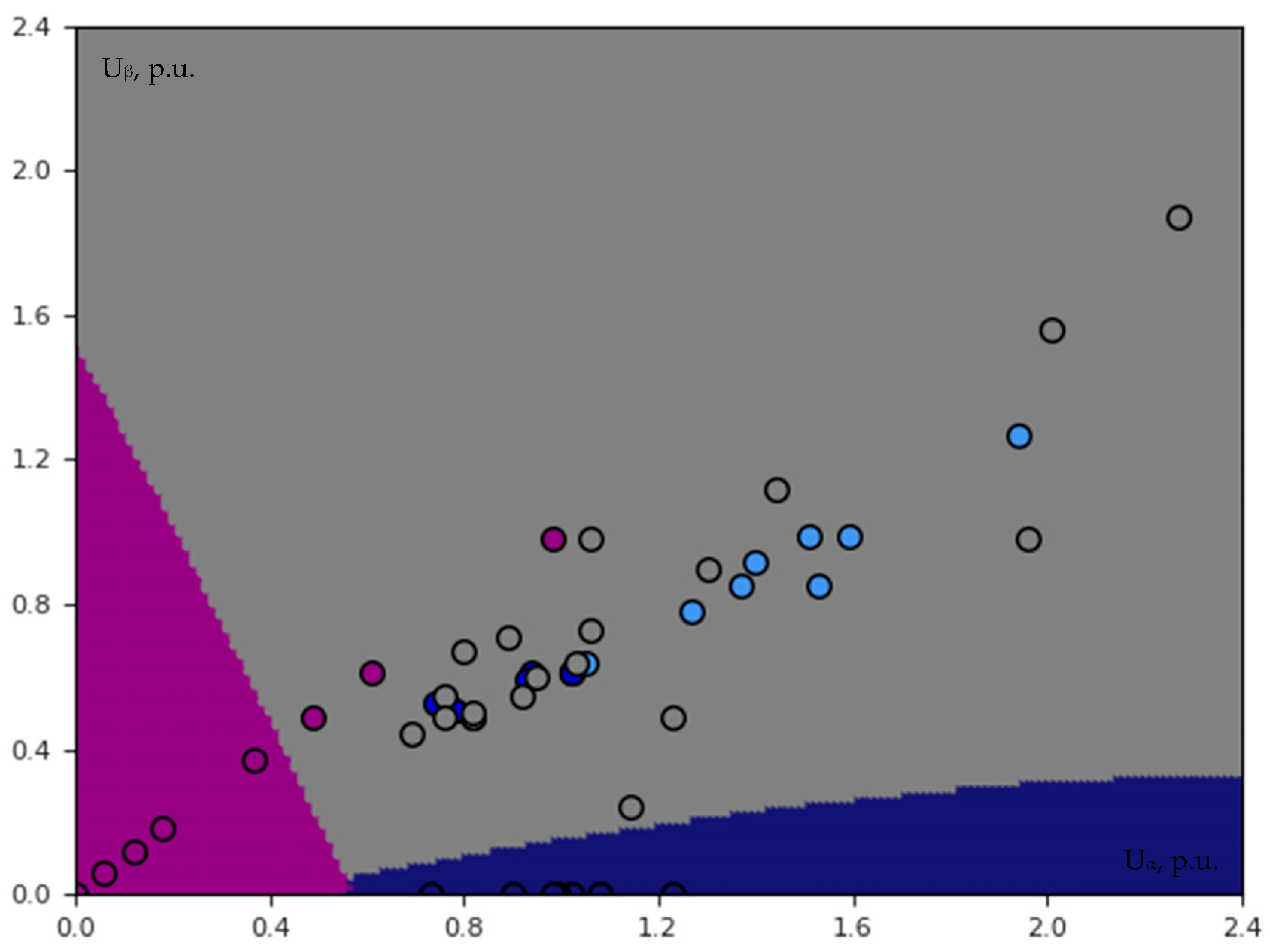
3.2.1. Single-Voltage Classification
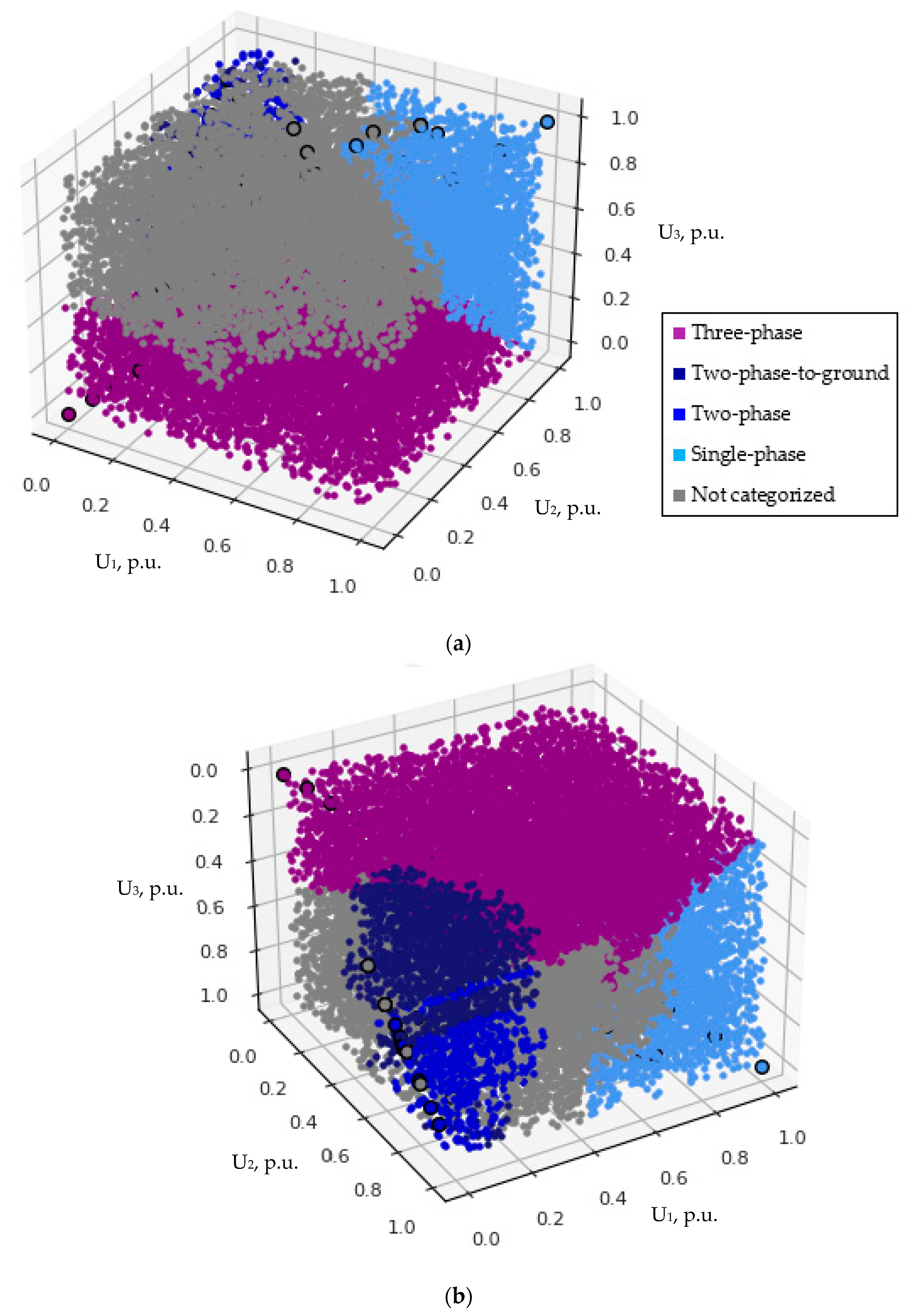
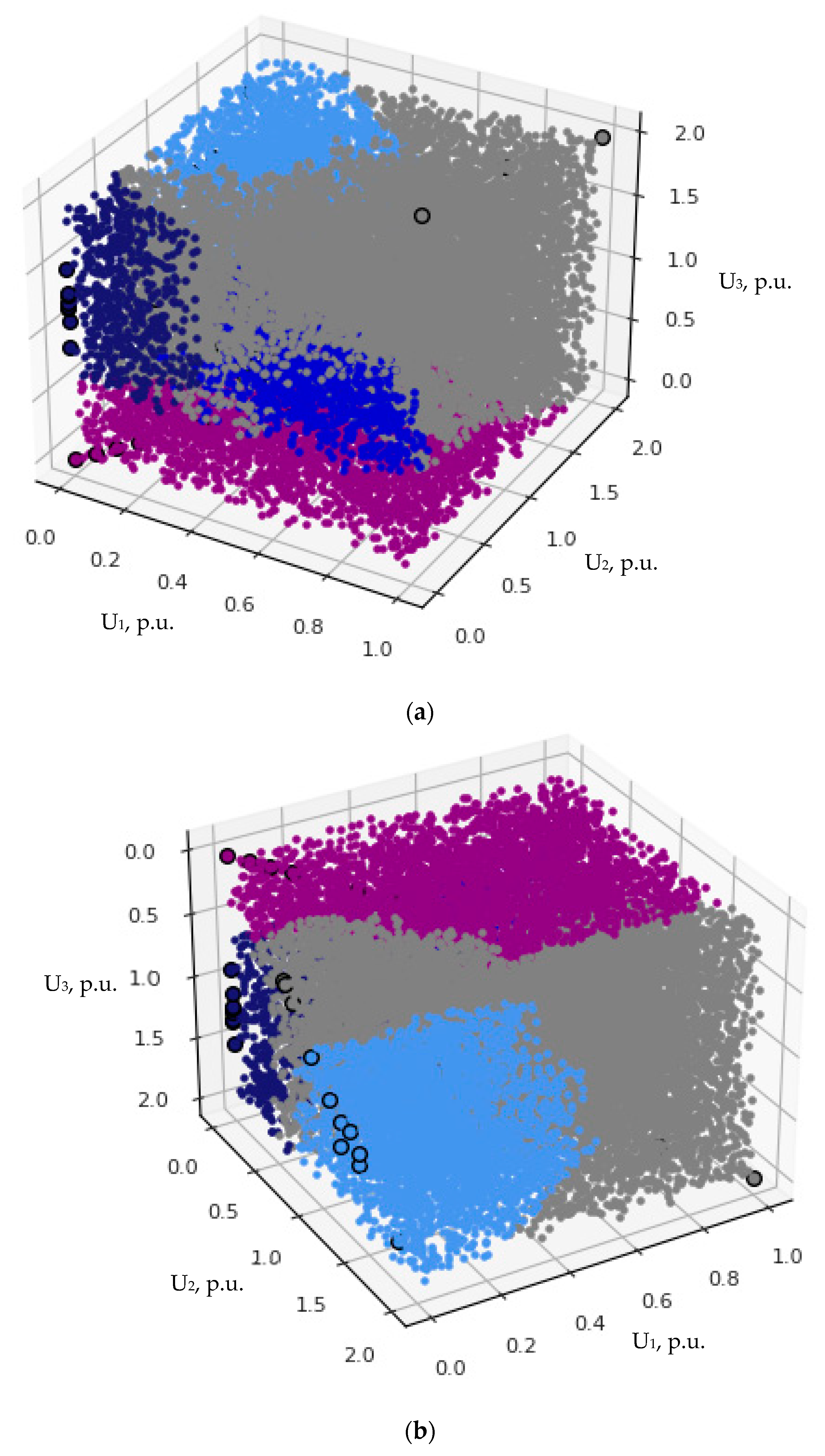
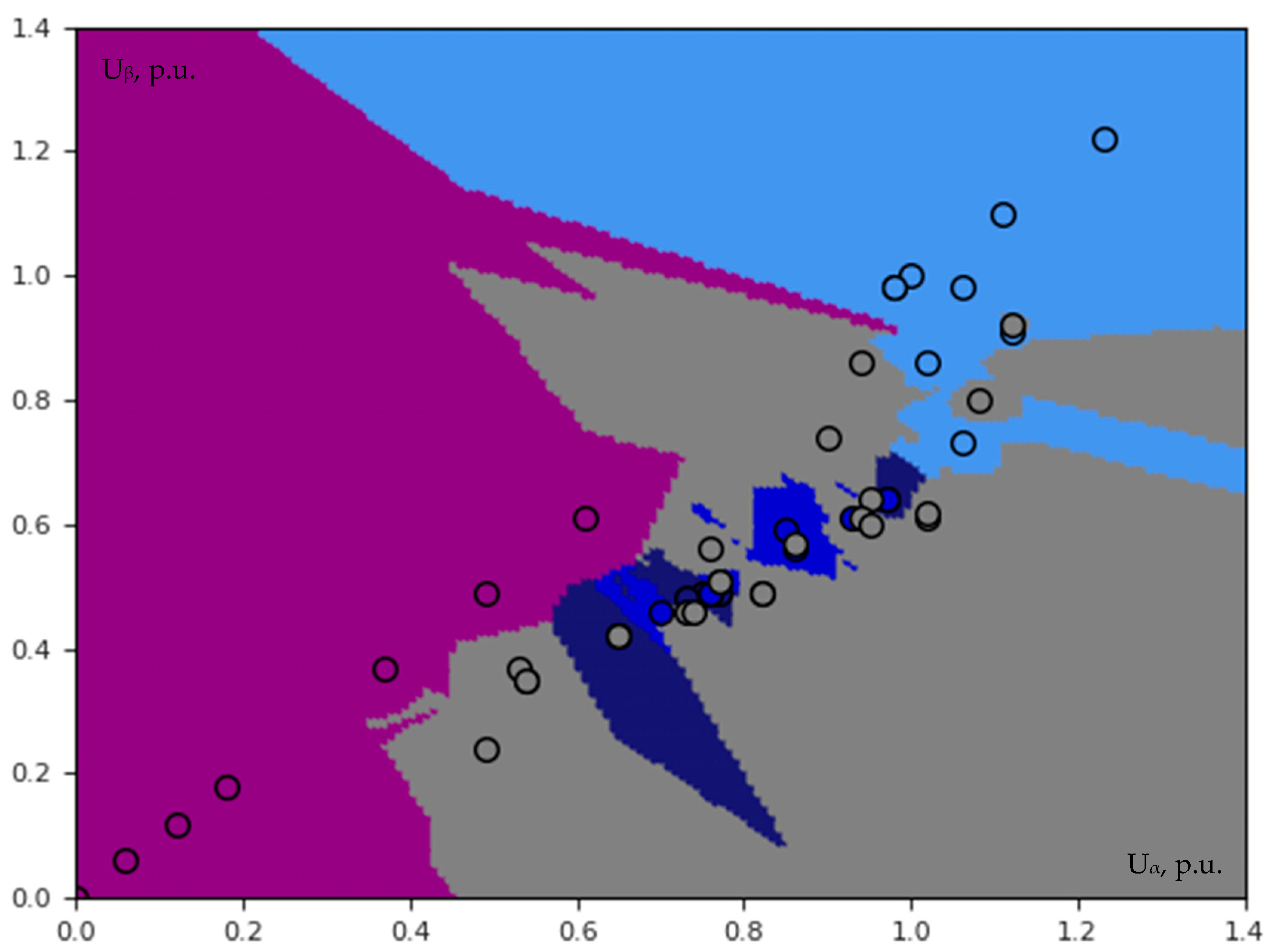
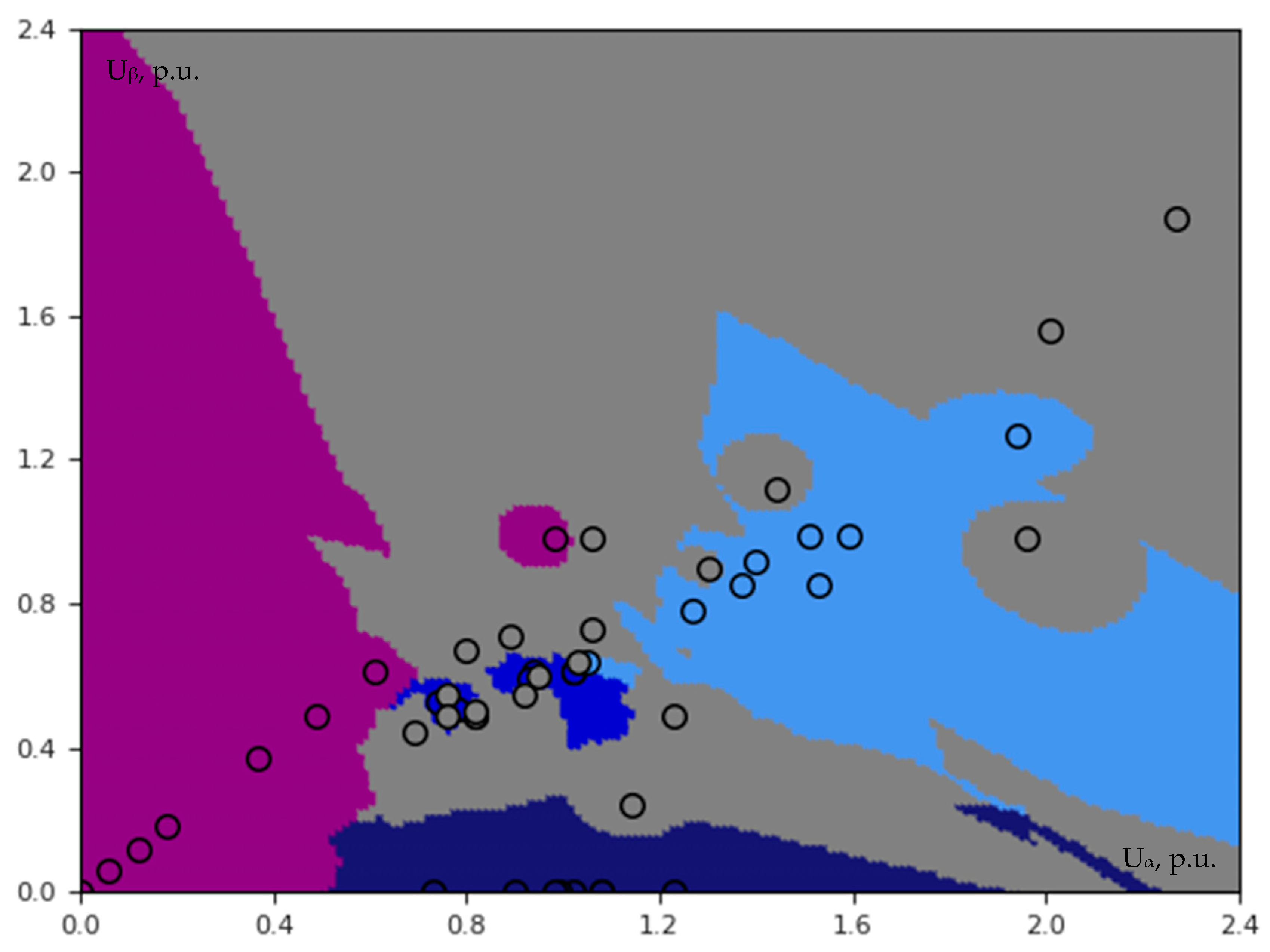
3.2.2. Three-Dimensional Voltage Classification
- In the case of a three-phase fault (Figure 23a), all points lie on the line belonging to the plane which forms the angles of 45° with both abscissa and ordinate.
- In the case of a two-phase-to-ground fault (Figure 23b), all points (of both phase-to-phase and phase-to-ground voltages) belong to the same coordinate hyperplane, i.e., are coplanar (see Equation (34)), which is defined by the pair of ordinate and applicate.
- In the case of a two-phase fault (Figure 23c), the phase-to-phase pattern is identical to the case of a two-phase-to-ground fault, while phase-to-ground points are encircled with the ellipse lying in the plane which forms the angles of 45° with both the abscissa and ordinate (analogously to the case of a three-phase fault).
- In the case of a single-phase fault (Figure 23d), phase-to-phase points are covered with one half of the paraboloid, while phase-to-ground points are encircled with the ellipse lying in the coordinate hyperplane defined by the pair of ordinate and applicate.
4. Discussion
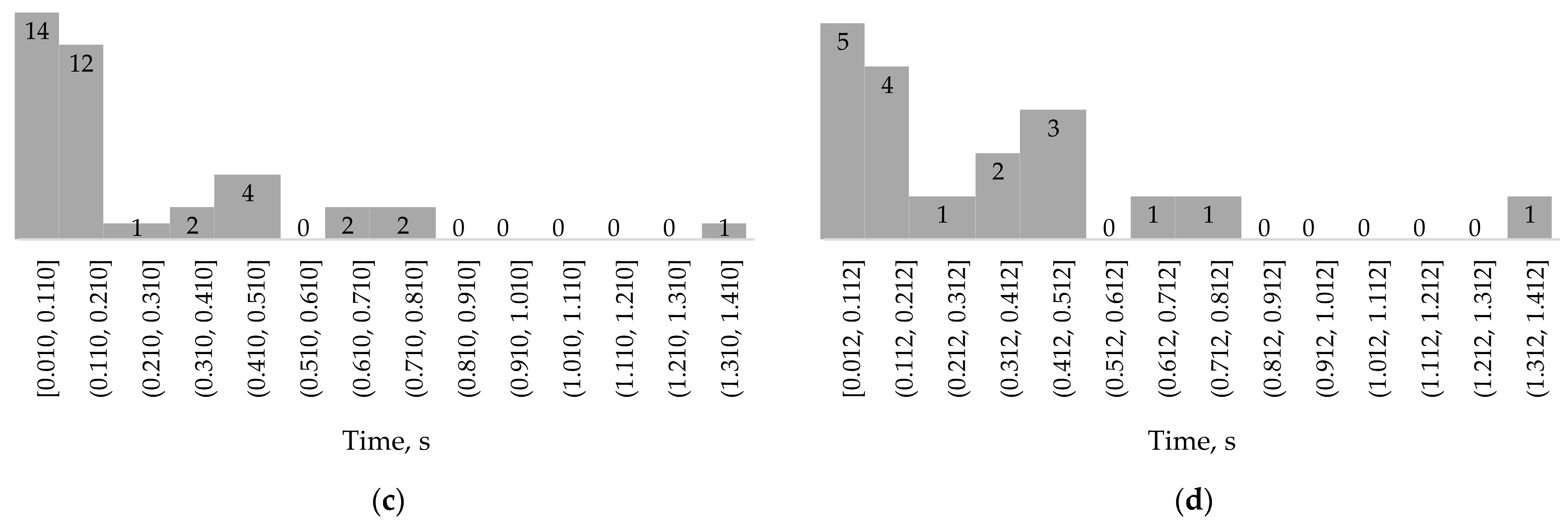
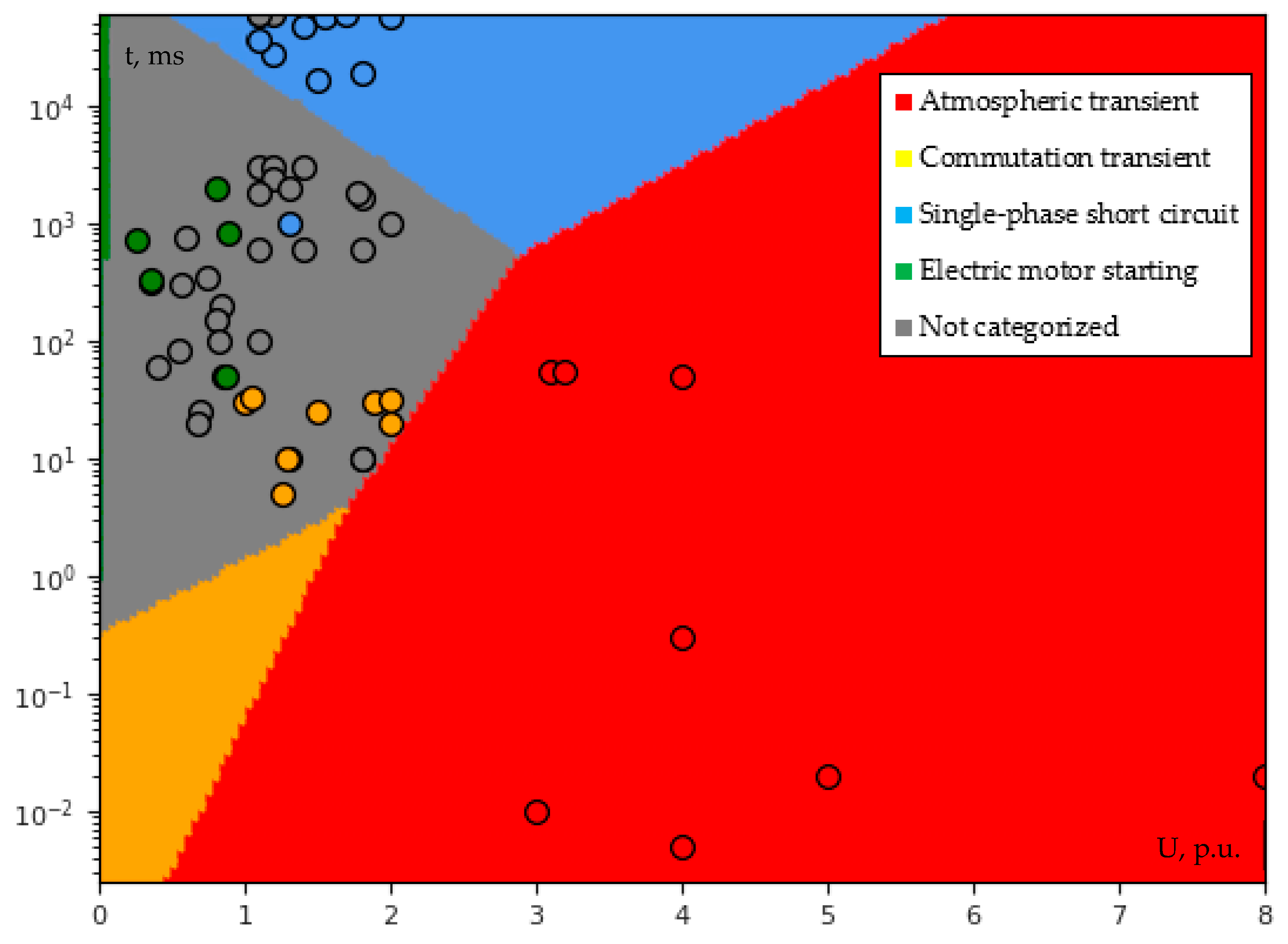
4.1. PQ Events Assessment
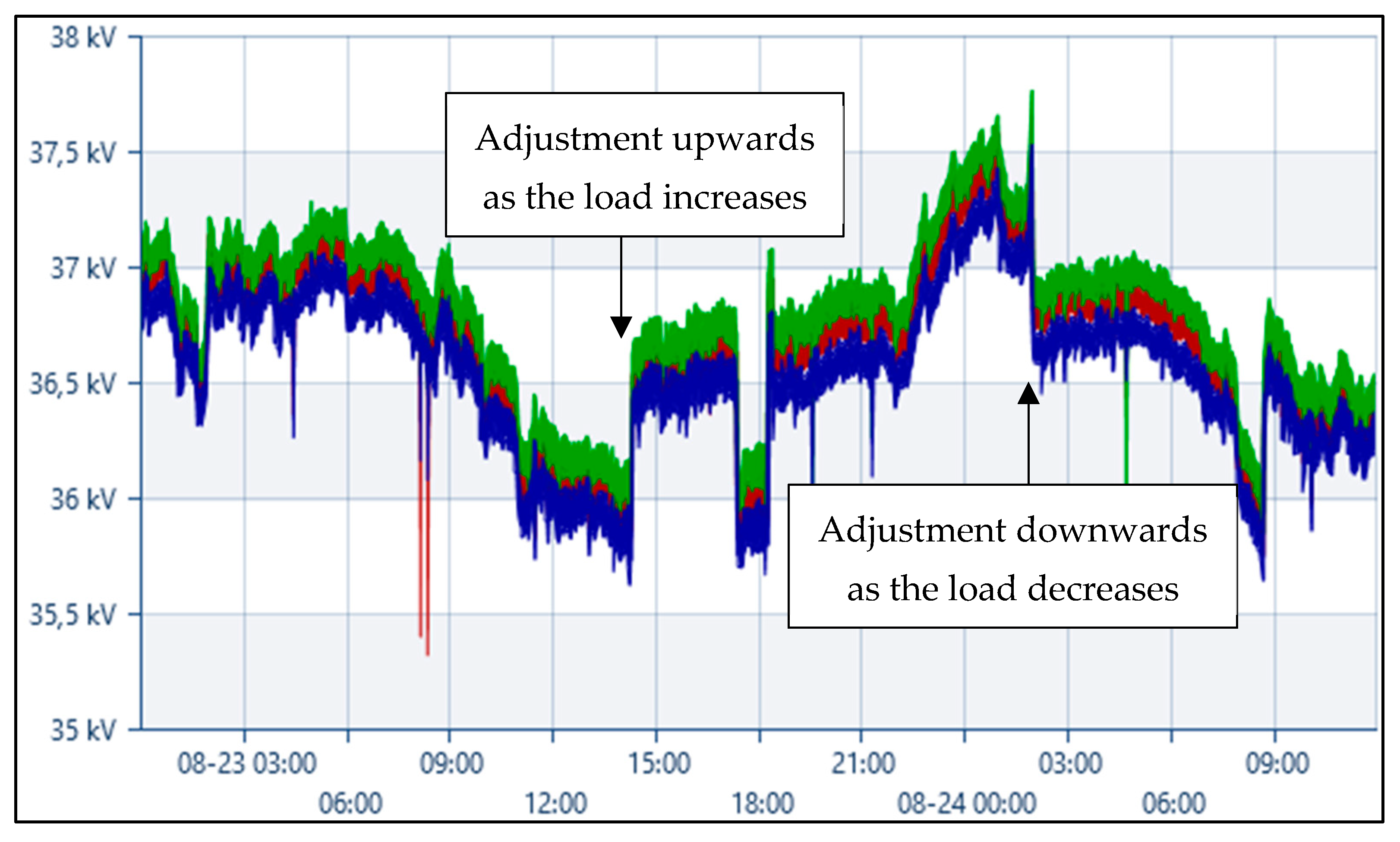
4.2. PQ—Part of Smart Grid and Its Communication Network
- Trial sites can have poor communication, hence: (1) this criterion should be considered during trial sites selection; (2) alternative sites with better communication should be considered; and (3) the availability of communication alternatives should be ensured. Surveys revealed that no single cellular network operator is capable of covering all sites, in particular with 4G LTE. In this case, roaming SIM cards can be used; thus, the communication hub will be able to utilize an available provider at each site.
- IEC 61850 can be implemented differently (particularly in terms of file transfer mechanisms), and this is not essentially desirable. Moreover, in the case of IEC 61850 usage, the monitor sometimes is unable to reply to all requests. This can lead to (small) data loss, which subsequently cannot be retrieved.
- The episodic instability of one monitor was solved by developing a method of remote triggering. This allows avoiding site visits when a reset is needed.
- Since PQ data do not need to be transmitted continuously, file transfer is preferred because it can be carried out asynchronously. This approach requires less resources and is more robust (resilient) to a temporary loss of communication.
- Monitors installation has been sped up by pre-configuring and pre-commissioning them and communication hubs prior to traveling to site.
- In comparison with more commonly used CSV and JSON file formats, the HDF format offers several advantages such as faster data retrieval, storage and memory saving.
4.3. Further Development of the Algorithms
4.3.1. Mathematical Methods
4.3.2. Integration with Other Applications: Case of PM of Grid Insulation
5. Conclusions
- Research on the fundamental grid component removal from a PQ signal has not been found in the existing literature. However, data processing with an IIR shelving filter showed that such filtering distorts PQ signals and converts them to the unsuitable form for a further analysis: (1) when is set to 1 Hz, a filter’s transient process lasts a relatively long time, concealing the signal, and (2) when is set to 25 Hz, the duration of the transient process is minimized but unfortunately in exchange for frequency response quality.
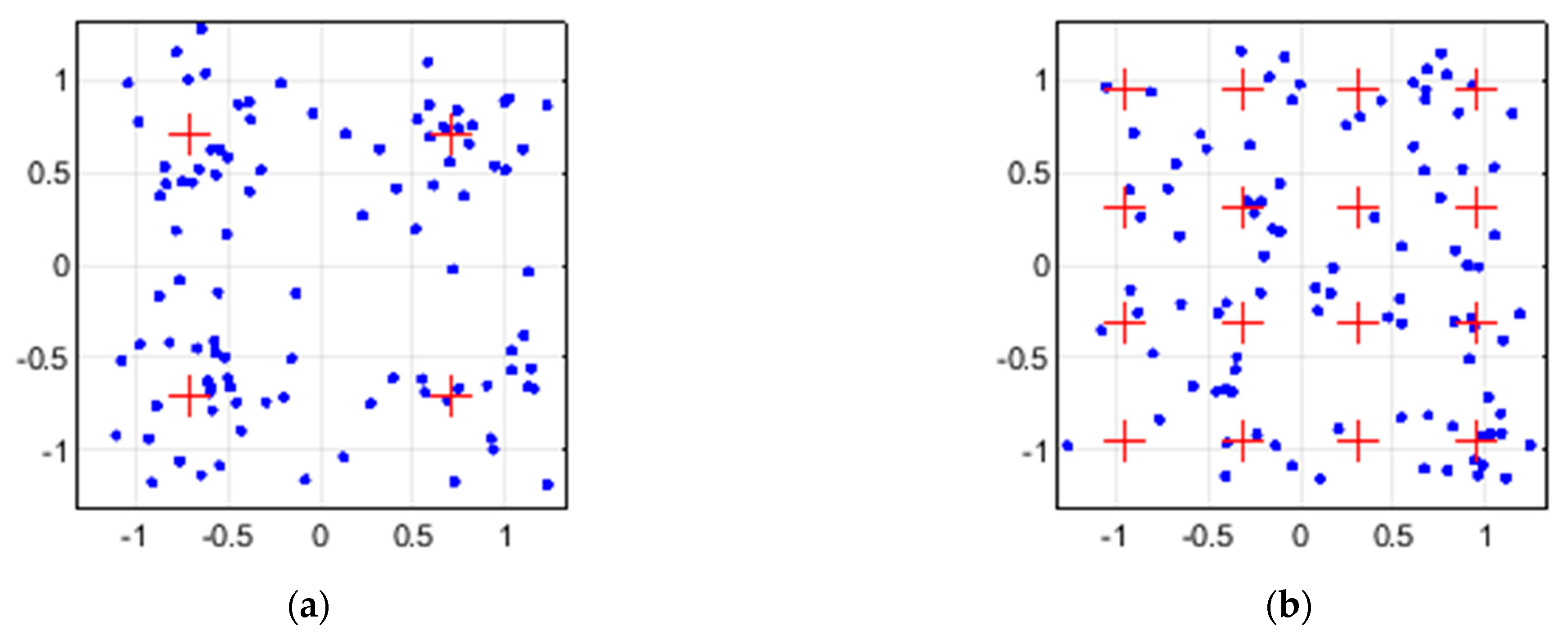
- Contrary to biometrics, a large database is not always needed for PQ machine learning. On the other hand, it is more difficult to create a high-quality PQ database due to insufficient PQ events occurrence frequency (especially at a single grid node), which highly correlates with the difficulty in covering all possible scenarios (situations). The results provided by KNN are much more satisfying than SVM; however, it does not mean that KNN alone can successfully cope with all arising classification challenges, for example, with clusters overlapping which perhaps could be solved by both AI ensemble and adding more additional dimensions to the feature vector.
- The proposed unique approach of three-dimensional voltage classification is a successful outcome achieved by using the simulation results presented in [9], and the geometric analysis of the feature clusters highlighted certain patterns, which has the potential to bring the problem significantly closer to successful completion. Moreover, developed the Clarke transformation-based method showed outstanding results; thus, it can be considered as a promising tool suitable for the simplification of short circuit data analysis in three-dimensional space. In order to successfully implement all proposed mathematical operations, it is important to maintain the same order of elements in the vectors.
- At present, many methodological gaps in PQ assessment inhibit AI application. Some of them have been noticed during the analysis of PQ data measured in the Lithuanian DSO grid: for example, regarding a multistage voltage sag, voltage sag burst, voltage sag followed by a power line disconnection, etc. It should be underlined that the majority of these solutions must be universally agreed upon in the form of PQ law amendments. It is noteworthy that such a discussion as that given in Section 4.1 is presented for the first time in the scientific literature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Khokhar, S.; Mohd Zin, A.A.B.; Mokhtar, A.S.B.; Pesaran, M. A Comprehensive Overview on Signal Processing and Artificial Intelligence Techniques Applications in Classification of Power Quality Disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Liubčuk, V.; Radziukynas, V.; Naujokaitis, D.; Kairaitis, G. Grid Nodes Selection Strategies for Power Quality Monitoring. Appl. Sci. 2023, 13, 6048. [Google Scholar] [CrossRef]
- McCorduk, P. Machines Who Think: A Personal Inquiry into the History and Prospects of Artificial Intelligence, 2nd ed.; A K Peters: Natick, MA, USA, 2004. [Google Scholar]
- Egypt Independent. Ancient Egyptians Invented First Robot 4000 Years Ago: Study. Available online: https://egyptindependent.com/ancient-egyptians-invented-first-robot-4000-years-ago-study (accessed on 30 September 2023).
- Maspero, G. Manual of Egyptian Archaeology and Guide to the Study of Antiquities in Egypt; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Aristotle. Aristotle’s Politics; Clarendon Press: Oxford, UK, 1885. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Pearson Education: London, UK, 2016. [Google Scholar]
- Hasija, Y. Artificial Intelligence and Digital Pathology Synergy: For Detailed, Accurate and Predictive Analysis of WSIs. In Proceedings of the 8th ICACCS, Coimbatore, India, 25–26 March 2022. [Google Scholar]
- Liubčuk, V.; Radziukynas, V.; Kairaitis, G.; Naujokaitis, D. Power Quality Monitors Displacement Based on Voltage Sags Propagation Mechanism and Grid Reliability Indexes. Appl. Sci. 2023, 13, 11778. [Google Scholar] [CrossRef]
- LST EN 61000-4-30:2015; Electromagnetic Compatibility (EMC)—Part 4–30: Testing and Measurement Techniques—PQ Measurement Methods (IEC 61000-4-30:2015). Lithuanian Standards Board: Vilnius, Lithuania, 2016.
- EN 50160:2010; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. CENELEC: Brussels, Belgium, 2010.
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE: New York, NY, USA, 2019.
- IEEE Std 1564-2014; IEEE Guide for Voltage Sags Indices. IEEE: New York, NY, USA, 2014.
- Kezunovic, M.; Liao, Y. A New Method for Classification and Characterization of Voltage Sags. Electr. Power Syst. Res. 2001, 58, 27–35. [Google Scholar] [CrossRef]
- Huang, N.; Peng, H.; Cai, G.; Chen, J. Power Quality Disturbances Feature Selection and Recognition Using Optimal Multi-Resolution Fast S-Transform and CART Algorithm. Energies 2016, 9, 927. [Google Scholar] [CrossRef]
- Khetarpal, P.; Tripathi, M.M. A Critical and Comprehensive Review on Power Quality Disturbance Detection and Classification. Sustain. Comput. Inform. Syst. 2020, 28, 100417. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, Y.; Li, Y.; Cao, H. A New Method for Recognition and Classification of Power Quality Disturbances Based on IAST and RF. Electr. Power Syst. Res. 2024, 226, 109939. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, C.; Chai, Z.; He, Y. Adversarial Attack and Training for Deep Neural Network Based Power Quality Disturbance Classification. Eng. Appl. Artif. Intell. 2024, 127, 107245. [Google Scholar] [CrossRef]
- Khan, M.A.; Asad, B.; Vaimann, T.; Kallaste, A.; Pomarnacki, R.; Hyunh, V.K. Improved Fault Classification and Localization in Power Transmission Networks Using VAE-Generated Synthetic Data and Machine Learning Algorithms. Machines 2023, 11, 963. [Google Scholar] [CrossRef]
- Fu, L.; Deng, X.; Chai, H.; Ma, Z.; Xu, F.; Zhu, T. PQEventCog: Classification of Power Quality Disturbances Based on Optimized S-Transform and CNNs with Noisy Labeled Datasets. Electr. Power Syst. Res. 2023, 220, 109369. [Google Scholar] [CrossRef]
- Khetarpal, P.; Tripathi, M.M. Power Quality Disturbance Classification Taking into Consideration the Loss of Data during Pre-Processing of Disturbance Signal. Electr. Power Syst. Res. 2023, 220, 109372. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, T.; Mohamed, M.A. A Novel Dual-Attention Optimization Model for Points Classification of Power Quality Disturbances. Appl. Energy 2023, 339, 121011. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Tian, D.; Lou, J.; Chen, Y.; Liu, X. Assessment of Voltage Sag/Swell in the Distribution Network Based on Energy Index and Influence Degree Function. Electr. Power Syst. Res. 2023, 216, 109072. [Google Scholar]
- Lin, W.-M.; Wu, C.-H. Fast Support Vector Machine for Power Quality Disturbance Classification. Appl. Sci. 2022, 12, 11649. [Google Scholar] [CrossRef]
- Salles, R.S.; Ribeiro, P.F. The Use of Deep Learning and 2-D Wavelet Scalograms for Power Quality Disturbances Classification. Electr. Power Syst. Res. 2023, 214, 108834. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Zhou, Y. Ensemble Deep Learning for Automated Classification of Power Quality Disturbances Signals. Electr. Power Syst. Res. 2022, 213, 108695. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Miraftabzadeh, S.M.; Bollen, M.H.J.; Longo, M. Voltage-Sag Source Detection: Developing Supervised Methods and Proposing a New Unsupervised Learning. Sustain. Energy Grids Netw. 2022, 32, 100855. [Google Scholar] [CrossRef]
- Upadhya, M.; Singh, A.K.; Thakur, P.; Nagata, E.A.; Ferreira, D.D. Mother Wavelet Selection Method for Voltage Sag Characterization and Detection. Electr. Power Syst. Res. 2022, 211, 108246. [Google Scholar] [CrossRef]
- Yang, L.; Guo, L.; Zhang, W.; Yang, X. Classification of Multiple Power Quality Disturbances by Tunable-Q Wavelet Transform with Parameter Selection. Energies 2022, 15, 3428. [Google Scholar] [CrossRef]
- Turonović, R.; Dragan, D.; Gojić, G.; Petrović, V.B.; Gajić, D.B.; Stanisavljević, A.M.; Katić, V.A. An End-to-End Deep Learning Method for Voltage Sag Classification. Energies 2022, 15, 2898. [Google Scholar] [CrossRef]
- Mohstaham, M.B.; Jalilian, A. Classification of Multi-Stage Voltage Sags and Calculation of Phase Angle Jump Based on Clarke Components Ellipse. Electr. Power Syst. Res. 2022, 205, 107725. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhou, X. Classification of Power Quality Disturbances Using Visual Attention Mechanism and Feed-Forward Neural Network. Measurements 2022, 188, 110390. [Google Scholar] [CrossRef]
- Chamchuen, S.; Siritaratiwat, A.; Fuangfoo, P.; Suthisopapan, P.; Khunkitti, P. High-Accuracy Power Quality Disturbance Classification Using the Adaptive ABC-PSO As Optimal Feature Selection Algorithm. Energies 2021, 14, 1238. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Salarpour, A.; Leborgne, R.C. Comprehensive Strategy for Classification of Voltage Sags Source Location Using Optimal Feature Selection Applied to Support Vector Machine and Ensemble Techniques. Electr. Power Energy Syst. 2021, 124, 106363. [Google Scholar] [CrossRef]
- Khoa, N.M.; Dai, L.V. Detection and Classification of Power Quality Disturbances in Power System Using Modified-Combination between the Stockwell Transform and Decision Tree Methods. Energies 2020, 13, 3623. [Google Scholar] [CrossRef]
- Nagata, E.A.; Ferreira, D.D.; Bollen, M.H.J.; Barbosa, B.H.C.; Ribeiro, E.G.; Duque, C.A.; Ribeiro, P.F. Real-Time Voltage Sag Detection and Classification for Power Quality Diagnostics. Measurements 2020, 164, 108097. [Google Scholar] [CrossRef]
- Bravo-Rodríguez, J.C.; Torres, F.J.; Borrás, M.D. Hybrid Machine Learning Models for Classifying Power Quality Disturbances: A Comparative Study. Energies 2020, 13, 2761. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Z.; Che, Y. Power Quality Disturbances Classification Based on DWT and Multilayer Perceptron Extreme Learning Machine. Appl. Sci. 2019, 9, 2315. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Q.S.; Zhang, G.L.; Liu, W.; Chen, F.R. Adaptive S Transform for Feature Extraction in Voltage Sags. Appl. Soft Comput. 2019, 80, 438–449. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Z.; Che, Y. Power Quality Disturbance Classification Based on Compressed Sensing and Deep Convolution Neural Networks. IEEE Access 2019, 7, 78336–78346. [Google Scholar] [CrossRef]
- Pukys, P. Teorinė Elektrotechnika II, 4th ed.; Bartkevičius, S., Lazauskas, V., Pukys, P., Stonys, J., Virbalis, A., Eds.; Kaunas University of Technology—Publishing House “Technologija”: Kaunas, Lithuania, 2011. [Google Scholar]
- Baublys, J.; Jankauskas, P.; Marckevičius, L.A.; Morkvėnas, A. Izoliacija ir Viršįtampiai; Kaunas University of Technology—Publishing House “Technologija”: Kaunas, Lithuania, 2008. [Google Scholar]
- LST EN 62305-1:2011; Protection Against Lightning—Part 1: General Principles (IEC 62305-1:2010). Lithuanian Standards Board: Vilnius, Lithuania, 2011.
- Vejuvić, S.; Lovrić, D. Exponential Approximation of the Heidler Function for the Reproduction of Lightning Current Waveshapes. Electr. Power Syst. Res. 2010, 80, 1293–1298. [Google Scholar] [CrossRef]
- Yu, Z.; Zhu, T.; Wang, Z.; Lu, G.; Zeng, R.; Liu, Y.; Luo, J.; Wang, Y.; He, J.; Zhuang, C. Calculation and Experiment of Induced Lightning Overvoltage on Power Distribution Line. Electr. Power Syst. Res. 2016, 139, 52–59. [Google Scholar] [CrossRef]
- Evdokunin, G.A.; Petrov, N.N. Lightning-Induced Voltage on Overheard Lines. In Proceedings of the 2016 ElConRusNW, St. Petersburg, Russia, 2–3 February 2016. [Google Scholar]
- IEEE Std 998-2012; IEEE Guide for Direct Lightning Stroke Shielding of Substations. IEEE: New York, NY, USA, 2013.
- Pedra, J.; Sainz, L.; Córdoles, F. Effects of Symmetrical Voltage Sag on Squirrel-Cage Induction Motors. Electr. Power Syst. Res. 2007, 77, 1672–1680. [Google Scholar] [CrossRef]
- Silva, B.F.; Vanço, W.E.; Da Silva Gonçalves, F.A.; Bissochi, C.A., Jr.; De Carvalho, D.P.; Guimarães, G.C. A Proposal for the Study of Voltage Sag in Isolated Synchronous Generators Caused by Induction Motor Start-up. Electr. Power Syst. Res. 2016, 140, 776–785. [Google Scholar] [CrossRef]
- Hashem, M.; Abdel-Salam, M.; Nayel, M.; El-Mohandes, M.T. Mitigation of Voltage Sag in a Distribution System During Start-up of Water-Pumping Motors Using Superconducting Magnetic Energy Storage: A Case Study. J. Energy Storage 2022, 55, 105441. [Google Scholar] [CrossRef]
- Boльдек, А.И. Электрические Мaшины, 3rd ed.; Тoлвинскaя, E.B., Ed.; «Энергия»: Leningrad, Russia, 1978. [Google Scholar]
- Marozas, V. (Biomedical Engineering Institute of Kaunas University of Technology, Kaunas, Lithuania). Personal communication, 2018. [Google Scholar]
- Orfanidis, S.J. Introduction to Signal Processing; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Haykin, S. (Ed.) Neural Networks and Learning Machines, 3rd ed.; Person Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Using a Hard Margin vs Soft Margin in Support Vector Machines. Available online: https://www.section.io/engineering-education/using-a-hard-margin-vs-soft-margin-in-support-vector-machines (accessed on 17 November 2023).
- Using a Hard Margin vs. Soft Margin in SVM. Available online: https://www.baeldung.com/cs/svm-hard-margin-vs-soft-margin (accessed on 17 November 2023).
- MathWorks. Clarke and Park Transforms. Available online: https://se.mathworks.com/solutions/electrification/clarke-and-park-transforms.html (accessed on 15 November 2023).
- MathWorks. Park Transform. Available online: https://se.mathworks.com/help/sps/ref/parktransform.html (accessed on 15 November 2023).
- De Santis, M.; Di Stasio, L.; Noce, C.; Varilone, P.; Verde, P. Indices of Intermittence to Improve the Forecasting of the Voltage Sags Measured in Real Systems. IEEE Trans. Power Deliv. 2021, 37, 1252–1263. [Google Scholar] [CrossRef]
- Council of European Energy Regulators. 5th CEER Benchmarking Report on the Quality of Electricity and Gas Supply; CEER: Brussels, Belgium, 2011. [Google Scholar]
- Svinkūnas, G.; Navickas, A. Elektros Energetikos Pagrindai, 2nd ed.; Kaunas University of Technology—Publishing House “Technologija”: Kaunas, Lithuania, 2013. [Google Scholar]
- Kundur, P. Power Systems Stability and Control, 1st ed.; Balu, N.J., Lauby, M.G., Eds.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Western Power Distribution. Primary Networks Power Quality Analysis. Six Monthly Project Progress Reports, 2018–2021. Available online: https://www.westernpower.co.uk/projects/primary-networks-power-quality-analysis-pnpqa (accessed on 5 May 2021).
- LST EN 61000-4-5:2014; Electromagnetic Compatibility (EMC)—Part 4–5: Testing and Measurement Techniques—Surge Immunity Test (IEC 61000-4-5:2014). Lithuanian Standards Board: Vilnius, Lithuania, 2014.
- What Is True RMS Measurement? Available online: https://www.electricalvolt.com/2018/09/what-is-true-rms-measurement/?utm_content=cmp-true (accessed on 22 October 2023).
- What Do RMS and True RMS Stand for? Available online: https://www.promaxelectronics.com/ing/news/561/what-do-rms-and-true-rms-stand-for-here-we-explain-you-the-differences (accessed on 22 October 2023).
- Ponce-Jara, M.A.; Ruiz, E.; Gil, R.; Sancristóbal, E.; Pérez-Molina, C.; Castro, M. Smart Grid: Assessment of the Past and Present in Developed and Developing Countries. Energy Strat. Rev. 2017, 18, 38–58. [Google Scholar] [CrossRef]
- Kašėta, S. Telekomunikacijų Teorija; Kaunas University of Technology—Publishing House “Technologija”: Kaunas, Lithuania, 2012. [Google Scholar]
- Communications Regulatory Authority of the Republic of Lithuania. Expected Coverage Areas of Cellular Networks. Available online: https://www.rrt.lt/judriojo-rysio-tinklu-tiketinos-aprepties-zonos/?highlight=RSRP (accessed on 10 October 2023).
- Faheem, M.; Shah, S.B.H.; Butt, R.A.; Raza, B.; Anwar, M.; Ashraf, M.W.; Ngadi, M.A.; Gungor, V.C. Smart Grid Communication and Information Technologies in the Perspective of Industry 4.0: Opportunities and Challenges. Comput. Sci. Rev. 2018, 30, 1–30. [Google Scholar] [CrossRef]
- IEEE Std 2030-2011; IEEE Guide for Smart Grid Interoperability of Energy Technology and Information Technology Operation with the Electric Power System (EPS), End-Use Applications, and Loads. IEEE: New York, NY, USA, 2011.
- IEEE Std 1159.3-2019; IEEE Recommended Practice for Power Quality Data Interchange Format (PQDIF). IEEE: New York, NY, USA, 2019.
- Youtube. Complex Integration, Cauchy and Residue Theorems [Video]. Available online: https://www.youtube.com/watch?v=EyBDtUtyshk (accessed on 23 November 2023).
- Kurienė, A. Chemija. In Trumpas Chemijos Kursas; “Gimtinė”: Vilnius, Lithuania, 1999. [Google Scholar]













| Reference 1 | Algorithm 2 | Task 3 | Target Group 4 | Data 5 | Parameters, Features | ||||
|---|---|---|---|---|---|---|---|---|---|
| [17] (2023) | ST, RF | C | ImT | OsT | Int | Sg | S, R | Maximum magnitudes (peaks) of FFT spectrum of the signal 6 | |
| Sw | F | H | N | C | |||||
| [18] (2023) | CNN-LSTM | C, S 7 | ImT | OsT | Int | Sg | S | Deep features of 1D time series signal 8 | |
| Sw | F | H | C | ||||||
| [19] (2023) | DT, KNN, RF, SVM, VAE | C, L 9 | Sg 10 | S 11 | Current, voltage, fault type and location | ||||
| Sw 10 | |||||||||
| [20] (2023) | CNN, ST | C | ImT | Sp 12 | OsT | Int | Sg | S, R | Deep features of 2D time–frequency matrix |
| Sw | F | H | N | C | |||||
| [21] (2023) | OFDT, PCA | C | Sp | OsT | Int | Sg | S | Power spectrum estimated by Welch’s method | |
| Sw | F | H | N | ||||||
| [22] (2023) | CNN, HT | C | ImT | OsT | Int | Sg | S, R 14 | Deep features of voltage amplitude envelope | |
| Sw | F 13 | H | N | C | |||||
| [23] (2022) | Not applicable | A | Sg | S | Voltage, time, energy index, influence degree (severity) | ||||
| Sw | |||||||||
| [24] (2022) | Fast SVM | C | Int | Sg | S | The input is the amplitude of one cycle of the distorted wave | |||
| Sw | H | C | |||||||
| [25] (2022) | 2D WT, CNN 15 | C | ImT | OsT | Int | Sg | S | Deep features of the colored image of the time–frequency plane | |
| Sw | |||||||||
| [26] (2022) | LSTM | C | ImT | Sp | OsT | Int | Sg | S | The input is the raw sample with its PQ event type |
| Sw | F | H | N | C | |||||
| [27] (2022) | DT, KNN, LR, RF, SVM | L | Sg 10 | S, R | 28 features extracted from voltage and current waveforms 16 | ||||
| Sw 10 | |||||||||
| [28] (2022) | WT | F | Sg | S | Voltage, time, cross-correlation coefficients with mother wavelets | ||||
| [29] (2022) | TQWT 17 | C | ImT | OsT | Int | Sg | S | Statistical parameters, sub-band energy ratio, zero crossings, etc. 18 | |
| Sw | F | H | N | C | |||||
| [30] (2022) | LSTM | C | Sg | S, R | Voltage, fault type 19 | ||||
| [31] (2021) | CT | C | Sg | S | Clarke components ellipse | ||||
| [32] (2021) | FNN | C | Sp | OsT | Int | Sg | S | Binary image of PQ signal waveform and its saliency map | |
| Sw | F | H | N | C | |||||
| [33] (2021) | ABC-PSO, MRA, PNN, WT | C | ImT | Sp | OsT | Int | Sg | S | Energy, entropy, standard deviation, mean and other statistical parameters |
| Sw | F | H | N | C | |||||
| [34] (2020) | EM, GA, SVM 20 | L | Sg 10 | S | 34 features extracted from voltage and current waveforms 16 | ||||
| Sw 10 | |||||||||
| [35] (2020) | DT, ST | C | OsT | Int | Sg | S, R | Maximum amplitude versus both time and frequency, THD, etc. | ||
| Sw | F | H | C | ||||||
| [36] (2020) | MLP, SVM | C | Sg 21 | S | Higher-order statistics (moments and cumulants), cause | ||||
| [37] (2020) | CSO, DT, GA, KNN, ST, SVM | C | ImT | OsT | Int | Sg | S | Statistical parameters, disturbance energy ratio | |
| Sw | F | H | N | C | |||||
| [38] (2019) | ELM, WT | C | Sp | OsT | Int | Sg | S, R | Statistical parameters, wavelet coefficients | |
| Sw | F | H | N | C | |||||
| [39] (2019) | ST | F | Sg 22 | S | First and second duration times, recovery time and magnitude, THD 23 | ||||
| Group | Data | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Atmospheric transient | 8 p.u. | 5 p.u. | 4 p.u. | 4 p.u. | 4 p.u. | 3.2 p.u. | 3.1 p.u. | 3 p.u. | ||||||||||||||||
| 0.02 ms | 0.02 ms | 50 ms | 0.3 ms | 0.005 ms | 55 ms | 55 ms | 0.01 ms | |||||||||||||||||
| Commutation transient | 2 p.u. | 2 p.u. | 1.88 p.u. | 1.8 p.u. | 1.5 p.u. | 1.3 p.u. | 1.29 p.u. | 1.25 p.u. | 1.05 p.u. | 1 p.u. | ||||||||||||||
| 31 ms | 20 ms | 30 ms | 10 ms | 25 ms | 10 ms | 10 ms | 5 ms | 33 ms | 30 ms | |||||||||||||||
| Single-phase short circuit | 2 p.u. | 1.8 p.u. | 1.7 p.u. | 1.55 p.u. | 1.5 p.u. | 1.4 p.u. | 1.3 p.u. | 1.2 p.u. | 1.1 p.u. | 1.1 p.u. | ||||||||||||||
| 55 s | 19 s | 60 s | 56 s | 16 s | 46 s | 1000 ms | 27 s | 60 s | 35 s | |||||||||||||||
| Electric motor starting | 0.88 p.u. | 0.87 p.u. | 0.85 p.u. | 0.8 p.u. | 0.35 p.u. | 0.35 p.u. | 0.25 p.u. | |||||||||||||||||
| 800 ms | 50 ms | 50 ms | 2000 ms | 327 ms | 307 ms | 710 ms | ||||||||||||||||||
| Not categorized | 2 p.u. | 1.8 p.u. | 1.8 p.u. | 1.8 p.u. | 1.78 p.u. | 1.4 p.u. | 1.4 p.u. | 1.3 p.u. | 1.2 p.u. | 1.2 p.u. | ||||||||||||||
| 1000 ms | 1600 ms | 600 ms | 10 ms | 1780 ms | 3000 ms | 600 ms | 60 s | 3000 ms | 2300 ms | |||||||||||||||
| 1.2 p.u. | 1.1 p.u. | 1.1 p.u. | 1.1 p.u. | 1.1 p.u. | 1.1 p.u. | 0.84 p.u. | 0.82 p.u. | 0.8 p.u. | 0.74 p.u. | |||||||||||||||
| 2000 ms | 60 s | 3000 ms | 1800 ms | 600 ms | 10 ms | 200 ms | 100 ms | 150 ms | 340 ms | |||||||||||||||
| 0.7 p.u. | 0.68 p.u. | 0.6 p.u. | 0.57 p.u. | 0.55 p.u. | 0.4 p.u. | |||||||||||||||||||
| 25 ms | 20 ms | 750 ms | 290 ms | 80 ms | 60 ms | |||||||||||||||||||
| Group | Data | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three-phase short circuit | 0.8 (0.98) | 0.5 (0.61) | 0.4 (0.49) | 0.3 (0.37) | 0.15 (0.18) | 0.1 (0.12) | 0.05 (0.06) | 0.0 (0.00) | ||||||||
| 0.8 (0.98) | 0.5 (0.61) | 0.4 (0.49) | 0.3 (0.37) | 0.15 (0.18) | 0.1 (0.12) | 0.05 (0.06) | 0.0 (0.00) | |||||||||
| 0.8 (0.00) | 0.5 (0.00) | 0.4 (0.00) | 0.3 (0.00) | 0.15 (0.00) | 0.1 (0.00) | 0.05 (0.00) | 0.0 (0.00) | |||||||||
| Two-phase-to-ground short circuit | 0.0 (0.97) | 0.0 (0.77) | 0.0 (0.76) | 0.0 (0.76) | 0.0 (0.75) | 0.0 (0.73) | 0.0 (0.65) | 0.0 (0.54) | ||||||||
| 0.9 (0.64) | 0.7 (0.49) | 0.7 (0.49) | 0.7 (0.49) | 0.69 (0.49) | 0.68 (0.48) | 0.6 (0.42) | 0.5 (0.35) | |||||||||
| 0.9 (0.52) | 0.72 (0.41) | 0.71 (0.41) | 0.7 (0.40) | 0.7 (0.40) | 0.68 (0.39) | 0.6 (0.35) | 0.5 (0.29) | |||||||||
| Two-phase short circuit | 0.0 (0.97) | 0.0 (0.93) | 0.0 (0.86) | 0.0 (0.85) | 0.0 (0.77) | 0.0 (0.76) | 0.0 (0.70) | 0.0 (0.65) | ||||||||
| 0.9 (0.64) | 0.86 (0.61) | 0.8 (0.56) | 0.79 (0.59) | 0.72 (0.51) | 0.7 (0.49) | 0.65 (0.46) | 0.6 (0.42) | |||||||||
| 0.9 (0.52) | 0.86 (0.49) | 0.8 (0.46) | 0.79 (0.46) | 0.72 (0.42) | 0.7 (0.40) | 0.65 (0.38) | 0.6 (0.35) | |||||||||
| Single-phase short circuit | 1.0 (1.23) | 0.9 (1.11) | 0.82 (1.00) | 0.8 (0.98) | 0.7 (1.06) | 0.7 (1.12) | 0.7 (1.02) | 0.6 (1.06) | ||||||||
| 1.0 (1.22) | 0.9 (1.10) | 0.82 (1.00) | 0.8 (0.98) | 0.9 (0.98) | 0.8 (0.91) | 0.7 (0.86) | 0.6 (0.73) | |||||||||
| 1.0 (0.00) | 0.9 (0.00) | 0.82 (0.00) | 0.8 (0.00) | 0.9 (0.12) | 1.0 (0.15) | 0.9 (0.12) | 1.0 (0.23) | |||||||||
| Not categorized | 0.7 (1.12) | 0.6 (0.94) | 0.6 (1.08) | 0.6 (0.90) | 0.52 (0.95) | 0.5 (1.02) | 0.5 (0.94) | 0.4 (1.02) | 0.4 (0.82) | 0.4 (0.73) | ||||||
| 0.8 (0.92) | 0.8 (0.86) | 0.7 (0.80) | 0.6 (0.74) | 0.52 (0.64) | 0.5 (0.61) | 0.5 (0.61) | 0.6 (0.62) | 0.4 (0.49) | 0.4 (0.49) | |||||||
| 1.0 (0.15) | 0.8 (0.12) | 1.0 (0.21) | 0.8 (0.12) | 0.9 (0.22) | 1.0 (0.29) | 0.9 (0.23) | 1.0 (0.31) | 0.8 (0.23) | 0.7 (0.17) | |||||||
| 0.3 (0.76) | 0.3 (0.82) | 0.3 (0.53) | 0.2 (0.49) | 0.1 (0.95) | 0.1 (0.74) | 0.0 (0.86) | 0.0 (0.77) | 0.0 (0.65) | 0.0 (0.54) | |||||||
| 0.6 (0.56) | 0.5 (0.49) | 0.3 (0.37) | 0.2 (0.24) | 0.8 (0.60) | 0.6 (0.46) | 0.8 (0.57) | 0.72 (0.51) | 0.6 (0.42) | 0.5 (0.35) | |||||||
| 0.7 (0.21) | 0.8 (0.25) | 0.5 (0.12) | 0.5 (0.17) | 0.9 (0.44) | 0.7 (0.32) | 0.8 (0.46) | 0.72 (0.42) | 0.6 (0.35) | 0.5 (0.29) | |||||||
| Group | Data | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Three-phase short circuit | 0.8 (0.98) | 0.5 (0.61) | 0.4 (0.49) | 0.3 (0.37) | 0.15 (0.18) | 0.1 (0.12) | 0.05 (0.06) | 0.0 (0.00) | ||||||||
| 0.8 (0.98) | 0.5 (0.61) | 0.4 (0.49) | 0.3 (0.37) | 0.15 (0.18) | 0.1 (0.12) | 0.05 (0.06) | 0.0 (0.00) | |||||||||
| 0.8 (0.00) | 0.5 (0.00) | 0.4 (0.00) | 0.3 (0.00) | 0.15 (0.00) | 0.1 (0.00) | 0.05 (0.06) | 0.0 (0.00) | |||||||||
| Two-phase-to-ground short circuit | 0.0 (1.23) | 0.0 (1.08) | 0.0 (1.08) | 0.0 (1.02) | 0.0 (0.99) | 0.0 (0.98) | 0.0 (0.90) | 0.0 (0.73) | ||||||||
| 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | 0.0 (0.00) | |||||||||
| 1.5 (0.87) | 1.32 (0.76) | 1.3 (0.76) | 1.25 (0.72) | 1.22 (0.70) | 1.2 (0.69) | 1.1 (0.64) | 0.9 (0.52) | |||||||||
| Two-phase short circuit | 0.5 (1.02) | 0.5 (1.02) | 0.5 (1.02) | 0.5 (0.94) | 0.48 (0.93) | 0.43 (0.74) | 0.42 (0.78) | 0.4 (0.78) | ||||||||
| 0.5 (0.61) | 0.5 (0.61) | 0.5 (0.61) | 0.5 (0.61) | 0.48 (0.59) | 0.43 (0.53) | 0.42 (0.51) | 0.4 (0.51) | |||||||||
| 1.0 (0.29) | 1.0 (0.29) | 1.0 (0.29) | 0.9 (0.23) | 0.9 (0.24) | 0.69 (0.15) | 0.75 (0.19) | 0.8 (0.19) | |||||||||
| Single-phase short circuit | 0.0 (1.94) | 0.0 (1.59) | 0.0 (1.51) | 0.0 (1.40) | 0.0 (1.53) | 0.0 (1.37) | 0.0 (1.27) | 0.0 (1.05) | ||||||||
| 1.8 (1.27) | 1.4 (0.99) | 1.4 (0.99) | 1.3 (0.92) | 1.2 (0.85) | 1.2 (0.85) | 1.1 (0.78) | 0.9 (0.64) | |||||||||
| 1.8 (1.04) | 1.5 (0.84) | 1.4 (0.81) | 1.3 (0.75) | 1.5 (0.79) | 1.3 (0.72) | 1.2 (0.69) | 1.0 (0.55) | |||||||||
| Not categorized | 1.0 (2.27) | 0.8 (2.01) | 0.8 (1.96) | 0.8 (1.06) | 0.6 (1.44) | 0.6 (1.06) | 0.58 (0.89) | 0.52 (1.03) | 0.5 (0.80) | 0.4 (0.92) | ||||||
| 2.0 (1.87) | 1.7 (1.56) | 0.8 (0.98) | 0.8 (0.98) | 1.2 (1.12) | 0.6 (0.73) | 0.58 (0.71) | 0.52 (0.64) | 0.6 (0.67) | 0.5 (0.55) | |||||||
| 2.0 (0.58) | 1.8 (0.55) | 2.0 (0.69) | 0.9 (0.06) | 1.3 (0.38) | 1.0 (0.23) | 0.8 (0.13) | 1.0 (0.28) | 0.7 (0.10) | 0.9 (0.26) | |||||||
| 0.4 (0.76) | 0.4 (1.23) | 0.4 (0.82) | 0.4 (0.82) | 0.3 (1.30) | 0.3 (0.82) | 0.2 (1.14) | 0.1 (0.95) | 0.0 (0.76) | 0.0 (0.69) | |||||||
| 0.5 (0.55) | 0.4 (0.49) | 0.4 (0.49) | 0.4 (0.49) | 1.1 (0.90) | 0.5 (0.50) | 0.2 (0.24) | 0.8 (0.60) | 0.7 (0.49) | 0.62 (0.44) | |||||||
| 0.7 (0.15) | 1.3 (0.52) | 0.8 (0.23) | 0.7 (0.23) | 1.2 (0.49) | 0.8 (0.25) | 1.3 (0.64) | 0.9 (0.44) | 0.7 (0.40) | 0.62 (0.36) | |||||||
| Requirement | General Information | Nuances in PQ Monitoring |
|---|---|---|
| Latency | Data transmission delay between smart grid components | PQ monitoring is not a time critical or real-time application; thus, the delay requirement can be not very strict [2] |
| Bandwidth | Wireless communication frequency determines its coverage and bandwidth (data rate) [70]; hence, low, medium and high frequencies will have their specific roles in a smart grid. Therefore, a detailed examination of data rate, transmission distance and other features is essential in order to select appropriate technology 1 | PQ monitoring is a wide area network application whose end-nodes are static (hence, handoff regions are not relevant). The required bandwidth can be diminished by feature extraction which, however, not always can be applied, for example, in the case of transient waveforms |
| Data rate | Various types of data (text, pictures, audio, video, etc.) will be generated by smart grid applications at different rates [70]. Hence, it is important to select appropriate ICT, considering its technical characteristics and cost efficiency | Data rate depends on feature extraction techniques. Probably, PQ application will be a part of a smart grid’s ICT network, and there are numerous possible ways to implement this task, including technology selection (e.g., see [2] for the list of potential ICTs) |
| Throughput | The sum of data transferred between smart grid components in a specific time interval [70] | PQ measurements must be carried out continuously. This is not essential for PQ data transmission: it could be scheduled considering an ICT network’s traffic profile and the memory of the monitor with an obvious exception in case of a high-priority request. Also, the throughput will depend on the monitors’ quantity optimization (including smart meters and other relevant devices), data redundancy factor, feature extraction, etc. |
| Reliability | Quantified success of proper data transferring. In [70], the reliability requirement is higher than 98% for all smart grid applications | Currently, the PQ system reliability can reach 98%; however, it must be significantly increased after the integration with SA. Also, perhaps, a reliability requirement could be slightly lowered with an increase in the data redundancy factor. The transferring of high-entropy messages is more valuable and thus must be more reliable than low-entropy messages 2 |
| Accuracy andprecision | Accuracy is the difference between a measurement and a true (accepted) value, while precision characterizes how close the measurements are to each other 3 | As already mentioned, along with well-known aspects such as the instrument error, the magnitude and phase frequency response of the measurement circuit also play an important role. In the case of frequency domain analysis, which is an integral part of PQ, even more less understood nuances emerge: for example, Heisenberg uncertainty, resolution bandwidth, spectrum aliasing, spectral leakage, etc. [2] |
| Validity | Characterizes information usefulness, strength, accuracy and other relevant features which are required to efficiently achieve the desired goal. It is closely related to feature extraction strategies: useful data must be retrieved | Validity depends directly on feature extraction. This aspect is important for every PQ task regardless of whether it is technical, economic or political |
| Accessibility | Access rules must be established for interested parties such as TSO, DSO, regulator, industry, and households. Equal opportunities must be offered for the members of each group without discrimination [70] | Probably, each user will have access to simplified and understandable to him information restricted to his narrow area of responsibility. Meanwhile, grid operators must possess full data |
| Interoperability | Various protocols and ICTs are expected in smart grids. Thus, a proper protocol conversion must be ensured to achieve the best possible interoperability | Various protocols and ICTs can be used for PQ data and its smooth interactions with other applications (AMI, OM, PM, SA, etc.) must be ensured. Along with popular general-purpose protocols and data formats, more specialized protocol could also be used such as PQDIF specified in IEEE Std 1159.3-2019 [72] |
| Security | Protection from both physical threats and cyberattacks | Currently, PQ data are not as critical as they will become in the future, especially after the integration with SA. All structural parts of the PQ monitoring process are potentially vulnerable, in particular local data assessment, data transmission and central data assessment. For example, [18] investigates classification defense from an adversarial attack. The question regarding minimum storage time of PQ history currently also remains unanswered [2] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liubčuk, V.; Kairaitis, G.; Radziukynas, V.; Naujokaitis, D. IIR Shelving Filter, Support Vector Machine and k-Nearest Neighbors Algorithm Application for Voltage Transients and Short-Duration RMS Variations Analysis. Inventions 2024, 9, 12. https://doi.org/10.3390/inventions9010012
Liubčuk V, Kairaitis G, Radziukynas V, Naujokaitis D. IIR Shelving Filter, Support Vector Machine and k-Nearest Neighbors Algorithm Application for Voltage Transients and Short-Duration RMS Variations Analysis. Inventions. 2024; 9(1):12. https://doi.org/10.3390/inventions9010012
Chicago/Turabian StyleLiubčuk, Vladislav, Gediminas Kairaitis, Virginijus Radziukynas, and Darius Naujokaitis. 2024. "IIR Shelving Filter, Support Vector Machine and k-Nearest Neighbors Algorithm Application for Voltage Transients and Short-Duration RMS Variations Analysis" Inventions 9, no. 1: 12. https://doi.org/10.3390/inventions9010012
APA StyleLiubčuk, V., Kairaitis, G., Radziukynas, V., & Naujokaitis, D. (2024). IIR Shelving Filter, Support Vector Machine and k-Nearest Neighbors Algorithm Application for Voltage Transients and Short-Duration RMS Variations Analysis. Inventions, 9(1), 12. https://doi.org/10.3390/inventions9010012






