Closed-Form Hyper-Rayleigh Mode Analysis of the Fluctuating Double-Rayleigh with Line-of-Sight Fading Channel

Abstract

The research studies hyper-Rayleigh behavior of a wireless communication system functioning in the presence of the generalized multipath fading. Although the initial metric (hyper-Rayleigh mode (HRM)) is quite informative, it is defined only asymptotically (i.e., for the infinitely increasing SNR). In spite of mathematical simplifications brought by such a definition (i.e., in this case most of the performance characteristics defining the HRM can be easily evaluated), it sufficiently limits its applications since, evidently, the real-life systems function in the presence of a finite (and usually not very high) SNR. The study presents a novel approach to the fading channel analysis (i.e., finite signal-to-noise ratio hyper-Rayleigh mode (fHRM)). The proposed metric (fHRM) is studied on the newly presented channel model-fluctuating double-Rayleigh with Line-of-Sight (fdRLoS) fading model. To accomplish this, the novel expressions for two channel-dependent system characteristics (i.e., the Amount of Fading (AoF) and the Outage Probability (OP)) were derived in exact form valid for arbitrary fading parameters. Based on the derived expressions, the finite SNR hyper-Rayleigh map is obtained, which helps to identify the parameters’ values corresponding to the specific propagation scenarios, which were further deployed to analyze the problem of the communication link physical layer security quantified in terms of the probability of strictly positive secrecy capacity (SPSC). Numerical verification of the derived closed-form expressions was performed. Several peculiarities of the system performance are observed and discussed.

1. Introduction

The development of wireless communication systems is accompanied by an increase in the diversity of signal propagation conditions. Modern and perspective communication systems (such as 5G [1], 6G [2] or Wi-Fi 7 [3]) are expected to work reliably in rural areas or in urban conditions, outside and inside buildings. In all the scenarios, the signal undergoes attenuation, shadowing, scattering, multiple re-reflections and multipath propagation. Severe conditions lead to a reduction in the coverage area of communication systems [3,4], and thus to the decrease of the number of propagation paths (especially for propagation inside buildings). That reduces the accuracy of communication performance forecasts and leads to underestimation or, more importantly, to overestimation of potential system characteristics. At the same time, the requirements for the communication quality are increasing. Under these conditions, even small changes in the physical properties of the channel lead to a significant change in the wireless system performance. Thus, for a correct channel prediction, an adequate mathematical or statistical model (capable of handling all the effects mentioned above) is required.

There are numerous fading channel models, both the simplest and quite complex. Especially for high-frequency and optical communication (including Free Space Optical communication (FSO) and Underwater Optical communication (UWOC)), such models as the well-renowned Gamma-gamma (see, for instance, [5,6]), Málaga distribution (see, for example, [7,8]) and the newly-presented Exponential-Generalized Gamma channel model [9,10] are widely applied. For the Radio Frequency (RF) counterparts of FSO/UWOC systems, the Two/N-wave with Diffuse Power (TWDP/NWDP) models are nowadays widely studied (see [11,12]). Although, delivering a very versatile description, they take in to the account only a single reflection (with various multiple components, i.e., multipath and line-of-sight, specular and diffuse).

For future communication systems, the most advanced models that take into account multiple re-reflections and other signal transmission peculiarities [13] are relevant. The approach originally proposed by Rice [14] that considered the presence of line of sight (LoS) along with multipath signal propagation was later developed involving multiple scattering [15,16,17]. Taking into account double scattering [18,19] for Rayleigh models has led to the emergence of new double-Rayleigh and double-Rayleigh with LoS models [20,21,22]. This made it possible to take into account more signal propagation features without significantly complicating the model.

Of particular interest is the Lopez-Fernandez et al. model published in 2022 [23]. It is a novel fluctuating double-Rayleigh with line-of-sight (fdRLoS) fading channel model, which generalized the double-Rayleigh with line-of-sight model [14] by including the Gamma-distributed shadowing of the LoS component. In addition to the initial statistical formulation of the model, the closed-form expressions for the probability density function (pdf) and for the cumulative distribution function (cdf) were obtained in [23] for a specific case of the integer values of fading parameter. The results allowed the authors to obtain simplified expressions for the pdf and cdf and apply them to the problem of the outage probability analysis. However, the presented result formulation did not make further analytical derivations possible, which sufficiently restricts its practical application. Moreover, the expressions were valid for the integer values of the shadowing parameter, though, it was shown for similar models [24] that the shadowing parameter extracted from the experimental results (e.g., [25]) efficiently can be non-integer and generally less than 1. Later, some new results were obtained for the fdRLoS model: A closed-form expression for bit error rate (BER) [26], BER for M-order quadrature amplitude and M-order phase shift keying modulations [26], the analysis of the fading parameters’ impact on the error rate [26], analytical and asymptotic expressions for the ergodic capacity under optimal rate and optimal power and rate adaptation scenarios [27].

It is worth mentioning that fdRLoS model (being a generalization of the double-Rayleigh with LoS scattering) successfully approximates [23] the so-called I-K-model widely applied in Optical Wireless Communications (OWC) [28,29,30,31]. The classical I-K distribution is usually applied to describe optical signal intensity fluctuations, while propagating through extended clear-air turbulence [32,33]. It was introduced as an extension of the K-distribution and was successfully experimentally verified for a wide variety of atmospheric turbulence conditions including weak turbulence, which is a theoretical applicability limitation of the K-distribution. Although, the I-K model demonstrated very good agreement with experimental studies within the tails of the pdf [34], it has some specific issues with fitting the mode [30,34]. In [23], it is stated that this well-known effect (basically explained by the spiky behavior of the I-K density function) can be alleviated by the fdRLoS model. Thus, it can be regarded as a promising candidate for the future OWC (FSO and UWOC) systems’ description, as well as for the joint RF-FSO systems.

As it is shown in [18], double-scattering in general demonstrates a larger fading severity compared to Rayleigh [35,36,37]. This is because two (or in general more) dominant waves with similar magnitudes may cancel each other out, while the diffuse power is reduced. As a result, the system performance decreases [38,39]. Therefore, it is necessary to identify the conditions under which the a channel will be better-than-Rayleigh or worse-than-Rayleigh, and to conduct detailed analysis of its functioning in the latter, which is often termed as the hyper-Rayleigh mode (RHM) (or hyper-Rayleigh regime) [35,36]. As of the current date, no results concerning the channel parameters’ value indicating the specific degree of hyper-Rayleigh are present for the fdRLoS model. Various measures have been proposed in the literature for a quantitative description of the hyper-Rayleigh regime (e.g., [40,41]). In the current research, we will follow the comprehensive and convenient approach outlined in [42].

Besides the quality and reliability of communications, another critical aspect of modern wireless systems is the link secrecy. Although security issues were studied for different two-beam fading models (e.g., [43,44]), the security of communication scenarios for the fdRLoS model has remained unexplored. From the physical layer security point of view, the reduction of the coverage area leads to the fact that an eavesdropper can be closer to both the transmitter and the receiver and can wiretap at a higher signal-to-noise ratio (SNR) than in long-distance communication systems, or even get into the same physical conditions of signal reception with a legitimate receiver. The random changes in signal amplitude and phase from the spatial positioning between a receiver and a transmitter refer to these situations as the co-called small-scale fading [45]. Therefore, it is especially important to be able to evaluate the secrecy parameters for severe scenarios of electromagnetic wave propagation and to choose a security strategy.

Physical phenomena in the communication channel can be taken into account within the physical layer security framework [46,47,48]. This approach has a number of advantages over cryptography [48]: Physical layer methods maintain the secure link even if the eavesdropper is not limited in computing resources; they ensure the operation of different networks, including self-organizing ones; they can act as an additional well-embedded communication security solution together with traditional ones.

There are many secrecy metrics in modern wireless communication systems [49,50]. In the present research, we will exemplify hyper-Rayleigh regime analysis by assessing the probability of a strictly positive secrecy capacity, being one of the basic and primary metrics.

Motivated by the problem stated above and the mentioned drawbacks of the existing solutions, the proposed research performs the closed-form analysis of the hyper-Rayleigh fading conditions of a wireless communication system operating in the presence of the multipath channel described by the fluctuating double-Rayleigh with line-of-sight model. The major contributions of the research can be summarized as follows:

• The closed-form expression is derived for the moment-function of the fluctuating double-Rayleigh with line-of-sight channel model, which helps to evaluate the exact expression for the amount of fading.
• Novel exact expressions for the cumulative distribution function and the outage probability of the fluctuating double-Rayleigh with line-of-sight channel model are derived, extending the existing result, and are valid for an arbitrary positive fading parameter m.
• A hyper-Rayleigh map, which associates the set of system parameter values with the specific propagation conditions, is obtained. The presented results are valid not only for an “asymptotic” definition of the hyper-Rayleigh map (as it is defined in classic technical literature), but for all possible values of the system and channel parameters.
• The performed analysis is exemplified with a problem of physical layer security analysis. A thorough numeric analysis of the strictly positive secrecy capacity is performed for all possible hyper-Rayleigh scenarios (i.e., channel parameters).
• The asymptotic parameters’ regions, where either the amount of fading, or the outage probability, or the ergodic capacity are nearly insensible to the channel parameter change are identified.

The remainder of the paper is organized as follows: Section 2 provides the general physical and statistical description of the fluctuating double-Rayleigh with line-of-sight channel model, describes the hyper-Rayleigh conditions, introduces the classification of possible hyper-Rayleigh cases, and presents a brief description of a physical layer security problem (strictly positive capacity analysis) adopted for illustration; Section 3 presents the derived analytical results; Section 4 contains a thorough numerical analysis of the derived expressions depending on various channel parameters’ values; and the conclusions are drawn in Section 5.

2. Materials and Methods

2.1. Physical Channel Model

The proposed fluctuating double-Rayleigh with line-of-sight fading channel model in [23] assumes that there are two components: The line-of-sight associated with the presence of a direct path between the transmitter and receiver and the Rayleigh diffuse component. The line-of-sight component exists in many scenarios of modern wireless communications, especially at higher frequencies [51,52], and fluctuates as the propagation conditions change during the communication session due to temporary shadowing of the LoS using relatively small and mobile objects such as th human body [53]. So the received signal S can be represented as the linear combination of two components [23]:

$$S=a_0\sqrt{\xi }{e}^{j\varphi }+a_2{G}_2{G}_3,$$

(1)

That is, of the shadowed LoS component (the first term) with average magnitude $a_0$ and double-Rayleigh fading (dRf) component (the second term) $a_2{G}_2{G}_3$, where $\xi$ is the shadowing parameter with unit power and shape coefficient m; $a_2$ is the average dRf component magnitude, and $G_2$, $G_3$ are the zero-mean complex normal random variables, which are the coefficients of the channel transfer function responsible for accounting the first and the second scattering at two transmission stages [15]. Here the phase of the LoS component is uniformly distributed $\varphi \sim U[0,2\pi$), the shadowing parameter $\xi$ is the Gamma distributed and $G_2$, $G_3$ are the zero-mean complex normal random variables (i.e., $G_2,G_3\sim \mathcal{CN}(0,1)$). Physically, this model corresponds to the propagation channel with constant amplitude LoS component that undergoes shadowing with unit power.

Such propagation conditions occur in a wide variety of applications: Millimeter wave communications [11,35,38], optical wireless communications [54], backscatter communications [15], indoor mobile links, vehicle-to-vehicle communications and others.

2.2. Statistical Channel Model

Following [23], let us assume that the channel is properly normalized to yield unit power of the received signal (i.e., $\mathbb{E}\left\{\right|S{|}^2\}=1$), and the probability density function of the instantaneous signal-to-noise ratio $\gamma$, defined as $\gamma =\overline{\gamma }{\left|S\right|}^2$ (with $\overline{\gamma }$—the average signal-to-noise ratio), is given by (see Equation (13) in [23])

$$f_{\gamma }\left(\gamma \right)={\int }_0^{\infty }{f}_{{\gamma }_x}\left(\gamma |x\right)e^{-x}dx,$$

(2)

where $f_{{\gamma }_x}\left(\gamma |x\right)$ is the conditional probability density function conditioned on $x=|G_3{|}^2$, which is defined as

$$f_{{\gamma }_x}\left(\gamma |x\right)=\frac{m^m(1+k_x)}{{\left(m+k_x\right)}^m{\overline{\gamma }}_x}{e}^{-\frac{1+k_x}{{\gamma }_x}\gamma }{}_1{F}_1\left(m,1,\frac{k_x(1+k_x)}{k_x+m}\frac{\gamma }{{\overline{\gamma }}_x}\right).$$

(3)

Here $k=\frac{a_0^2}{a_2^2}$ denotes the Rician K-factor, $k_x=\frac{k}{x}$, ${\overline{\gamma }}_x=\frac{k+x}{k+1}\overline{\gamma }$ and ${}_1{F}_1(·)$ is the confluent hypergeometric function [55].

The model can be used to predict the performance of a wide spectrum of wireless communications systems types: Suburban, urban, forest [15], indoor [56], indoor-to-outdoor and vice versa [57], peer-to-peer [58], or railway [59]. Moreover, what is especially important is that the model allows us to deal with the signal propagation affected by the keyhole effect [54], which can occur under propagation in the presence of diffracting elements, such as building corners, roofs, elements of urban small architecture, etc.

2.3. Hyper Rayleigh Mode

A formal definition of the hyper-Rayleigh mode (HRM) is based on the use of three metrics [42]: Amount of fading (AoF), outage probability ($P_{out}$) and the average capacity.

The amount of fading is defined as the normalized second moment of the instantaneous SNR $\gamma$ [60]:

$$AoF=\frac{\mathbb{V}ar\left\{\gamma \right\}}{{\left(\mathbb{E}\left\{\gamma \right\}\right)}^2}=\frac{\mathbb{E}\left\{{\gamma }^2\right\}}{{\overline{\gamma }}^2}-1,$$

(4)

where $\overline{\gamma }=\mathbb{E}\left\{\gamma \right\}$ is the average SNR.

The outage probability is the probability that the instantaneous SNR falls below a given threshold value ${\gamma }_{th}$:

$$P_{out}=F_{\gamma }\left({\gamma }_{th}\right),$$

(5)

where $F_{\gamma }\left(·\right)$ is the cdf of $\gamma$.

The average capacity $\overline{C}$ per unit bandwidth is the instantaneous capacity averaged over all possible fading states [42]:

$$\overline{C}=\underset{0}{\overset{\infty }{\int }}{log}_2\left(1+\gamma \right)f_{\gamma }\left(\gamma \right)d\gamma .$$

(6)

According to [42], a fading model can demonstrate hyper-Rayleigh behavior for a set of model parameters if the following conditions hold:

• amount of fading is greater than AoF for the Rayleigh model, i.e., 1:

  $$AoF>Ao{F}^{Ray}=1$$

  (7)
• Or for equal values of the asymptotic (in sense of ${\gamma }_{th}\ll \overline{\gamma }$) outage probability the average SNR is greater than the Rayleigh average SNR
• Or for equal average SNRs, the asymptotic (in sense of $\overline{\gamma }\to \infty$) average capacity is less than that for the Rayleigh model.

In contrast to [42], where HRM is established only for the asymptotic values of the outage probability and average capacity, in our case arbitrary metric values will be assumed, which is a significant extension of the existing results.

Following [42], who considered situations to one of four cases depending on the number of hyper-Rayleigh criteria implemented, we will consider HRM as full hyper-Rayleigh regime if all three criteria are met simultaneously, strong HRM if two of the three conditions are satisfied, and weak HRM if only one criterion is met. If none of the conditions are fulfilled, we will assume that HRM is not demonstrated by the system.

2.4. Secrecy Communication Metrics

To illustrate the performance of the fdRLoS channel, we will assume the problem is of the wireless communication link secrecy. It is usually described as a three acting agents model [61] with a communication link between the transmitter and the destination point of a legitimate receiver (described with the model (2)–(3) and parameters $m_D,k_D,{\overline{\gamma }}_D$), and a wiretap link to the eavesdropper (described with the channel model (2)–(3) and parameters $m_E,k_E,{\overline{\gamma }}_D$).

As it was mentioned earlier, there are numerous metrics that can assist in the security assessment [49,50]. Among them, the primary role is given to the Probability of Strictly Positive Secrecy Capacity (SPSC), which is the probability that the positive secrecy capacity exists (i.e., that the secure communication can be established):

$$SPSC=\mathbb{P}\{C>0\}=1-P_{out}\left(0\right),$$

(8)

where $P_{out}$ is the secrecy outage probability for a fixed threshold capacity $C_{th}$ defined as

$$P_{out}\left(C_{th}\right)=\mathbb{P}\{C\le C_{th}\}.$$

(9)

Since in modern urban communication systems the coverage area tends to shrink, a practically important setup of closely spaced receiver and eavesdropper appears. From a practical viewpoint, this case can be assumed as a worst-case scenario, since in this situation the parameters of both channels are almost the same and the only factor that helps to establish a secure link is the average SNR in the main channel (which implies hard restrictions on the receiver). Thus, for further analysis we will resort to this specific situation, i.e., $m_D=m_E$, $k_D=k_E$.

Moreover, we will assess SPSC of the fdRLoS channel for all the possible fading scenarios, choosing the channel parameters in such a way as to correspond: (a) No HRM, (b) weak HRM, (c) strong HRM, and (d) full HRM.

3. Results

The joint hyper-Rayleigh map is a region-plot comprised of subregions corresponding to the specific HRM. In order to obtain such a map, one needs to evaluate the regions that correspond to HRM for each of the metrics: AoF, outage probability and ergodic capacity. Thus, closed-form expressions presenting those metrics for arbitrary values of channel parameters are required.

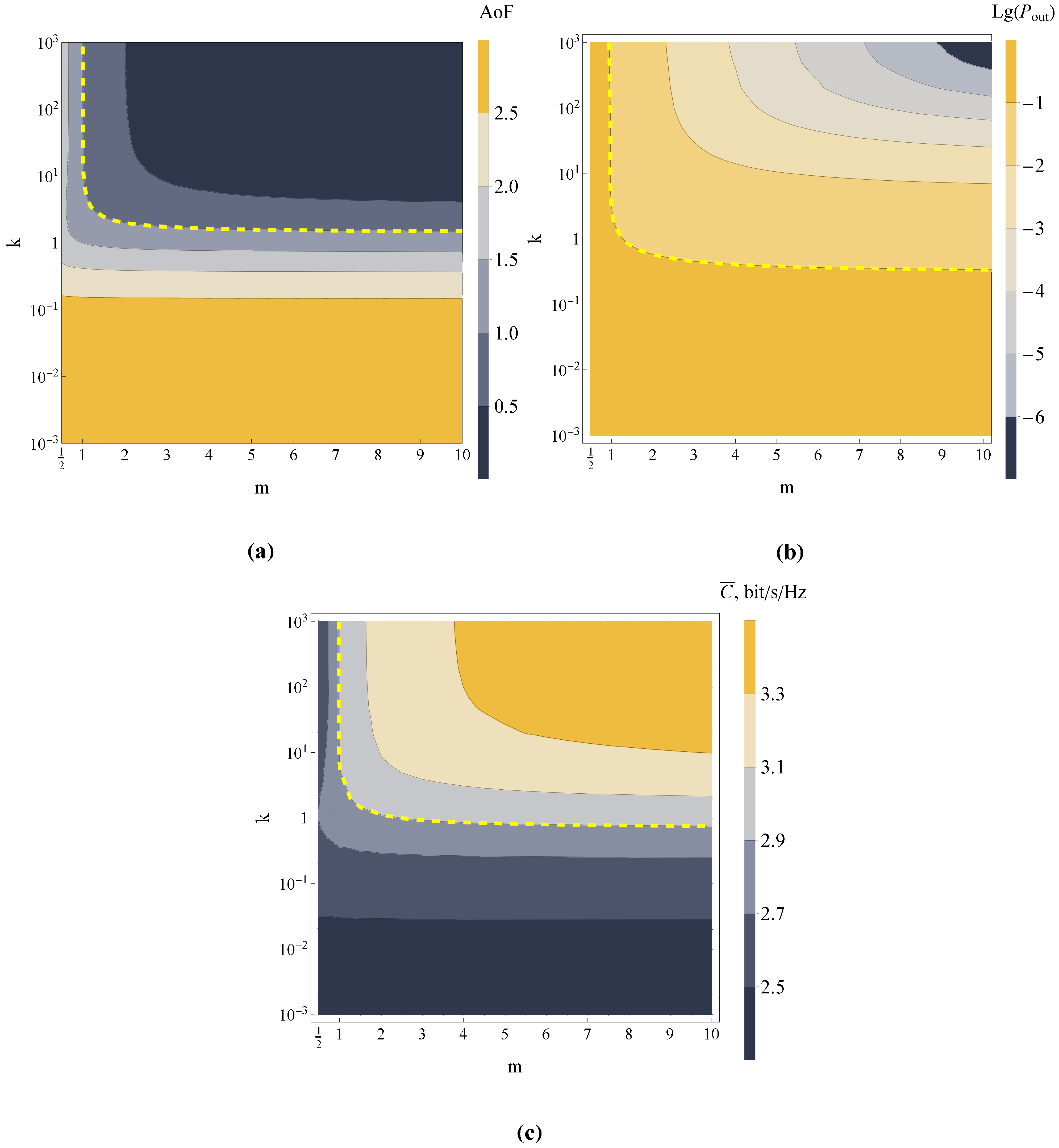
3.1. Amount of Fading

To derive the closed-form expression for the amount of fading, one starts with the redefining of the fdRLoS instantaneous SNR pdf $f_{\gamma }\left(\gamma \right)$ (given in (2)) and conditional pdf $f_{{\gamma }_x}\left(\gamma \right|x)$ (given in (3)) in a compact notation:

$$f_{{\gamma }_x}\left(\gamma \right|x)=C_0{e}^{-\alpha \gamma }{}_1{F}_1\left(m;1;\beta \gamma \right),$$

(10)

with the following set of coefficients:

$$\begin{array}{}\hfill \mathrm{(11a)}& \hfill {\mathrm{C}}_0& \hfill =& \frac{m^m\left(k+1\right)x^{m-1}}{{\left(k+mx\right)}^m\overline{\gamma }},\hfill \hfill \mathrm{(11b)}& \hfill \alpha & \hfill =& \frac{\left(k+1\right)}{x\overline{\gamma }},\hfill \hfill \mathrm{(11c)}& \hfill \beta & \hfill =& \frac{k\left(k+1\right)}{x\left(k+mx\right)\overline{\gamma }}.\hfill \end{array}$$

Since the amount of fading is defined in terms of the first two raw moments (i.e., $\mathbb{E}\left\{\gamma \right\}$ and $\mathbb{E}\left\{{\gamma }^2\right\}$) of the instantaneous signal-to-noise ratio, their evaluation is a prerequisite for further reasoning.

To broaden the analysis, we will derive an expression for the arbitrary-order moment (the raw-moment function) of the fdRLoS channel, given by the following theorem and its corollary.

Theorem 1.

The rth-order raw moment of the instantaneous signal-to-noise ratio ${\mu }_r$ for the fluctuating double-Rayleigh with line-of-sight channel model can be expressed as follows:

$${\mu }_r={\left(r!\right)}^2{\left(\frac{\overline{\gamma }}{k+1}\right)}^r\sum _{l=0}^r\frac{{\left(m\right)}_l}{{\left(l!\right)}^2}{\left(\frac{k}{m}\right)}^l,$$

(12)

where ${(·)}_r$ is the Pochhammer symbol [62].

Proof. 

For proof, see Appendix A. □

With the help of the stated result, the closed-form expression can be easily obtained.

Corollary 1.

The Amount of Fading for the fluctuating double-Rayleigh with line-of-sight channel model is given by

$$AoF=\frac{k^2+2km+3m}{m{(k+1)}^2}.$$

(13)

Proof. 

The proof of the corollary is easily obtained with the help of Theorem 1, by setting $r=1$ (to obtain $\mathbb{E}\left\{\gamma \right\}$) and $r=2$ (for $\mathbb{E}\left\{{\gamma }^2\right\}$). After some algebraic simplifications, the result (13) is obtained. □

Since for the Rayleigh case the $Ao{F}^{Ray}=1$ [60], henceforward we will assume the fdRLoS channel with parameters $(m,k)$ to be in a hyper-Rayleigh regime if $AoF>Ao{F}^{Ray}$, i.e.,

$$\frac{k^2+2km+3m}{m{(k+1)}^2}>1,$$

(14)

which is equivalent to the following set of inequalities:

$$\left\{\begin{array}{cc}k>\sqrt{\frac{2m}{m-1}},\hfill & \\ m>1.\hfill \end{array}\right.$$

(15)

3.2. Outage Probability

As it was mentioned earlier, the expression for the outage probability was initially derived in [23] (with the introduction of the fdRLoS model). However, due to the complexity of integration procedures, the authors have confined themselves to the case of integer-valued fading parameter m. Since, it is expected that the case of $m<1$ can possibly correspond to the hyper-Rayleigh scenario; moreover, in practical situations it is usually non-integer, the existing results are not valid for the current research. To eliminate this drawback, an exact expression for the $P_{out}$ for arbitrarily-valued $(m,k)$ was derived, as given by the following theorem and its corollary.

Theorem 2.

The cumulative distribution function of the instantaneous signal-to-noise ratio for the fluctuating double-Rayleigh with line-of-sight channel model for arbitrary non-negative channel parameters can be expressed as follows:

$$F_{\gamma }\left(\gamma \right)=1-m^m\sum _{l=0}^{\infty }\sum _{h=0}^{l+1}\frac{{\left(m\right)}_l}{l!}\frac{k^l}{h!}{\left((k+1)\frac{\gamma }{\overline{\gamma }}\right)}^h{I}_{2_{h,l}},$$

(16)

where the coefficients $I_{2_{h,l}}$ are defined in (A25).

Proof. 

For proof, see Appendix B. □

It should be noted that, although, $I_{2_{h,l}}$ does not admit a simple closed-form representation, it can be easily evaluated by numerically applying one of the numerous fast calculation procedures. Nevertheless, integer m, $I_{2_{h,l}}$ can be expressed in the exact form, but since in our research we are aiming at the cases of arbitrary m (especially $0.5\le m\le 1$), those simplifications are not employed.

Corollary 2.

The Outage Probability for some threshold SNR value ${\gamma }_{th}$ of the fluctuating double-Rayleigh with line-of-sight channel model is given by

$$P_{out}\left({\gamma }_{th}\right)=F_{\gamma }\left({\gamma }_{th}\right).$$

(17)

Proof. 

The proof of the corollary is trivial in view of the derived expression for the cdf (see Theorem 2). □

Since for the Rayleigh case the $P_{out}^{Ray}\left({\gamma }_{th}\right)=1-e^{\frac{{\gamma }_{th}}{\overline{\gamma }}}$ [2], henceforward we will assume the fdRLoS channel with parameters $(m,k)$ to be in a hyper-Rayleigh regime if $P_{out}>P_{out}^{Ray}$, i.e.,

$$P_{out}\left({\gamma }_{th}\right)>1-e^{\frac{{\gamma }_{th}}{\overline{\gamma }}}.$$

(18)

3.3. Channel Capacity

The last metric that is used to evaluate the HRM of the fdRLoS channel is the average capacity.

In [27], the closed-form expressions of the ergodic capacities for the assumed channel were derived for various adaptation strategies (including the optimal rate adaptation that is of primary interest for the current study). Moreover, since in [27] the results were presented both for integer and non-integer values of channel parameters (covering all the possible conditions), henceforth they will be assumed for further evaluation of the hyper-Rayleigh regime (specifically Theorem 1 and 2 from [27] will be employed).

As before, the HRM is defined as the situation when $\overline{C}<{\overline{C}}^{Ray}$. The ergodic capacity of the Rayleigh channel was derived in [63] (with further corrections in [64]), and is presented in the following form:

$${\overline{C}}^{Ray}=\frac{1}{ln2}{E}_1\left(\frac{1}{\overline{\gamma }}\right)e^{\frac{1}{\overline{\gamma }}},$$

(19)

where $E_1(·)$ is the exponential integral function [62].

It is worth stressing out again, that all the derived results and analysis assume arbitrary channel parameter values. This specifically includes the average (and threshold) SNR, in contrast to the pioneering work [42], where only asymptotic behavior was considered.

4. Discussion

The derived expressions made it possible to perform a thorough HRM analysis.

The numerical simulation was executed in accordance within the general framework described in Section 2 (see Section 2.1 for the physical channel model and Section 2.2 for the statistical description), Section 2.3 (see for HRM definition and classification), Section 2.4 (see for SPSC definition), and Section 3 (see for close-form expression of the AoF, $P_{out}$ and $\overline{C}$ used for analysis).

The channel parameters’ ranges (presented in

Table 1. Numeric simulation setup: system and channel parameters.

Parameter	Parameter Value
Shadowing coefficient (m)	$\frac{1}{2}\dots 20$
Rician K-factor (k)	${10}^{-3}\dots {10}^3$
Average SNR ($\overline{\gamma }$), dB	$-20\dots 50$
Threshold SNR (${\gamma }_{th}$), dB	$-10\dots 30$

) were chosen in such a way to cover the whole region of their possible practical values and be in coherence with the existing real-life measurement campaigns (for instance, for closely-related channel models see Rician K-factor measurements in [65,66] and fading parameter estimation in [67,68]).

To this extent, several important notes should be pointed out:

• For the simulation, the shadowing parameter m is upper-bounded by $m=20$ (although the plots are presented for $m<10$), since numerous studies [26,27] showed that the values $m>5÷10$ (depending on the problem under consideration) can be assumed as ”almost asymptotic”. This generally means that its increase does not deliver significant changes in the result.
• The lower bound of the shadowing parameter was set to 0.5, although, $0<m<0.5$ are also possible (since the shadowing is introduced via Gamma-distributed model). But numerous simulations demonstrated that $m<0.5$ do not make any contribution to the current research, thus were omitted.
• The Rician K-factor was chosen in order to be consistent with practical scenarios of real-life measurements (i.e., from $-30$ dB to 30 dB).
• The expression (16) is given in terms of an infinite series, thus for further numerical calculations it was truncated to 200 terms to yield at least 4-digit accuracy compared with the brute-force numerical integration. Moreover, if an extra precision (for a fixed number of summands) is required, well-established techniques for convergence increase can be applied (for example, Richardson extrapolation or Shanks’ transformation (see [69])).

Furthermore, the Section is divided into two following parts: HRM analysis and an illustration of its application to the problem of SPSC analysis. In Figure 1 and Figure 2, the results obtained with the help of the following derived expressions: For the AoF analysis in Section 3.1, the plots of the outage probability (obtained via numeric simulation) are calculated via expression derived in Section 3.2, and capacity analysis is performed with the help of the expression presented in Theorem 1 and 2 from [27] (as it is stated in Section 3.3).

4.1. Hyper-Rayleigh Regime Numerical Analysis

Hyper-Rayleigh mode metrics for the fdRLoS channel model with various k and m are displayed in Figure 1 as contour maps, which are marked with dashed lines corresponding to the Rayleigh channel values of metrics. This bound corresponds to the analytical expression (15) for AoF and is obtained numerically for other hyper-Rayleigh metrics.

The conditions for the parameter m to be considered asymptotic depend on the value of the parameter k: if $k<1$, then almost any m can be considered asymptotic; when $k\sim 10$, the HRM metrics are almost insensible to m for $m\ge 5$, and with $k\sim {10}^2$, for $m\ge 10$.

The performed analysis demonstrates the fact that the three hyper-Rayleigh metrics distinctly identify the degree of hyper-Rayleigh. If the observed outage probability falls below the $P_{out}^{Ray}$, then the values of the other two hyper-Rayleigh criteria (AoF and $\overline{C}$) will automatically correspond to the full HRM.

On the other hand, even if AoF becomes greater than $Ao{F}^{Ray}$ (i.e., $AoF>1$), it is not guaranteed that $\overline{C}$ and $P_{out}$ will be worse than Rayleigh; hence, the system behavior mode may be hyper-Rayleigh, depending on the specific values of $\overline{C}$ and $P_{out}$. That is, the outage probability implies the most severe restrictions.

Figure 2 shows the joint hyper-Rayleigh map of the fdRLoS channel: red—region full hyper-Rayleigh mode; orange region—to the strong hyper-Rayleigh regime; yellow sector corresponds to the weak hyper-Rayleigh fading; in the green region, the channel exhibits no hyper-Rayleigh properties.

These four types of hyper-Rayleigh regime correspond to different practical situations. No hyper-Rayleigh regime assumes a channel with strong LoS and small fading. This occurs, for example, in such cases as: Indoor office communication at short distances (from 4 to 21 m in office hallways, lobbies, halls, as shown with experiments on 5G communication at 28 and 73 GHz in [70]); UWOC in clear water with low absorption and no scattering from the smallest inhomogeneities in water; FSO communication systems at small distances, e.g., up to 200 m at 3.5 GHz in urban areas [71]. Full hyper-Rayleigh regime is the most interesting for communication security tasks: There is a heavily obstructed LoS with the intensive fading in the channel. This occurs, for example, in urban areas, inside buildings or at public places, where a lot of people create random, temporary and heavy line-of-sight shadowing [72]. The other two regimes correspond to various scenarios of LoS shadowing, depending on visibility for FSO communication [73], scattering from inhomogenities or turbulence influence in UWOC and when using RF communication systems at relatively large distances, e.g., up to 500 m at 3.5 GHz in urban area [71].

For $k<0.4$ and $m<1$ the system can demonstrate only full RHM. For the case of $k>0.4$ with the increase of m (and for $m>1$ with the increase of k), the system smoothly transits from the state of full HRM to the state of no HRM. Thus, it can be stated that a change in one of the parameters ($m,k$) does not lead to a change in the hyper-Rayleigh degree for $k>5$ or $m>5$.

To describe the performance of the fdRLoS channel, 4 distinct parameter combinations (points on the joint hyper-Rayleigh map) corresponding to the above-mentioned hyper-Rayleigh modes are chosen for the further physical layer security analysis of the wireless communication link: $m=5$, $k=5$ for no HRM, $m=5$, $k=1$ for weak HRM $m=2$, $k=1$ for strong HRM and $m=1$, $k=1$ for full HRM.

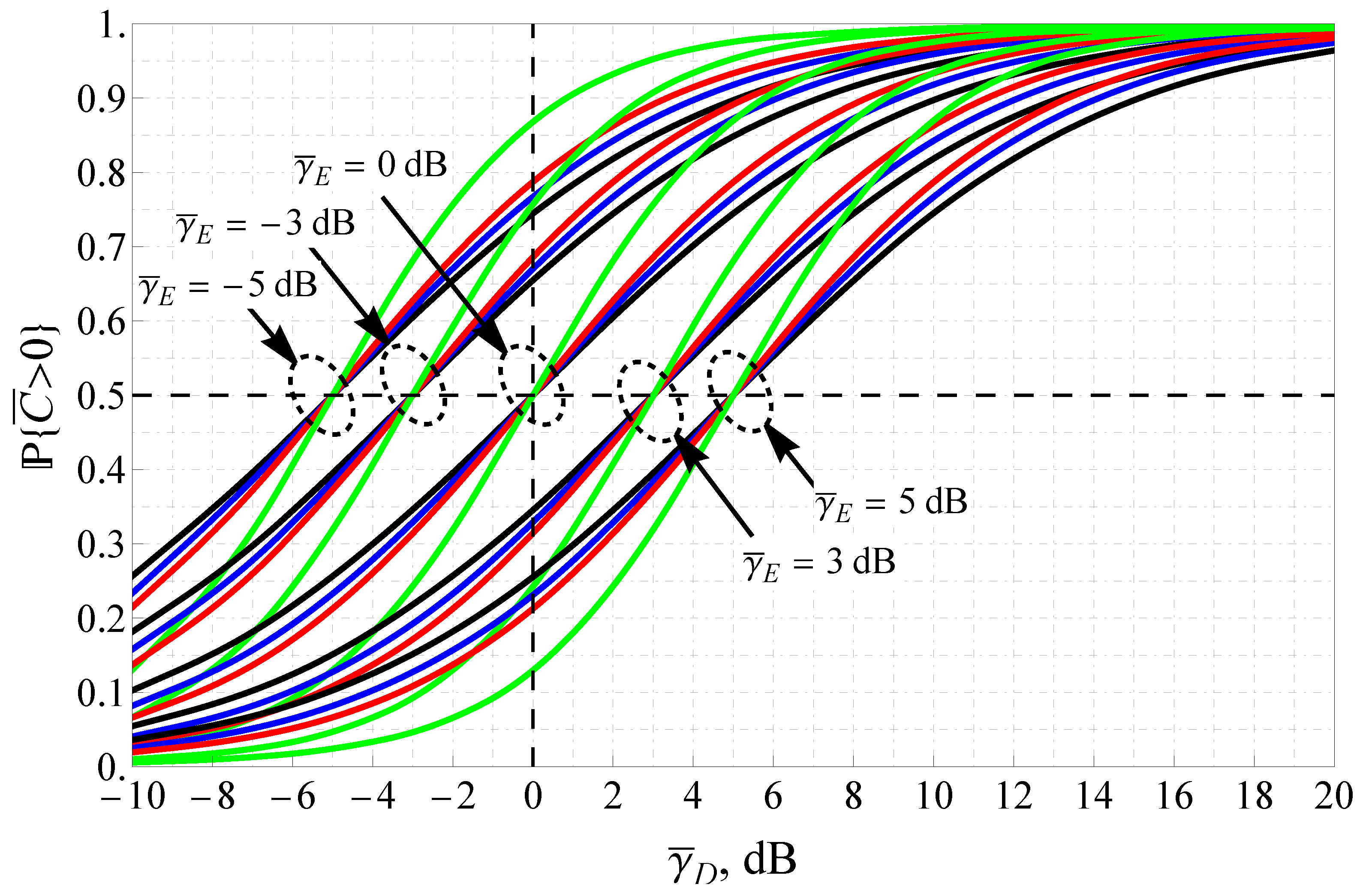
4.2. Illustrative Example: SPSC in Hyper-Rayleigh Regime

The probability of the strictly positive secrecy capacity for the fdRLoS model $\mathbb{P}\{\overline{C}>0\}$ (SPSC) as a function of the average SNR in the main channel ${\overline{\gamma }}_D$ for different average SNR in the wiretap channel ${\overline{\gamma }}_E$ is shown in Figure 3: Green lines denote no HRM (with channel parameters $m=5$, $k=5$), red lines denote weak HRM (for $m=5$, $k=1$), blue lines correspond to strong HRM ($m=2$, $k=1$), and black lines denote full HRM ($m=1$, $k=1$).

It can be pointed out that the proposed research assumes a physical layer secrecy scenario when channel parameters for the eavesdropper and destination channels are equal, which from the practical point of view corresponds to the situation when the eavesdropper is placed close to the receiver and passively and concealed wiretaps the communication link. This situation can occur in in an overcrowded and small environment, which is typical for public places supplied with high speed telecommunication systems (5G-NR, Wi-Fi-6 etc.).

With the gain in ${\overline{\gamma }}_D$, the value of SPSC monotonically increases to 1, and the values achieved are determined by the specific hyper-Rayleigh regime and SNRs in destination and eavesdropper channels. Security capacity is classically defined as the difference between the capacities of both channels. If there is no fading, the classical theory states that the security capacity is zero. However, under fading conditions, it becomes statistically possible to establish a secure link with non-zero capacity even in situations where ${\overline{\gamma }}_D$ is less than ${\overline{\gamma }}_E$. For example, if at ${\overline{\gamma }}_D=0$ dB the SNR in the eavesdropper’s channel ${\overline{\gamma }}_E$ worsens from 5 to 0 dB, then the SPSC increases from 0.22 to 0.5, with a further decrease in ${\overline{\gamma }}_E$ from 0 to −5 dB, SPSC changes from 0.5 to 0.78. So when ${\overline{\gamma }}_D<{\overline{\gamma }}_E$ SPSC is less than 0.5, but greater than 0.

There is a unique relationship between the values of SNR in the destination and eavesdropper channels (i.e., ${\overline{\gamma }}_D={\overline{\gamma }}_E$), at which the SPSC is indifferent to the degree of hyper-Rayleigh and is equal to 0.5 for any of them because of the identity of the destination and the eavesdropper channels that can be demonstrated analytically. Near this point, there is a change in the order in which the degrees of hyper-Rayleigh affect the SPSC: For ${\overline{\gamma }}_D<{\overline{\gamma }}_E$), the SPSC grows with the hyper-Rayleigh impairment, $\overline{\gamma }>{\overline{\gamma }}_E$) improves.

The curves for various hyper-Rayleigh scenarios are generally closer to each other than to the curve of the scenario in which the system does not exhibit hyper-Rayleigh behavior, with the maximum difference in the values of SPSC of about 0.15.

It is worth noting that any of the hyper-Rayleigh modes imposes greater energy requirements for achieving some predefined communication link secrecy level. For example, to achieve $\mathbb{P}\{\overline{C}>0\}=0.9$ in the best of the situations under consideration (i.e., ${\overline{\gamma }}_E=-5$ dB), the required ${\overline{\gamma }}_D$ should be around 1.3 dB for no-HRM, and almost 4 dB in full HRM (which is 2.7 dB greater). In the worst situation of ${\overline{\gamma }}_E=5$ dB, the requirements become tougher: ${\overline{\gamma }}_D=16$ dB is required for full HRM versus 11 dB needed for the no-HRM channel.

5. Conclusions

Modern wireless communication systems, RF or OWC, are highly sensitive to the signal propagation conditions. The presented research studies hyper-Rayleigh behavior of wireless communication systems functioning in the presence of the generalized multipath fading. The use of the recently published fdRLoS channel model, which takes into account many features of signal propagation, made it possible to obtain the closed-form analytical description of the finite SNR hyper-Rayleigh regime, including the closed-form expression for the amount of fading and the exact expression for the outage probability valid for arbitrary fading parameters. This allows not only to describe the severity of channel fading and shadowing, predict the performance of communication link in specific environmental conditions, but also to identify the hyper-Rayleigh mode on the go and reconfigure the system in order to improve the quality, reliability and secrecy. For instance, if the channel parameters m and k increase, one can expect a transition from the full HRM to the strong/weak/none HRM, that helps to predict the possible change of the system performance. Such changes may be caused by variation of propagation conditions, for example, due to the movement of the transmitter, receiver, scatterers or due to the fluctuation of the shadowing conditions, for example, due to the random nature of shadowing objects’ movement or due to an increase in their number along the path of the line-of-sight component. Artificial techniques can also be used to change the HRM severity, for example, such as the use of intelligent reflecting surfaces. As the exception, one can mention channel parameters’ regions, where the increase of the parameters themselves does not yield any improvement in hyper-Rayleigh mode, including the full HRM (e.g., for m < 1 and increasing k, or for $k\le 0.3$ and increasing m), and the regions where the parameters do not change sufficiently (e.g., m can be considered asymptotic if $k<1$).