Gradient Heatmetry in a Burners Adjustment
Abstract
1. Introduction
2. Experimental Procedure
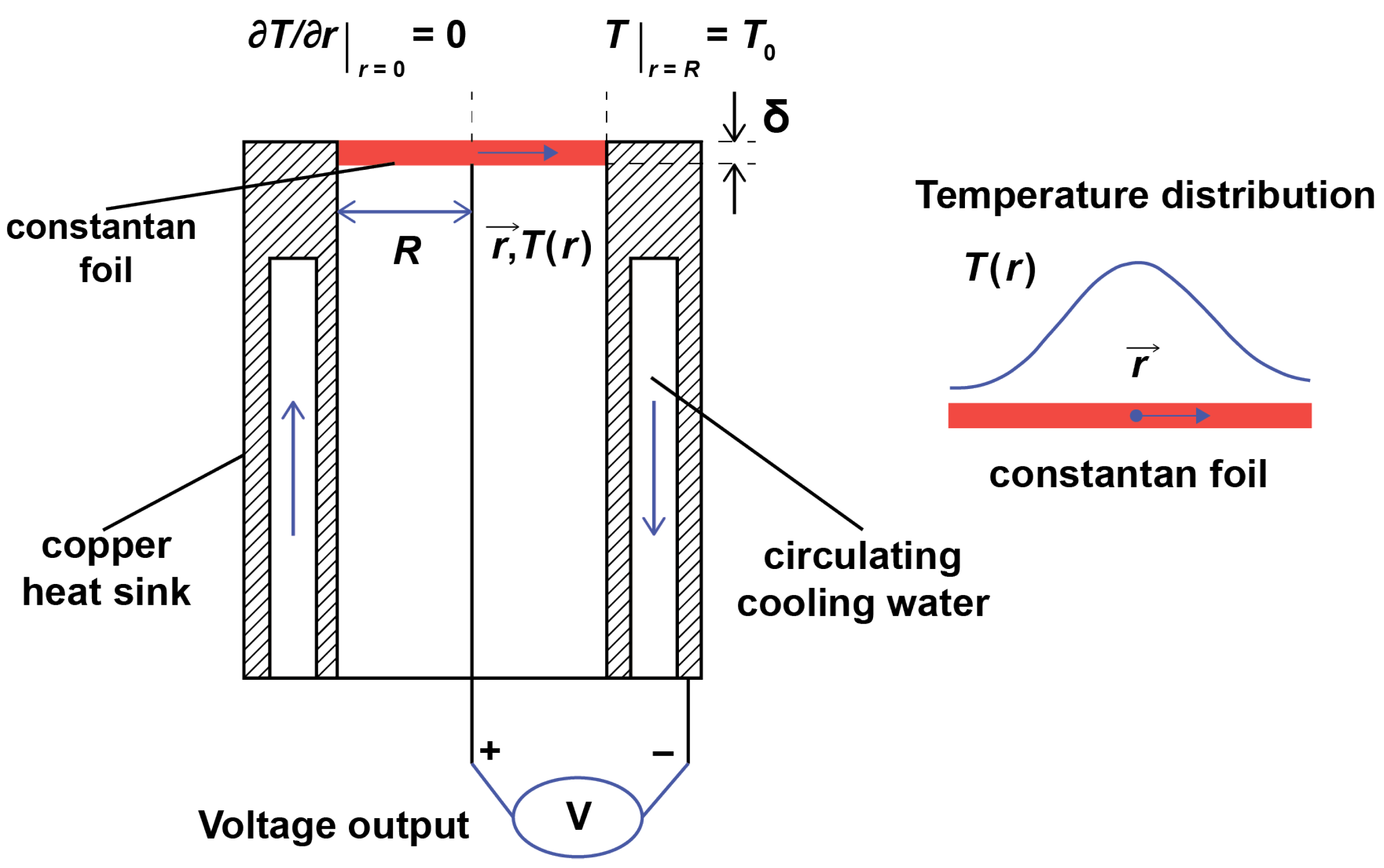
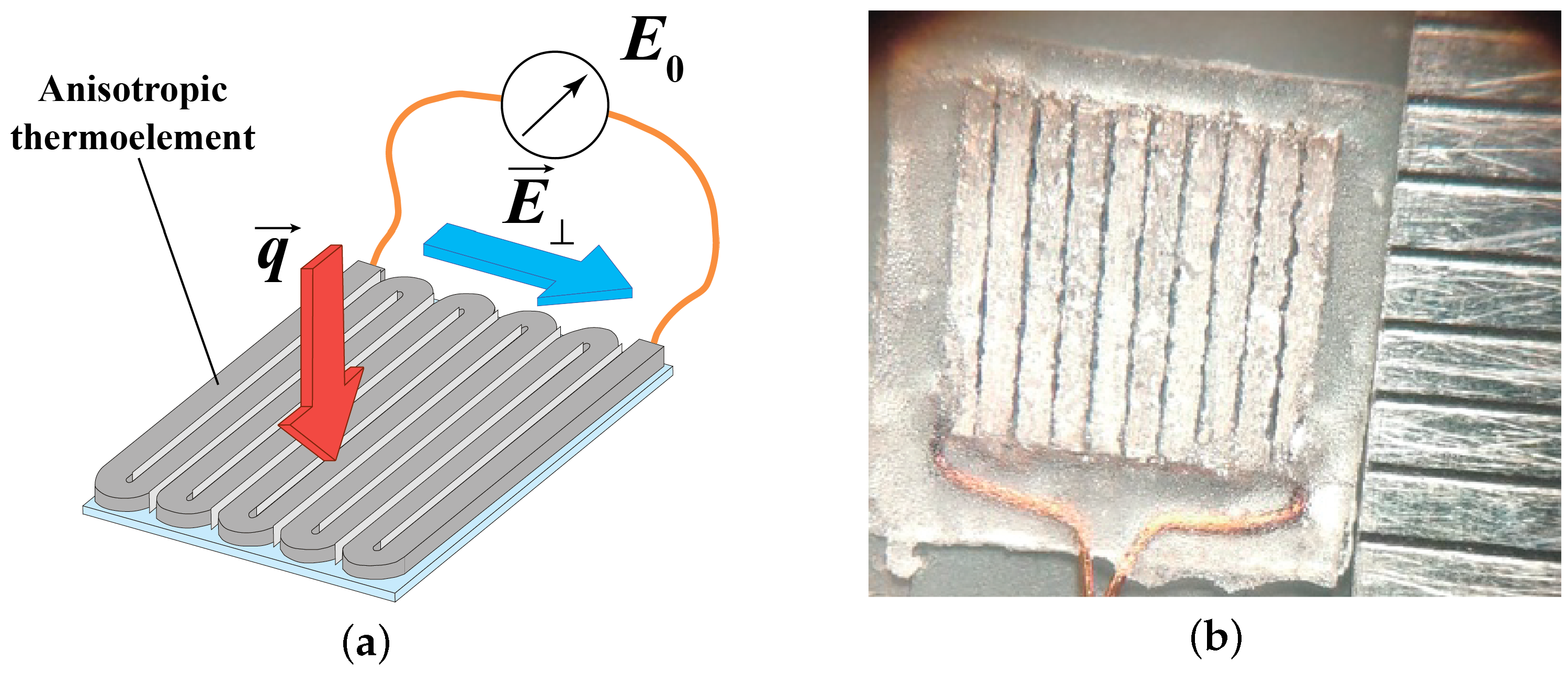
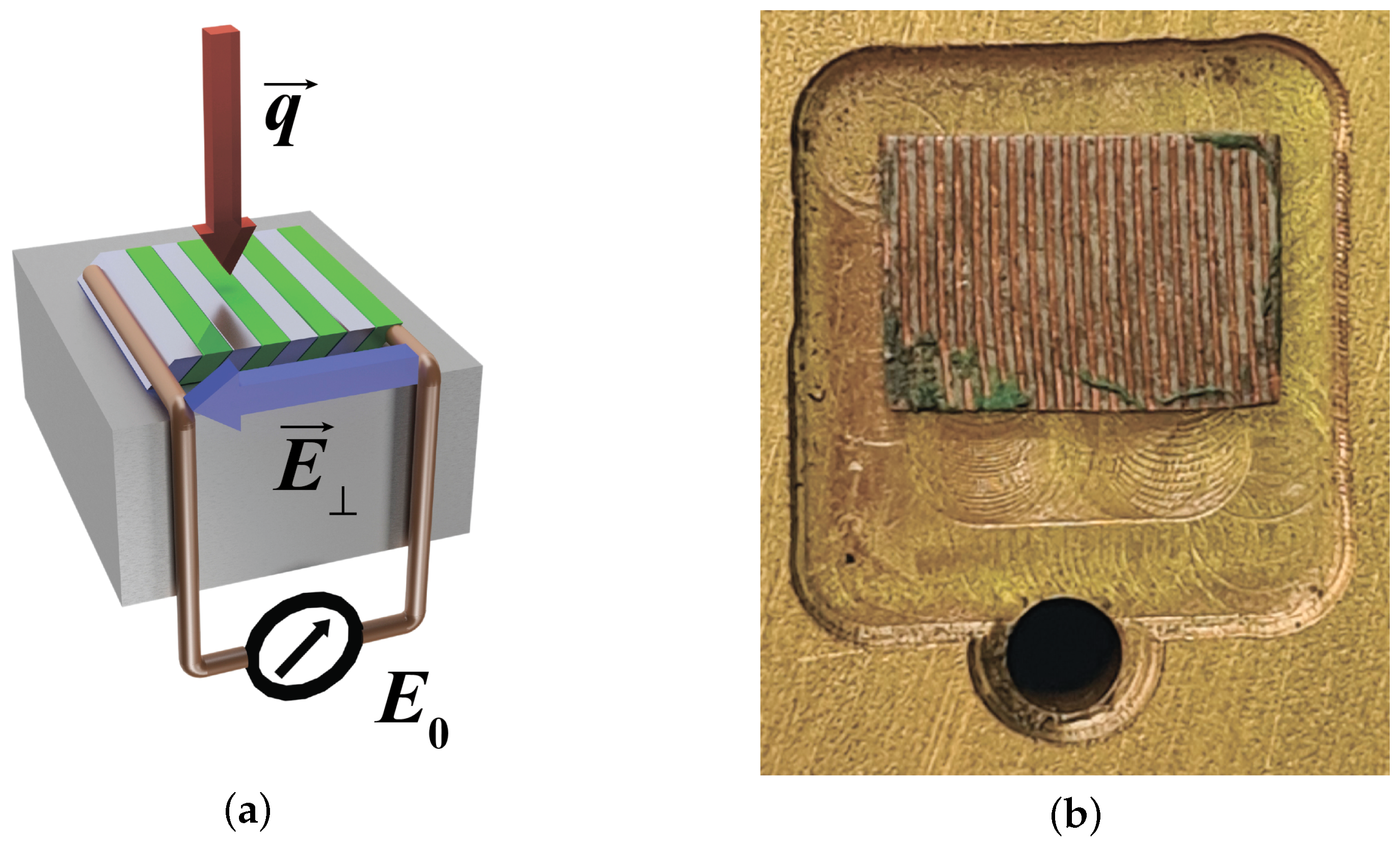
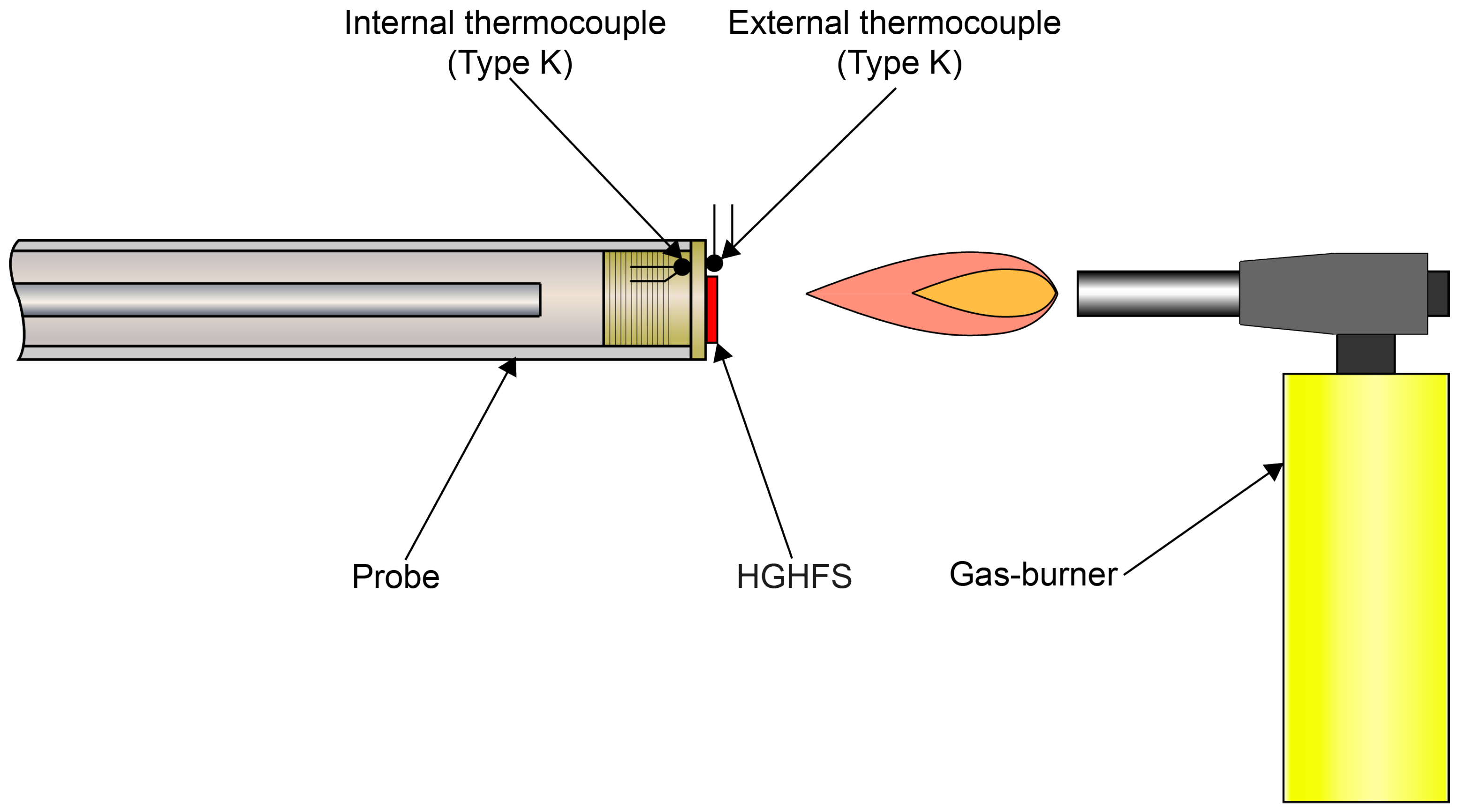
2.1. Gradient Heatmetry
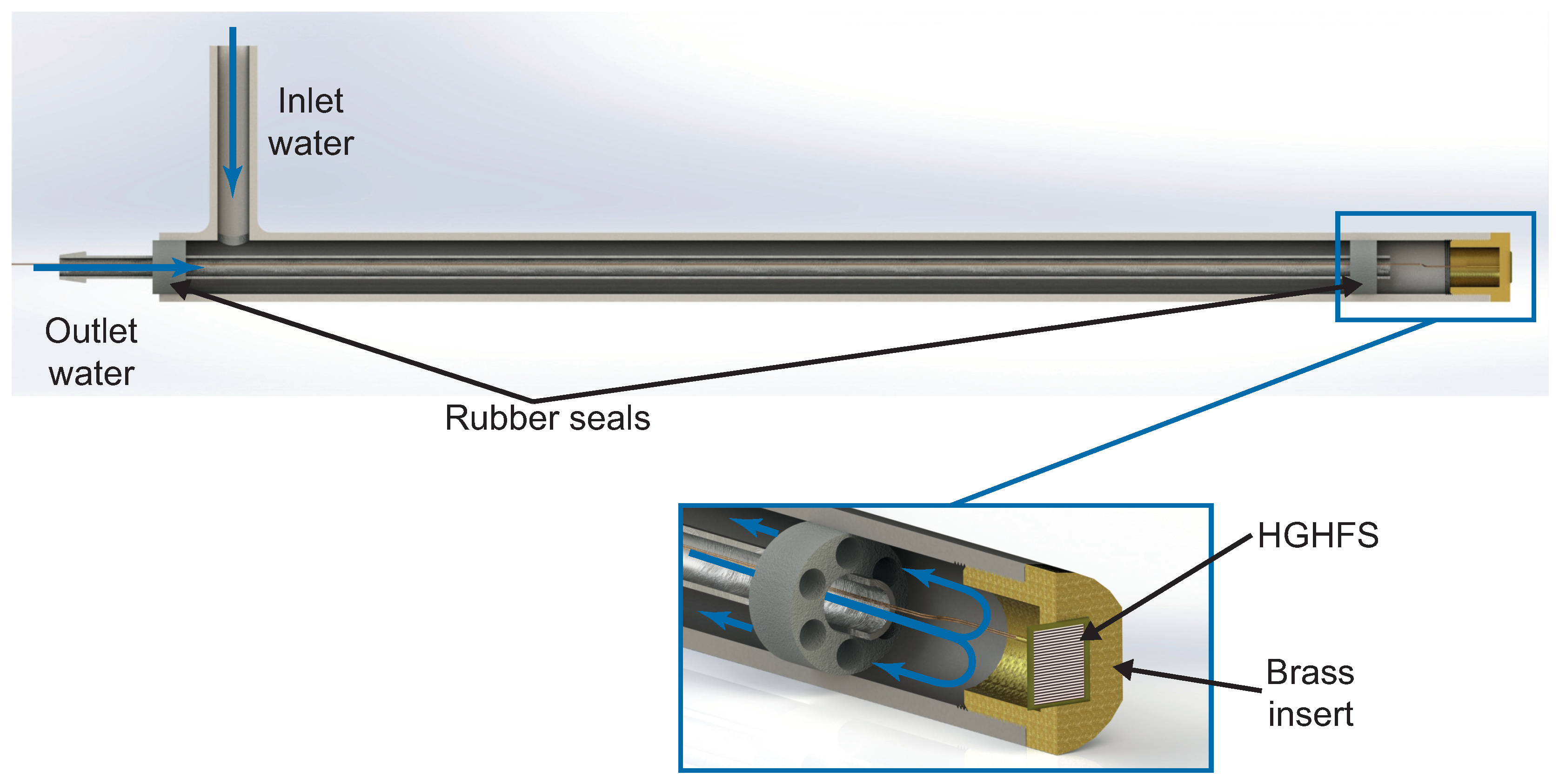
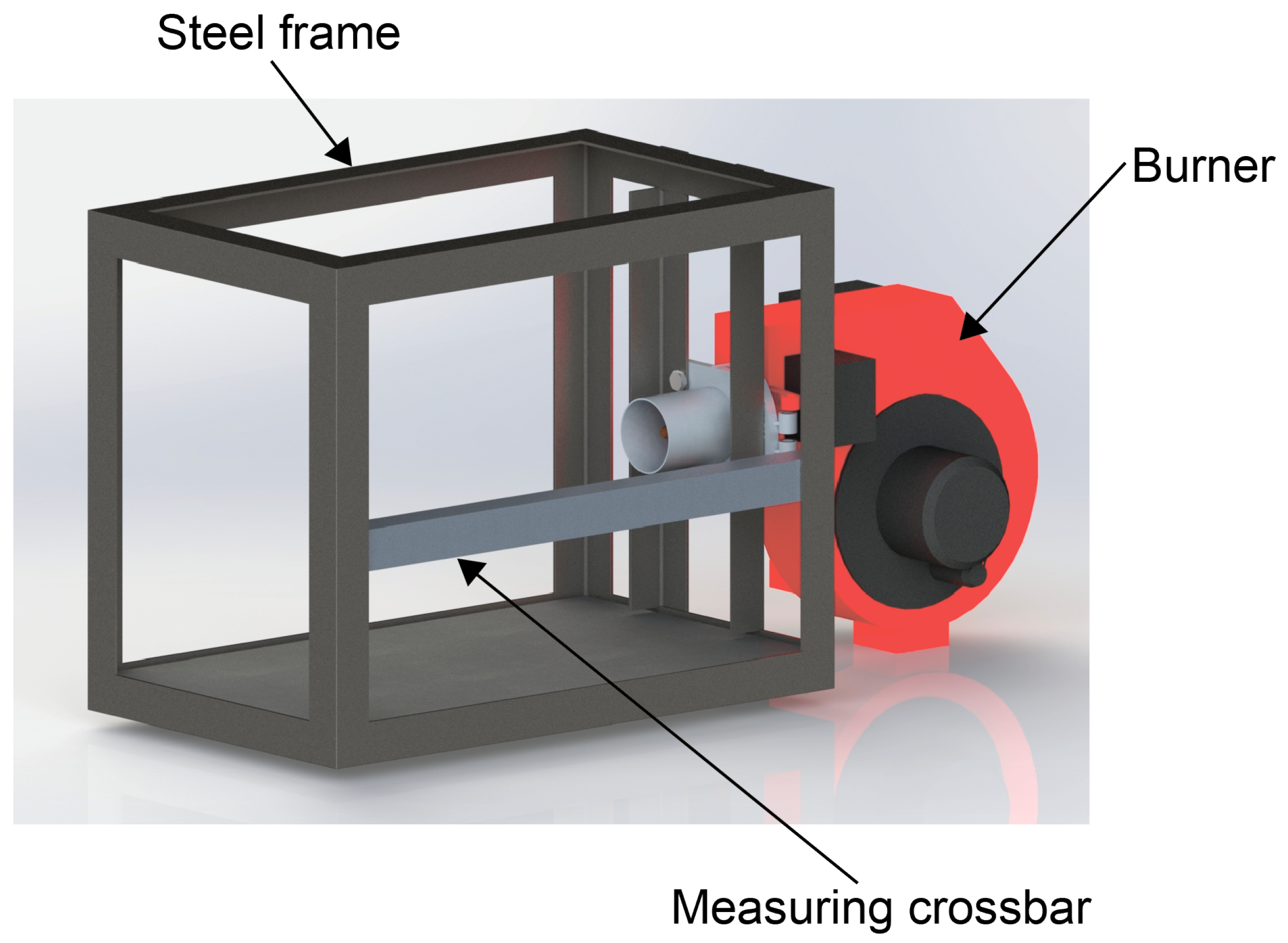
2.2. Experimental Setup
- The measuring insert dimensions must be small enough in comparison with the the flame size and large enough in comparison with the HGHFS plan-area.
- The measuring insert must be made of a material with high thermal conductivity, and the probe itself must be made of a material with low thermal conductivity.
- The dimensions of the probes and inserts should be convenient for mounting thermocouples and HGHFS, outputting wires, and supplying cooling water.
2.3. Measurement Uncertainty
- Error in the GHFS volt-watt sensitivity
- Error in measuring the GHFS area
- Errors in measurement using ADC
3. Experimental Results
3.1. Pilot Experiments
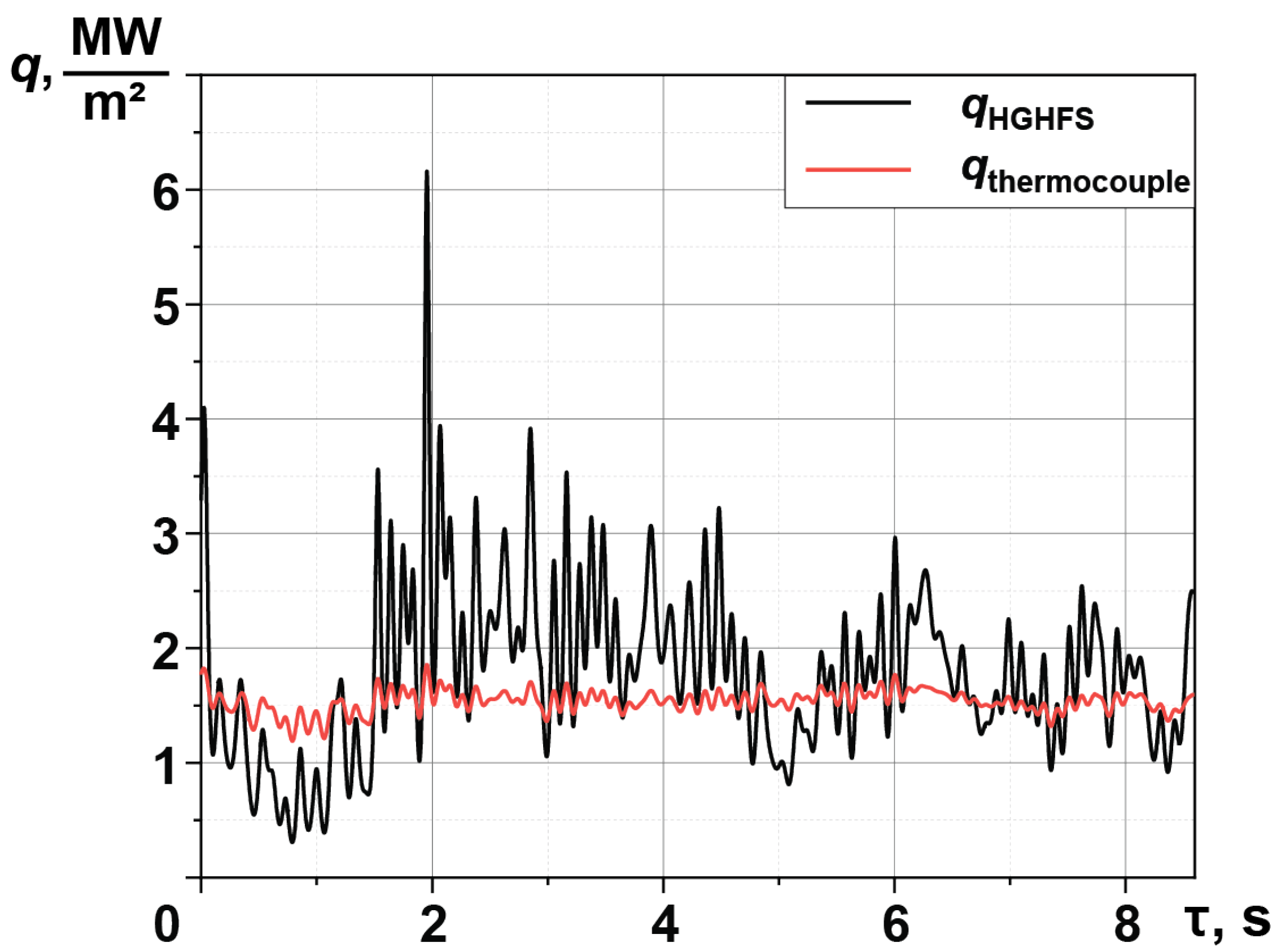
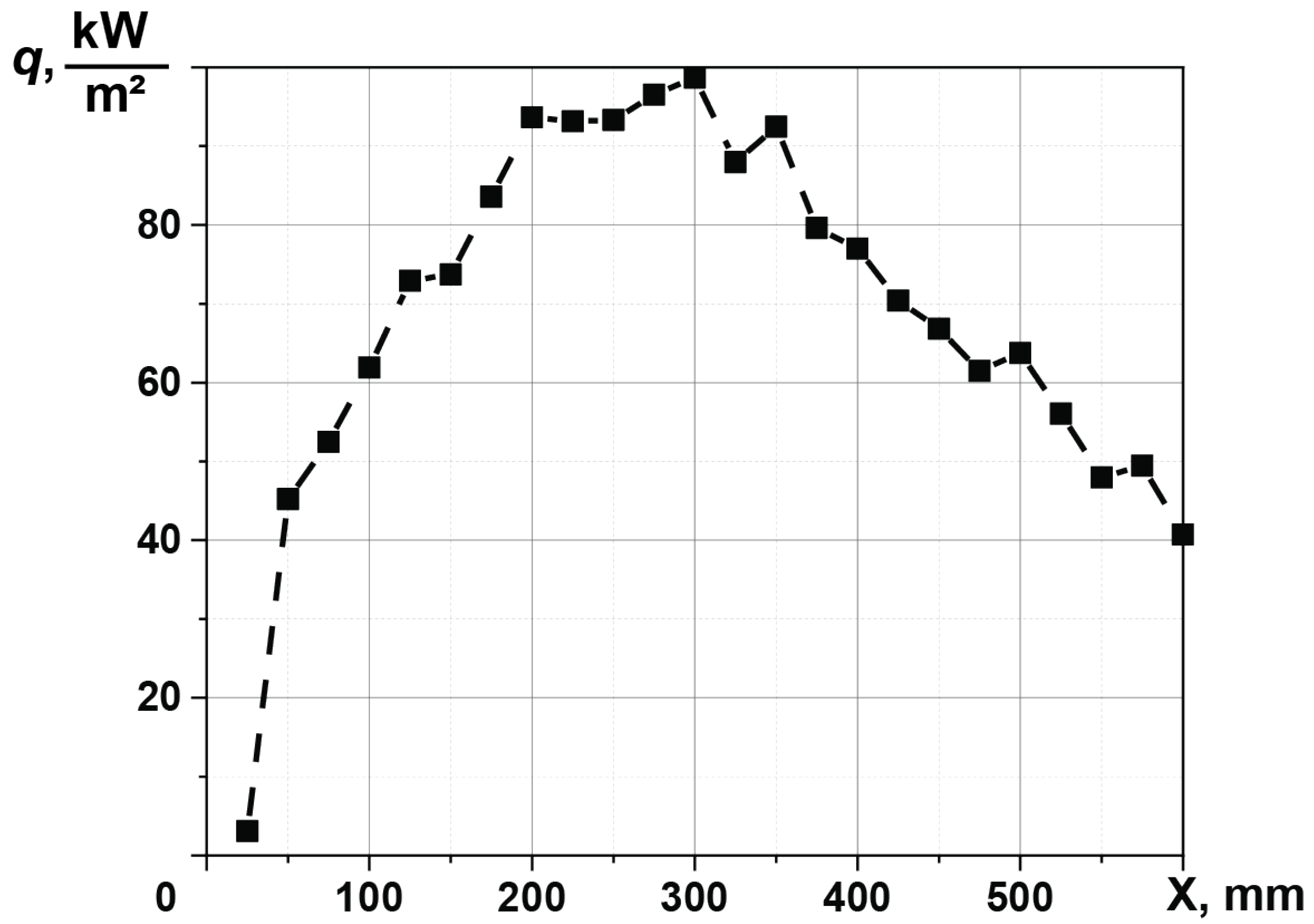
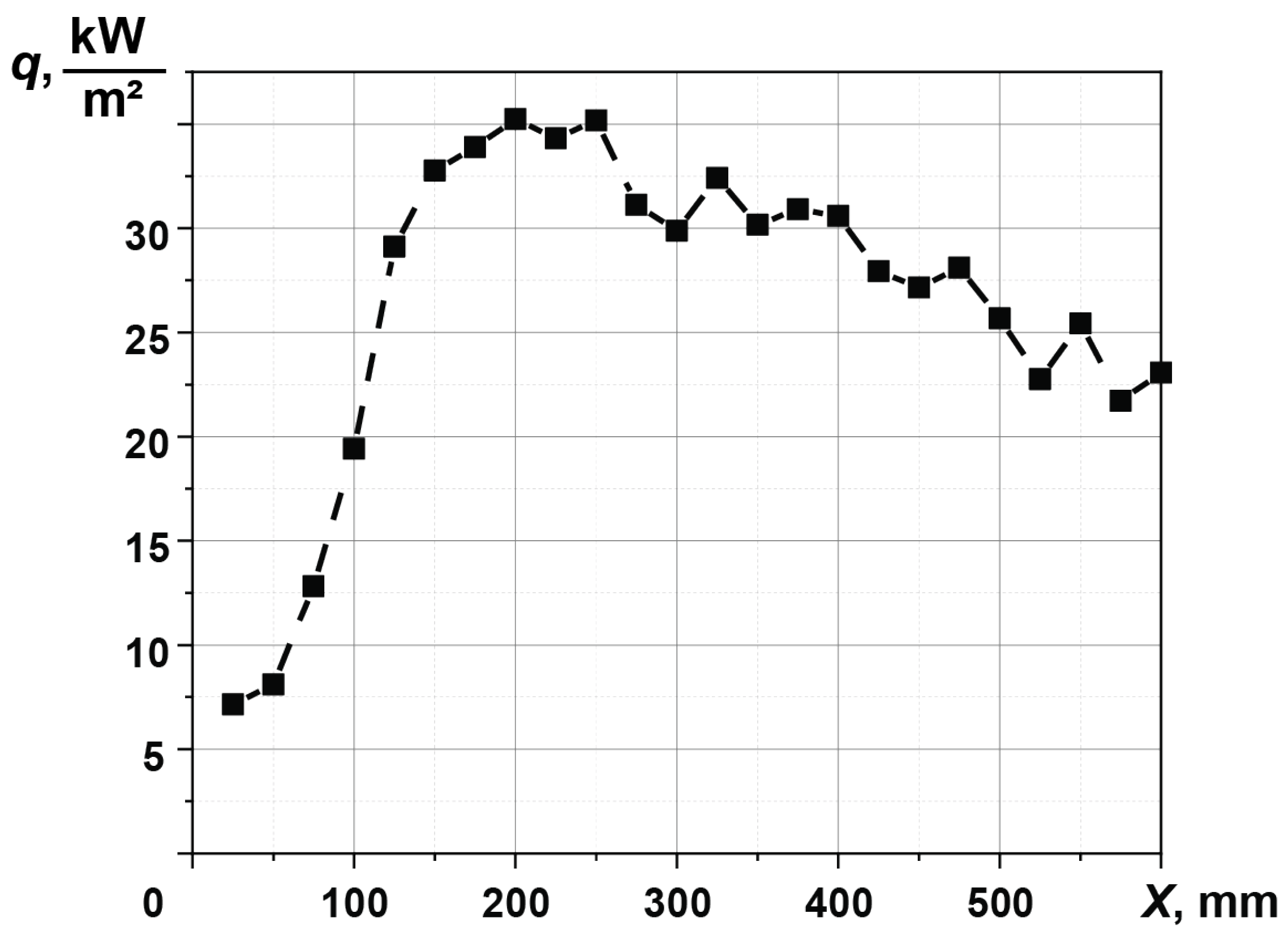
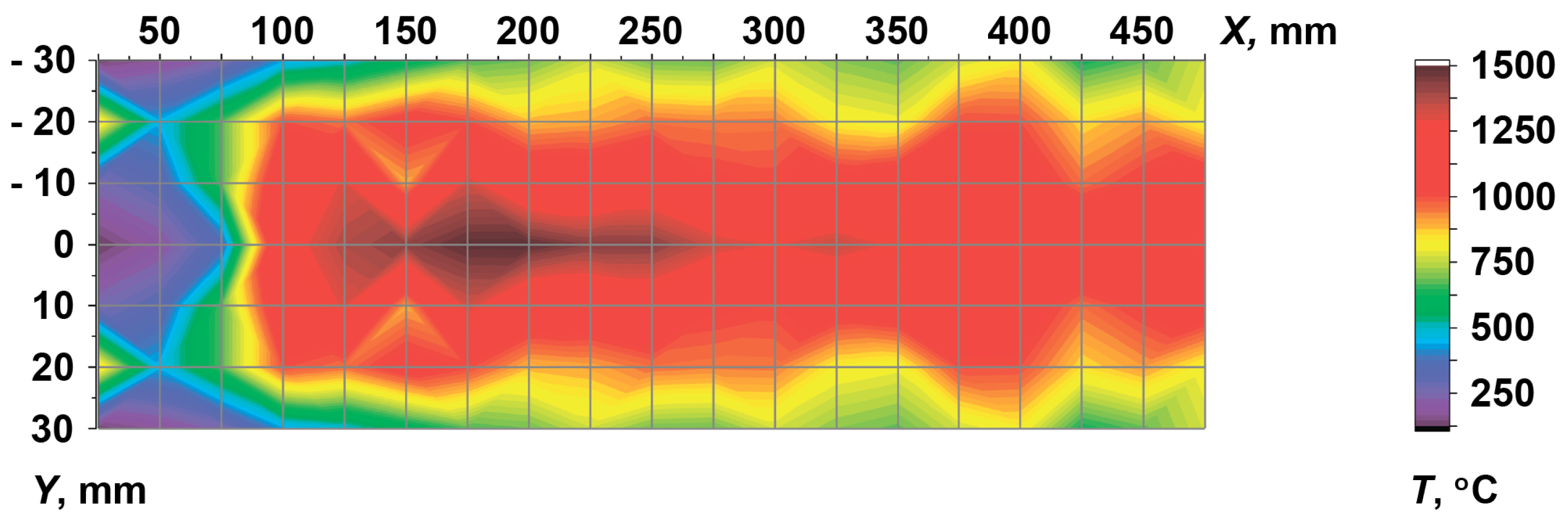
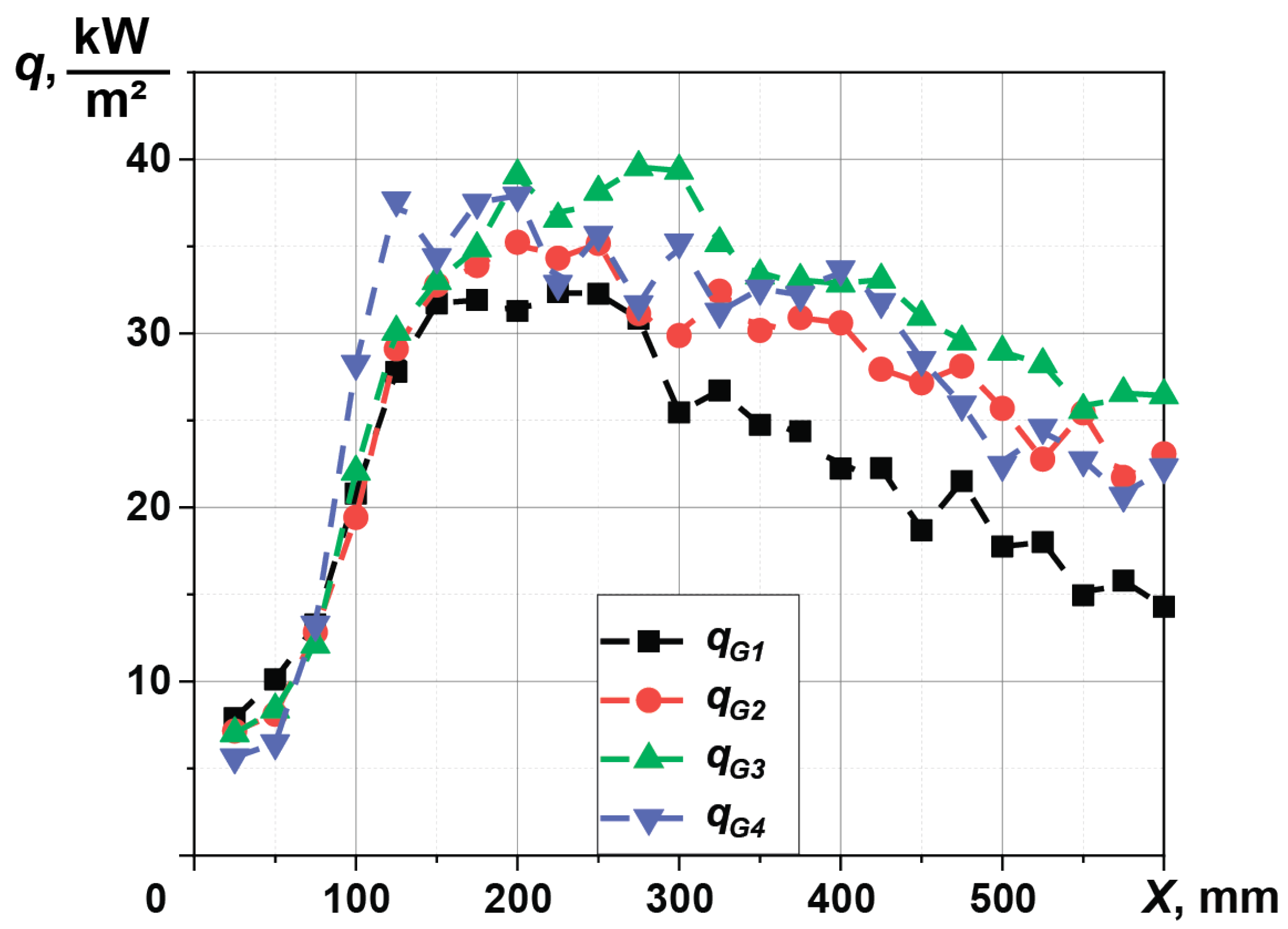
3.2. Gas Flame
3.3. Diesel Flame
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LHV | Lower Heating Value |
| GHFS | Gradient Heat Flux Sensor |
| ATE | Anisotropic Thermoelemnt |
| HGHFS | Heterogeneous Gradient Heat Flux Sensor |
| ADC | Analog to Digital Converter |
References
- Glassman, I.; Yetter, R.A.; Glumac, N.G. Combustion, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2014; 757p. [Google Scholar]
- Kemelman, D.N.; Eskin, N.B.; Davidov, A.A. Adjustment of Boiler Installations: Handbook; Energiya Publ.: Moscow, Russia, 1976; p. 344. [Google Scholar]
- Zhang, D.; Shi, H.; Meng, C.; Wu, Y.; Zhang, H.; Zhou, W.; Ran, S. Measurements on Heat Flux Distribution in a Supercritical Arch-Fired Boiler. In Clean Coal Technology and Sustainable Development; Yue, G., Li, S., Eds.; Springer: Singapore, 2016; pp. 207–212. [Google Scholar]
- Martucci, A.; De Gregorio, F.; Musto, M.; Petrella, O.; Marciano, L.; Rotondo, G.; Gaudino, E. Innovative calibration methodology for gardon gauge heat flux meter. In Proceedings of the IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 22–24 June 2020; pp. 288–293. [Google Scholar]
- Pullins, C.A.; Diller, T.E. Direct Measurement of Hot-Wall Heat Flux. J. Thermophys. Heat Transf. 2012, 26, 430–438. [Google Scholar] [CrossRef]
- Guillot, E.; Alxneit, I.; Ballestrin, J.; Sans, J.L.; Willsh, C. Comparison of 3 heat flux gauges and a water calorimeter for concentrated solar irradiance measurement. Energy Procedia 2014, 49, 2090–2099. [Google Scholar] [CrossRef]
- Northover, E.W.; Hitchcock, J.A. A heat flux meter for use in boiler furnaces. J. Sci. Instrum. 1967, 44, 371–374. [Google Scholar] [CrossRef]
- Arai, N.; Matsunami, A.; Churchill, S.W. A review of Measurements of Heat Flux Density Applicable to the Field of Combustion Experimental. Therm. Fluid Sci. 1996, 12, 452–460. [Google Scholar] [CrossRef]
- Schulte, E.H.; Kohl, R.F. A review of measurements of heat flux density applicable to the field of combustion. Exp. Therm. Fluid Sci. 1969, 40, 1420–1427. [Google Scholar]
- Hager, N.E., Jr. Thin Foil Heat Meter. Rev. Sci. Instrum. 1965, 36, 1564–1570. [Google Scholar] [CrossRef]
- Klems, J.H.; DiBartolomeo, D. Large-area, high-sensitivity heat-flow sensor. Rev. Sci. Instrum. 1982, 53, 1609–1612. [Google Scholar] [CrossRef]
- Mityakov, A.V.; Mityakov, V.Y.; Sapozhnikov, S.Z.; Chumakov, Y.S. Measurement of Instantaneous Values of a Heat Flux on a Vertical Heated Surface under Conditions of Free-Convection Heat Transfer. High Temp. 2002, 40, 620–625. [Google Scholar] [CrossRef]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V. Bismuth-Based Gradient Heat-Flux Sensors in Thermal Experiment. High Temp. 2004, 42, 629–638. [Google Scholar] [CrossRef]
- Sapozhnikov, S.; Mityakov, V.; Mityakov, A. Heatmetry: The Science and Practice of Heat Flux Measurement; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Seroshtanov, V.V.; Gusakov, A.A. The Combination of PIV and Heat Flux Measurement in Study of Flow and Heat Transfer Near a Circular Finned Cylinder. In Proceedings of the International Conference on Optical Methods of Flow Investigation, Moscow, Russia, 24–28 June 2019; Volume 1412. [Google Scholar]
- Mityakov, V.Y.; Sapozhnikov, S.Z.; Zainullina, E.R.; Babich, A.Y.; Milto, O.A.; Kalmykov, K.S. Gradient Heat Flux Measurement while Researching of Saturated Water Steam Condensation. In Proceedings of the International Conference “Problems of Thermal Physics and Power Engineering” (PTPPE-2017), Moscow, Russia, 9–11 October 2017; Volume 891. [Google Scholar]
- Sapoznikov, S.Z.; Mityakov, V.Y.; Gusakov, A.A.; Pavlov, A.V.; Bobylev, P.G. Gradient Heatmetry for Boiling of Underheated Water on Spherical Surface. J. Phys. Conf. Ser. 2020, 1683, 1683. [Google Scholar] [CrossRef]
- Available online: https://oilon.spb.ru/ (accessed on 11 November 2022).
- ISO/IEC Guide 98-1:2009–Uncertainty of Measurement—Part 1: Introduction to the Expression of Uncertainty in Measurement. Available online: www.iso.org/standard/ (accessed on 12 November 2022).
- Available online: https://flukeshop.ru/multimetr-fluke-287/ (accessed on 30 November 2022).
- Benjamin, G. Heat Transfer; McGraw-Hill: New York, NY, USA, 1961; p. 454. [Google Scholar]
- Available online: https://www.danfoss.com/ (accessed on 11 November 2022).
- Lakshminarayanan, P.A.; Aghav, Y.V. Modelling Diesel Combustion; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Available online: https://www.testo.ru/ (accessed on 13 November 2022).



| Quantity | Value | Standart Uncertainty | Probability Distribution | Sensitivity Coefficient | Uncertainty Contribution |
|---|---|---|---|---|---|
| , mV/W | 4.97 | 0.17 | B | −7238 | 1230.5 |
| A, m | 25 × 10 | 2.8 × 10 | B | −144.2 × 10 | 40.32 |
| E, mV | 4.488 | 0.025 | B | 16.1 × 10 | 401.6 |
| q, W/m | 36.05 × 10 | 1295.0 | B | ||
| , % | 7.18 |
| Flow-Rate, kg/h | CO | nCO | O |
|---|---|---|---|
| 7.11 | 0.80 | 1.00 | 0.92 |
| 7.95 | 0.62 | 0.22 | 1.00 |
| 8.58 | 1.00 | 0.07 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobylev, P.G.; Pavlov, A.V.; Proskurin, V.M.; Andreyev, Y.V.; Mityakov, V.Y.; Sapozhnikov, S.Z. Gradient Heatmetry in a Burners Adjustment. Inventions 2022, 7, 122. https://doi.org/10.3390/inventions7040122
Bobylev PG, Pavlov AV, Proskurin VM, Andreyev YV, Mityakov VY, Sapozhnikov SZ. Gradient Heatmetry in a Burners Adjustment. Inventions. 2022; 7(4):122. https://doi.org/10.3390/inventions7040122
Chicago/Turabian StyleBobylev, Pavel G., Andrey V. Pavlov, Vyacheslav M. Proskurin, Yuriy V. Andreyev, Vladimir Yu. Mityakov, and Sergey Z. Sapozhnikov. 2022. "Gradient Heatmetry in a Burners Adjustment" Inventions 7, no. 4: 122. https://doi.org/10.3390/inventions7040122
APA StyleBobylev, P. G., Pavlov, A. V., Proskurin, V. M., Andreyev, Y. V., Mityakov, V. Y., & Sapozhnikov, S. Z. (2022). Gradient Heatmetry in a Burners Adjustment. Inventions, 7(4), 122. https://doi.org/10.3390/inventions7040122






