Impact of Electroosmosis and Wall Properties in Modelling Peristaltic Mechanism of a Jeffrey Liquid through a Microchannel with Variable Fluid Properties
Abstract
:1. Introduction
2. Physical Model
3. Methodology
3.1. Perturbation Solution
3.1.1. Zeroth Order System
3.1.2. First Order System
4. Results and Discussion
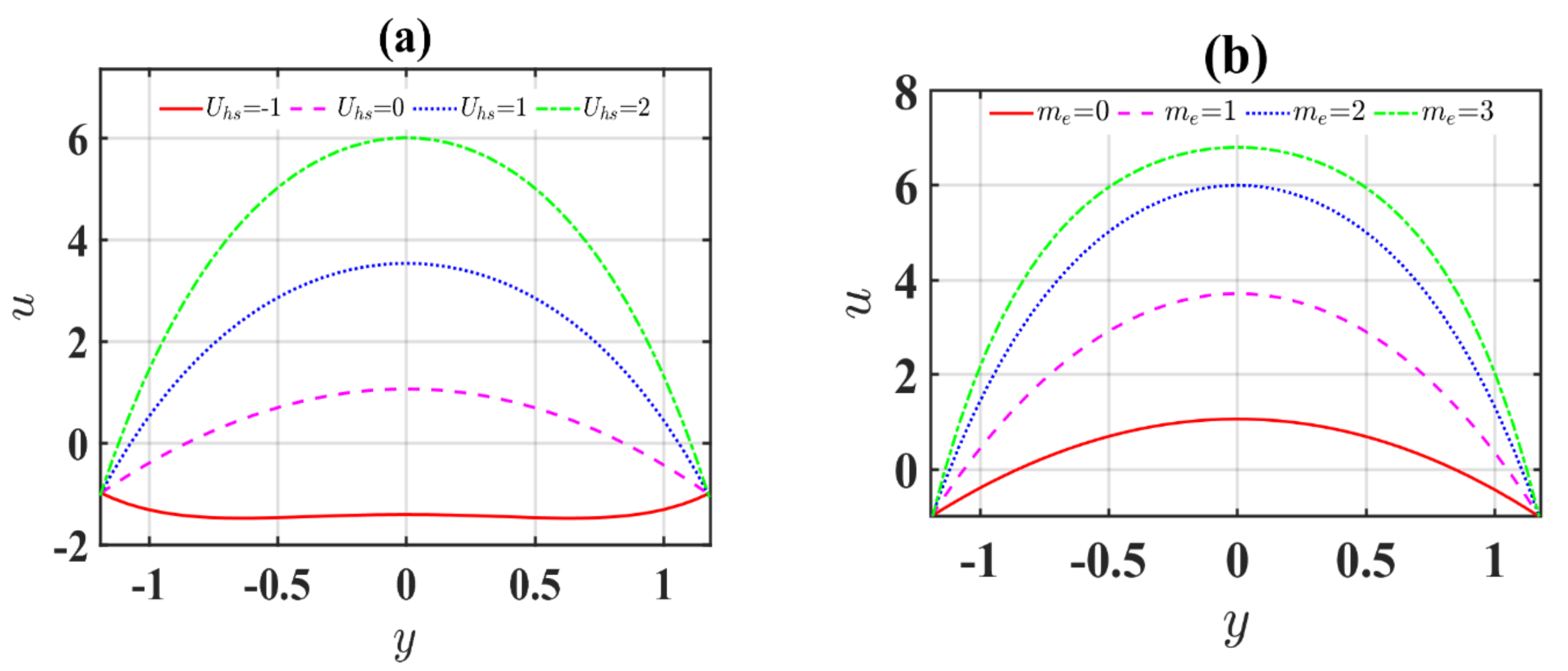
4.1. Velocity Profiles
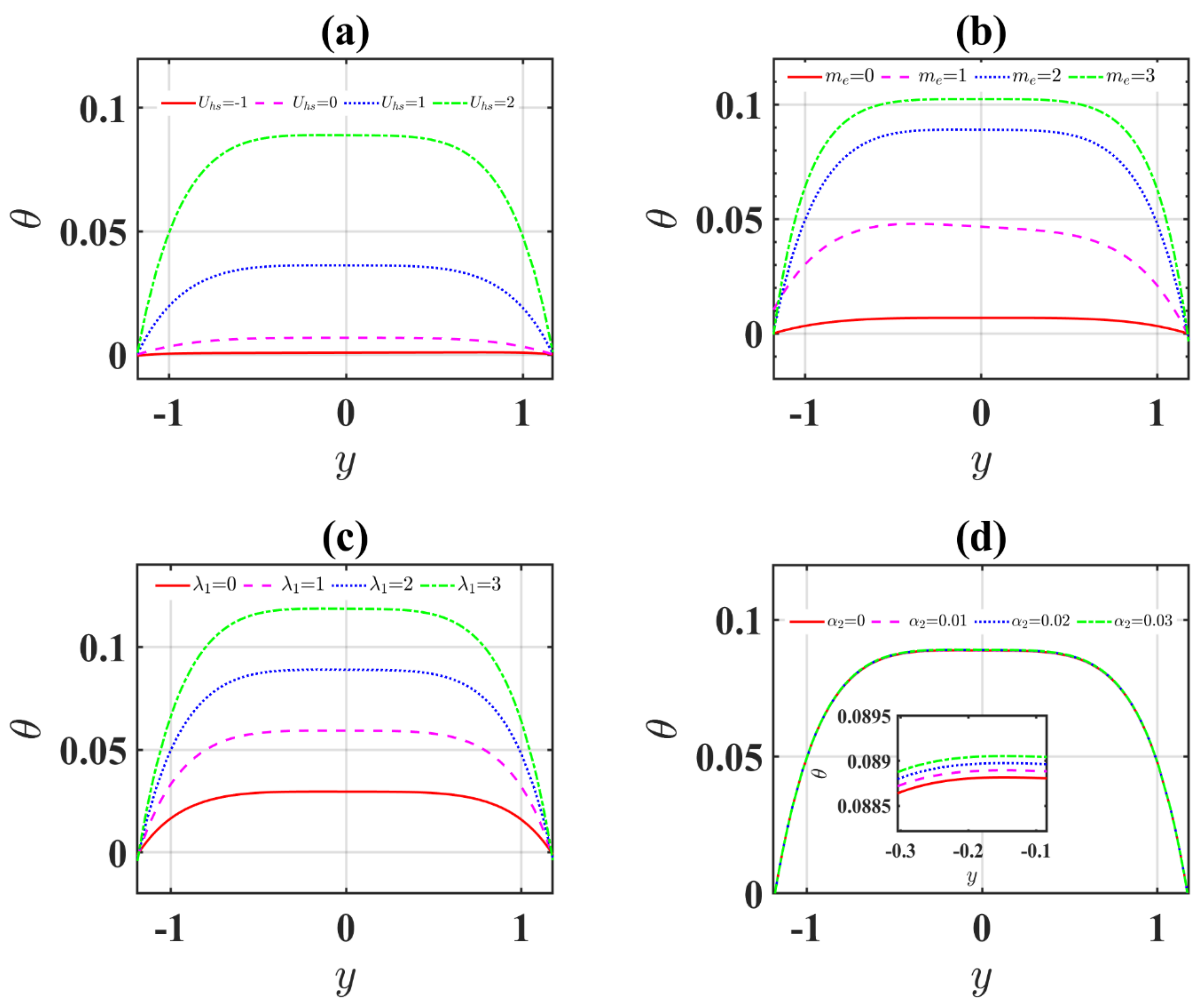
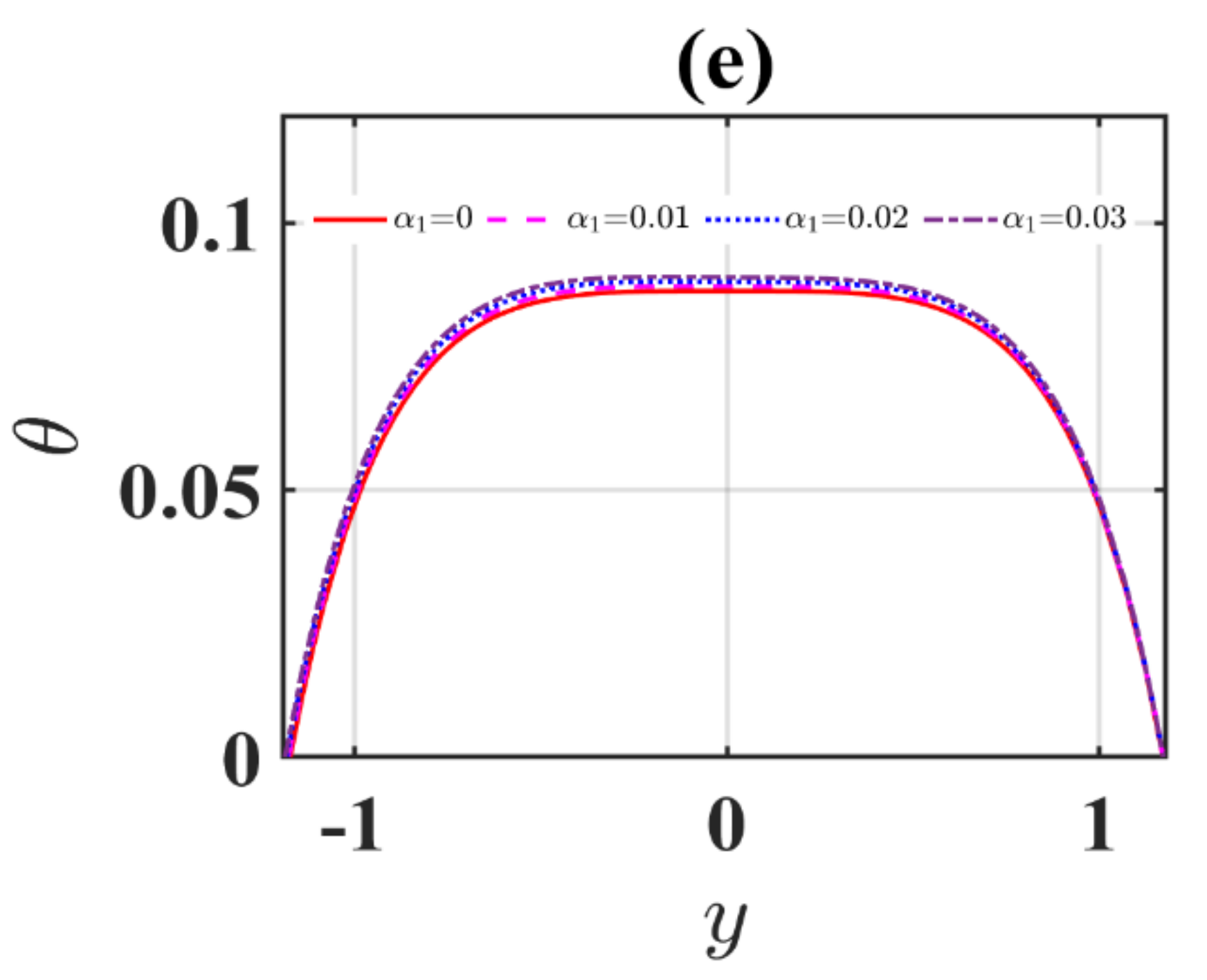
4.2. Temperature Profiles
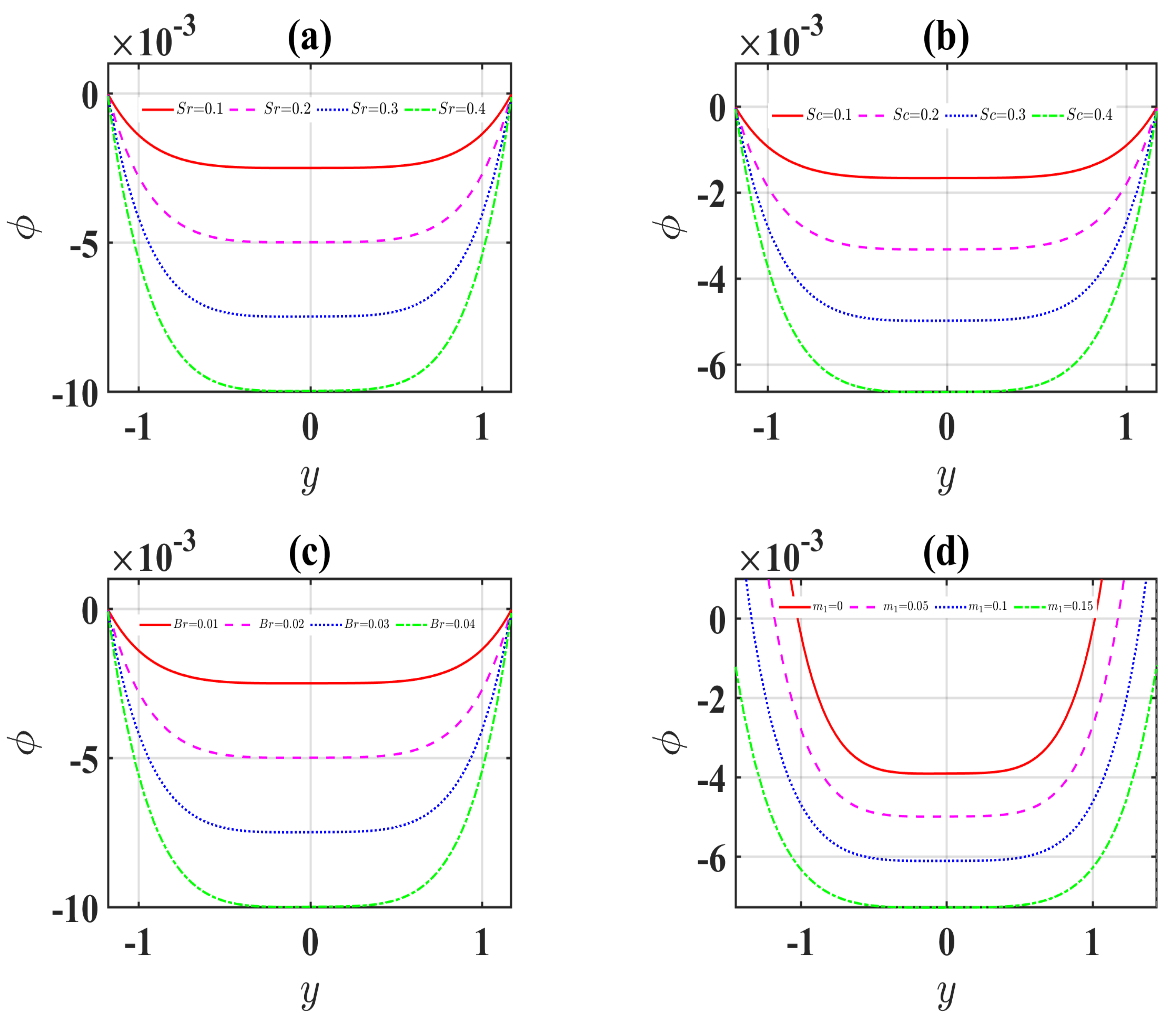
4.3. Concentration Profiles
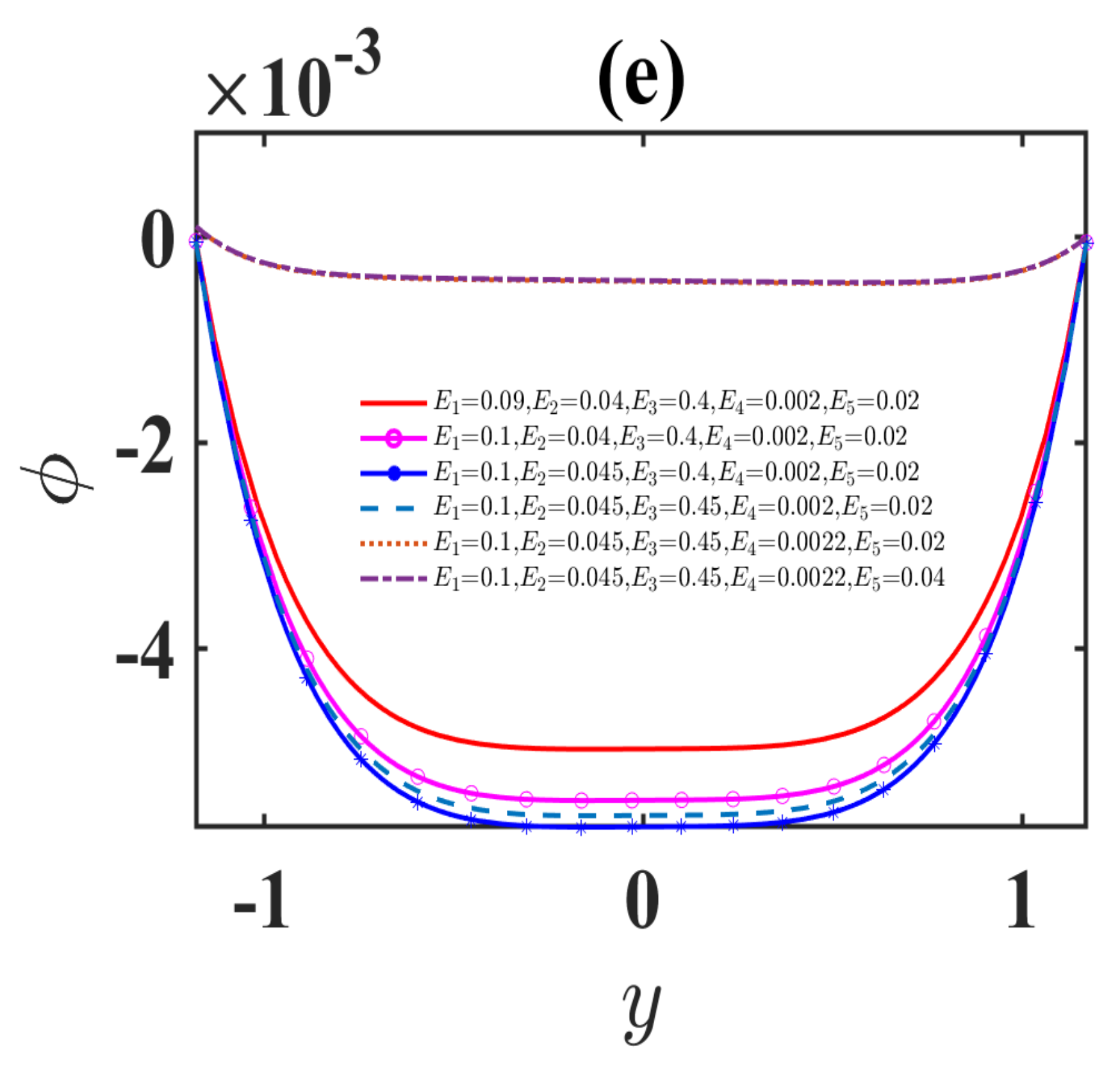
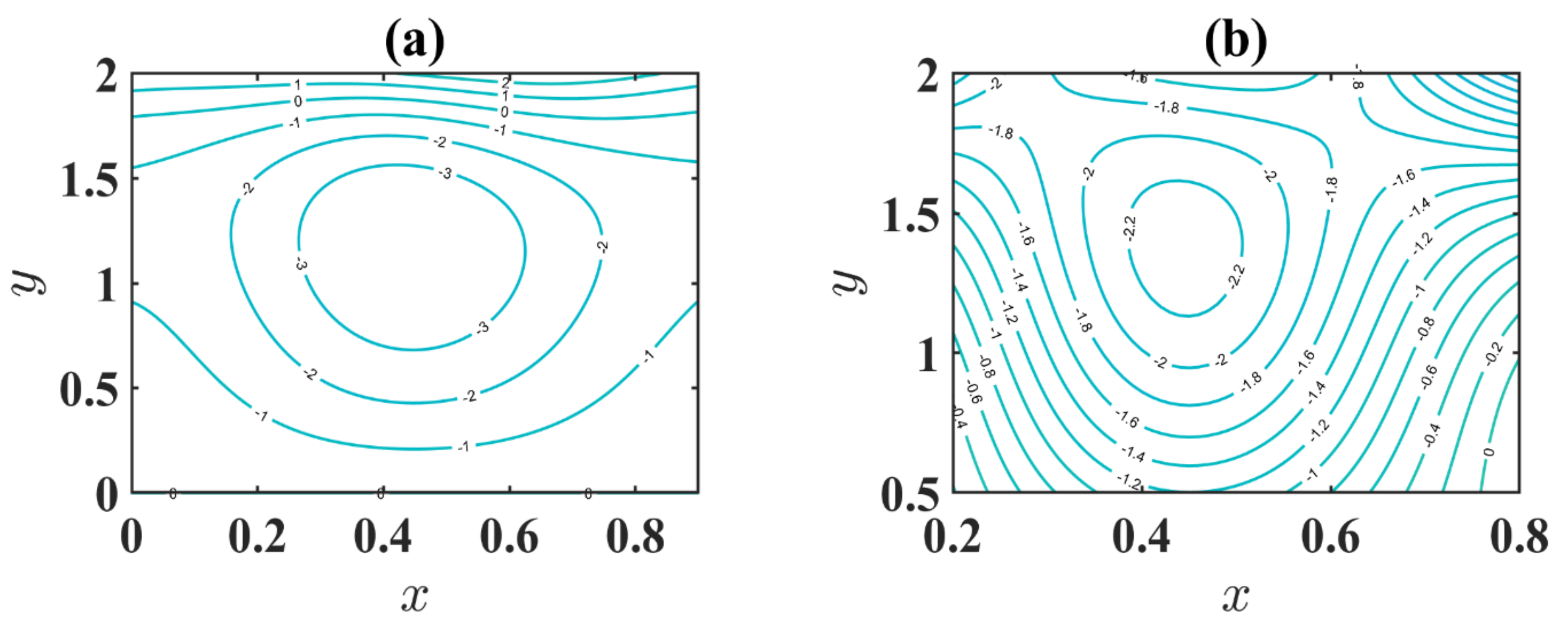
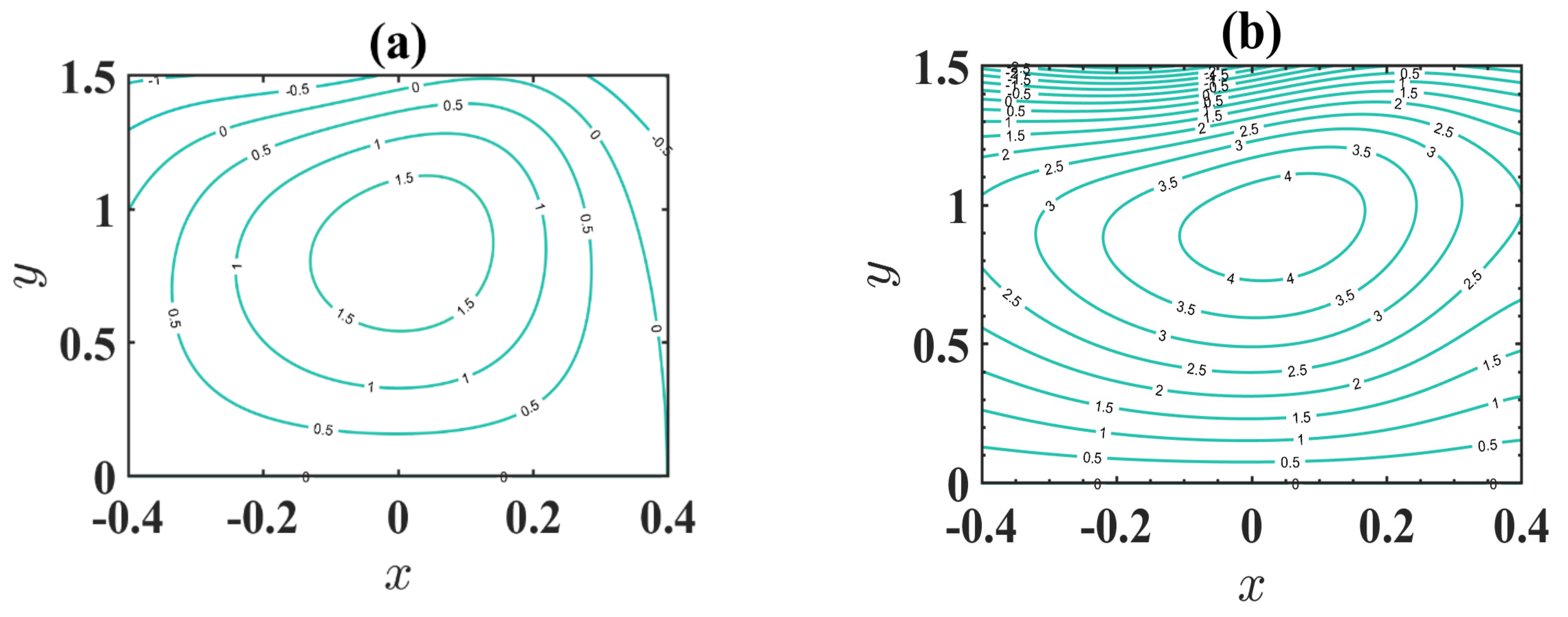
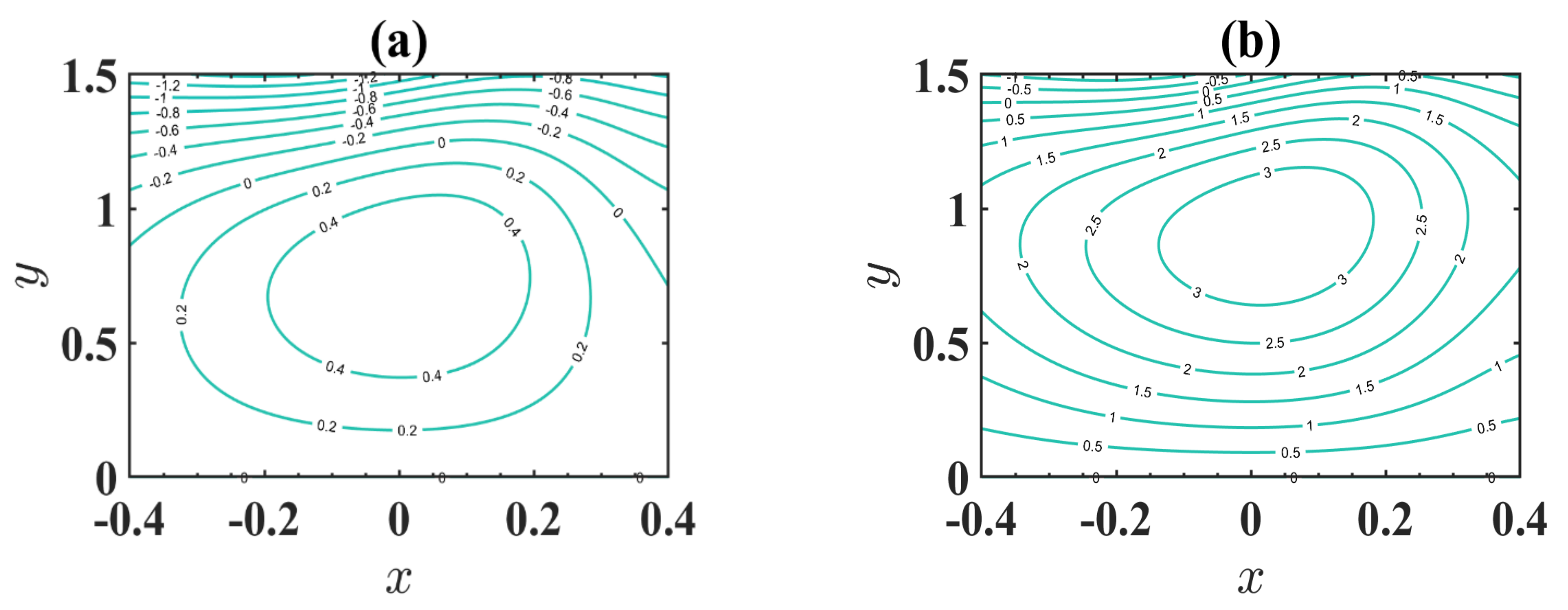
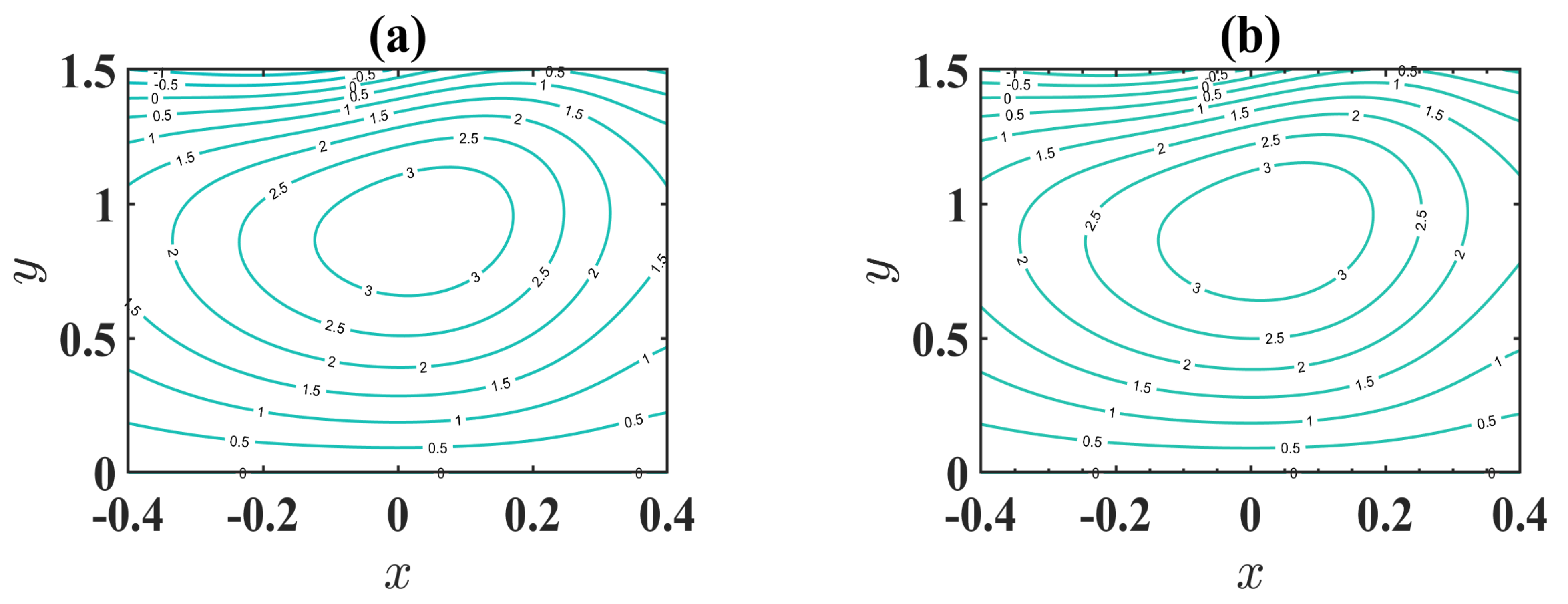
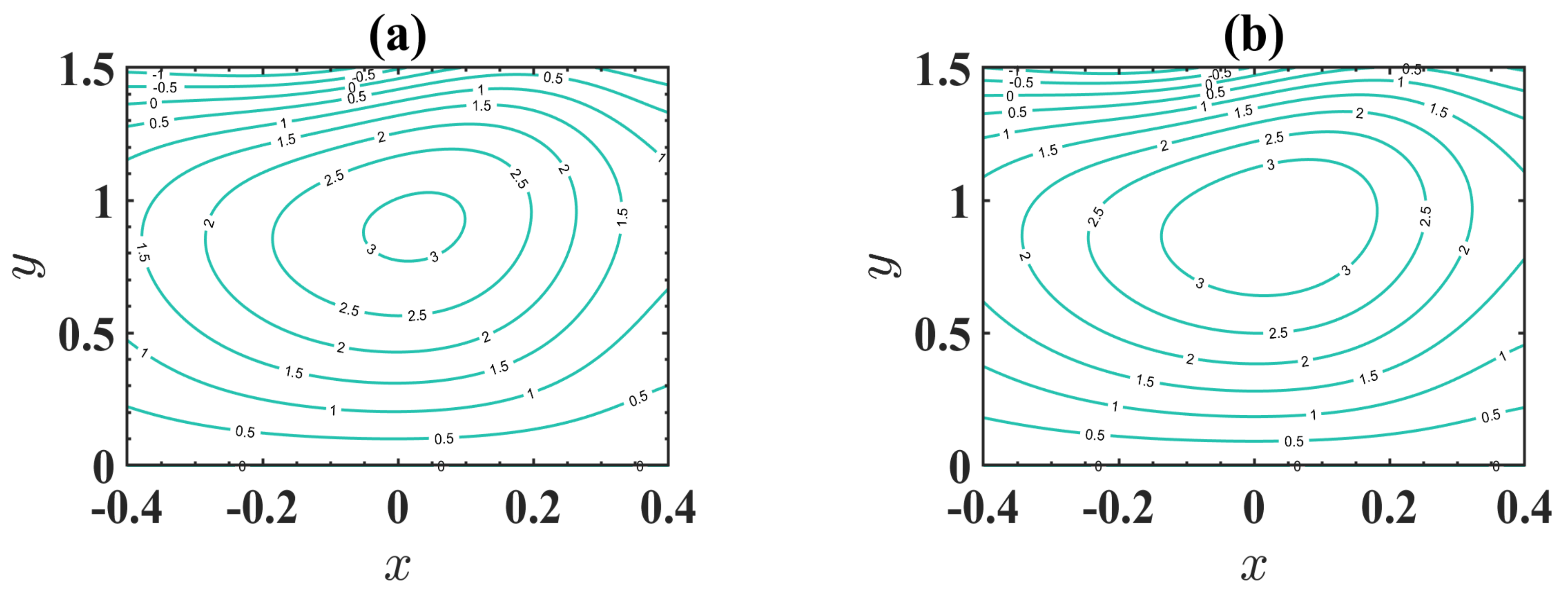
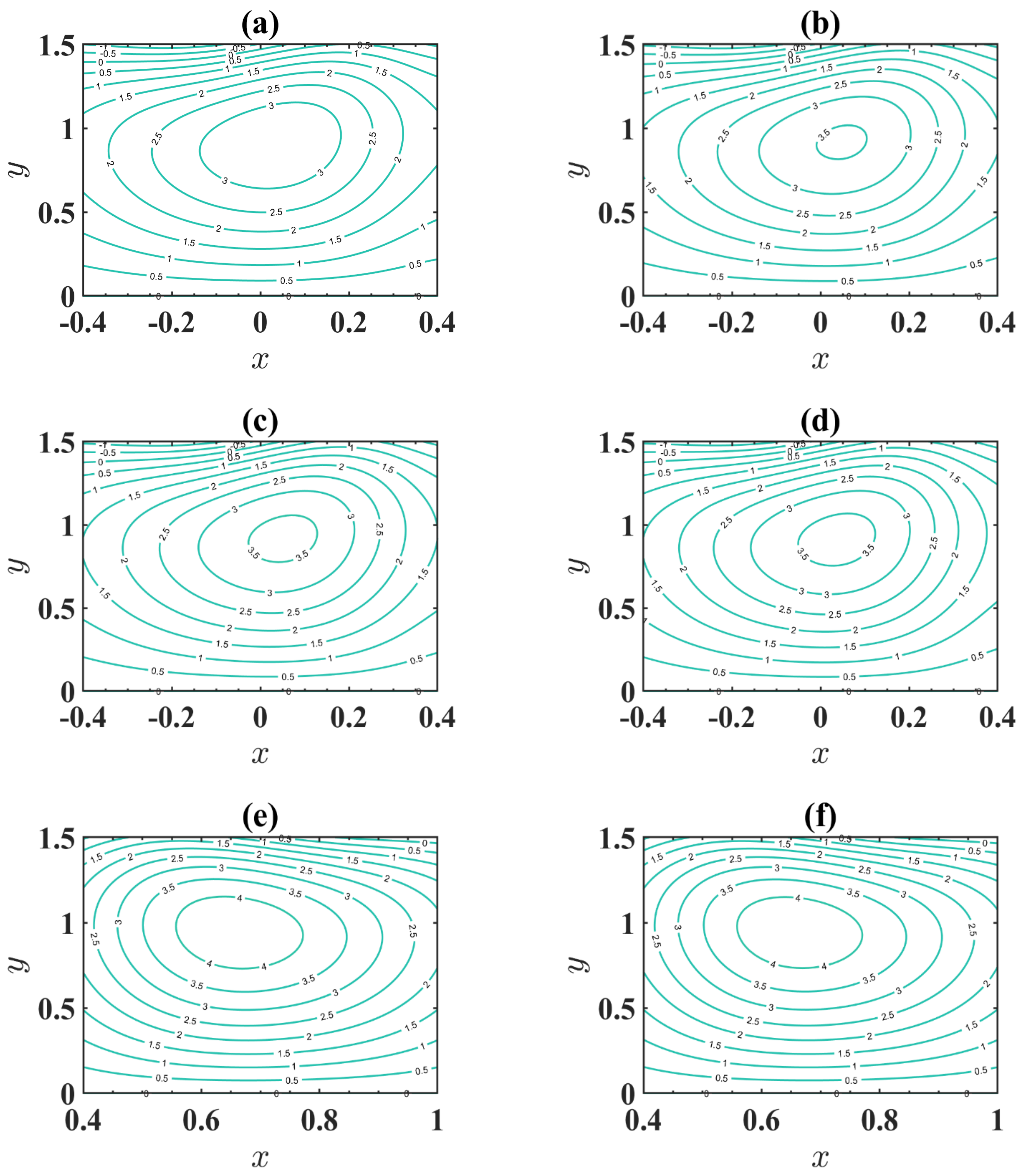
4.4. Trapping Phenomenon
5. Conclusions
- The impact of optimum electroosmotic velocity enhances the velocity profiles.
- Electroosmotic specification is a decreasing function of velocity.
- The increasing values of the Brinkman number and the non-uniform parameter enhance the velocity profiles.
- The Jeffrey term boosts the temperature and velocity profiles.
- The changeable viscosity and variable thermal conductivity boost the velocity and temperature profiles.
- The concentration profiles significantly diminish for more significant values of the Schmidt and Soret numbers.
- The influence of enhances the velocity and temperature profiles for Newtonian fluids, and it decreases for .
- The size of the trapped bolus increases through an expansion in the estimation of changeable viscosity.
- Accumulation of streamlines decreases with an increase in maximum electroosmotic velocity.
- The number of enclosed boluses is augmented through a boost in the electroosmotic criterion.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| average temperature | |
| axial and radial coordinates | |
| Boltzmann constant | |
| Brinkmann number | |
| bulk concentration | |
| charge balance | |
| Eckert number | |
| elastic parameters | |
| electronic charge | |
| electroosmotic term | |
| extra stress tensor | |
| Helmholtz–Smoluchowski velocity | |
| identity tensor | |
| length of the channel | |
| mass per unit area | |
| mass per unit surface | |
| Prandtl number | |
| pressure | |
| Reynold’s number | |
| Schmidt number | |
| Soret number | |
| time | |
| velocity components | |
| viscous damping coefficient | |
| wave speed | |
| Greek Letters | |
| amplitude ratio | |
| angle of inclination | |
| Cauchy stress tensor | |
| concentration | |
| Debye length | |
| density | |
| dielectric permittivity | |
| elastic tension | |
| electric potential | |
| fluid flow parameter | |
| ratio of relaxation to retardation | |
| retardation time | |
| shear rate | |
| streamline | |
| temperature | |
| thermal conductivity coefficient | |
| total charge density | |
| variable thermal conductivity | |
| variable viscosity | |
| wave length |
References
- Latham, T.W. Fluid Motions in a Peristaltic Pump. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Raju, K.; Devantahan, R. Peristaltic transport of non-Newtonian fluid. Rheol. Acta 1972, 11, 170–178. [Google Scholar] [CrossRef]
- Manjunatha, G.; Rajashekhar, C. Slip Effects on Peristaltic Transport of Casson Fluid in an Inclined Elastic Tube with Porous Walls. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 43, 67–80. [Google Scholar]
- Vaidya, H.; Rajashekhar, C.; Manjunatha, G.; Prasad, K.V. Rheological Properties and Peristalsis of Rabinowitsch Fluid Through Compliant Porous Walls in an Inclined Channel. J. Nanofluids 2018, 8, 970–979. [Google Scholar] [CrossRef]
- Manjunatha, G.; Rajashekhar, C.; Vaidya, H.; Prasad, K.; Makinde, O.D. Effects Wall Properties on Peristaltic Transport of Rabinowitsch Fluid through an Inclined Non-Uniform Slippery Tube. Defect Diffus. Forum 2019, 392, 138–157. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Fares, R.; Aissa, A.; Lewis, R.; Abu-Hamdeh, N.H. Entropy and convection effect on magnetized hybrid nano-liquid flow inside a trapezoidal cavity with zigzagged wall. Int. Commun. Heat Mass Transf. 2021, 125, 105279. [Google Scholar] [CrossRef]
- Shafiq, A.; Mebarek-Oudina, F.; Sindhu, T.N.; Abidi, A. A study of dual stratification on stagnation point Walters’ B nanofluid flow via radiative Riga plate: A statistical approach. Eur. Phys. J. Plus 2021, 136, 1–24. [Google Scholar] [CrossRef]
- Vajravelu, K.; Radhakrishnamacharya, G.; Radhakrishnamurty, V. Peristaltic flow and heat transfer in a vertical porous annulus, with long wave approximation. Int. J. Non-linear Mech. 2007, 42, 754–759. [Google Scholar] [CrossRef]
- Srinivas, S.; Kothandapani, M. Peristaltic transport in an asymmetric channel with heat transfer—A note. Int. Commun. Heat Mass Transf. 2008, 35, 514–522. [Google Scholar] [CrossRef]
- Ali, N.; Sajid, M.; Javed, T.; Abbas, Z. Heat transfer analysis of peristaltic flow in a curved channel. Int. J. Heat Mass Transf. 2010, 53, 3319–3325. [Google Scholar] [CrossRef]
- Tanveer, A.; Hayat, T.; Alsaedi, A.; Ahmad, B. Heat Transfer Analysis for Peristalsis of MHD Carreau Fluid in a Curved Channel Through Modified Darcy Law. J. Mech. 2018, 35, 527–535. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Vafai, K. Effects of heat and mass transfer on peristaltic flow in a non-uniform rectangular duct. Int. J. Heat Mass Transf. 2014, 71, 706–719. [Google Scholar] [CrossRef]
- Iftikhar, N.; Rahman, A. Peristaltic flow of an Eyring Prandtl fluid in a diverging tube with heat and mass transfer. Int. J. Heat Mass Transf. 2017, 111, 667–676. [Google Scholar] [CrossRef]
- Magesh, A.; Kothandapani, M. Heat and mass transfer analysis on non-Newtonian fluid motion driven by peristaltic pumping in an asymmetric curved channel. Eur. Phys. J. Plus 2021, 230, 1447–1464. [Google Scholar]
- Warke, A.S.; Ramesh, K.; Mebarek-Oudina, F.; Abidi, A. Numerical Investigation of Nonlinear Radiation with Magnetomicropolar Stagnation Point Flow past a Heated Stretching Sheet. J. Therm. Anal. Calorim. 2021, 135, 533–549. [Google Scholar]
- Rajashekhar, C.; Mebarek-Oudina, F.; Vaidya, H.; Prasad, K.V.; Manjunatha, G.; Balachandra, H. Mass and heat transport impact on the peristaltic flow of a Ree–Eyring liquid through variable properties for hemodynamic flow. Heat Transf. 2021, 50, 5106–5122. [Google Scholar] [CrossRef]
- Mittra, T.K.; Prasad, S.N. On the influence of wall properties and Poiseuille flow in peristalsis. J. Biomech. 1973, 6, 681–693. [Google Scholar] [CrossRef]
- Srinivas, S.; Kothandapani, M. The influence of heat and mass transfer on MHD peristaltic flow through a porous space with complaint walls. Appl. Math. Comput. 2009, 213, 197–208. [Google Scholar]
- Hayat, T.; Javed, M.; Hendi, A.A. Peristaltic transport of viscous fluid in a curved channel with com-plaint walls. Int. J. Heat Mass Transf. 2011, 54, 1615–1621. [Google Scholar] [CrossRef]
- Eldesoky, I.M.; Abumandour, R.M.; Kamel, M.H.; Abdelwahab, E.T. The combined influences of heat transfer, complaint wall properties and slip conditions on the peristaltic flow through tube. SN Appl. Sci. 2019, 1, 897. [Google Scholar] [CrossRef] [Green Version]
- Javed, M.; Naz, R. Peristaltic flow of a realistic fluid in a complaint channel. Phys. A Stat. Mech. Appl. 2020, 551, 123895. [Google Scholar] [CrossRef]
- Nadeem, S.; Hayat, T.; Akbar, N.S.; Malik, M. On the influence of heat transfer in peristalsis with variable viscosity. Int. J. Heat Mass Transf. 2009, 52, 4722–4730. [Google Scholar] [CrossRef]
- Sinha, A.; Shit, G.C.; Ranjit, N.K. Peristaltic transport of MHD flow and heat transfer in an asym-metric channel: Effects of variable viscosity, velocity slip and temperature jump. Alex. Eng. J. 2015, 54, 691–704. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, S.; Akbar, N.S. Influence of temperature dependent viscosity on peristaltic transport of a Newtonian fluid: Application of an endoscope. Appl. Math. Comput. 2010, 216, 3606–3619. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Effects of temperature dependent viscosity on peristaltic flow of a Jeffrey-six constant fluid in a non-uniform vertical tube. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 3950–3964. [Google Scholar] [CrossRef]
- Vaidya, H.; Rajashekhar, C.; Manjunatha, G.; Prasad, K.V.; Makinde, O.D.; Sreenadh, S. Peristaltic Motion of Non-Newtonian Fluid with Variable Liquid Properties in a Convectively Heated Non-Uniform Tube: Rabinowitsch Fluid Model. J. Enhanc. Heat Transf. 2019, 26, 277–294. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Nazeer, M.; Khan, M.I.; Ali, W.; Zafar, Z.; Kadry, S.; Abdelmalek, Z. Entropy analysis in the Rabinowitsch fluid model through inclined Wavy Channel: Constant and variable properties. Int. Commun. Heat Mass Transf. 2020, 119, 104980. [Google Scholar] [CrossRef]
- Rajashekhar, C.; Vaidya, H.; Prasad, K.V.; Tili, I.; Patil, A.; Nagathan, P. Unsteady flow of Rabinowitsch fluid peristaltic transport in a non-uniform channel with temperature-dependent properties. Alex. Eng. J. 2020, 59, 4745–4758. [Google Scholar] [CrossRef]
- Vaidya, H.; Rajashekhar, C.; Manjunatha, G.; Prasad, K.V. Effect of variable liquid properties on peristaltic flow of a Rabinowitsch fluid in an inclined convective porous channel. Eur. Phys. J. Plus 2019, 134, 231. [Google Scholar] [CrossRef]
- Vaidya, H.; Rajashekhar, C.; Mebarek-Oudina, F.; Animasaun, I.L.; Prasad, K.V.; Makinde, O.D. Combined effects of homogeneous and heterogeneous reactions on peristalsis of Ree-Eyring liquid: Application in hemodynamic flow. Heat Transf. 2021, 50, 2592–2609. [Google Scholar] [CrossRef]
- Chakraborty, S. Augmentation of peristaltic microflows through electro-osmotic mechanisms. J. Phys. D Appl. Phys. 2006, 39, 5356–5363. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: Oxford, UK, 2008; Volume 18, p. 346. [Google Scholar]
- Ai, Y.; Yalcin, S.E.; Gu, D.; Baysal, O.; Baumgart, H.; Qian, S.; Beskok, A. A low-voltage nano-porous electroosmotic pump. J. Colloid Interface Sci. 2010, 350, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Rajasekaran, P.R.; Martin, C.R. An Alternating Current Electroosmotic Pump Based on Conical Nanopore Membranes. ACS Nano 2016, 10, 4637–4643. [Google Scholar] [CrossRef] [PubMed]
- Asandei, A.; Schiopu, I.; Chinappi, M.; Seo, C.H.; Park, Y.; Luchian, T. Electroosmotic trap against the electrophoretic force near a protein nanopore reveals peptide dynamics during capture and translocation. ACS Appl. Mater. Interfaces 2016, 8, 13166–13179. [Google Scholar] [CrossRef] [PubMed]
- Bengtsson, K.; Robinson, N.D. A large-area, all-plastic, flexible electroosmotic pump. Microfluid. Nanofluid. 2017, 21, 178. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Willems, K.; Soskine, M.; Wloka, C.; Maglia, G. Electro-osmotic capture and ionic discrimination of peptide and protein biomarkers with FraC nanopores. Nat. Commun. 2017, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chinappi, M.; Yamaji, M.; Kawano, R.; Cecconi, F. Analytical Model for Particle Capture in Nanopores Elucidates Competition among Electrophoresis, Electroosmosis, and Dielectrophoresis. ACS Nano 2020, 14, 15816–15828. [Google Scholar] [CrossRef]
- Talapatra, S.; Chakraborty, S. Squeeze-Flow Electroosmotic pumping between charged parallel plates. Int. J. Fluid Mech. Res. 2009, 36, 460–472. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Tripathi, D.; Chakraborty, S. Electroosmosis-modulated peristaltic transport in microfluidic channels. Phys. Fluids 2016, 28, 052002. [Google Scholar] [CrossRef]
- Waheed, S.; Noreen, S.; Hussanan, A. Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels. Appl. Sci. 2019, 9, 2164. [Google Scholar] [CrossRef] [Green Version]
- Waheed, S.; Noreen, S.; Tripathi, D.; Lu, D. Electrothermal transport of third-order fluids regulated by peristaltic pumping. J. Biol. Phys. 2020, 46, 45–65. [Google Scholar] [CrossRef]
- Noreen, S.; Waheed, S.; Lu, D.; Tripathi, D. Heat stream in electroosmotic bio-fluid flow in straight microchannel via peristalsis. Int. Commun. Heat Mass Transf. 2021, 123, 105180. [Google Scholar] [CrossRef]
- Tripathi, D.; Prakash, J.; Reddy, M.G.; Misra, J.C. Numerical simulation of double diffusive convection and electroosmosis during peristaltic transport of a micropolar nanofluid on an asymmetric microchannel. J. Therm. Anal. Calorim. 2021, 143, 2499–2514. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajashekhar, C.; Mebarek-Oudina, F.; Sarris, I.E.; Vaidya, H.; Prasad, K.V.; Manjunatha, G.; Balachandra, H. Impact of Electroosmosis and Wall Properties in Modelling Peristaltic Mechanism of a Jeffrey Liquid through a Microchannel with Variable Fluid Properties. Inventions 2021, 6, 73. https://doi.org/10.3390/inventions6040073
Rajashekhar C, Mebarek-Oudina F, Sarris IE, Vaidya H, Prasad KV, Manjunatha G, Balachandra H. Impact of Electroosmosis and Wall Properties in Modelling Peristaltic Mechanism of a Jeffrey Liquid through a Microchannel with Variable Fluid Properties. Inventions. 2021; 6(4):73. https://doi.org/10.3390/inventions6040073
Chicago/Turabian StyleRajashekhar, Choudhari, Fateh Mebarek-Oudina, Ioannis E. Sarris, Hanumesh Vaidya, Kerehalli V. Prasad, Gudekote Manjunatha, and Hadimane Balachandra. 2021. "Impact of Electroosmosis and Wall Properties in Modelling Peristaltic Mechanism of a Jeffrey Liquid through a Microchannel with Variable Fluid Properties" Inventions 6, no. 4: 73. https://doi.org/10.3390/inventions6040073
APA StyleRajashekhar, C., Mebarek-Oudina, F., Sarris, I. E., Vaidya, H., Prasad, K. V., Manjunatha, G., & Balachandra, H. (2021). Impact of Electroosmosis and Wall Properties in Modelling Peristaltic Mechanism of a Jeffrey Liquid through a Microchannel with Variable Fluid Properties. Inventions, 6(4), 73. https://doi.org/10.3390/inventions6040073







