Implementation Aspects Regarding Closed-Loop Control Systems Using Evolutionary Algorithms

Abstract

When an optimal control problem requires an important computational effort, a metaheuristic algorithm (MA) can be a useful approach. An MA is conceived to solve a specific optimal control problem having a characteristic objective function. This algorithm solely yields only an optimal offline solution. The desideratum to have a closed-loop implementation can be fulfilled through a supplementary “tool”, the Receding Horizon Control (RHC) structure. This paper addresses a particular case and integrates Evolutionary Algorithms into the RHC structure. The main objective is to propose a general harmonization between the Controller of the closed loop and the Evolutionary Algorithm. Some details concerning the implementation of the closed loop and Controller are described. The impact of the RHC’s prediction technique upon the control sequences’ encoding is also analyzed. Two general structure Controllers are proposed, one of them conceived to cope with restrictive time constraints. Practical ideas have been illustrated through a case study: the well-known optimal control of a fed-batch reactor for ethanol production. This time, our implementation achieves a closed-loop solution. The results from the programs and simulation series validate the Controllers, EAs, and the closed-loop structure. Generally speaking, the association between RHC and EA can be a realistic solution to optimal process control.

1. Introduction

Optimal control of a dynamic system is a usual task in process engineering. If the process has mathematical properties sufficient to apply theoretical control laws, this task can sometimes be achieved without significant computational complexity. Other times the computational effort is important, or we do not dispose of known control techniques. In this case, metaheuristic algorithms integrated within appropriate control structures constitute a realistic solution. This kind of algorithms (see [1,2,3]) have been used intensively in control engineering (see [4,5,6,7]) because of their robustness and capacity to cope with big complexity problems.

A metaheuristic algorithm (MA), like simulated annealing, genetic algorithm, evolutionary algorithm (AE), ant colony systems, particle swarm optimization, etc., is not by itself prepared to achieve a closed-loop control structure. That is why it needs to be integrated into a structure like Receding Horizon Control (RHC) (see [8,9,10]) or Model Predictive Control ([11,12]). Both structures use prediction techniques that could involve MAs because prediction is usually optimization.

This work has rather practical relevance because it is first addressed to a practicing professional engineer who wants to implement an optimal control structure using an Evolutionary Algorithm (see [11,13,14,15]). More precisely, there are several requests and given data that define our work:

• A real process has to be controlled over a given control horizon;
• We dispose of a process model (usually nonlinear), usually a set of all algebraic and differential constraints imposed by the dynamic environment;
• A closed-loop control structure has to solve an Optimal Control Problem (OCP). Its Controller should optimize an objective function and meet some constraints over the control horizon. The objective function contains a terminal penalty term, which renders the prediction of the optimal control sequence a complex task;
• A basic version of the EA can find the optimal value of the objective function over the control horizon.

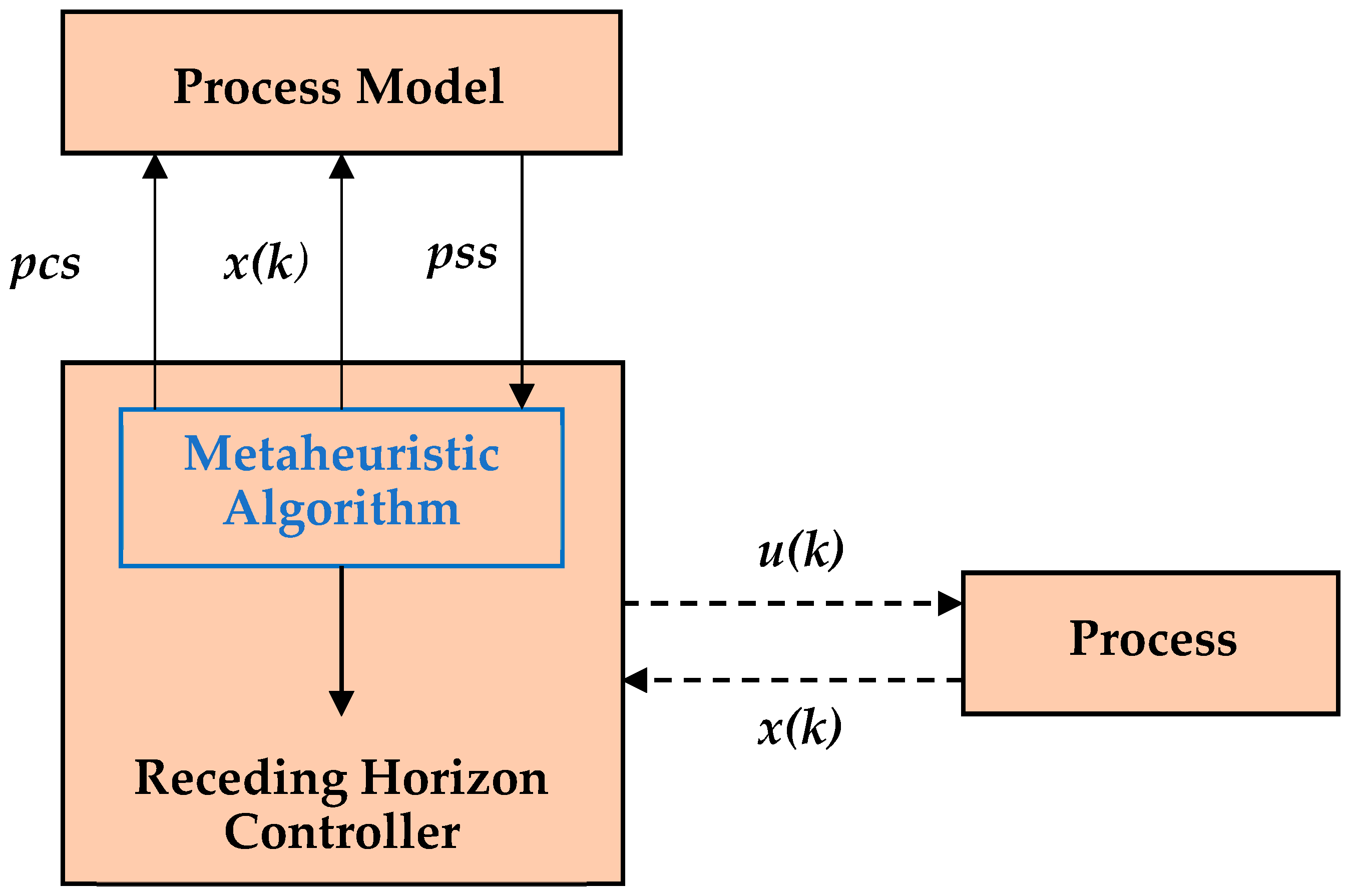
The RHC structure is a general and simple control structure involving a prediction technique that can fit with an evolutionary algorithm. For this reason, the solution proposed by this paper is based on the RHC structure whose Controller makes optimal predictions using an EA. The implementation aspects emphasized in our presentation mainly refer to two topics:

• The harmonization between the prediction RHC structure technique and the EA;
• The implementation of a Controller based on an EA with an acceptable computational complexity.

Section 2 briefly presents the elements that define an OCP and introduces the notations used in the next sections.

After recalling the RHC structure, Section 3 proposes the first version of the Controller. This is organized as a function and includes the slightly modified basic version of the EA. At each sampling moment, the EA is executed to determine the optimal control sequence covering the prediction horizon. The Controller takes the first value of this sequence and makes it its current control output. After that, this value is applied to the process. At each call, the prediction horizon decreases and keeps the final moment of the control horizon (see for comparison [9,10,11]).

In this work, we propose two versions of the Controller. The EA calls for a numerical integration function using a discretization step equal to the closed-loop sampling period. Consequently, the encoding of a control sequence uses a number of genes proportional to the prediction horizon’s length. The greater computation effort of the Controller is sustained in the first sampling period when the prediction horizon is the largest. Using simulations, the implementer has to decide whether the Controller’s execution time is less than the sampling period; that is, the Controller can be implemented.

The second version of the Controller, proposed in Section 4, improves the computational complexity such that the execution time would be lower than a sampling period. Regardless of the prediction horizon’s length, the discretization steps’ number is constant. In other words, the encoding of a control sequence always uses the same number of genes. If the increase of the discretization steps does not significantly affect the computation accuracy, this version can improve the computational complexity and assure the feasibility of the Controller.

Section 5 presents a case study concerning a particular OCP and the controller implementation using an adequate EA. The performance index is a terminal penalty. The main objective is to show how a peculiar OCP can be solved and implemented using such a controller. Notice that we do not aim to solve a particular OCP and compare our solution with other approaches but, rather, highlight some implementation aspects. The resulting RHC structure will be simulated to validate the quasi-optimal behaviour of the closed loop.

The addressed problem deals with the optimal control of a fed-batch reactor for ethanol production (OCEP). First of all, an EA is chosen to solve this problem and yield an open-loop solution. Section 5.1 describes an evolutionary algorithm (EAv0) that solves the OCEP problem. Although EAv0 does not refer to a closed-loop implementation, it will prove its capacity to solve the open-loop problem. It also allows us to assess the computational complexity. A simulation series is conducted to evaluate the performances of a typical solution and its state evolution.

The implementation of the Receding Horizon Controller for the OCEP problem is presented in Section 5.2. EAv0 is slightly modified to obtain EAv1, which is a constituent of the Controller. The control sequence is encoded by a vector of real values whose dimension is proportional to the prediction horizon’s length. The closed-loop evolution (Controller’s outputs and the process’ states) is simulated, considering the real process, which is identical to the process model. The computation complexity is evaluated on the overall control horizon, using simplifying hypothesis.

A Controller’s second version—used to solve the OCEP problem—which can improve the computation complexity, is presented in Section 5.3. Algorithm EAv0 is modified to generate EAv2, such that a control sequence is encoded by a constant number of real values, regardless of the prediction horizon’s length. The evolution of the closed loop, including the new Controller, is simulated. The computation complexity of EAv2 is analyzed in contrast with EAv1 to prove that the first one is smaller, at least in the first sampling periods.

The results of the simulation series have proved that the RHC structure with the Controller that is able to integrate an EA is feasible with good quasi-optimal behaviour.

2. Defining Elements of an Optimal Control Problem

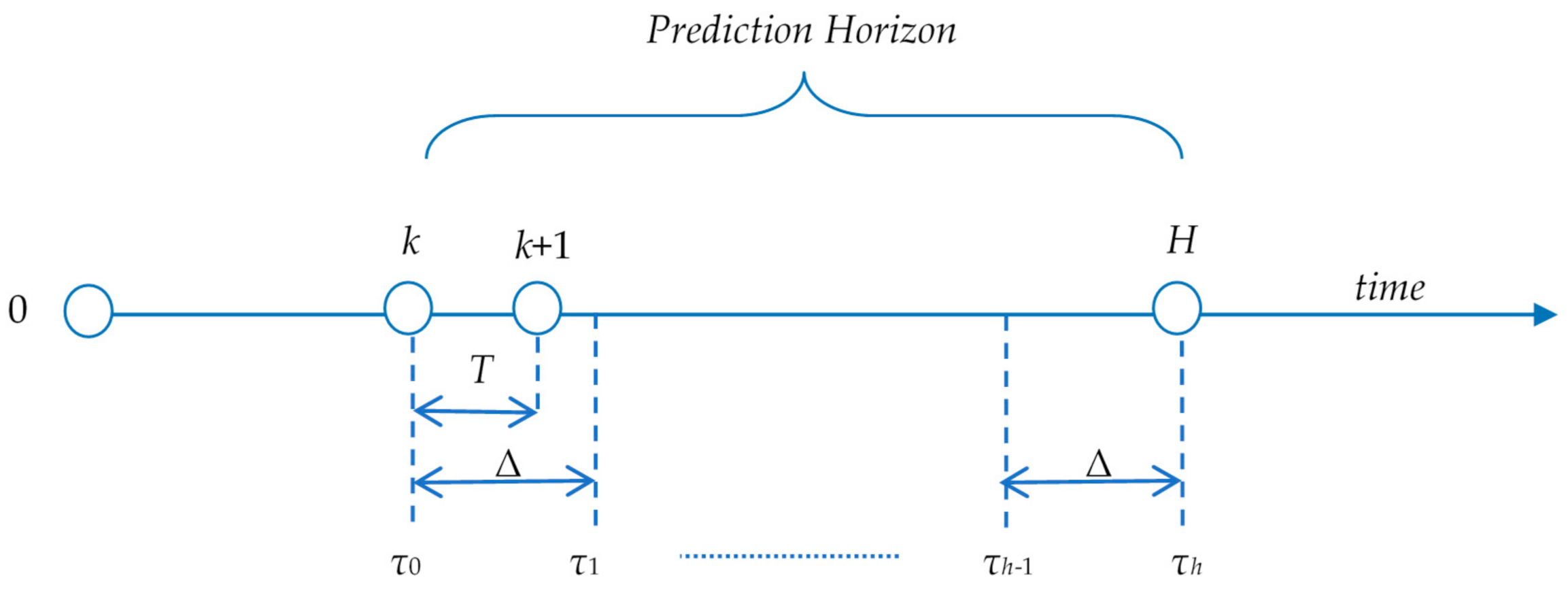
In the upcoming sections, we briefly recall the defining elements of an optimal control problem (OCP) and their usual notations, but we do so in a way that is adapted to the presentation of the next sections. Let us consider an OCP whose control horizon is finite, for example $\left[0, H\cdot T\right]$, where H is a positive integer and T is the sampling period. The discrete moments $t_k=k·T$ will be specified simply by $k=0,1,\cdots ,H$.

We suppose that a discrete process model, used to simplify the presentation, is available and given in Equation (1). An eventual continuous model can always be converted into a discrete one.

$$x(k+1)=f(k,x(k),u(k)); k=0, 1,\cdots , H-1,$$

(1)

The vectors $u(k)$, $x(k)$ have m and n elements ($m,n\in N^{+}$), respectively, and f is an n-dimensional vector function with all regularity properties demanded by the calculations.

Any control sequence $U_0$, defined as below, meets certain constraints and determines the system evolution over the control horizon:

$$U_0\stackrel{D}{=} <u(0), u(1),\dots , u(H-1)>$$

(2)

This system evolution has to be optimal under a performance index. The latter minimizes a specific objective function, which has the discrete form presented in Equation (3).

$$J(k,x(k),U(k))={\displaystyle \sum _{i=k}^{H-1}L(i,x(i)},u(i))+TP(x(H)),k=0, 1,\cdots , H-1$$

(3)

$$U(k)\stackrel{D}{=} <u(k), u(k+1),\dots , u(H-1)>$$

(4)

Equation (3) refers to the prediction horizon $\left[k, H\right]$ and the state trajectory that starts with $x(k)$. The system evolution is generated by a control sequence $U(k)$ having the structure presented in Equation (4). The resulting state trajectory can be denoted by

$$X(k)\stackrel{D}{=} <x(k), x(k+1),\dots , x(H)>; k=0, 1,\cdots , H-1.$$

(5)

The first part of the sum presented in Equation (3) is a Lagrange-type term that measures quality along the trajectory of the dynamic system. The scalar value $L(i,x(i),u(i))$ is the contribution of the interval $\left[i,i+1\right]$ to the quality measure J. The second part is a Mayer-type term that measures the quality of the trajectory in its final extremity. This term will be called the terminal penalty in the upcoming sections. The function TP(x) penalizes the final state x.

The performance index $I_0$ of an optimal solution over the control horizon minimizes the objective function J as below:

$$I_0=\underset{U_0}{\min } J(0,x_0,U_0); x_0=x(0)$$

(6)

Obviously, J’s minimization (or maximization) can be subjected to constraints regarding the control inputs and the state variables.

3. Controller Implementation Using Evolutionary Algorithms

3.1. RHC Using Metaheuristic Algorithms

If problem solving requires an important computational effort, a metaheuristic algorithm can be a useful approach. An MA is conceived to solve a specific OCP having a characteristic objective function. However, the desideratum to have a closed-loop implementation can be fulfilled through a supplementary “tool”: the RHC structure.

Figure 1 recalls the principle of the RHC and suggests how it is able to implement the predictive control technique in a particular case when a metaheuristic algorithm is used.

The objective of RHC is to implement closed-loop control systems under circumstances involving optimal evolution. The RHC is among the very few control strategies supporting a closed-loop implementation using an MA. The Receding Horizon Controller uses the MA to accomplish the prediction technique: it calculates the optimal control sequences (ocs) that optimize the performance index on the current prediction horizon $\left[k,H\right]$.

At moment k, the MA calculates the optimal solution, which is represented by a series of control inputs, as in Equation (4). We can consider the MA as a generic function that returns the following optimal solution:

$$U^{*}(k)=\arg \underset{U(k)}{\min }J(k,x(k),U(k)),k=0, 1,\cdots , H-1.$$

(7)

The process state $x(k)$ is acquired from the dynamic environment and represents the initial state for the control horizon $\left[k,H\right]$.

We may suppose that the MA is based on a population of solutions because we shall use an EA in this work. Hence, the MA generates and evolves a population of individuals within an iterative process for each sampling period. An individual of the population is represented by a predicted control sequence (pcs). A numerical integration function can use the process model, the pcs and the current initial state $x(k)$, and return the predicted state sequence (denoted by pss). The MA will make an optimal prediction for the interval $\left[k,H\right]$ that becomes the prediction horizon (briefly denoted as Phz) and has H-k sampling periods. The objective function J over the Phz is optimized and subject to certain constraints through an optimal control sequence (7).

Finally, the Controller sends to the process the control input $u(k)$, the first element of the sequence $U^{*}(k)$. The Controller calls the MA that yields the vector $U^{*}(k)$ to the first time at k = 0.

A systematic procedure to implement the control structure depicted in Figure 1 is presented in [8].

3.2. Controller Using an Evolutionary Algorithm

In the upcoming sections, we shall consider the EA as an MA able to solve this kind of problem. We will refer to the EA with a large abstraction degree, such that we do not need to give, for the moment, all of the details concerning its implementation. In this way, the implementation aspects described below maintain generality. In one way or another, a particular EA calculates the optimal solution for the considered OCP meeting the initial conditions.

The considerations made up until now are valid whatever the EA’s implementation would be (except Equation (7), where the min operator can be replaced by max). We shall consider a particular implementation called EAv1 (EA version 1), which adopts a natural solution encoding in the upcoming sections. The control input u(t) is a step function whose discretization step equals the sampling period. A candidate solution is a sequence (pcs) that covers the Phz and has the following structure:

$$pcs=<u\left(k|k\right), \cdots , u\left(k+i|k\right),\cdots , u\left(H-1|k\right)>,$$

(8)

where $u\left(k+i|k\right)$, $i=0,\dots ,H-k-1$ is the predicted value for the control input $u\left(k+i\right)$ based on knowledge up until moment $k$. The control input $u\left(k+i|k\right)$ is kept constant within the sampling period $\left[k+i, k+i+1\right)$, such that a pcs represents a step function.

Note that:

$$u\left(k+i|k\right) \ne u\left(k+i\right).$$

The value $u\left(k+i|k\right)$ is a future control input predicted at the present moment, whereas the value $u(k+i)$ is the future real control input that is unknown at the present moment. We can assert the same thing for the state variables. Using Equations (1) and (8), the process model returns the predicted state sequence (pss) as below:

$$pss=<x\left(k+1|k\right), . . . ,x\left(H |k\right)>,$$

(9)

where $x\left(k+i|k\right)$, $i=0,\dots ,H-k$ is the predicted value of the state $x\left(k+i\right)$ based on knowledge up until moment k.

The EAv1 has now the necessary data to compute the objective function J over the prediction horizon. At the end of the iterative process, the EAv1 returns to the optimal control sequence (ocs):

$$ocs=<u^{*}\left(k|k\right),\dots , u^{*}\left(H-1|k\right)>.$$

(10)

After that, the Controller will send the first element of ocs sequence, namely $u(k)=u^{*}(k|k)$, to the process as a real control input for the current sampling period. The Controller then shifts the beginning of the Phz by one sample and restarts the optimization for the next interval $[k+1, H]$.

Table 1. Outline of Receding Horizon Controller using an EAv1.

1	Get the current value of the state vector, x(k).
2	$ocs\leftarrow \mathrm{EAv}1(k,x(k))$
3	$u(k)\leftarrow u^{*}(k\left|k)\right.$
4	Send $u\left(k\right)$ towards the dynamic system
5	Shift the prediction horizon and wait for the next sampling period

presents an outline of the Controller’s actions for every sampling period. The execution of the EAv1 is presented in Line #2 as a function call, whose input parameters are the current sampling period and the process state vector. It returns the ocs over the interval $[k,H]$ according to Equation (10). Line #3 sets the output of the Controller $u\left(k\right)$ at the value $u^{*}(k|k)$. In Line #2, the function $\mathrm{EAv}1(k,x(k))$ can be replaced by a new version, $\mathrm{EAv}2(k,x(k))$, developed in the next section.

Remarks:

• This work addresses OCPs whose objective function (3) includes a terminal penalty. The Phz has to be $[k,H]$ even if the integral term is missing. The Phz “recedes” at each sampling period but keeps the final extremity. Hence, its length decreases by one unit at each sampling period;
• For the current sampling period, $[k,k+1)$, the Phz is $[k,H]$, and its length is $H-k$. Consequently, the computational complexity of the EAv1 is variable and depends on this value: $H-k$. Let us note that the discretization step used by the EAv1 for encoding a pcs is equal to the sampling period T. Therefore, the length of the ocs is variable along the control horizon and decreases at each sampling period;
• The most restrictive time constraint for the algorithm presented in Table 1 is that the execution time has to be smaller than the sampling period. The length of the Phz could be very large at the beginning of the control horizon, especially in the first sampling period. If the time constraint is met initially, it will also be fulfilled in the next sampling period because the length of the Phz decreases;
• The choice of T is related to control engineering aspects, such as continuous signal discretization and time constants of the considered dynamic system. Therefore, the increase of T is not an option for solving constraint #3. Before implementation, the control system designer must verify the fulfilment of this constraint using simulations. Generally speaking, RHC using an MA is suitable for processes having relatively large time constants.

4. Controller Implementation with Improved Computational Complexity

The Controller improvement can be done using a new version of the EA. The latter keeps its general structure and the most parameter values, but it will consider fewer gene encoding predicted control sequences.

4.1. EA with Variable Discretization Step

This section proposes a version of the EA called EAv2 (version 2), which can reduce the Controller’s computational complexity compared to the first version. The aforementioned Remark #2 underlines that EAv1 uses a constant discretization step equal to the sampling period T.

In the proposed new version, inside the EAv2, the number of discretization steps is constant and independent of the length of the Phz. Consequently, the discretization step is variable and, as we shall see, greater than or equal to T.

With h, let us denote the number of the discretization steps. As we already saw, for the current sampling period $[k,k+1)$, the Phz is $[k,H]$. Expressed in time units, the Phz is

$$\left[t_k, t_H\right]=\left[k\cdot T, H\cdot T\right]$$

This interval will be discretized using h steps. Figure 2 shows the new discretization of the Phz in contrast with the old one involved in the sampling period.

Hence, the EAv2 will use pcs having the form

$$pcs=<u\left({\tau }_0|k\right), u\left({\tau }_1|k\right), \cdots , u\left({\tau }_j|k\right),\cdots , u\left({\tau }_{h-1}|k\right)>.$$

(11)

If the discretization step is denoted by $\Delta$, the discretization moments ${\tau }_j$ are defined below:

$$\begin{gathered} {\tau }_j=t_k+j\cdot \Delta ; j=0,\cdots ,h-1; \\ {\tau }_0=t_k; {\tau }_h=t_H \end{gathered}$$

We recall here that the predicted value for the control input $u\left({\tau }_j\right)$ based on knowledge up until the moment $t_k$ is the value

$$u\left({\tau }_j|k\right), j=0,\dots ,h-1.$$

Because our goal is to reduce the computational complexity of EAv2 in contrast with EAv1, the following constraint has to be met:

$$h\le H-k.$$

(12)

If the constraint introduced by Equation (12) is met, a smaller number of predicted values will cover the prediction horizon. A possibility, which also simplifies the implementation, is to set the number of discretization steps using the rule below:

$$\begin{array}{cc}h=& \left\{\begin{array}{ccc}{h}_0,\hfill & \mathrm{for} \hfill & k=0, 1,\cdots ,H-h_0\hfill \\ H-k\hfill & \mathrm{for} \hfill & k=H-h_0+1,\cdots ,H-1\hfill \end{array}\right.\end{array}$$

(13)

The value of the constant integer $h_0$ is chosen such that

$$h_0<H.$$

4.2. Computational Complexity

This section makes a comparison between the computational complexity of the two EAs. Usually, an effective way to compare two MAs is to evaluate the calls number of the objective function. In our work, all the EAs have the structure corresponding to Lines #9—#19 of the pseudo-code described in

Table 2. Outline of the EAv2 with improved computational complexity.

	startEA(k, x(k))
1	/* Initialize the parameters of EA*/
2	if $k\le H-h_0$
3	$h\leftarrow h_0$;
4	$\Delta \leftarrow T\cdot (H-k)/h_0$;
5	else
6	$h\leftarrow H-k$;
7	$\Delta \leftarrow T$;
8	end
9	Generation of the initial population
10	Calculation of the performance indexes
11	$g\leftarrow 1$ /* g: current generation number */
12	while ($g\le NGen$) /* optimization iterative process */
13	parent selection;
14	offspring generation; /*calculate the performance indexes*/
15	self-adaptive mutation; /*update the performance indexes*/
16	replacement;
17	population sorting
18	$g\leftarrow g+1$
19	end /*while*/
20	returnocs (the best of the population)

. Hence, the structure of the two algorithms, EAv1 and EAv2, will basically be the same and only differ by few initializing instructions. One can count the call number of the objective function:

• $\mu$ calls within Line #11: Calculation of the performance indexes for the initial population having μ individuals;
• $\lambda$ calls within Line #14: offspring generation ($\lambda$ individuals);
• $p\cdot \lambda$calls within Line #15: $p$ is the offspring’s probability of undergoing mutation.

If the iterative optimization process evolves on NGen generations, then the average call number for J is

$$\mathrm{Ncalls}=\mu +NGen\cdot \mathit{\lambda }\cdot (1+p).$$

(14)

As such, the call number for J will actually be the same, as we shall confirm using simulations in Section 6.

The most time-consuming part of the objective function execution is the process model integration determining the state evolution. The question that one can raise is whether the integration time is significantly different for the new version. The integration time interval is $[k,H]$ in both cases. As such, the process model’s integration has the same initial state and time interval and similar input functions u(t), which are step functions. The different number of genes involves different step numbers for the two input functions. This fact has a small influence on the integration time. Simulation tests show that the integration of input functions takes a similar amount of time while in these conditions.

In conclusion, the computation effort to calculate the objective function is similar for the two versions of the EA.

On the other side, pcs encoding is decisive for the algorithm’s complexity. EAv1 encodes pcs using $H-k$ real values (genes), while EAv2 only uses $h_0$ values. Since it holds $h_0<H$, the EAv2 obviously has a smaller computational complexity for all genetic operators (selection, crossover, mutation, replacement) and initializations.

Finally, one can say that EAv2 is better than EAv1 from the point of view of computational complexity. The number of discretization steps is $h_0$, while $k\le H-h_0$ and decreases from $h_0-1$ toward 1, for $k>H-h_0$.

NB:

If Equation (13) is fulfilled, the implementation issue stated by Remark #3 can be avoided. On the other hand, this value must be a trade-off between the computational complexity and the ocs accuracy.

4.3. General Implementation of the EAv2

Equation (13) allows the calculation of the discretization step $\Delta$. Because h has a constant value for the initial segment, the $\Delta$ value will be variable in return. From (11) and (13), it holds that:

$$\Delta =\left\{\begin{array}{cc}T\cdot \frac{H-k}{h_0} >T\hfill & \mathrm{for} k=0, 1,\cdots ,H-h_0-1\hfill \\ T\hfill & \mathrm{for} k=H-h_0,\cdots ,H-1\hfill \end{array}\right..$$

(15)

According to Equation (11), a pss will have the form

$$pss=<x\left({\tau }_1|k\right), . . . ,x\left({\tau }_h |k\right)>$$

The main output of the EAv2 is the ocs for the current Phz, which has the following structure:

$$ocs=<u^{*}\left({\tau }_0|k\right), \cdots , u^{*}\left({\tau }_j|k\right),\cdots , u^{*}\left({\tau }_{h-1}|k\right)>$$

(16)

Table 2 schematically describes the EAv2 included in a controller with improved computational complexity. EAv2 has specific parts that cannot be detailed here. Therefore, the following sketch describes them with a large degree of extraction. The outline only presents the details allowing the management of the length of the pcs.

The iterative optimization process evolves on NGen generations counted by the variable g. Lines #13–#17 call for functions implementing well-known genetic operators. We recall here that the offspring generation also calculates the performance indexes of the new pcs (solutions). The self-adaptive mutation also updates the performance indexes of the solutions that are subjected to mutation.

Remarks:

5.

The encoding of the pcs and ocs according to (11) and (16) can obviously diminish the computational complexity when generating ocs. However, on the other hand, the discretization with fewer intermediary points affects the ocs accuracy, that is, its capacity to represent the optimal solution to our problem. The question is, to what extent this accuracy is affected? Using simulations, the control system designer must verify that the ocs representation is not degraded and the quasi-optimality is still kept before implementation.

6.

Equation (15) shows that, for each sampling period, it holds:

$$\Delta \ge T.$$

(17)

Considering the inequality of Equation (17), the first element of the ocs covers the sampling period:

$$[{\tau }_0, {\tau }_1]=[t_k,t_k+\Delta ] \supseteq [t_k,t_k+T].$$

Hence, the first ocs value, i.e., $u^{*}\left({\tau }_0|k\right)$, will be sent to the process as the optimal control input for the current sampling period (as in Line #4 from Table 1).

5. Case Study

This section will present an example of implementing a metaheuristic-based controller that integrates an RHC structure.

We have considered a well-known problem that has been described in many articles, among which we recall [16,17]. This problem is known as the optimal control of a fed-batch reactor for ethanol production (OCEP) and concerns a nonlinear dynamic system. Different sub-cases are presented in these papers, which differ in control horizon and control bounds. We have considered the OCEP problem stated in Appendix A, which presents all of the basic elements. Because our main objective is to construct the Controller using an AE, we have considered a fixed final time in contrast with other versions of the problem. Keeping notations, it holds:

$$n=4; m=1; t_f=H\cdot T=54h$$

The process model has n state variables $x_1,x_2,x_3,x_4$ representing the cell mass, substrate, product concentration (g/L), and volume (L). The control variable is the feed rate (L/h) that meets the following constraint:

$$0\le u(t)\le 12$$

The state variable x₄ has to meet the following constraint:

$$x_4(t_f)\le 200$$

(18)

The objective function given below has to be maximized:

$$J\left(x(t_f)\right)=x_3(t_f)\cdot x_4(t_f)$$

Although this one is a terminal penalty and the integral component is missing, the implementation maintains its difficulty: the process evolution of the entire control horizon must be determined when a pcs is adopted.

5.1. Open-Loop Solution Using an Evolutionary Algorithm

In this section, we present preliminary work before constructing the Controller for the closed-loop control structure. We have implemented and conducted an evolutionary algorithm (see [1,2,3]) that solves the OCEP problem. It will be denoted by EAv0 (EA version 0) in the upcoming sections. The implementation of the EAv0 and the simulations were conducted using the MATLAB language and system. We have employed special functions devoted to integrating the differential equations for the simulation of the process evolution.

Let us recall that EAv0 determines the following quasi-optimal control input because our problem looks for the maximum value of J:

$$U^{*}(0)=\arg \underset{U(0)}{\max }J(0,x_0,U(0))$$

This means that the control horizon is [0, H], and the initial state is x₀.

This algorithm is the basis for the two versions of EA used inside the Controller. EAv0 is modified and adapted to become part of the optimal Controller.

As mentioned previously, EAv0 uses direct encoding and has the usual characteristics listed below:

• For each generation, the population has μ individuals;
• The children population has λ individuals ($\lambda <\mu$);
• The population evolves over NGen generations;
• The selection strategy uses stochastic universal sampling and the rank of individuals. The latter is scaled linearly using selection pressure (s); see [3] (pp. 205–221);
• A BLX-α crossover operator;
• Inside the mutation operator, the mutation step is subjected to a global variance adaptation. This one is conducted according to the “1/5 success rule”; see [1] (pp. 245–274);
• The replacement strategy involves that the children replace the λ worst individuals of the generation.

The most important parameters are given in

Table 3. The main parameters of EAv0.

EAv0	λ	μ	NGen	H	s	α
	20	30	70	20	1.8	0.4

.

This algorithm yields a solution that is actually a quasi-optimal sequence of control inputs. It can be only used within an open-loop control structure. For the reasons mentioned before, this sequence is useless for a closed-loop control structure. Nevertheless, this phase is mandatory because it can validate the aptitude of the EA to solve the problem and evaluate the computational complexity.

The resulting simulation program has a stochastic character; therefore, we cannot conclude after a single execution. We must repeat the execution more times to confer consistency to statistical parameters. That is why we have conducted a simulation series that has repeated times the execution of EAv0 30 times. The results, namely a performance index statistic, the quasi-optimal control input u(t), and state evolution, are presented in

Table 4. Results of the open-loop simulation series using EAv0.

Jmin	Javg	Jmax	Sdev	Jtypical
18,973.0	19,906.4	20,395.2	312.5	19,885.7

and Figure 3.

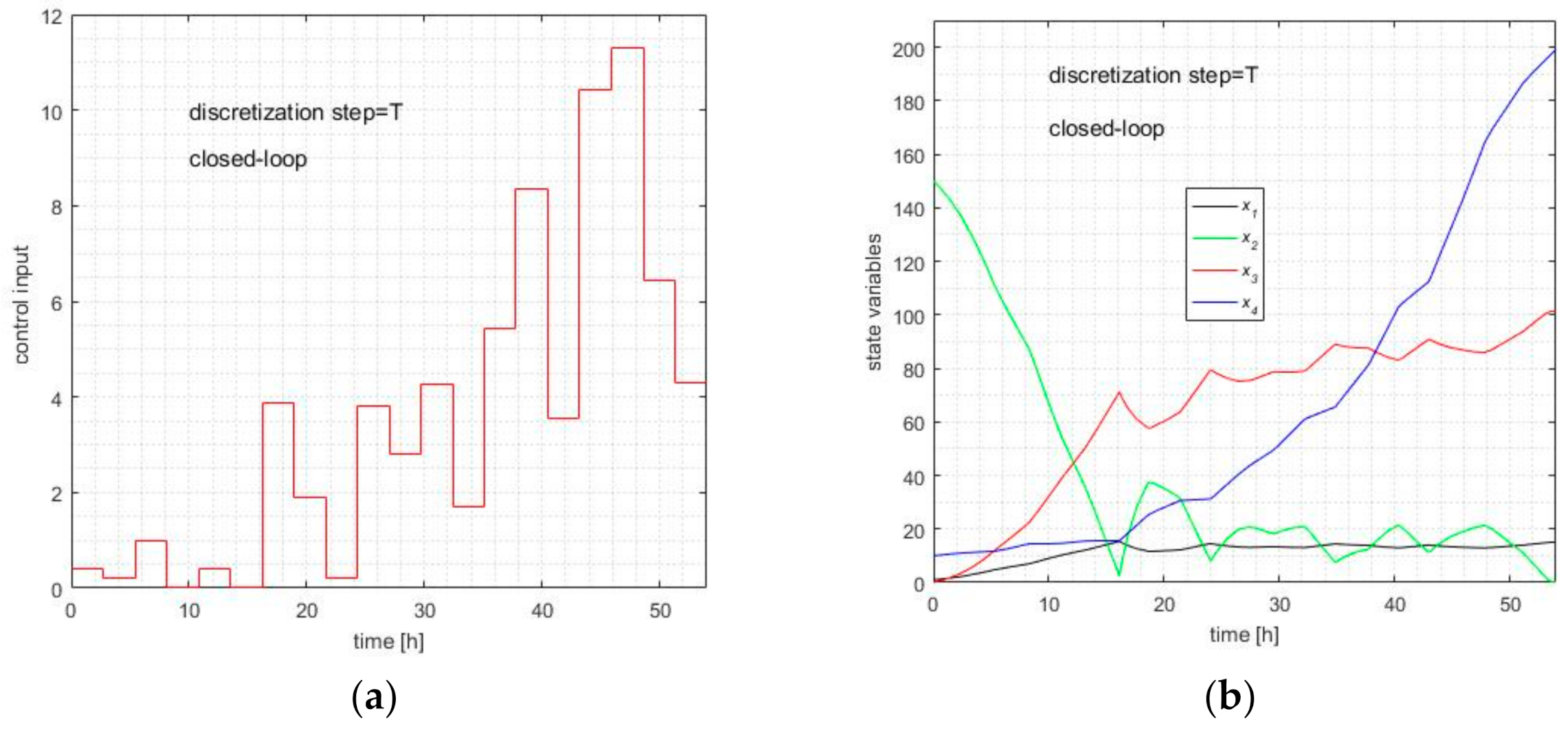
Table 4 shows some statistical parameters characterizing the 30 executions of EAv0. The minimum, average, and maximum values and standard deviation are indicated for the performance index. We consider typical execution as the particular simulation among the 30 that produce the values that are the closest to the average performance index. In our simulation series, there is an execution that yields Jtypical = 19885.7. The quasi-optimal control input for the typical execution is depicted in Figure 3a, and its state evolution in Figure 3b.

Further details concerning EAv0 are given in Appendix B.

5.2. Closed-Loop Solution Using an EA with Constant Discretization Step

This section aims to achieve the closed-loop control of the dynamic system involved in the OCEP problem using the Controller based on EAv1. We have implemented the Controller and a program that simulates how the closed loop works. The process model has been used to predict the ocs. We have also considered the same model to simulate the real process.

The Controller has the same structure as the one presented in Table 1, except that it includes EAv1 (does not call a function). It is organized as a function called for each sampling period (see Appendix B).

The Controller has the following characteristics:

• Input parameters: k and x(k);
• Output parameter: $u(k)$ (the first element of the best solution, i.e., $u^{*}(k\left|k)\right.$);
• Control horizon: $\left[k,H\right]$, with $k=0,1,\cdots ,H-1$; H = 20;
• Number of genes: $H-k$ (see (8));
• Discretization step: T;
• Other parameters such as those in Table 3.

EAv1—which is included not called by the Controller—has the same structure and characteristics as EAv0 (given in Section 5.1).

The program that simulates the closed-loop optimal control has the outline presented in

Table 5. Outline of the closed-loop optimal control using EAv1.

1	Initializations /* for OCEP problem, controller and simulation*/
2	for $k=0,1,\cdots ,H-1$
3	$u(k)\leftarrow Controller\_EA(k)$
4	Compute the state vector $x\left(k+1\right)$ of the process model using $u\left(k\right)$;
5	$x_0\leftarrow x\left(k+1\right)$
6	end
7	display$J^{*}$ and $u^{*}(k) ; k=0,1,\cdots ,H-1$

. Essentially, the closed loop is achieved by a loop that simulates the Controller’s call for each sampling period and the feedback from the real process.

The Controller’s call is done in Line #3. It uses as an input parameter, which is the initial state that is stored in the global variable $x_0$. The numerical integration of the process model is accomplished in Line #4. This algorithm is implemented as a MATLAB script.

We conducted a simulation series that executed the script “Closed-loop.m” 30 times. In our simulation series, there was an execution that yielded Jtypical = 20,153.5. The performance index statistic, the quasi-optimal control input u(t), and the state evolution are presented for typical execution in

Table 6. Results of the closed-loop simulation series using the Controller with EAv1.

Jmin	Javg	Jmax	Sdev	Jtypical
19,127.7	20,136.7	21,014.9	449.5	20,153.5

, Figure 4a,b, respectively.

5.3. Closed-Loop Solution Using an EA with Improved Computational Complexity

This section aims to implement the closed-loop control of the dynamic system under consideration using the Controller based on EAv2. We have implemented the Controller and a program that simulates the closed-loop working (see “Closed-loop2.m”, inside the folder “EA_Etanol_loop2”). The latter is basically the same as that described in Table 5, except for a few initializations.

The new Controller has the structure that was presented in Table 1, except that it includes EAv2. It is also organized as a function called for each sampling period (see the script “Controller_EA2.m”). It has the following characteristics:

• Input parameters: k and x(k);
• Output parameter: $u(k)$ (the first element of the best solution, i.e., $u^{*}(k\left|k)\right.$);
• Control horizon: $\left[k,H\right]$, with $k=0,1,\cdots ,H-1$; $H=20$;
• Number of genes: $h_0$, for the first $H-h_0$ sampling periods, and $h_0-1,\cdots , 2, 1$ for the last sampling periods (see (13)); $h_0=10$;
• Discretization step: $\Delta \ge T$ variable (see (15));
• Other parameters such as those in Table 3.

The EAv2 algorithm —which is included and not called by the Controller—has the same structure and characteristics as EAv0 (given in Section 5.1)

Because OCEP maximizes the objective function, the best solution is as below:

$$U^{*}(k)=\arg \underset{U(k)}{\max }J(k,x(k),U(k)),k=0, 1,\cdots , H-1.$$

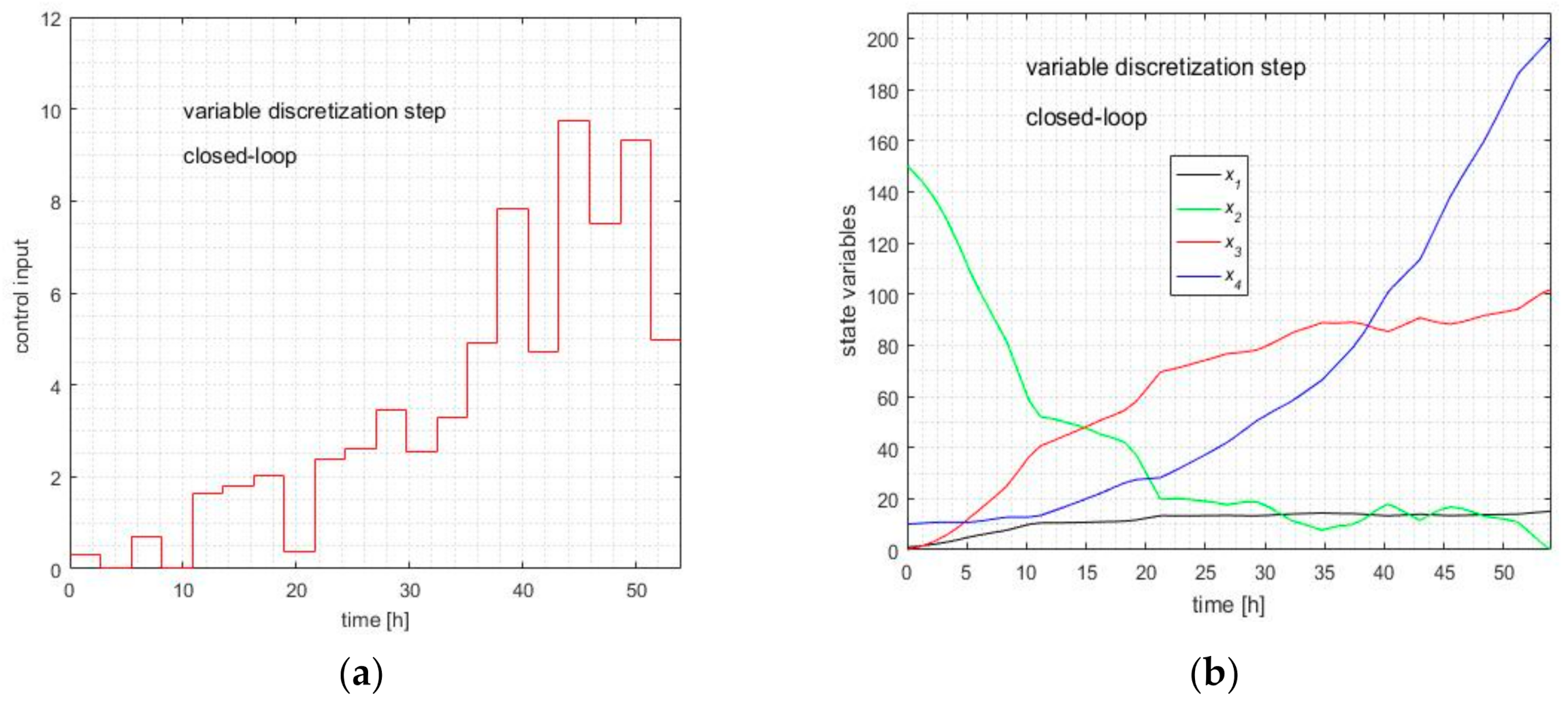
We conducted a simulation series that executes the script “Closed-loop2.m” 30 times. In our simulation series, there was an execution that yielded Jtypical = 20319.0. A statistic of the performance index achieved by the closed loop is presented in

Table 7. Results of the closed-loop simulation series using the Controller with EAv2.

Jmin	Javg	Jmax	Sdev	Jtypical
19,497.0	20,323.0	20,982.0	353.0	20,319.0

. The quasi-optimal control input calculated by the Controller for typical execution is depicted in Figure 5a, and its state evolution is depicted in Figure 5b.

6. Discussion

We can now verify the statement made in Section 4.2, which was that the Controller based on EAv2 has a smaller computational complexity than the one based on EAv1.

Table 8. The call number of the objective function.

	Nmin	Navg	Nmax	Ncalls
EAv1	2674	2691	2719	2690
EAv2	2666	2690.8	2711

shows the call number of the objective function recorded at the time of the closed-loop simulations. This number refers to the call of only one Controller, determining the optimal control input for the current sampling period. Its value is independent of the prediction horizon’s length. The first three columns represent the minimum, average, and maximum recorded values. The last column presents the theoretical value calculated with Equation (14) and Table 3. The adopted offspring’s probability of undergoing mutation is p = 0.9.

Hence the call number is the same for the two Controller versions.

For the same prediction horizon [k, H], the process model’s integration works over the same time interval and has similar input functions u(t), which are step functions. The step number of u(t) is not so important for the integration time. Hence, under these circumstances, the integration durations are similar.

Considering the two aspects mentioned above, we can conclude that the computational complexity regarding the objective function evaluation is similar for the two Controllers.

The aspect that makes the difference between the two controllers is related to encoding a pcs, namely the gene number. The Controller based on EAv1 uses a variable number of genes: $H, H-1,\cdots , 2, 1$. Constraint #3 can be prohibitive, especially in the first sampling period.

The Controller based on EAv2 only has $h_0$ genes and $h_0<H$. Hence, EAv2 obviously has a smaller computational complexity for all genetic operators (selection, crossover, mutation, replacement) and initializations. The confirmation of this statement is given by

Table 9. Execution time for the two controllers.

k	tv1[s]	tv2[s]	k	tv1[s]	tv2[s]	k	tv1[s]	tv2[s]	k	tv1[s]	tv2[s]
1	84.4	60.7	6	62.9	36.0	11	53.9	35.2	16	43.1	18.9
2	78.8	51.3	7	62.2	41.3	12	51.8	41.1	17	37.1	20.4
3	91.3	49.0	8	62.0	50.4	13	46.1	25.8	18	26.6	11.9
4	84.6	49.8	9	62.4	38.8	14	44.8	22.7	19	23.1	7.9
5	70.7	55.7	10	59.0	33.8	15	44.8	19.0	20	13.0	7.0

, which gives the execution time for the two controllers. These durations have been recorded at the time of the closed-loop simulations for each sampling period. The columns labelled by k give the sampling period rank within the control horizon. The columns labelled by tv1 and tv2 give the execution times (in seconds) for the Controller based on EAv1 and EAv2, respectively.

The durations indicated in the two columns show that the Controller based on EAv2 has undoubtedly smaller computational complexity than EAv1.

In our case, because the durations tv1 are less than T, even the first Controller can be used in a closed-loop control structure. Generally speaking, constraint #3 can be prohibitive for other OCPs, and the Controller based on EAv2 could be the solution. The price to pay for this Controller’s computational complexity is underlined by Remark #5. The simulations should prove that the optimal accuracy of the control sequence is not seriously affected. In our case, the values of the performance indexes shown in Table 7 prove that the best solution accuracy is more than acceptable.

The third line of

Table 10. Performance indexes recorded within the simulation series.

	Jmin	Javg	Jmax	Sdev	Jtypical
Open-loop EAv0	18,973.0	19,906.4	20,395.2	312.5	19,885.7
Closed-loop EAv1	19,127.7	20,136.7	21,014.9	449.5	20,153.5
Closed-loop EAv2	19,497.0	20,323.0	20,982.0	353.0	20,319.0

proves that EAv2 works very well in a closed loop with only ten genes.

The curves depicted in Figure 3, Figure 4 and Figure 5 have similar aspects. Moreover, Figure 4 and Figure 5 show that the control action is present and the closed-loops work. To facilitate the comparison among the performance indexes for the three situations, Table 9 unites Table 4, Table 5 and Table 6. We recall that each simulation series has 30 program executions. Some explanations concerning the differences among the three lines are necessary.

One can remark that the values of J from in the first line are less than those accomplished by the two controllers. This explanation is related to the extent of the search operation. EAv0 searches for the best solution using only 2690 calls (Ncalls) of the objective function, while the controllers use 20 times more calls (2690 calls for each sampling period). In other words, the execution of EAv0 is equivalent to the Controller’s call for the first sampling period.

EAv1 finds the best performance index in the closed loop J = 21,014.9, which is greater than the corresponding value of EAv2, J = 20,982. This time, the explanation is related to the bigger number of genes that involve a finer representation of the pcs. From this point of view, EAv1 is superior to EAv2. More accurate representation leads to better optimization.

At the same time, the bigger number of genes involves a greater explorative character and a greater representation power for u(t). That is why EAv1 has a standard deviation greater than the corresponding value of EAv2. In comparison with EAv0, EAv1 has 20 times more chances to strengthen its explorative character. This fact explains the smaller value of the standard deviation in the open loop.

Our closed-loop simulations had two entities: the Controller based on EA and the controlled process. The Controller already uses a process model to implement the RHC structure (to make predictions). In this work, the real process is also simulated using the process model. That is a simplification because the real process is almost always affected by unmodeled dynamics and noises. One may ask: at what extent could the real process degrade the closed-loop functioning? The answer can always be found through simulation using a real process model. For example, a real process model could be obtained from the process model to which a simulated “noise” is added. We have simulated closed-loop functioning using this technique, but quantitative results are not included in this paper to avoid a presentation that is too complex.

We can notice a degradation of quasi-optimal behaviour according to the amplitude of the noise. The increase of the noise implies the decrease of the performance index. The closed loop does or does not work well depending on whether the performance index value is acceptable.

Generally speaking, it is relatively easy to deal with the constraints regarding the control input $u(k), k=0,\cdots ,H-1$. This can be done when generating new pcs. Finally, each component belongs to a certain domain, $u(k)\in U_k$, and the construction of a new pcs could meet this constraint. What is more difficult is the handling of the constraints regarding the state variables $x(k), k=0,\cdots ,H-1$. A valid pcs will yield the resulting state trajectory $X(k)$ defined by Equation (5). For a specific OCP, state path constraints involving a trajectory that is a pss could be imposed. The most general constraint could have a form that involves an admissible domain for each k: $x(k)\in D_k, k=0,\cdots ,H$. In our case study, Constraint (18) limits the produced ethanol’s volume in the final state to the reactor’s volume.

The pss is calculated through the integration procedure. A good strategy is to verify if the component of the pss meet the path constraints just after the calculation of the pss within the objective function. If at least one constraint is not fulfilled, the cause associated with this effect, namely the pcs, must be moved away. A correct approach is to assign an infinite value (for minimization) to its performance index. In this way, the MA will replace the considered pcs, and the stochastic character of the population evolution will not be corrupted.

At successive time moments, the pcs values are randomly set. Thus, the difference between two successive values could be quite big in one sense or another. This fact does not fit with the certain and desired smoothness of the control profile. Actually, this is the price to pay for the stochastic nature of the EA. The latter can integrate the so-called step control technique, which implements the following differential constraint:

$$\left|\frac{du(t)}{dt}\right|\le \Delta s_{\max }$$

The value $\Delta s_{\max }$ is the maximal accepted slope. If the step control technique is implemented, it will involve a certain smoothness at the level of the state trajectory. Starting from this remark and assimilating gradient-based optimization with evolutionary optimization, in principle, we could facilitate the state evolution toward the optimal pcs. Within a future work, this idea could help to make the control action of the proposed receding horizon controller more effective.

Besides the EA, other metaheuristic algorithms have been used by the authors to implement receding horizon controllers. Both population-based metaheuristic methods (firefly algorithm, harmony search, Gaussian adaptation, memetic algorithm, etc.) and Swarm algorithms (Ant Colony Optimization, the Artificial Bee Colony Algorithm, the Bees Algorithm, Cuckoo search, Lévy flights for global optimization, particle swarm optimization, etc.) have been used to solve OCPs. The communication skills among agents are not making swarm algorithms always more effective than the population-based algorithms. Our first perception is that the effectiveness of the Controller mainly depends on the dynamic process nature. A systematic comparison can be made within a future investigation, and more implementation aspects could be revealed.

7. Conclusions

This paper presented some implementation aspects regarding the optimal control of a process using a Controller based on an evolutionary algorithm. This solution is addressed when other analytical or numerical solutions are not available and when using a metaheuristic algorithm yields a flexible and robust solution.

Using a metaheuristic algorithm involves a control structure that can use such an algorithm. The RHC structure is adequate from this point of view because the prediction technique can fit with an evolutionary algorithm.

We have presented some implementation aspects concerning the harmonization between the prediction technique and the evolutionary algorithm. Metaheuristic algorithms are known to have a large computational complexity. This paper has addressed a method to thwart this drawback and fulfil the time constraint for an evolutionary algorithm.

For the case study presented in this work, we have illustrated the proposed algorithm using simulation programs. The material attached to this work includes the simulation programs that show how the RHC structure, Controller, and prediction with an EA can be implemented with good results.