Agriculture Model Comparison Framework and MyGeoHub Hosting: Case of Soil Nitrogen †
Abstract
1. Introduction
- A high-fidelity complex agriculture model requires more execution time and space, whereas a comparable accuracy reduced model is desirable for fast prototyping;
- Lack of high quality temporal resolution data as the basis for model comparison;
- Programs for calibration and decision-making are typically in a separate language from that of the model, making the interfacing slow that needs to be sped-up as well;
- A complex agriculture model is generally not accessible across platforms and requires local download and installation, which needs to be addressed;
- A lean model can be used for quick initial exploration of a global search space for optimization routine (whether for automated calibration or decision making), which can then seed a subsequent more refined local search utilizing a complex model, increasing the usefulness of a basic lean model.
- Develop a framework to compare any two models where high quality field data for calibrating a test model against a benchmark model is not directly available;
- Survey of soil nitrogen models and ranking those based on a number of N-pools and parameters, which are indicative of model complexity;
- Implement and compare a lean N-model [10] against a high-fidelity complex agriculture model RZWQM and measuring the degree of fit as well as a speed-up in simulation time;
- Implement both the lean N-model and the routine for automated calibration in the same programming language for fast interfacing;
- Host the lean soil nitrogen model in MyGeoHub, making the model cloud accessible through a browser and cross-platform, thus eliminating local installation.
2. Review of Soil Nitrogen Models
3. Materials and Methods
3.1. Soil Nutrient (C and N) Module in RZWQM
3.2. A Lean Nutrient Model
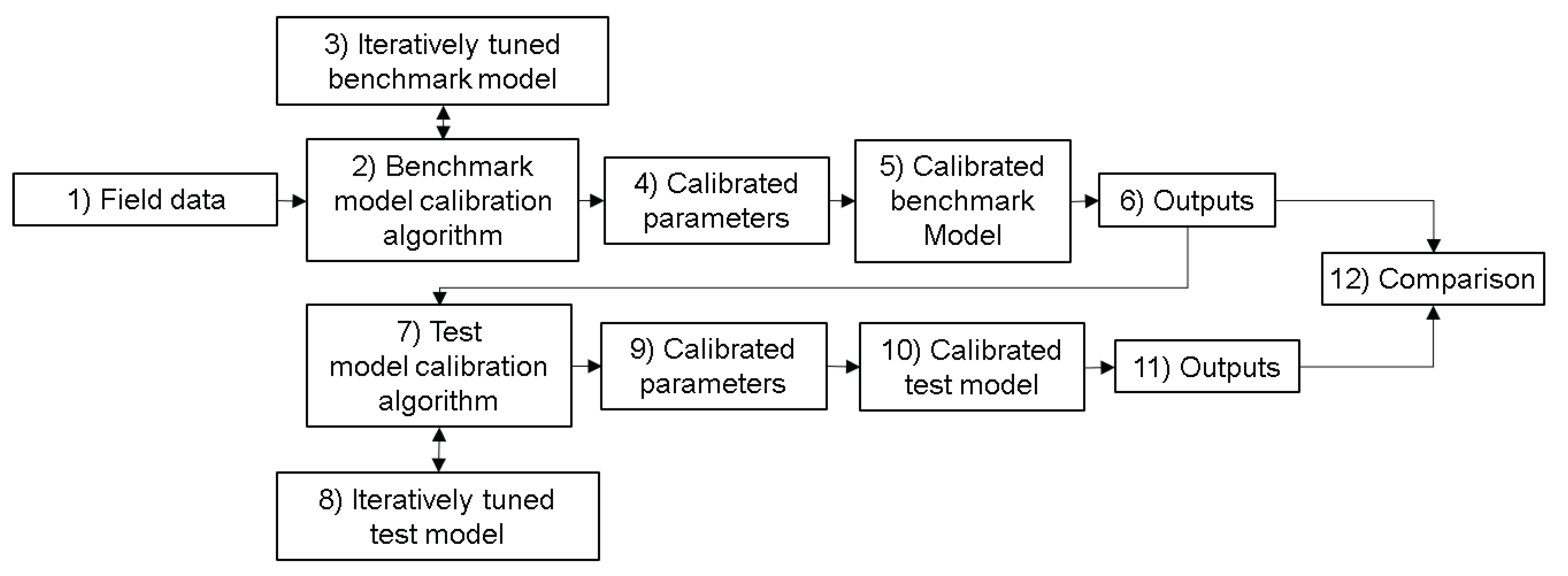
3.3. RZWQN vs. Lean Model Comparison Setup
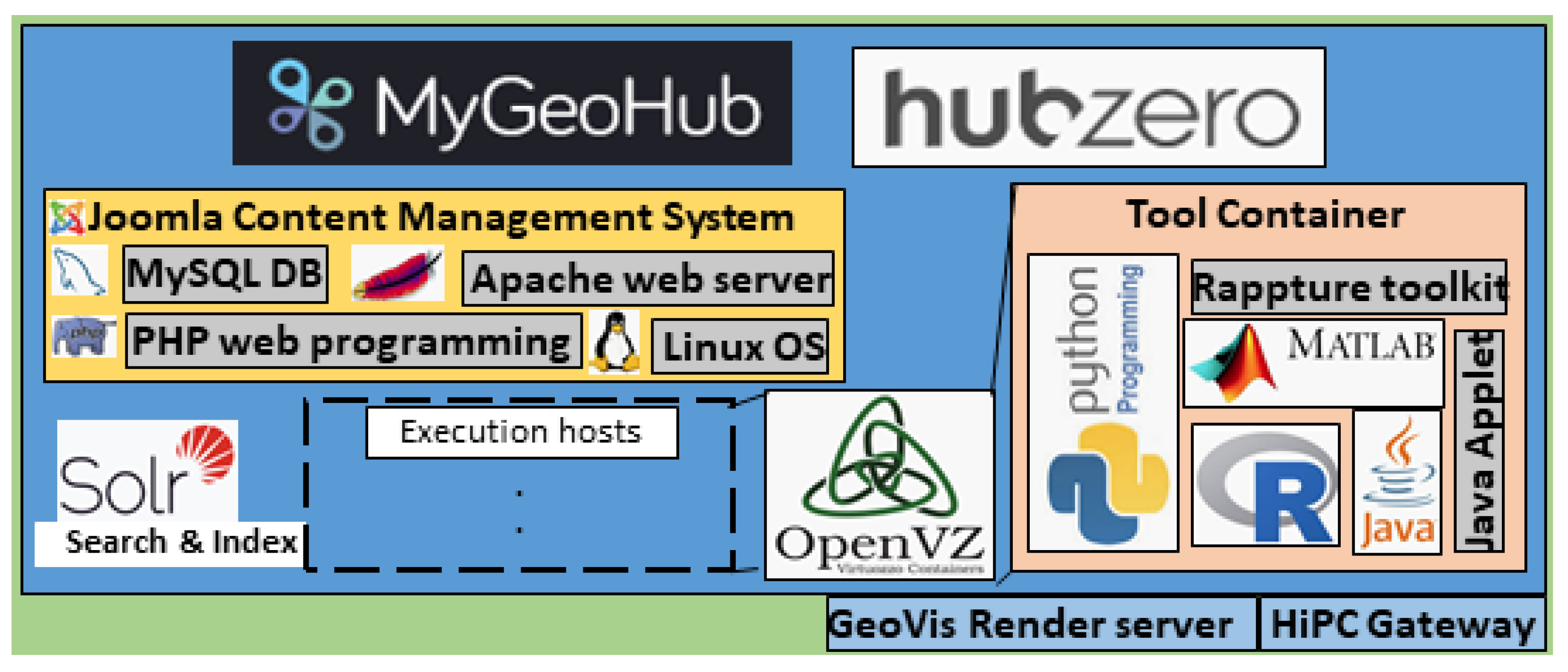
3.4. MyGeoHub Cyber-Infrastructure
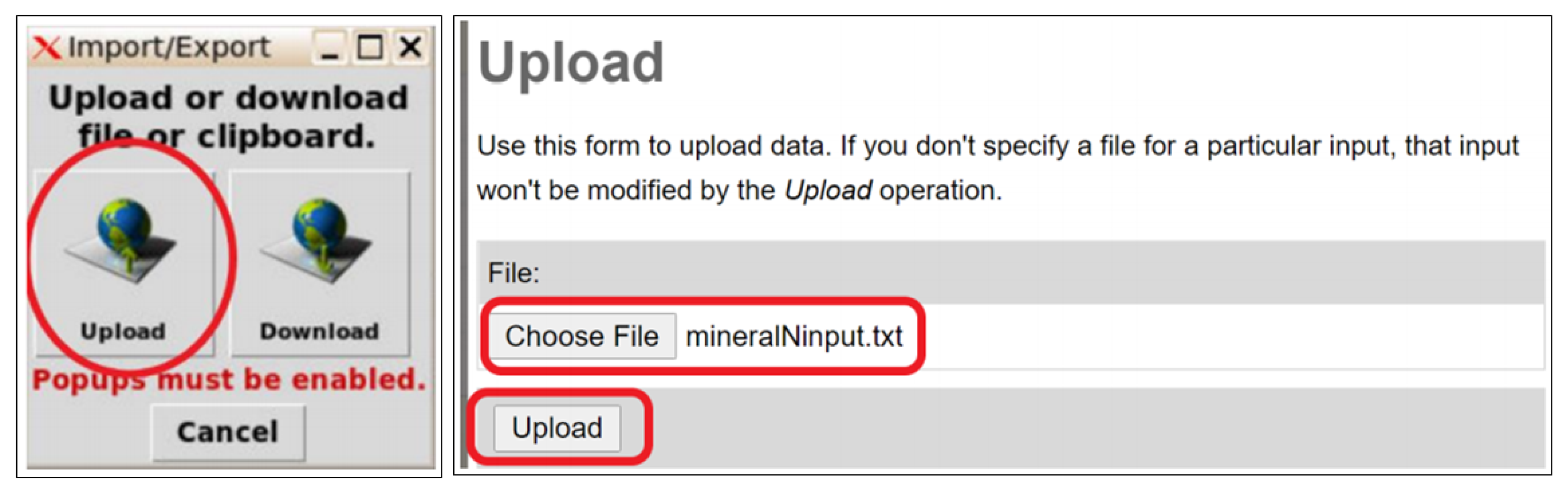
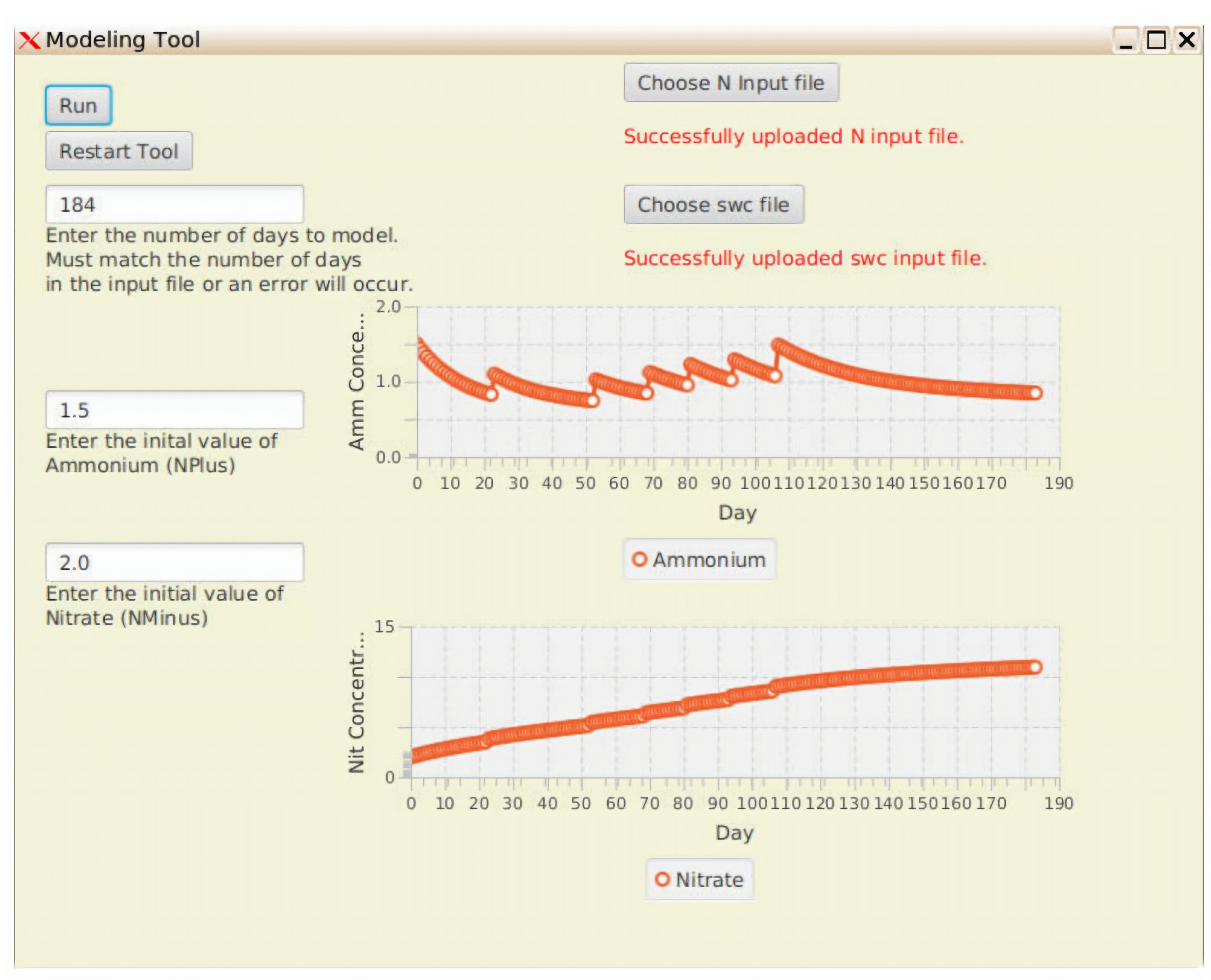
3.4.1. Hosting of Lean N-Model in MyGeoHub
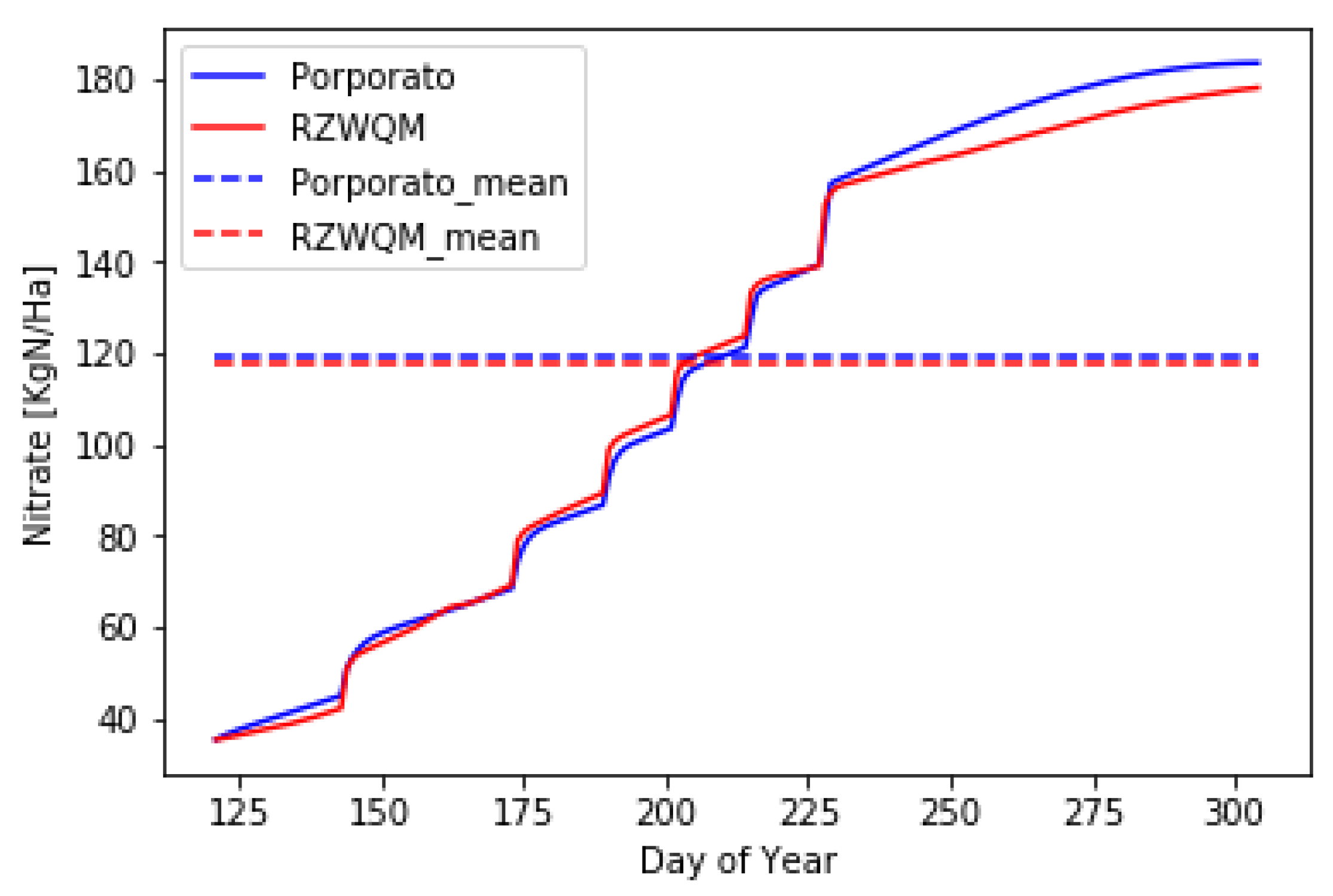
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2017, 155, 240–254. [Google Scholar] [CrossRef]
- De Wit, C.T. Transpiration and Crop Yields; Technical Report; WILEY: Hoboken, NJ, USA, 1958. [Google Scholar]
- Van Bavel, C. A Drought Criterion and Its Application in Evaluating Drought Incidence and Hazard 1. Agron. J. 1953, 45, 167–172. [Google Scholar] [CrossRef]
- Shaffer, M.J.; Pierce, F.J. A user’s guide to NTRM, a soil-crop simulation model for nitrogen, tillage, and crop-residue management. In Conservation Research Report (USA); U.S. Dept. of Agriculture, Agricultural Research Service: Washington, DC, USA, 1987. [Google Scholar]
- Shaffer, M.; Halvorson, A.; Pierce, F. Nitrate leaching and economic analysis package (NLEAP): Model description and application. In Managing Nitrogen for Groundwater Quality and Farm Profitability; Soil Science Soc Amer: Madison, WI, USA, 1991; pp. 285–322. [Google Scholar]
- Molina, J.; Clapp, C.; Shaffer, M.; Chichester, F.; Larson, W. NCSOIL, a model of nitrogen and carbon transformations in soil: Description, calibration, and behavior. Soil Sci. Soc. Am. J. 1983, 47, 85–91. [Google Scholar] [CrossRef]
- Parton, W. The CENTURY model. In Evaluation of Soil Organic Matter Models; Springer: Berlin/Heidelberg, Germany, 1996; pp. 283–291. [Google Scholar]
- Parton, W.J.; Hartman, M.; Ojima, D.; Schimel, D. DAYCENT and its land surface submodel: Description and testing. Glob. Planet. Chang. 1998, 19, 35–48. [Google Scholar] [CrossRef]
- Hansen, S.; Jensen, H.; Shaffer, M. Developments in modeling nitrogen transformations in soil. In Nitrogen Fertilization in the Environment; Marcel Dekker: New York, NY, USA, 1995; pp. 83–107. [Google Scholar]
- Porporato, A.; D’odorico, P.; Laio, F.; Rodriguez-Iturbe, I. Hydrologic controls on soil carbon and nitrogen cycles. I. Modeling scheme. Adv. Water Resour. 2003, 26, 45–58. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Dzotsi, K.; Jones, J.; Adiku, S.; Naab, J.; Singh, U.; Porter, C.; Gijsman, A. Modeling soil and plant phosphorus within DSSAT. Ecol. Model. 2010, 221, 2839–2849. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosion/Productivity Impact Calculator. I: Model Documentation. II: User Manual. In Technical Bulletin-United States Department of Agriculture; US Department of Agriculture: Washington, DC, USA, 1990. [Google Scholar]
- Jones, C.; Cole, C.; Sharpley, A.; Williams, J. A simplified soil and plant phosphorus model: I. Documentation. Soil Sci. Soc. Am. J. 1984, 48, 800–805. [Google Scholar] [CrossRef]
- Williams, J.; Izaurralde, R.; Steglich, E. Agricultural policy/environmental extender model. Theor. Doc. Version 2008, 604, 2008–2017. [Google Scholar]
- Taiz, L.; Zeiger, E.; Møller, I.M.; Murphy, A. Plant Physiology and Development; Sinauer Associates Incorporated: Sunderland, MA, USA, 2015. [Google Scholar]
- Thornley, J.H.; France, J. Mathematical Models in Agriculture: Quantitative Methods for the Plant, Animal and Ecological Sciences; CABI: Wallingford, UK, 2007. [Google Scholar]
- Williams, J.; Jones, C.; Kiniry, J.; Spanel, D.A. The EPIC crop growth model. Trans. ASAE 1989, 32, 497–0511. [Google Scholar] [CrossRef]
- Ritchie, J. Description and performance of CERES wheat: A user-oriented wheat yield model. In ARS Wheat Yield Project; USDA-ARS: Ames, IA, USA, 1985; pp. 159–175. [Google Scholar]
- Van Diepen, C.v.; Wolf, J.; Van Keulen, H.; Rappoldt, C. WOFOST: A simulation model of crop production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- SimUnek, J.; Van Genuchten, M.T.; Sejna, M. The HYDRUS Software Package for Simulating the Two-And Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Porous Media. In Technical Manual; 2012; Available online: www.researchgate.net/ (accessed on 31 January 2021).
- Radcliffe, D.E.; Simunek, J. Soil Physics with HYDRUS: Modeling and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Douglas-Mankin, K.; Srinivasan, R.; Arnold, J. Soil and Water Assessment Tool (SWAT) model: Current developments and applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Saxton, K.E.; Willey, P.H. The SPAW model for agricultural field and pond hydrologic simulation. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2005; pp. 400–435. [Google Scholar]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.; Feddes, R.; Kabat, P.; Van Walsum, P.; Groenendijk, P.; Van Diepen, C. Theory of SWAP Version 2.0; Simulation of Water Flow, Solute Transport and Plant Growth in the Soil-Water-Atmosphere-Plant Environment; Technical Report; DLO Winand Staring Centre: Wageningen, The Netherlands, 1997. [Google Scholar]
- Holzworth, D.P.; Huth, N.I.; de Voil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM–evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Stockle, C.O.; Martin, S.A.; Campbell, G.S. CropSyst, a cropping systems simulation model: Water/nitrogen budgets and crop yield. Agric. Syst. 1994, 46, 335–359. [Google Scholar] [CrossRef]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Ahuja, L.; Rojas, K.; Hanson, J. Root Zone Water Quality Model: Modelling Management Effects on Water Quality and Crop Production; Water Resources Publication: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Zhang, Y.; Li, C.; Zhou, X.; Moore, B., III. A simulation model linking crop growth and soil biogeochemistry for sustainable agriculture. Ecol. Model. 2002, 151, 75–108. [Google Scholar] [CrossRef]
- Thorp, K.; Youssef, M.; Jaynes, D.; Malone, R.; Ma, L. DRAINMOD-N II: Evaluated for an agricultural system in Iowa and compared to RZWQM-DSSAT. Trans. ASABE 2009, 52, 1557–1573. [Google Scholar] [CrossRef]
- Kozak, J.A.; Aiken, R.M.; Flerchinger, G.N.; Nielsen, D.C.; Ma, L.; Ahuja, L. Comparison of modeling approaches to quantify residue architecture effects on soil temperature and water. Soil Tillage Res. 2007, 95, 84–96. [Google Scholar] [CrossRef]
- Wiborg, T. A Comparison of Agricultural Sector Models: CRAM, DRAM, SASM and the KVL Model; Technical Report; 2000; Available online: https://ageconsearch.umn.edu/record/24211/files/ew000002.pdf (accessed on 28 March 2021).
- Parajuli, P.B.; Nelson, N.O.; Frees, L.D.; Mankin, K.R. Comparison of AnnAGNPS and SWAT model simulation results in USDA-CEAP agricultural watersheds in south-central Kansas. Hydrol. Process. Int. J. 2009, 23, 748–763. [Google Scholar] [CrossRef]
- Bhar, A.; Kumar, R.; Qi, Z.; Malone, R. Coordinate descent based agricultural model calibration and optimized input management. Comput. Electron. Agric. 2020, 172, 105353. [Google Scholar] [CrossRef]
- Bhar, A.; Kumar, R. Model-Predictive Real-Time Fertilization and Irrigation Decision-Making Using RZWQM. In Proceedings of the 2019 ASABE Annual International Meeting. American Society of Agricultural and Biological Engineers, Boston, MA, USA, 7–10 July 2019; p. 1. [Google Scholar]
- Kalyanam, R.; Zhao, L.; Song, C.; Biehl, L.; Kearney, D.; Kim, I.L.; Shin, J.; Villoria, N.; Merwade, V. MyGeoHub—A sustainable and evolving geospatial science gateway. Future Gener. Comput. Syst. 2019, 94, 820–832. [Google Scholar] [CrossRef]
- McLennan, M.; Kennell, R. HUBzero: A platform for dissemination and collaboration in computational science and engineering. Comput. Sci. Eng. 2010, 12, 48–53. [Google Scholar] [CrossRef]
- Wu, L.; McGechan, M.; McRoberts, N.; Baddeley, J.; Watson, C. SPACSYS: Integration of a 3D root architecture component to carbon, nitrogen and water cycling—Model description. Ecol. Model. 2007, 200, 343–359. [Google Scholar] [CrossRef]
- Sadhukhan, D.; Qi, Z.; Zhang, T.; Tan, C.S.; Ma, L.; Andales, A.A. Development and evaluation of a phosphorus (P) module in RZWQM2 for phosphorus management in agricultural fields. Environ. Model. Softw. 2019, 113, 48–58. [Google Scholar] [CrossRef]
- Hansen, S.; Jensen, H.; Nielsen, N.; Svendsen, H. DAISY: Soil plant atmosphere system model. NPO Rep. A 1990, 10, 272. [Google Scholar]
- Liang, H.; Hu, K.; Batchelor, W.D.; Qi, Z.; Li, B. An integrated soil-crop system model for water and nitrogen management in North China. Sci. Rep. 2016, 6, 25755. [Google Scholar] [CrossRef]
- Jansson, P.E. CoupModel: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1337–1344. [Google Scholar] [CrossRef]
- Smith, J.; Gottschalk, P.; Bellarby, J.; Chapman, S.; Lilly, A.; Towers, W.; Bell, J.; Coleman, K.; Nayak, D.; Richards, M.; et al. Estimating changes in Scottish soil carbon stocks using ECOSSE. I. Model description and uncertainties. Clim. Res. 2010, 45, 179–192. [Google Scholar] [CrossRef]
- Gerik, T.; Williams, J.; Francis, L.; Greiner, J.; Magre, M.; Meinardus, A.; Steglich, E.; Taylor, R. Environmental Policy Integrated Climate Model-User’s Manual Version 0810; Blackland Research and Extension Center; Texas A&M AgriLife: Temple, TX, USA, 2014. [Google Scholar]
- Parton, B.; Ojima, D.; Del Grosso, S.; Keough, C. CENTURY Tutorial: Supplement to CENTURY User’s Manual. In Great Plain System Research Unit Technical Report; 2001; Available online: https://www2.nrel.colostate.edu/projects/century/century_tutorial.pdf (accessed on 28 March 2021).
- Li, C.; Frolking, S.; Frolking, T.A. A model of nitrous oxide evolution from soil driven by rainfall events: 1. Model structure and sensitivity. J. Geophys. Res. Atmos. 1992, 97, 9759–9776. [Google Scholar] [CrossRef]
- Johnsson, H.; Bergstrom, L.; Jansson, P.E.; Paustian, K. Simulated nitrogen dynamics and losses in a layered agricultural soil. Agric. Ecosyst. Environ. 1987, 18, 333–356. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.; Singh, V.; Frevert, D. The APEX model. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2006; pp. 437–482. [Google Scholar]
- Li, Y.; White, R.; Chen, D.; Zhang, J.; Li, B.; Zhang, Y.; Huang, Y.; Edis, R. A spatially referenced water and nitrogen management model (WNMM) for (irrigated) intensive cropping systems in the North China Plain. Ecol. Model. 2007, 203, 395–423. [Google Scholar] [CrossRef]
- Kersebaum, K.C. Application of a simple management model to simulate water and nitrogen dynamics. Ecol. Model. 1995, 81, 145–156. [Google Scholar] [CrossRef]
- Nendel, C. MONICA: A simulation model for nitrogen and carbon dynamics in agro-ecosystems. In Novel Measurement and Assessment Tools for Monitoring and Management of Land and Water Resources in Agricultural Landscapes of Central Asia; Springer: Berlin/Heidelberg, Germany, 2014; pp. 389–405. [Google Scholar]
- Kersebaum, K.C. Modelling nitrogen dynamics in soil–crop systems with HERMES. In Modelling Water and Nutrient Dynamics in Soil–Crop Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 147–160. [Google Scholar]
- Franko, U.; Oelschlägel, B.; Schenk, S. Simulation of temperature-, water-and nitrogen dynamics using the model CANDY. Ecol. Model. 1995, 81, 213–222. [Google Scholar] [CrossRef]
- Franko, U.; Oelschlägel, B.; Schenk, S.; Puhlmann, M.; Kuka, K.; Mallast, J.; Thiel, E.; Prays, N.; Meurer, K.; Bönecke, E. CANDY Manual—Description of Background; UFZ; Halle: Leipzig, Germany, 2015. [Google Scholar]
- De Willigen, P. Nitrogen turnover in the soil-crop system; comparison of fourteen simulation models. In Nitrogen Turnover in the Soil-Crop System; Springer: Berlin/Heidelberg, Germany, 1991; pp. 141–149. [Google Scholar]
- De Willigen, P.; Neeteson, J. Comparison of six simulation models for the nitrogen cycle in the soil. Fertil. Res. 1985, 8, 157–171. [Google Scholar] [CrossRef]
- Wu, L.; McGechan, M. A review of carbon and nitrogen processes in four soil nitrogen dynamics models. J. Agric. Eng. Res. 1998, 69, 279–305. [Google Scholar] [CrossRef]
- Manzoni, S.; Porporato, A. Soil carbon and nitrogen mineralization: Theory and models across scales. Soil Biol. Biochem. 2009, 41, 1355–1379. [Google Scholar] [CrossRef]
- Shaffer, M.J.; Ma, L.; Hansen, S. Modeling Carbon and Nitrogen Dynamics for Soil Management; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Dessureault-Rompré, J.; Zebarth, B.J.; Georgallas, A.; Burton, D.L.; Grant, C.A.; Drury, C.F. Temperature dependence of soil nitrogen mineralization rate: Comparison of mathematical models, reference temperatures and origin of the soils. Geoderma 2010, 157, 97–108. [Google Scholar] [CrossRef]
- Rodrigo, A.; Recous, S.; Neel, C.; Mary, B. Modelling temperature and moisture effects on C–N transformations in soils: Comparison of nine models. Ecol. Model. 1997, 102, 325–339. [Google Scholar] [CrossRef]
- Antonopoulos, V.Z. Comparison of different models to simulate soil temperature and moisture effects on nitrogen mineralization in the soil. J. Plant Nutr. Soil Sci. 1999, 162, 667–675. [Google Scholar] [CrossRef]
- Trout, T.J.; Bausch, W.C. USDA-ARS Colorado maize water productivity data set. Irrig. Sci. 2017, 35, 241–249. [Google Scholar] [CrossRef]
- Qi, Z.; Ma, L.; Bausch, W.C.; Trout, T.J.; Ahuja, L.R.; Flerchinger, G.N.; Fang, Q. Simulating maize production, water and surface energy balance, canopy temperature, and water stress under full and deficit irrigation. Trans. ASABE 2016, 59, 623–633. [Google Scholar]
- Wilkins-Diehr, N.; Gannon, D.; Klimeck, G.; Oster, S.; Pamidighantam, S. TeraGrid science gateways and their impact on science. Computer 2008, 41, 32–41. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y. TeraGrid GIScience gateway: Bridging cyberinfrastructure and GIScience. Int. J. Geogr. Inf. Sci. 2009, 23, 631–656. [Google Scholar] [CrossRef]
- Klimeck, G.; McLennan, M.; Brophy, S.P.; Adams, G.B., III; Lundstrom, M.S. nanohub. org: Advancing education and research in nanotechnology. Comput. Sci. Eng. 2008, 10, 17. [Google Scholar] [CrossRef]
- Allison, J.; Backman, D.; Christodoulou, L. Integrated computational materials engineering: A new paradigm for the global materials profession. Jom 2006, 58, 25–27. [Google Scholar] [CrossRef]
- Goff, S.A.; Vaughn, M.; McKay, S.; Lyons, E.; Stapleton, A.E.; Gessler, D.; Matasci, N.; Wang, L.; Hanlon, M.; Lenards, A.; et al. The iPlant collaborative: Cyberinfrastructure for plant biology. Front. Plant Sci. 2011, 2, 34. [Google Scholar] [CrossRef]
- CIF21 DIBBs: PD: Cyberinfrastructure Tools for Precision Agriculture in the 21st Century. Available online: https://www.nsf.gov/awardsearch/showAward?AWD_ID=1724843 (accessed on 28 March 2021).
- Tarboton, D.G.; Idaszak, R.; Ames, D.; Goodall, J.; Horsburgh, J.; Band, L.; Merwade, V.; Song, C.; Couch, A.; Valentine, D.; et al. HydroShare: An Online, Collaborative Environment for the Sharing of Hydrologic Data and Models; 2012; Available online: https://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=3691&context=cee_facpub (accessed on 28 March 2021).
- Rosenzweig, C.; Jones, J.W.; Hatfield, J.L.; Ruane, A.C.; Boote, K.J.; Thorburn, P.; Antle, J.M.; Nelson, G.C.; Porter, C.; Janssen, S.; et al. The agricultural model intercomparison and improvement project (AgMIP): Protocols and pilot studies. Agric. For. Meteorol. 2013, 170, 166–182. [Google Scholar] [CrossRef]
- Bhar, A.; Qi, Z.; Malone, R.W.; Kumar, R. Sensor data driven parameter estimation for Agricultural Model using Coordinate Descent. In Proceedings of the 2018 ASABE Annual International Meeting, American Society of Agricultural and Biological Engineers, Detroit, MI, USA, 29 July–1 August 2018; p. 1. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Xu, Z.; Wang, X.; Weber, R.J.; Kumar, R.; Dong, L. Nutrient sensing using chip scale electrophoresis and in situ soil solution extraction. IEEE Sens. J. 2017, 17, 4330–4339. [Google Scholar] [CrossRef]
- Pandey, G.; Kumar, R.; Weber, R.J. A low RF-band impedance spectroscopy based sensor for in situ, wireless soil sensing. IEEE Sens. J. 2014, 14, 1997–2005. [Google Scholar] [CrossRef]
- Pandey, G.; Weber, R.J.; Kumar, R. Agricultural cyber-physical system: In-situ soil moisture and salinity estimation by dielectric mixing. IEEE Access 2018, 6, 43179–43191. [Google Scholar] [CrossRef]
- Kashyap, B.; Kumar, R. Sensing Methodologies in Agriculture for Soil Moisture and Nutrient Monitoring. IEEE Access 2021, 9, 14095–14121. [Google Scholar] [CrossRef]
- Tabassum, S.; Kumar, R.; Dong, L. Nanopatterned optical fiber tip for guided mode resonance and application to gas sensing. IEEE Sens. J. 2017, 17, 7262–7272. [Google Scholar] [CrossRef]
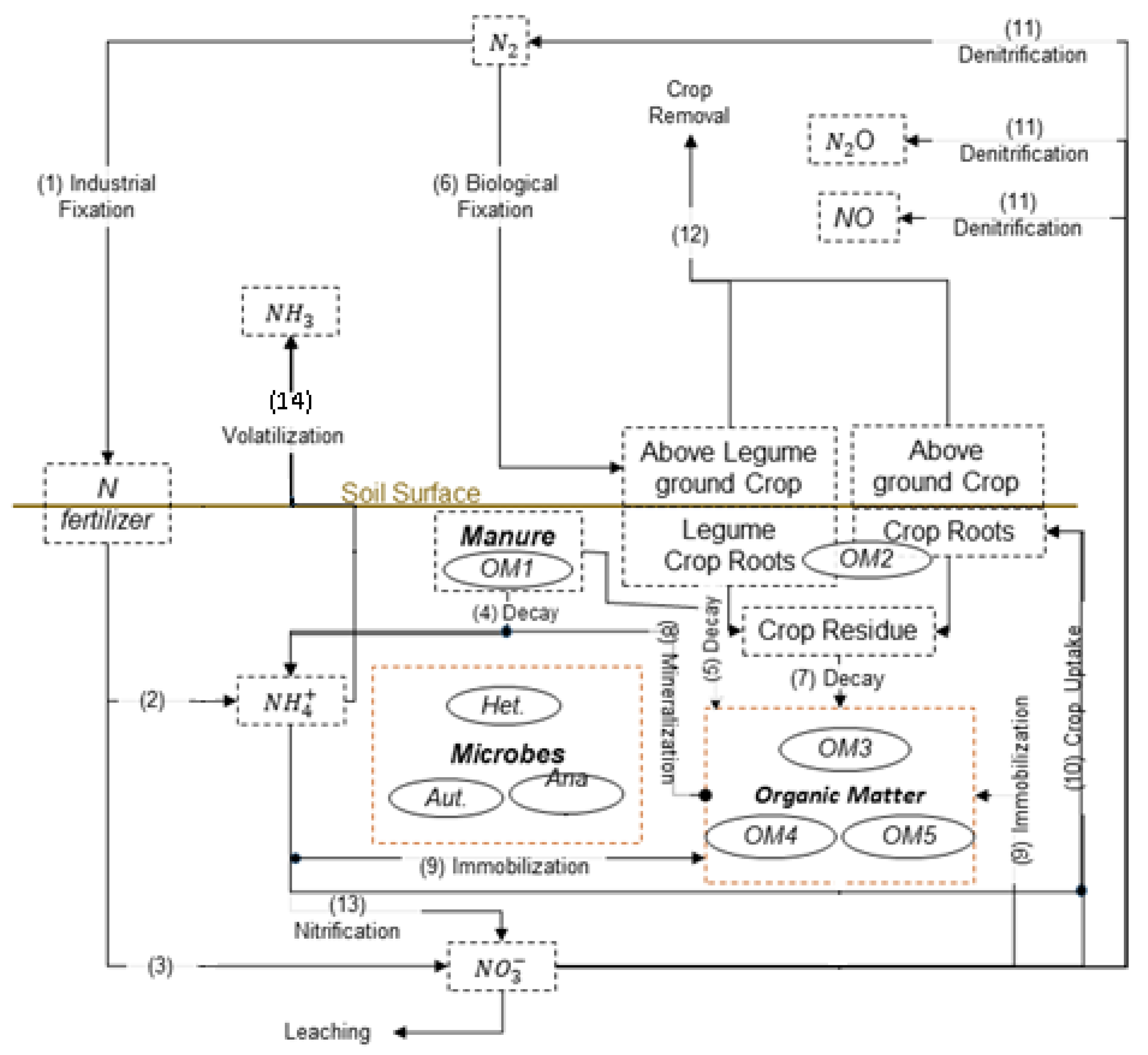
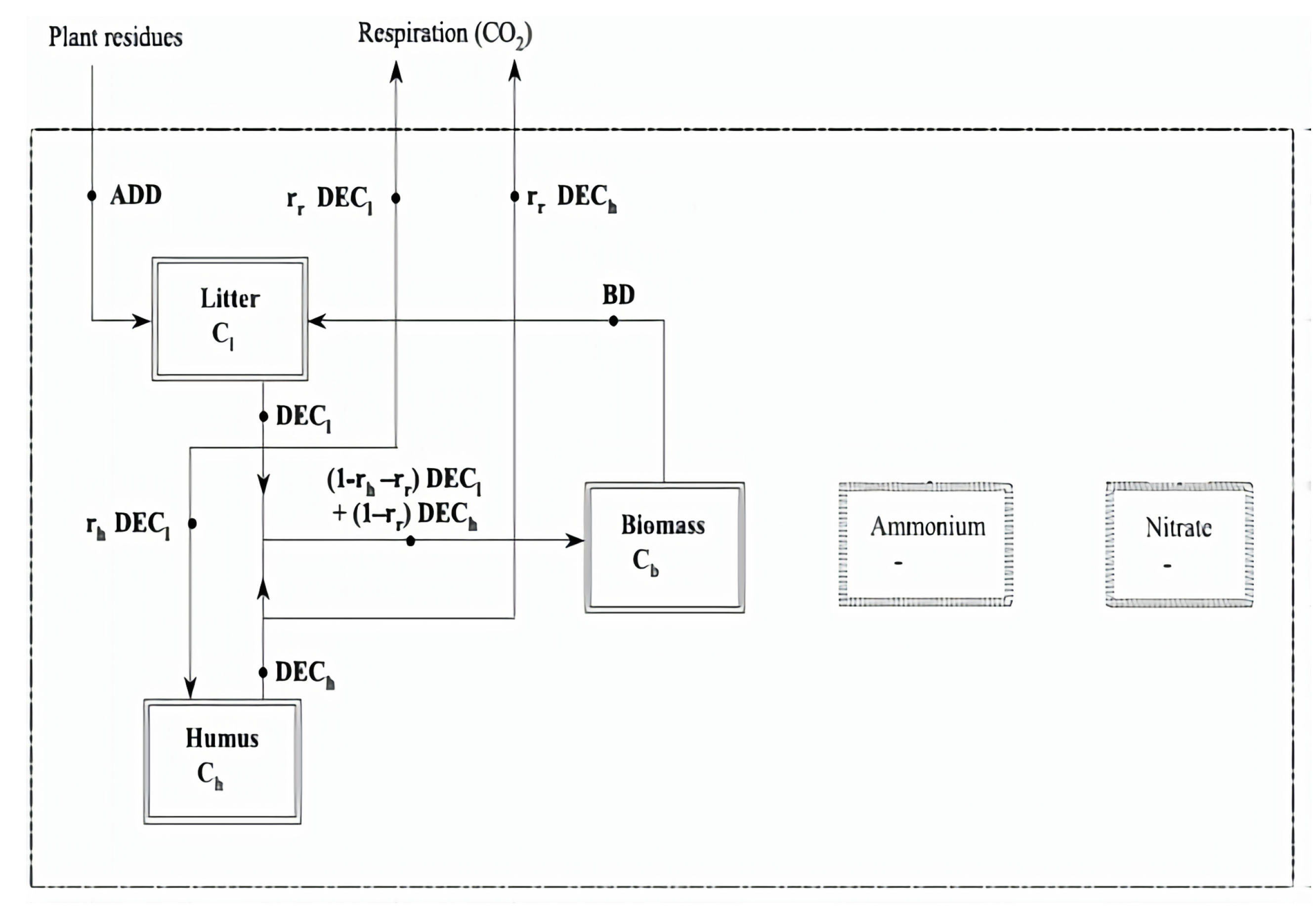
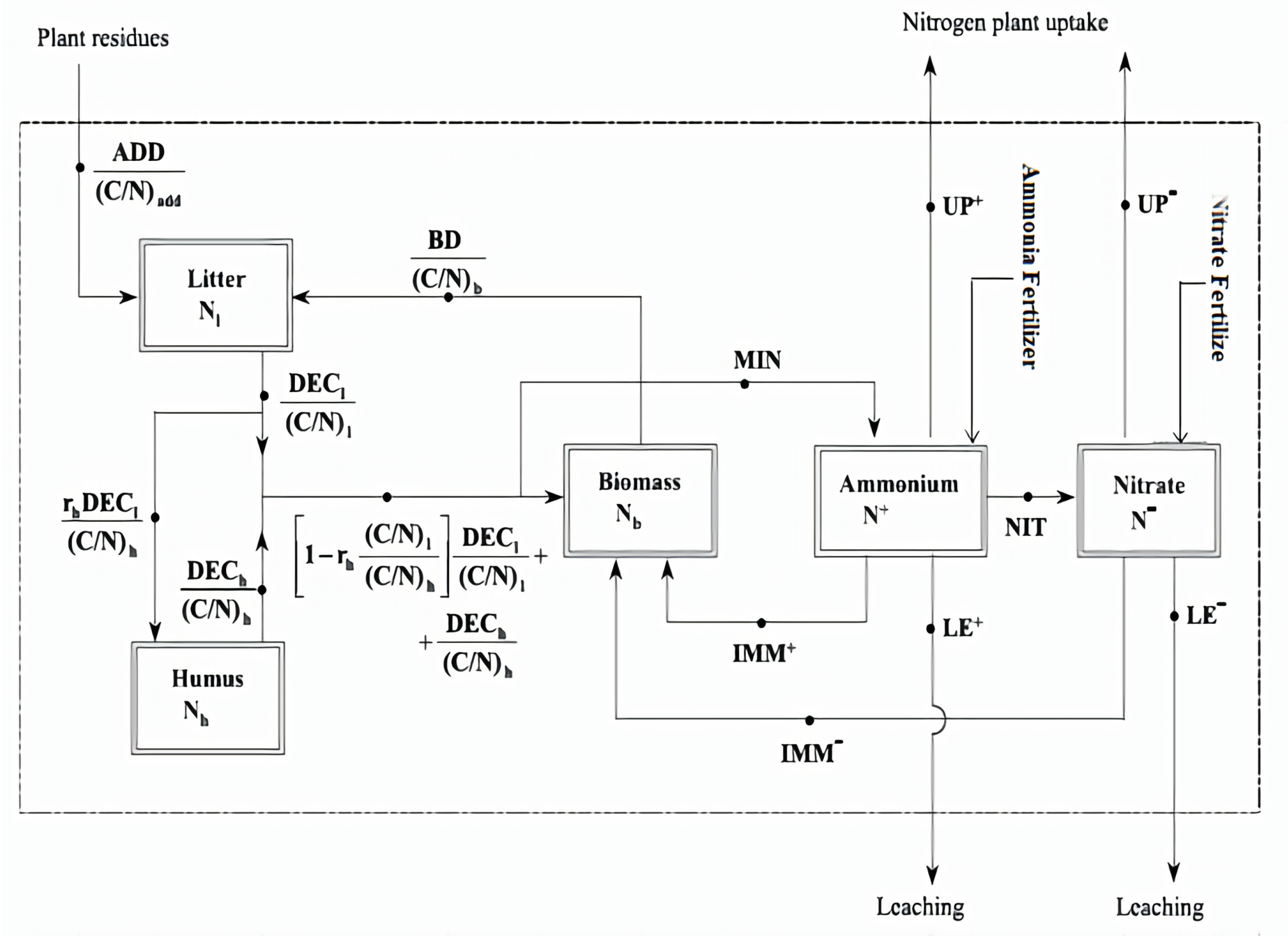
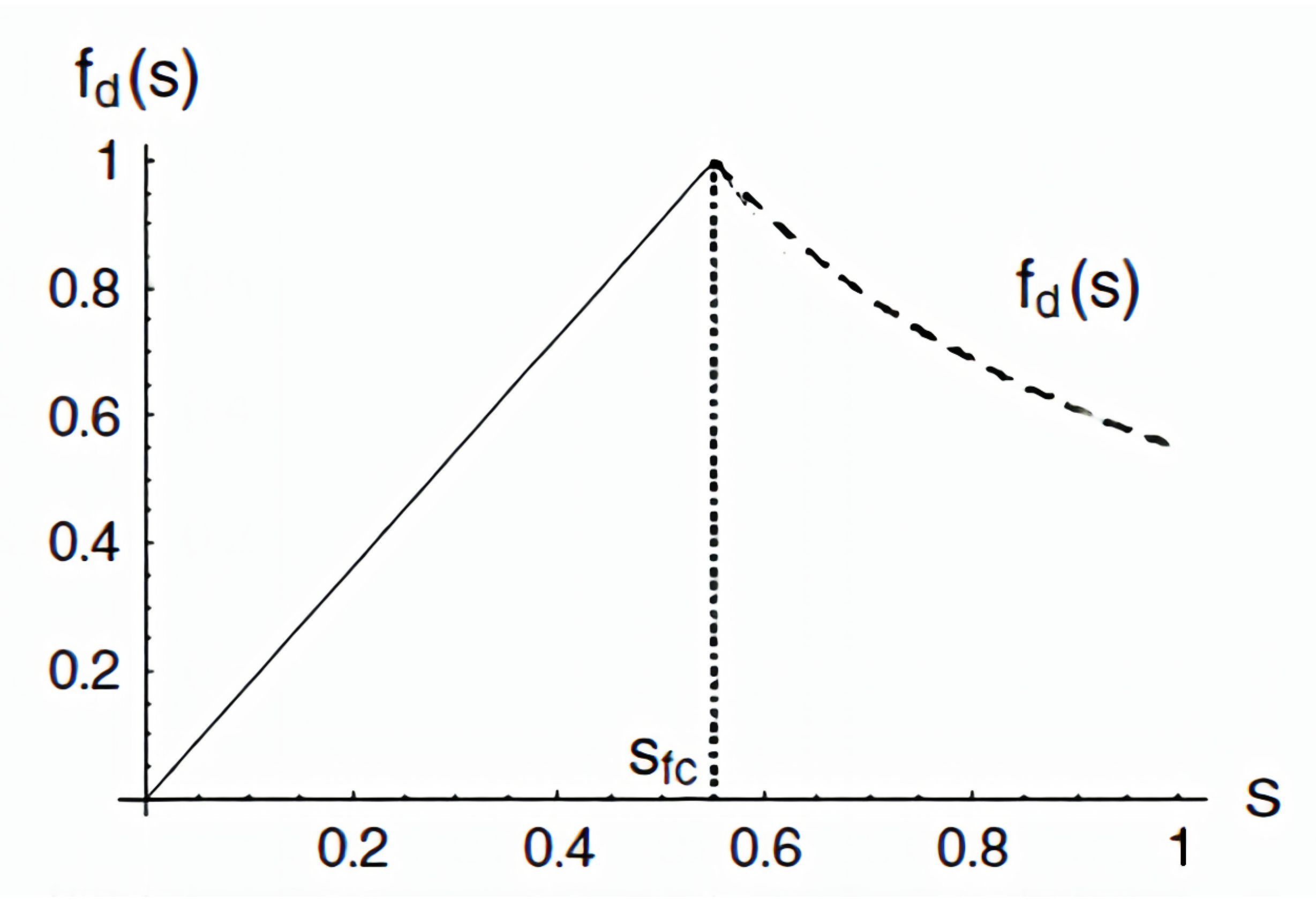

| # | Name | * | * | Additional Input | Additional Process | Ref. & Remark |
|---|---|---|---|---|---|---|
| (1) | SPACSYS | 27 | 45 | P cycle; N fixation; 3D root; | Wu et al. [41] (2007) rothamsted.ac.uk/rothamsted-spacsys-model | |
| (2) | RZWQM | 19 | 44 | ammonia volatilisation; urea hydrolysis; pesticide; P cycle [42] | Ahuja et al. [31] (2000) ars.usda.gov/plains-area/fort-collins-co/ | |
| (3) | DAISY | 14 | 35 | GIS | Hansen et al. [43] (1990) daisy.ku.dk/ | |
| (4) | CoupModel | 12 | 35 | GIS | Liang et al. [44] (2016). N model is based on DAISY | |
| (5) | WHCNS | 10 | 35 | ammonia volatilisation; | Jansson [45] (2012) http://www.coupmodel.com/ | |
| (6) | ECOSSE | 8 | 35 | GIS | methane dynamics; | Smith et al. [46] (2010) abdn.ac.uk/staffpages/uploads/soi450/ECOSSE%20User%20manual%20310810.pdf |
| (7) | EPIC | 12 | 25 | ammonia volatilisation; N fixation; erosion; P cycle; pesticide; | Sharpley and Williams [13] (1990), Gerik et al. [47] (2014) epicapex.tamu.edu/epic/. Inspired from CENTURY [48] | |
| (8) | DNDC | 16 | 20 | GIS | methane dynamics; ammonia volatilisation; urea hydrolysis; | Li et al. [49] (1992). dndc.sr.unh.edu/ |
| (9) | SOILN | 13 | 20 | Johnsson et al. [50] (1987) | ||
| (10) | APEX | 12 | 25 | erosion; grazing; pesticide; P cycle; N fixation; ammonia volatilisation; watershed, reservoir, ground water, sediment. | Williams et al. [51] (2006) epicapex.tamu.edu/apex/. Extension of EPIC. | |
| (11) | WNMM | 12 | 15 | GIS | Li et al. [52] (2007) | |
| (12) | MONICA | 11 | 14 | N fixation; Ammonia Volatilisation; Urea hydrolysis; | Kersebaum [53] (1995), Nendel [54] (2014) https://github.com/zalf-rpm/monica/wiki. Uses DAISY’s C dynamics. Extension of HERMES [55] model. | |
| (13) | CANDY | 6 | 18 | soil loosening/compaction; pesticide; ammonia volatilisation; | Franko et al. [56] (1995), Franko et al. [57] (2015) https://www.ufz.de/index.php?de=39503 | |
| (14) | A “Lean” Model | 8 | 12 | no denitrification; | Porporato et al. [10] 2003 |
| Parameter | Lower Range | Calibrated Value | Upper Range |
|---|---|---|---|
| 0.5 | 0.943 | 1.0 | |
| 0.0001 | 0.0787 | 0.1 | |
| b | 1 | 6.05 | 13 |
| 0.01 | 0.6647 | 2.2 | |
| 0.01 | 0.01 | 0.99 | |
| 0.01 | 0.322 | 0.99 | |
| 0.0001 | 0.0185 | 0.0999 | |
| 0.0001 | 0.0047 | 0.9999 | |
| 0.1 | 0.482 | 1.1 | |
| 0.1 | 0.405 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhar, A.; Feddersen, B.; Malone, R.; Kumar, R. Agriculture Model Comparison Framework and MyGeoHub Hosting: Case of Soil Nitrogen. Inventions 2021, 6, 25. https://doi.org/10.3390/inventions6020025
Bhar A, Feddersen B, Malone R, Kumar R. Agriculture Model Comparison Framework and MyGeoHub Hosting: Case of Soil Nitrogen. Inventions. 2021; 6(2):25. https://doi.org/10.3390/inventions6020025
Chicago/Turabian StyleBhar, Anupam, Benjamin Feddersen, Robert Malone, and Ratnesh Kumar. 2021. "Agriculture Model Comparison Framework and MyGeoHub Hosting: Case of Soil Nitrogen" Inventions 6, no. 2: 25. https://doi.org/10.3390/inventions6020025
APA StyleBhar, A., Feddersen, B., Malone, R., & Kumar, R. (2021). Agriculture Model Comparison Framework and MyGeoHub Hosting: Case of Soil Nitrogen. Inventions, 6(2), 25. https://doi.org/10.3390/inventions6020025







