Design and Construction of a Novel Simple and Low-Cost Test Bench Point-Absorber Wave Energy Converter Emulator System
Abstract
1. Introduction
2. Description of Wave Energy Characteristics
2.1. Extraction of Wave Energy
Hydrodynamics of Point-Absorber WECs
3. Materials and Methodology
3.1. Emulation Technique
3.2. Experimental Setup
3.3. Logic of the Motor Rotation
3.4. Experimental Setup for the Real Point-Absorber WEC
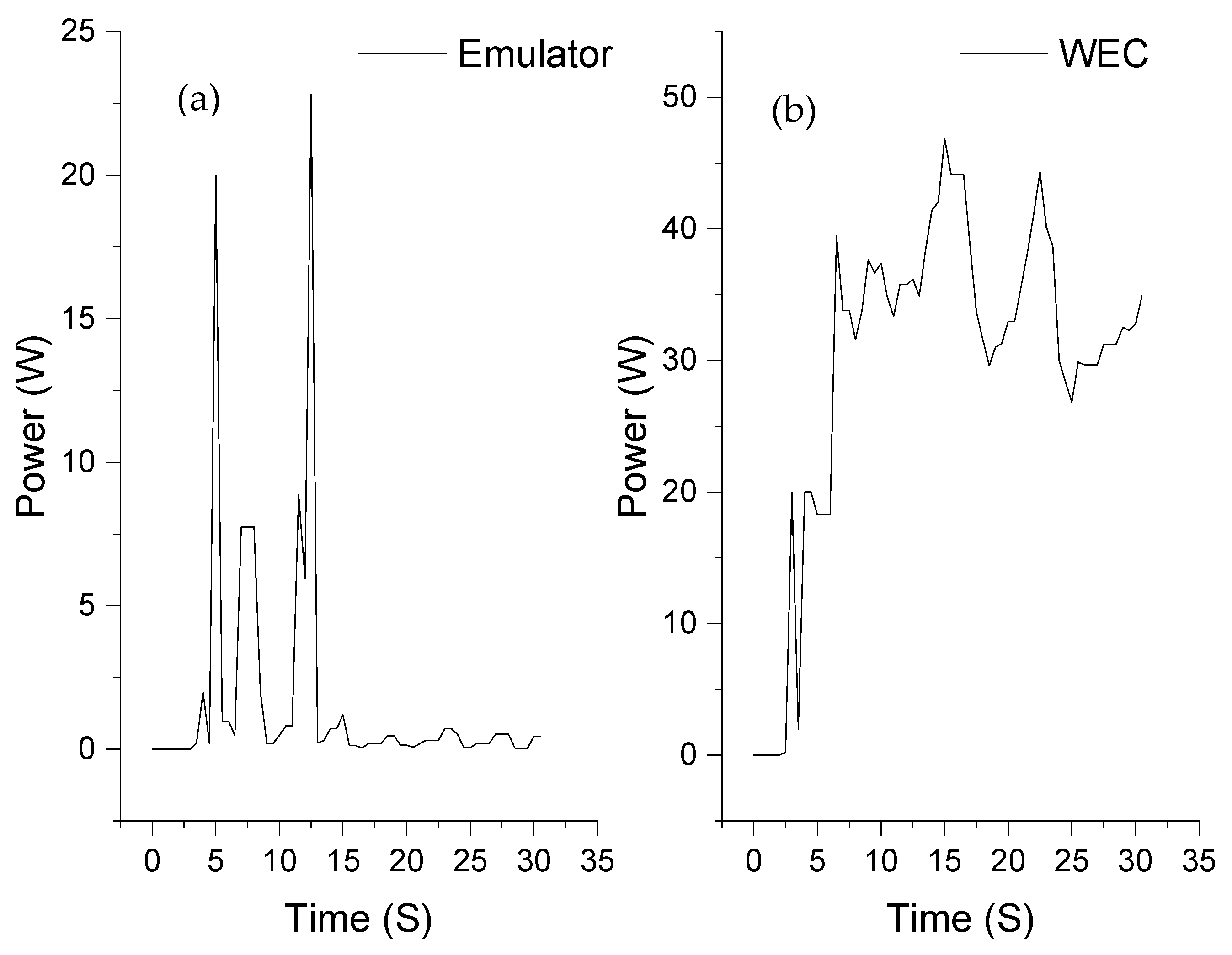
4. Results and Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agyekum, E.B. Energy poverty in energy rich Ghana: A SWOT analytical approach for the development of Ghana’s renewable energy. Sustain. Energy Technol. Assess. 2020, 40, 100760. [Google Scholar] [CrossRef]
- Agyekum, E.B. Techno-economic comparative analysis of solar photovoltaic power systems with and without storage systems in three different climatic regions, Ghana. Sustain. Energy Technol. Assess. 2021, 43, 100906. [Google Scholar] [CrossRef]
- Faraggiana, E.; Chapman, J.; Williams, A.; Masters, I. Genetic based optimisation of the design parameters for an array-on-device orbital motion wave energy converter. Ocean Eng. 2020, 218, 108251. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Velkin, V.I. Optimization and techno-economic assessment of concentrated solar power (CSP) in South-Western Africa: A case study on Ghana. Sustain. Energy Technol. Assess. 2020, 40, 100763. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Nutakor, C. Feasibility study and economic analysis of stand-alone hybrid energy system for southern Ghana. Sustain. Energy Technol. Assess. 2020, 39, 100695. [Google Scholar] [CrossRef]
- Agyekum, E.; Velkin, V.I.; Hossain, I. Sustainable energy: Is it nuclear or solar for African Countries? Case study on Ghana. Sustain. Energy Technol. Assess. 2020, 37. [Google Scholar] [CrossRef]
- Isaacs, J.D.; Castel, D.; Wick, G.L. Utilization of the energy in ocean waves. Ocean Eng. 1976, 3, 175–187. [Google Scholar] [CrossRef]
- Li, X.; Chen, C.; Li, Q.; Xu, L.; Liang, C.; Ngo, K.; Parker, R.G.; Zuo, L. A compact mechanical power take-off for wave energy converters: Design, analysis, and test verification. Appl. Energy 2020, 278, 115459. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. The economics of wave energy: A review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Akpınar, A.; Kömürcü, M.I. Assessment of wave energy resource of the Black Sea based on 15-year numerical hindcast data. Appl. Energy 2013, 101, 502–512. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Choosing the site for the first wave farm in a region: A case study in the Galician Southwest (Spain). Energy 2011, 36, 5525–5531. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Hazra, S.; Bhattacharya, S. Modeling and Emulation of a Rotating Paddle Type Wave Energy Converter. IEEE Trans. Energy Convers. 2017, 33, 594–604. [Google Scholar] [CrossRef]
- Hazra, S.; Shrivastav, A.S.; Gujarati, A.; Bhattacharya, S.; Hazra, S.; Gujarati, A.; Bhattacharya, S. Dynamic emulation of oscillating wave energy converter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 1860–1865. [Google Scholar]
- Biligiri, K.; Harpool, S.; Von Jouanne, A.; Amon, E.; Brekken, T. Grid emulator for compliance testing of Wave Energy Converters. In Proceedings of the 2014 IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 24–26 July 2014; pp. 30–34. [Google Scholar]
- Abanades, J.; Greaves, D.M.; Iglesias, G. Wave farm impact on the beach profile: A case study. Coast. Eng. 2014, 86, 36–44. [Google Scholar] [CrossRef]
- Frid, C.; Andonegi, E.; Depestele, J.; Judd, A.; Rihan, D.; Rogers, S.I.; Kenchington, E. The environmental interactions of tidal and wave energy generation devices. Environ. Impact Assess. Rev. 2012, 32, 133–139. [Google Scholar] [CrossRef]
- López, I.; Iglesias, G. Efficiency of OWC wave energy converters: A virtual laboratory. Appl. Ocean Res. 2014, 44, 63–70. [Google Scholar] [CrossRef]
- Leijon, M.; Danielsson, O.; Eriksson, M.; Thorburn, K.; Bernhoff, H.; Isberg, J.; Sundberg, J.; Ivanova, I.; Sjöstedt, E.; Ågren, O.; et al. An electrical approach to wave energy conversion. Renew. Energy 2006, 31, 1309–1319. [Google Scholar] [CrossRef]
- Portillo, J.; Collins, K.; Gomes, R.; Henriques, J.; Gato, L.; Howey, B.; Hann, M.; Greaves, D.; Falcão, A. Wave energy converter physical model design and testing: The case of floating oscillating-water-columns. Appl. Energy 2020, 278, 115638. [Google Scholar] [CrossRef]
- Têtu, A. Power Take-Off Systems for WECs. In Quantitative Monitoring of the Underwater Environment; Springer International Publishing: Cham, Switzerland, 2016; pp. 203–220. [Google Scholar] [CrossRef]
- Tongphong, W.; Kim, B.-H.; Kim, I.-C.; Lee, Y.-H. A study on the design and performance of ModuleRaft wave energy converter. Renew. Energy 2021, 163, 649–673. [Google Scholar] [CrossRef]
- Al Shami, E.; Wang, X.; Ji, X. A study of the effects of increasing the degrees of freedom of a point-absorber wave energy converter on its harvesting performance. Mech. Syst. Signal Process. 2019, 133. [Google Scholar] [CrossRef]
- Muthukumar, S.; Jayashankar, V. Micro-controller based emulation of a wave energy converter. In Proceedings of the 2011 International Conference on Emerging Trends in Electrical and Computer Technology, Nagercoil, India, 23–24 March 2011; pp. 186–189. [Google Scholar]
- Blanco, M.; Moreno-Torres, P.; Lafoz, M.; Beloqui, M.; Castiella, A. Development of a laboratory test bench for the emulation of wave energy converters. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 2487–2492. [Google Scholar]
- Hazra, S.; Kamat, P.; Shrivastav, A.; Bhattacharya, S. Emulation of oscillating wave energy converter for laboratory test bed. In Proceedings of the 3rd Marine Energy Technology Symposium, Washington, DC, USA, 27–29 April 2015; p. 8. [Google Scholar]
- Wahyudie, A.; Susilo, T.B.; Jama, M.; Mon, B.F.; Shaaref, H. Design of a double-sided permanent magnet linear generator for laboratory scale ocean wave energy converter. In Proceedings of the OCEANS 2017—Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–5. [Google Scholar]
- Duquette, J.; O’Sullivan, D.; Ceballos, S.; Alcorn, R. Design and Construction of an Experimental Wave Energy Device Emulator Test Rig. In Proceedings of the European Wave and Tidal Energy Conference, Uppsala, Sweden, 7 September 2009. [Google Scholar]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- Ilyas, A.; Kashif, S.A.; Saqib, M.A.; Asad, M.M. Wave electrical energy systems: Implementation, challenges and environmental issues. Renew. Sustain. Energy Rev. 2014, 40, 260–268. [Google Scholar] [CrossRef]
- Steinn, G. Hydrodynamic Investigation of Wave Power Buoys; KTH Royal Institute of Technology: Stockholm, Sweden, 2013. [Google Scholar]
- Yuce, M.I.; Muratoglu, A. Hydrokinetic energy conversion systems: A technology status review. Renew. Sustain. Energy Rev. 2015, 43, 72–82. [Google Scholar] [CrossRef]
- Rourke, F.O.; Boyle, F.; Reynolds, A. Marine current energy devices: Current status and possible future applications in Ireland. Renew. Sustain. Energy Rev. 2010, 14, 1026–1036. [Google Scholar] [CrossRef]
- Faizal, M.; Ahmed, M.R.; Lee, Y.-H. A Design Outline for Floating Point Absorber Wave Energy Converters. Adv. Mech. Eng. 2014, 6. [Google Scholar] [CrossRef]
- Falnes, J.; Lillebekken, P.M. Budal’s latching-controlled-buoy type wave-power plant. In Proceedings of the 5th European Wave Energy Conference; 2003; p. 12. Available online: https://core.ac.uk/download/pdf/30849835.pdf (accessed on 18 March 2021).
- Backer, G.D. Hydrodynamic Design Optimization of Wave Energy Converters Consisting of Heaving Point Absorbers; Ghent University: Ghent, Belgium, 2009. [Google Scholar]
- Al Shami, E.; Zhang, R.; Wang, X. Point Absorber Wave Energy Harvesters: A Review of Recent Developments. Energies 2018, 12, 47. [Google Scholar] [CrossRef]
- Sjökvist, L.; Göteman, M.; Rahm, M.; Waters, R.; Svensson, O.; Strömstedt, E.; Leijon, M. Calculating buoy response for a wave energy converter—A comparison of two computational methods and experimental results. Theor. Appl. Mech. Lett. 2017, 7, 164–168. [Google Scholar] [CrossRef]
- Falnes, J. On non-causal impulse response functions related to propagating water waves. Appl. Ocean Res. 1995, 17, 379–389. [Google Scholar] [CrossRef]
- Urbikain, G.; De Lacalle, L.L.; Campa, F.; Fernández, A.; Elías, A. Stability prediction in straight turning of a flexible workpiece by collocation method. Int. J. Mach. Tools Manuf. 2012, 54-55, 73–81. [Google Scholar] [CrossRef]
- Hai, L.; Svensson, O.; Isberg, J.; Leijon, M. Modelling a point absorbing wave energy converter by the equivalent electric circuit theory: A feasibility study. J. Appl. Phys. 2015, 117, 164901. [Google Scholar] [CrossRef]
- Aubry, J.; Ben Ahmed, H.; Multon, B.; Babarit, A.; Clément, A. Wave Energy Converters. In Marine Renewable Energy Handbook; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 323–366. [Google Scholar]
- Hossain, I.; Velkin, V.I.; Shcheklein, S.E.; Eliseev, A.V. Structural Design Development of a Float Type Wave Micro Power Plant. IOP Conf. Ser. Mater. Sci. Eng. 2019, 481, 012007. [Google Scholar] [CrossRef]
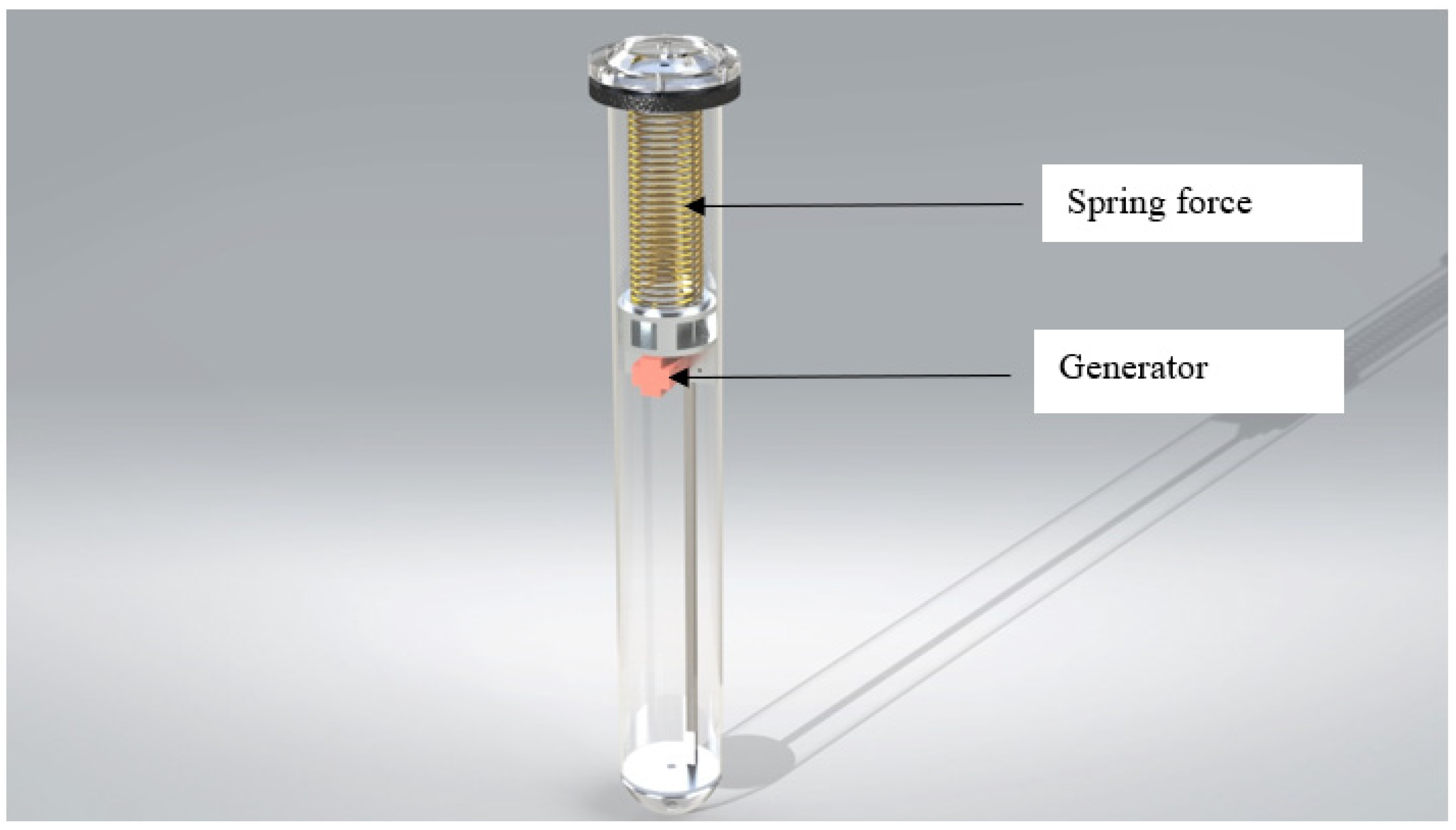
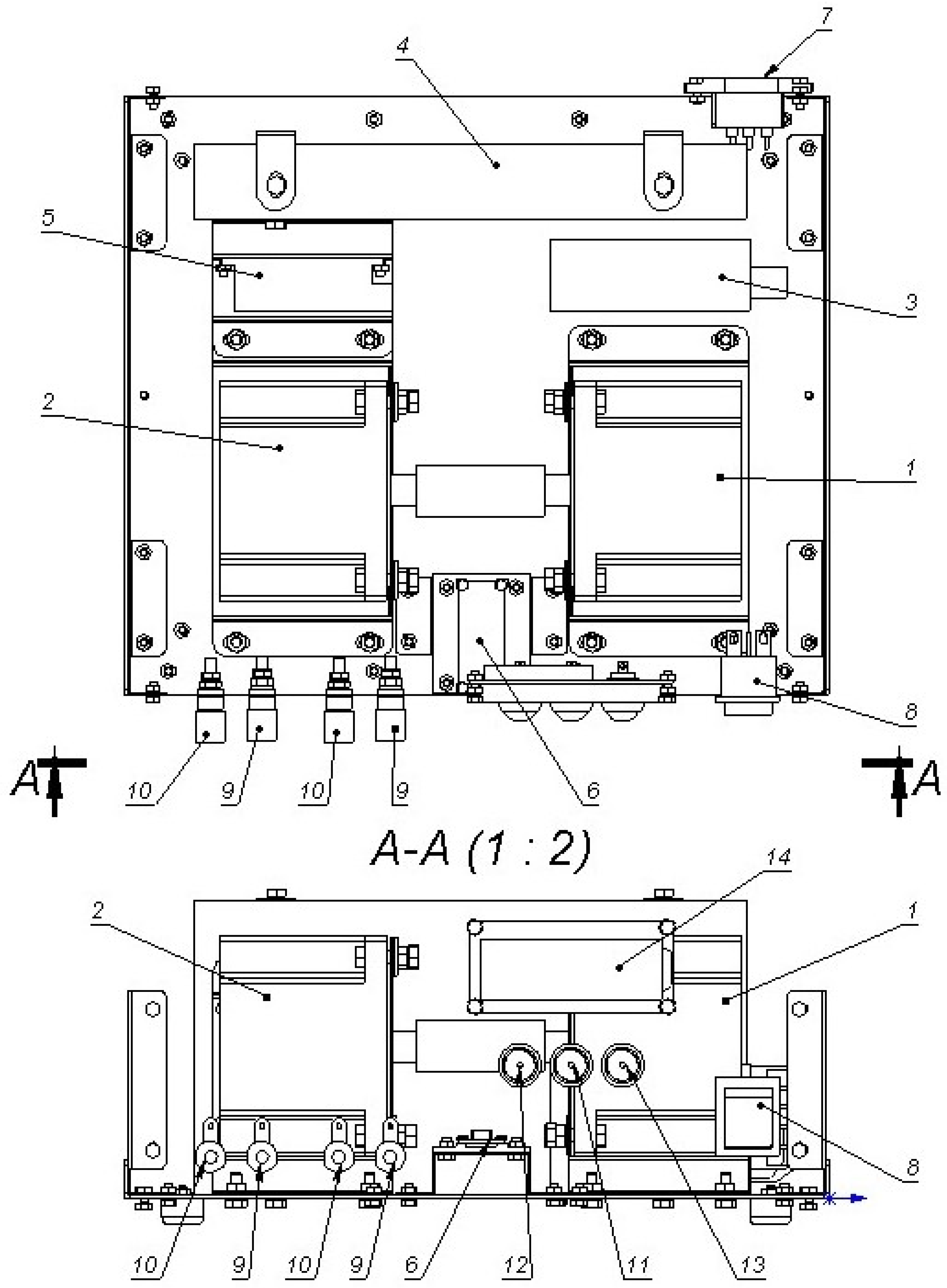





| Number | Designation | Quantity |
|---|---|---|
| 1 | Lead stepper motor | 1 |
| 2 | Driven stepper motor | 1 |
| 3 | RS-25 power supply | 1 |
| 4 | Power supply LRS-350-48 | 1 |
| 5 | G210 Driver | 1 |
| 6 | Arduino Nano | 1 |
| 7 | Network socket C14 on REX ANT housing | 1 |
| 8 | Rocker switch 250 V 16 A | 1 |
| 9 | Panel socket 10-0019 red | 2 |
| 10 | Panel socket 10-0019 black | 2 |
| 11 | Switch-push button 250 V 1 A yellow | 1 |
| 12 | Switch-push button 250 V 1 A green | 1 |
| 13 | Switch-push button 250 V 1 A blue | 1 |
| 14 | Liquid-crystal display (LCD) | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agyekum, E.B.; PraveenKumar, S.; Eliseev, A.; Velkin, V.I. Design and Construction of a Novel Simple and Low-Cost Test Bench Point-Absorber Wave Energy Converter Emulator System. Inventions 2021, 6, 20. https://doi.org/10.3390/inventions6010020
Agyekum EB, PraveenKumar S, Eliseev A, Velkin VI. Design and Construction of a Novel Simple and Low-Cost Test Bench Point-Absorber Wave Energy Converter Emulator System. Inventions. 2021; 6(1):20. https://doi.org/10.3390/inventions6010020
Chicago/Turabian StyleAgyekum, Ephraim Bonah, Seepana PraveenKumar, Aleksei Eliseev, and Vladimir Ivanovich Velkin. 2021. "Design and Construction of a Novel Simple and Low-Cost Test Bench Point-Absorber Wave Energy Converter Emulator System" Inventions 6, no. 1: 20. https://doi.org/10.3390/inventions6010020
APA StyleAgyekum, E. B., PraveenKumar, S., Eliseev, A., & Velkin, V. I. (2021). Design and Construction of a Novel Simple and Low-Cost Test Bench Point-Absorber Wave Energy Converter Emulator System. Inventions, 6(1), 20. https://doi.org/10.3390/inventions6010020







