Analysis of Firefly–Fuzzy Hybrid Algorithm for Navigation of Quad-Rotor Unmanned Aerial Vehicle

Abstract

In the present scenario for the development of the unmanned aerial vehicle (UAV), artificial intelligence plays an important role in path planning and obstacle detection. Due to different environments, it is always a task to achieve the proper moment for achieving the target goal while avoiding obstacles with minimum human interference. To achieve the goal with the avoidance of obstacles, individual optimization techniques with metaheuristic algorithms such as fuzzy, particle swarm optimization (PSO), etc. were implemented in various configurations. However, the optimal solution was not attained. Thus, in order to achieve an optimal solution, a hybrid model was developed by using the firefly algorithm and the fuzzy algorithm, establishing multiple features of the individual controller. The path and time optimization were achieved by a standalone controller and a hybrid firefly–fuzzy controller in different conditions, whereby the results of the controller were validated by simulation and experimental results, highlighting the advantages of the hybrid controller over the single controller.

1. Introduction

Over the most recent couple of decades, the utilization of multicopters has generally been considered in military and civil purpose settings with different kinds of uses such as surveillance, target-based missions, mapping and weather forecasting, etc. As unmanned aerial vehicles (UAVs) have to follow a defined path, path planning or navigation is an important parameter of UAVs, which allows them to perform intelligently and compute the shortest optimum flight path between an initial position and an end checking point, to fulfill their missions with specific constraints such as path length, obstacle avoidance, etc., as path planning is also related to obstacle avoidance. Path planning process development has undergone rapid growth in recent years and the problem has been solved especially with the help of various advancements in genetic and metaheuristic algorithms happening in recent days, such as the ant colony advance algorithm, swarm intelligence, firefly, simulated annealing, etc.

Many genetic or metaheuristic algorithms provide an optimal solution such as swarm intelligence, which gives results inspired from observing the behavior of swarms of animals, for example ants, bees, glowworms, etc., to get more complex results. An inspirational swarm intelligence algorithm that was inspired by the behavior of ant colonies for solving combinatorial optimization problems is ant colony optimization (ACO), which provides optimal results for a virtual environment. ACO works cooperatively to reach the optimal solution to a problem on the basis of virtual colonies of artificial ants. A property of communication with other ants through pheromone trails is adopted in this algorithm. A tracking hybrid controller for UAVs was developed using an adaptive neuro-fuzzy inference system (ANFIS) and particle swarm optimization (PSO) algorithm. This hybrid controller gave good results compared to an individual algorithm-based controller for a quadrotor UAV [1]. Sarthi et al. [2] developed the bio-inspired metaheuristic approach named antlion optimization for local searching on the basis of total routing distance.

Fuzzy algorithm has been evolved in the path optimization of UAVs but the limited possibilities have been analyzed. For the control of a multicopter with a conceivable solution, the latest evolving fuzzy controllers were reviewed [3].

The firefly algorithm is a very well-known metaheuristic algorithm developed by Yang [4] and was inspired by the flashing behavior of fireflies. It is stochastic in nature as it follows the randomness of the environment and it works on the principles of trial and error for finding the optimal solution in a realistic amount of time. In one study, the firefly algorithm was a hybrid with particle swarm optimization for solving continuous optimization problems [5].

The study presented here was designed with a firefly and fuzzy-based optimal solution for path planning of a quadrotor UAV in an unstructured environment. We found that, despite many researchers exploring the navigation of robots using genetic algorithms, there was a lack of results available for quadcopters. On the other hand, many studies have explored the optimal solutions for the navigation of unmanned aerial vehicles (multicopters) using genetic algorithms, or other techniques which have been presented in static and dynamic environments [6,7,8,9].

A hybrid algorithm was developed for the application of the firefly algorithm with an artificial bee colony for the enhancement of optimized values by minimizing the randomness in each step [10].

The research discussed above outlined the application of various algorithms with specific configurations for path planning and obstacle detection. The problem of trajectory optimization of multirotors was stated by Pradeep et.al. [11] as follows: in attaining the goal of path planning, certain obstacles that are dynamic in nature often present themselves, thus algorithms should be good enough to overcome the dynamic obstacles presented by many researchers investigating navigation [12,13].

Path planning for a unmanned combat aerial vehicle was optimized by using various algorithms like firefly and modified firefly [14], as well as a fuzzy hybrid scheme consisting of a fuzzy logic controller and a regulation pole-placement tracking (RST) controller with a model reference adaptive control (MRAC), in which the adaptive gains of the RST controller were fine-tuned by a fuzzy logic controller and done on a trimotor [15]. However, no studies have investigated hybridization of the firefly and fuzzy algorithms.

In order to hybridize the firefly algorithm (FFA) and the fuzzy logic (FL) for an efficient controller, the FFA was used as an initial filter, while the FL was used as a secondary filter. This was done because fuzzy logic uses a gradient-based algorithm which reduces the performance and results in low convergence rates when using training parameters. This limitation of the gradient method is minimized when using the FFA. The FFA with least squares estimation was used to train the initial parameters, thereby providing optimal results. The FFA provides a well-trained parameter to the controller to achieve tasks with few errors. The FFA is a metaheuristic algorithm influenced by the behavior of fireflies, hence its conversion rate is higher than others when solving a high-level optimization problem.

In this paper, a new firefly–fuzzy-based hybrid approach for navigational properties such as path planning and obstacle avoidance for a quadcopter in a various static and dynamic environments was analyzed and compared to a standalone controller. A comparison of path length and time was done for both the standalone controller and the hybrid controller. Section 2 describes the input parameters of the hybrid algorithm in different environments. The FFA and the FL are described in Section 3 and Section 4. In Section 5, simulation and experimental analyses are carried out on the results of the standalone and the hybrid algorithms. In Section 6, the results and conclusions are presented.

2. Firefly Mechanism (FFA)

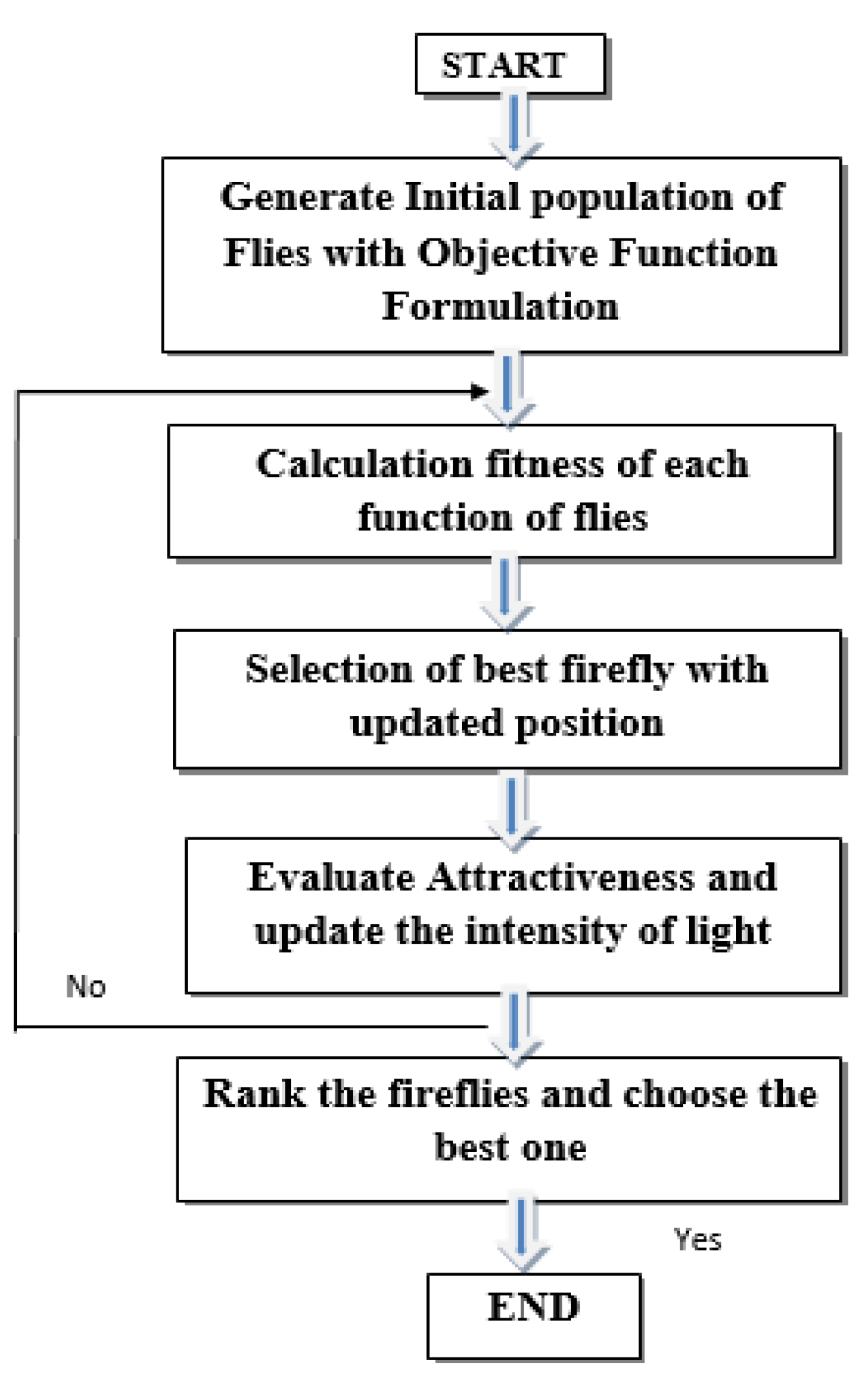
The firefly algorithm is a genetic algorithm that was inspired by the nature of fireflies and was created by Yang in the year 2008. This algorithm provides optimal solutions based on the flashing behavior of flies. Different optimization problems are solved through the nature-based technique in which the fireflies generate light, usually at night, by the property of bioluminescence (energy released by chemical reactions).

The light generated is used by the flies to protect them from enemies, as well as to communicate with other flies for selecting their mates. From the flashing light, the flashing intensity and amount of flashing time are observed as the important parameters for the algorithm. The objective function to optimize the algorithm is developed from the light of fireflies. The FFA is analyzed by the intensity of light created by the fireflies, which should be unique in order to attract each other. The algorithm follows different rules, where the first rule states the attraction of flies and depends on the genders of the flies, and in order to get optimal results all flies should be unisex. In the second rule, the flies will be attracted to each other with their intensity of light. In the third rule, the intensity of light (brightness) of the fireflies is decided. The FFA is presented in the form of the flowchart in Figure 1.

In the FFA, β, α and γ are the parameters denoting attractiveness, randomization, and light absorption coefficient respectively. The positions of the first and second fireflies are denoted by x_i and x_j. The iteration and the random number of the flies are denoted by r and t. The distance between two flies is denoted by d and the value of the firefly in the K^th dimension is given by x_i^k.

A comparison of the attractiveness of the fireflies (i.e., low bright fly and high bright fly) is given by Equation (1).

$$\beta (r)={\beta }_0\exp (-\gamma r^m);m\ge 1$$

(1)

Two fireflies are approximated with the distance given below in Equation (2).

$$r_{ij}=\Vert x_i-x_j\Vert =\sqrt{{\displaystyle \sum _{k=1}^d{(x_i^k-x_j^k)}^2}}$$

(2)

The attraction of the fireflies towards each other is calculated by Equation (3).

$$x_i^k(t+1)=x_i^k(t)+{\beta }_0\exp (-\gamma r_{ij}{}^2)((x_j^k(t)-x_i^k(t))+\alpha (r-\frac{1}{2})$$

(3)

3. Basic Fuzzy-Logic Mechanism

Fuzzy logic methods were developed by Lotfi Zadeh in the year 1965 [16], and act like a mechanism based on human decisions. Fuzzy logic refers to the various factors that are unclear and it gives a real-world representation by its if–then, rule-based mechanism. Its process depends on inexact and partial data for different problems. Fuzzy logic models complex data problems with maximum uncertainty to the linear one. The basic fuzzy inference model is explained in the flowchart Figure 2.

Key steps for the fuzzy logic mechanism are given as follows:

• Fuzzification: Input variables are converted by a membership function.
• Inference and Aggregation: Final output by fuzzy-based rules.
• Defuzzification: Crisp value conversion from fuzzified output.

3.1. Fuzzy Inference

For mapping the sensory input data with the output variable, the if–then rule is used which also has the base for its decision making. Let the collection of objects (x) denoted by X and x be the known ordered pair for fuzzy set A.

$$A=\{(x,\mu A(x)\in X\}$$

(4)

From Equation (4), $\mu A(x)$ states the fuzzy membership function provided for set A. However, the membership values used to measure x will be 0 to 1. In fuzzy logic the problem is solved by two types of membership function, i.e., trapezoidal and triangular.

The triangular membership function is stated as

$$Triangle(x,p,q,r)=\{\begin{array}{c}0,x<p\\ \frac{x-p}{q-p},p\le x\le q\\ \frac{r-x}{r-q},q\le x\le r\\ 0,r\le X\end{array}$$

(5)

As per the principle of maxima and minima, Equation (5) can be represented by

$$\mathrm{Triangle} (\mathrm{x},\mathrm{p},\mathrm{q},\mathrm{r}) = \max .(\min .\{\frac{x-p}{q-p}, \frac{r-x}{r-q}\}, 0)$$

(6)

Similarly, the trapezoidal membership function can be specified by using the four-parameter {p,q,r,s} as represented in Equation (7).

$$trapezoid\left(x;p,q,r,s\right)=\{\begin{array}{c}0,x<p\\ \begin{array}{l}\frac{x-p}{q-p},p\le x\le q\\ 1,q\le x\le r\end{array}\\ \frac{s-x}{s-r},r\le x\le s\\ 0,s\le X.\end{array}$$

(7)

By using a minimum and a maximum, the above equation can also be represented by the following equation:

$$trapezoid(x;p,q,r,s)=\max .(\min .\left(\frac{x-p}{q-p},1,\frac{s-x}{s-r}\right),0)$$

(8)

where (p,q,r,s) determines the value of the x-coordinates (with p < q < r < s) of the corners of the defuzzification–trapezoidal membership function.

3.2. Defuzzification

Defuzzification is mathematically represented as in the equation given below, which works on the center of gravity concept and converts the fuzzy set into a crisp value.

$${\mathsf{\mu }}^{crisp}= \frac{{\sum }_i{b}_i\int {\mu }_i}{{\sum }_i{\int }^{ }{\mu }_i}$$

(9)

Here the crisp value output is defined by μ^crisp and the center of the membership function is given by b_i. Consequently, rule i and ${{\displaystyle \mathsf{\mu }}}_{\left(\mathrm{i}\right)}$ give the area under the membership function.

4. Proposed Hybrid Firefly–Fuzzy Controller

The firefly–fuzzy controller is a hybrid controller using firefly and fuzzy mechanisms for optimizing different parameters such as quadcopter to obstacle distance, quadcopter to goal distance, and mutual distance between the quadcopter with its motion. All these navigational parameters are defined in the controller to provide the necessary turning angle for the quadcopter. In Section 2, it was shown that the firefly algorithm gets optimal parameters from the system. 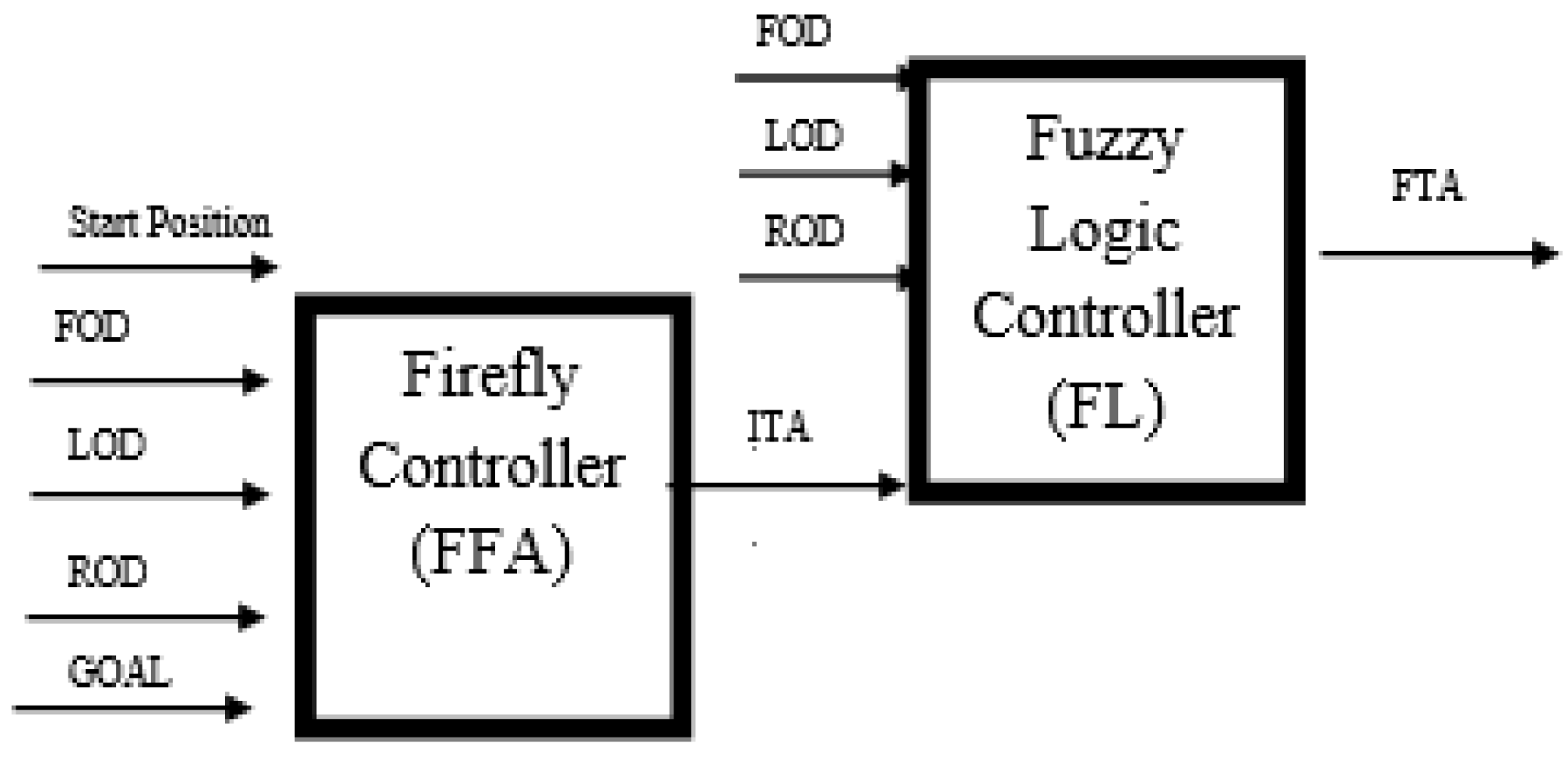Figure 3 describes the model of the firefly–fuzzy hybrid controller for the calculation of the required parameters for path planning of the quadcopter.

In the first part, front obstacle distance (FOD), left obstacle distance (LOD), and right obstacle distance (ROD) are the input parameters provided to the firefly controller (FFA), whereas intermediate turning angle (ITA) is the output of the FFA. This output ITA stated by FFA controller, will be the input for the fuzzy logic controller and the existing position of the quadcopter including FOD, LOD, and ROD will also be its input parameters for FL controller as shown in Figure 4. For the detection of these parameters (FOD, LOD, ROD), the quadcopter is fitted with IR sensors which are connected to an Arduino board, and these sensors also detect the position of the given goal.

The input from the FFA controller will be considered by the fuzzy controller as a hybrid controller, whereas its obstacle would be given to the ITA. The ITA is used to train the final turning angle (FTA) for all conditions. For the performance of the multicopter in a real-time environment, a quadcopter is used, which is embedded with a microcontroller.

Sensors are equipped to calculate the distance of the quadcopter from obstacle to goal, as the initial input or the information to be provided first for the environment plays an important role in the objective function selection parameter. In the FFA approach, the efficient position of the firefly with respect to its group will be decided by the position of the obstacle which is nearest, and those flies which have a safe distance from the obstacle. These flies update its position until it clears all the obstacles.

The distance between the best firefly with respect to its obstacle is given in Equation (10) and this distance is known as Euclidean distance.

$$D_{fo}= \sqrt{{\left(x_o-x_{f1}\right)}^2+{\left(y_o-y_{f1}\right)}^2}$$

(10)

Here, D_fo = Euclidean distance (firefly to nearest obstacle); x_fi and x_o = x are the firefly position and obstacle respectively; y_fi and y_o = y are the firefly position and obstacle respectively.

D_RO is the distance between the nearest obstacle and the quadcopter. In a complex environment it is necessary to select the nearest obstacle and this distance is calculated by the equation given below.

$$D_{RO}= \sqrt{{\left(x_O-x_R\right)}^2+{\left(y_O-y_R\right)}^2}$$

(11)

X_on and x_R = x are the obstacle position and quadcopter position respectively and y_on and y_R = y are the firefly position and obstacle respectively.

The selection of the best fly among the group of flies will be considered with different parameters. According to the first parameter, the brighter fly will have a maximum distance from an obstacle and the second parameter will be that at the same time the brighter fly will be nearer to the goal. This system will continue until it reaches the goal by successfully avoiding all the obstacles. The distance from the quadcopter to the final position is calculated as the Euclidean distance (D_fg) and is formulated as

$$D_{fe}= \sqrt{{\left(x_e-x_{f1}\right)}^2+{\left(y_e-y_{f1}\right)}^2}$$

(12)

where x and y are the positions of the goal.

The final objective function of the FFA is given as

$$f_1= K_i \frac{1}{min{o}_n \in o_s \parallel D_{fo}\parallel }+ K_2 \parallel D_{fg}\parallel$$

(13)

For getting an optimal solution by using the objective function, the parameters α, β, and γ are tested variably. After testing the parameters for many trials, the best values obtained are given as α = 0.5, β = 0.2, and γ = 0.5.

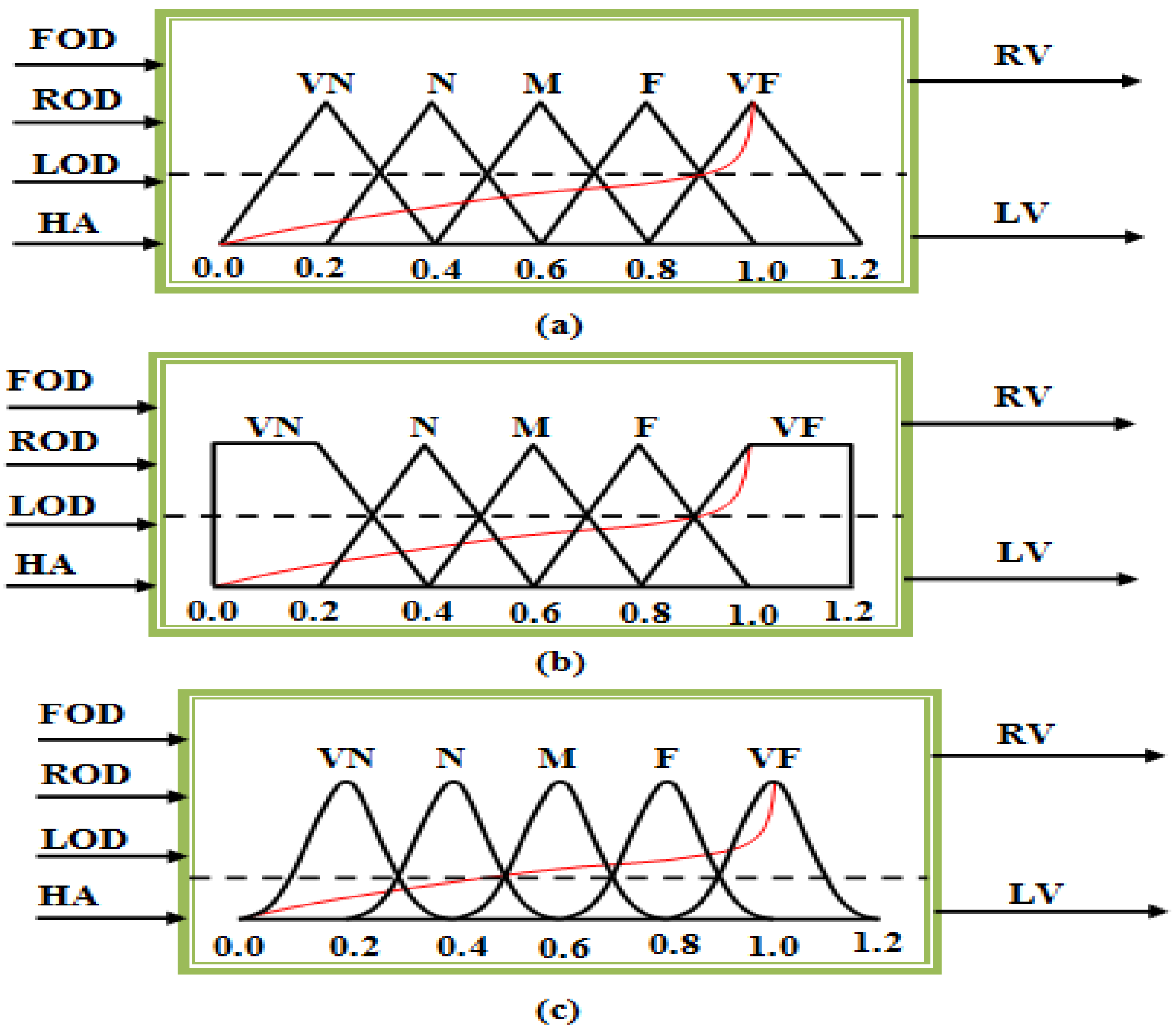
Fuzzy logic is also known as a universal approximator and it can do the mapping of sensory data and output variables. The terms given for various parameters are stated in Figure 5.

The final output in terms of turning angle (TA) is stated by more negative, negative, zero, positive, and more positive respectively as shown in

Table 1. Few Fuzzy logic rules for navigation of the quadcopter.

Sl. No.	FOD	LOD	ROD	TA	LV	RV
1	N	N	F	Positive	Slow	Fast
2	M	N	F	Zero	Medium	Medium
3	F	N	F	Negative	fast	Slow
4	N	N	M	Positive	Slow	Fast
5	M	N	M	Zero	Medium	Medium
6	F	N	M	Negative	fast	Slow
7	N	N	N	Positive	Slow	Fast
8	M	N	N	Zero	Medium	Medium
9	F	N	N	Negative	fast	Slow
10	N	M	F	Positive	Slow	Fast

. By the fuzzy logic mechanism, the if–then function is used when the obstacle is in the way of the quadcopter and when there is no obstacle the fuzzy mechanism will not be activated as described in

Table 2. Fuzzy logic parameters (obstacle).

Linguistic Variable	Very Near (VN)	Near (N)	Medium (M)	Far (F)	Very Far (VF)
LOD	0.0	0.2	0.4	0.6	0.8
ROD	0.0	0.2	0.4	0.6	0.8
FOD	0.4	0.6	0.8	1.0	1.2

and

Table 3. Fuzzy logic parameters (Turning angle).

Linguistic Variable	More Negative (MN)	Negative (N)	Zero (Z)	Positive (P)	More Positive (MP)
Target Turning Angle	−180	−120	−10	10	60
	−120	−60	0.0	60	120
	−60	0	10	120	180

. Triangular, triangular–trapezoidal and Gaussian membership functions are presented in Figure 6.

5. Analysis of Firefly–Fuzzy Hybrid Controller

The hybrid controller was tested by experimental work which was validated by simulation through MATLAB software, for the experimental work quadcopter having an Arduino board as a flight controller with six IR sensors fitted around its periphery. The coding of Arduino was done using embedded C and navigation in a realtime environment is shown in Figure 7 and Figure 8.

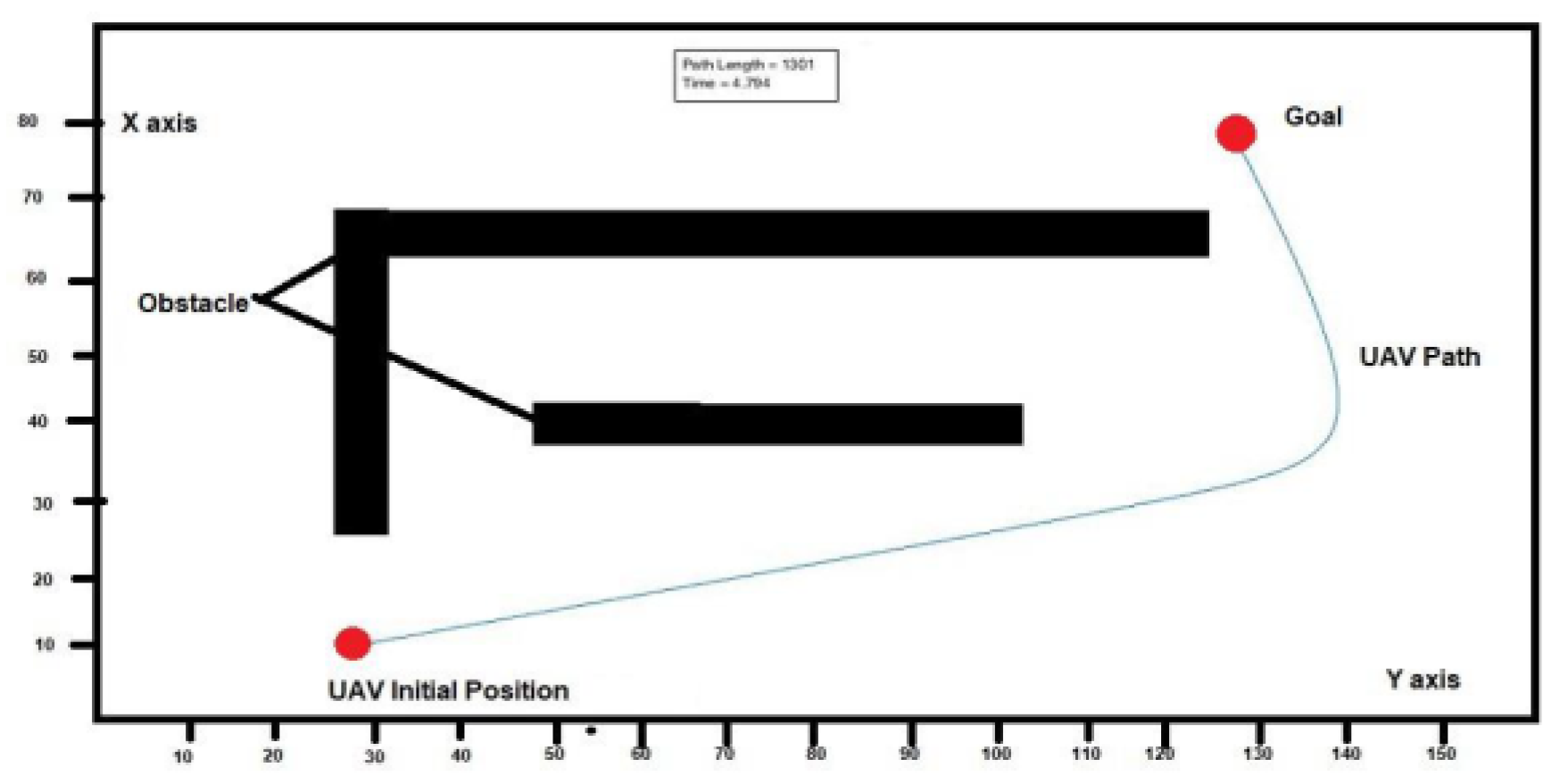
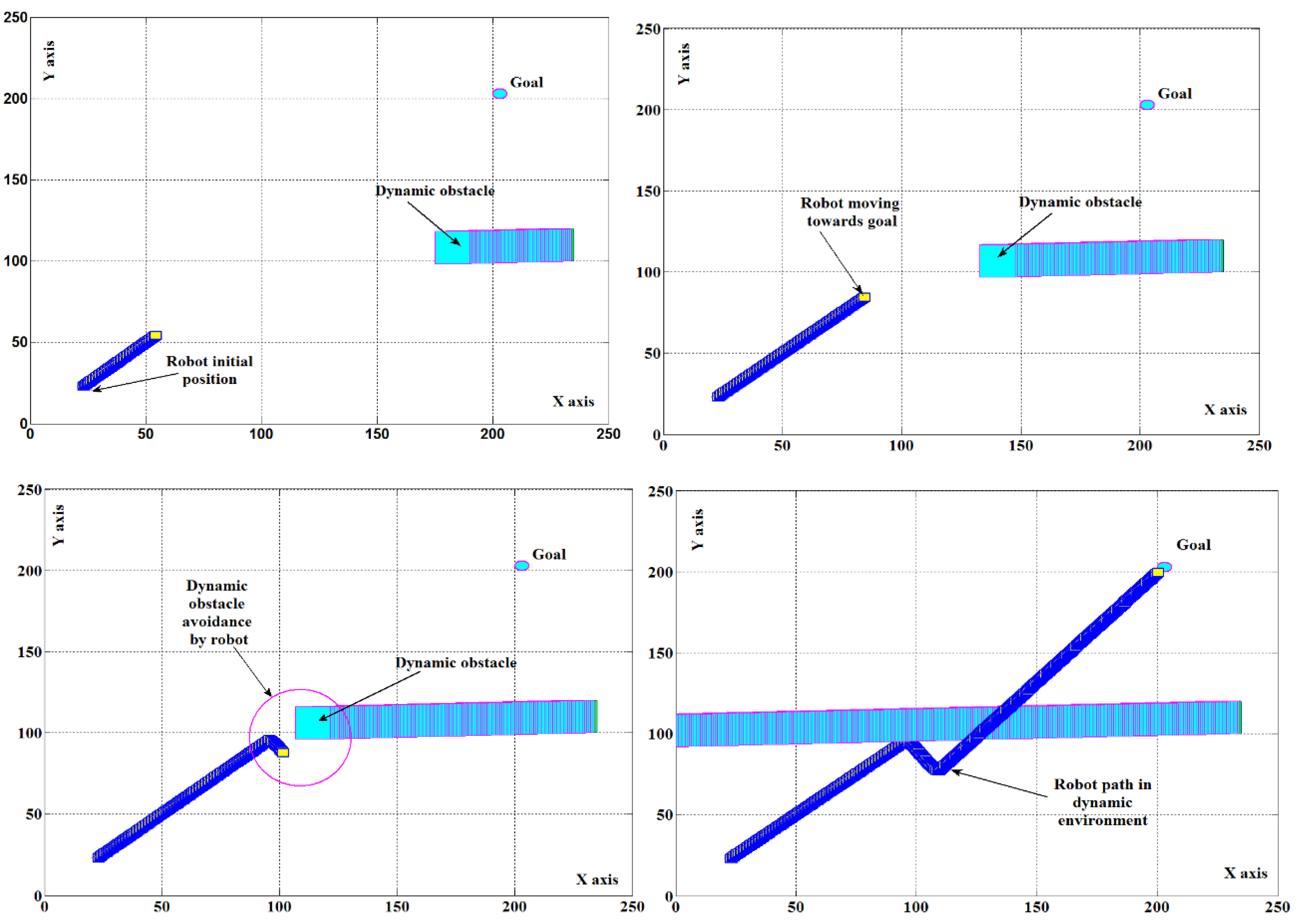
For the simulation, MATLAB software was used and results were generated for both static and dynamic obstacles in different environmental conditions. Navigation using three controllers was used and the output was taken, which is shown in Figure 9, Figure 10 and Figure 11, and similarly, the analysis of dynamic obstacles was simulated in MATLAB and the results are shown in Figure 12.

In the case of a dynamic environment, the hybrid controller was tested under a moving obstacle as shown in Figure 12. For validation of the results, the hybrid firefly–fuzzy controller was compared with standalone firefly and standalone fuzzy controllers with the same environment in both simulation and experimental cases. These results are presented over its path length and navigational time as shown in Figure 13 and Figure 14.

Table 4. Path length comparison over similar environmental setup.

Sl. No.	Controller	Experimental Path Length (in ‘cm’)	Simulational Path Length (in ‘cm’)	% of Deviation
1	FFA	684.04	650.77	5.11
2	FL	633.27	605.17	4.64
3	FFA-FL	602.92	577.13	4.71

and

Table 5. Navigational time comparison over similar environmental setup.

Sl. No.	Controller	Experimental Time (in ‘sec’)	Simulational Time (in ‘sec’)	% of Deviation
1	FFA	33.98	29.90	5.56
2	FL	32.23	30.73	4.63
3	FFA-FL	26.57	25.30	4.77

provide the optimal values of all the three controllers tested over 10 runs.

6. Conclusions and Future Scope

In this investigation, for both experiment and simulation it was found that there are more possible ways for developing controllers that provide optimal results, which has been proved in this paper through the successful testing of a firefly–fuzzy-based new controller for navigation of a quadcopter in the stated environment with a static or dynamic obstacle. The results in Section 5 show that the deviation is less than 6%. The navigational time required to accomplish the task in simulation and in the experimental environment with the hybrid firefly–fuzzy algorithm was less when compared to standalone controllers. The simulation and experimental results show that the path obtained by the hybrid controller had optimal results compared to a standalone controller for both static and dynamic environments. Making the firefly controller an initial filter provides a key feature to get the optimal values because it can easily train and update its parameters and do calculations in each step.

In future work, more metaheuristic or genetic algorithms like a blue whale, antlion, grey wolf, etc. can be tested for more optimal results. In this investigation, the FFA and the FL were used for hybridization, so further studies with more genetic algorithms used for hybridization could give better results. In this study, experimental work was carried out with a static obstacle, so for future work the model could be tested for dynamic obstacles experimentally. This hybrid controller could be tested in robots, underwater drones or any unmanned autonomous vehicle.