1. Introduction
Sustainable development of contemporary power system towards systems based on renewable energy sources (RES) requires facing some problems. These problems are mainly related to the inherent difficulty in predicting the availability of RES at a given time. This problem is made more difficult with the time-variation of the load and volatility of energy prices on the wholesale markets. One of the key aspects of reliable operation of the power system is proper planning of the supply versus demand, which, due to the RES generation uncertainty, becomes a struggle for responsible entities. The inaccuracy, of for instance wind generation forecasts, entails consequences of two primary natures: (i) technical—divergence of the forecasts around planned RES generation which impedes the transmission system operators’ (TSOs) ability to properly and accurately plan the fulfilment of actual demand by available power capacity; and (ii) economical—the uncertainty of the total forecasted wind power supply translates into the uncertainty of the day-ahead and balancing market prices, which can result in financial losses of the market participants.
This study will examine the economic aspect identified above. Wind power variability influences the wholesale market price. This considerable impact is caused by the relatively low marginal cost of the energy from wind farms, because wind energy is not burdened with fuels costs. Therefore, an injection of the wind energy, featured by the lowest unit cost, shifts the supply-demand curve to the right, which results in a reduction of the market prices.
In the literature, numerous publications can be found which support the hypothesis that the wind energy forecast is a valuable input in wholesale market price forecasting. Moreover, a wide range of mathematical models have been developed as well (e.g., [
1,
2,
3])—however, their universalism has not been tested on divergent market environments, such as Polish and Portuguese ones.
The abovementioned concerns have led to the statement of several research problems which are addressed by this paper. The main contributions of the research are the following:
The quality of overall wind power forecasts in Poland and Portugal, as well as distinguishing the most relevant features of the forecasting errors. To address this issue, an evaluation of the wind power prognoses will be made using statistical measures, which will give a quantitative picture of the accuracy, characteristics and tendencies observed. The comparison of obtained statistic description for both countries will allow to distinguish the main differences between the forecasts and point out the main sources of uncertainty.
The cost of inaccurate wind power forecasting globally from the perspective of wind power producers in both countries. This is accomplished by using market and wind generation data available for both countries to calculate the financial loss from inaccurate wind power predictions. This will illustrate the range and importance of appropriate and accurate wind generation forecasts.
The extent to which the information on expected wind generation improves the accuracy of the wholesale market prices forecasts in both examined countries. The verification of whether wind generation has an impact in predicting market prices requires developing mathematical models. For this study, the four models commonly used in dealing with spot market prices time series will be approached: ARMA—auto-regressive moving average; ARMAX—auto-regressive moving average with exogenous inputs; NAR—non-linear auto-regressive neural network and NARX—non-linear auto-regressive with exogenous inputs neural network. The modelling process will be carried out independently using data from Polish and Portuguese systems. This will evaluate if the inclusion of wind generation data improves the spot prices predictions in both countries, and examine if a given model can be successfully applied for the data coming from diametrically different power and market systems.
The current stage of wind energy development in Poland and Portugal is comparable. Citing the Portuguese TSO, at the end of 2019, the installed onshore wind power capacity accounted for about 5.2 GW, while, in Poland, according to the state’s Energy Regulatory Office, 2019 ended with 5.9 GW of wind power connected to the power system. So far, none of the countries has offshore wind installed capacity. After years of substantial and steady growth, in both cases, a plateau has been observed from 2016 onwards, and increases of installed power year to year are reaching no more than several dozens of MW. With regard to offshore wind power, both in Poland and in Portugal, no energy has been generated as of the end of 2019. In Portugal, a pre-commercial 25 MW offshore wind park using an innovative floating technology is being currently installed in deep waters. Though in Poland no construction works have been initiated yet, the special zone on the Baltic sea has been delimited, in order to develop offshore wind power of over 7 GW in the coming years.
The main objective of the study is to quantitatively evaluate the applicability of selected electricity price forecasting time series models in different datasets corresponding to Poland and Portugal market electricity prices. Moreover, we have verified the usefulness of wind power forecast as supplementary explaining variables of the models.
In the literature review concerning this research, a wide range of studies concerning the predictions of wind energy as well as spot market prices has been found. Although, usually, in the collected publications, a focus was put only on a single case of particular power system/power market. To the best knowledge of the authors, a multi-subject study has not been performed to reveal whether a given forecasting methodology applies to the separate cases of different national market environments, such as in Poland and Portugal. Although the Polish and Portuguese wind power capacity in the system is similar in amount when considering the share of this kind of energy the differences are substantial.
The main innovation of the paper is the use of the same methodology to analyse the influence of wind power forecasts in the market electricity prices of two differently conditioned power systems (Portugal and Poland), with a set of distinguishing features. This is accomplished by using a single data source, therefore making the comparison results robust and fully comparable.
The paper is organised as follows. To introduce the reader to the context of the abovementioned problems,
Section 2 is devoted to the state-of-the-art research on the topics of wind power and spot market prices forecasting, together with particular focus on their interrelation. An overview of Portuguese and Polish RES sector and energy exchange institutions is offered in
Section 3. Moreover, a description of the methodologies applied in solving the research problems stated in the introduction, including the basic statistical measures for dealing with forecasting error analysis and fundamentals of time series models constructed in terms of this study is presented in
Section 4. In
Section 5, the study results will be displayed, beginning from the statistical description of the wind generation forecasts error for Portugal and Poland, and related potential penalties suffered by the wind power producer globally. Finally, the spot prices forecasting results will be presented for the developed time-series models, with their comparative evaluation. At the end of this paper, the most significant findings will be highlighted in
Section 6.
2. State-of-the-Art Review
Contemporarily, when the electricity is traded on wholesale markets, the uncertainty regarding the amount of wind energy supplied to the system has a direct influence on the market prices. Every excess or deficiency of energy in the system has a consequence in the financial outcomes of energy suppliers/receivers [
1]. This elaboration concerns the two crucial problems in sustaining modern power systems, being a subject of intensive research within last decades, which are wind power forecasting (WPF) and electricity price forecasting (EPF). The increasing share of wind energy in the power systems, together with the tendency for equalisation of wind power producers with all the remaining electricity market participants, leads to the enhancement of the interaction between the WPF and EPF.
The impact of increased wind power penetration in power grid on the market player’s behaviour and their decisions has been studied by Usaola (2008), who estimated that the uncertainty of wind power supplied to the system leads to significant reduction of the energy producers revenues, reaching 10% of maximum obtainable revenue [
1].
The same finding has been obtained by Crespo-Vasquez et al. (2017), who constructed a decision-making model of the windfarm owner which underlined the loss of incomes resulting from the uncertainty of wind power output—in this case, the losses constituting 4% of the total earnings [
4].
The analysed publications indicate that the improvement of WPF is crucial from the perspective of increasing the effectiveness of market actions taken by its contributors [
1,
2,
4]. It also should be pointed out that the uncertainty of the energy produced in a system has not only negative consequences. The presence of the day-ahead market, as well as the balancing market, may allow members to increase their revenues, who may speculate the prices and gain profits only from buying/selling the energy depending on the market or imbalance prices [
1].
A comprehensive and condensed study on WPF methods has been delivered by Zhao (2011), which gives a view on numerous aspects related to this issue. Above all, two main approaches in WPF models can be distinguished: (i) physical: the models are created based on the measurements, technical data of the windmills and air parameters provided by weather prognoses; (ii) statistical: including the artificial intelligence, based on the statistical models [
5].
Among the most important issues related to the WPF is its scalability, which has been pointed out by Rasheed et al. (2014). The author emphasises that, for two instances of the same weather conditions in the wind farm, the power output may differ significantly, which is caused by the complexity of the terrain on which the installation has been set up [
6].
The fact that there are not universally optimal WPF models for all the windfarms has been highlighted by Banerjee et al. (2017), who demonstrated that the most appropriate modelling approach depends also on the evaluation criterion [
7].
The achievable WPF errors entail the necessity of knowing the primary sources of uncertainty. In a paper published by Monforti et al. (2017) the authors have attempted to detect and weight the main factors affecting inaccurate wind power predictions. The lack of comprehensive knowledge of the technical parameters of the wind farms and insufficient information on the wind fields are mentioned as the two main sources of WPF inaccurateness [
8].
The desire for knowing the market prices in advance with acceptable reliability has become the subject of many studies. A remarkable focus has been put on forecasting the spot market prices [
9,
10,
11]. Bessec et al. (2014) distinguish three main modelling methods for predicting the energy prices on the market: equilibrium and game theory, simulation and time series forecasting methods [
12]. The basic models for prediction of time series include smoothing methods like averaging, exponential smoothing (e.g., Brown’s, Holt’s and Winter’s methods). However, the results of these models suffer relatively high prediction errors [
9].
Throughout numerous scientific publications, most attention is paid to the autoregressive (AR), moving average (MA) and their combination—ARMA—models, which have had success in forecasting economic phenomena [
13]. The ARMA model can be useful in stationary processes, which are characterised by a constant value of the average in throughout the time domain. Since a lot of processes indicate a presence of a trend, the ARMA model cannot be applied directly—this problem is solved by extension of the ARMA model by including integration (the I term in ARIMA), which transforms the process with trend into a stationary one (ARIMA). Another difficulty comes from the seasonality of some time series in a short time, which has been addressed by the seasonal (SARIMA) model.
In the age of computers, artificial neural networks (ANN), a branch of computational intelligence (CI), has become increasingly popular in all range of predictions, mainly because of their forecasting accuracy and availability of dedicated software. Neural networks can be used successfully in circumstances which prevent statistical methods being applied. One main advantage of ANN is its adaptability for complex, dynamic and nonlinear relations. On the other hand, Weron (2014) emphasises that the neural networks can be susceptible to unexpected, rapid changes in the process [
14].
Kolmek and Navruz (2012) performed the parallel forecasting processes for the Turkish energy spot prices utilising the ARIMA and ANN model, with the learning dataset constituting historical observations for time-period of 342 days. The latter model was achieved a smaller error, which was concluded as the main advantage of this method for statistical techniques (15.60% MAPE for ARIMA vs. 14.15% MAPE for ANN, calculated for a time horizon of 1 week) [
15].
In his explicit study, Weron (2014) [
14] lists the strengths and weaknesses of the electricity spot prices forecast in terms of the aforementioned methods, which have often been used separately a particular modelling approach. The weaknesses of each model are reduced though combining the modelling tools through dedicated computer software. The hybrid EPF models often result in performance improvements [
16,
17].
The most recent studies devoted to WPF and EPF strongly affirm the continuous necessity for proper projections of the wind power supplied to the system and their helpfulness in making decisions concerning the electricity market prices. Maldonado et al. [
18], in their attempt to systematise the literature review concerning WPF, concludes that the field of improvement is sought more often in the direction of ANNs, which brings more promising results. However, what was highlighted by Santhosh et al. in paper [
19], is that even the most advanced techniques do not solve the problem of generalisation capability, and do not assure suitability of a given model for individual windfarms. In the scope of the same study, Santhosh indicates the latest development of hybrid models and highlight the importance of probabilistic forecasting. The influence of RES generation forecast on the day-ahead market prices have been confirmed by the study by Frade et al. [
20], which was conducted based on the Iberian market data.
3. Portuguese and Polish RES Sector and Energy Exchange Institutions
Portugal is a country characterised by a very high share of RES in the total energy mix. Poland, while representing a steady growth in this area, does not reach the Portuguese share by far. It should be stressed that direct comparison on the RES share is improper since, throughout the continent, countries have developed diverse and specific energy systems, depending mainly on available domestic resources. Other key factors determining the shape of energy systems are climatic conditions (e.g., temperature), as well as the maximum energy independence. Although Poland has seen a considerable increase of RES in total energy production, the dominant primary energy source is coal, which is one of the most CO
2-intensive electricity generation technologies. Contrary to Poland, Portugal’s energy mix is diverse, with no single dominant energy production technology [
21,
22].
The continuation of the European Union’s (EU’s) plans for clean and sustainable energy requires the adequate and optimal utilisation of the wide range of RES technologies to make it not only efficient, but also profitable. Poland and Portugal are countries separated by a vast distance, which results in different climatic conditions and different available sources of renewable energy generation. Taking into account the average annual wind speed, in both countries, the obtained measures are similar [
23]. On the other hand, the solar energy in Portugal has a much higher potential for utilisation, with measures of the yearly solar irradiation being 1800 kWh/m
2 in Portugal and around 1200 kWh/m
2 in Poland.
The Towarowa Giełda Energii (TGE) was established in 1999, as the Polish government recognised the need to have an institution managing the energy trading on the emerging liberalised competitive market. Half a year after commission, the spot market was launched for market participants. Currently, TGE is the only company licensed by the state for managing the energy exchange. During the two recent decades, TGE expanded its area of activity into the emissions market exchange and origin certificates trading platform. In 2008, TGE introduced the Commodity Forward Instruments market, which allows it to maintain relatively constant prices across a wider time-horizon, as well as to optimise the costs of sales and purchases of energy [
24].
While the TGE activities are limited to the within the country borders, the Iberian Electricity Market (MIBEL) is an example of the energy market expanded to the regional scale. It is a result of joint efforts of the Spanish and Portuguese governments. This convergence, having its origins in 2001, allows every market participant to make deals with other agents from all over the Iberian Peninsula. The integration of the hitherto separated energy systems required a series of undertakings, including the harmonisation of the electric network, laws, and economic environment. In 2004, both parts of the Santiago Agreement declared the creation of two sub-institutions, responsible for different aspects of the proper operation of the system as a whole. These were the OMI-Polo Português (OMIP), responsible for the forward market and OMI-Polo Español (OMIE), which was brought to existence to manage the spot market. The period between the Santiago Agreement and the launch of the Iberian Market (1 July 2007) was influenced by many factors, including political changes.
5. Results and Discussion
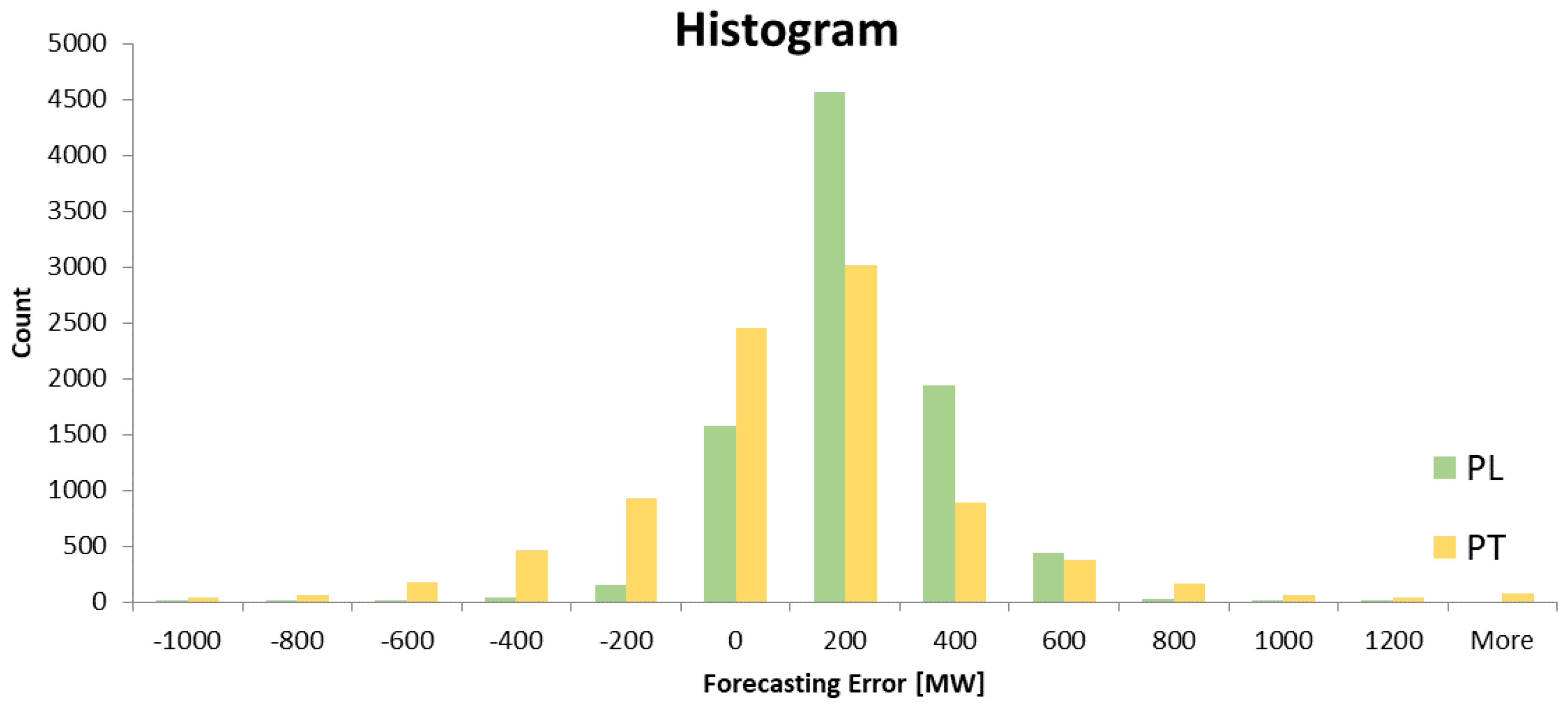
The wind power error value (expressed as the difference between the realisation of the variable and its corresponding forecasted value) has been calculated for each hour of 2016, and divided into ranges to present the error distribution on a histogram, as shown in
Figure 2.
The main conclusion from the analysis of the above chart is that the wind generation forecasts are generally underestimated in both countries, since the result of subtracting the forecasted value from the actual value of power results in positive values, between 0 and 200 MW.
To get a deeper view of the characteristics of the error distribution, the statistical parameters of the examined dataset have been calculated. The statistical description has been carried out to quantitatively compare the inaccuracies of wind power forecasts for both countries, including the calculation of statistical measures, which are presented in
Table 3 and are referred to in
Section 3.
Analysing
Table 3, one may conclude that both Polish and Portuguese forecasts are underestimated, because the average error values exceed 0 significantly, especially in Poland, reaching 118 MW. Although the average is much higher in Poland compared to Portugal, the Portuguese forecast is characterised by higher volatility, which is indicated by the values of kurtosis and standard deviation. Comparing the kurtosis of both forecasts’ errors, the higher tendency for clustering of the error near the average value occurs in the forecast prepared for Poland. In both cases, the extreme values of the forecast error reached gigawatts. Comparing the MAPE values, the Polish forecasts perform considerably better, reaching 15% on average. The skewness values of examined samples took the opposite sign for Poland and Portugal, which means that the asymmetry of the error distributions has the opposite direction. Comparing the wind generation forecasts error (up to 2 GW) with the overall generation rates in the countries (reaching up to about 10 GW in Portugal and 50 GW in Poland) leads to the question in what extent these forecasts influence the total energy system and energy markets.
The potential financial losses have been calculated assuming that the entire forecasted wind power is traded on the spot market, and the divergence between the wind forecast and actual production is traded on the balancing market. The results of the performed calculations are presented in
Table 4:
Although the total wind-generated imbalanced energy volume in 2016 is not significantly different between Poland and Portugal, the financial losses in the case of the Iberian country reached almost EUR 21 million, which was over ten times more than in the case of Poland. Although the yearly-aggregated forecast deviation brought losses, there were hours, when it resulted in positive income (L < 0). In Poland, more than half of hours in the year brought benefits from incorrect forecasts (4510 h in 8784 of total).
To directly compare the results, the unit costs of the forecast error was calculated by the division of the total imbalance by the total financial loss in 2016. As shown in
Table 4, a 1 MWh planning error in Portugal resulted in EUR 10.7 of costs, which was almost 10 times larger when compared with Poland. Such a significant discrepancy comes from the imbalance pricing system, which is different in these countries. In Portugal, there are two levels of balancing market price, depending on the character of imbalance (surplus/deficiency). In Poland, there is only one universally valid imbalance price, which allows for market speculation. In the circumstance of a single, uniform imbalance price, there exists a considerable probability of obtaining income from selling energy on the balancing market instead of the spot market. The Polish wind energy seller may speculate on the difference between the spot and imbalance prices, which may encourage him to intentionally distort the production plan. In contrast, the Portuguese energy seller may expect only the negative outcomes from an inappropriate production plan.
As far as the influence of wind energy forecasts on spot prices is concerned, the forecasting results with the use of ARMA, ARMAX, NAR and NARX models are presented in
Table 5 and
Table 6, respectively. Results where the inclusion of wind power forecasts led to better performance when compared to the case without wind power information are in bold text. The information of the key model parameters is also shown. Moreover, the uncertainty of the sale as defined in Equation (11) is also displayed.
To have a reference of the models constructed in this paper, the persistence model has been simulated as well. Applying Equation (9) to the validation dataset (December 2016), the persistence model has been constructed and evaluated by obtaining the value of MAPE, which took a value of 6.92% in Poland and 4.50% in Portugal.
The S1, S2 and D2 cases have not been highlighted, because in these examples the ARMAX model’s nb coefficient was zero. This is the order of polynomial composed of external variable values, which means that the ARMAX model becomes ordinary ARMA model.
Analysis of
Table 5 and
Table 6 show that when comparing the forecasting results globally, the Portuguese spot market prices are significantly more predictable than the Polish case using the models constructed for this study. Another finding is that usually, the dynamic cases perform worse than the static ones thus the model estimation should include wider ranges of data. Additionally, in the right-hand-side column, the difference between the sales uncertainty (SU) of the models with and without the inclusion of the wind generation forecast has been calculated. The SU value varied between EUR 55,000 and EUR 235,000, in the case of models based on Portuguese data.
Recalling the reference forecasts of the persistence model (6.92% MAPE in Poland and 4.50% in Portugal), it can be observed that in the case of Poland the obtained models rarely perform better than the persistence one, while, in Portugal, the MAPE obtained by time series models is often below 4%.
Comparing country-to-country, it can be observed that the wind generation forecast is valuable for predicting the spot prices in Portugal, because in seven out of eight cases, the “X” model returned more accurate results than its counterpart without information of wind generation forecast (ARMA vs. ARMAX and NAR vs. NARX). In the case of predicting the Polish spot market prices, only in two instances out of eight did the addition of wind production forecasts improve the model output. The cumulated simulation results show that wind generation forecasts influence the spot market prices in Portugal. In the case of the Polish market, has been shown that the forecasts do not have an impact on the spot market price. As a source of this difference, the authors consider the significant divergence in the wind generation share in the total electricity production. In the case of Portugal, the relative amount of the energy injected to the system from wind turbine generators is much higher, thus, may have a greater impact on the market behaviour.
As a general tendency, the Portuguese spot market prices were more predictable than the Polish time series. This is shown by the one-sided difference of the MAPE measure in all the cases.
Moreover, when comparing the results obtained from the four models for the individual learning dataset approaches (S1, S2, D1 and D2), a global result is that the models of “static” character, those being estimated on a fixed dataset, resulted in obtaining lower errors. As for the reason, the authors assume the instantaneous peaks of the prices occurring within a week or a day, which may significantly influence the estimation and impact the model’s prediction accuracy. In the situation when the time range of the data was wider (1 month, 11 months), this impact was mitigated.
The results answer the fundamental question of this study because as it is observed, the impact of wind power on the market prices is not unequivocal. An application of a given model with wind power variable as input occurred to be more accurate in the case of Portugal, while in Poland not.
The outcome of the study demonstrates consistency with former research on the topic. As highlighted in the study by Maciejowska et al. [
28], the RES generation forecasts published on the ENTSO-E platform are encumbered with systematic errors, which gives space for future improvement in EPF. The analysis of WPF and EPF for Poland and Portugal confirmed the relevance of the forecasting error, which translated to the level of financial loss or gain, strongly amplifying the uncertainty of sales. The calculated values of MAPE for ARMA and ANN models, compared to the ones reported in the studies devoted to spot market forecasting (e.g., Kolmek and Navruz, [
15]), can be found satisfactory. However, direct comparison between studies in the literature should be performed with caution. Our parallel study addressed this deficiency by comparatively analyse the separate cases of two countries, but with a data feed completely correspondent to one another in time and scope. That allowed to unambiguously evaluate the accurateness of EPF models and their receptivity for external data input as the wind power forecast.
6. Conclusions
The analysis of the wind power forecasts for Poland and Portugal resulted in significant forecasting errors, based on calculations made by the use of data from the ENTSO-E platform. Large discrepancies have been observed for both analysed countries. Analysis of the wind forecast error distribution revealed that there exists a difference in the estimation of the wind generation forecast among the countries. In Portugal, the forecast often predicted lower values than the actual ones. In the case of Poland, these forecast values overestimated the production compared to actual values. This finding opens a new research opportunity which would investigate the application of systematic error correction in overall wind production forecasts.
Calculation of the financial losses from inaccurate wind power forecasts led to the conclusion that the uncertainty of the wind energy production forecasting results in remarkable potential income losses for the wind energy producers, reaching millions of EUR in global (national) scale. As shown in this study, in the Polish case, there exists a large possibility of market speculation, since, in many instances, the sales on the balancing market were more profitable than in the spot market.
Analysis of the spot price forecasting models shows that in the case of Poland, the applicability of wind power as the input to a particular model is uncertain. On the other hand, a decrease of MAPE values has been demonstrated when adding the wind power input variable to the models based on Portuguese data, which translated into lower values of sales uncertainty of the generated wind power. These opposite observations reveal that the advantage of models including wind power information is not universal among the individual countries.