The Current Spectrum Formation of a Non-Periodic Signal: A Differential Approach
Abstract
:1. Introduction
2. Theoretical Assumptions
2.1. Task Definition
2.2. Task Solution
3. Results
3.1. Experimental Design
- By graphical representation of calculated coefficients and reconstructed signals;
- On the Central Processing Unit (CPU) time during calculations;
- Relative performance, defined as the percentage of the difference between the time estimates of calculations performed using the classical (see Equation 1) and the developed algorithms, and the time of calculation using the classical algorithm; and,
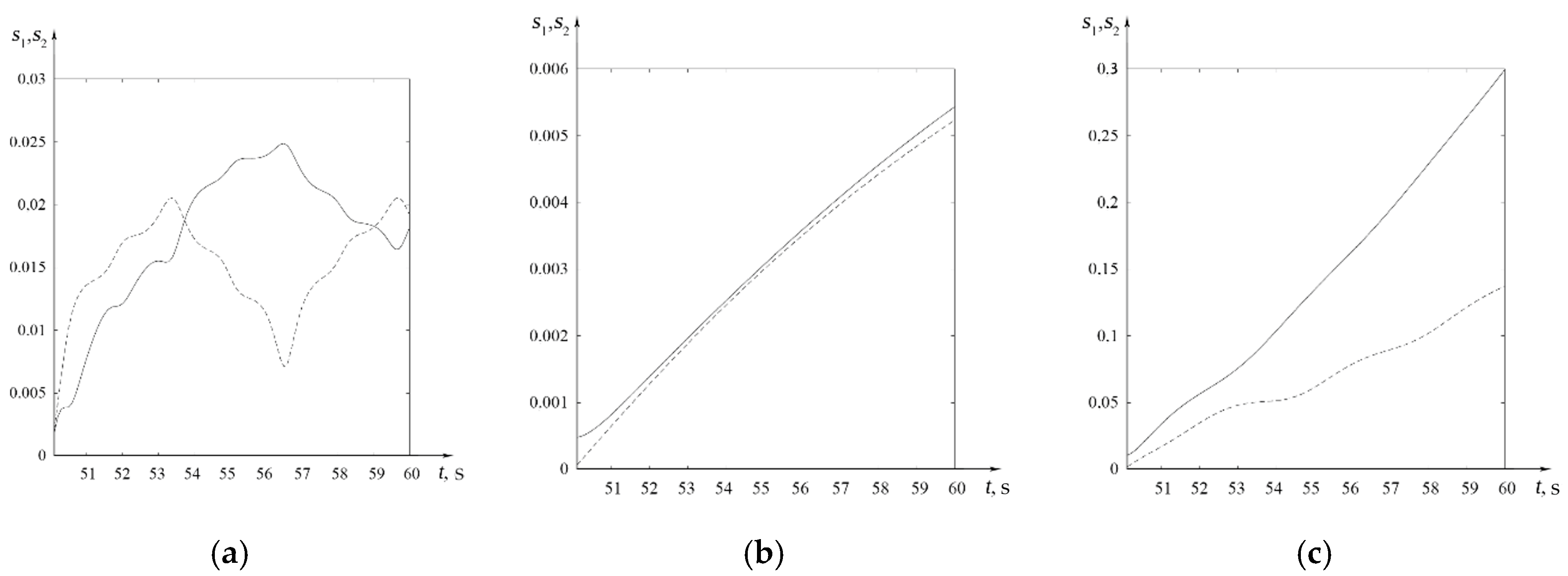
- Based of the standard deviations analysis of the spectral coefficients values ak[i] and bk[i] calculated by the above algorithm from the reference values akr[i] and bkr[i] calculated by the integral transformation (1).
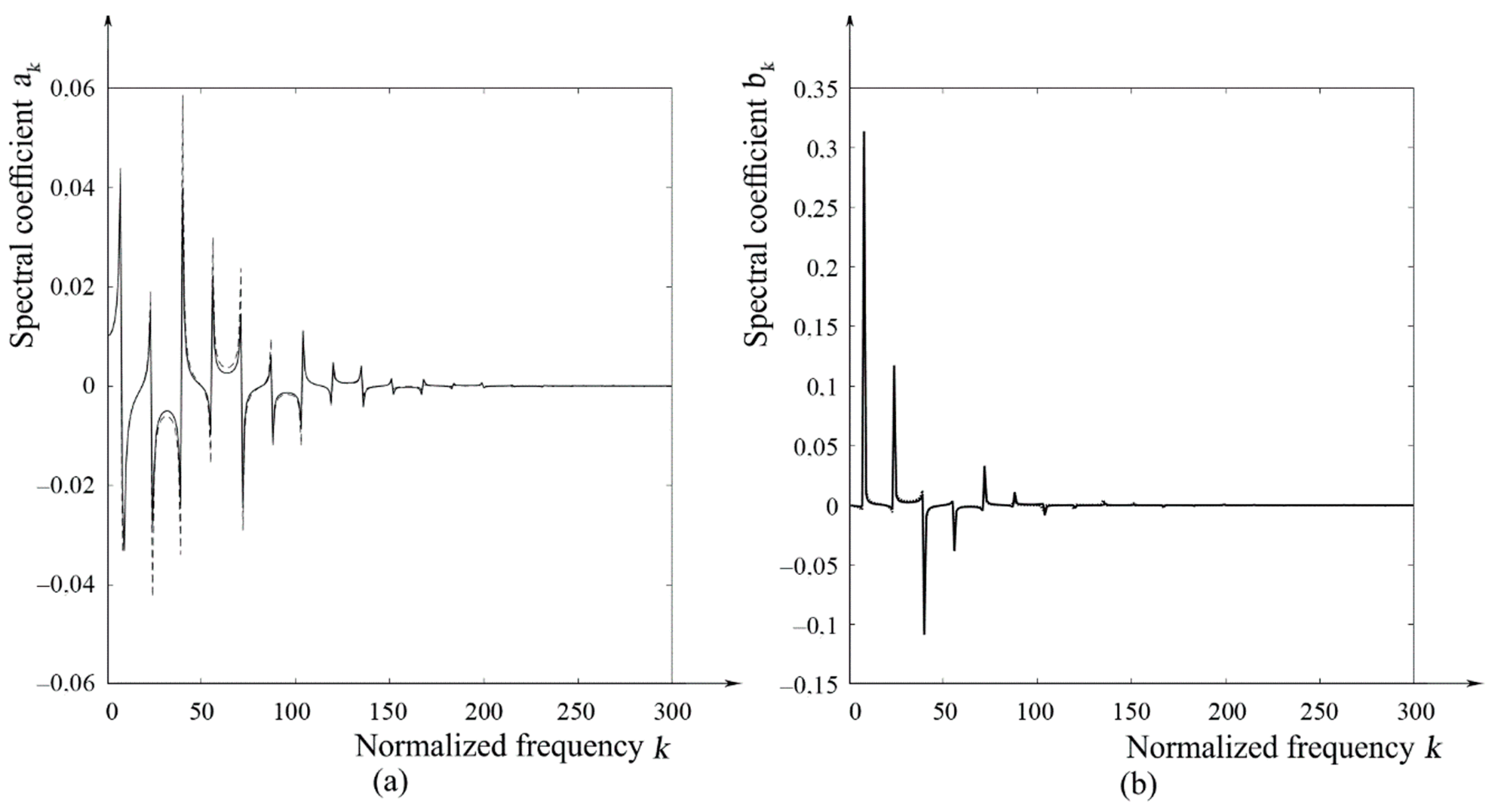
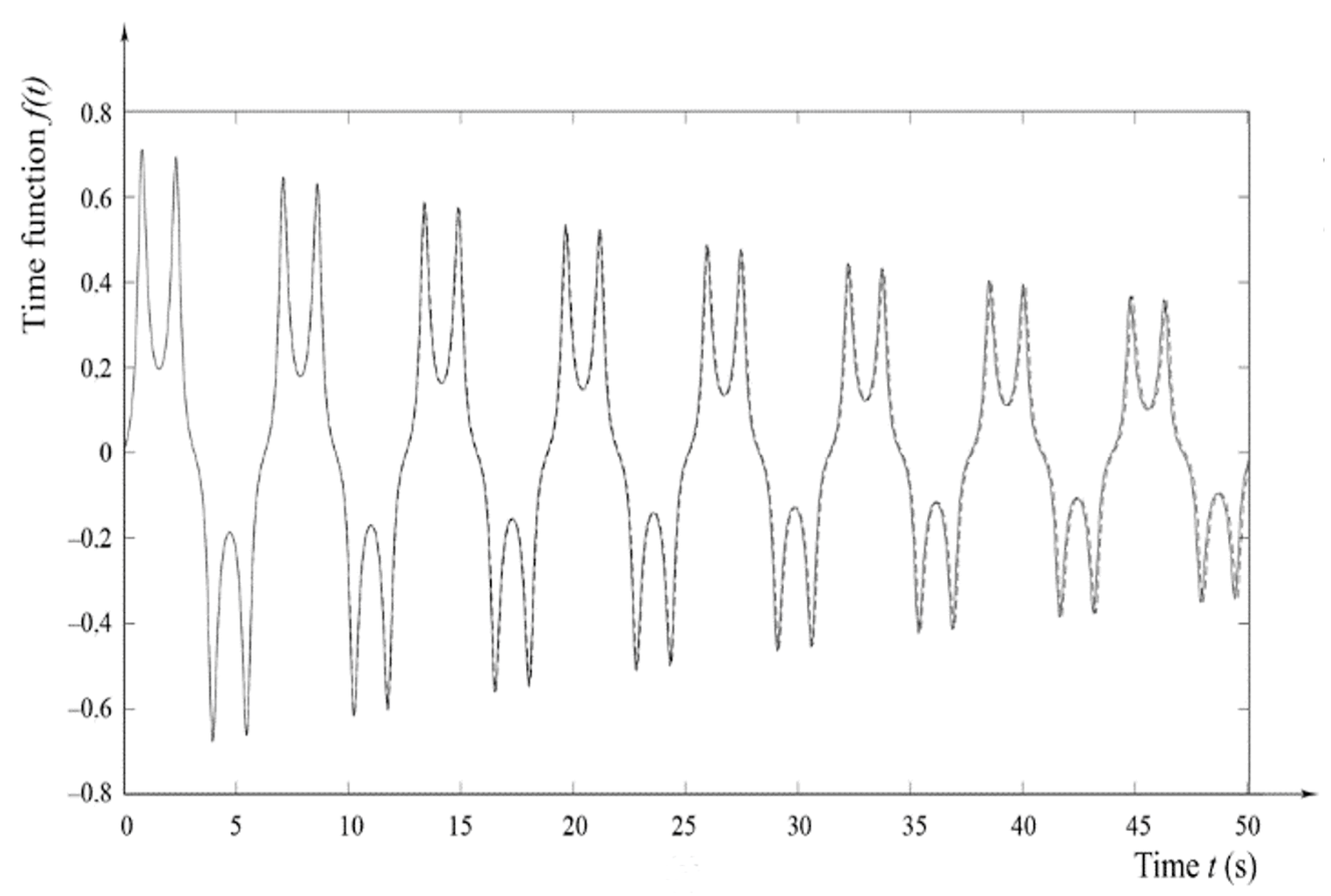
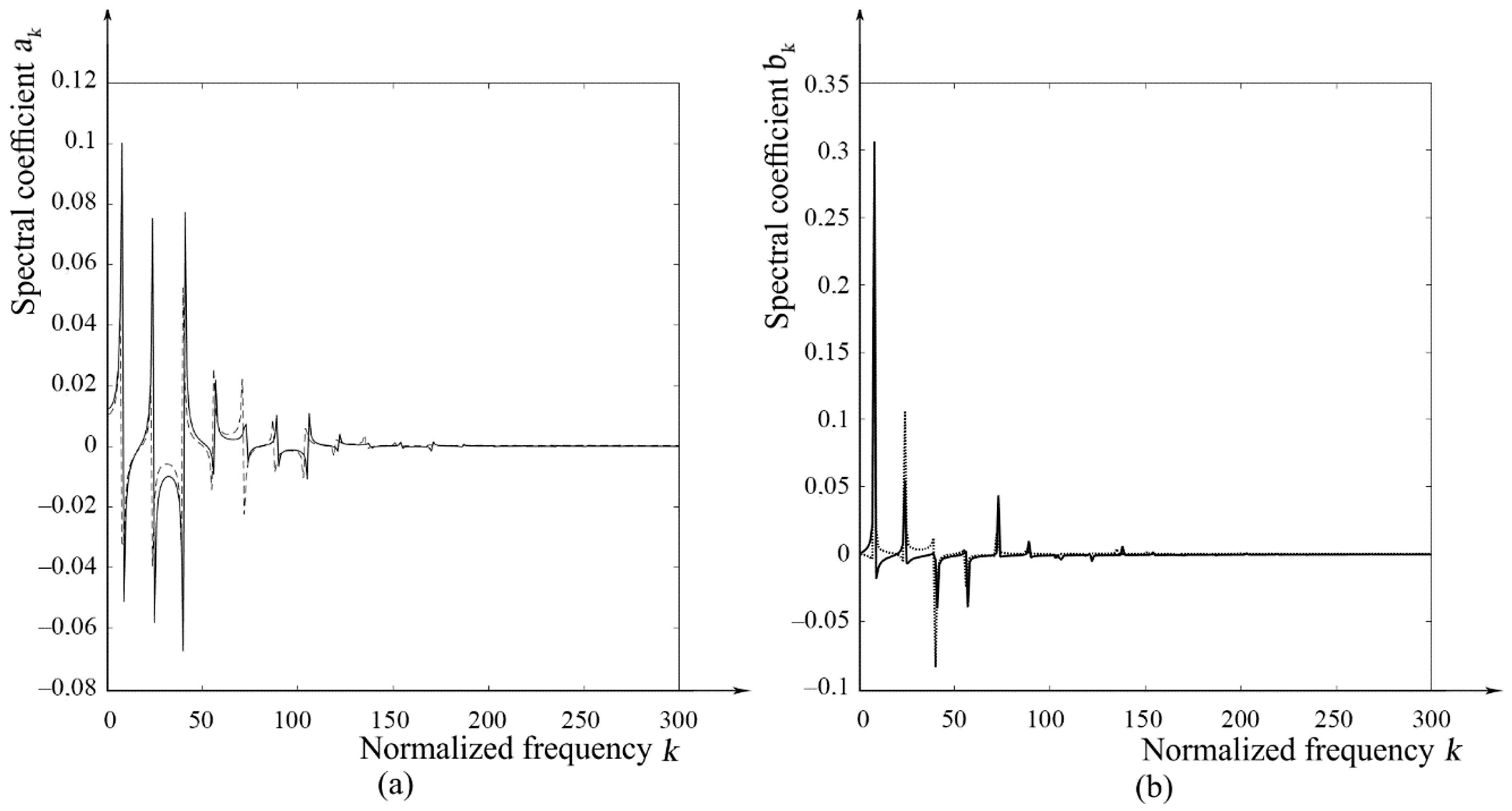
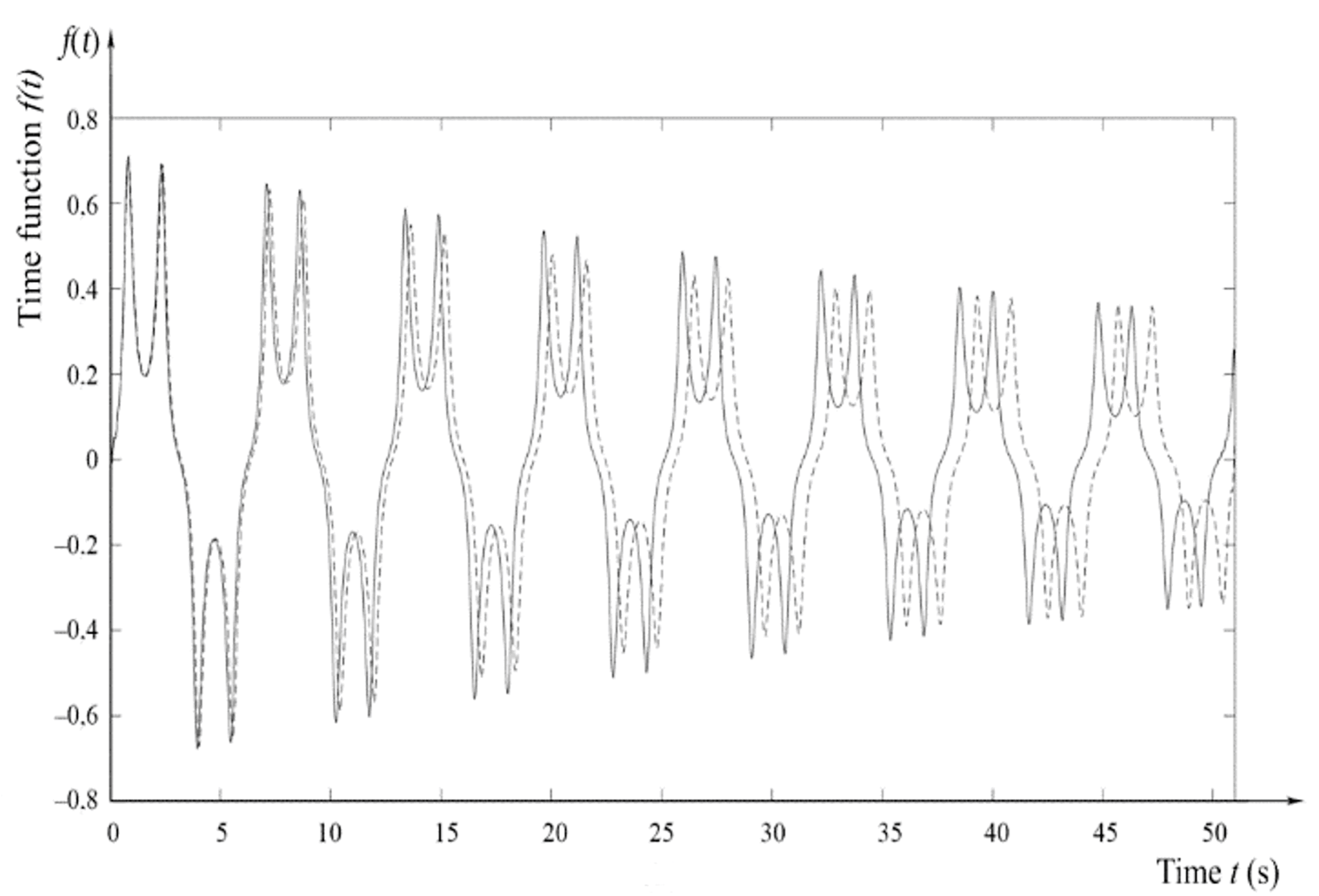
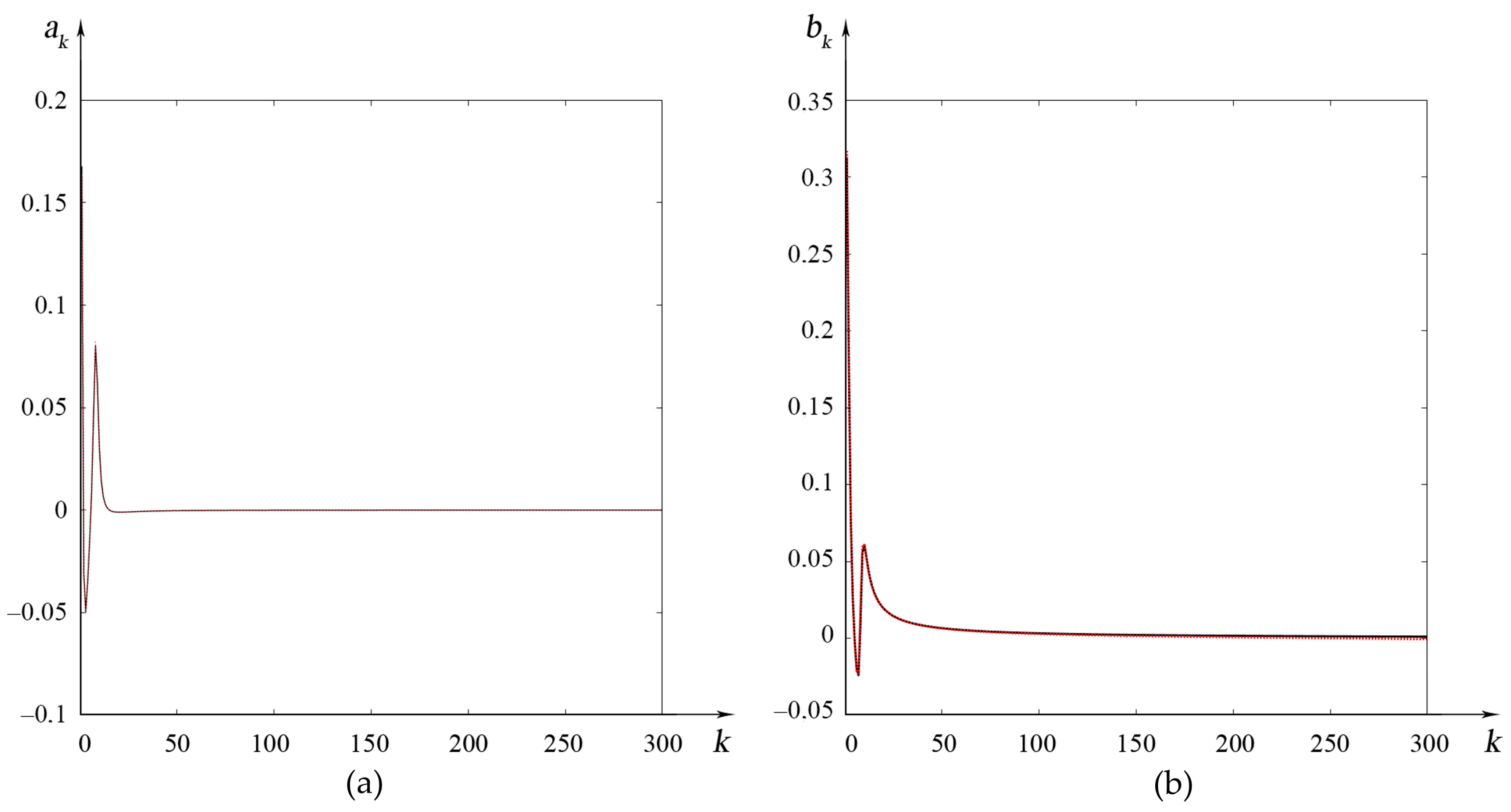
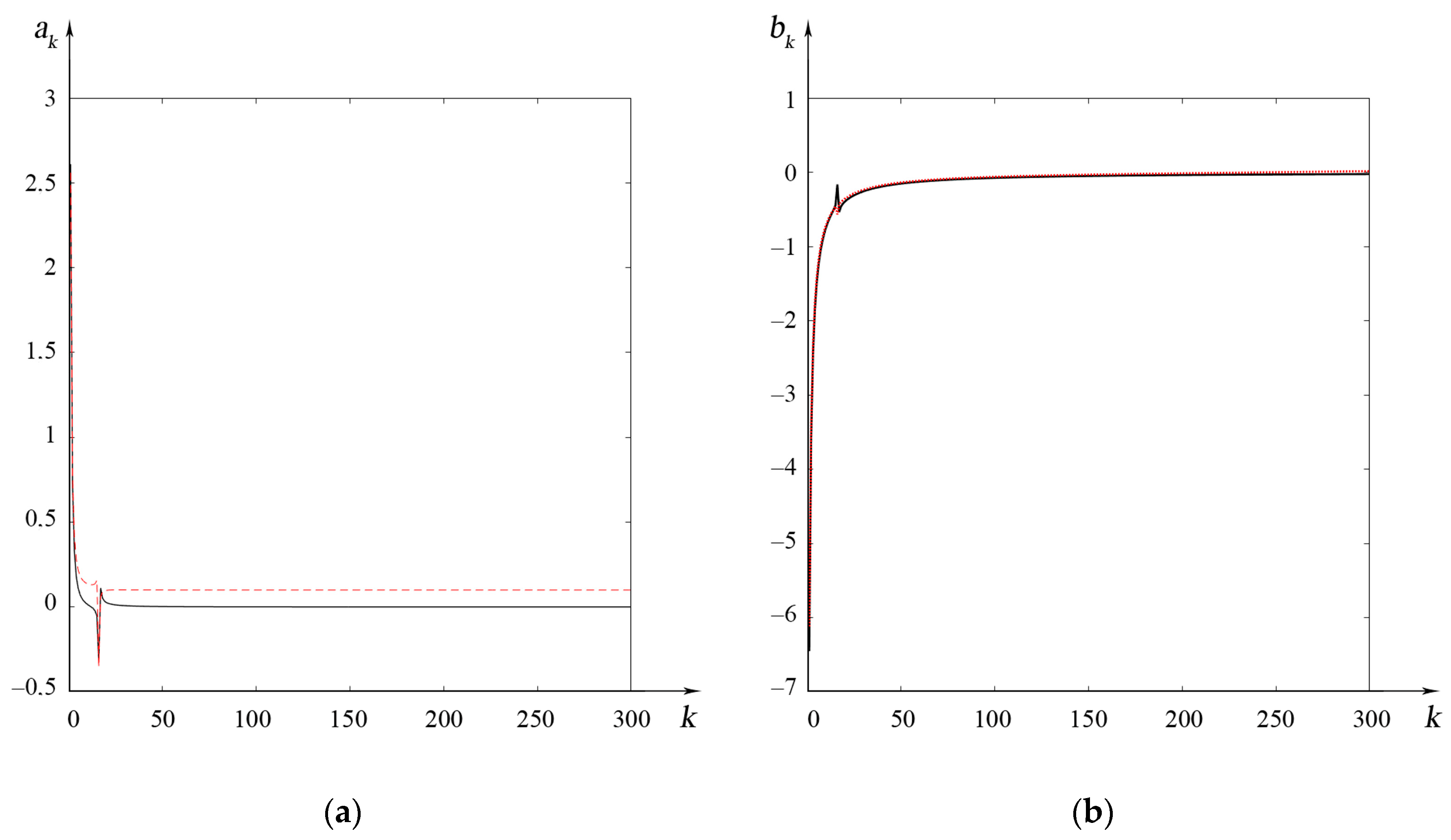
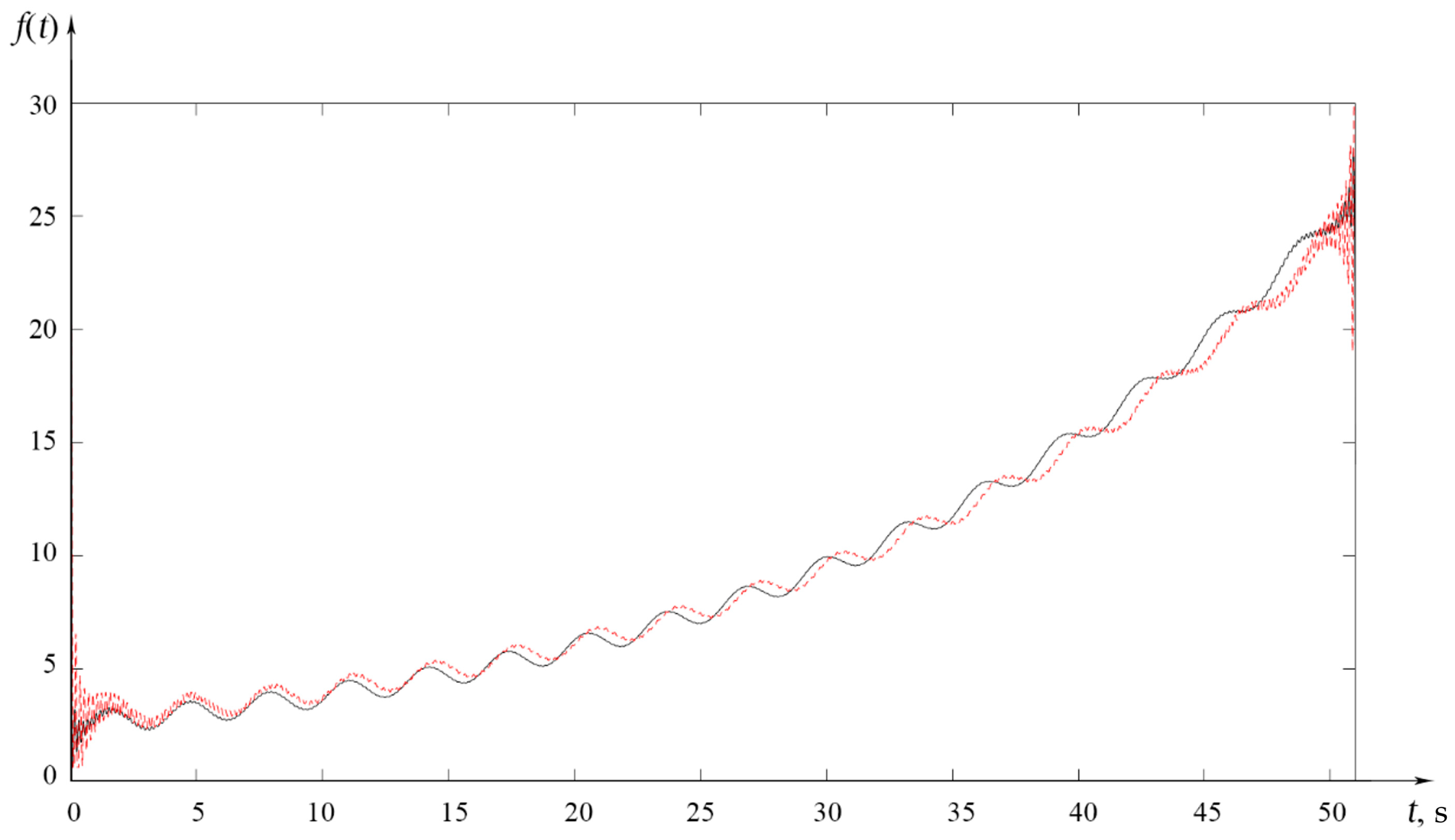
3.2. Numerical Modelling
3.3. Evaluation of Numerical Modelling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dyakonov, V. Modern digital spectrum analyzers. Components Technol. 2010, 5, 185–195. [Google Scholar]
- Isermann, R.; Münchhof, M. Identification of Dynamic Systems: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-540-78878-2. [Google Scholar]
- Iglesias, V.; Grajal, J.; Sanchez, M.A.; Lopez-Vallejo, M. Implementation of a Real-Time Spectrum Analyzer on FPGA Platforms. IEEE Trans. Instrum. Meas. 2015, 64, 338–355. [Google Scholar] [CrossRef]
- Sergienko, A.B. Digital Signal Processing, 3rd ed.; BHV-Petersburg: St. Petersburg, Russia, 2011; ISBN 5977506066. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson: London, UK, 2010. [Google Scholar]
- Lyons, R.G. Understanding Digital Signal Processing, 3rd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2004; ISBN 8131764362. [Google Scholar]
- Marks, R.J., II. The Joy of Fourier: Analysis, Sampling Theory, Systems, Multidimensions, Sto-Chastic Processes, Random Variables, Signal Recovery, POCS, Time Scales, & Applications; Baylor University: Waco, TX, USA, 2006. [Google Scholar]
- Blahut, R.E. Fast Algorithms for Signal Processing; Cambridge University Press: New York, NY, USA, 2010; ISBN 1139487957. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Applications; McGraw Hill: Singapore, 2000. [Google Scholar]
- Averchenko, A.P.; Zhenatov, B.D. Estimation of the gain of computational costs of Hartley transform before Fourier transform. Omsk Sci. Bull. 2015, 2, 190–194. [Google Scholar]
- Avramchuk, V.S.; Yakovleva, E.M. Application of lattice periodic functions in spectral analysis of narrowband periodic signals. Bull. Tomsk Politech. Univ. 2006, 309, 40–44. [Google Scholar]
- Bogner, R.E.; Constantinides, A.G. Introduction to Digital Filtering; Wiley: New York, NY, USA, 1975; ISBN 0471085901. [Google Scholar]
- Chakraverty, S.; Mahato, N.R.; Karunakar, P.; Rao, T.D. Advanced Numerical and Semi-Analytical Methods for Differential Equations; Wiley: Hoboken, NJ, USA, 2019; ISBN 9781119423423. [Google Scholar]
- Korolova, O.; Popp, M.; Mathis, W.; Ponick, B. Performance of Runge-Kutta family numerical solvers for calculation of transient processes in AC machines. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Radzi, H.M.; Majid, Z.A.; Ismail, F.; Suleiman, M. Four step implicit block method of Runge-Kutta type for solving first order ordinary differential equations. In Proceedings of the 2011 Fourth International Conference on Modeling, Simulation and Applied Optimization, Kuala Lumpur, Malaysia, 19–21 April 2011; pp. 1–5. [Google Scholar]

| Time Interval | T0 = 50.1 s | T0 = 51.0 s | ||||
|---|---|---|---|---|---|---|
| Evaluation Criterion | Standard Deviation for ak[i] | Standard Deviation for bk[i] | Performance, % | Standard Deviation for ak[i] | Standard Deviation for bk[i] | Performance, % |
| f1(t) | 0.0020 | 0.0018 | 96.4 | 0.0147 | 0.0089 | 80.8 |
| f2(t) | 0.000066253 | 0.0004806 | 97.0 | 0.0006512 | 0.00082342 | 79.4 |
| f3(t) | 0.0020 | 0.0107 | 98.8 | 0.0172 | 0.0342 | 79.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolov, S.; Marshakov, D.; Novikov, A. The Current Spectrum Formation of a Non-Periodic Signal: A Differential Approach. Inventions 2020, 5, 15. https://doi.org/10.3390/inventions5020015
Sokolov S, Marshakov D, Novikov A. The Current Spectrum Formation of a Non-Periodic Signal: A Differential Approach. Inventions. 2020; 5(2):15. https://doi.org/10.3390/inventions5020015
Chicago/Turabian StyleSokolov, Sergey, Daniil Marshakov, and Arthur Novikov. 2020. "The Current Spectrum Formation of a Non-Periodic Signal: A Differential Approach" Inventions 5, no. 2: 15. https://doi.org/10.3390/inventions5020015
APA StyleSokolov, S., Marshakov, D., & Novikov, A. (2020). The Current Spectrum Formation of a Non-Periodic Signal: A Differential Approach. Inventions, 5(2), 15. https://doi.org/10.3390/inventions5020015






