Study of Two-Phase Newtonian Nanofluid Flow Hybrid with Hafnium Particles under the Effects of Slip

Abstract

This paper investigates the role of slip in a two-phase flow of Newtonian fluid. The nano-size Hafnium particles are used in the base fluid. The fluid under consideration is studied for two cases namely (i) fluid phase (ii) phase of particles. Both cases are examined for three types of geometries. The governing equations are simplified in nondimensional form for each phase along with boundary conditions. The resulting equations have been analytically solved to get exact solutions for both fluid and particle phases. Different features of significant physical factors are discussed graphically. The flow patterns have been examined through streamlines.

1. Introduction

The multiphase flows contribute a great role to shaping human lives for centuries, such as water flowing down from top of the hills, high waves produced in the oceans with different speed, air in the windmills, drilling of crude oil under earth surface, blood flowing in the circulatory system that deal with single, double, or multiphase flows. More precisely, the air and water flows are the examples of single-phase flow whereas flows such as solid–liquid flow, bubbly flows, particulate flows, droplets (multi-directional) flow, and water and stream flow, are the most common examples of two-phase flow. Moreover, from a medical point of view, the best example of two-phase flow is plasma-platelet in the blood flow. The multiphase flow involves such materials which has chemically different features, for example, a mixture of liquids and different types of gases, or two types of liquids that do not mix with each other. The multiphase flow term is used for any kind of fluid flow which consists of more than one component or phase. Multiphase flow was particularly studied widely in the context of the oil industry due to the increasing dependence of petroleum. In the industry, multiphase flows technology are used at a large scale nowadays, few examples among several are suspension of fibers in contractions, fluidized bed, nuclear reactors, sediment transport, manufacturing process of paper and pulp, etc. Moshizi et al. [1] have presented a theoretical model on two-phase nanofluid with heat generation and absorption. Sheikholeslami et al. [2] numerically investigated the two-phase model for magnetohydrodynamics (MHD) nanofluid with convection. Chamkha [3] reported the flow of two-phase with hydromagnetic. Akbari et al. [4] have presented the mixture model of a two-phase nanofluid. Goodarzi et al. [5] examined the two-phase flow for shallow cavity with a mixture model. Sheikholeslami et al. [6] conducted the study of magnetohydrodynamics nanofluid with heat transfer by employing a two-phase model. Recently, Sadeghi et al. [7] investigated porosity effects for the two-phase flow. Significant developments for two-multiphase flows are contained in [8,9,10,11,12,13,14].

Moreover, nanoparticles have a size between 1 and 100 (nm). In nanotechnology, a nanoparticle is such a tiny particle which acts as a whole unit with reference to its transport and properties. Several special issues noteworthy of theoretical, numerical, and experimental studies on nanofluids and its applications can be seen in [15,16,17,18,19,20,21,22,23].

Furthermore, the Hafnium particles have great importance and demand in nuclear reactor due to its unique character of absorbing neutrons and corrosion resistance. That unique character motivated the trend of research in this sense. Nanoparticles associated with Hafnium particles built a bridge between bulk materials and atomic or molecular structures that ultimately linked with medical science as delivery agents for anticancer, drugs, and vaccines. They can easily approach physical properties that can be measured for complete description, such as, shape, size, surface properties, crystalline, and dispersion state [24,25]. Hafnium metal and its compound have been a focus of scientists in recent decades, owing to unique physical properties. The primarily application of the metal is to control and use as a safety mechanism in nuclear reactors [26]. This is only possible due to its high cross-section for neutron absorption and high corrosion resistance. Nanostructured Hafnium base ally [27] such as Hafnium dioxide ($Hf{O}_2)$ is used to manufacture circuits and transistor to control the flow of current, due high melting point, neutron absorption cross section, chemical stability, and due to high dielectric constant. Recent developments in the field of medical sciences [28], have brought new clinical options such as photodynamic therapy (PDT) to kill cancer cells depending on the bombardment of nanosized hafnium particles. Marill et al. [29] considered Hafnium oxide and NBTXR3 nanoparticles that were designed for high dose energy deposition within cancer cells when exposed to ionizing radiation. In the same connection, Maggiorella et al. [30] have also utilized Hafnium oxide nanoparticles for the treatment of tissues via radiotherapy.

In addition, electroosmosis [31] is a fundamental electrokinetic effect involving the movement of the bulk solution against a charged solid surface under the influence of an electric field. The electroosmotic flow (EOF) [32] arises from the formation of an electrical double layer at a solid–liquid interface. Prakash and Tripathi [33] endeavor is related to the peristaltic transport of EOF of nanofluid. The osmotic flow was suspended with the Williamson fluid through tapered channel. This model can help study the intrauterine fluid dynamics governed by electroosmosis mechanism. Noreen et al. [34] study is based on lubrication and Debye–Hückel linearization approximation of an electroosmotic flow of nanofluid. The theoretical investigation offers peristaltic nanoflow under the influence of entropy generation in double-diffusive convection. In [35], Sheikholeslami and Bhatti have studied applied electric field on the nanofluid by means of electro-hydrodynamics (EHD) which augment the rate of heat. Similarly, some notable researches have been reported in [36,37,38,39] which involve the application of electroosmosis and different kinds of nanofluid flows.

In addition, it is obvious that in slip phenomena, the velocity of fluid at surface is directly proportional to shear stress at surface, consequently the slip condition affects the velocity of fluid. The slip mostly appears in two situations (i) when the fluids have elastic character and (ii) in the case of field gases. In both said cases slippage acts subject to the large tangential traction. Through experimental studies it is perceived that an existence of slippage is also possible in the Newtonian and non-Newtonian fluids such as molten polymer and in the case of polymer solutions [40,41,42,43,44,45,46,47].

In view of the above-mentioned studies, it is perceived that hafnium nanoparticles are widely used in biosciences to target cancer cells such as “Ionizing radiation”, a new approach to cancer therapy. The aqueous solution of hafnium nano-crystallites go through different shapes and forms of arteries and veins, in the process to reach damaged tissues. The theoretically studied lubrication effects on the nanoflow will help expedite the healing process which is yet not available in existing literature. Motivated by these facts, we aim to devote our efforts to fill this gap.

2. Mathematical Model

If $\overline{V}=\left[\overline{u}\left(\overline{\xi },\overline{\eta }\right) \overline{v}\left(\overline{\xi },\overline{\eta }\right) \overline{w}\left(\overline{\xi },\overline{\eta }\right)\right]$, the velocity of Newtonian fluid has features, i.e., viscous, incompressible, steady, and electrically conducting containing 40% of Hafnium particles. Investigating the multiphase flow through various geometries, paved the way on how one can face new challenges in the days to come. Here, we have considered the following three diverse geometries as shown in Figure 1, Figure 2 and Figure 3 for illustration:

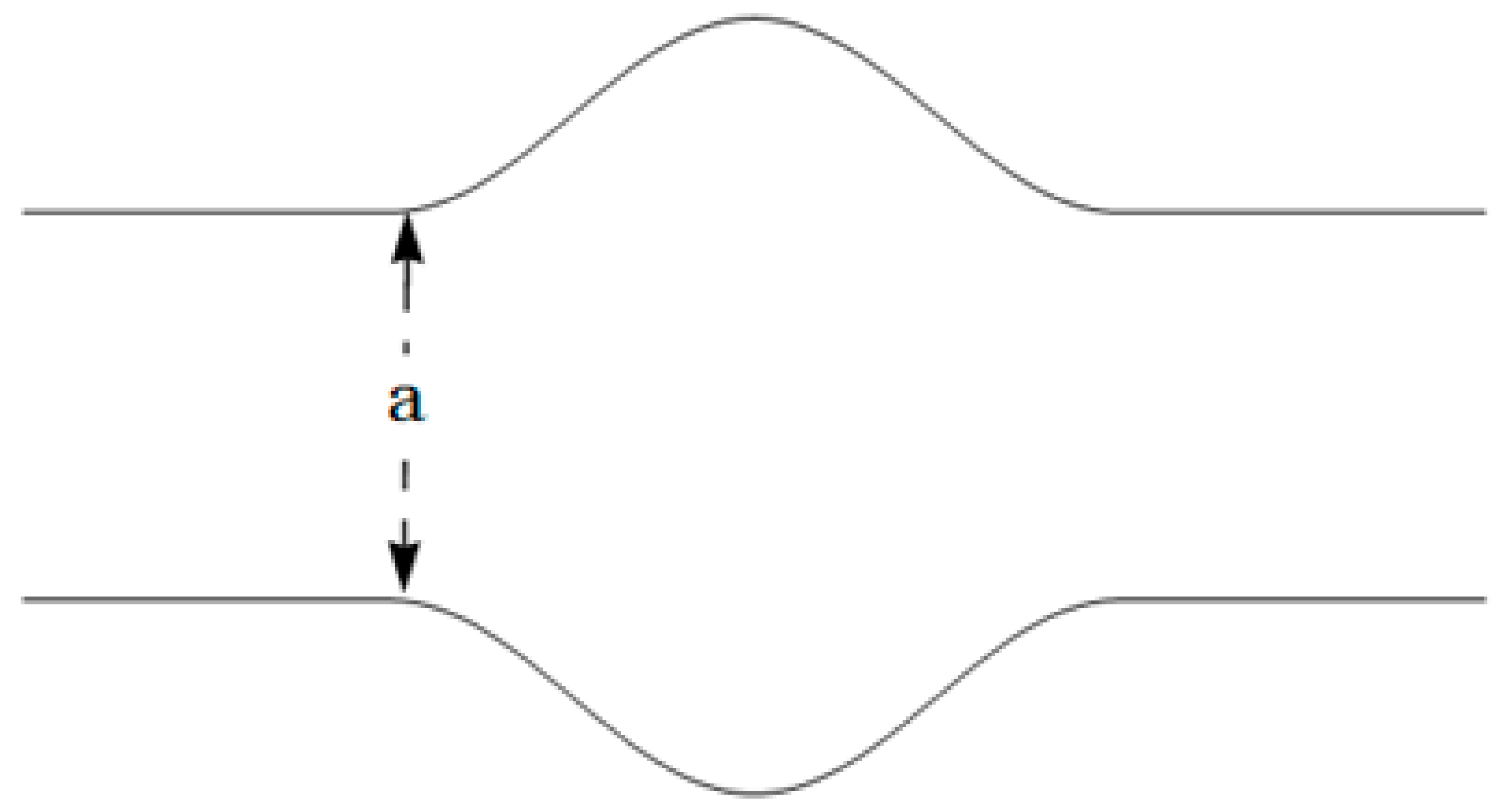
2.1. Geometries

First geometry:

$$H\left(\overline{\xi }\right)=\{\begin{array}{ll}a-b\sqrt{1-\cos \left(\frac{\pi \overline{\xi }}{\lambda }\right)};& for \frac{11}{7}<\overline{\xi }<\frac{33}{7},\\ 0.5 a;& \mathrm{otherwise}.\end{array}$$

(1)

Second geometry:

$$H\left(\overline{\xi }\right)=\{\begin{array}{ll}b+a\left(\frac{0.5 \lambda -\overline{\xi }}{3.5 \lambda }\right);& for 0.5<\lambda <\overline{\xi },\\ 0.5 a;& \mathrm{otherwise}.\end{array}$$

(2)

Third geometry:

$$H\left(\overline{\xi }\right)=\{\begin{array}{ll}a-b Si{n}^2 \left(\frac{\pi \overline{\xi }}{\lambda }\right);& for \frac{11}{7}<\overline{\xi }<\frac{33}{7},\\ 0.5 a;& \mathrm{otherwise}.\end{array}$$

(3)

The associated velocities of fluid and particle phases are given:

$${\overline{V}}_f=\left[{\overline{u}}_f\left(\overline{\xi },\overline{\eta }\right){\overline{v}}_f\left(\overline{\xi },\overline{\eta }\right){\overline{w}}_f\left(\overline{\xi },\overline{\eta }\right)\right]$$

(4)

$${\overline{V}}_p=\left[{\overline{u}}_p\left(\overline{\xi },\overline{\eta }\right){\overline{v}}_p\left(\overline{\xi },\overline{\eta }\right){\overline{w}}_p\left(\overline{\xi },\overline{\eta }\right)\right]$$

(5)

If flow is in an axial direction, then Equations (4) and (5) can be written:

$${\overline{V}}_f=\left[{\overline{u}}_f\left(\overline{\xi },\overline{\eta }\right)00\right]$$

(6)

$${\overline{V}}_p=\left[{\overline{u}}_p\left(\overline{\xi },\overline{\eta }\right)00\right].$$

(7)

2.2. Mathematical Model

In view of Equations (6) and (7), the resulting mathematical model for fluid and particle phase in components from [48] are given as:

(i) For the case of phase fluid:

$$\frac{\partial {\overline{u}}_f}{\partial \overline{\xi }}+\frac{\partial {\overline{v}}_f}{\partial \overline{\eta }}=0,$$

(8)

$$\begin{array}{cc}\hfill {\rho }_f\left(1-C\right)\left[{\overline{u}}_f\frac{\partial {\overline{u}}_f}{\partial \overline{\xi }}+{\overline{v}}_f\frac{\partial {\overline{u}}_f}{\partial \overline{\eta }}\right]=& \left(C-1\right)\frac{\partial \overline{p}}{\partial \overline{\xi }}-{\mu }_s\left(C-1\right)\left[\frac{{\partial }^2{\overline{u}}_f}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2{\overline{u}}_f}{\partial {\overline{\eta }}^2}\right]-\sigma B_o{}^2{\overline{u}}_f\hfill \\ & +CS\left({\overline{u}}_p-{\overline{u}}_f\right)+\left(\frac{{\partial }^2\overline{\Phi }}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2\overline{\Phi }}{\partial {\overline{\eta }}^2}\right){\overrightarrow{E}}_{\xi }\hfill \end{array}\}.$$

(9)

Here, C is concentration, $\mu$ is viscosity, and $“S”$ denotes the drag coefficient of interaction for the force exerted by the particles on the base liquid [49].

(ii) For the case of particle phase:

$$\frac{\partial {\overline{u}}_p}{\partial \overline{\xi }}+\frac{\partial {\overline{v}}_p}{\partial \overline{\eta }}=0,$$

(10)

$${\rho }_{f}C\left[{\overline{u}}_p\frac{\partial {\overline{u}}_p}{\partial \overline{\xi }}+{\overline{v}}_p\frac{\partial {\overline{u}}_p}{\partial \overline{\eta }}\right]=CS\left({\overline{u}}_f-{\overline{u}}_p\right)-C\frac{\partial \overline{p}}{\partial \overline{\xi }}$$

(11)

2.3. Boundary Conditions

Associated boundary conditions for fluid phase are:

$$(\mathrm{i}).{\overline{u}}_f=-L{\frac{\partial u_f}{\partial \eta }|}_{at upper wall}; at \overline{\eta }=H\left(\overline{\xi }\right),$$

(12)

$$(\mathrm{ii}).{\overline{u}}_f=L{\frac{\partial u_f}{\partial \eta }|}_{at lower wall}; at \overline{\eta }=-H\left(\overline{\xi }\right).$$

(13)

Invoking the following transformation

$$\begin{array}{c}\xi =\frac{\overline{\xi }}{\lambda },\eta =\frac{\overline{\eta }}{a},u_f=\frac{{\overline{u}}_f}{U_o},u_p=\frac{{\overline{u}}_p}{U_o},v_f=\frac{{\overline{v}}_f}{\delta U_o},v_p=\frac{{\overline{v}}_p}{\delta U_o},\overline{h}=\frac{H}{a},p=\frac{a\delta \overline{p}}{U_o{\mu }_s},{\beta }_1=\frac{L}{a},\beta =\frac{b}{a},\\ \Phi =\frac{\overline{\Phi }}{\zeta },\psi =\frac{\overline{\psi }}{a U_o},\delta =\frac{a}{\lambda },U_{HS}=\frac{-ϵ \zeta {\overrightarrow{E}}_{\xi } }{U_o{\mu }_s},m=aez\sqrt{\frac{2 n_o}{ϵK_{B}T}},M=a{B}_o\sqrt{\frac{\sigma }{{\mu }_s}}\end{array}\}.$$

(14)

The dimensionless form of Equations (1) to (3) and (8) to (13) are obtained as:

$$\overline{ h}\left(\xi \right)=\{\begin{array}{ll}1-\beta \sqrt{1-\cos \pi \xi };& for 0.5<\xi <1.5,\\ 0.5;& \mathrm{otherwise}.\end{array}$$

(15)

$$\overline{h}\left(\xi \right)=\{\begin{array}{ll}\beta -\left(\frac{\xi -0.5}{3.5}\right);& for 0.5<\xi ,\\ 0.5;& \mathrm{otherwise}.\end{array}$$

(16)

$$\overline{h}\left(\xi \right)=\{\begin{array}{ll}1-\beta Si{n}^2\left(\pi \xi \right);& for 0.5<\xi <1.5,\\ 0.5;& \mathrm{otherwise}.\end{array}$$

(17)

$$\frac{\partial u_f}{\partial \xi }+\frac{\partial v_f}{\partial \eta }=0,$$

(18)

$$\frac{d^2{u}_f}{d{\eta }^2}\left(\frac{M^2}{C-1}\right)u_f+\frac{a^{2}CS\left(u_p-u_f\right)}{\left(1-C\right){\mu }_s}+\left(\frac{m^2{U}_{HS}}{C-1}\right)\mathsf{\Phi }\left(\eta \right)=\frac{dp}{d\xi }$$

(19)

$$(\mathrm{i}).u_f=-{\beta }_1{\frac{\partial u_{f }}{\partial \eta }|}_{at upper wall}; \mathrm{at} \eta =\overline{h}\left(\xi \right),$$

(20)

$$(\mathrm{ii}).u_f={\beta }_1{\frac{\partial u_{f }}{\partial \eta }|}_{at lower wall}; \mathrm{at} \eta =-\overline{h}\left(\xi \right).$$

(21)

$$\frac{\partial u_{ p}}{\partial \xi }+\frac{\partial v_{ p}}{\partial \eta }=0,$$

(22)

$$\frac{{\mu }_s}{a\delta \lambda }\frac{dp}{d\xi }=S\left(u_f-u_p\right).$$

(23)

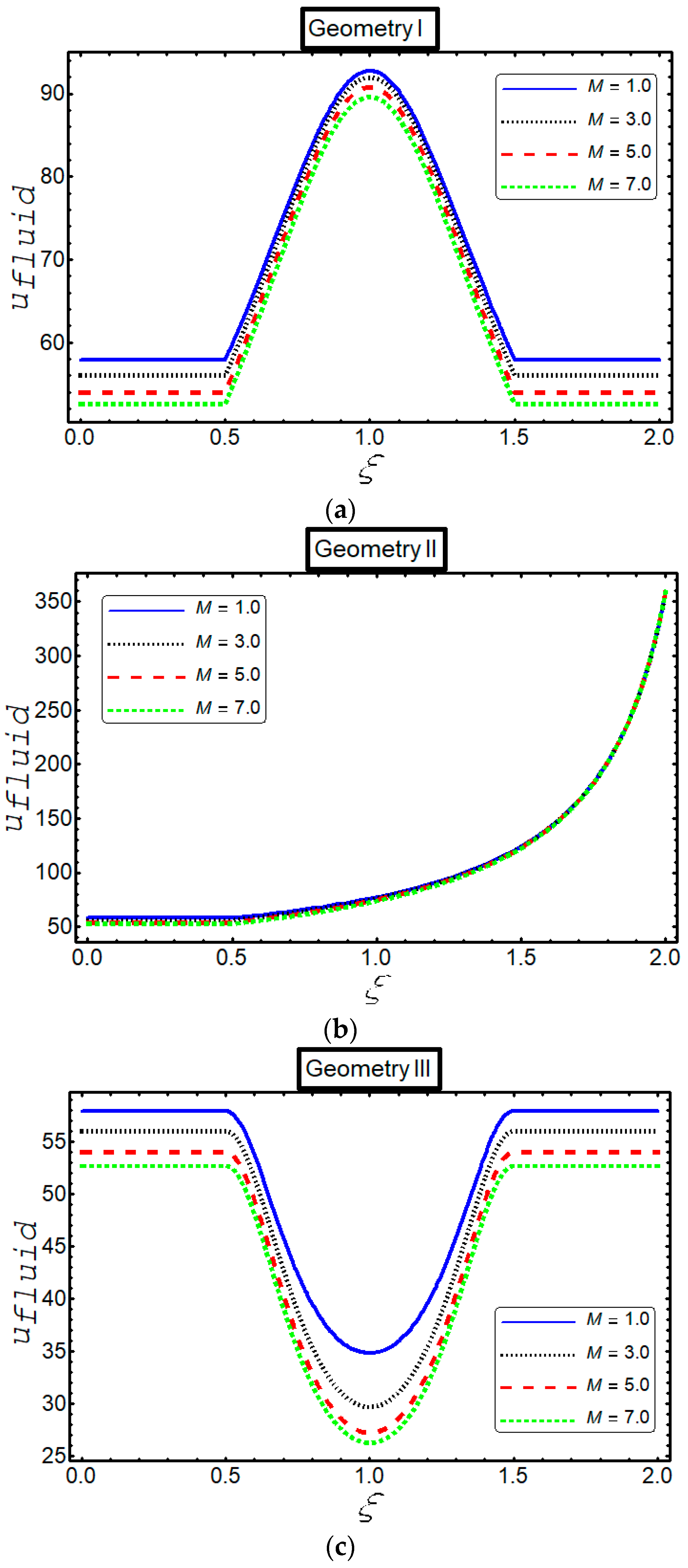
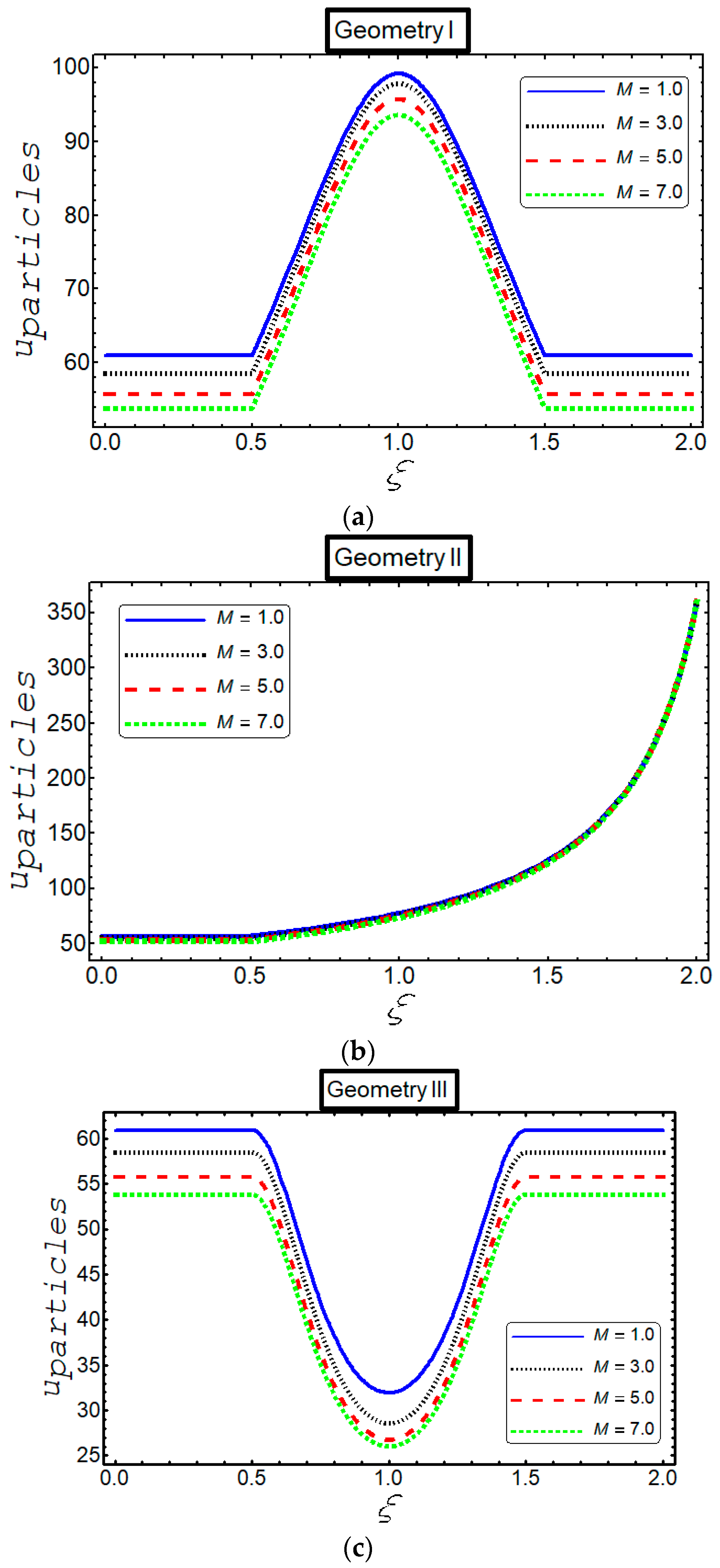
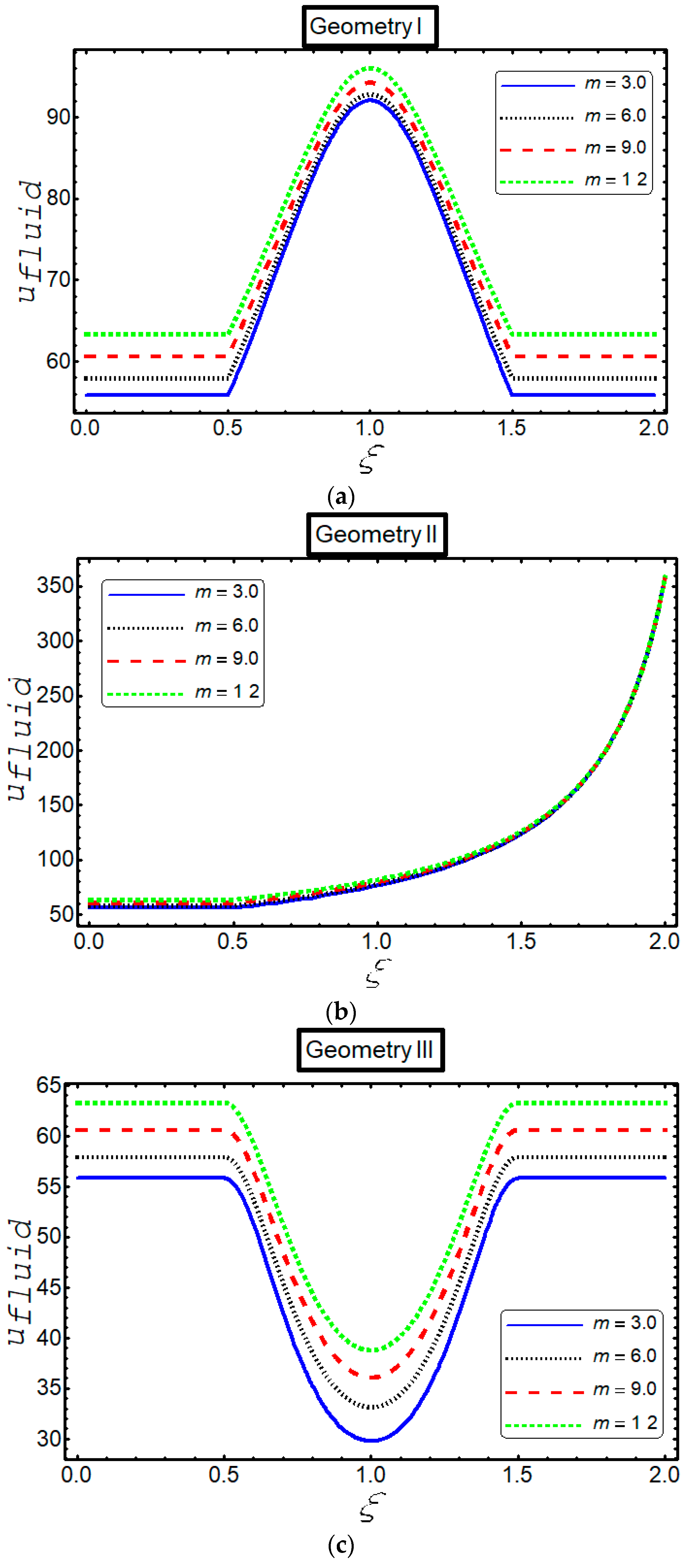
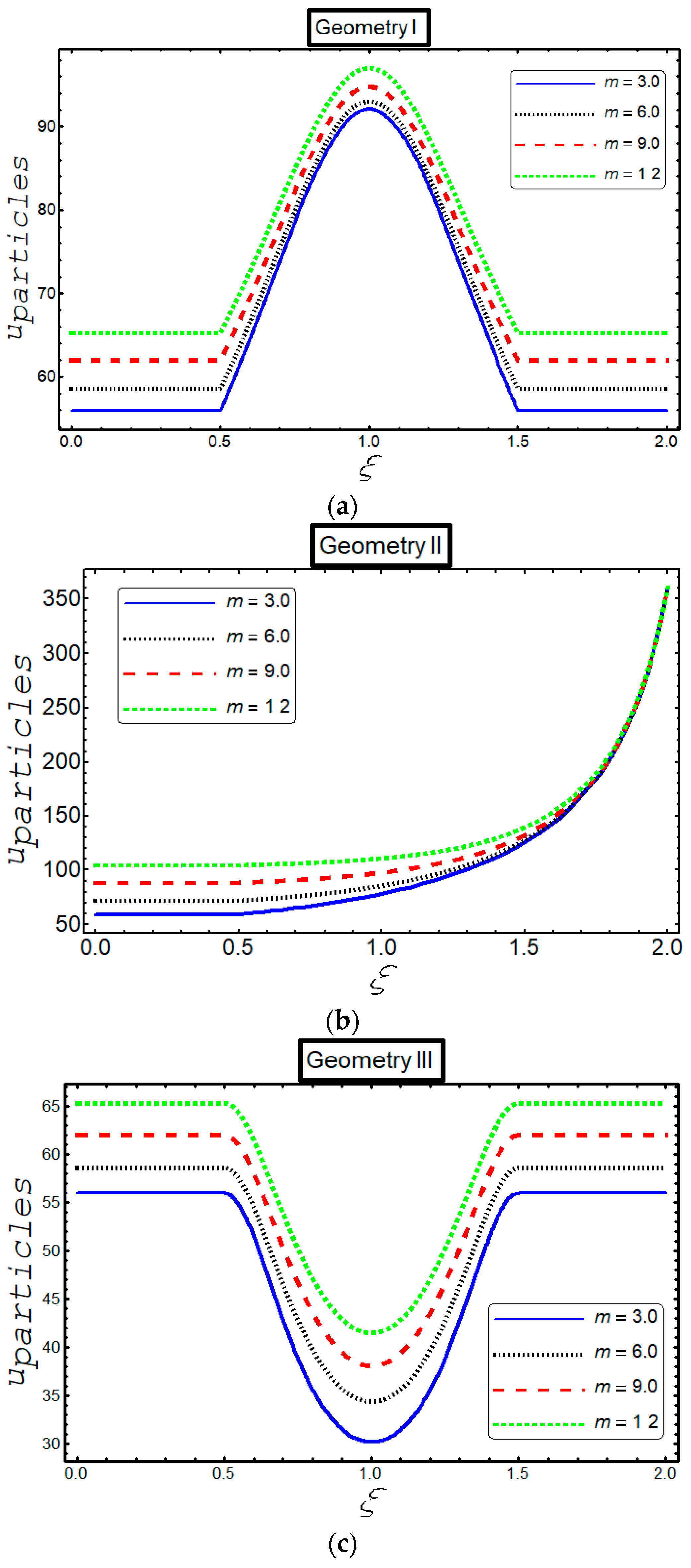
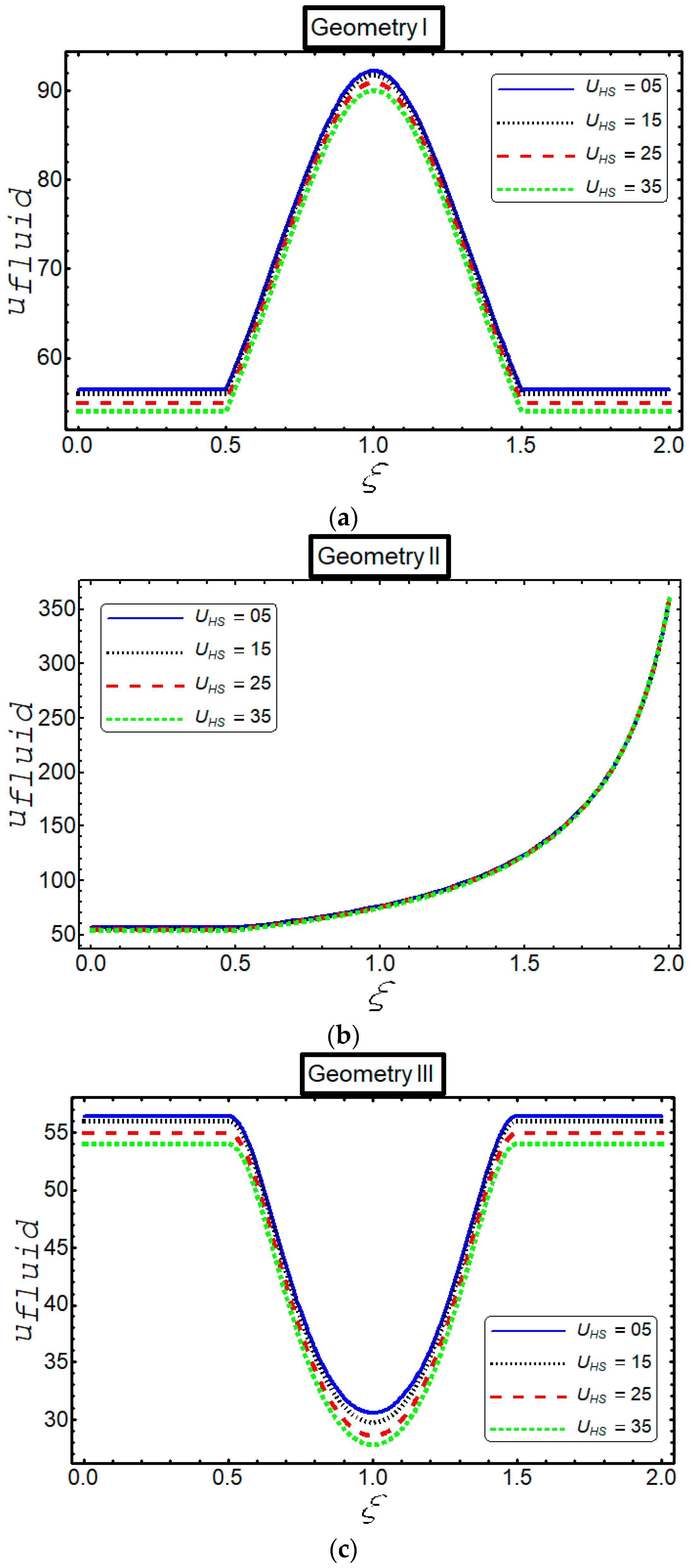
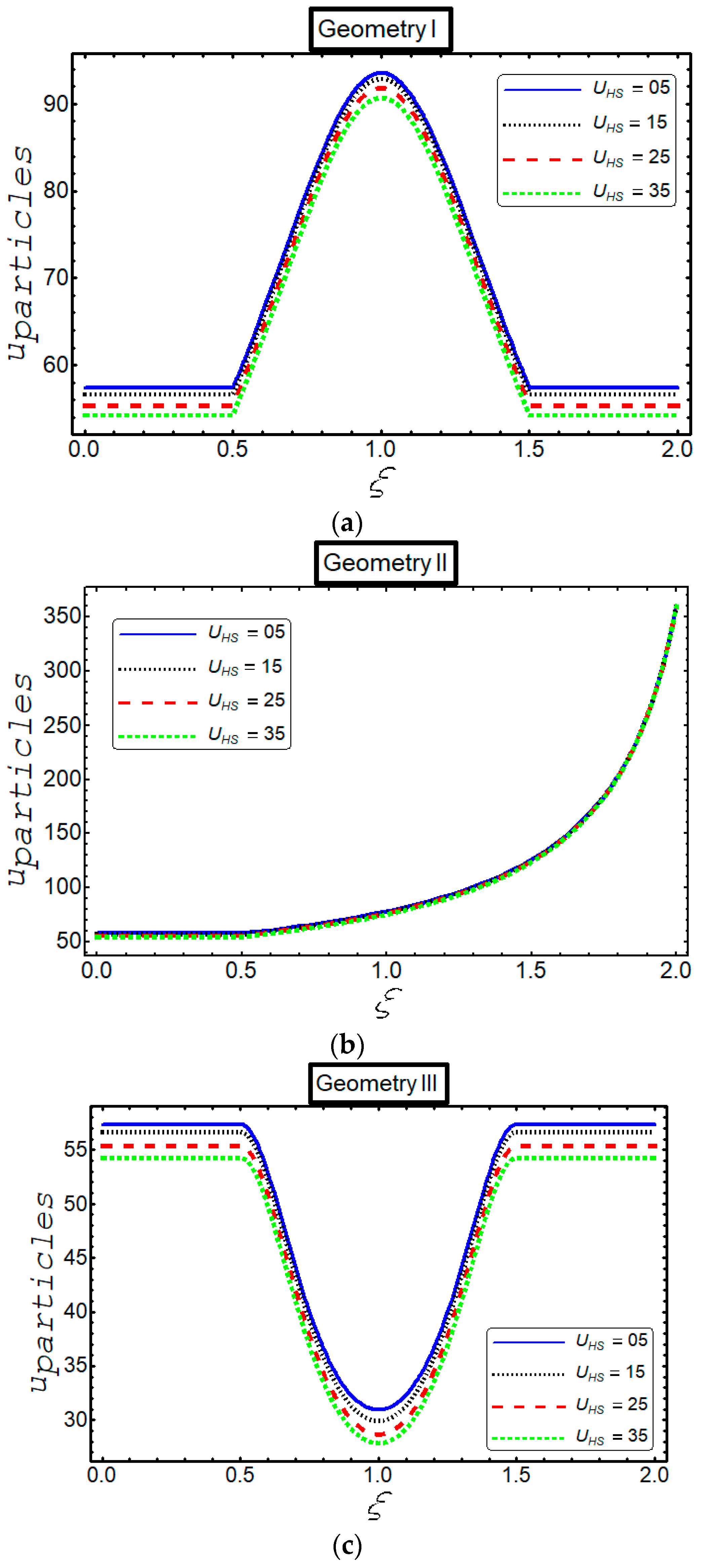
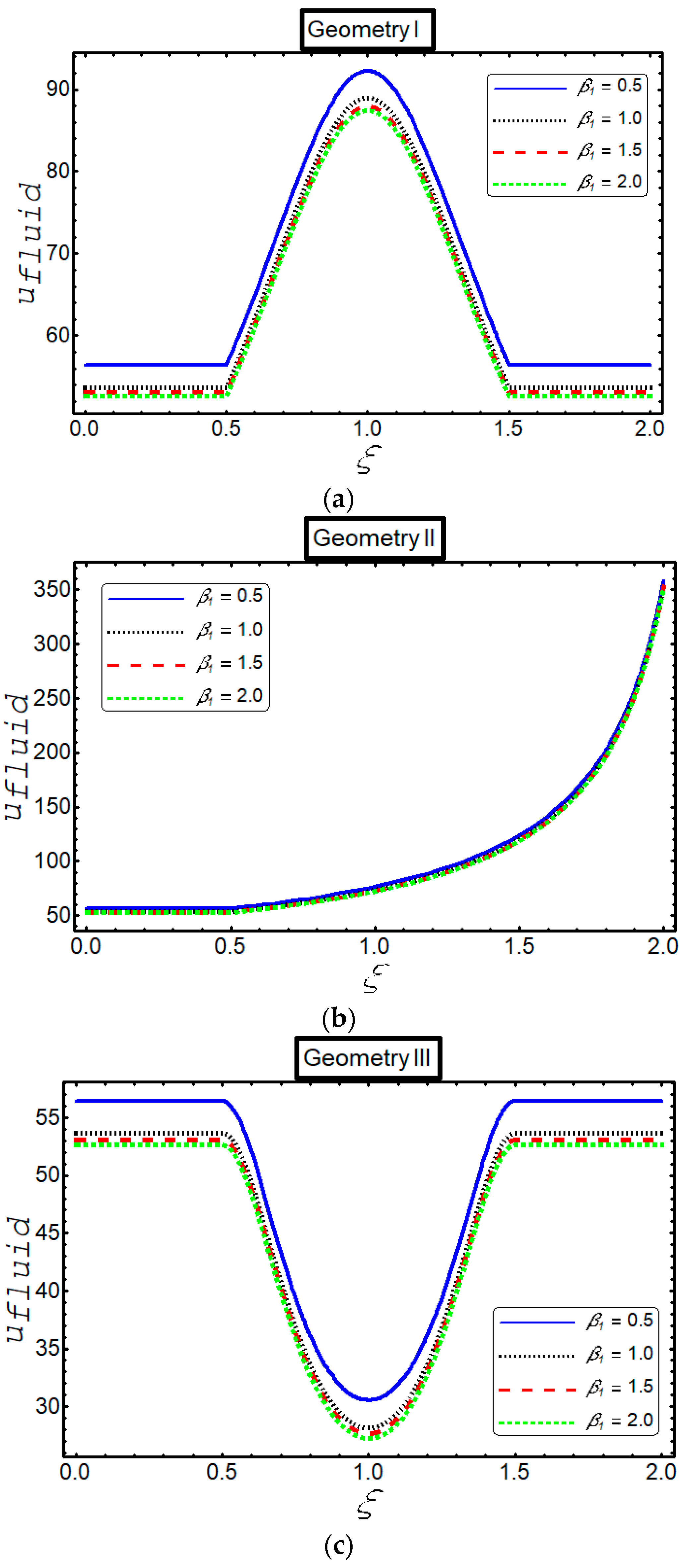
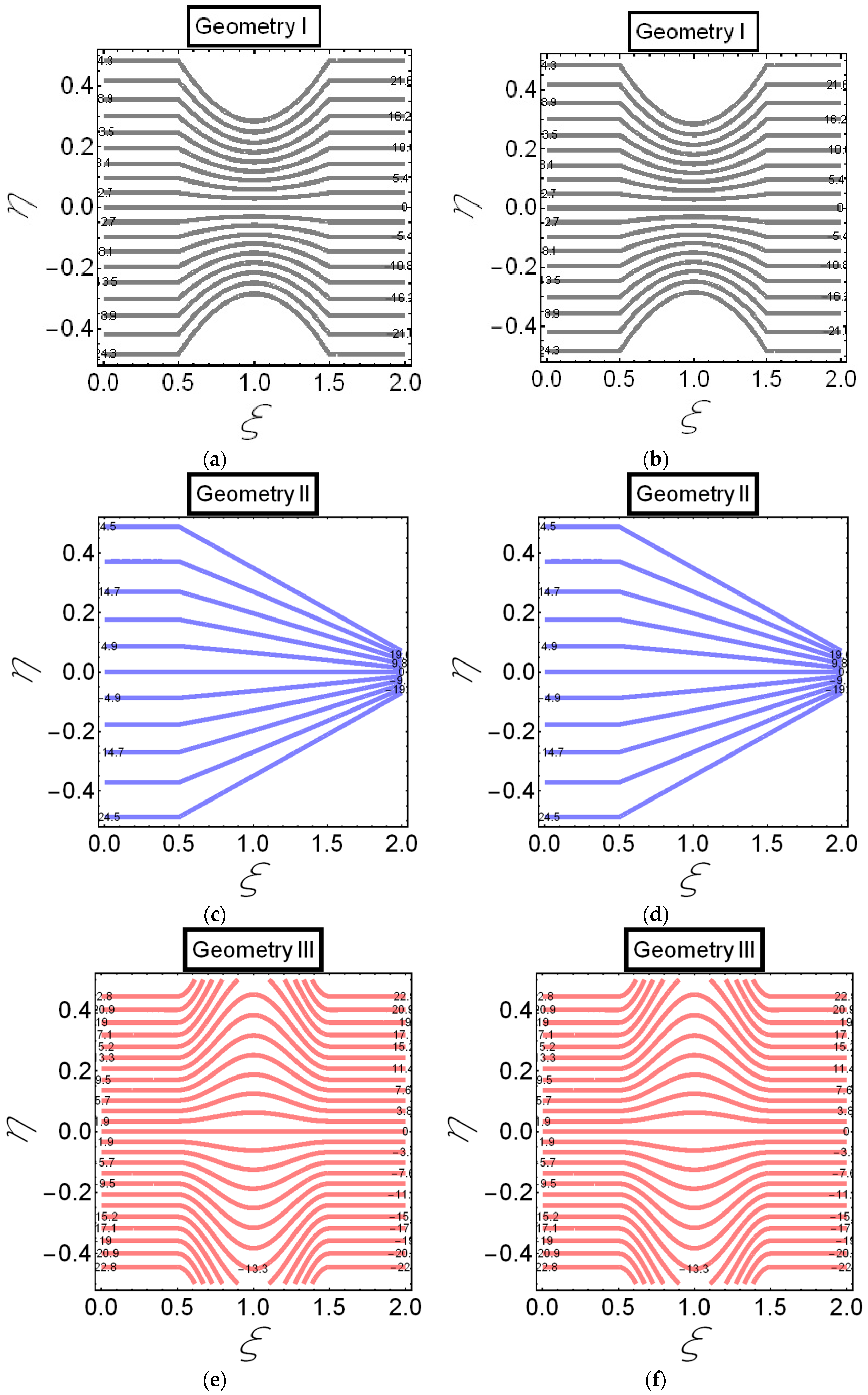
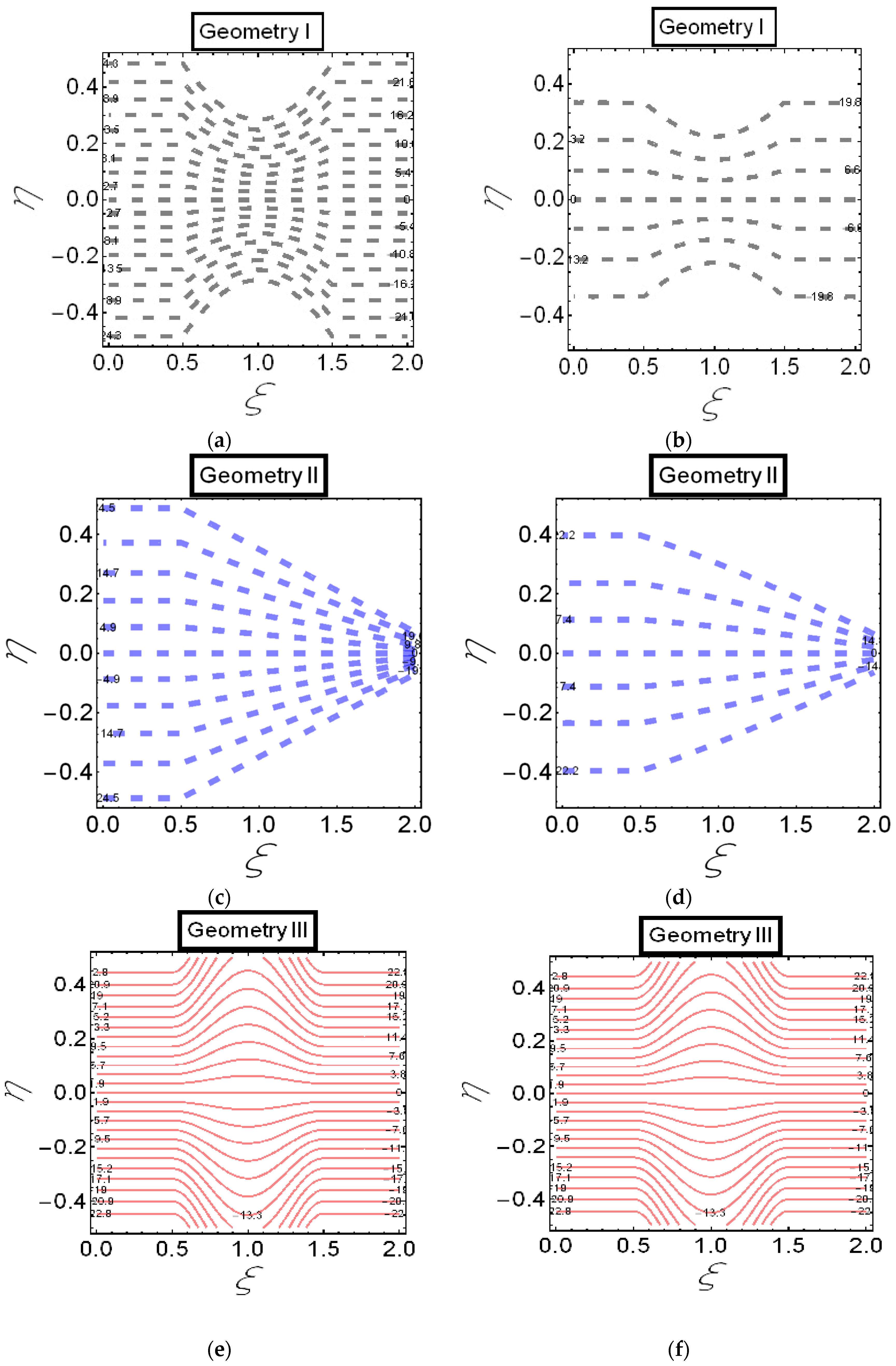
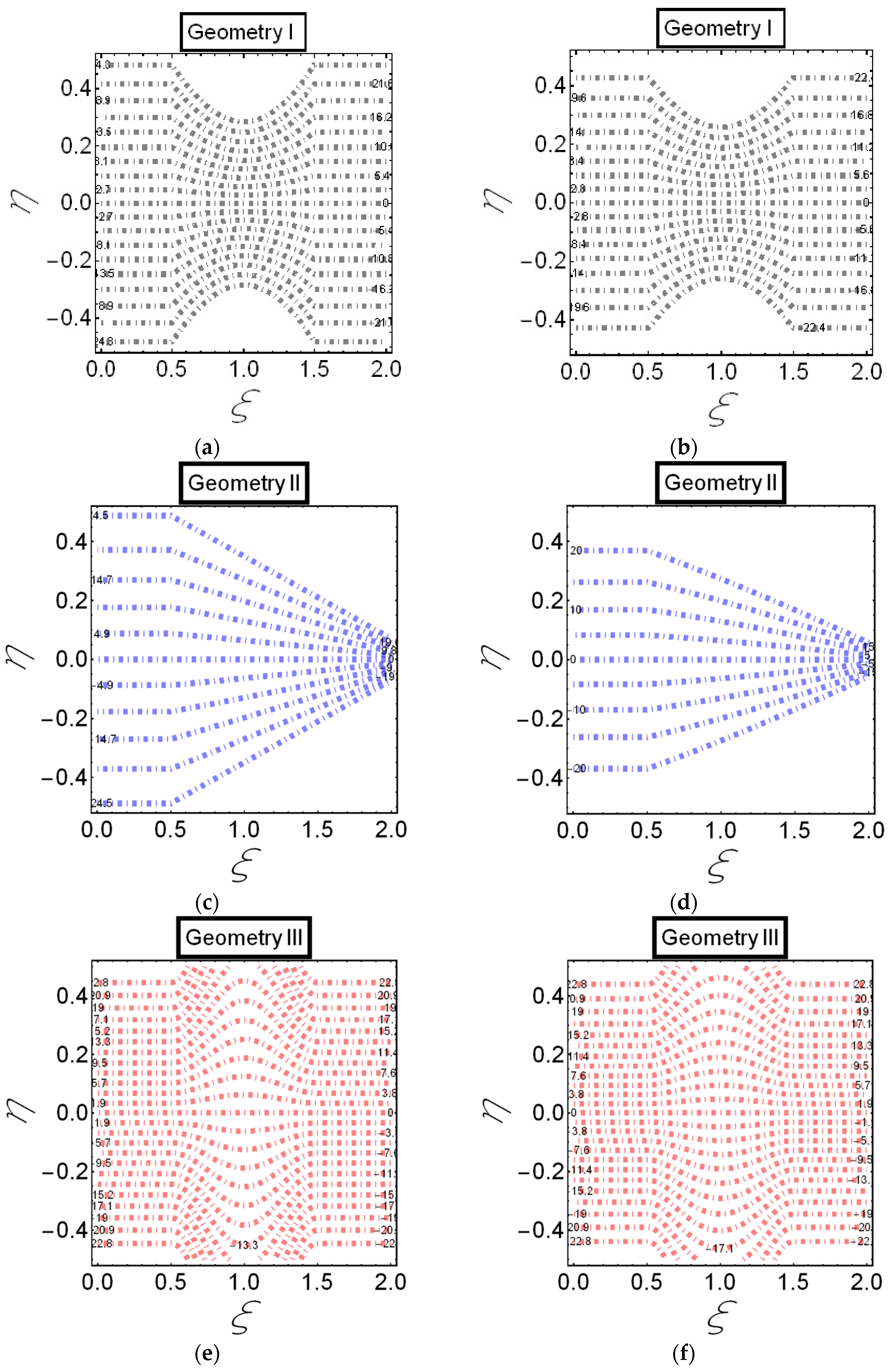
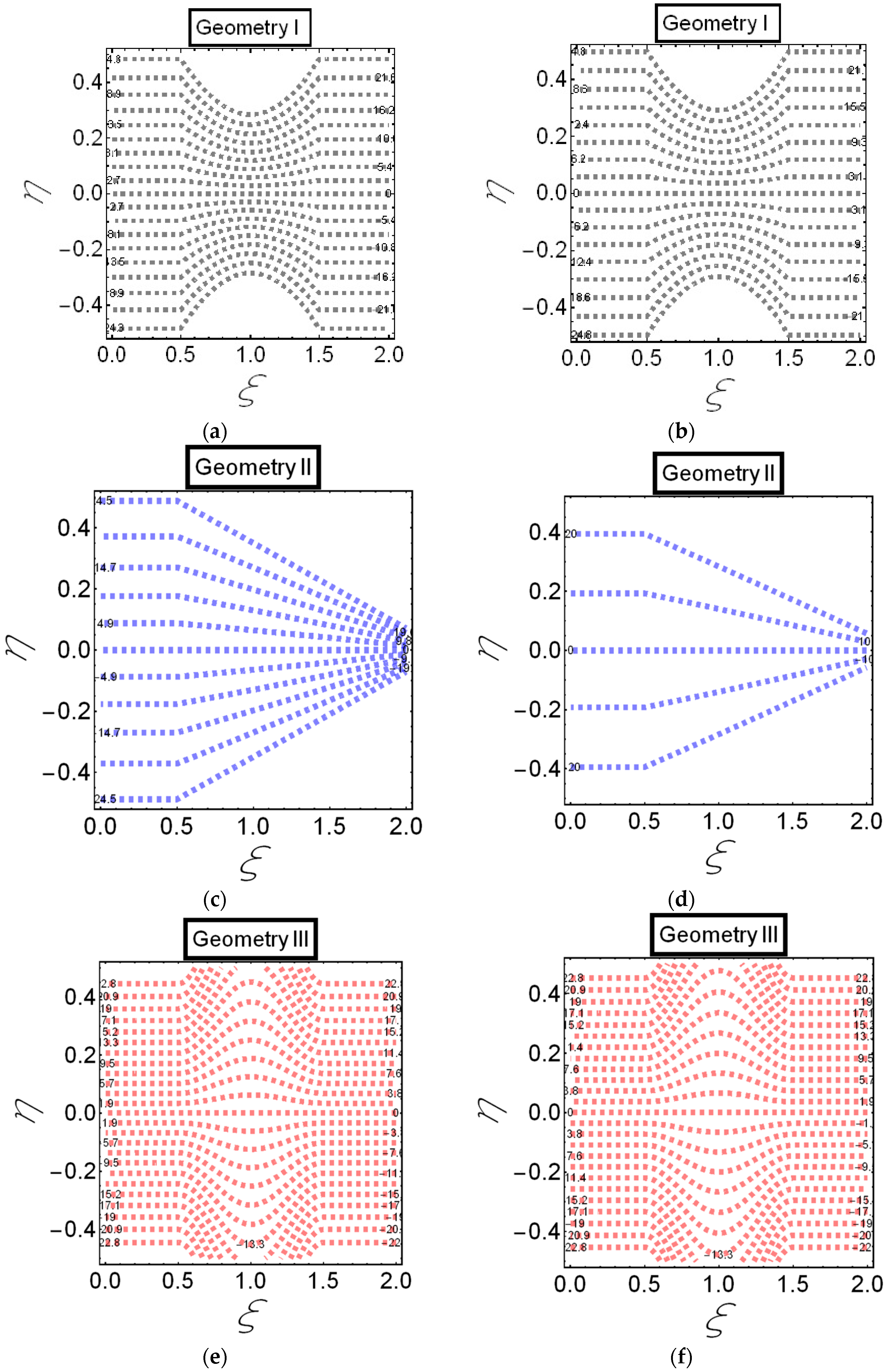
3. Results

After basic manipulation, the electro-osmotic potential function $\mathsf{\Phi }\left(\eta \right),$ given in Equation (19), can be attained as

$$\mathsf{\Phi }\left(\eta \right)=\frac{\cosh \left(m \eta \right)}{\cosh \left(m \overline{h}\right)}$$

(24)

In view of Equation (24), Equation (19) can be written as

$$\frac{d^2{u}_f}{d{\eta }^2}+\left(\frac{M^2}{C-1}\right)u_f+\frac{a^{2}CS\left(u_p-u_f\right)}{\left(1-C\right){\mu }_s}+\left(\frac{m^2{U}_{HS}}{C-1}\right)\frac{\cosh \left(m\eta \right)}{\cosh \left(m\overline{h}\right)}=\frac{dp}{d\xi }$$

(25)

The velocity of the particles in view of Equation (23) can be expressed as

$$u_p=u_f-\left(\frac{{\mu }_s}{a \delta \lambda S}\right)\frac{dp}{d\xi }$$

(26)

Using Equation (26) in Equation (25), yields

$$\frac{d^2{u}_f}{d{\eta }^2}+\left(\frac{M^2}{C-1}\right)u_f=\left(1+\frac{aCS}{\left(C-1\right)\delta \lambda S}\right)\frac{dp}{d\xi }+\left(\frac{m^2{U}_{HS}}{1-C}\right)\frac{\cosh \left(m\eta \right)}{\cosh \left(m\overline{h}\right)}$$

(27)

By using routine calculation, the exact solution of the second order linear but nonhomogeneous ordinary differential Equation (27) by means of boundary conditions in Equations (20) and (21) yield

$$\begin{array}{cc}\hfill u_f=& \left\{\begin{array}{c}\frac{\frac{dp}{d\xi }\left(\left(1-C\right)\delta \lambda -aC\right)}{\delta \lambda M^2}-\left(\frac{m^2{U}_{HS}}{m^2\left(C-1\right)-M^2}\right)\\ -\left(\frac{m^3{U}_{HS}\tanh \left(m\overline{h}\right)}{m^2\left(C-1\right)-M^2}\right){\beta }_1\end{array}\right\}\frac{\cosh \left(\frac{M\eta }{\sqrt{C-1}}\right)}{\left({\beta }_1\left(\frac{M\eta }{\sqrt{C-1}}\right)\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)+\cosh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\right)}\hfill \\ & +\frac{\frac{dp}{d\xi }\left(\left(1-C\right)\delta \lambda -aC\right)}{\delta \lambda M^2}+\frac{m^2{U}_{HS}\cosh \left(m\eta \right)}{\left(m^2\left(C-1\right)-M^2\right)\cosh \left(m\overline{h}\right)}.\hfill \end{array}$$

(28)

Further simplification of Equation (28) yields:

$$u_f=\{\begin{array}{c}\left\{\begin{array}{c}\frac{m^2{U}_{HS}}{M^2+m^2\left(C-1\right)}+\frac{\frac{dp}{d\xi }\left(\delta \lambda -C\left(a+\delta \lambda \right)\right)}{\delta \lambda M^2}\\ +\left(\frac{m^3{U}_{HS}\tanh \left(m\overline{h}\right)}{M^2+m^2\left(C-1\right)}\right){\beta }_1\end{array}\right\}\frac{\cosh \left(\frac{M\eta }{\sqrt{C-1}}\right)}{\left({\beta }_1\left(\frac{M\eta }{\sqrt{C-1}}\right)\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)+\cosh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\right)}\hfill \\ +\frac{\frac{dp}{d\xi }\left(aC+\left(C-1\right)\delta \lambda \right)}{\delta \lambda M^2}-\frac{m^2{U}_{HS}\cosh \left(m\eta \right)\sec \mathrm{h}\left(\mathrm{m}\overline{h}\right)}{M^2+m^2\left(C-1\right)}.\hfill \end{array}$$

(29)

Which is the required velocity of the base fluid.

By using the base fluid values given above in Equation (29) in Equation (26) one gets

$$u_p=\{\begin{array}{c}\left\{\begin{array}{c}\frac{\frac{dp}{d\xi }\left(\delta \lambda -C\left(a+\delta \lambda \right)\right)}{\delta \lambda M^2}+\left(\frac{m^3{U}_{HS}\tanh \left(m\overline{h}\right)}{M^2+m^2\left(C-1\right)}\right){\beta }_1\\ +\frac{m^2{U}_{HS}}{M^2+m^2\left(C-1\right)}\end{array}\right\}\frac{\cosh \left(\frac{M\eta }{\sqrt{C-1}}\right)}{\left({\beta }_1\left(\frac{M\eta }{\sqrt{C-1}}\right)\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)+\cosh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\right)}\hfill \\ +\frac{dp}{d\xi }\left(\frac{\left(aC+\left(C-1\right)\delta \lambda \right)}{\delta \lambda M^2}\right)-\frac{m^2{U}_{HS}\cosh \left(m\eta \right)\sec \mathrm{h}\left(\mathrm{m}\overline{h}\right)}{M^2+m^2\left(C-1\right)}-\left(\frac{{\mu }_s}{a \delta \lambda S}\right)\frac{dp}{d\xi }.\hfill \end{array}$$

(30)

Simplification of Equation (30) further leads to

$$u_p=\{\begin{array}{c}\left\{\begin{array}{c}\frac{m^2{U}_{HS}}{M^2+m^2\left(C-1\right)}+\frac{\frac{dp}{d\xi }\left(\delta \lambda -C\left(a+\delta \lambda \right)\right)}{\delta \lambda M^2}\\ +\left(\frac{m^3{U}_{HS}tanh\left(m\overline{h}\right)}{M^2+m^2\left(C-1\right)}\right){\beta }_1\end{array}\right\}\frac{\cosh \left(\frac{M\eta }{\sqrt{C-1}}\right)}{\left({\beta }_1\left(\frac{M\eta }{\sqrt{C-1}}\right)\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)+\cosh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\right)}\hfill \\ -\frac{\frac{dp}{d\xi }\left(aS\left(C-1\right)\delta \lambda +a^{2}CS-M^2{\mu }_s\right)}{a\delta \lambda M^{2}S}-\frac{m^2{U}_{HS}\cosh \left(m\eta \right)\sec \mathrm{h}\left(\mathrm{m}\overline{h}\right)}{M^2+m^2\left(C-1\right)}.\hfill \end{array}$$

(31)

Now, for fluid and particle phases, the volumetric flow rates are obtained as:

$$Q_f={{\displaystyle \int }}_0^{\overline{h}}{u}_{f}d\eta ,$$

(32)

$$Q_p={{\displaystyle \int }}_0^{\overline{h}}{u}_{p}d\eta .$$

(33)

However, the total fluid particle volumetric flow rate can be obtained as:

$$Q=Q_f+Q_p,$$

(34)

$$\mathrm{Q}=\{\begin{array}{c}2\left(\frac{\overline{h}aC+\delta \lambda \overline{h}\left(C-1\right)}{a\delta \lambda M^{2}S}\right)\frac{dp}{d\xi }-\left(\frac{\overline{h}{\mu }_s}{a\delta \lambda S}\right)\frac{dp}{d\xi }-\frac{2m{U}_{HS}\tanh \left(m\overline{h}\right)}{M^2+m^2\left(C-1\right)}+\hfill \\ 2\sinh \left(\frac{\overline{h}M}{\sqrt{C-1}}\right)\left\{\frac{\frac{m^2{U}_{HS}}{M^2+m^2\left(C-1\right)}-\frac{\frac{dp}{d\xi }\left(aC+\left(C-1\right)\delta \lambda \right)}{\delta \lambda M^2}+\left(\frac{m^3{U}_{HS}\tan \mathrm{h}\left(m\overline{h}\right)}{M^2+m^2\left(C-1\right)}\right){\beta }_1}{\frac{M}{\sqrt{C-1}} \left({\beta }_1\left( \frac{M}{\sqrt{C-1}} \right) \sin \mathrm{h}\left( \frac{M\overline{h}}{\sqrt{C-1}} \right)+ \cos \mathrm{h}\left( \frac{M\overline{h}}{\sqrt{C-1}} \right)\right)}\right\}\hfill \end{array}$$

(35)

Pressure gradient is the most important feature of the considered fluid. By simplifying the expression for pressure gradient from Equation (35).

$$\frac{dp}{d\xi }=\frac{a\delta \lambda M^{2}S\left\{-\frac{1}{\sqrt{C-1}}M\cosh \left(\frac{\overline{h}M}{\sqrt{C-1}}\right)\left(\begin{array}{c}\left(\left(M^2+m^2\left(C-1\right)\right)Q+2m{U}_{HS}\tanh \left(m\overline{h}\right)\right)+\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\\ \left(\begin{array}{c}-\left(\frac{M^2}{1-C}\right){\beta }_{1}MQ\left(M^2+m^2\left(C-1\right)\right)+2m^2{U}_{HS}\\ +2m{\beta }_1{U}_{HS}\left(-\left(\frac{M^2}{1-C}\right)+m^2\right)tanh\left(m\overline{h}\right)\end{array}\right)\end{array}\right)\right\}}{\left(M^2+m^2\left(C-1\right)\right)\left\{\begin{array}{c}\frac{M\overline{h}}{\sqrt{C-1}}\left(M^2{U}_{HS}-2aS\left(aC+\left(C-1\right)\delta \lambda \right)\right)\cosh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\\ +\left(\left(aSC+\left(C-1\right)\delta \lambda S\right)\left(2a-2a{\beta }_1\left(\frac{M^2\overline{h}}{\left(C-1\right)}\right)\right)+{\beta }_1\left(\frac{M^4\overline{h}{U}_{HS}}{\left(C-1\right)}\right)\right)\sinh \left(\frac{M\overline{h}}{\sqrt{C-1}}\right)\end{array}\right\}}$$

(36)

4. Discussion

A brief debate on the role of active factors, namely Helmholtz–Smoluchowski velocity $U_{HS}$, Hartmann number $M$, electro-osmotic parameter $m$, and slip parameter ${\beta }_1$ that effectively contribute to the bi-liquid flow through three diverse geometries are illustrated in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. In Figure 4a–c the motion of fluid phase is observed against the Hartmann number. It is noted that the velocity of fluid drops down for higher values of the Hartmann number. In Figure 5a–c, the velocity of particles phase also declines due to variation in magnetic field. This phenomenon basically is caused in the response of Lorentz force which resists the flow. Moreover, the magnetic effects are intense for the case of diverging type of geometry (i.e., geometry III) as observed in Figure 4c and Figure 5c, respectively. This also confirms that the magnetic induction is much stronger for diverging-converging nozzles, as compared to geometry I and II. The variation of electro-osmotic parameter $m$, is displayed in Figure 6 and Figure 7. One sees that the motion of both fluid and Hafnium particles is supported by the concerned parameter, by considering the flow in any form of geometry. However, the influences of $m$ are so prominent in the convergent type of geometry. Therefore, the velocity of fluid and particles inclines rapidly, as shown in Figure 6a–c and Figure 7a–c, respectively. This changing trend is the contribution of the electrokinetic term in the governing equation.

An opposite behavior in the flow is observed for Helmholtz–Smoluchowski velocity $U_{HS}.$ By looking at each diagram shown in Figure 8a–c and Figure 9a–c, the velocity of both phases reduces in strength for the higher values of $U_{HS}.$ The most significant parameter of this survey, is the lubrication parameter ${\beta }_1$, which is shown in Figure 10a–c and Figure 11a–c. The effects of lubrication at both walls of each geometry resist the performance of fluid and particle. Therefore, by increasing the slip parameter velocity of the fluid, the particle also declines.

The pattern of fluid flow through the given geometries, can be described by stream lines. In this regard, Figure 12, Figure 13, Figure 14 and Figure 15 have been sketched. Deterioration in velocities is observed in both phases for the increasing values of M which indicates hindrance in the course of flow. Thus, escalation in M causes the emergence in terms of extra stream lines as observed in Figure 12a,b,e,f, for geometries I and III whereas for geometry II, the fluid’s velocity gets the highest momentum, thus the lines of magnetic fields can only manage to compress the streamlines inwards and the same is seen in Figure 12c,d. Consequently, the fall in velocity of the fluid–particle suspension is perceived. The role of $m$ on streamlines varies in all cases. The streamlines that shrink against higher m is detected in Figure 13a,b. One can detect that fluid flow gets stress-free having no hurdle in its way in geometry $\mathrm{I}$, whereas streamlines remain unchanged in the rest of two geometries II and III, as displayed in Figure 13c–f. It is noted that streamlines of Helmholtz–Smoluchowski velocity $U_{HS}$, remain unchanged while maximizing the value of parameter. No prominent change is observed on the structure of streamlines one way or another for all geometries in Figure 14a–f. Streamlines of slip parameter ${\beta }_1$, remain unchanged by increasing the value of parameter. No prominent change is observed on the structure of streamlines one way or another for all geometries in Figure 15a–f.

5. Conclusions

The expressions of the velocities for fluid and particle phase are analytically obtained in the multiphase flow of water and Hafnium particles $\left(HF-H_{2}O\right)$. The flow is examined through three different geometries for various parameters. The effects of slip is studied on multiphase flow synthesis of nano-sized particles. Some important observations are listed as:

• The velocity decreases against Hartmann number $M$ and Helmholtz–Smoluchowski $U_{HS}$ in all cases.
• The velocity of particle phase decreases against the slip parameter, ${\beta }_1$ in geometry I and geometry II whereas it increases in geometry III.
• The velocity increases against $m$, in the three geometries for both particles and fluid phases.
• Inclined behavior of velocity is observed for both phases in three geometries against $m$.
• In the case of Hartmann number $M$, Helmholtz–Smoluchowski $U_{HS}$, and slip parameter ${\beta }_1$, the graphs of streamlines are the same for all three geometries. However, the reduction of the streamlines for electro-osmotic parameter $m$, is observed. This behavior is due to the curve-like structure of the channel.