Abstract
Movement of sand particles is a complicated phenomenon that occurs in nature. In this paper, the main goal is to provide an analytic model for the deposition profile of sand particles downstream of a fence. The analytic model was derived with respect to governing equations and shear flows for upstream and downstream regions. In this approach, we obtain a new expression for the downstream velocity of the fence, which allows for the determination of potential areas of deposition particles by assuming a log-normal distribution profile. A discrete-phase flow (DPM) was used to inject particles in the simulation domain. The DPM gives capabilities to capture spatiotemporal velocities components, as we can define the probability of deposition particles in the downstream of the fence. The proposed model was validated with a numerical model and experimental results. The comparison with field data and numerical results shows that the deposition profile is in acceptable agreement. With some assumptions and modifications about the properties of particles, the results of this research can be extended to snow accumulation downstream of a fence.
1. Introduction
Significant research has been conducted to investigate aeolian transportation of particles. In general, we can classify this research into three categories: experimental, numerical, and analytical. Experimental investigations have been performed in the form of wind tunnel and fieldwork, which are expensive and in some cases are not possible because of difficulties in measuring turbulent flow near the surface. One of the main challenges in calculating soil erosion rates, boundary layer turbulent parameters, and probability of sand transport is the choosing of averaging time [1]. A small miscalculation in the wind velocity leads to inaccurate predictions of wind erosion [2]. Usually, windy conditions are common in natural desert regions because of the stratification layer of the atmosphere [3,4]. Wind and erosion influence the shape of sand particles; therefore, desert sands are more rounded and denser than coastal sand particles [5]. Wind makes the movement of sand particles that occurs through creep, saltation, and suspension processes (Figure 1) [6,7]. Larger sand particles move through creeping on the surface, the majority move through saltation, which uplifts them into the air when striking the surface, and smaller particles are suspended in the air and are transported long distances in the air.
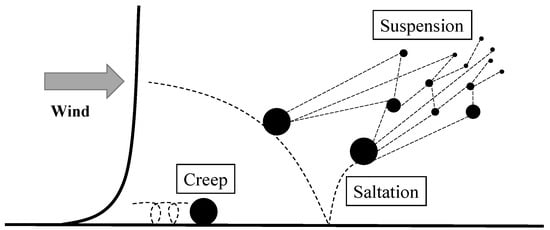
Figure 1.
Transportation of sand particles by wind in a desert.
There are several techniques for reducing effects of erosion. Vegetation reduces the movement of sand particles, which mitigates the erosion of an area [8]. The large eddy simulation (LES) has been used to compare the normalized wind velocity and momentum flux simulated over vegetated surfaces of shrubs and trees by Dupont et al. [9]. As a consequence, trees have a better performance than shrubs to reduce sand erosion. Wang and Young [10] investigated the behavior of vegetation-coated sand particles, which was consistent with experimental work based on an image processing model used in computer graphics.
The amount of sand deposition depends on different factors (e.g., porosity, number, and height of a fence). Using a solid fence generates strong vorticities in the downstream. Saif et al. [11] investigated a numerical solution of fences with two segment variable porosities. They used a simplistic algorithm, k–ε model to find that the most effective velocity reduction was in the case with a lower section of 20% and a higher 40% porosity composition. Owing to the fence design with a two-segment variable porosity, compared to a uniformity of 30%, it provided a small shift of high turbulent kinetic energy (TKE) away from the fence. Bitog et al. [12] investigated the movement of three adjacent fences. In this study, the distances between fences were 2, 4, and 6 m, the fence heights were 0.6, 0.8, and 1 m, and the porosities were 0, 0.2, 0.4, and 0.6. They recommended the distance between fences should be at least 6 m, with a height of 0.6 and an optimum porosity of 20%. Dong et al. [13] investigated velocity particles near the surface in a wind tunnel and showed that the probability density function of sand particles’ lift-off, incident velocities, and their vertical components were a function of sand particles and wind velocity. Liu et al. [14] performed a numerical research comparison by computational fluid dynamic (CFD) with an actual-sized experimental model fence, and they realized some flow characteristics near the fence cannot be captured in the reduced-scale experimental or numerical model.
Lima et al. [15] found that the optimal fence height was around 50 cm, and using a fence with a height more than 1.25 m did not have reasonable economic benefits. Furthermore, Lavasani et al. [16] have proven that increases in the height of a fence from 1 to 1.5 m was not helpful in reducing sand deposition. Nishi and Kimura’s results from a field study confirmed that most deposited sand particles progressed from the lee of a fence to the upwind of the fence by decreasing the porosity of the fence [17,18]. Jensen [19] defined the shelter effect parameter as a velocity deficit to an inlet velocity. His results indicated that the optimal porosity for the maximum sheltering was around 35%–40%. Bruno et al. [20] discussed the mean wind flow, streamlines, and related deposition levels for different porous fences. The wind pattern, formation of the eddy zones, vortex structure, and accumulation potential were directly related to the fence porosity. The reattachment distance in the downstream of the fence can be decreased from 15 to 9 h by increasing the porosity from 10% to 20% [21].
Naegëli [22] found the relative wind velocities ( around fences (leeward and windward) with different porosities, where was the time-averaged upstream wind velocity and was the time-averaged undisturbed wind velocity. In the lee of lower-porosity fences, the reduction of the wind speed was higher, and the range of the relative velocity at the fence was between 0.3 and 0.7. Phillips and Willetts [23] found the distributions of shear velocity ( around fences (leeward and windward) with different porosities, where was the time-averaged upstream shear velocity and was the time-averaged undisturbed shear velocity. In this paper, we proposed a new analytical approach with fundamental equations to find the profile of deposition in the downstream.
2. Method
In this chapter, we used governing equations to find where a region had more potential to deposit sand particles in the downstream of a fence [24,25]. This model consisted of three steps: (1) the minimum velocity behind the fence was computed, corresponding to the properties of the fence and the shear profile; (2) the maximum deposition profile was defined with respect to wake parameters; (3) the deposition profile was determined with local conditions. Figure 2 presents the control volume of a domain that was divided into the upstream and downstream regions of the fence. First, we did not consider sand particles in the domain and assumed that the inlet wind velocity was steady and incompressible. We reached the following expressions from governing and energy equations between boundary conditions 1 and 2, where is a kinetic energy factor. Particularly, in this methodology, we regarded the shear profile as a kinetic energy factor parameter.
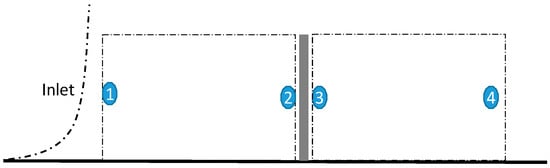
Figure 2.
Control volume of an upstream and downstream fence.
We can follow the same approach and derive Equation (2) between boundary conditions 3 and 4. By some mathematic work, we reached the following expression for the change of the average pressure in the upstream and downstream fence:
According to Darcy’s equations [26] and Idelchik [27], the pressure drop in a porous medium was written as:
where and are the coefficients of resistance. The wake in the downstream of the fence is expanded. Therefore, the downstream shear rate is lower than the upstream one. We defined the parameter to be proportional to the ratio, which was approximately between 1 and 1.05, and was equal to . According to Equations (3) and (4), was described as:
The upstream logarithmic form of velocity is a function of surface roughness that is characteristic of a local terrain. We assumed the wake behind the fence is expanded linearly with a slope line of , which is a function of turbulent and surface roughness of a terrain, since the porous medium thickness is small (). According to the continuity between boundary conditions 3 and 4, Equations (6)–(8) were obtained:
where , , b, and D are the maximum probability deposition profile, porosity, thickness, and height of the fence, respectively. If we do not consider the effect of the local geographic, uplift, saltation, and creep for the particles, the deposition profile of sand particles should be symmetric along the streamwise. We suppose the deposition sand profile is a log-normal distribution with positive skews, and the mode profile was calculated from Equation (8). The mean and standard deviation of the probability density function depended on the geographic features of locations.
3. Simulation and Discussion
Figure 3 summarizes the main steps in the simulation. In general, sand particles are injected into the simulation domain corresponding to each time step. Then, considering the minimum velocity at the boundary layer, the probability density function for the particles to be deposed is identified. The density of particles is 2650 kg/m3 with a Rosin-Rammler distribution [28], which is an exponential relation between the particle diameter and the mass fraction [29,30]. Further details are available in Reference [16]. Figure 4 shows the velocity magnitude of sand particles in the downstream of the simulation. The particles near the surface with a lower velocity have more potential to deposit.
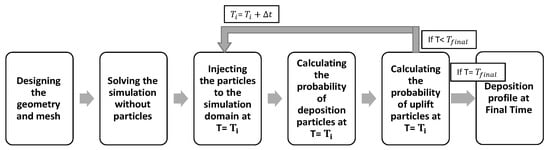
Figure 3.
Flow chart of the main steps in the simulation.
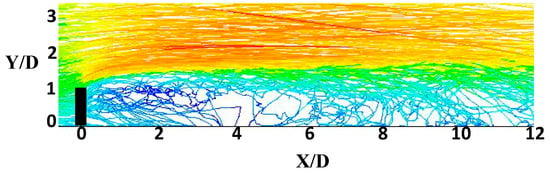
Figure 4.
Contours of the sand particles.
We used the ANSYS Fluent [30] software in our simulation, and sand particles were injected into the domain by the Lagrange method. The simple algorithm was used to solve pressure–velocity coupling. The boundary condition of the fence was the porous jump, the inlet profile followed the logarithmic law as a function of friction velocity and surface roughness, and the pressure outlet airflow was considered fully developed for the outlet. The mesh independency was checked for critical parameters.
The results for the fence with a porosity of 50% and a height of 1 m were validated with Tabler [31] field data, the Iversen wind tunnel [32], and simulation results [16] (Figure 5).
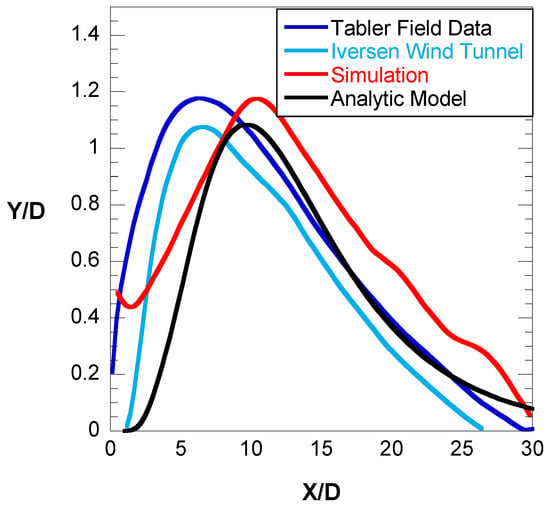
Figure 5.
Deposition profiles of sand particles in the downstream of the fence.
4. Conclusions
A new analytic model was proposed to predict the profile of sand deposition in a downstream fence. The proposed model considered the properties of the fence and the aerodynamic conditions of the atmosphere. In the first step, governing equations in the presence of a shear flow were applied to find out a new expression for a lower-region velocity downstream. A log-normal distribution profile was considered for the deposition profile in the downstream fence. The mode of the deposition profile in the wake can be computed as:
In the simulation, a discrete-phase flow (DPM) was used to calculate the probability of deposition of sand particles for different porosities and heights of fences. The results were validated for the fence with a porosity of 50% and a height of 1 m. The peak profile of deposition was around X = 10D for the fence. There is good agreement between the proposed analytic model and field data and numerical data. The correlation of the log-normal profile parameters with experimental studies and field data will be addressed in future work.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shen, Y.; Zhang, C.; Huang, X.; Wang, X.; Cen, S. The effect of wind speed averaging time on sand transport estimates. CATENA 2019, 175, 286–293. [Google Scholar] [CrossRef]
- Van Donk, S.; Wagner, L.E.; Skidmore, E.L.; Tatarko, J. Comparison of the Weibull model with measured wind speed distributions for stochastic wind generation. Trans. ASAE 2005, 48, 503–510. [Google Scholar] [CrossRef]
- Nickling, W.G. The initiation of particle movement by wind. Sedimentology 1988, 35, 499–511. [Google Scholar] [CrossRef]
- Shi, F.; Huang, N. Measurement and simulation of sand saltation movement under fluctuating wind in a natural field environment. Phys. A Stat. Mech. Its Appl. 2012, 391, 474–484. [Google Scholar] [CrossRef]
- Goudie, A.; Watson, A. The shape of desert sand dune grains. J. Arid Environ. 1981, 4, 185–190. [Google Scholar] [CrossRef]
- Kalinske, A.A. Criteria for determining sand-transport by surface-creep and saltation. Eos Trans. Am. Geophys. Union 1942, 23, 639–643. [Google Scholar] [CrossRef]
- Baas, A.C.W. Grains in Motion. In Aeolian Geomorphology; Livingstone, I., Warren, A., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 2019; pp. 27–60. [Google Scholar]
- Tominaga, Y.; Okaze, T.; Mochida, A. Wind tunnel experiment and CFD analysis of sand erosion/deposition due to wind around an obstacle. J. Wind Eng. Ind. Aerodyn. 2018, 182, 262–271. [Google Scholar] [CrossRef]
- Dupont, S.; Bergametti, G.; Simoëns, S. Modeling aeolian erosion in presence of vegetation. J. Geophys. Res. Earth Surf. 2014, 119, 168–187. [Google Scholar] [CrossRef]
- Wang, N.; Hu, B.-G. Aeolian sand movement and interacting with vegetation: A gpu based simulation and visualization method. In Proceedings of the 2009 Third International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications, Beijing, China, 9–13 November 2009; pp. 401–408. [Google Scholar]
- Saif, A.; Mohamed, A.; Alam Eldein, A. Variable porosity wind fences to control aeolian sand transport. In Proceedings of the Tenth International Congress of Fluid Dynamics, Ain Soukhna Red Sea, Egypt, 16–19 December 2010. [Google Scholar]
- Bitog, J.P.; Lee, I.B.; Shin, M.H.; Hong, S.W.; Hwang, H.S.; Seo, I.H.; Yoo, J.I.; Kwon, K.S.; Kim, Y.H.; Han, J.W. Numerical simulation of an array of fences in Saemangeum reclaimed land. Atmos. Environ. 2009, 43, 4612–4621. [Google Scholar] [CrossRef]
- Xie, L.; Dong, Z.; Zheng, X. Experimental analysis of sand particles’ lift-off and incident velocities in wind-blown sand flux. Acta Mech. Sin. 2006, 21, 564–573. [Google Scholar] [CrossRef]
- Liu, B.; Qu, J.; Zhang, W.; Tan, L.; Gao, Y. Numerical evaluation of the scale problem on the wind flow of a windbreak. Sci. Rep. 2014, 4, 6619. [Google Scholar] [CrossRef] [PubMed]
- Lima, I.A.; Araújo, A.D.; Parteli, E.J.R.; Andrade, J.S.; Herrmann, H.J. Optimal array of sand fences. Sci. Rep. 2017, 7, 45148. [Google Scholar] [CrossRef] [PubMed]
- Lavasani, A.M.; Razia, P.; Mehdipourb, R. Numerical Solution of Fence Performance for Reduction of Sand Deposition on Railway Tracks. Int. J. Eng.-Trans. A Basics 2016, 29, 1014–1021. [Google Scholar]
- Li, B.; Sherman, D.J. Aerodynamics and morphodynamics of sand fences: A review. Aeolian Res. 2015, 17, 33–48. [Google Scholar] [CrossRef]
- Hotta, S.; Kraus, N.C.; Horikawa, K. Function of sand fences in controlling wind-blown sand. In Coastal Sediments; ASCE: Reston, VA, USA, 1987; pp. 772–787. [Google Scholar]
- Jensen, M.J.P. Shelter Effect, Investigations into the Aerodynamics of Shelter and its Effects on Climate and Crops; Danish Techn.: Krbenhavn, Denmark, 1954. [Google Scholar]
- Bruno, L.; Horvat, M.; Raffaele, L. Windblown sand along railway infrastructures: A review of challenges and mitigation measures. J. Wind Eng. Ind. Aerodyn. 2018, 177, 340–365. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Wang, H. A wind tunnel simulation of the mean velocity fields behind upright porous fences. Agric. For. Meteorol. 2007, 146, 82–93. [Google Scholar] [CrossRef]
- Nägeli, W. Weitere Untersuchungen über die Windverhältnisse im Bereich von Windschutzstreifen. Mitteilungen für die Schweizerische Anstalt für das Forstliche Versuchswesen 1946, 24, 660–737. [Google Scholar]
- Phillips, C.J.; Willetts, B.B. Predicting sand deposition at porous fences. J. Waterway Port Coast. Ocean Div. 1979, 105, 15–31. [Google Scholar]
- Chamorro, L.P.; A Arndt, R.E. Non-uniform velocity distribution effect on the Betz-Joukowsky limit. Wind Energy 2013, 16, 279–282. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø National Laboratory: Roskilde, Denmark, 1983; ISBN 87-550-0971-9. [Google Scholar]
- Darcy, H.P.G. Les Fontaines Publiques de la Ville de Dijon. Exposition et Application des Principes à Suivre et des Formules à Employer Dans les Questions de Distribution D’eau, Etc.; V. Dalamont: Paris, France, 1856. [Google Scholar]
- Idelchik, I.E. Handbook of Hydraulic Resistance; Hemisphere Publishing Corp.: Washington, DC, USA, 1986; 662p. [Google Scholar]
- Rosin, P. Laws governing the fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Mehdipour, R.; Baniamerian, Z. A new approach in reducing sand deposition on railway tracks to improve transportation. Aeolian Res. 2019, 41, 100537. [Google Scholar] [CrossRef]
- Fluent 6.2 User’s Guide; Fluent Inc.: Lebanon, IN, USA, 2006.
- Tabler, R.D. Geometry and Density of Drifts Formed by Snow Fences. J. Glaciol. 1980, 26, 405–419. [Google Scholar] [CrossRef][Green Version]
- Iversen, J.D. Comparison of wind-tunnel model and full-scale snow fence drifts. J. Wind Eng. Ind. Aerodyn. 1981, 8, 231–249. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).