State of Charge Estimation of a Composite Lithium-Based Battery Model Based on an Improved Extended Kalman Filter Algorithm
Abstract
1. Introduction
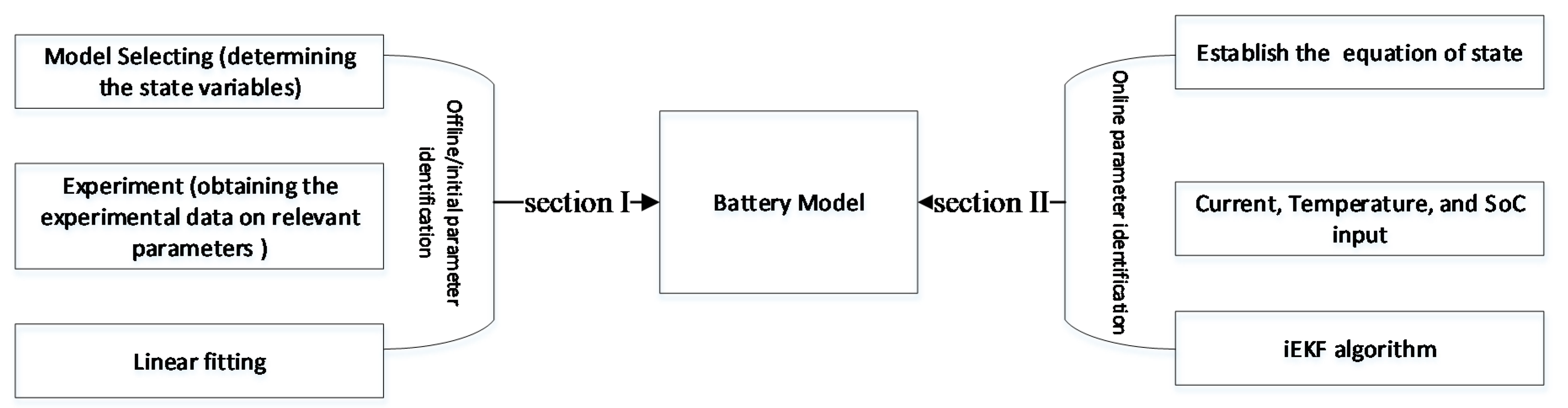
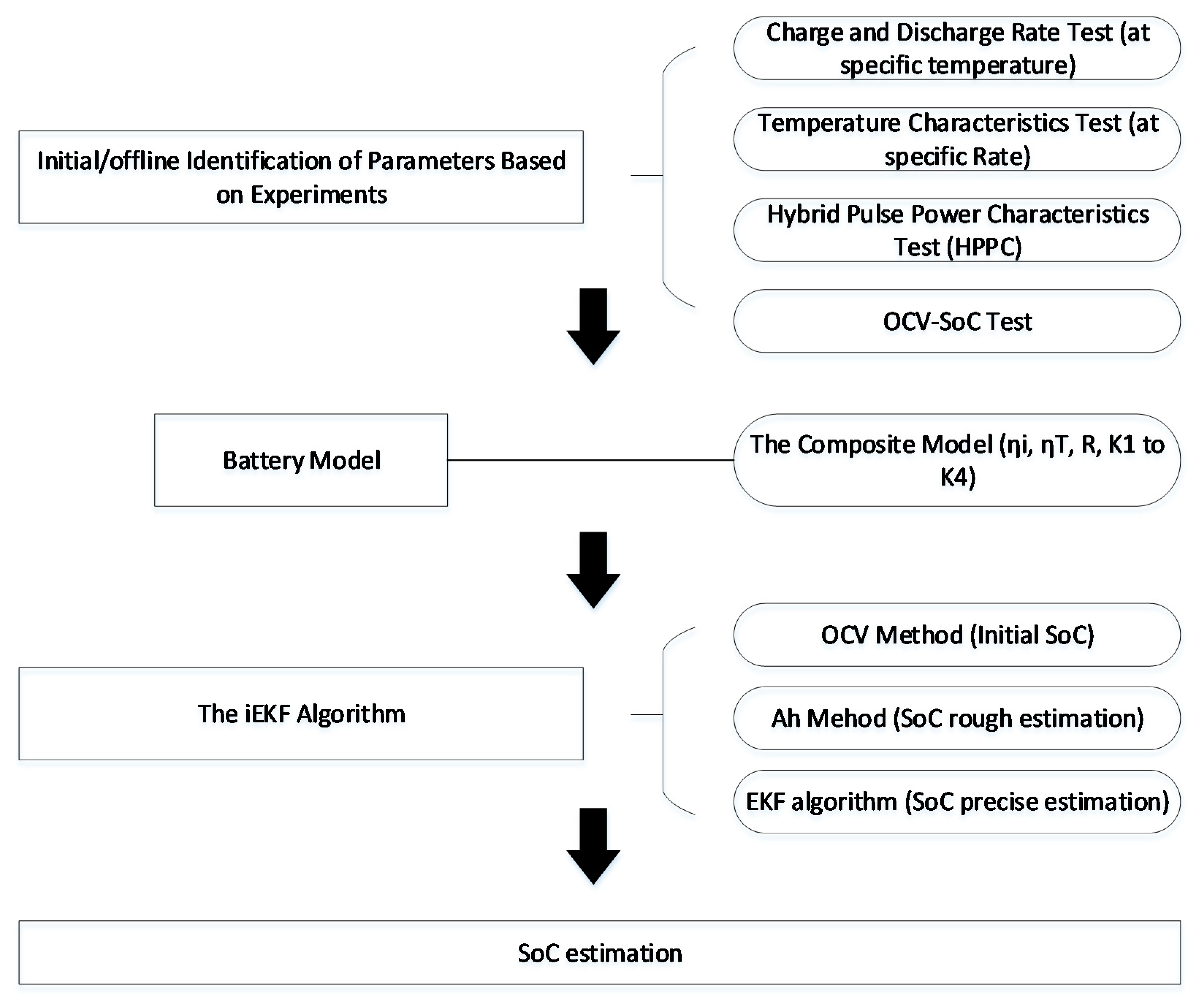
2. The Battery Model
- Selecting the battery model (A novel composite electrochemical model).
- Determining the different parameters to be identified based on the selected model.
- Performing a series of characteristics tests on the battery.
- Linear fitting of the experimental data (offline identification).
- Building the model in MATLAB.
- Obtaining the equation of state.
- Developing the online estimation algorithm (iEKF).
- Inputting the current, temperature and SoC (simulations in static and dynamic conditions).
The Composite Battery Model
3. The Experiments and Offline Parameter Identification
3.1. Charge and Discharge Rate Test
3.2. Temperature Characteristics Test
3.3. Hybrid Pulse Power Characterization (HPPC) Test
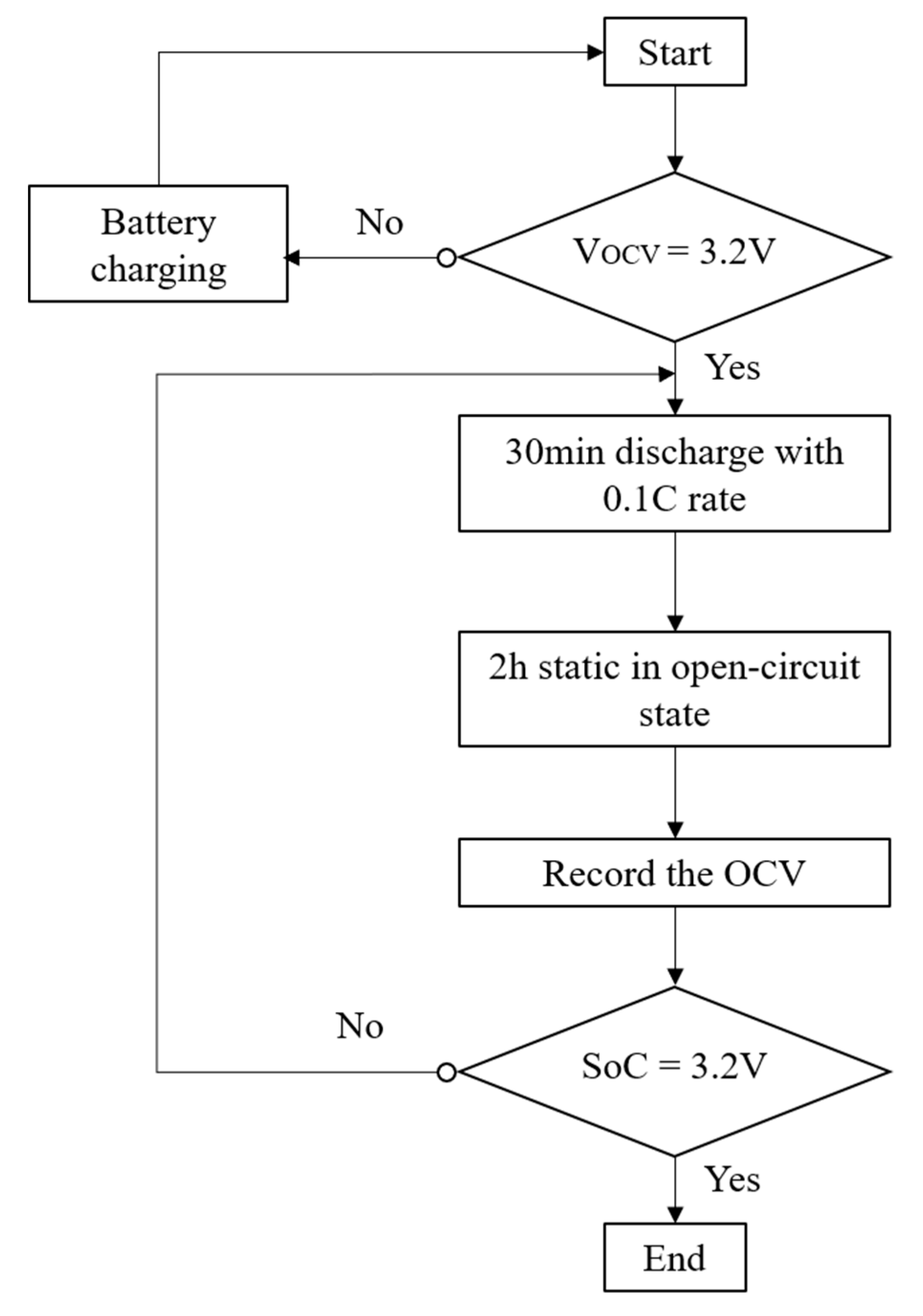
3.4. OCV-SoC Test
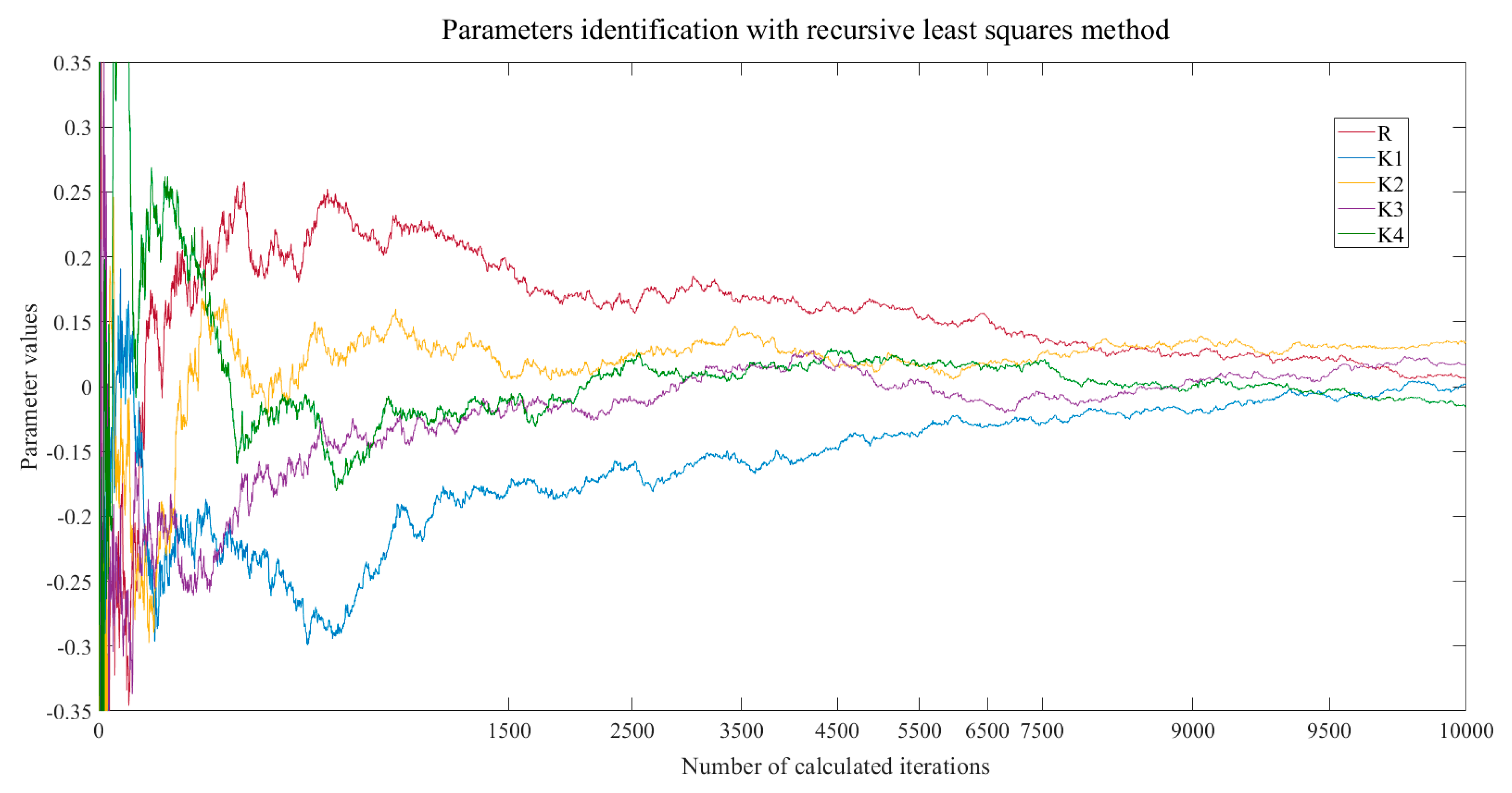
3.5. Offline Parameter Identification
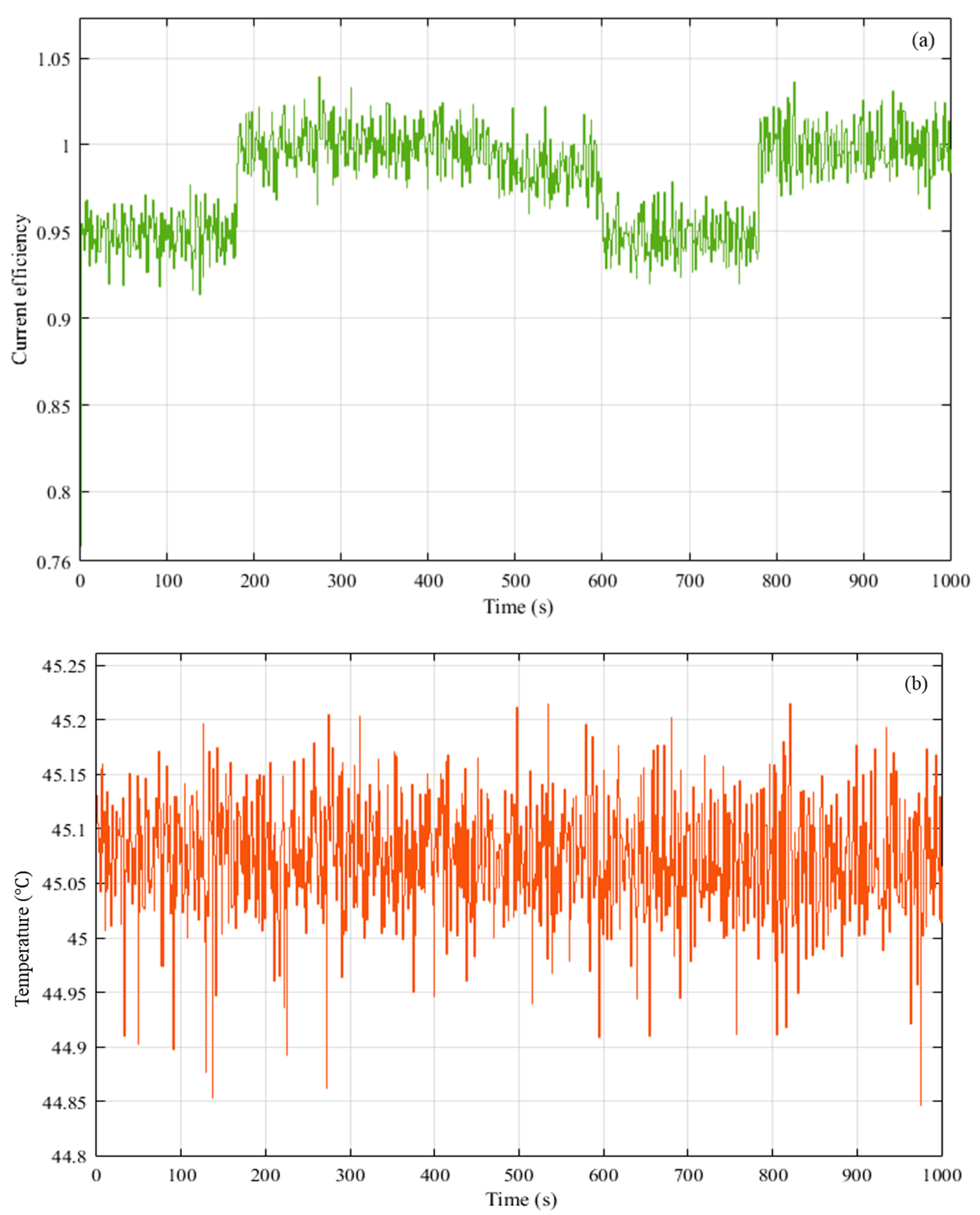
4. The SoC Estimation Based on an Improved EKF Algorithm
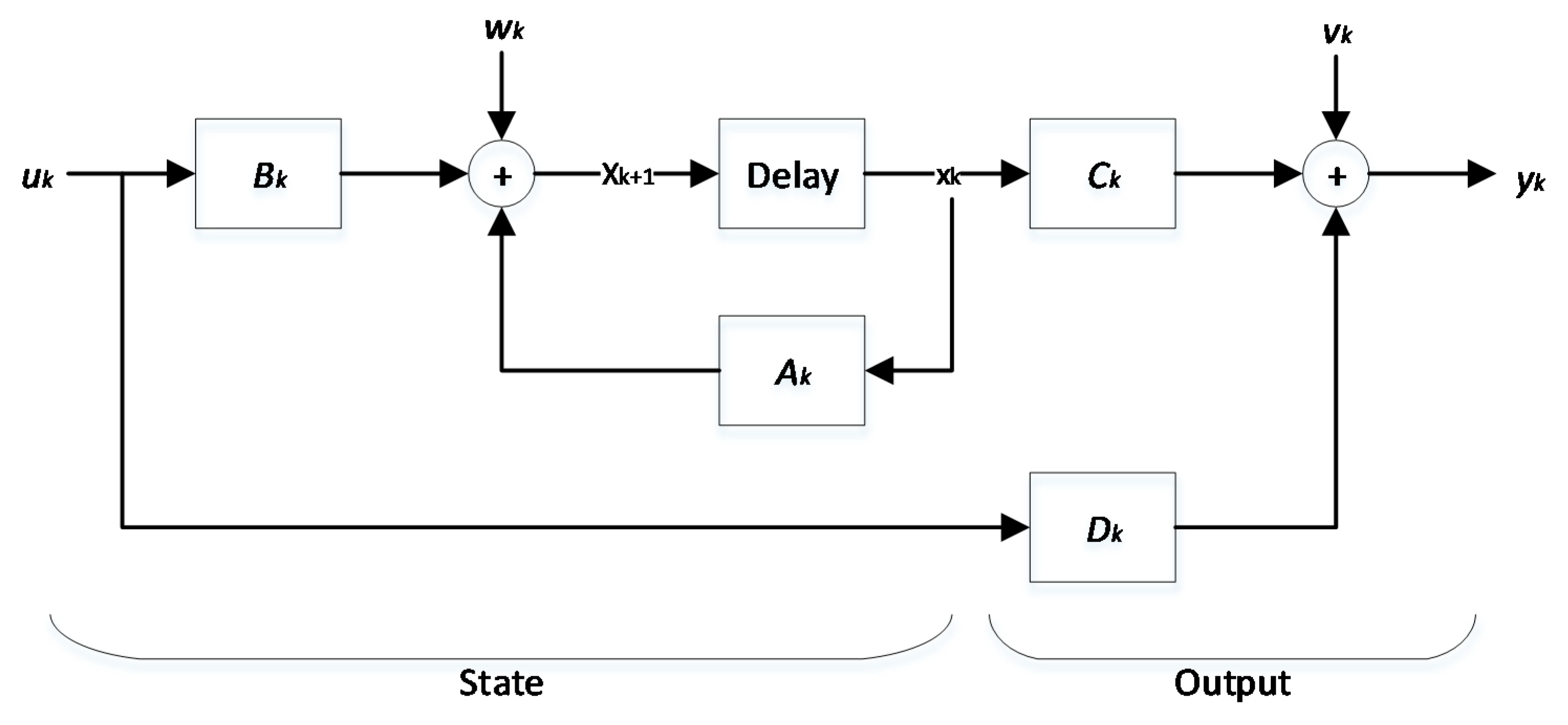
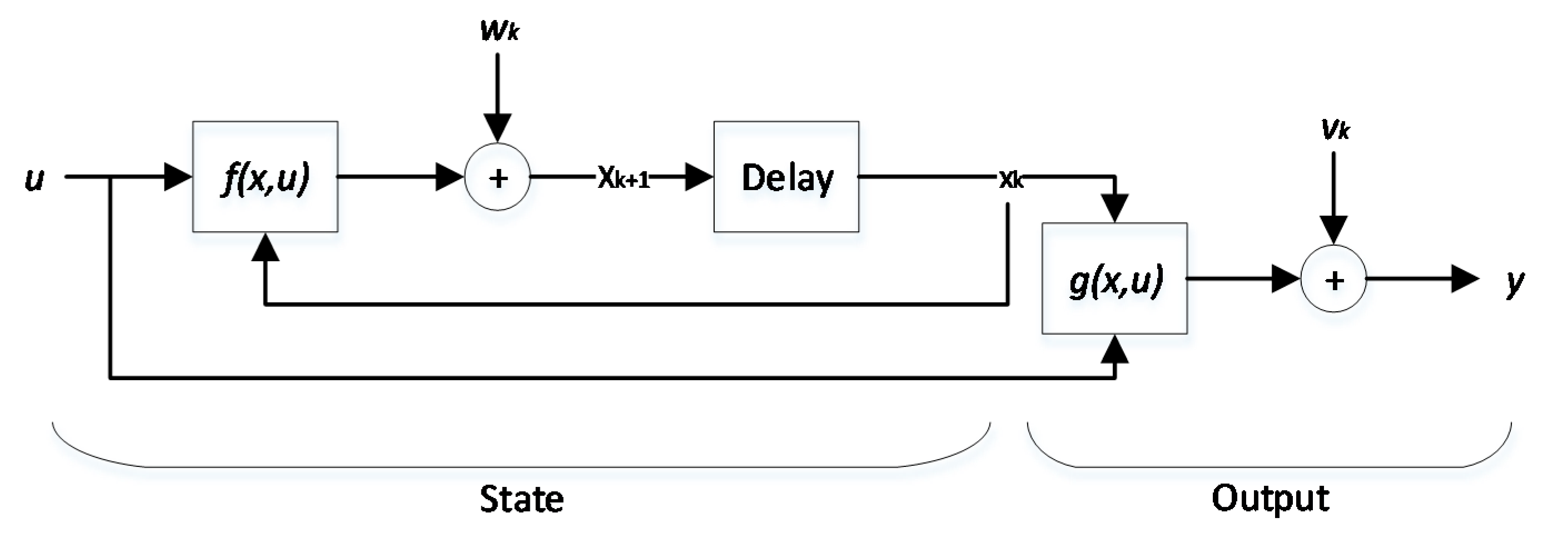
4.1. Analysis of the KF and EKF Algorithm
- Initial value of and :
- Predictive estimate of the and :
- KF gain Lk (weighting coefficient matrix)
- Optimal estimate of the and :where Dw and Dv in Equations (14) and (15) are the covariance of the process noise wk and the measurement noise vk, respectively.
4.2. The SoC Estimation Model Corrected by EKF Based on Composite Model
- Model establishment: Use Equations (6) and (7).
- Determination of system parameters:
- Initialization of the state variable and the covariance.
- Iterative calculation of the EKF.
5. The Simulation Validation of the Improved EKF Algorithm
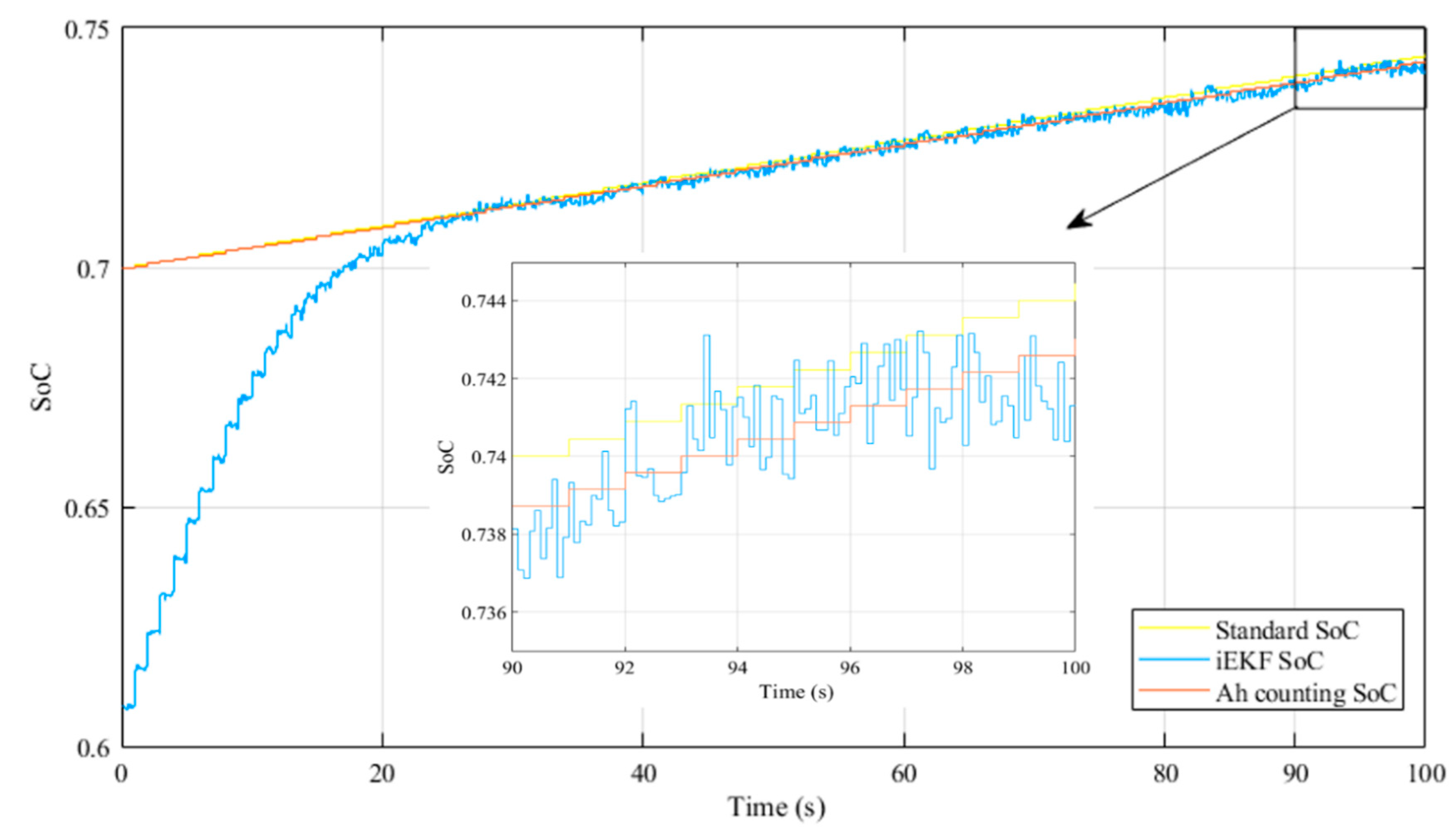
5.1. The Validation of the Improved EKF Algorithm
5.2. The Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiong, R.; Zhang, Y.; Wang, J.; He, H.; Peng, S.; Pecht, M. Lithium-ion battery health prognosis based on a real battery management system used in electric vehicles. IEEE Trans. Veh. Technol. 2018, 68, 4110–4121. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.; Hossain, E. A comprehensive study of key electric vehicle (EV) components, technologies, challenges, impacts, and future direction of development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Sources 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Cuma, M.U.; Koroglu, T. A comprehensive review on estimation strategies used in hybrid and battery electric vehicles. Renew. Sustain. Energy Rev. 2015, 42, 517–531. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Zhang, P.; Schmidt, C.; Gomadam, P.; Gorka, T. Data-driven method based on particle swarm optimization and k-nearest neighbor regression for estimating capacity of lithium-ion battery. Appl. Energy 2014, 129, 49–55. [Google Scholar] [CrossRef]
- Malkhandi, S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery. Eng. Appl. Artif. Intell. 2006, 19, 479–485. [Google Scholar] [CrossRef]
- Antón, J.Á.; Nieto, P.G.; de Cos Juez, F.J.; Lasheras, F.S.; Vega, M.G.; Gutiérrez, M.R. Battery state-of-charge estimator using the SVM technique. Appl. Math. Model. 2013, 37, 6244–6253. [Google Scholar] [CrossRef]
- Zheng, Y.; Lu, L.; Han, X.; Li, J.; Ouyang, M. LiFePO4 battery pack capacity estimation for electric vehicles based on charging cell voltage curve transformation. J. Power Sources 2013, 226, 33–41. [Google Scholar] [CrossRef]
- Xu, J.; Cao, B.; Chen, Z.; Zou, Z. An online state of charge estimation method with reduced prior battery testing information. Int. J. Electr. Power Energy Syst. 2014, 63, 178–184. [Google Scholar] [CrossRef]
- Dai, H.; Wei, X.; Sun, Z.; Wang, J.; Gu, W. Online cell SOC estimation of Li-ion battery packs using a dual time-scale Kalman filtering for EV applications. Appl. Energy 2012, 95, 227–237. [Google Scholar] [CrossRef]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on state of charge estimation of batteries with adaptive extended Kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Pavković, D.; Krznar, M.; Komljenović, A.; Hrgetić, M.; Zorc, D. Dual EKF-Based State and Parameter Estimator for a LiFePO4 Battery Cell. J. Power Electron. 2017, 17, 398–410. [Google Scholar] [CrossRef]
- Yousefizadeh, S.; Bendtsen, J.D.; Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. EKF-based Predictive Stabilization of Shipboard DC Microgrids with Uncertain Time-varying Load. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 901–909. [Google Scholar] [CrossRef]
- Fang, Y.; Xiong, R.; Wang, J. Estimation of Lithium-Ion Battery State of Charge for Electric Vehicles Based on Dual Extended Kalman Filter. Energy Procedia 2018, 152, 574–579. [Google Scholar] [CrossRef]
- Guo, F.; Hu, G.; Xiang, S.; Zhou, P.; Hong, R.; Xiong, N. A multi-scale parameter adaptive method for state of charge and parameter estimation of lithium-ion batteries using dual Kalman filters. Energy 2019, 178, 79–88. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, C. State-of-charge estimation of valve regulated lead acid battery based on multi-state Unscented Kalman Filter. Int. J. Electr. Power Energy Syst. 2011, 33, 472–476. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Wang, C.; Wang, L.; Liu, Y. Adaptive state of charge estimation for Li-ion batteries based on an unscented Kalman filter with an enhanced battery model. Energies 2013, 6, 4134–4151. [Google Scholar] [CrossRef]
- Gao, S.; Kang, M.; Li, L.; Liu, X. Estimation of state-of-charge based on unscented Kalman particle filter for storage lithium-ion battery. J. Eng. 2019, 2019, 1858–1863. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The state of charge estimation of lithium-ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 2013, 63, 1614–1621. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Barillas, J.K.; Li, J.; Günther, C.; Danzer, M.A. A comparative study and validation of state estimation algorithms for Li-ion batteries in battery management systems. Appl. Energy 2015, 155, 455–462. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Xiong, R.; Gong, X.; Mi, C.C.; Sun, F. A robust state-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter. J. Power Sources 2013, 243, 805–816. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Plett, G. LiPB dynamic cell models for Kalman-filter SOC estimation. In The 19th International Battery, Hybrid and Fuel Electric Vehicle Symposium and Exhibition; Pusan, Korea, 2002; pp. 1–12. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=.+LiPB+dynamic+cell+models+for+Kalman-filter+SOC+estimation.+In+The+19th+International+Battery%2C+Hybrid+and+Fuel+Electric+Vehicle+Symposium+and+Exhibition&btnG= (accessed on 31 October 2019).
- Han, H.; Xu, H.; Yuan, Z.; Zhao, Y. Modeling for Lithium-ion Battery Used in Electric Vehicles. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August 2014; pp. 1–5. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Chang, W.-Y. The state of charge estimating methods for battery: A review. ISRN Appl. Math. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Hunt, G.; Motloch, C. Freedom Car Battery Test Manual for Power-Assist Hybrid Electric Vehicles; INEEL, Idaho Falls: Idaho Falls, ID, USA, 2003. [Google Scholar]
- Doughty, D.H.; Crafts, C.C. FreedomCAR: Electrical Energy Storage System Abuse Test Manual for Electric and Hybrid Electric Vehicle Applications; Sandia National Laboratories: Albuquerque, NM, USA, 2006. [Google Scholar]
- Hu, Y.; Yurkovich, S. Battery cell state-of-charge estimation using linear parameter varying system techniques. J. Power Sources 2012, 198, 338–350. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Signal Processing, Sensor Fusion, and Target Recognition VI; SPIE Digital Library: Bellingham, WA, USA, 1997; pp. 182–194. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Norwood, MA, USA, 2003. [Google Scholar]
- Best, M.C.; Gordon, T.; Dixon, P. An extended adaptive Kalman filter for real-time state estimation of vehicle handling dynamics. Veh. Syst. Dyn. 2000, 34, 57–75. [Google Scholar]
- Pérez, G.; Garmendia, M.; Reynaud, J.F.; Crego, J.; Viscarret, U. Enhanced closed loop State of Charge estimator for lithium-ion batteries based on Extended Kalman Filter. Appl. Energy 2015, 155, 834–845. [Google Scholar] [CrossRef]
- Marvasti, F. Nonuniform Sampling: Theory and Practice; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Pang, S.; Farrell, J.; Du, J.; Barth, M. Battery state-of-charge estimation. In Proceedings of the 2001 American Control Conference (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; pp. 1644–1649. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.; Ren, H.; Zhao, Y. Model-based unscented Kalman filter observer design for lithium-ion battery state of charge estimation. Int. J. Energy Res. 2018, 42, 1603–1614. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, Y.; Li, C. SOC Performance Evaluation Analysis in Electric Vehicle Power Battery Operation. Inn. Mong. Electr. Power 2016, 34, 81–84. [Google Scholar]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison study on the battery SoC estimation with EKF and UKF algorithms. Energies 2013, 6, 5088–5100. [Google Scholar] [CrossRef]
- Liu, C.; Liu, W.; Wang, L.; Hu, G.; Ma, L.; Ren, B. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]

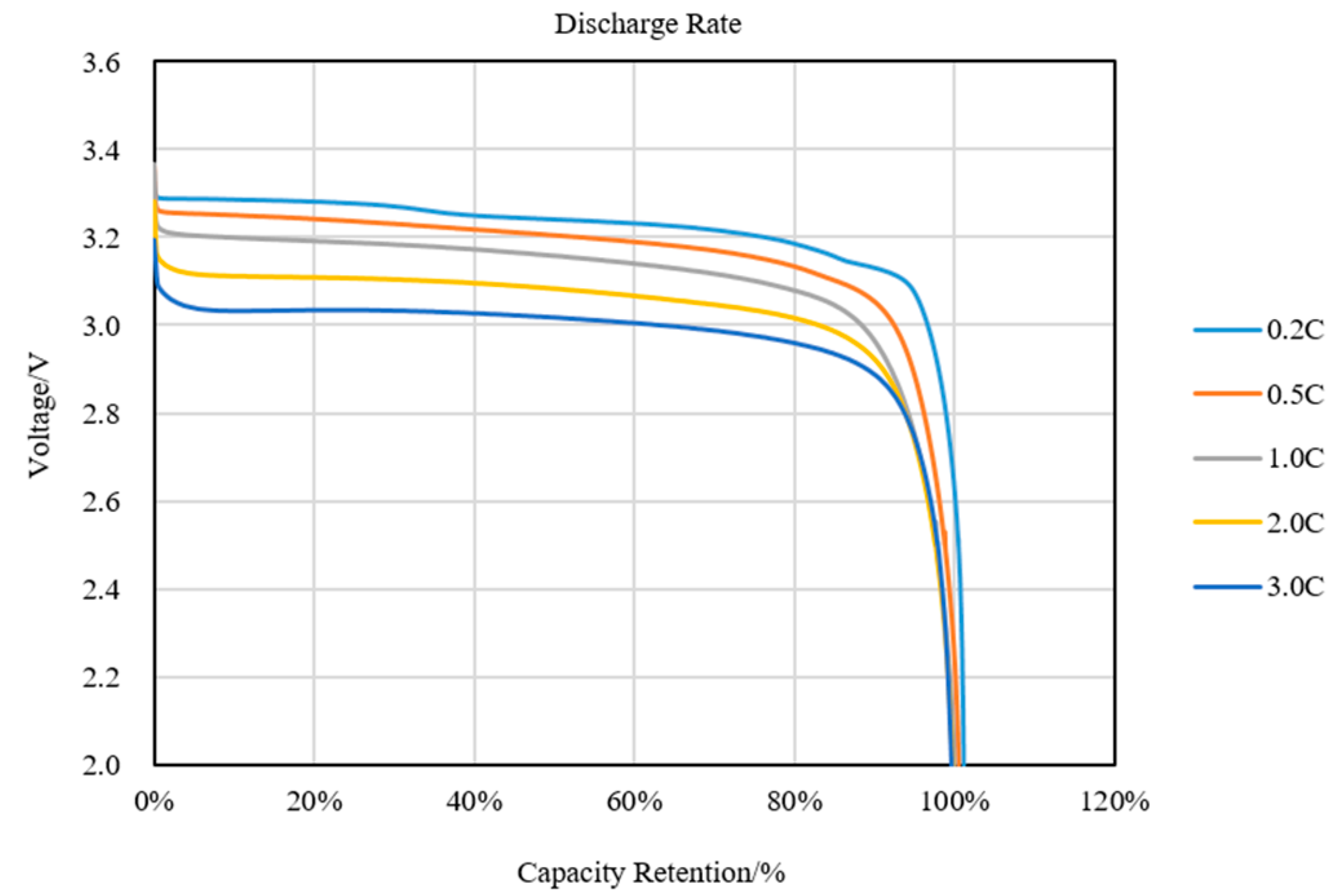




| Charge Rate Test | 0.2 C | 0.5 C | 1.0 C | 2.0 C | 3.0 C |
|---|---|---|---|---|---|
| Capacity/Ah | 211.45 | 208.95 | 206.88 | 204.07 | 194.76 |
| Capacity retention rate/% | 102.21 | 101.00 | 100.00 | 98.64 | 94.14 |
| Energy/Wh | 707.76 | 706.36 | 708.04 | 712.64 | 692.15 |
| Energy retention rate/% | 99.96 | 99.76 | 100.00 | 100.65 | 97.76 |
| Charge Rate Test | 0.2 C | 0.5 C | 1.0 C | 2.0 C | 3.0 C |
|---|---|---|---|---|---|
| Capacity/Ah | 214.31 | 212.94 | 211.84 | 211.28 | 211.08 |
| Capacity retention rate/% | 101.16 | 100.52 | 100.00 | 99.74 | 99.64 |
| Energy/Wh | 687.83 | 672.22 | 657.33 | 641.41 | 628.45 |
| Energy retention rate/% | 104.64 | 102.26 | 100.00 | 97.58 | 95.61 |
| Temperature Characteristic Test | −20 °C | −10 °C | 0 °C | 25 °C | 45 °C |
|---|---|---|---|---|---|
| Capacity/Ah | 194.18 | 201.14 | 205.49 | 211.27 | 211.35 |
| Capacity retention rate/% | 91.91 | 95.20 | 97.26 | 100.00 | 100.00 |
| Energy/Wh | 523.18 | 566.18 | 600.52 | 657.80 | 668.46 |
| Energy retention rate/% | 79.54 | 86.07 | 91.29 | 100.00 | 101.62 |
| SoC | 206Ah 4C Discharge/3C Charge | |||||
|---|---|---|---|---|---|---|
| Discharge | Charge | |||||
| Vbefore (mV) | Vafter (mV) | DCR (mΩ) | Vbefore (mV) | Vafter (mV) | DCR (mΩ) | |
| 90% | 3328.30 | 2910.70 | 0.45 | 3277.20 | 3613.20 | 0.49 |
| 80% | 3327.40 | 2893.70 | 0.47 | 3267.20 | 3612.90 | 0.50 |
| 70% | 3327.40 | 2881.60 | 0.48 | 3258.90 | 3610.10 | 0.51 |
| 60% | 3296.70 | 2857.40 | 0.48 | 3244.90 | 3586.90 | 0.50 |
| 50% | 3289.00 | 2829.80 | 0.50 | 3230.40 | 3580.40 | 0.51 |
| 40% | 3288.00 | 2805.90 | 0.52 | 3217.30 | 3577.30 | 0.52 |
| 30% | 3284.30 | 2775.60 | 0.55 | 3201.50 | 3570.10 | 0.53 |
| 20% | 3254.50 | 2707.40 | 0.59 | 3169.90 | 3539.40 | 0.53 |
| 10% | 3209.60 | 2422.10 | 0.86 | 3110.40 | 3497.00 | 0.56 |
| Operation Condition | Maximum Error (%) | Average Error (%) | Relative Error (%) |
|---|---|---|---|
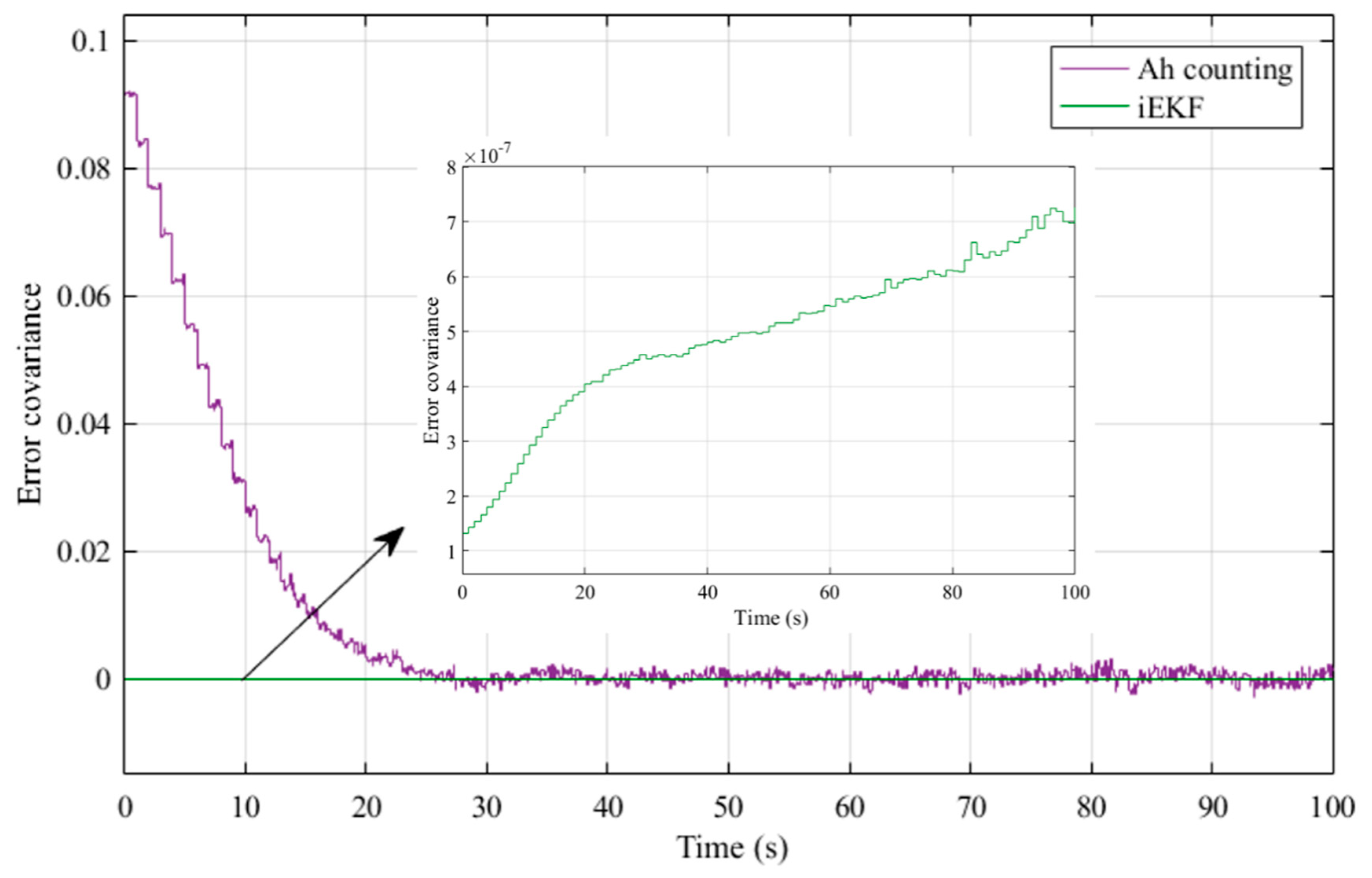
| Static | 2.39 | 1.43 | 1.20 |
| Dynamic | 6.76 | 3.94 | 2.15 |
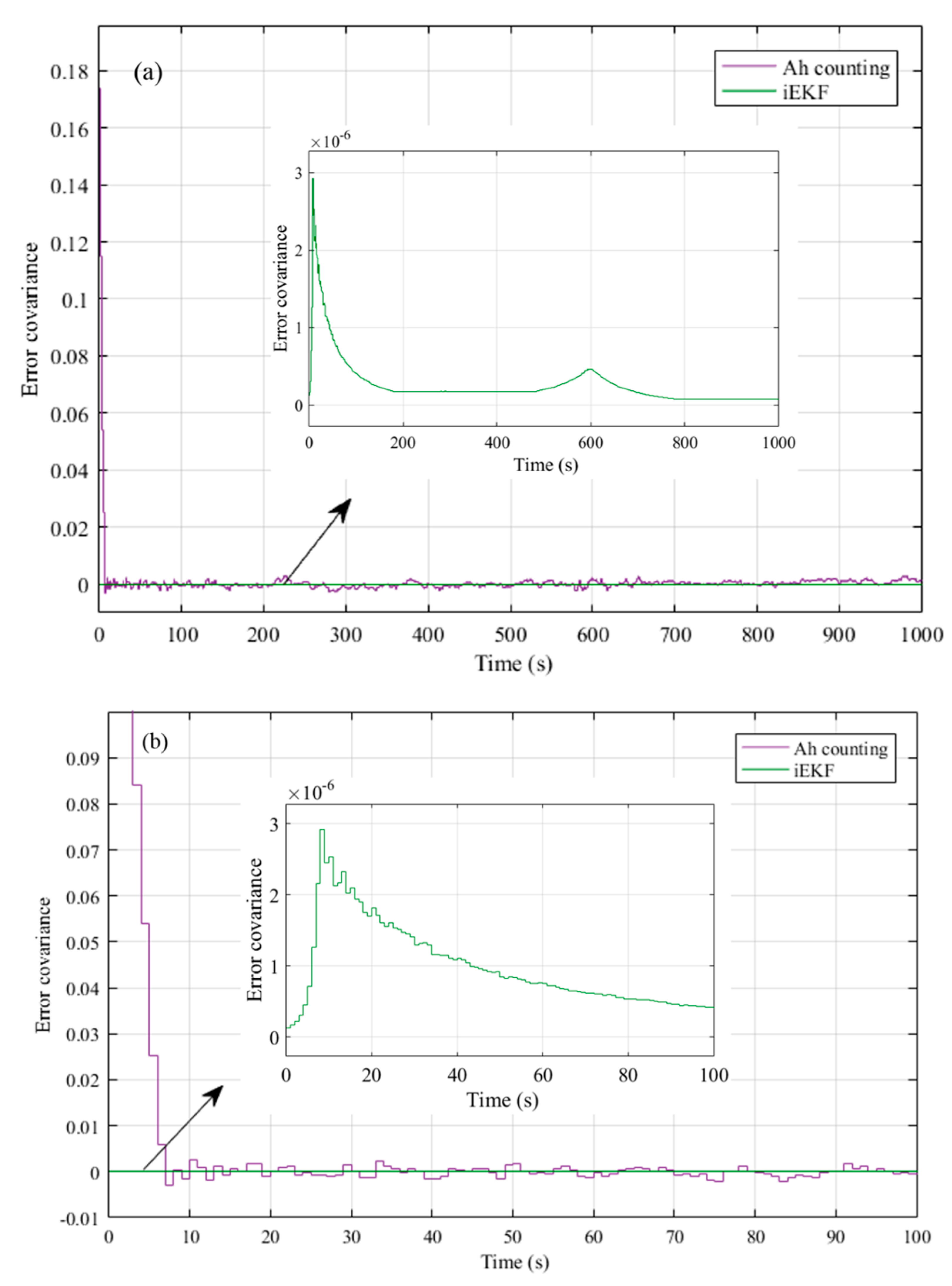
| Estimation Error | Initial SoC of 20% | Initial SoC of 50% | Initial SoC of 70% | ||||
|---|---|---|---|---|---|---|---|
| Operation | Ah Counting | iEKF | Ah Counting | iEKF | Ah Counting | iEKF | |
| Static | 14.9 | 0.8 | 15.3 | 1.0 | 15.0 | 1.2 | |
| Dynamic | 17.7 | 1.7 | 18.5 | 2.0 | 19.7 | 2.1 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, N.; Prasad, K.; Lie, T.T.; Cui, J. State of Charge Estimation of a Composite Lithium-Based Battery Model Based on an Improved Extended Kalman Filter Algorithm. Inventions 2019, 4, 66. https://doi.org/10.3390/inventions4040066
Ding N, Prasad K, Lie TT, Cui J. State of Charge Estimation of a Composite Lithium-Based Battery Model Based on an Improved Extended Kalman Filter Algorithm. Inventions. 2019; 4(4):66. https://doi.org/10.3390/inventions4040066
Chicago/Turabian StyleDing, Ning, Krishnamachar Prasad, Tek Tjing Lie, and Jinhui Cui. 2019. "State of Charge Estimation of a Composite Lithium-Based Battery Model Based on an Improved Extended Kalman Filter Algorithm" Inventions 4, no. 4: 66. https://doi.org/10.3390/inventions4040066
APA StyleDing, N., Prasad, K., Lie, T. T., & Cui, J. (2019). State of Charge Estimation of a Composite Lithium-Based Battery Model Based on an Improved Extended Kalman Filter Algorithm. Inventions, 4(4), 66. https://doi.org/10.3390/inventions4040066






