Prediction of Solar Irradiance Based on Artificial Neural Networks
Abstract
1. Introduction
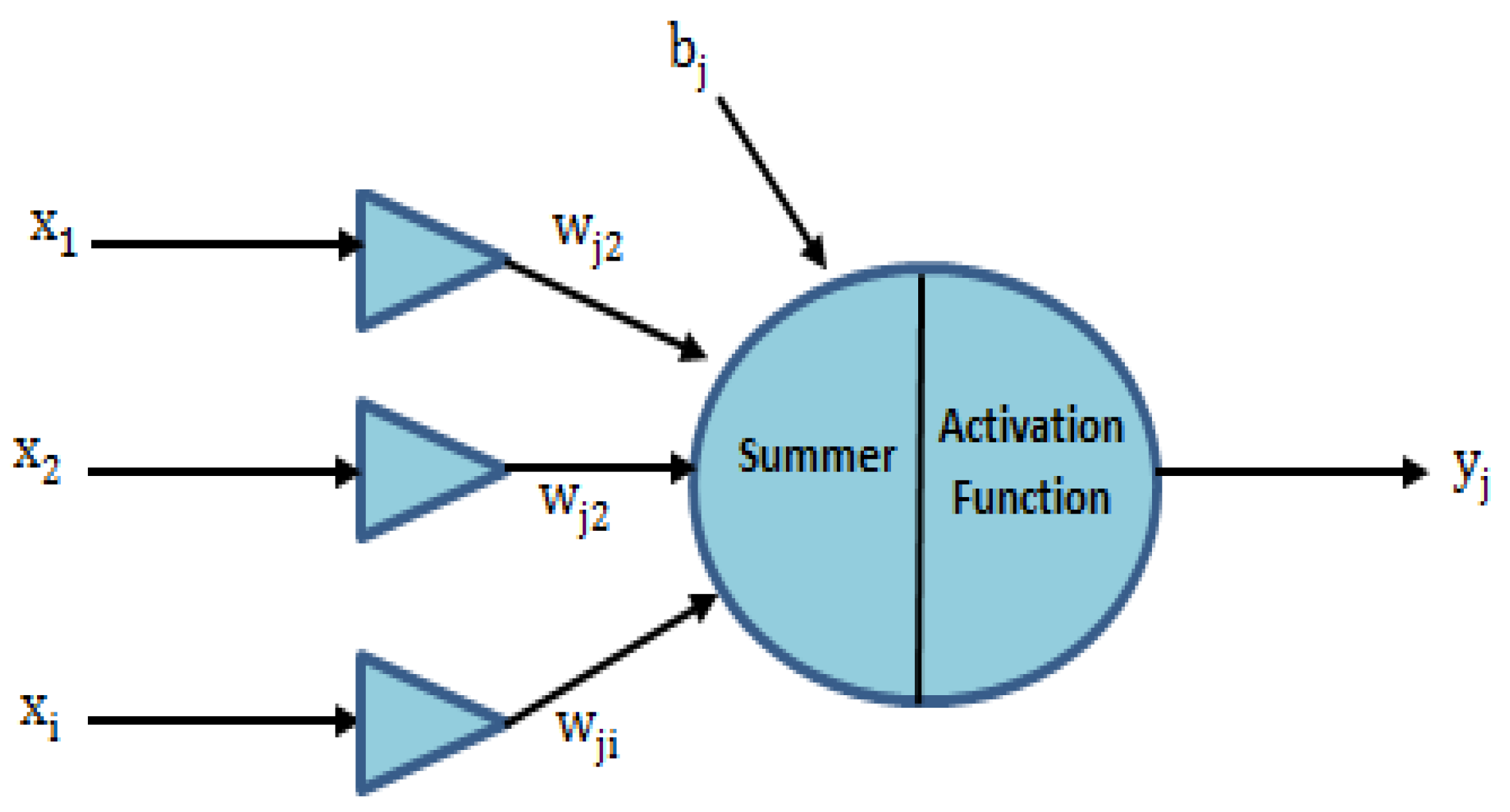
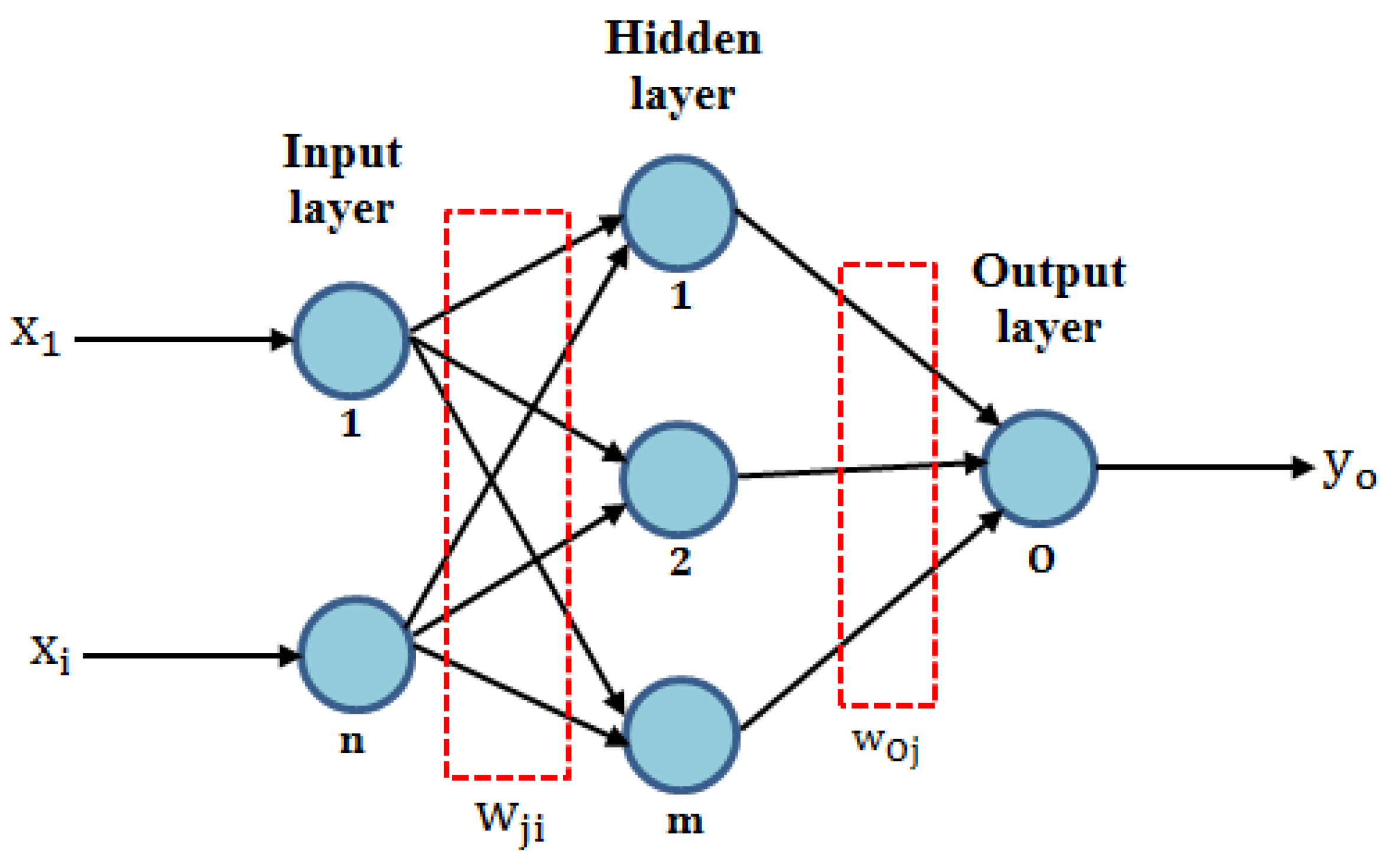
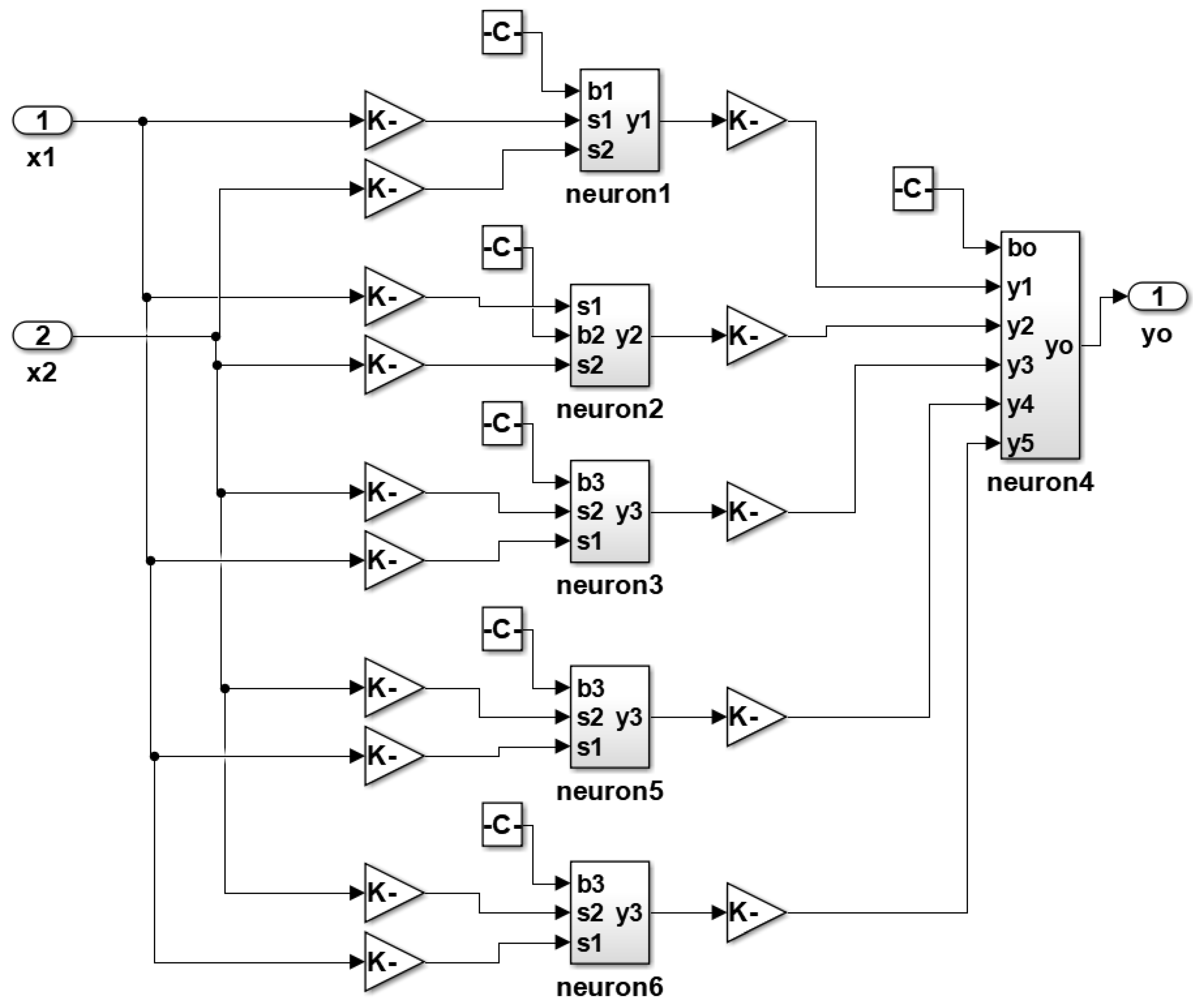
2. Artificial Neural Network
- (1)
- For the weights between the output and hidden neurons, the delta rule () is calculated as follows:
- (2)
- For weights between the hidden and input neurons, the delta hidden rule () is calculated as follows:where is the weight matrix between the output and hidden neurons, and is the desired output at k-input pattern.
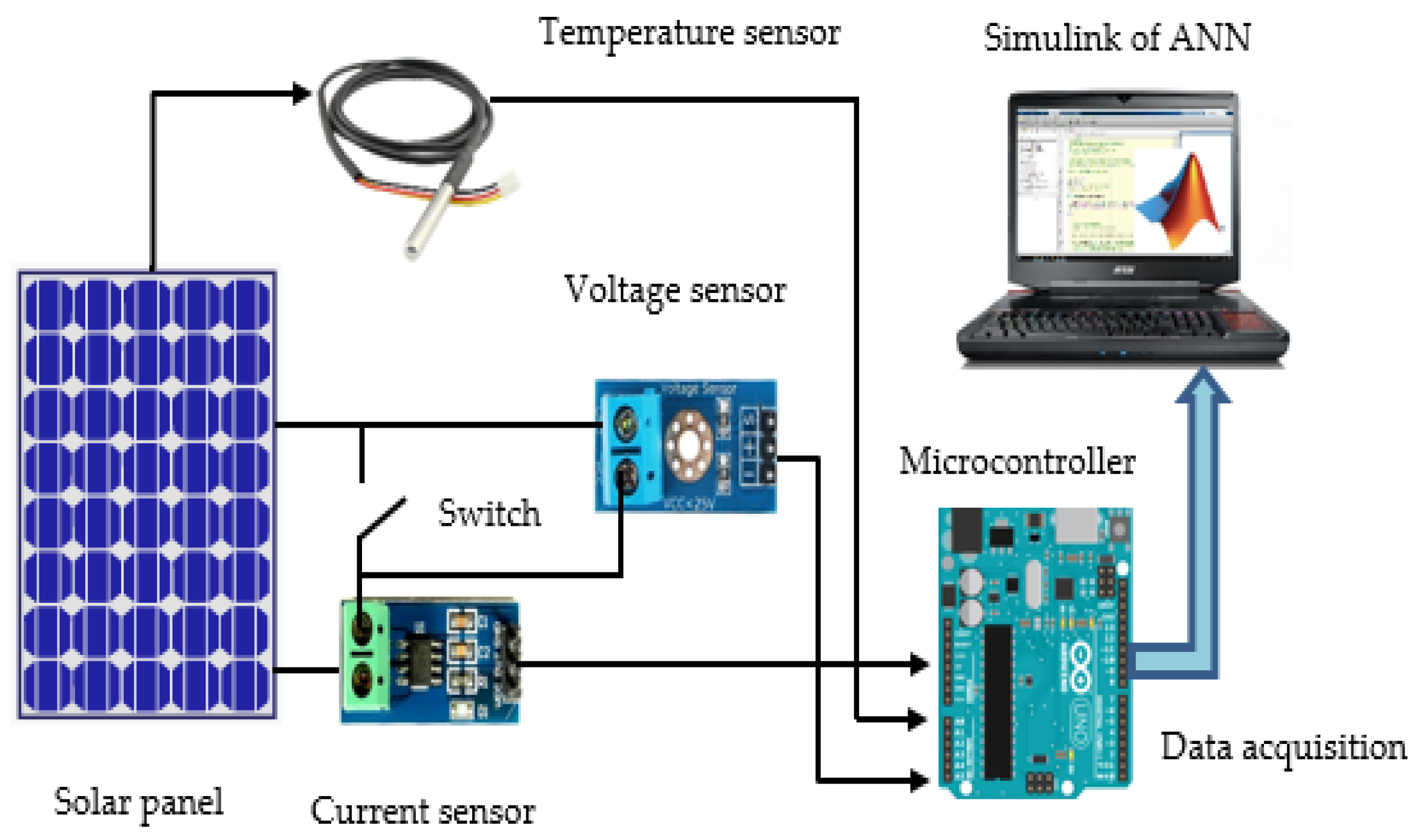
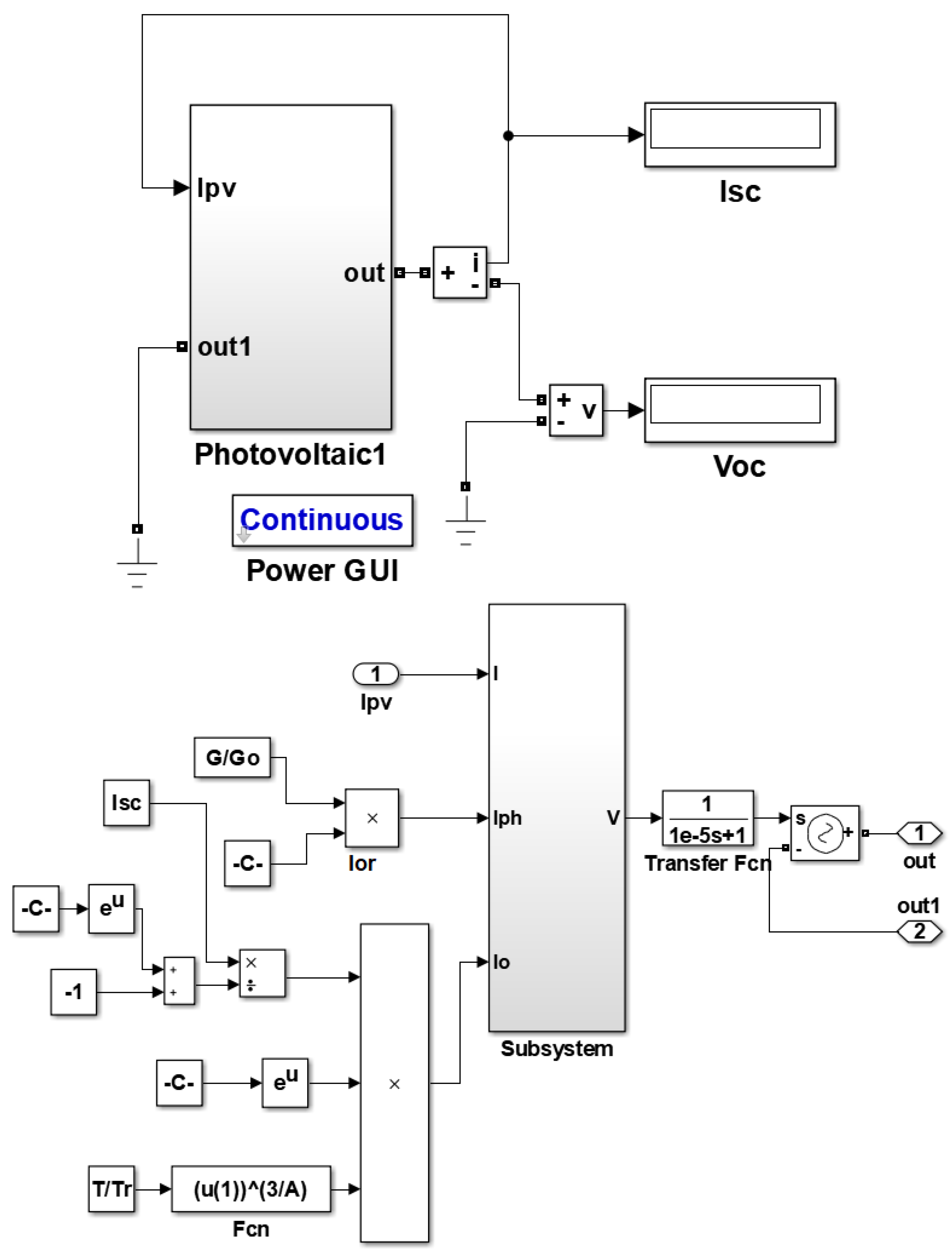
3. Irradiance Prediction Using ANN
- : short-circuit current at standard test conditions (STC) (Gr = 1000 w/m2 and Tr = 25 C),
- : short-circuit current at any G and T,
- β: coefficients for temperature.
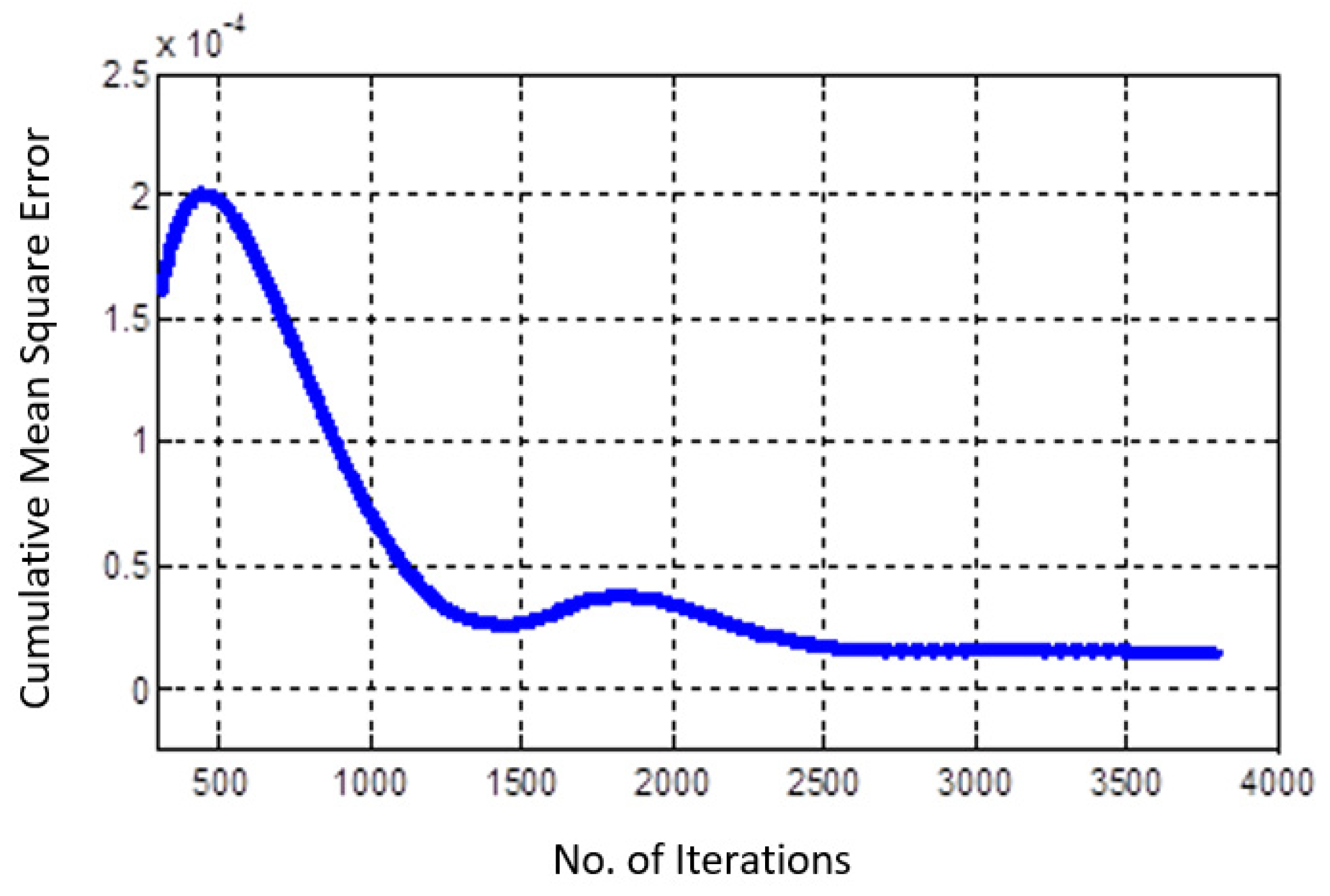
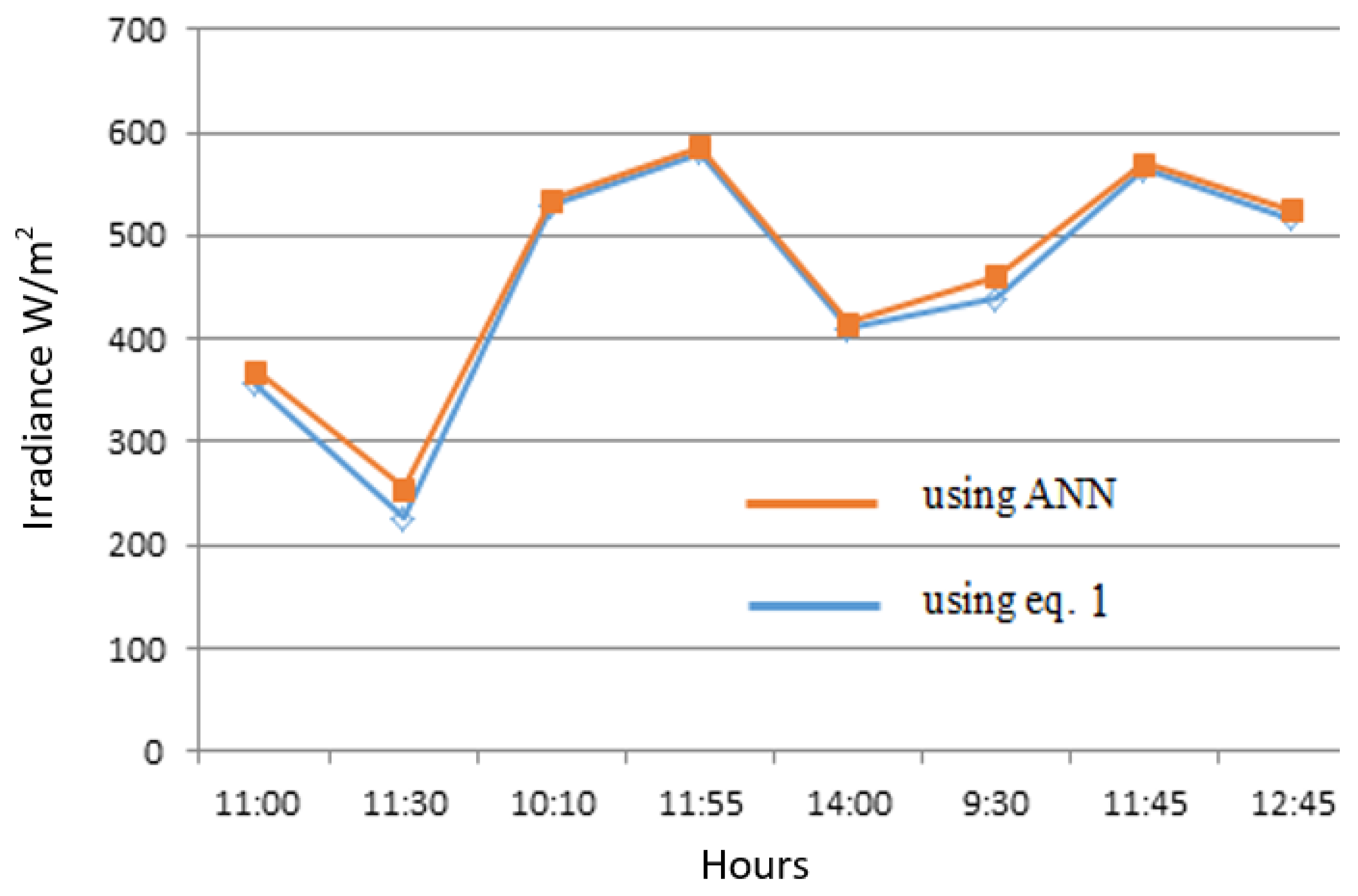
4. Simulation and Measurement Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eltawila, M.A.; Zhao, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Petitta, M.; Wagner, J.E.; Belluardo, G.; Moser, D.; Castelli, M.; Zebisch, M.; Tetzlaff, A. Wind effect on PV module temperature: Analysis of different techniques for an accurate estimation. Energy Proc. 2013, 40, 77–86. [Google Scholar] [CrossRef]
- Rivera, E.I.O.; Peng, F.Z. Algorithms to estimate the temperature and effective irradiance level over a photovoltaic module using the fixed point theorem. In Proceedings of the IEEE Annual Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 2911–2912. [Google Scholar]
- Tiwari, G.N.; Tiwari, A.S. Handbook of Solar Energy Theory Analysis and Applications; Springer Science+Business Media: Singapore, 2017. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering Processes and Systems, 2nd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2009; pp. 1–815. [Google Scholar]
- Mubarak, R.; Hofmann, M.; Riechelmann, S.; Seckmeyer, G. Comparison of modelled and measured tilted solar irradiance for photovoltaic applications. Energies 2017, 10, 1688. [Google Scholar] [CrossRef]
- Marzouq, M.; El Fadili, H.; Lakhliai, Z.; Zenkouar, K. A review of solar radiation prediction using artificial neural networks. In Proceedings of the IEEE International Conference on Wireless Technologies, Embedded and Intelligent Systems, Fez, Morocco, 19–20 April 2017. [Google Scholar]
- Ciulla, G.; Lo Brano, V.; Franzitta, V.; Trapanese, M. Assessment of the operating temperature of crystalline PV modules based on real use conditions. Int. J. Photoenergy Hindawi Publ. Corp. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Truatmoraka, P.; Waraporn, N.; Suphachotiwatana, D. Water level prediction model using back propagation neural network. In Proceedings of the IEEE 4th International Symposium on Computational and Business Intelligence, Olten, Switzerland, 5–7 September 2016. [Google Scholar]
- Aitkenhead, M.; Aitkenhead-Peterson, J.A.; McDowell, W.H.; Smart, R.P.; Cresser, M.S. Modelling DOC export from watersheds in Scotland using neural networks. Comput. Geoscis. 2007, 33, 423–436. [Google Scholar] [CrossRef]
- Jinming, Z.; Yi, H.; Sung-Sau, S. Overview of artificial neural networks. Ser. Methods Mol. Biol. Springer 2009, 458, 14–22. [Google Scholar]
- Hameed, W.I.; Kadhim, A.S.; Al-Thuwaynee, A.A.K. Field weakening control of a separately excited DC motor using neural network optimized by social spider algorithm. Eng. J. Sci. Res. Publ. Inc. 2016, 8, 1–10. [Google Scholar]
- Burns, R.S. Advanced Control Engineering; Elsevier Ltd.: Gurugram, India, 2001; pp. 1–464. [Google Scholar]
- Saleh, A.L.; Obaid, B.A.; Obed, A.A. Motion control of linear induction motor based on optimal recurrent wavelet neural network-PID controller. Int. J. Eng. Technol. 2018, 7, 2028–2034. [Google Scholar] [CrossRef]
- Sumathi, S.L.; Surekha, K.A.P. Solar PV and Wind Energy Conversion Systems An Introduction to Theory, Modeling with MATLAB/SIMULINK, and the Role of Soft Computing Techniques; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–790. [Google Scholar]
- Jazayeri, M.; Uysal, S.; Jazayeri, K. A simple matlab/SIMULINK simulation for PV modules based on one-diode model. In Proceedings of the IEEE High Capacity Optical Networks and Emerging/Enabling Technologies Conference, Magosa, Cyprus, 11–13 December 2013. [Google Scholar]
- Ortiz-Rivera, E.; Peng, F.Z. Analytical model for a photovoltaic module using the electrical characteristics provided by the manufacturer data sheet. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 2087–2091. [Google Scholar]
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy Elsevier 2009, 8, 614–624. [Google Scholar] [CrossRef]
- Hameed, W.I.; Saleh, A.L.; Sawadi, B.A.; Al-Yasir, Y.I.; Abd-Alhameed, R.A. Maximum power point tracking for photovoltaic system by using fuzzy neural network. Inventions 2019, 4, 33. [Google Scholar] [CrossRef]
- Gil-Antonio, L.; Saldivar, B.; Portillo-Rodríguez, O.; Ávila-Vilchis, J.C.; Martínez-Rodríguez, P.R.; Martínez-Méndez, R. Flatness-based control for the maximum power point tracking in a photovoltaic system. Energies 2019, 12, 1843. [Google Scholar] [CrossRef]


| Data No. | Voc (V) | Isc (A) | G (W/m2) |
|---|---|---|---|
| 1 | 24 | 3 | 1000 |
| 2 | 23.7 | 2.44 | 800 |
| 3 | 23.4 | 1.8 | 600 |
| 4 | 22.8 | 1.22 | 400 |
| 5 | 22 | 0.6 | 200 |
| 6 | 21.2 | 3.1 | 1000 |
| 7 | 20.9 | 2.48 | 800 |
| 8 | 20.5 | 1.86 | 600 |
| 9 | 19.9 | 1.24 | 400 |
| 10 | 18.8 | 0.6 | 200 |
| 11 | 18.3 | 3.1 | 1000 |
| 12 | 17.9 | 2.5 | 800 |
| 13 | 17.5 | 1.88 | 600 |
| 14 | 16.9 | 1.25 | 400 |
| 15 | 16 | 0.6 | 200 |
| Wji | −0.1502 | −3.9070 | |||
| 51.4654 | −155.6956 | ||||
| 45.7296 | −51.6981 | ||||
| −4.3849 | 7.0656 | ||||
| 79.0253 | −123.8607 | ||||
| bj | 12.7440 | ||||
| 34.1014 | |||||
| 20.4454 | |||||
| 2.8674 | |||||
| 32.3323 | |||||
| Wo | −8.3171 | −0.2174 | 0.0757 | −0.0026 | −0.2278 |
| bo | 9.0913 | ||||
| Day/Month | Time | Measured Voc (V) | Measured Isc (A) | PV Module Temp. °C | Irradiance Estimated Using Equation (9) (W/m2) | Irradiance Estimated Using ANN (W/m2) | Weather State |
|---|---|---|---|---|---|---|---|
| 14/11 | 11:00 A.M. | 20.5 | 1.1 | 27 | 355 | 369 | cold–cloudy |
| 11:30 A.M. | 20.38 | 0.706 | 26.5 | 226 | 255 | ||
| 18/11 | 10:10 A.M. | 21.3 | 1.64 | 25 | 529 | 535 | cold–sunny |
| 11:55 A.M. | 20.9 | 1.8 | 30 | 581 | 587 | ||
| 02:00 P.M. | 20.7 | 1.27 | 29 | 410 | 416 | ||
| 21/11 | 09:30 A.M. | 21.3 | 1.36 | 21.7 | 439 | 461 | cold–sunny |
| 11:45 A.M. | 20.9 | 1.75 | 29.5 | 564 | 570 | ||
| 12:45 P.M. | 20.6 | 1.6 | 31.7 | 516 | 525 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hameed, W.I.; Sawadi, B.A.; Al-Kamil, S.J.; Al-Radhi, M.S.; Al-Yasir, Y.I.A.; Saleh, A.L.; Abd-Alhameed, R.A. Prediction of Solar Irradiance Based on Artificial Neural Networks. Inventions 2019, 4, 45. https://doi.org/10.3390/inventions4030045
Hameed WI, Sawadi BA, Al-Kamil SJ, Al-Radhi MS, Al-Yasir YIA, Saleh AL, Abd-Alhameed RA. Prediction of Solar Irradiance Based on Artificial Neural Networks. Inventions. 2019; 4(3):45. https://doi.org/10.3390/inventions4030045
Chicago/Turabian StyleHameed, Waleed I., Baha A. Sawadi, Safa J. Al-Kamil, Mohammed S. Al-Radhi, Yasir I. A. Al-Yasir, Ameer L. Saleh, and Raed A. Abd-Alhameed. 2019. "Prediction of Solar Irradiance Based on Artificial Neural Networks" Inventions 4, no. 3: 45. https://doi.org/10.3390/inventions4030045
APA StyleHameed, W. I., Sawadi, B. A., Al-Kamil, S. J., Al-Radhi, M. S., Al-Yasir, Y. I. A., Saleh, A. L., & Abd-Alhameed, R. A. (2019). Prediction of Solar Irradiance Based on Artificial Neural Networks. Inventions, 4(3), 45. https://doi.org/10.3390/inventions4030045









