Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation
Abstract
1. Introduction
- As simple as possible;
- As accurately as necessary; and
- Easy to implement in an electronic circuit simulator.
- Which goals are achieved with the models?
- Which parameterization options are available?
- Which simulation environment is provided for implementation?
2. Overview of Battery Models
2.1. Mathematical and Electrochemical Models
2.2. Thermal Models
2.3. Electrical Models
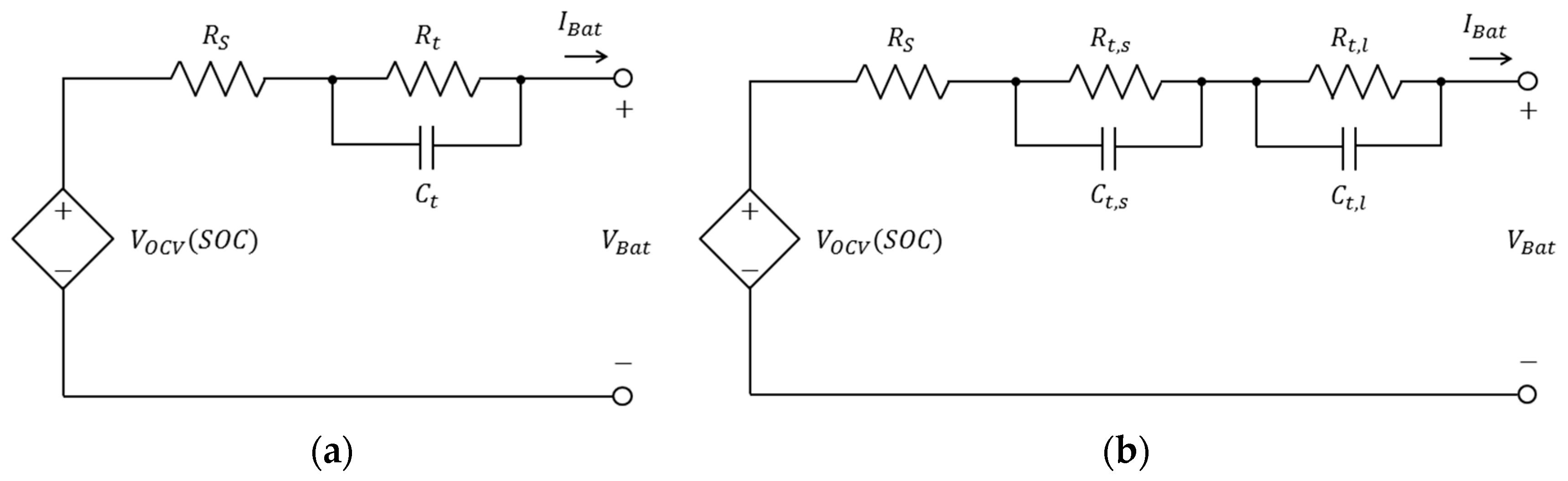
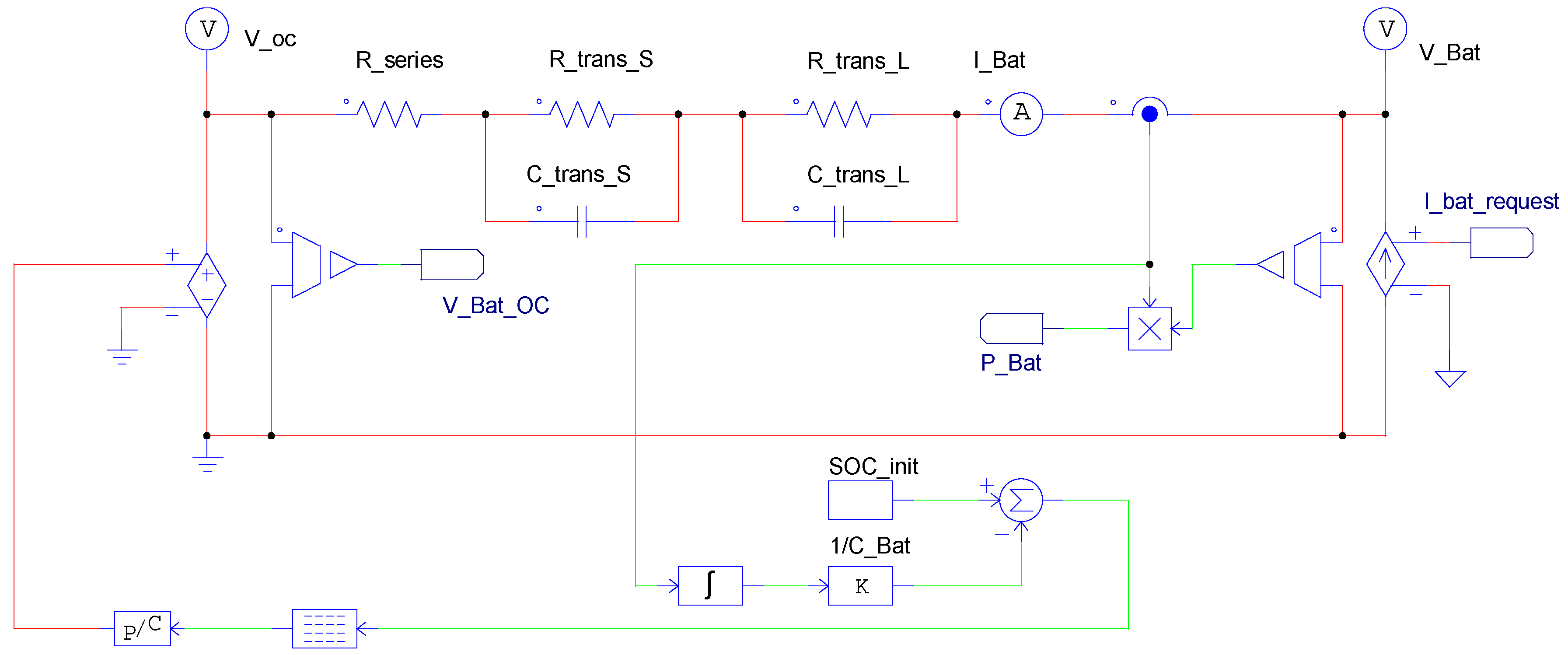
2.3.1. Thevenin-Based Electrical Model
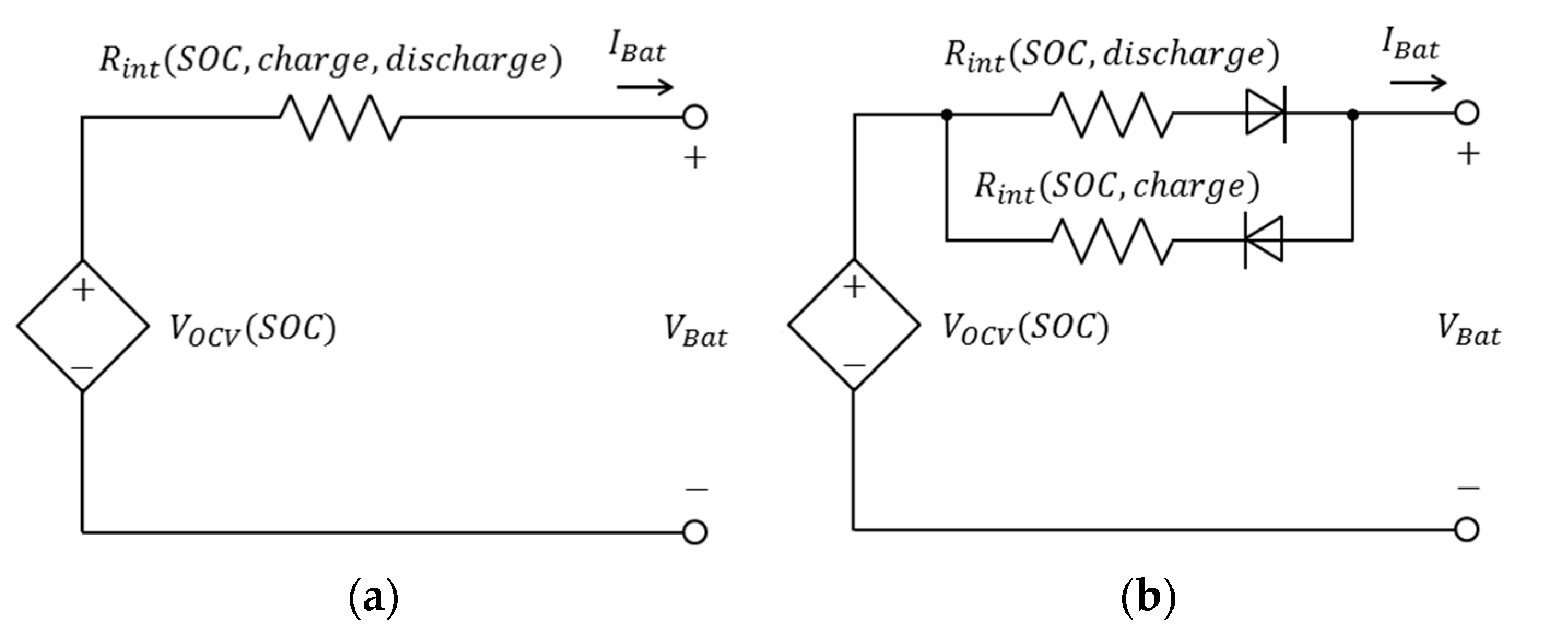
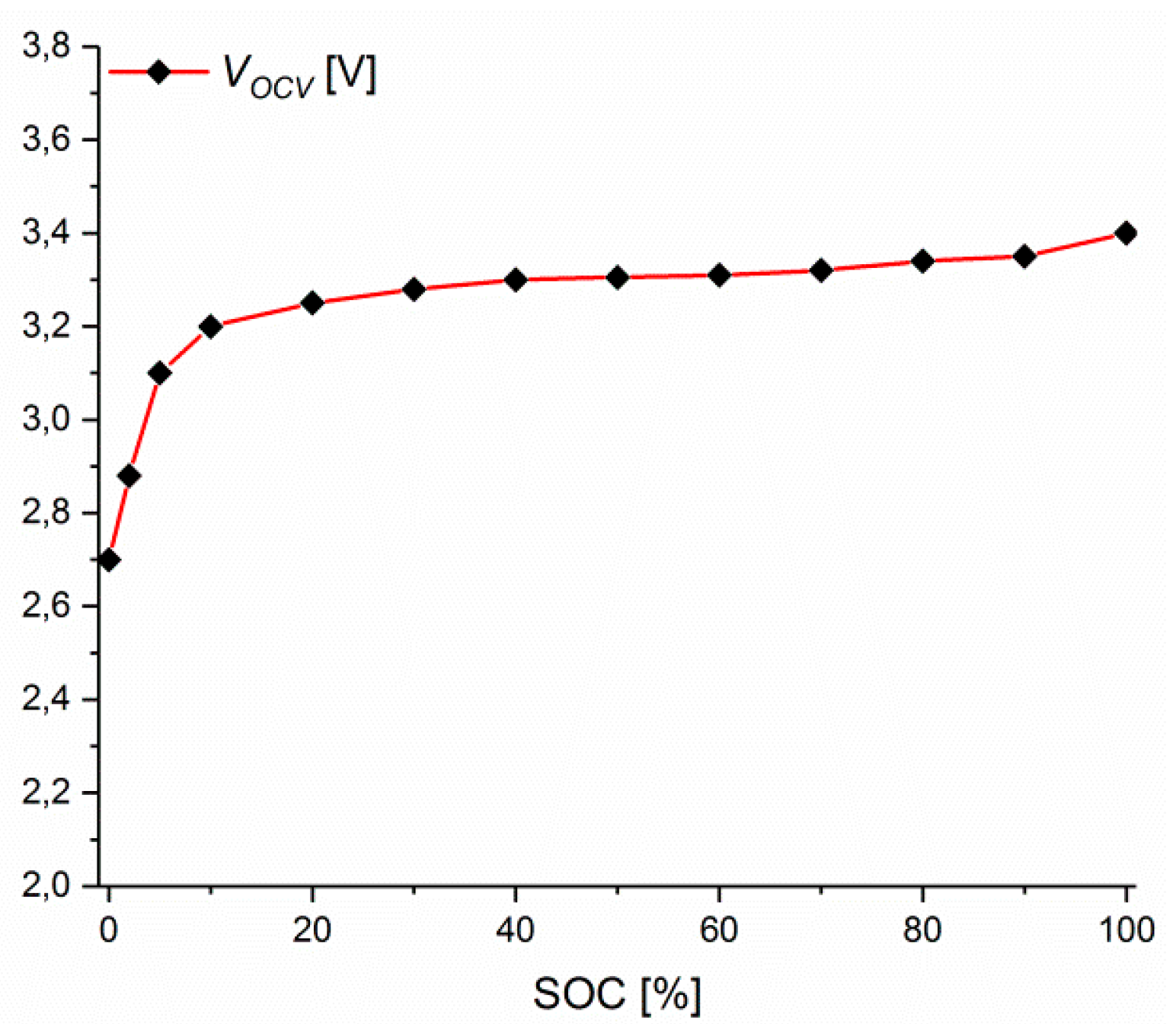
2.3.2. Rint Electrical Model
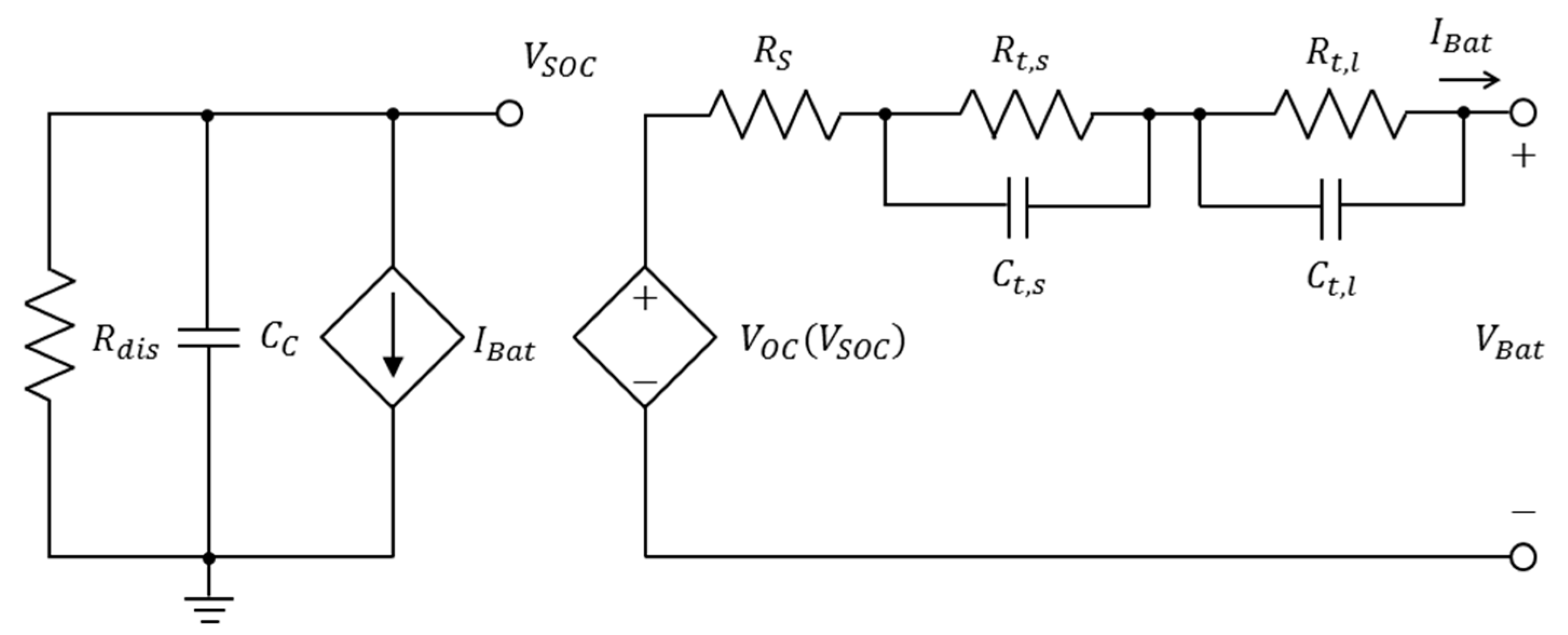
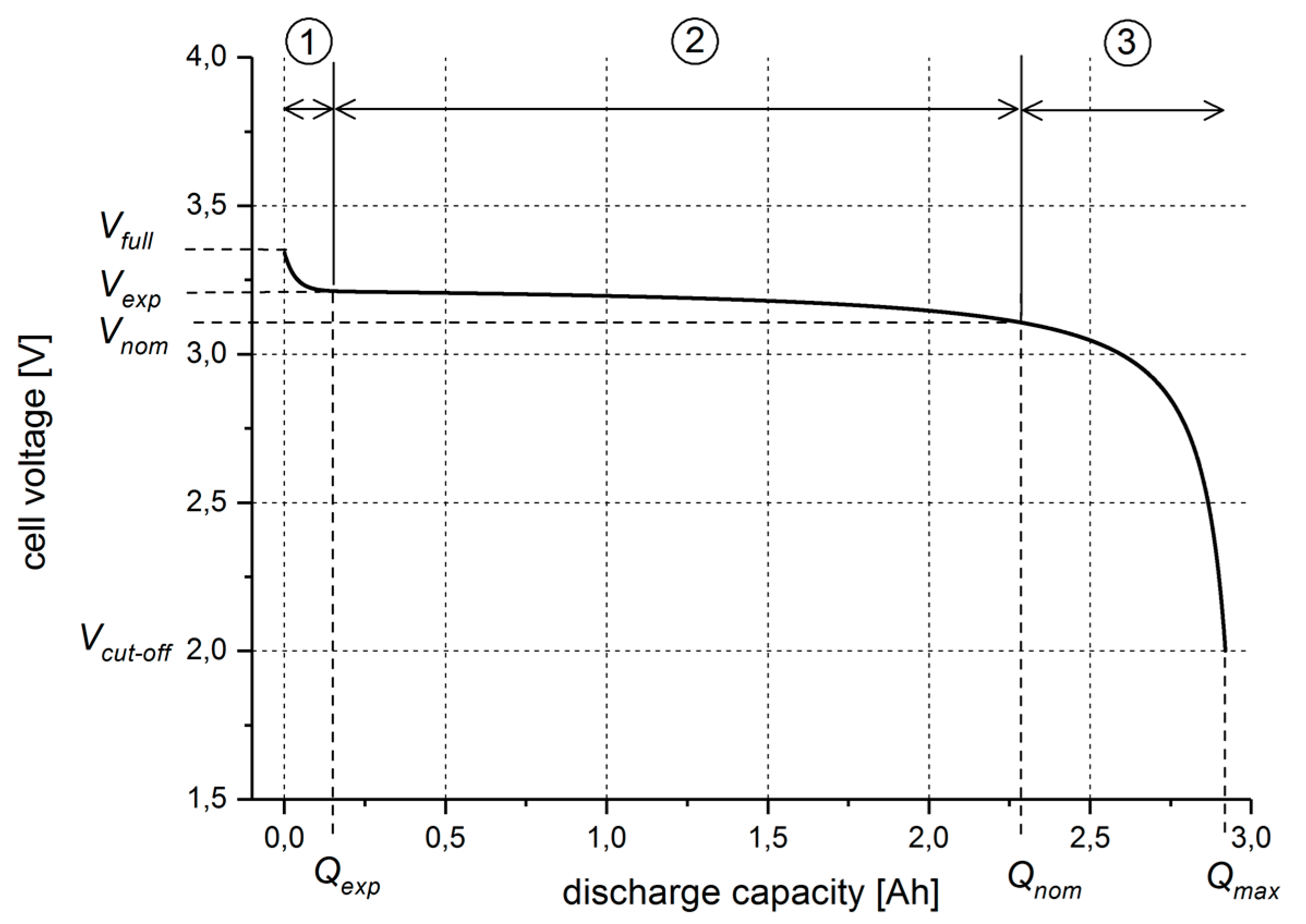
2.3.3. Runtime-Based Electrical Model
2.3.4. Impedance-Based Electrical Model
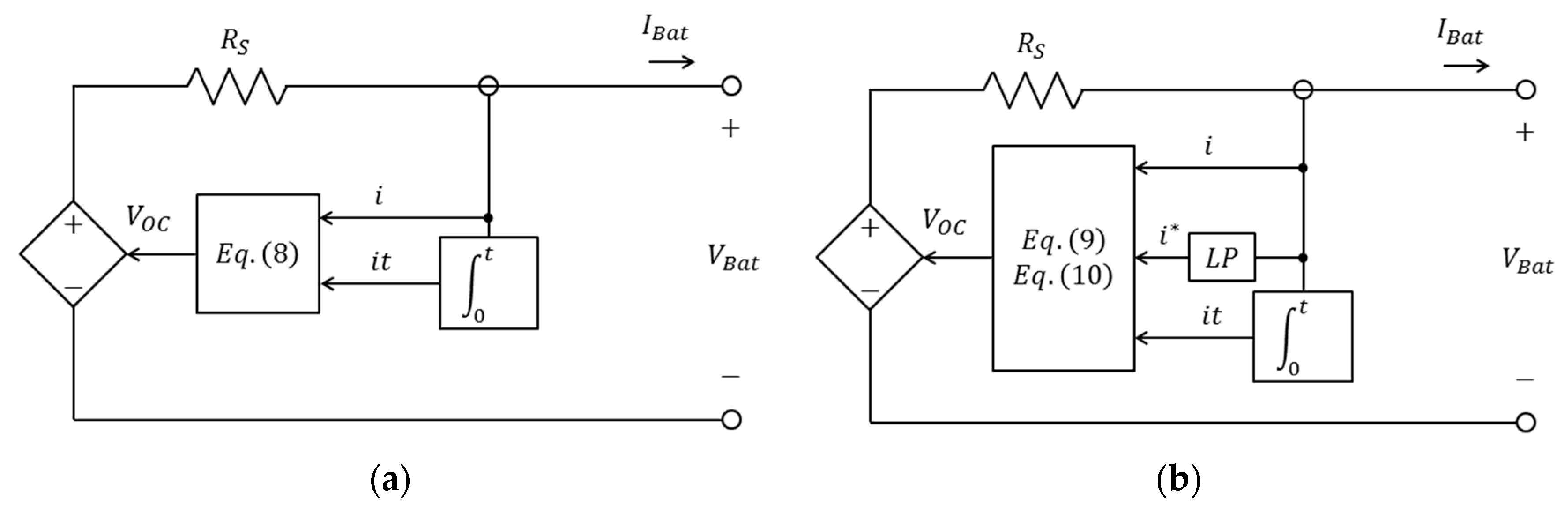
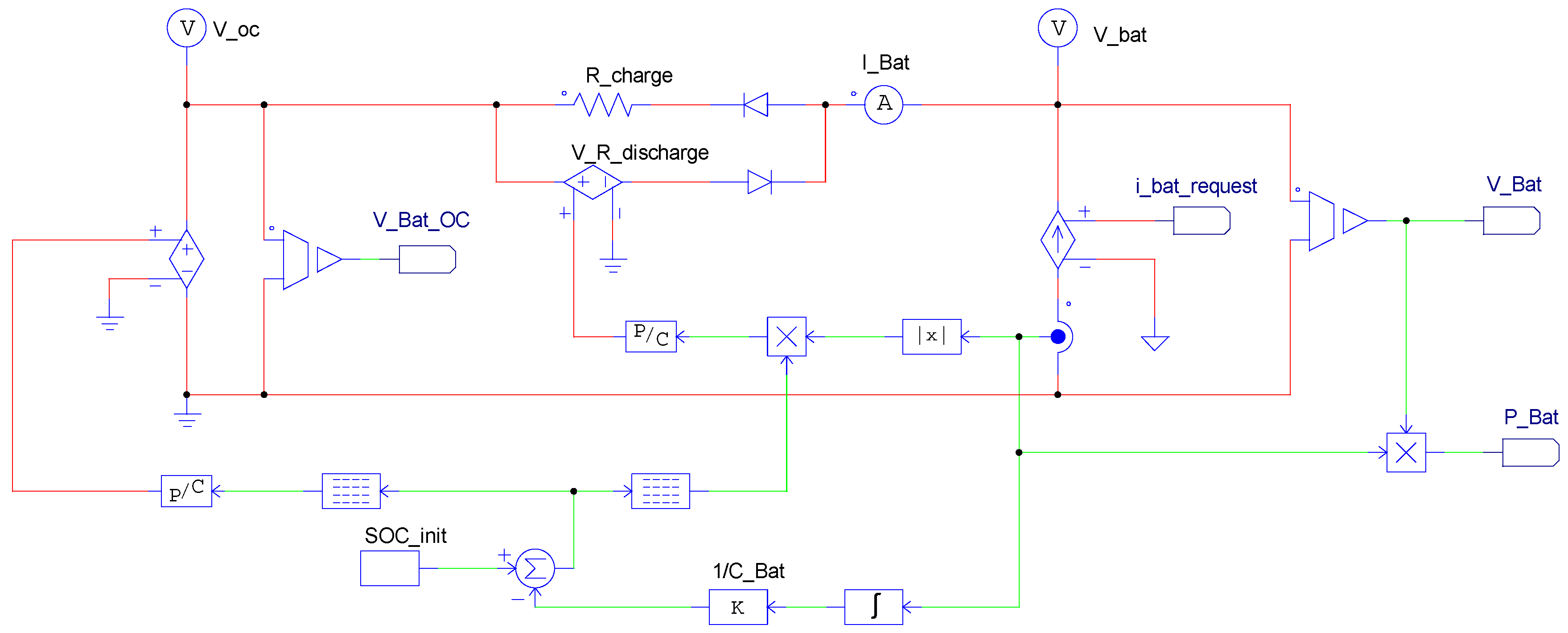
2.3.5. Shepherd’s Model
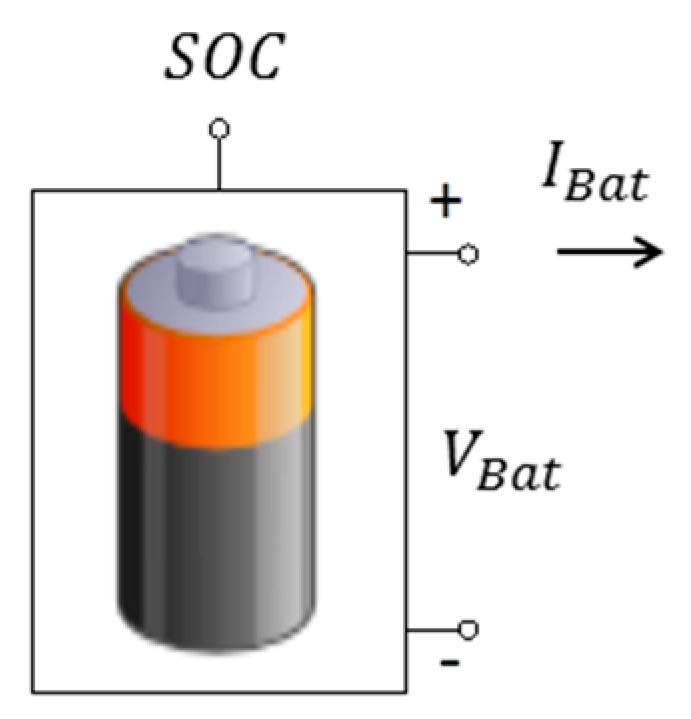
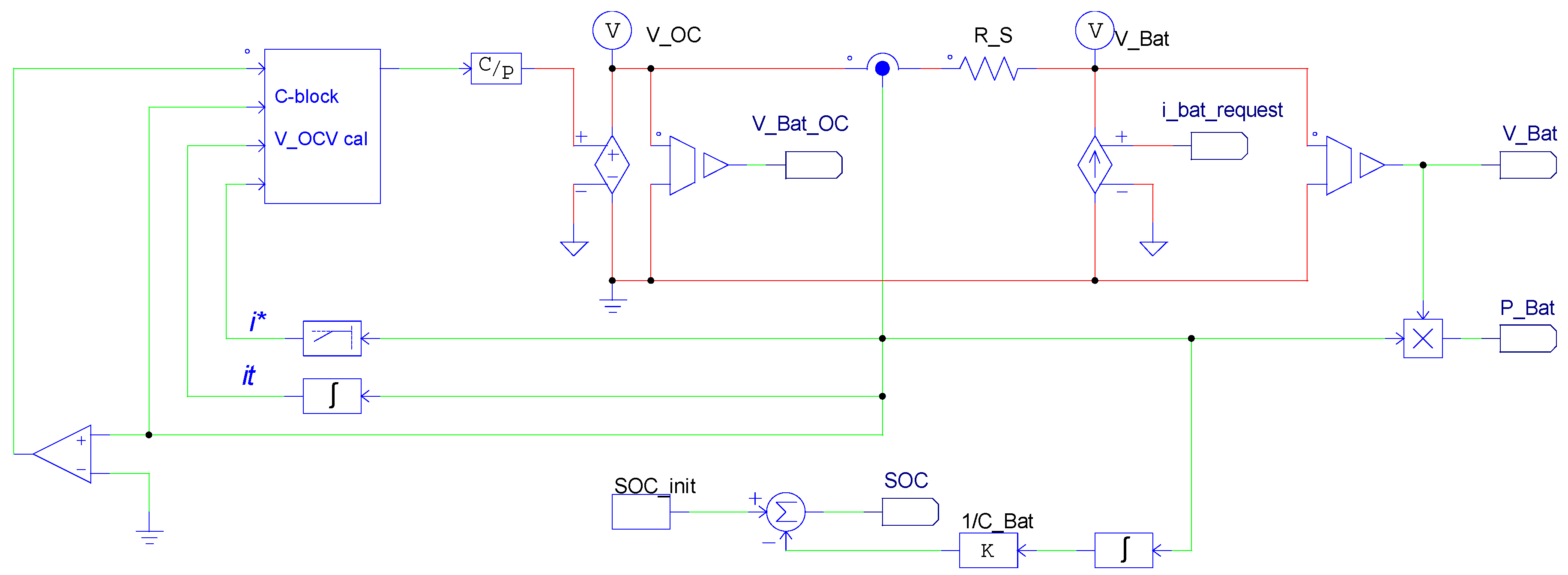
2.3.6. Generic Library Model
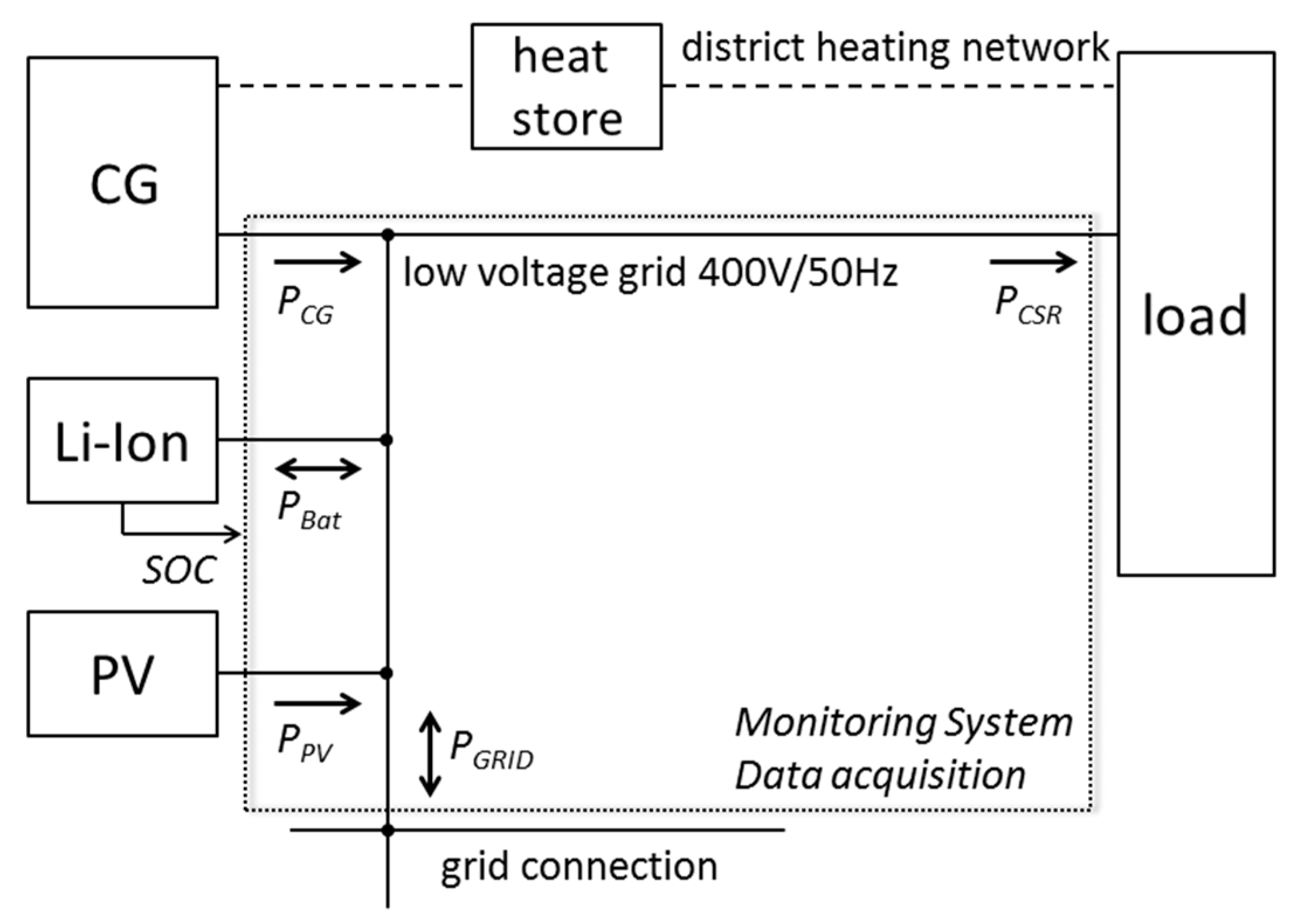
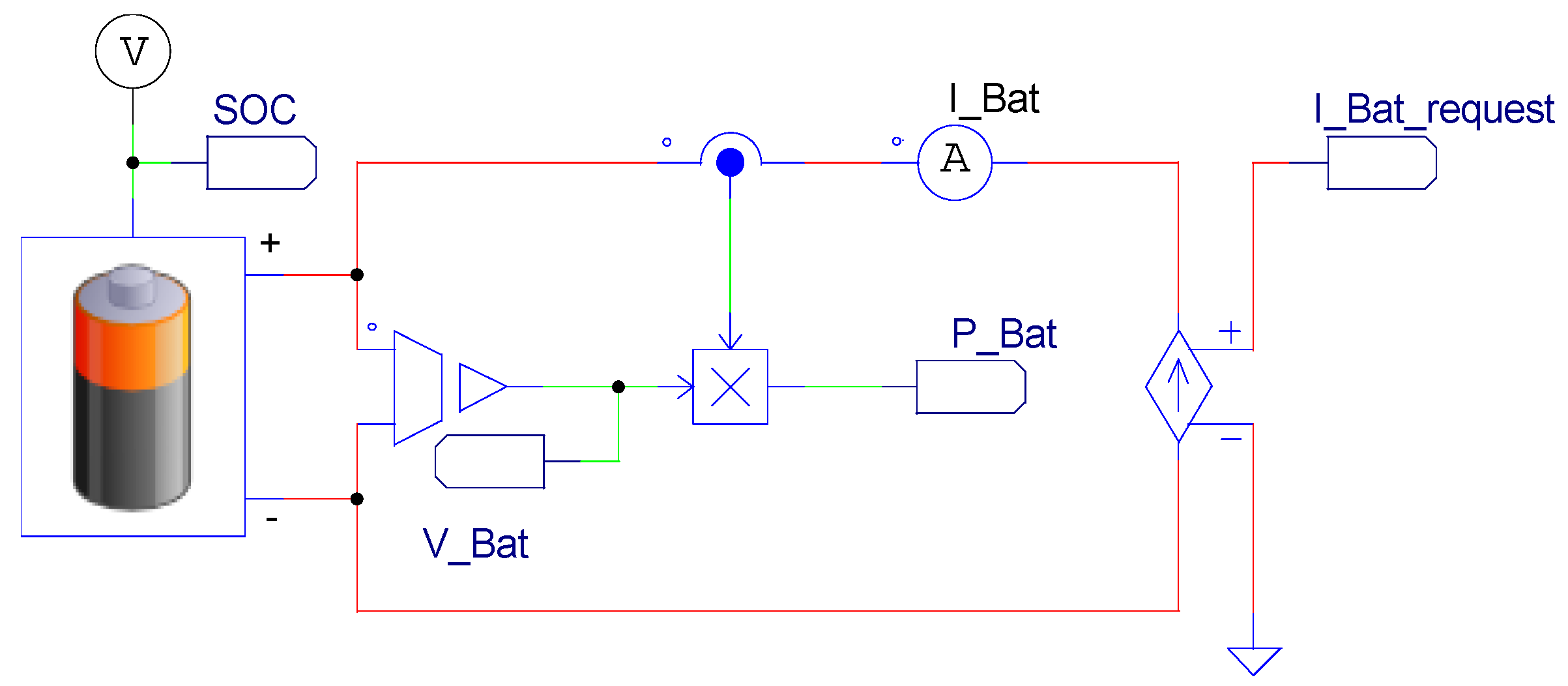
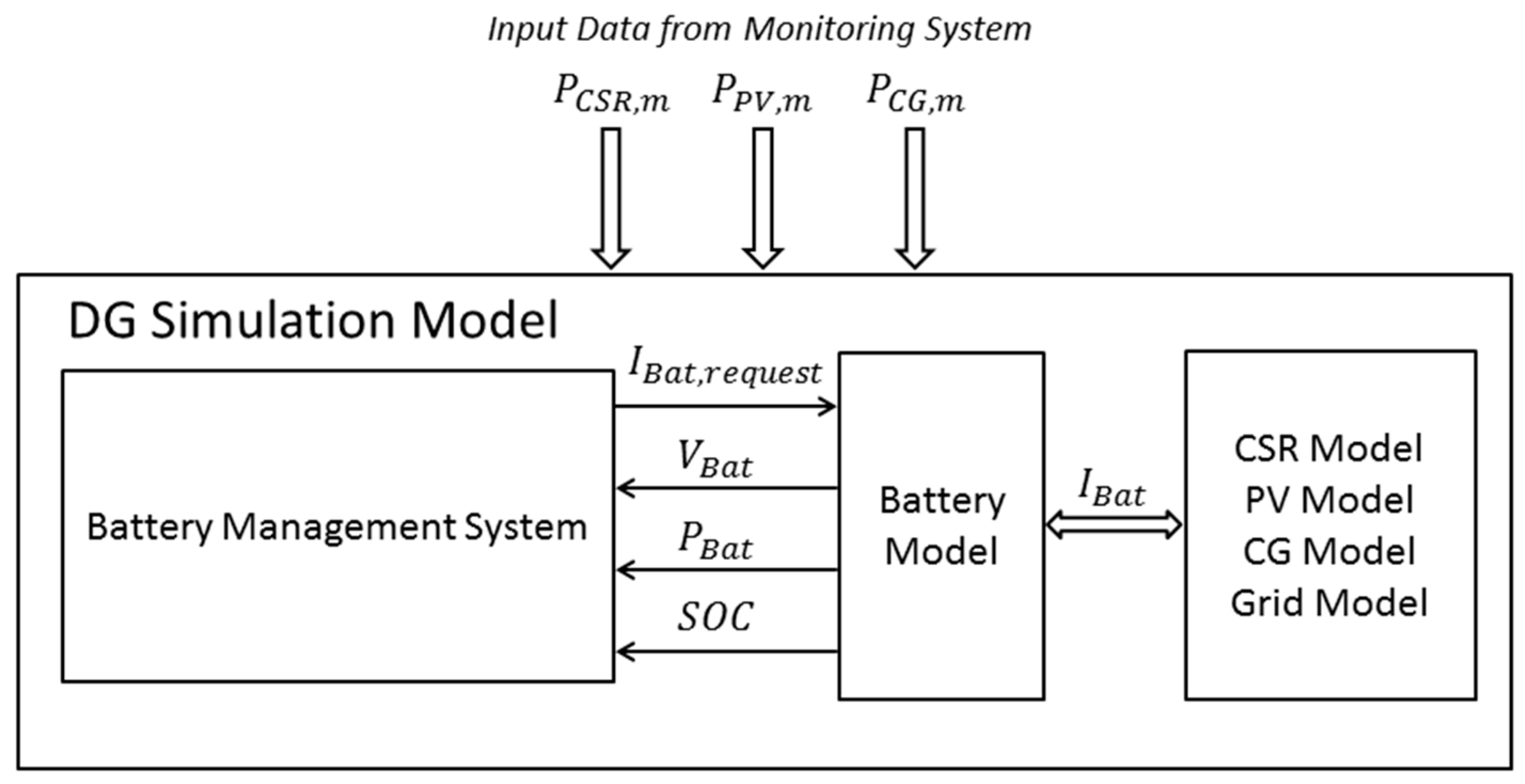
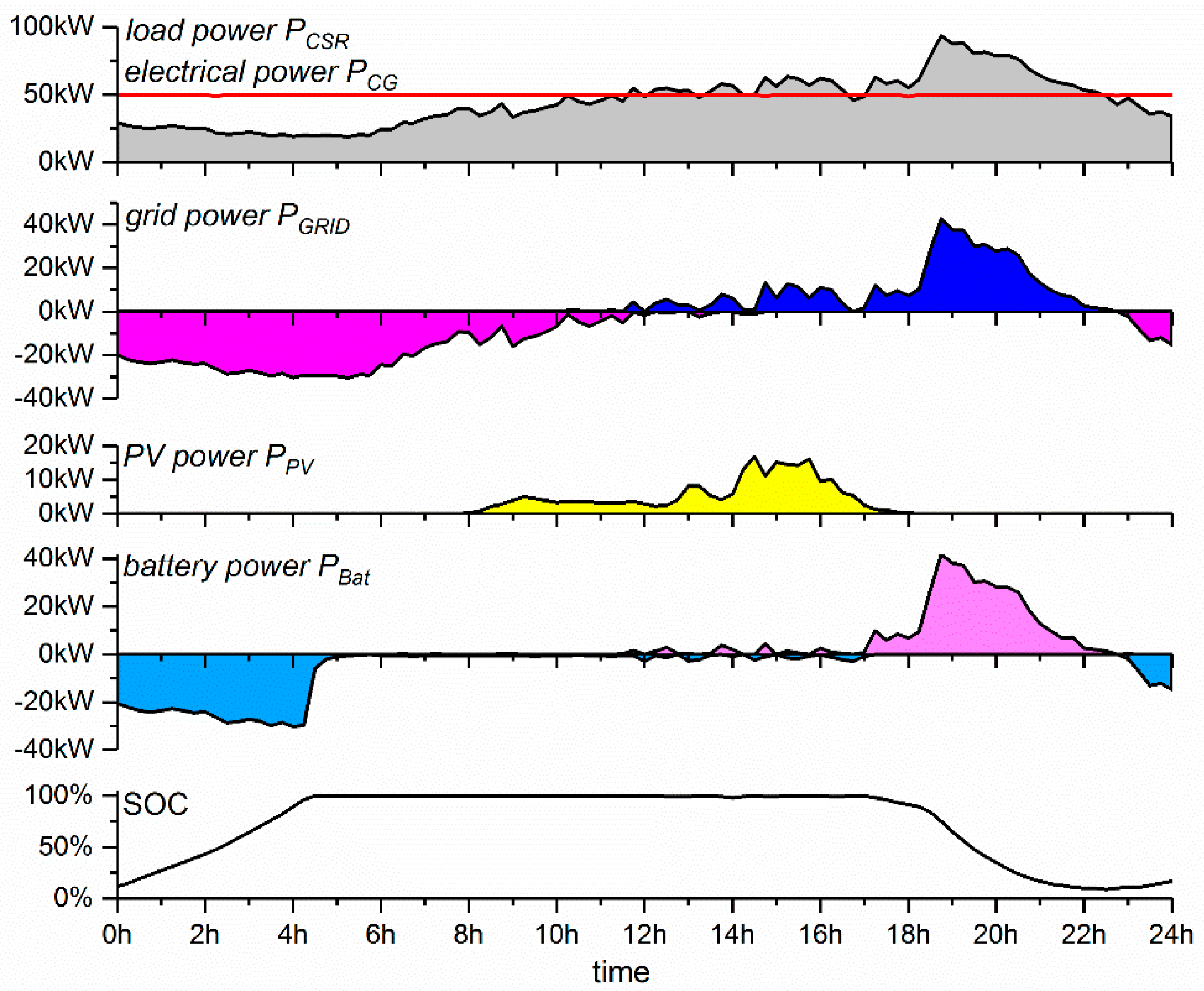
3. Case Study
3.1. Implementation of the Thevenin-Based Model
3.2. Implementation of the Rint Model
3.3. Implementation of the Shepherd’s Model
3.4. Implementation of the Generic Library Model
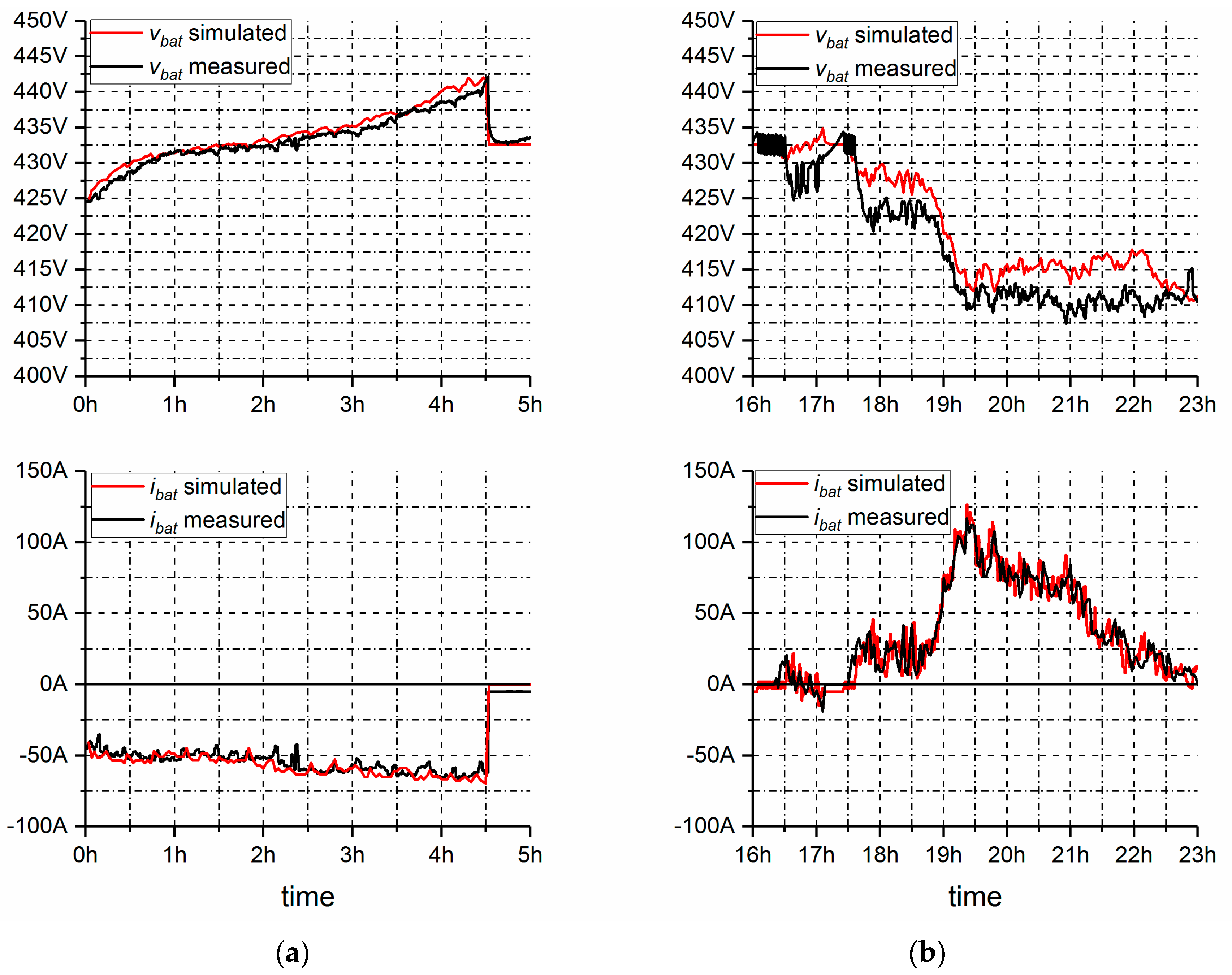
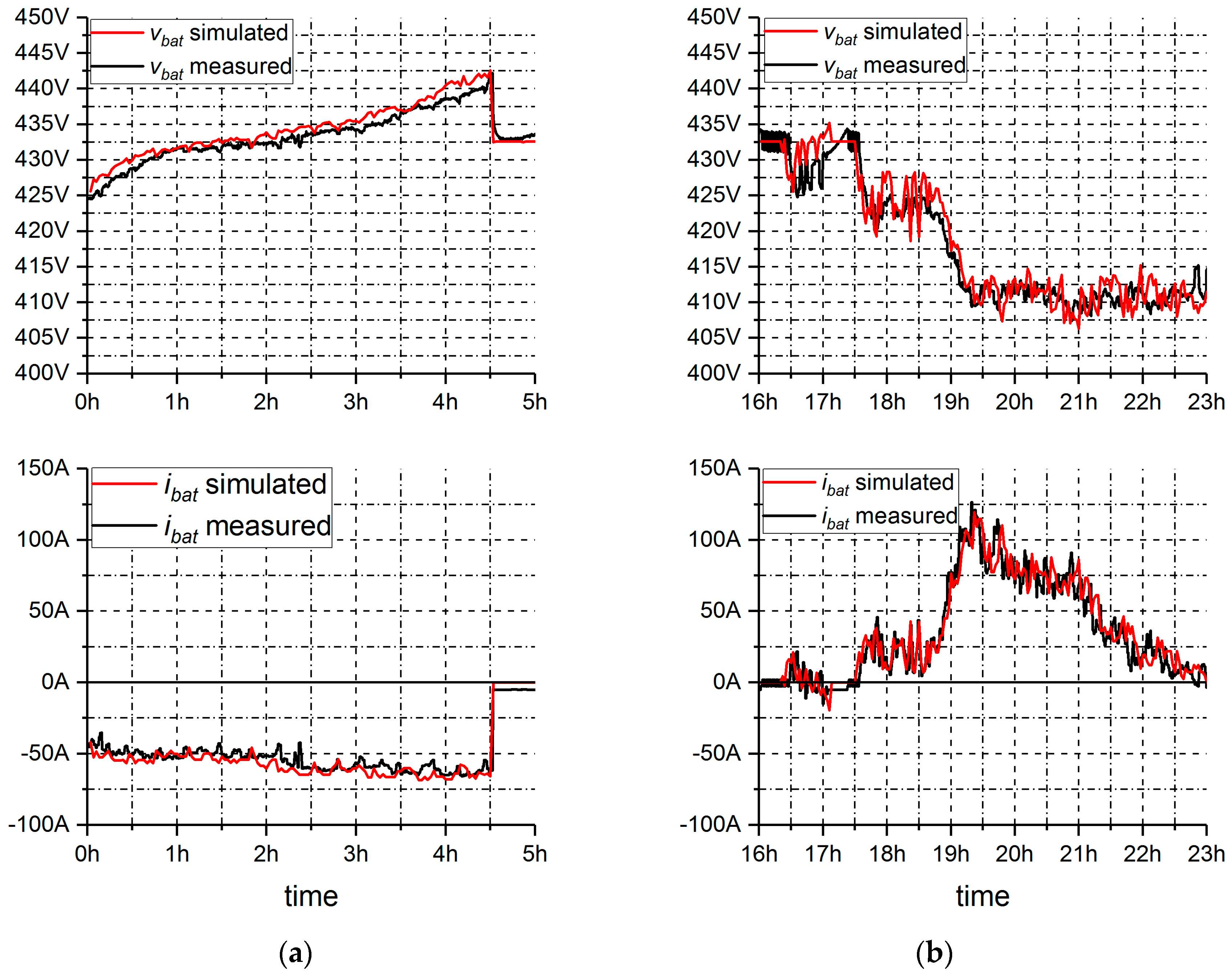
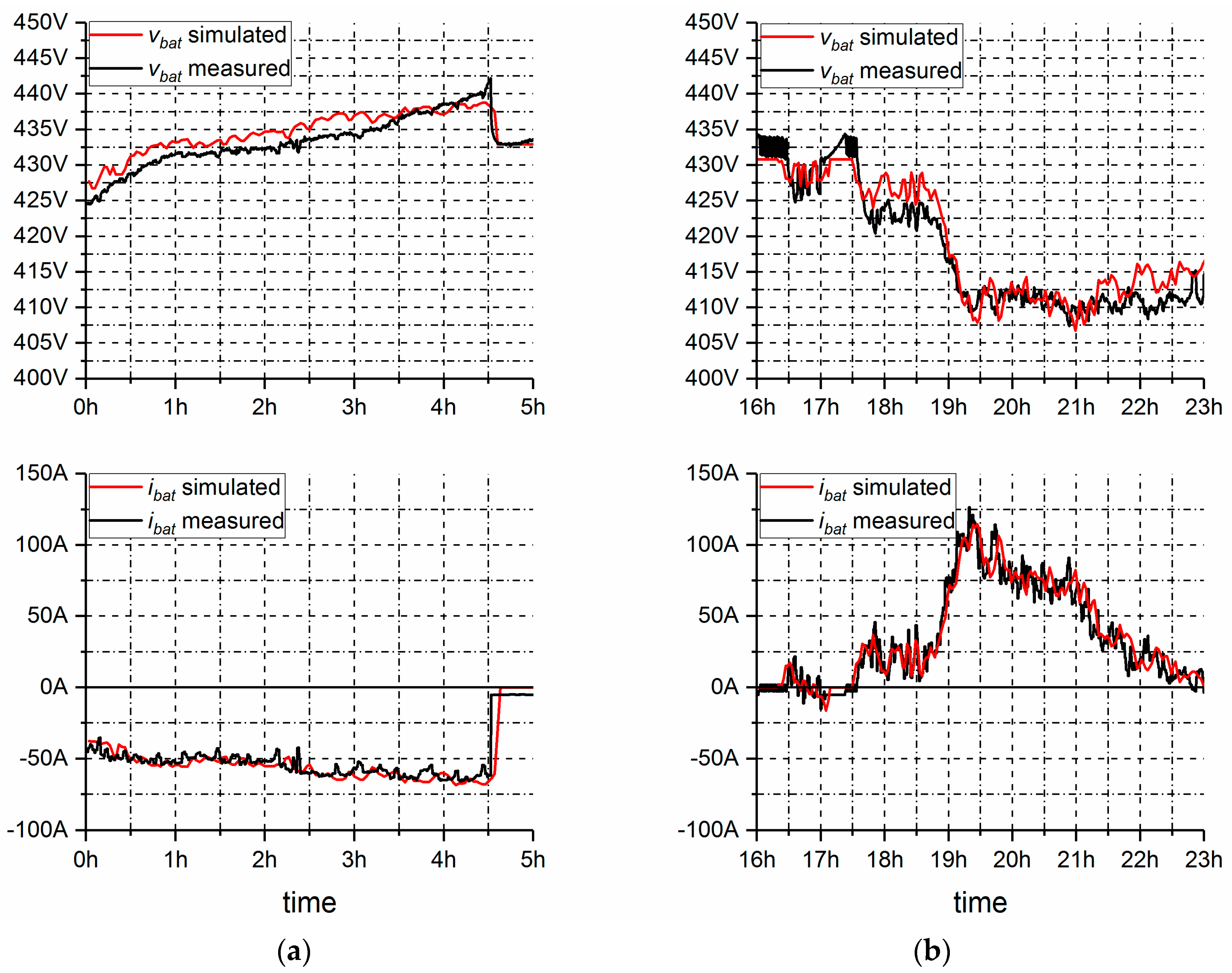
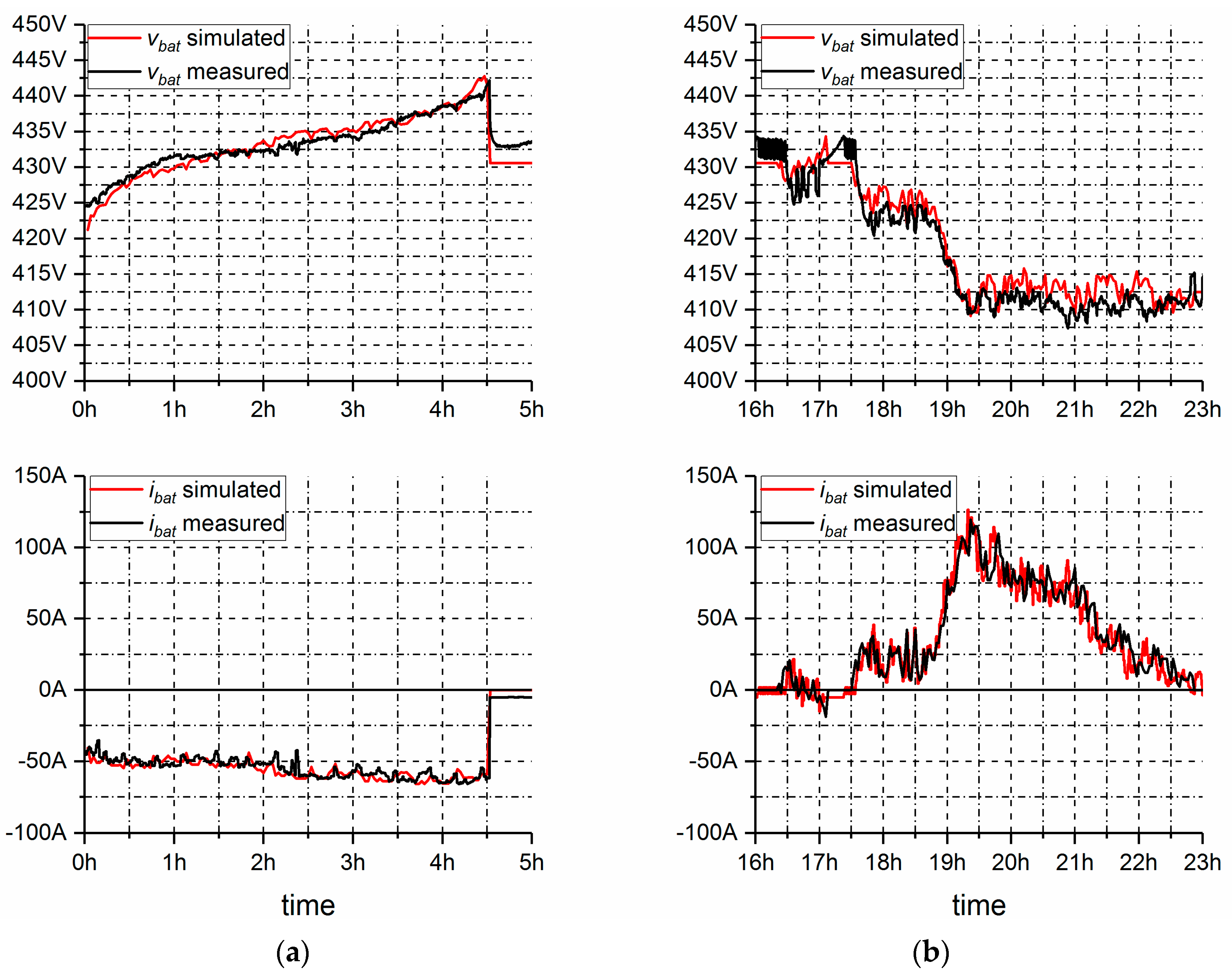
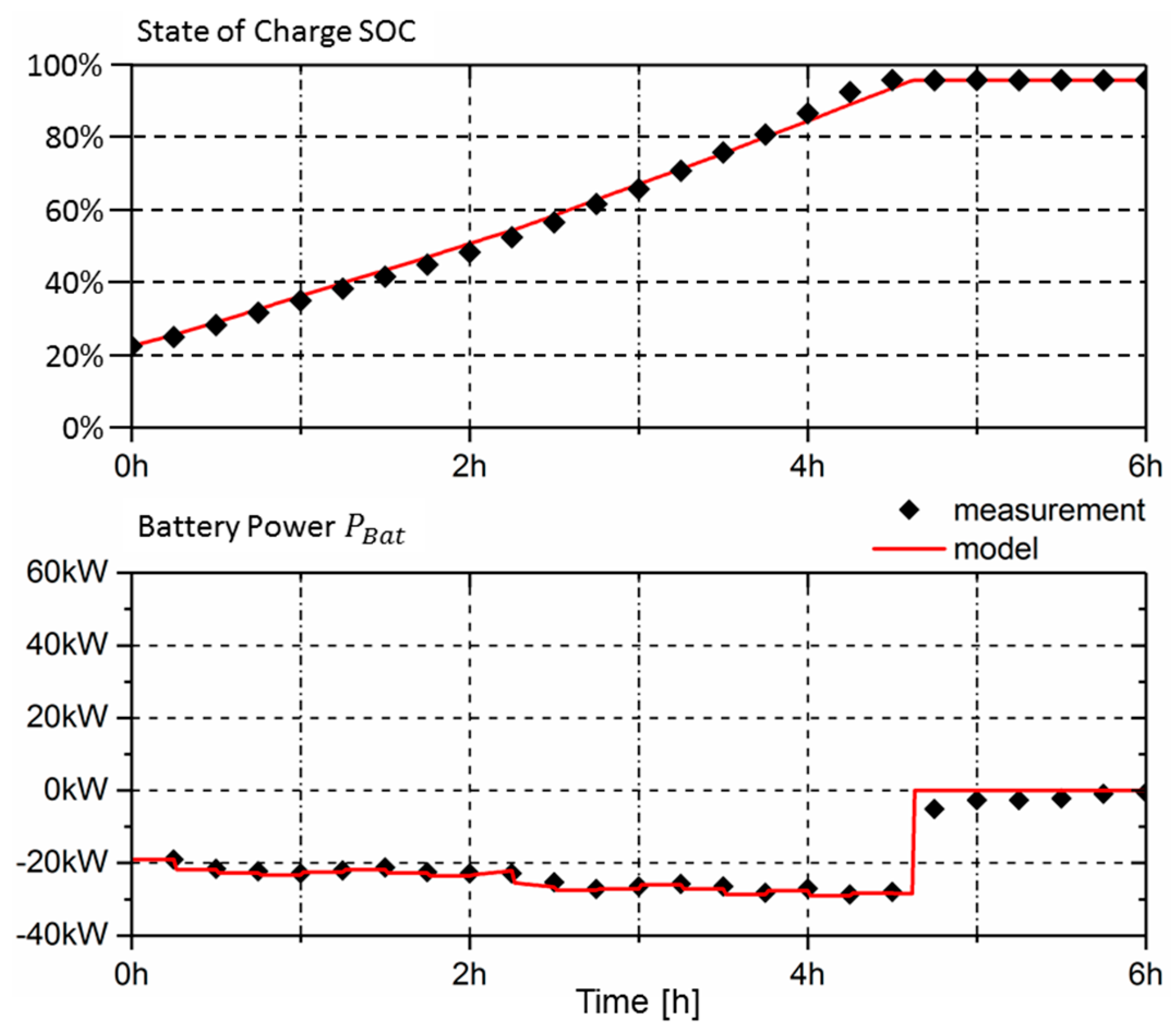
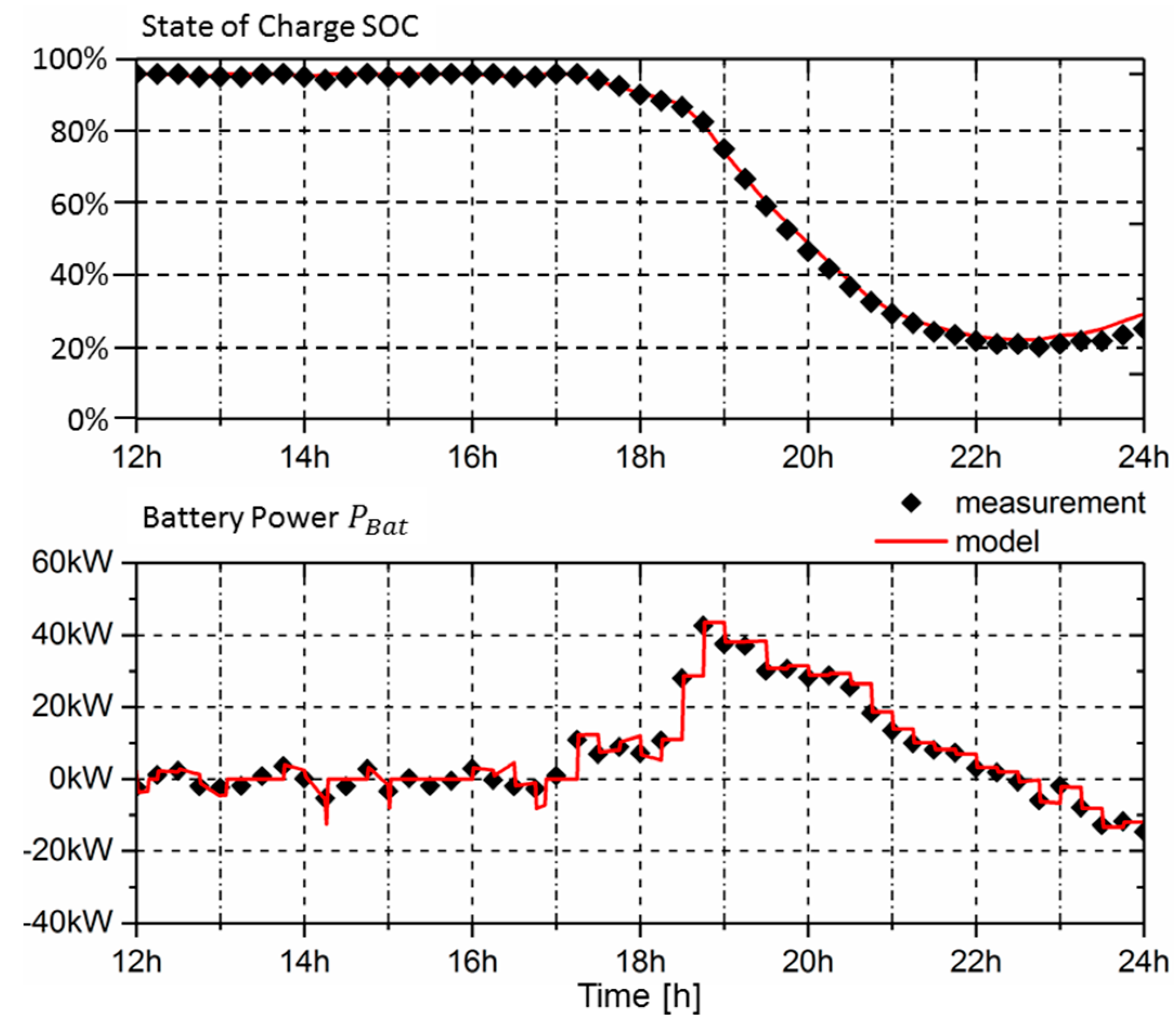
3.5. Model Validation
3.5.1. Predicting I–V Performance
3.5.2. Predicting SOC Performance
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Exxon Mobil 2018 Outlook for Energy: A View to 2040. Report 2017. Available online: https://corporate.exxonmobil.com/energy-and-environment/energy-resources/outlook-for-energy/2018-outlook-for-energy-a-view-to-2040 (accessed on 2 August 2019).
- Schaeffer, M.; Rogelj, J.; Roming, J.; Sferra, F.; Hare, B.; Serdeczny, O. Feasibility of Limiting Warming to 1.5 and 2 °C. Climate Analytics Report 2015. Available online: https://climateanalytics.org/briefings/feasibility-of-limiting-warming-to-below-15c/ (accessed on 2 August 2019).
- Dröge, S. The Paris Agreement 2015, Turning Point for the International Climate Regime. SWP Research Paper, German Institute for International and Security Affairs 2016. Available online: https://www.ssoar.info/ssoar/handle/document/46462 (accessed on 2 August 2019).
- Cox, S.; Gagnon, P.; Stout, S.; Zinman, O.; Watson, A.; Hotchkiss, E. Distributed Generation to Support Development-Focused Climate Action. National Renewable Energy Laboratory 2016. Available online: https://www.climatelinks.org/resources/distributed-generation-support-development-focused-climate-action (accessed on 2 August 2019).
- Matvoz, D.; Leskovec, R.; Maksić, M. Optimized reactive power characteristics for distributed generation sources in the low voltage network. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Jedrychwski, R.; Sereja, K. Control system for distributed generation in low voltage network systems. Przegląd Elektrotechniczny 2018, 94, 50–53. [Google Scholar] [CrossRef]
- Anaya, K.L.; Pollitt, M.G. Integrating Distributed Generation: Regulation and Trends in Three Leading Countries. Energy Policy 2015, 85, 475–486. [Google Scholar] [CrossRef]
- Lowder, T.; Zhou, E.; Tian, T. Evolving Distributed Generation Support Mechanisms: Case Studies from United States, Germany, United Kingdom, and Australia; National Renewable Energy Laboratory, Technical Report 2017; National Renewable Energy Laboratory: Lakewood, CO, USA, 2017.
- Thielmann, A.; Sauerand, A.; Wietschel, M. Overall Roadmap Stationary Energy Storage 2030 (Original German Title: Gesamt-Roadmap Stationäre Energiespeicher 2030); Fraunhofer Institute for Systems and Innovation Research ISI, Karlsruhe Germany: Karlsruhe, Germany, 2015. [Google Scholar]
- Eaton Powerquality Power Xpert 9395P UPS 250–1200 kVA. Datasheet 2015. Available online: https://www.eaton.com/us/en-us/products/backup-power-ups-surge-it-power-distribution/backup-power-ups.html (accessed on 9 June 2019).
- Electrotechnical Commission. White Paper—Electrical Energy Storage, International; Electrotechnical Commission: Geneva, Switzerland, 2011. [Google Scholar]
- Ding, C.; Zhang, H.; Li, X.; Liu, T.; Xing, F. Vanadium Flow Battery for Energy Storage: Prospects and Challenges. J. Phys. Chem. Lett. 2013, 4, 1281–1294. [Google Scholar] [CrossRef] [PubMed]
- Coote, N.; Milne, G. 1 MW Battery, Shetland; Scottish and Southern Energy Power Distribution: Perth, UK, 2013. [Google Scholar]
- Lemmon, J.P. Planar ZEBRA battery for renewable integration and grid applications. In Proceedings of the IBA Meeting, Cape Town, South Africa, 12–14 April 2011. [Google Scholar]
- Vasconcelos, J. Electricity storage: How to facilitate its deployment and operation in the EU, THINK. In Proceedings of the 7th EU Framework Program, Final Report, 21–22 June 2012. Available online: https://www.eui.eu/Projects/THINK/Documents/Thinktopic/THINKTopic8online.pdf (accessed on 9 June 2019).
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef]
- Li, K.; Tseng, K.J. An electrical model capable of estimating the state of energy for lithium-ion batteries used in energy storage systems. In Proceedings of the IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016. [Google Scholar]
- Rodrigues, E.M.G.; Godina, R.; Osório, G.J.; Lujano-Rojas, J.M.; Matias, J.C.O.; Catalão, J.P.S. Comparison of Battery Models for Energy Storage Applications on Insular Grids. In Proceedings of the Australasian Universities Power Engineering Conference, Wollongong, Australia, 27–30 September 2015. [Google Scholar]
- Xia, T.; Li, M.; Zi, P.; Tian, L.; Qin, X.; An, N. Modeling and Simulation of Battery Energy Storage System (BESS) Used in Power System. In Proceedings of the 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Changsha, China, 26–29 November 2015. [Google Scholar]
- Fortenbacher, P.; Mathieu, J.L.; Andersson, G. Modeling, Identification, and Optimal Control of Batteries for Power System Applications. In Proceedings of the Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014. [Google Scholar]
- Fortenbacher, P.; Mathieu, J.L.; Andersson, G. Modeling and Optimal Operation of Distributed Battery Storage in Low Voltage Grids. IEEE Trans. Power Syst. 2017, 32, 4340–4350. [Google Scholar] [CrossRef]
- Smith, K.; Saxon, A.; Keyser, M.; Lundstrom, B. Life Prediction Model for Grid-Connected Li-ion Battery Energy Storage System. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017. [Google Scholar]
- Hinz, H.; Stefanov, Y.; Kilz, J. Integration of a Photovoltaic and Battery System into a Decentralized Power Generation. In Proceedings of the PCIM Asia; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 24–26 June 2015. [Google Scholar]
- Hussein, A.A.H.; Batarseh, I. An Overview of Generic Battery Models. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011. [Google Scholar]
- Sun, K.; Shu, Q. Overview of the Types of Battery Models. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011. [Google Scholar]
- Mousavi, G.; Nikdel, N. Various battery models for various simulation studies and applications. Renew. Sustain. Energy Rev. 2014, 32, 477–485. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, W. A Review on Electric Vehicle Battery Modelling: From Lithium-ion toward Lithium-Sulfur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery I. Discharge behavior of a single cell. J. Electrochem. Soc. 1995, 142, 3274–3281. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery II. Temperature profiles in a cell stack. J. Electrochem. Soc. 1995, 142, 3282–3288. [Google Scholar] [CrossRef]
- Alhanouti, M.; Gießler, M.; Blank, T.; Gauterin, F. New Electro-Thermal Battery Pack Model of an Electric Vehicle. Energies 2016, 9, 563. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.O.; Park, J.W. A Comprehensive Battery Equivalent Circuit Based Model for Battery Management Application. In Proceedings of the ASME Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013; pp. 1520–1529. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Chen, M.; Rincón-Mora, G.A. An Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thevenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of Li-Ion Batteries Using Equivalent Circuit Diagrams. Available online: http://www.red.pe.org.pl/articles/2012/7b/40.pdf (accessed on 7 June 2019).
- He, Z.; Yang, G.; Lu, L. A Parameter Identification Method for Dynamics of Lithium Iron Phosphate Batteries Based on Step-Change Current Curves and Constant Current Curves. Energies 2016, 9, 444. [Google Scholar] [CrossRef]
- Hsieh, V.-C.; Lin, T.-D.; Chen, R.-J.; Lin, H.-Y. Electric circuit modelling for lithium-ion batteries by intermittent discharging. IET Power Electron. 2014, 7, 2672–2677. [Google Scholar] [CrossRef]
- Hagemann, S.C. Simple pspice models let you simulate common battery types. Electron. Design. News 1993, 38, 117–129. [Google Scholar]
- Bohlen, O.; Buller, S.; De Doncker, R.W.; Glbke, M.; Naumann, R. Impedance Based Battery Diagnosis for Automotive Applications. In Proceedings of the 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 2792–2797. [Google Scholar]
- Buller, B.; Thele, M.; De Doncker, R.W.; Karden, E. Impedance-Based Simulation Models of Supercapacitors and Li-Ion Batteries for Power Electronic Applications. IEEE Trans. Ind. Appl. 2005, 41, 742–774. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of Lithium-Ion Battery Models Based on Electrochemical Impedance Spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef]
- Shepherd, C.M. Design of Primary and Secondary Cells—Part 2. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A. Experimental Validation of a Battery Dynamic Model for EV Applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A.; Dekkiche, A.-I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007. [Google Scholar]
- Raszmann, E.; Baker, K.; Shi, Y.; Christensen, D. Modeling Stationary Lithium-Ion Batteries for Optimization and Predictive Control. In Proceedings of the IEEE Power and Energy Conference, Champaign, IL, USA, 23–24 February 2017. [Google Scholar]
- Yasuda, M. Sony Energy Storage System Using Olivine Type Battery. Product Presentation Sony Energy Devices, 13 March 2013. [Google Scholar]
- Battery: Implement Generic Batter Model. Available online: https://www.mathworks.com/help/physmod/sps/powersys/ref/battery.html (accessed on 7 June 2019).
- PSIM Tutorial Lithium-Ion Battery Model. POWERSIM, October 2016.
- Sony’s Energy Storage System—The Sony Lithium Ion Iron Phosphate (LFP) Advantage, Product Description 2013. Available online: https://docplayer.net/21498677-Sony-s-energy-storage-system-the-sony-lithium- ion-iron-phosphate-lfp-advantage.html (accessed on 30 July 2019).
- Hekert, J. Regionalverband FrankfurtRheinMain—Deutsches Institut für Urbanistik (German Institute of Urban Affairs). Press Release June 2015. Available online: www.region-frankfurt.de/media/custom/2005_1683_1.PDF?1436270389 (accessed on 30 July 2019).
- Zhang, L.; Peng, H.; Ning, Z.; Mu, Z.; Sun, C. Comparative Research on RC Equivalent Circuit Models for Lithium-Ion Batteries of Electric Vehicles. Appl. Sci. 2017, 7, 1002. [Google Scholar] [CrossRef]
- Safaria, M.; Delacourta, C. Modeling of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, 562–571. [Google Scholar] [CrossRef]
- Kin, T.; Qiao, W. A Hybrid Battery Model Capable of Capturing Dynamic Circuit Characteristics and Nonlinear Capacity Effects. IEEE Trans. Energy Convers. 2011, 26, 1172–1180. [Google Scholar]
- Naumann, M. Techno-Economic Evaluation of Stationary Battery Energy Storage Systems with Special Consideration of Aging. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]



| <100 kWh | 0.1–1 MWh | 1 MWh–1 GWh | |
|---|---|---|---|
| <1 h | lead-acid lithium-ion lithium-air | lead-acid lithium-ion lithium-sulphur | lead-acid lithium-ion |
| <1 day | lead-acid lithium-ion vanadium-redox sodium-sulphur sodium-nickel-chloride lithium-sulphur | lead-acid lithium-ion vanadium-redox sodium-sulphur sodium-nickel-chloride zinc-air lithium-air | lead-acid vanadium-redox sodium-sulphur sodium-nickel-chloride |
| >1 day | lead-acid lithium-ion vanadium-redox sodium-sulphur sodium-nickel-chloride zinc-air lithium-sulphur | vanadium-redox sodium-sulphur sodium-nickel-chloride | vanadium-redox |
| Energy/Capacity | Nominal Voltage | Maximum Discharge Current/Power |
|---|---|---|
| / |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinz, H. Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation. Inventions 2019, 4, 41. https://doi.org/10.3390/inventions4030041
Hinz H. Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation. Inventions. 2019; 4(3):41. https://doi.org/10.3390/inventions4030041
Chicago/Turabian StyleHinz, Hartmut. 2019. "Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation" Inventions 4, no. 3: 41. https://doi.org/10.3390/inventions4030041
APA StyleHinz, H. (2019). Comparison of Lithium-Ion Battery Models for Simulating Storage Systems in Distributed Power Generation. Inventions, 4(3), 41. https://doi.org/10.3390/inventions4030041





