Analysis of an H∞ Robust Control for a Three-Phase Voltage Source Inverter
Abstract
1. Introduction
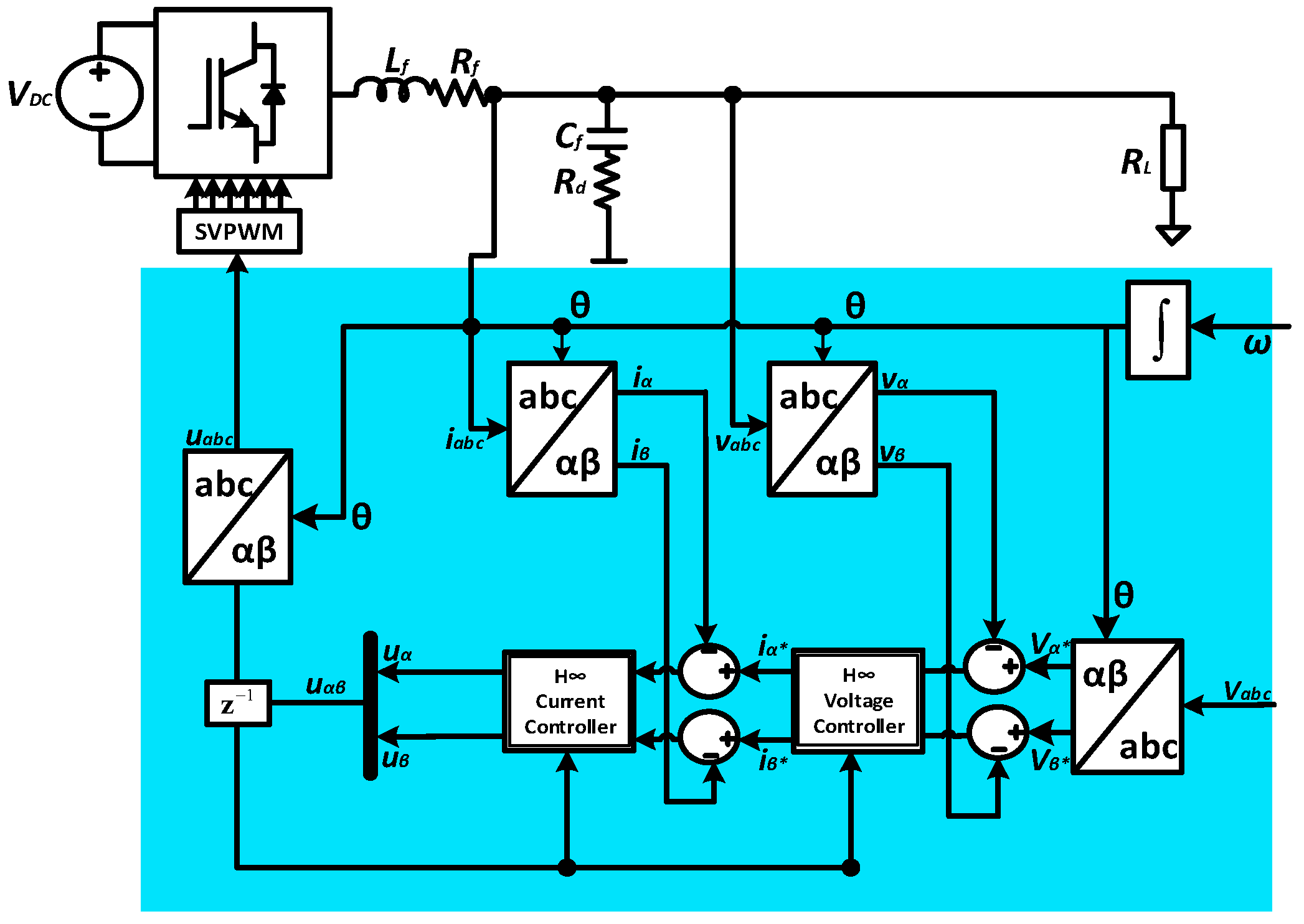
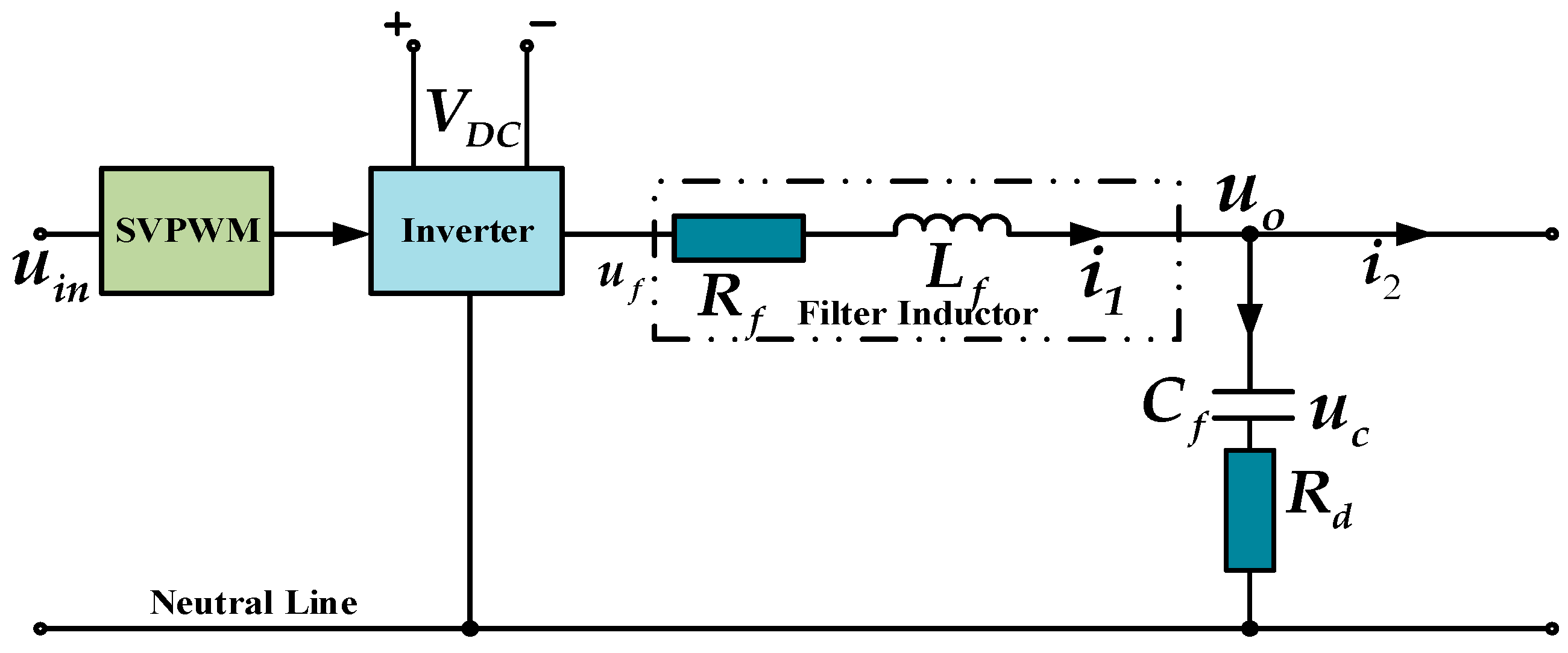
2. Proposed Control Scheme
3. State Space Model of the Augmented Plant
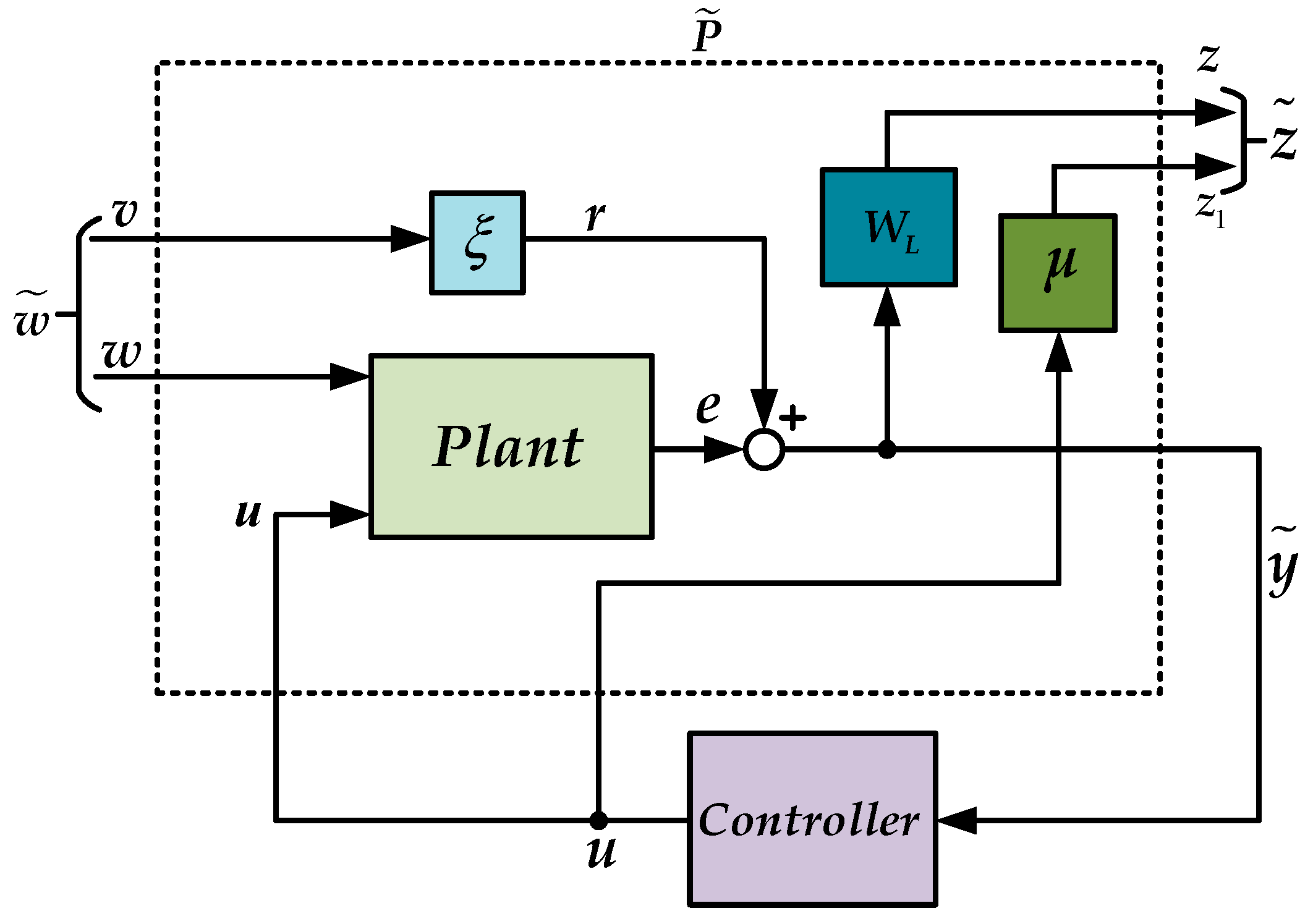
4. Formulation of the Standard H∞ Control Problem
5. Design Example
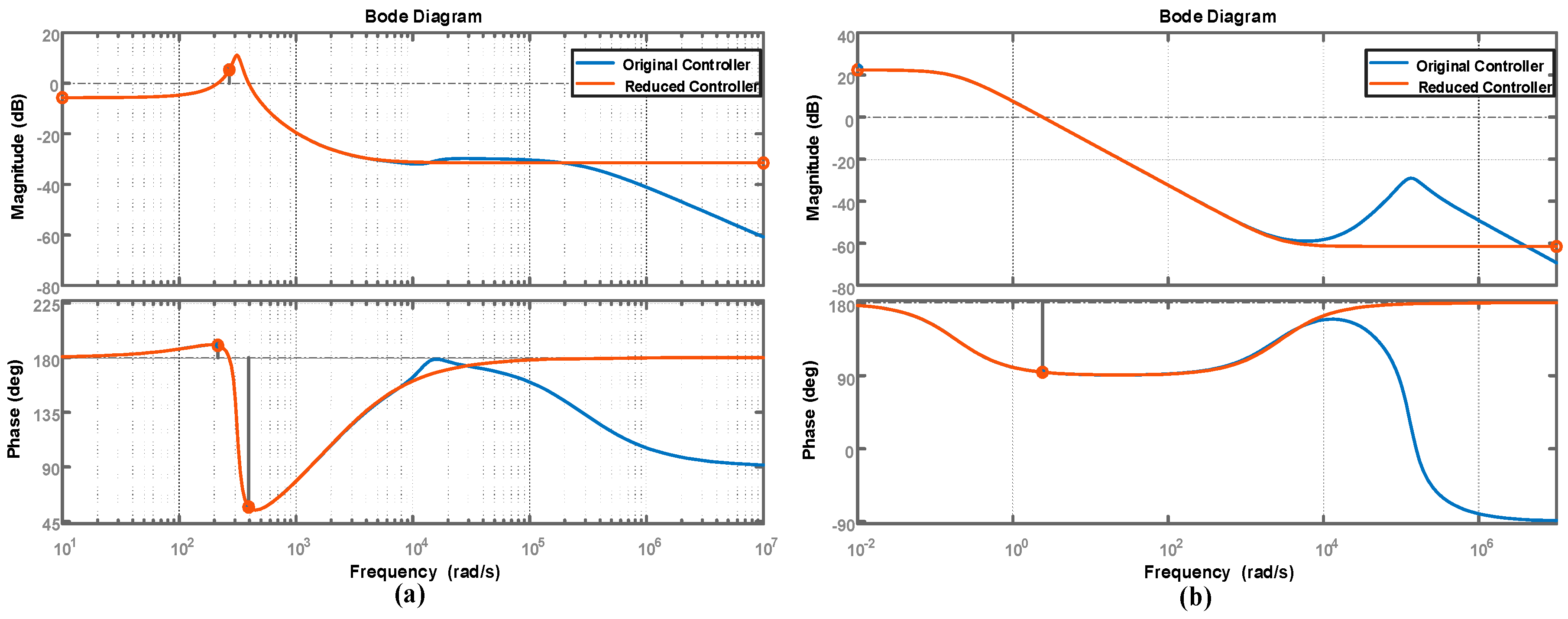
5.1. Design of H∞ Current Controller
5.2. Design of the H∞ Voltage Controller
5.3. Design of PI and DB Predictive Control Schemes
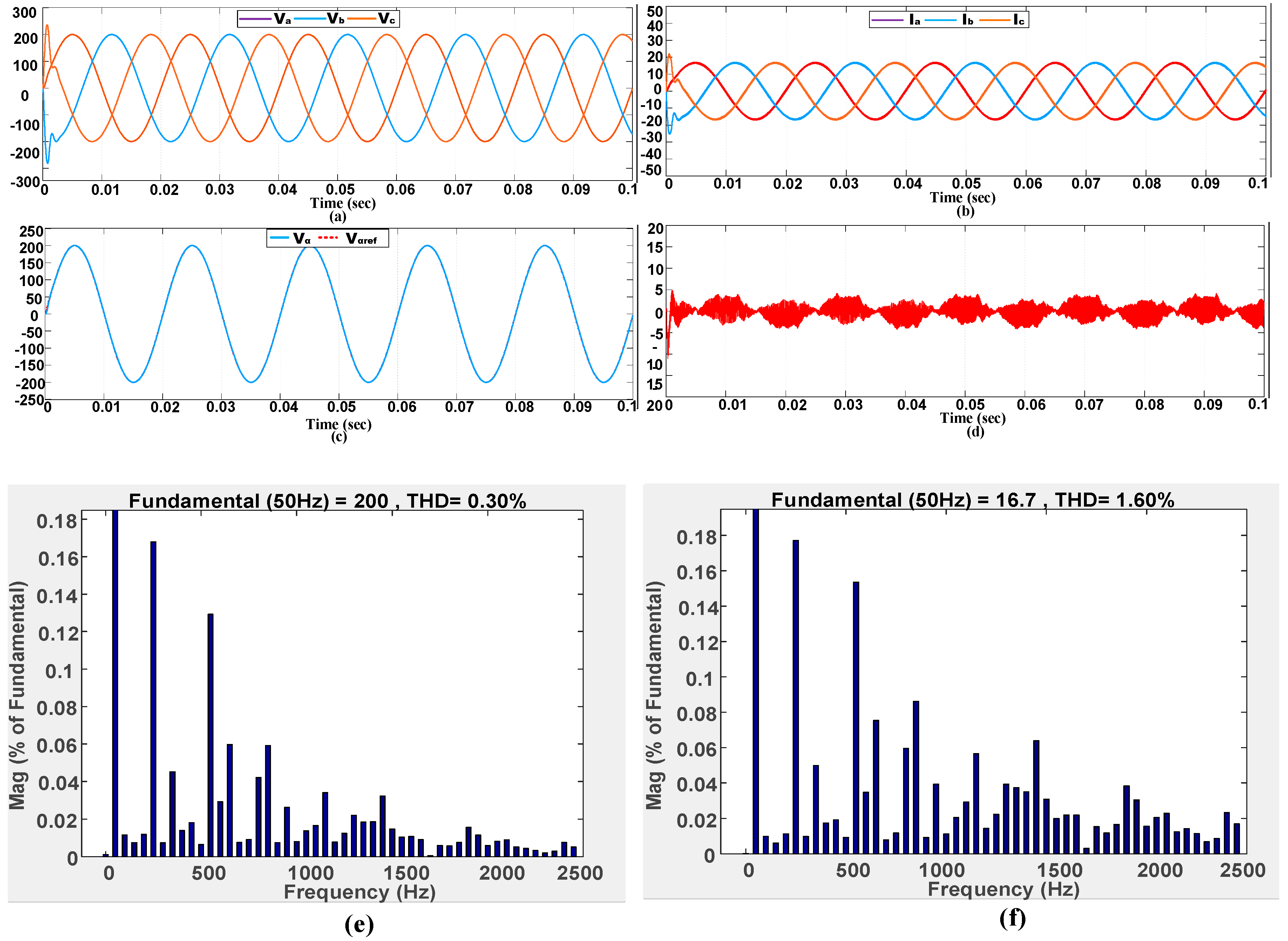
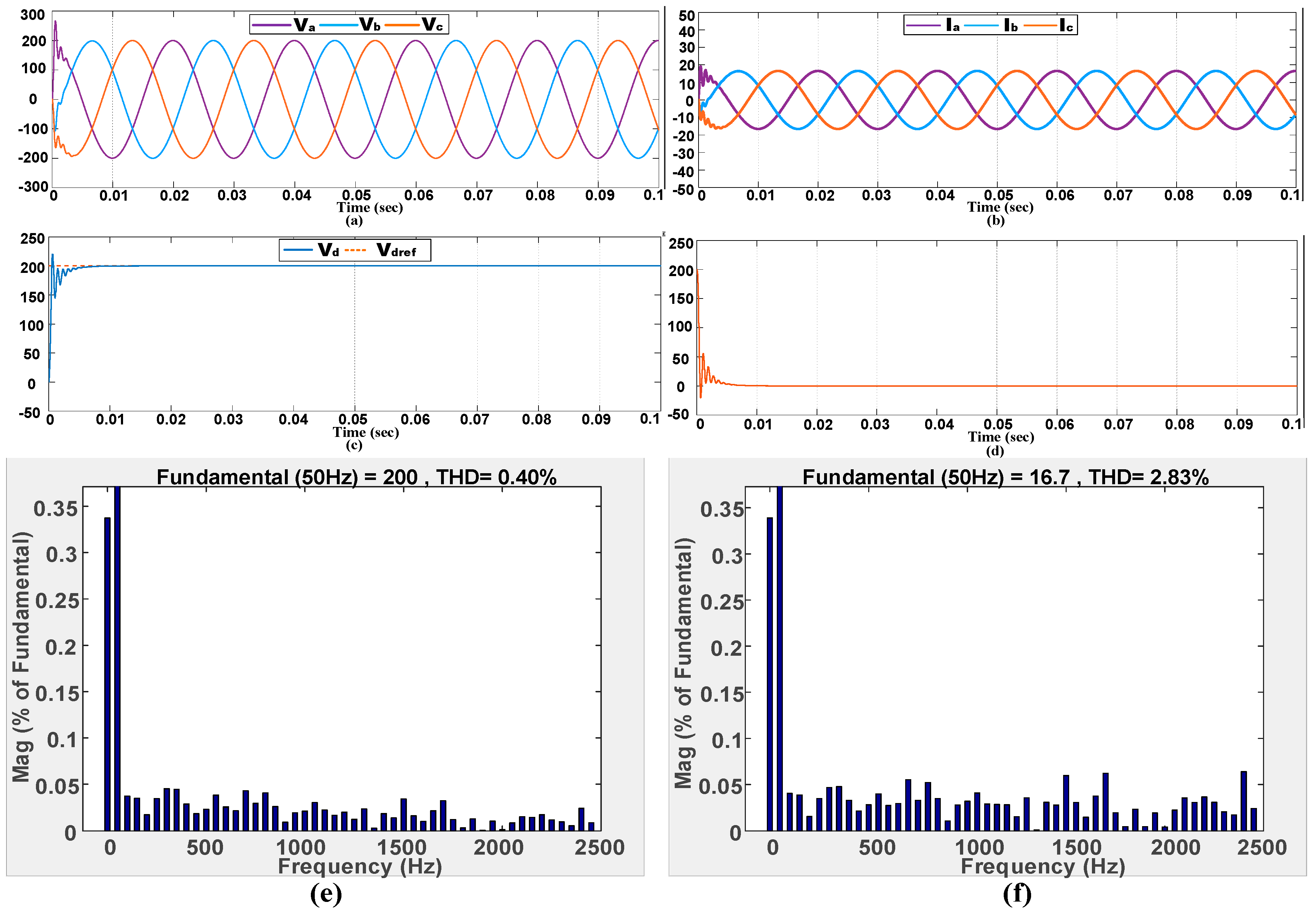
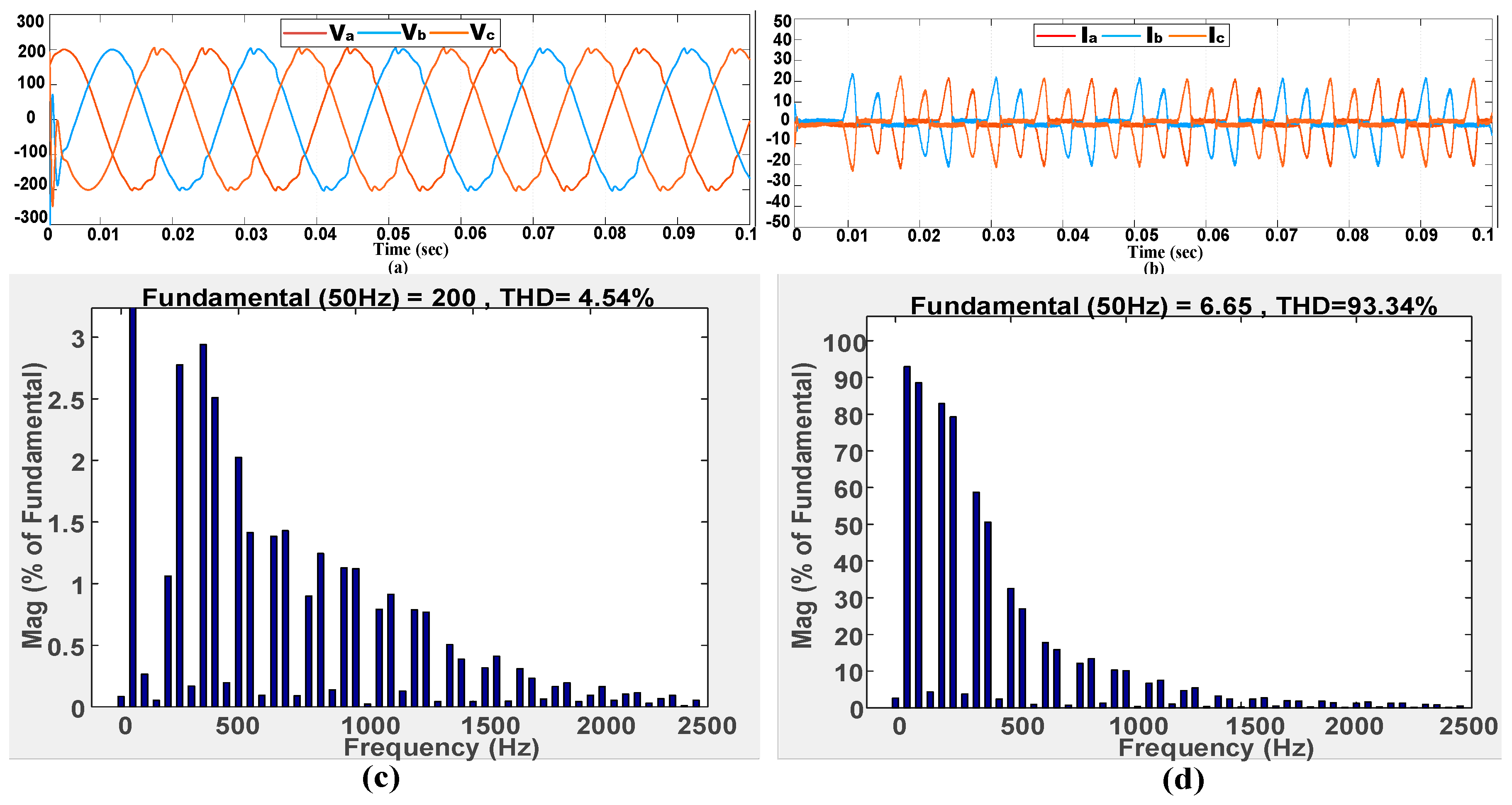
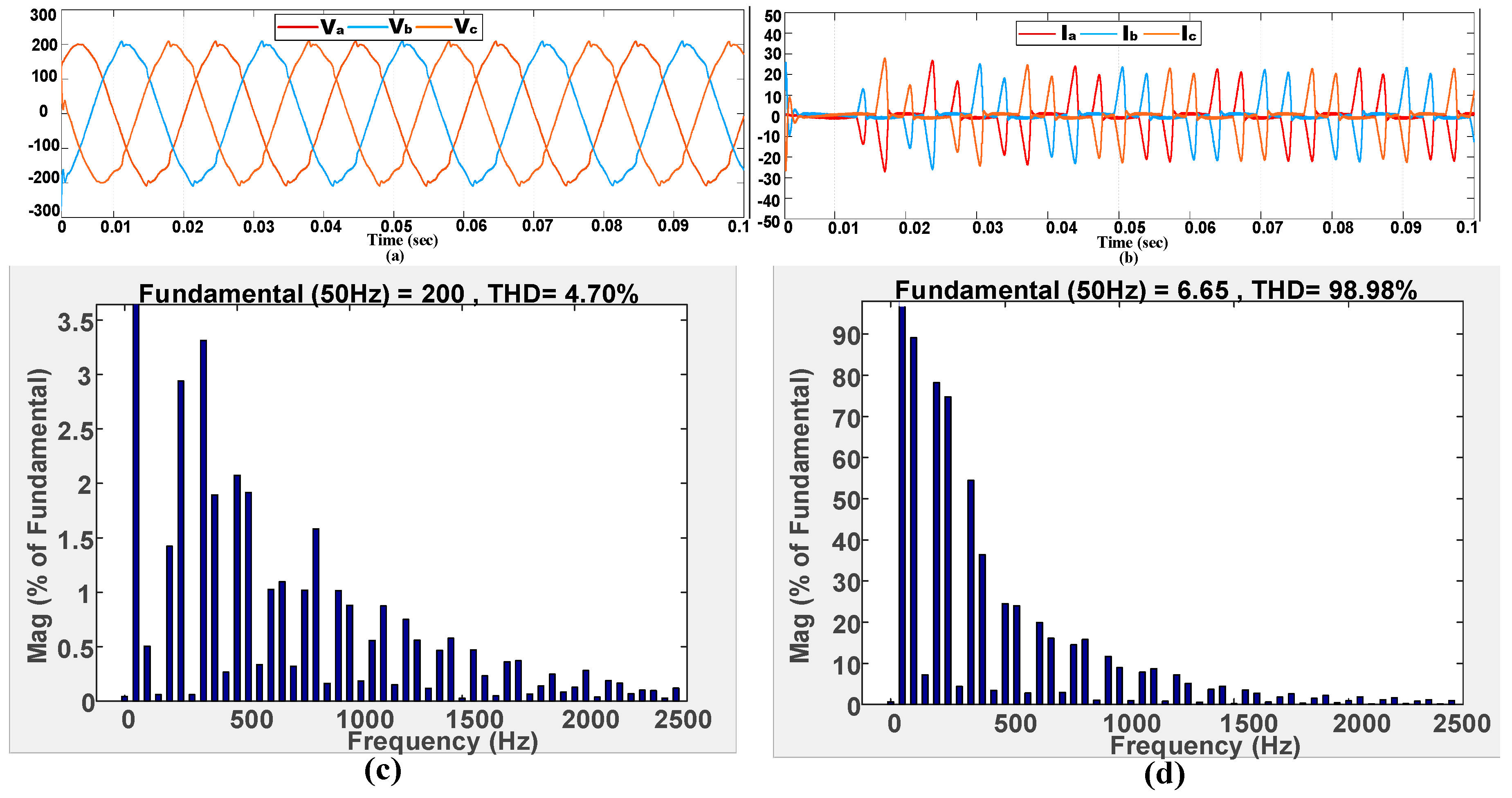
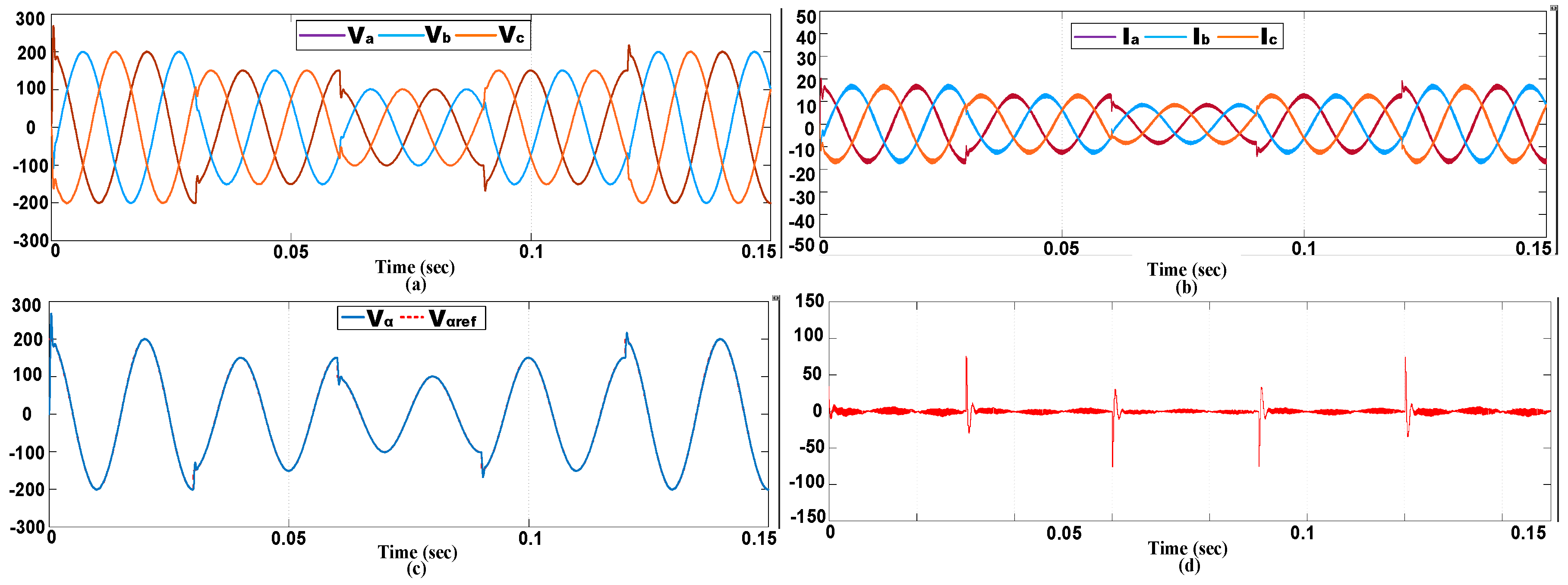
6. Simulation Results
6.1. Steady-State Performance in Stand-Alone Mode
6.1.1. Steady-State Performance with a Resistive Load
6.1.2. Steady-State Performance with Non-Linear Load
6.1.3. Transient Response with Resistive Load
7. Conclusion
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Liserre, M.; Fuchs, F.W.; Blaabjerg, F.; Dannehl, J.; Pena-Alzola, R.; Sebastian, R. Systematic Design of the Lead-Lag Network Method for Active Damping in LCL-Filter Based Three Phase Converters. IEEE Trans. Ind. Inform. 2013, 10, 43–52. [Google Scholar] [CrossRef]
- Dou, C.X.; Jin, S.J.; Jiang, G.T.; Bo, Z.Q. Multi-agent based control framework for microgrids. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Shahani, A.; Basu, K.; Mohan, N. LCL filter design for grid-connected inverters by analytical estimation of PWM ripple voltage. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition- APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1281–1286. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A.; McGrath, B.P.; Kong, W.Y. Optimized Design of Stationary Frame Three Phase AC Current Regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Abdelhakim, A.; Yang, Y.; Zhou, K. Control of Single-Phase and Three-Phase DC/AC Converters; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128052457. [Google Scholar]
- Hornik, T.; Zhong, Q.C. A current-control strategy for voltage-source inverters in microgrids based on H∞and Repetitive Control. IEEE Trans. Power Electron. 2011, 26, 943–952. [Google Scholar] [CrossRef]
- Lee, T.; Chang, J. H∞ Loop-Shaping Controller Designs for the Single-Phase Inverters. IEEE Trans. Power Electron. 2001, 16, 473–481. [Google Scholar]
- Chowdhury, M.A.; Kashem, S.B.A. H∞ loop-shaping controller design for a grid- connected single-phase photovoltaic system. Int. J. Sustain. Eng. 2018, 11, 196–204. [Google Scholar] [CrossRef]
- Komurcugil, H. Rotating-sliding-line-based sliding-mode control for single-phase UPS inverters. IEEE Trans. Ind. Electron. 2012, 59, 3719–3726. [Google Scholar] [CrossRef]
- Tahir, S.; Wang, J.; Baloch, M.; Kaloi, G. Digital Control Techniques Based on Voltage Source Inverters in Renewable Energy Applications: A Review. Electronics 2018, 7, 18. [Google Scholar] [CrossRef]
- Quan, X.; Huang, A.Q.; Dou, X.; Wu, Z.; Hu, M. A novel adaptive control for three-phase inverter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1014–1018. [Google Scholar] [CrossRef]
- Espi, J.M.; Castello, J.; Garcia-Gil, R.; Garcera, G.; Figueres, E. An Adaptive Robust Predictive Current Control for Three-Phase Grid-Connected Inverters. IEEE Trans. Ind. Electron. 2011, 58, 3537–3546. [Google Scholar] [CrossRef]
- Colak, I.; Kabalci, E.; Bayindir, R. Review of multilevel voltage source inverter topologies and control schemes. Energy Convers. Manag. 2011, 52, 1114–1128. [Google Scholar] [CrossRef]
- Trivedi, A.; Singh, M. Repetitive Controller for VSIs in Droop-Based AC-Microgrid. IEEE Trans. Power Electron. 2017, 32, 6595–6604. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Zaid, S.A.; Abu-Elyazeed, M.F.; Elsayed, H.M. Classical methods and model predictive control of three-phase inverter with output LC filter for UPS applications. In Proceedings of the 2013 International Conference on Control, Decision and Information Technologies (CoDIT), Hammamet, Tunisia, 6–8 May 2013; pp. 483–488. [Google Scholar] [CrossRef]
- Cortés, P.; Ortiz, G.; Yuz, J.I.; Rodríguez, J.; Vazquez, S.; Franquelo, L.G. Model predictive control of an inverter with output LC filter for UPS applications. IEEE Trans. Ind. Electron. 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
- Mattavelli, P. An improved deadbeat control for UPS using disturbance observers. IEEE Trans. Ind. Electron. 2005, 52, 206–212. [Google Scholar] [CrossRef]
- Ibrahim Mohamed, Y.A.R.; El-Saadany, E.F. An improved deadbeat current control scheme with a novel adaptive self-tuning load model for a three-phase PWM voltage-source inverter. IEEE Trans. Ind. Electron. 2007, 54, 747–759. [Google Scholar] [CrossRef]
- Hornik, T.; Zhong, Q.-C. H∞ repetitive voltage control of grid-connected inverters with a frequency adaptive mechanism. IET Power Electron. 2010, 3, 925. [Google Scholar] [CrossRef]
- Laub, A.J.; Heath, M.T.; Paige, C.C.; Ward, R.C. Computation of System Balancing Transformations and Other Applications of Simultaneous Diagonalization Algorithms. IEEE Trans. Automat. Contr. 1987, 32, 115–122. [Google Scholar] [CrossRef]
- Rasool, M.A.U.; Khan, M.M.; Faiz, M.T.; Zhang, W.; Tahir, S. An Optimized Disturbance Observer Based Digital Deadbeat Control Technique for Three-Phase Voltage Source Inverter. In Proceedings of the 2018 International Conference on Electronics and Electrical Engineering Technology, Tianjin, China, 19–21 September 2018; pp. 27–33. [Google Scholar] [CrossRef]
- Pichan, M.; Rastegar, H.; Monfared, M. Deadbeat Control of the Stand-Alone Four-Leg Inverter Considering the Effect of the Neutral Line Inductor. IEEE Trans. Ind. Electron. 2017, 64, 2592–2601. [Google Scholar] [CrossRef]
- Chung, I.Y.; Liu, W.; Cartes, D.A.; Collins, E.G.; Moon, S. Il Control methods of inverter-interfaced distributed generators in a microgrid system. IEEE Trans. Ind. Appl. 2010, 46, 1078–1088. [Google Scholar] [CrossRef]





| Description | Variable | Value |
|---|---|---|
| DC-Link Voltage | VDC | 440 V |
| Rated Power Output | Po | 9 kW |
| Filter Capacitance | Cf | 15 μF |
| Filter Inductance | Lf | 2.7 mH |
| Filter Resistance | Rf | 0.1 Ω |
| Damping Resistance | Rd | 1 Ω |
| Frequency PWM | fS | 12.8 kHz |
| Controller | Gain | Value |
|---|---|---|
| Current Loop Proportional Gain | kpc | 3.0 |
| Current Loop Integral Gain | kic | 5.21 |
| Voltage Loop Proportional Gain | kpv | 0.1756 |
| Voltage Loop Integral Gain | kpi | 0.25449 |
| Luenburger Gain | LM | |
| Observer Gain | η | 0.1 |
| Controller | H∞ Robust | DB Predictive | Proportional Integral |
|---|---|---|---|
| Linear Loads (Voltage) | 0.30% | 0.60% | 0.40% |
| Linear Loads (Current) | 1.60% | 3.38% | 2.83% |
| Controller | H∞ Robust | DB Predictive | Proportional Integral |
|---|---|---|---|
| Non-Linear Loads (Voltage) | 3.06% | 4.54% | 4.70% |
| Non-Linear Loads (Current) | 85.96% | 93.34% | 98.98% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasool, M.A.U.; Khan, M.M.; Ahmed, Z.; Saeed, M.A. Analysis of an H∞ Robust Control for a Three-Phase Voltage Source Inverter. Inventions 2019, 4, 18. https://doi.org/10.3390/inventions4010018
Rasool MAU, Khan MM, Ahmed Z, Saeed MA. Analysis of an H∞ Robust Control for a Three-Phase Voltage Source Inverter. Inventions. 2019; 4(1):18. https://doi.org/10.3390/inventions4010018
Chicago/Turabian StyleRasool, Muhammad Ahmad Usman, Muhammad Mansoor Khan, Zahoor Ahmed, and Muhammad Abid Saeed. 2019. "Analysis of an H∞ Robust Control for a Three-Phase Voltage Source Inverter" Inventions 4, no. 1: 18. https://doi.org/10.3390/inventions4010018
APA StyleRasool, M. A. U., Khan, M. M., Ahmed, Z., & Saeed, M. A. (2019). Analysis of an H∞ Robust Control for a Three-Phase Voltage Source Inverter. Inventions, 4(1), 18. https://doi.org/10.3390/inventions4010018






