Abstract
Tidal power technology is at its mature stage and large deployments are soon expected. The characteristics of tidal energy and its advantage to be predictable make it an ideal type of resource to be coupled with energy storage facilities. Despite this, most energy storage facilities are expensive. The fact that water has a high specific heat capacity makes this a potential cost-effective medium to be used for storing large amounts of thermal energy for balancing renewable energy output. This paper is an investigation on the possible application of integrating hot water reservoirs for storing tidal energy during power output peaks for domestic use. The main objective of this study is to evaluate the major factors incident on the proposed solution and to provide considerations on which real remunerations the proposed idea could bring to communities or to single families. For this purpose, a simplified numerical analysis, concerning three different scenarios, was performed. These scenarios differ by type of buildings and type of thermal energy demand. The study mainly concerns remote communities. Findings indicated that the proposed idea is technically feasible and if applied in the context of residential compounds, this could be more attractive in economic terms.
Keywords:
Tidal energy; remote communities; energy storage; renewable energy; hot water; off-grid; marine 1. Introduction
Nowadays, the development of marine renewable energy sector is at its take-off point. Tidal energy is one of the resources which, due to its nature, is at the first position to be highly exploited. Despite this, as it can be for other renewable energy resources, a main disadvantage of using such resource concern variability [1,2]. Nevertheless, contrarily to other renewable energy resources, tidal energy is cyclical and predictable. In fact, tidal energy output can be characterized by different harmonic components; these determine cyclical variations between high, low and nil power output values.
Not many cost effective solutions exist to deal with renewable energy sources variability and intermittency. Conventional energy storage systems are often not suitable to handle large amounts of renewable power produced and these normally are expensive. At the present time, frequently the renewable energy produced is directly delivered into the electricity network and no energy storage system is available. But as the renewable energy share is rapidly increasing, the electricity network infrastructure in many cases cannot deal with the high input of power [3]. In various locations, due to economics and resources available, coupling a tidal power with energy storage plants could reasonably reduce the final local cost of energy and also provide economic advantages. Therefore, by linking a tidal plant with a storage utility, community-wide benefits would occur. These, for instance, may regard energy self-sufficiency matters and profits from possible export of the locally produced energy.
A limited number of studies were carried out focusing on general aspects concerning applying tidal power for coastal settlements [4,5]. Further studies were dedicated to the specific topic about short-term energy storage with tidal power plants [6,7,8]. In Canada, researchers studied a way for increasing renewable energy production with tidal power by developing an energy storage system [9]. Differently, in the UK, an earlier study focused on energy storage in the context of a tidal barrage [7]. More recently, the improvement of the short-term inherent energy storage of tidal farms in channels by varying somehow the farms’ drag coefficients, were also discussed [8].
Few projects concerning energy storage generated from tidal power have recently begun. An energy storage project based on hydrogen production from tidal power has been initialized in the Orkney Islands by the European Marine Energy Centre (EMEC) [10]. The purpose of the plant is to use the tidal energy to produce hydrogen when the electrical network cannot absorb the excess power from tidal turbines. Similarly, a company based on the Shetland Islands developed a project regarding the integration of a tidal farm with a battery storage utility for allowing delivery baseload power to the community exclusively from the tidal energy resource [11].
In general, for remote communities located in areas where tidal power resources are abundant, it is crucial to find practical solutions to deal with tidal power variability. A number of possible energy storage technologies can be used to balance the tidal power output. Energy can be stored in form of mechanical, chemical or thermal energy. For what concerns electricity, storage techniques can be divided into four categories: low power applications; medium power application; network connection applications with peak levelling; and power control applications [2].
Existing energy storage technologies vary from simple pumped hydro storage to high-tech hydrogen production systems. Obviously, every type of technology has its advantages and its disadvantages; while complex methods such as hydrogen or flow batteries energy storage systems are very expensive to be developed, mechanical energy storage methods in certain contexts may be a more cost-effective option but often involve technical challenges.
Another type of energy storage technology is thermal energy. Nowadays, thermal energy storage is mostly applied to solar thermal power plants. An example is the 50 MW power station named Andasol 1 in Spain. Also, when for eight hours there is no direct sun radiation at the power plant, thanks to 28,000 metric tons of hot molten salt, constant power output from the station is guaranteed [12]. Energy storage facilities can be used for storing energy for different scales of time. Most common cases concern energy storages that are designed to store energy for relatively short periods, e.g., a few hours. On the other hand, there are also other kinds of long period thermal storages that are capable of storing heat for entire seasons. This refers to seasonal thermal stores [13].
The main objective of this paper is to evaluate an idea based on smoothing out the large dynamic range of tidal power output by using a thermal energy storage system over a period of about 14 days, corresponding to the neap-spring tidal cycle. In particular, the option of storing thermal energy in the form of hot water is proposed. The context of where to implement this type of energy storage arrangement is given to be single households or small residential buildings. The energy exploited from tidal streams is planned to be stored and used for domestic purposes only. Communities that can benefit from the proposed tidal energy storage utility can be any coastal or island settlements located close to places where tidal resources are economically viable.
In particular, the idea investigated in this study could be applied to every region close to consistent tidal stream energy resources, e.g., the UK’s north coastal communities. The concept is assessed for three hypothetical scenarios. The first two concern storing energy just for satisfying the hot water consumption demand. In the third scenario, the energy stored is supposed to be used also for satisfying the thermal energy demand of a single house situated in a high latitude location. Taking into consideration that normal households located in such areas consume a large amount of thermal energy, the type of buildings considered for this last scenario, was given to be a low-energy house.
2. Methodology
The feasibility of the concept was investigated by creating a numerical model representing possible realistic scenarios. The model is explained in this section and was used to validate the proposed idea. In order to explain the logical approach that was followed, major steps of the method implemented are shown in Figure 1. First steps related to the creation of a modulated tidal power input signal. Besides, the energy demand concerning the Domestic Hot Water (DHW) and space heating is estimated. Initially, a guessed value of the hot water tank volume was set. This volume was then adjusted by performing a number of iterations. The inputs where computed by solving differential equations describing the problem in the time-domain. Various simulations were systematically performed to obtain quantitative information on which system design parameters were affecting system performances the most.
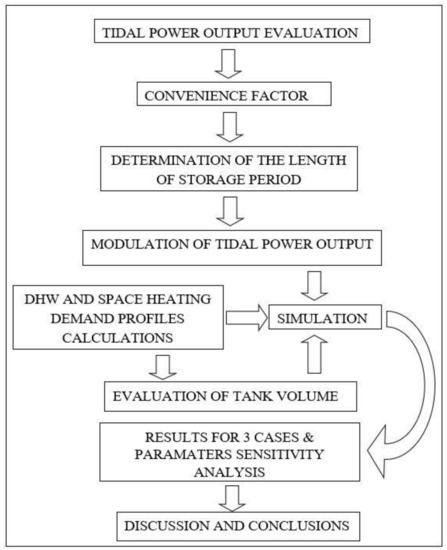
Figure 1.
Logical approach followed for conducting the feasibility study.
2.1. Evaluation of Tidal Power Output
The method used to estimate tidal stream is the one related to Stage-1 of the Tidal Resource Assessment Methodology publicised by EMEC. This consists of considering the solar and lunar principal harmonic constituents (S2 and M2), taking into account spring and neap tidal stream peaks and superimposing sinusoids [14].
Spring and neap stream velocity peaks were obtained from the ABP MER marine renewable atlas [15]. In order to find the tidal stream velocities for a month period of time (at different time steps i.e., 1 and 10 minutes) Equations (1) and (2) were used:
where, is the tidal stream speed (m/s), is the average speed between Neap and Spring peak velocities considered (m/s), is the variability of tidal stream associated to neap-spring cycle (m/s), is the spring tidal stream peak speed (m/s) is the neap tidal stream peak speed (m/s), is the angular frequency associated to semidiurnal period of 745 min (rad/s), is the angular frequency associated to neap-spring period of 21,262 min (rad/s) and is time (min).
In particular, by assuming no differences between flood and ebb tidal stream speeds, a 30 day tidal stream speed profile was created, as shown in Figure 2.
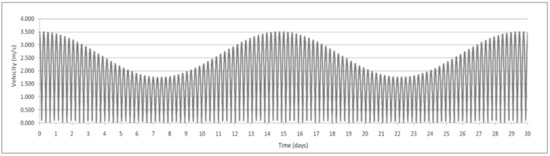
Figure 2.
Thirty day tidal current velocities profile.
After, obtaining the previous tidal stream speed values and determining the tidal turbine characteristics, the power output values were calculated. These lasts were found by implementing the following system of equations (Equation (3)) [16]:
where, are same as for Equation (1) and the other parameters are: , the turbine cut-in velocity, the turbine cut-out velocity, the turbine rated power tidal stream speed and is the drive train efficiency.
In order to choose the type of turbine, for maximizing energy output form particular site, detailed studies are required. However, as this is not the scope of the study, in this work the turbine characteristics are assumed to correspond to those of the SeaGen turbine [17]. To note that turbine’s characteristics as parameters of cut-in and rated power speed influence average energy output during the neap-spring cycle, specifications of the turbine considered and parameters used for obtaining power output profile are reported in Table 1.

Table 1.
Parameters used for obtaining simplified tidal power profile.
By considering the limits of cut-in, rated power speeds and imposing these to the previously calculated velocities, it was possible to calculate the power output profile shown in Figure 3.
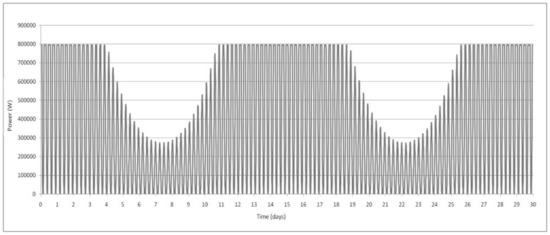
Figure 3.
Evaluated power output profile for 30 days of a tidal turbine by considering previous velocities.
2.2. Convenience Factor
In order to compare the amount of the daily available energy from one day to another, a convenience factor was defined. For every specific day, this is given by dividing the energy available in this day by the energy available in the day of maximum energy output. In particular, this is a value comprised in the range of 0 to 1 and is assigned to each day of the neap-spring cycle. This factor was defined in order to smooth down the power output dynamic range over the neap-spring cycle. This was used for ensuring that opportune amount of energy is stored at the appropriate time. In practice, by using this factor the most energy is stored during days of high tidal energy (spring days) and the least energy is stored when only low tidal energy is available (neap days).
2.3. Daily Average Energy Profile
For evaluating the length of the period for which storing heat in the form of hot water produced by the power output profile, a daily average energy profile for all the 30 days considered was defined. For this scope the convenience factor was used. An example of a daily average profile is shown in Figure 4.
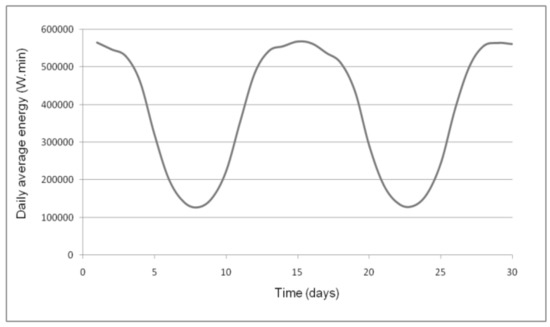
Figure 4.
Daily average extracted energy profile.
2.4. Modulated Power Profile for SIMULINK Models
An intermittent power output profile, to be used as input in to the models, was then obtained. Precisely, in order to have intermittent rated power output (Figure 5), a basic filter to the previous calculated profile (Figure 3) was applied.

Figure 5.
Intermittent power profile used for simulations.
In fact, the electric heating element in the hot water tank (HWT) is designed to operate at constant rated power. The profile was created for determining the exact energy to provide to the storage system. Though, different and more complex options depending on specific control system applied to the HWT, could be considered.
2.5. Defining Demand Profiles
About 56% of the total energy consumption in UK households is used for space heating and about 24% for domestic hot water, while the rest of it is used for electrical devices [18]. However, hot water consumption varies from one house to another depending on various factors which can be grouped in the following two main categories [18]:
- Behavioural determinants, very little related to climate, but depending on human factors.
- Physical determinants, little related to human habits, but essentially depending on physical characteristic of the building, climate and losses/efficiency of the appliances.
Hot water energy demand in a household is given to be the energy used for: bath or shower; wash hand basin; dish washing and cloths washing. Instead, space heating energy demand is intended to be the energy that through the heating system is delivered to the household environment merely for space heating purposes.
In order to define the domestic hot water (DHW) consumption, the DHW-calc program was used [19]. This program is a simple tool that generates domestic hot water request profiles. It creates flow rate values for a set time step. By configuring this program, with parameters reported in Table 2, the DHW demand profile for a period of a year was calculated. The output of the program was a file containing information on the water volume draw-offs related to every 10 minute time step.

Table 2.
Settings used in the DHW-calc program for calculating domestic hot water (DHW) demand.
Afterwards, the energy content was found with Equation (4) [20]:
where, is the energy consumption for increasing water temperature (J), is the specific water heat (J/(m3 K)), is the hot water volume (m3), is the number of days of a specific month and is the temperature rise (°C), this depends on the month considered. Values concerning the UK are reported in Table 3 [20].

Table 3.
Temperature (°C) rise for every month of the year (UK averages) [20]
Consequently, from the values of water volume and by taking into account the temperature rise values for each month, the DHW load profiles for each month were calculated (Figure 6).
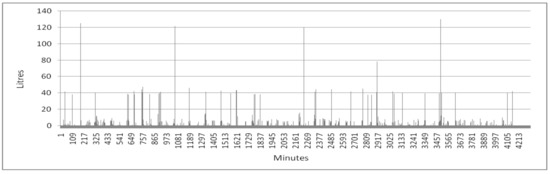
Figure 6.
Example of domestic hot water (DHW) profile for a three-member family, this represents all hot water (HW) draw-off during a generic February.
2.6. Space Heating Energy Demand Profile and Solar Gains
For the third scenario, where space heating demand was considered, the space heating demand of a generic household was also evaluated. For this purpose, the following relations were considered:
where, is the internal house temperature (given, constantly, to be 20 °C), is the outdoor temperature (values obtained from weather station archive), is the equivalent thermal resistance of the house, is the thermal resistance of walls (m2 K /W) and is the thermal resistance windows (m2 K /W).
For each month, average solar gains by following the standard assessment procedure SAP were calculated. This procedure consists of using a series of formulas for calculating solar fluxes at given latitude. In particular, the method takes into account: windows orientation; inclination; type; and dimensions [20]. For illustrative proposes, Figure 7 shows the space heating demand (SHD) profile for the month of December.
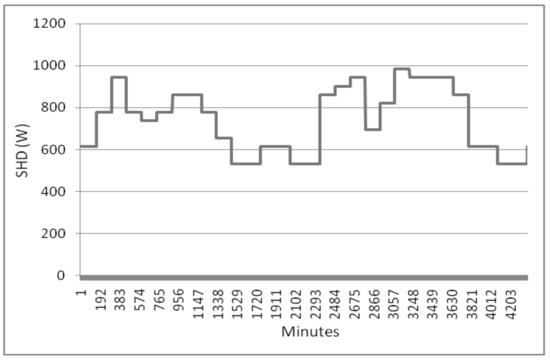
Figure 7.
Example of Space Heating Demand (SHD) profile (December).
3. SIMULINK Models
For three scenarios investigated, a generic model was at first defined. The generic model was applied for all systems numerically investigated, this is schematised in Figure 8. The first scenario represents a single household where only energy for DHW consumption is stored and space heating demand is not considered. The second scenario concerns a ten families building option. The last scenarios relate to a single household for which the space heating demand was also estimated. Two specific SIMULINK models were defined. While the first SIMULINK model was used for assessing the first and second scenarios, the second was used for evaluating the third scenario.
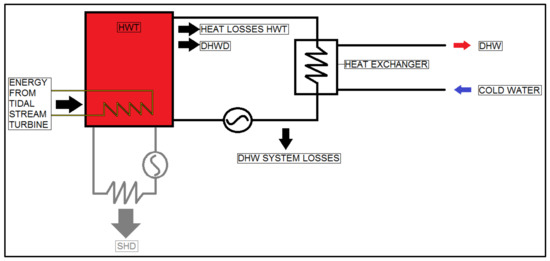
Figure 8.
Schematic representation of the systems modelled. In grey is indicated the space heating (SH) branch, only considered in the third scenario. Black and grey arrows indicate energy flow.
In all the three options the hot water system is given to be closed and the temperature, for all regions inside the tank, is given to be uniform. Thus, the same water re-circulates in pipes and in the HWT. Tap water, coming from the aqueduct, through heat exchangers is heated up. In order to permit that domestic heat exchangers to work in an efficient way, a minimum of about 20 °C difference between the water inside the tank and the tap water was preserved.
Energy losses in the pipes, heat exchangers and components of the hot water system are given to be a percentage of the demand. These last factors were taken into account by adding an estimated quantity to the total energy demand. In particular, for the first model, losses were defined as 10% of demand. For the second and third models, losses equal to 15% of the demand were instead assumed.
3.1. Single Household Model for DHW Demand (First Scenario)
The first model created in SIMULINK is reported in Figure 9. This represents the energy balance defined by the first law of thermodynamics, i.e., given by Equation (5).
where, is the mass of water in the HWT (kg), is the specific heat capacity of water (J/(kg K)), is the HWT temperature (C°), is time (min), is the tidal generator power output profile + initial input (J/min) and is the DHW load profile + heat losses HWT (J/min).
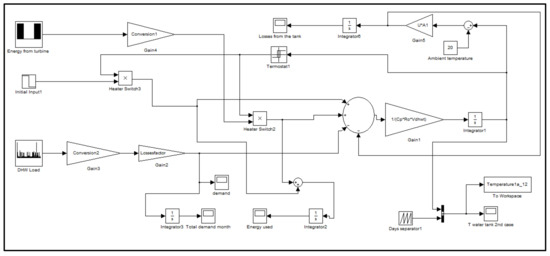
Figure 9.
Matlab-Simulink model created for investigating the feasibility of first and second scenarios.
Heating losses of HWT, by the following formula were defined as:
where,is the U-value of the HWT, (W/m2 K) is the external area of the HWT, (m2) is the water temperature inside the HWT and (C°) is the house ambient temperature (20 °C). Equation (8), after integration, gives temperature values for each time step.
3.2. Ten Families Model for DHW Demand (Second Scenario)
After having calculated different DHW demand profiles and used the first SIMULINK model, the ten families option was evaluated. For this scenario the HW demand was found by summing up forecasted draw-offs for 30 people. The input power was increased to a reasonable value.
3.3. Single Household Model For DHW And Space Heating Demand (Third Scenario)
While for the first model the specific characteristics of the house were not necessary, in the second SIMULINK model, a simple household with characteristics reported in Table 4, was modelled. The SIMULINK model, in this case, is an extension of the previous model. This is illustrated in Figure 10. After a number of preliminary simulations, it was found that for normal houses, due to the high energy consumption requirements, an unrealistically large hot water tank was necessary. Therefore, the house considered in the study was set to be low-energy (well insulated), with consumption of space heating of less than 30 kWh year per m2 [21].

Table 4.
Specifications of the simplified house considered.
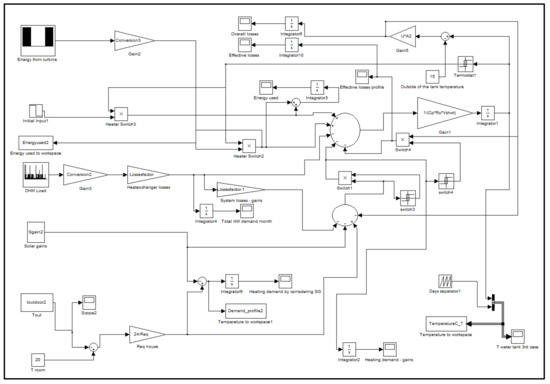
Figure 10.
Matlab-Simulink model created for investigating the feasibility of the third scenario considered.
In this option, the model was developed by adding the heating demand and heat gains to the first model which were taken as a template. In particular, it was considered that the water tank was installed inside the house or in a basement where the air is circulating. Thus, heat losses from the HWT become internal gains and these contribute to space heating.
In order to simulate the option considered, again Equation (8) was implemented. However, in this circumstance, was specified differently. The third SIMULINK model, (Figure 10) represents Equation (8) and relations defined by Equations (10)–(12).
where, is the domestic hot water energy demand (J/min), is the space heating energy demand (J/min), is the hot water tank losses (J/min), is house heat losses (J/min) and is solar gains (J/min).
3.4. Characteristics Of Systems Modelled And Limitations
In order to define the models used in this study, the proposed design was simplified, and particular assumptions were implemented. The following are the major characteristics and limitations of the models developed:
- The power needed for actuating the water pumps of the hot water systems is low. Thus, the energy required for the pumps is assumed to be negligible compared to the energy in form of heat needed to satisfy the hot water and heating demands. For instance, a hot water recirculation pump for a single household consumes in the order of about 3 kWh/year [22]. Compared to an estimated value of 1460 kWh/year of energy required for DHW production, the energy absorbed by the pump would be less than about 0.3% of the thermal energy demand. For simplicity, this little extra energy requirement is given to be available from other external energy sources. These may be any extra renewable energy sources coupled with batteries or be of conventional type (i.e., a grid connection or a diesel generator). In fact, in all cases, it is expected that extra sources of energy in form of electricity are needed for all other domestic applications such as lights and other electric appliances.
- HWT losses are given by simply considering a heat transfer coefficient. Thus, the tanks are given to be ideally insulated (no other type of heat exchanges are existing, except heat losses considered by a linear transmission coefficient). However, if tanks are not perfectly insulated, losses can be as much as five times higher [23].
- Real DHW storage tanks usually are regulated for the temperature range of 80 to 60 °C. However, as this project does not focus on system specification, a maximum temperature of 95 °C was considered feasible.
- Concerning the third model, internal house air circulation is given to be adequate and the energy required for ventilation is coming from external sources. Consequently, heat losses of the HWT contribute to space heating demand. The energy required for ventilation is assumed to be insignificant.
- The ambient temperature, by a thermostat, at 20 °C is maintained. Therefore, hot water will circulate in the heating system if the ambient temperature is below 20 °C. If the temperature is higher than this value, the water pump will be closed.
- In the third model, external temperature data input has daily resolution. By assuming that the building maintains heat during periods when the temperature drops down, hourly variations, due to change of temperature, are being neglected.
- Concerning solar gains, these were included with months-long average values. Hence, simulations did not reproduce daily and hourly related effects.
- In all options, temperature rise data was constant for each entire month. Consequently, models do not take into account minimal changes of the tap water temperature, which during a month, can slightly differ from one day to another.
- The temperature inside DHW tanks is uniform (no stratification assumption).
It was expected that for the purpose of the study the above limitations and characteristics of the models do not affect the resulting findings.
3.5. Simulations
System components were sized by running a set of simulations and systematically regulating system parameters. In order to evaluate systems’ performances, the resistance coil value and DHW tank volume parameters were optimized for the coldest month. Successively simulations for each month of the year were run. The MATLAB ode-45 solver in all options was used. Following this, different output results concerning HWT temperature and losses were registered.
Concerning the first two models, by taking into account a storage period of 7 days and DHW average maximum consumption per occupant, different HWT volume values were evaluated. In particular, by taking into account a DHW system sizing criteria [24], dimensions of the tanks were initially calculated with Equations (13) and (14).
where, is the energy needed daily per occupant (J), is the length of storage period (days), is the maximum temperature ranges in the HWT (C°), is the design purposes water consumption volume per day per occupant (m3) and is the maximum temperature rise value during the year (occurring during February in C°) (see Table 3).
Only one size of HWT was evaluated for the third scenario where also space heating demand (SHD) was considered.
4. Results
4.1. First Scenario—Single Household (Only HW Demand Considered)
The first scenario investigated concerned the use of the system proposed for storing only energy to be used for hot water (HW) demand. This scenario concerned three cases named Cases 1a, 1b and 1c.
Concerning the first case (1a), initially, a maximum consumption value of 80 litres per occupant per day was chosen [24]. Consequently, a volume of 2 m3 for the HWT was found. Successively, by assuming a daily DHW consumption of 60 litres a day per person for a 3 people family, a 25% smaller tank was evaluated, i.e., of a size of 1.5 m3 (Case 1b). For both cases by evaluating the system response for the month of February in which the temperature rise value is the highest, the coil resistance value at 2.7 KW was set (by considering 97% efficient coil). Subsequently, in order to understand which results can be obtained with a relatively small commercially available HWT, a further tank was considered. This last, had the volume of 1 m3 (Case 1c).
In Figure 11 is shown the temperature graph for the whole year of the 2 m3 HWT. Minimum temperatures of about 60 °C occur in February (red line). For all year round temperatures are above this value. Initial input period can be noticed for each month. For this period temperature increases steadily. Obviously, this period would occur only once.
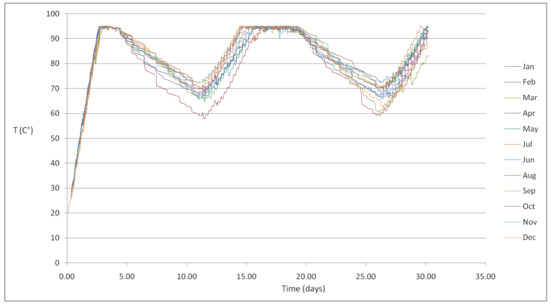
Figure 11.
The temperature in the 2 m3 hot water tank (HWT) (Case 1a).
Also, by setting the volume of the tank to 1.5 m3 (Case 1b), it was found that, for almost all of the year, the temperature in the water tank is above 60 °C (Figure 12). Only in a few hours, it drops below this value. Except for few circumstances, the temperature is all time over the 60°C threshold, this could indicate that if a backup system is installed, the tank volume could be significantly reduced.
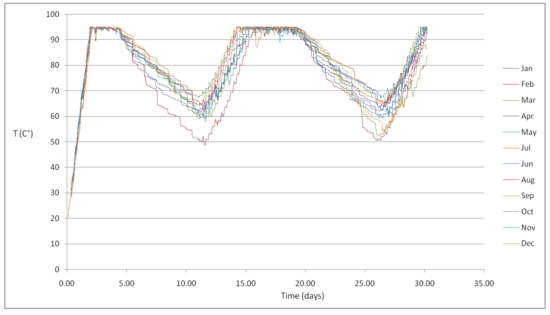
Figure 12.
The temperature in the 1.5 m3 HWT (Case 1b).
The temperature trends for the 1 m3 are shown in Figure 13. For this option it can be noticed minimum HWT temperature of 60 °C is not maintained in all months, however, except for a few occasions, the temperature does not drop below 50 °C. Thus, if low difference temperature heat exchangers are used, the HWT even in this case, could give significant contributions to the DHWD all year round.
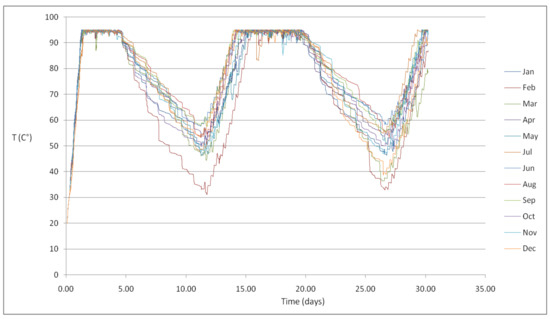
Figure 13.
The temperature in the 1 m3 HWT (Case 1c).
4.2. Second Scenario—Ten Families Building (Only HW Demand Considered)
Due to the fact that by centralizing the storage, fewer energy losses could be achieved and the demand could be more uniform, it was decided to investigate a storage facility for a larger and more populated building. For this purpose, the two cases named 2a and 2b were investigated. Precisely, a ten family (30 people) demand profile was examined. 15 and 10 m3 tanks with a 20.5 KW rated coil were chosen for this set of simulations.
Temperature graphs of 15 m3 and 10 m3 HWTs concerning the second scenario are reported in Figure 14 and Figure 15. Similar to the case of the 1.5 m3 HWT, storage volume per occupant, in 15 m3 HWT was specified to be 60 l/day. However, using a 15 m3 tank demand appears to be more uniform. This is due to the facts that, by adding together ten families’ DHW consumption, peaks of demand are slightly smoothed down. Different to the 1.5 m3 tank (Case 1b) where temperatures never reach values below 56 °C.
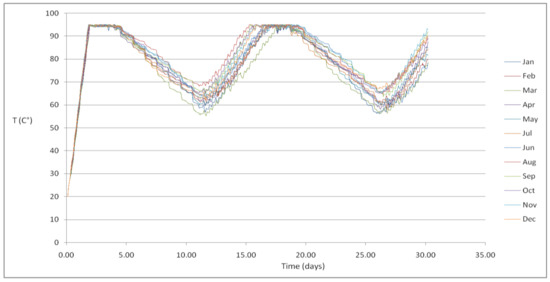
Figure 14.
The temperature in the 15 m3 HWT for energy demand for 10 families (Case 2a).
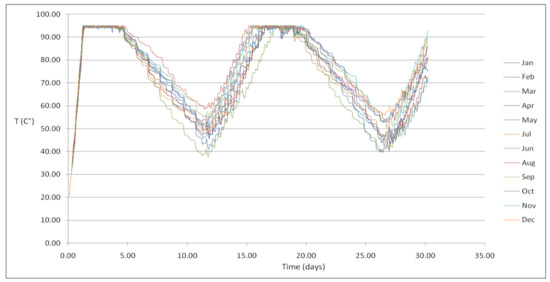
Figure 15.
Temperature in 10 m3 HWT for energy demand for 10 families (Case 2b).
For what concerns the 10m3 HWT temperature profiles are similar to the 1 m3 tank.
4.3. Third Scenario—Single Household (Considering Both HW And SH Demands)
The third model was created for investigating the possibility of using the energy storage system for both, DHWD and space heating demand (SHD) (Case 3). This model was developed for evaluating the implementation of the proposed idea for a single household. Due to the fact that a simulation concerning a real house could be dependent of many different complex factors, a simplified ideal house was defined during this study. The thermal energy demand is assumed to be satisfied thanks to heat exchanges. Heat gains and losses of the building were given to be only due to conduction, solar and internal heat gains.
The HWT, in this case, was sized for a house that could be completely autonomous from external thermal energy sources. In particular, by monitoring the system performance during a specific cold month, i.e., December 2010, system parameters were optimized. Initially, it was set that a minimum water temperature of 60 °C had to be maintained at all times. In this way, a water tank volume of 5 m3 was fixed. In order to have enough system response, a 3.14 KW rated coil was specified. Performances of the HWT, in terms of losses and temperature profiles, were registered.
In Figure 16 the temperature graph of the 5 m3 HWT for the second storage period for every month of the year 2010 is reported. Minimum temperature was registered in December due to low outdoor temperatures and, thus, high space heating demand. It was noticed that, exclusively for February and December the temperature goes below 70°C, while in the other months the temperatures are relatively higher. Consequently, by considering a backup system, that could provide energy on certain occasions, the HWT volume could be radically reduced and the storage facility could be more feasible.
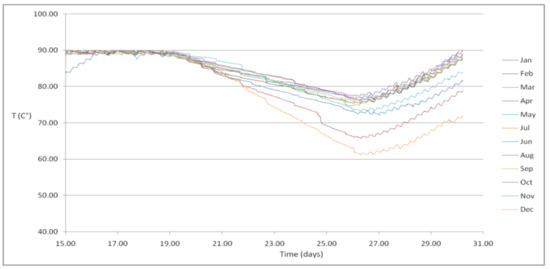
Figure 16.
Temperature profiles in the 5 m3 HWT for the second storage period of every month obtained with outdoor temperatures for the year 2010 (Case 3).
4.4. Overall Results
Two sets of simulations were run and energy losses were monitored. Main results concerned: Losses by limiting the temperature of the tank to 90 °C all the year round (Table 5); and the losses that could exist, if a basic control system for regulating the maximum monthly temperature of the HWT is applied (Table 6).

Table 5.
Thermal energy losses (kWh) registered for every case considered in a year period.

Table 6.
Thermal energy losses (kWh) computed by setting maximum temperature values depending on every month. To note that not for every month maximum temperature was regulated (Max T. Not Regulated cells). As in these months, the temperature goes below minimum values, the energy demand cannot be fully satisfied. However, the system works at 100% of its capability.
During simulation, depending on the different cases, temperature ranges were defined. Given these ranges, performances of the HWTs were quantified by registering how many times the temperature does drop below the minimum value, and in this way it was possible to understand the reliability of systems. Below 55 °C the risk of legionella diseases largely increases and below 50 °C heat exchangers (depending on the type) may start to not be efficient. Detailed results for all cases investigated are reported in Table 5 and Table 6. In the first table, there are summarized results for all configurations investigated without limiting the maximum HW temperature. Temperature graphs of these cases were reported in previous sections. Differently, in the second table are reported results for again all configurations but, in these cases, a basic control strategy for improving system performances was implemented. This control strategy concerned regulating the maximum temperature of the HWT depending on each month.
5. Discussion
Factors, which determine the effectiveness of a HWT energy storage medium coupled with a tidal energy source are various, and these affect, in different ways, performance of the proposed system. One of the main problems to consider is the one related to heat losses. In fact, regarding all examined cases, it was found that losses are relatively large compared to demand. By implementing energy-saving systems, reducing wasted energy in the house and implementing heat recovery systems, the HWT volume can be significantly reduced. Consequently, as losses are reduced, with smaller HWT the proposed system could be much more technically feasible.
The temperature profile of the first model HWT varies on the hourly scale more than the other cases. This is happening because the HWT for the first model is considerably smaller compared to the HWTs of the second and third models. For what concerns the third case, due to the large volume of water, the temperature varies mainly because of the effect of space heating (SH) demand and losses. Thus the effect of the DHW demand, in this latter case, has little significance.
Concerning the third case, the heat demand consumption for the whole year was found to be 26 kWh year/m2. This value indicated that the model correctly reproduced a low-energy houses SH demand (30 kWh year/m2) [21]. However, even by implementing the basic control strategy, losses in HWT are relatively high, especially when the energy demand is less (during summer). Consequently, the temperature inside the house may be too high. This characteristic may be a problem of the proposed system that needs to be addressed. Practical solutions to overcome this problem may concern increasing the insulation of tanks or ensuring good air circulation and natural cooling during warmer periods, e.g., by implementing smart actuators that open windows when refreshing is needed.
Given a specific system design, the aspects that determine the energy available for all the storage periods are very dependent on demand profiles. In order to successfully keep a minimum temperature value, the extreme heating demand periods should be somehow minimized. While, for space heating there is nothing to do except improving house designs, concerning DHW demand appropriate other actions for limiting the consumption could be taken. For example, a mechanism of local tariffs, by which minimum heat requirements can be guaranteed, could be created. In particular, if customers use much more energy than what is needed, prices of energy should progressively increase. The solution could eventually be implemented by installing smart meters.
It should be noted that the indicative thermal conductivity U-value equal to 0.23 W/m2K for the HWT was assumed; this is a common value for a well-insulated tank. However, thermal insulation can be higher if better and extra insulation is added. But this latter option would involve extra major costs.
In order to maximize heat stored in the HWT during a certain period, the range of feasible temperatures in HWT should be as large as feasible. If heat exchangers are used for heating water, as for the case of this study, a minimum temperature should not be less than about 50 °C. On the other hand, the maximum temperature could not exceed 100 °C, otherwise, a pressurized HWT is needed and this could be less feasible in economic terms. The maximum range of HWT temperature depends also on the systems’ sub-components.
In order to implement a HWT for storing tidal energy, solutions on how to warm up the DHW at various temperature differences have to be found. A possible solution could be the one of implementing smart high rated heat exchangers, by which even with smaller temperatures differences water can still be heated up. Another aspect to be considered concerns how to practically deliver water at the right temperature. For example, a solution would be to install automatic temperature controller faucets. In this way, energy could be saved and high domestic water temperatures dangerous to users could be avoided.
5.1. HWT Control Strategy
Depending on the month or occupancy, in order to reduce losses and to increase the functionality of the HWT medium, a control system would be beneficial. This was proved by results of simulations run with a basic control strategy implemented. More in detail, for investigating to which extend HWTs losses could be reduced, a second set of simulations regarding same 6 cases (by controlling maximum temperature) were run. The aim of the control strategy implemented was to raise the temperature to a tuned maximum value of HWT temperature. This indicated that losses could be slightly reduced when the control strategy is applied. Results for this case are reported in Table 6. In particular, daily ranges of temperature were calculated for establishing the minimum heat to store, this later needed to satisfy the demand during energy storage days.
5.2. Viability
Depending on particular remote communities, different implementations of the idea proposed could be developed. In order to quantify the viability and potential economic advantages of the proposed idea, various factors must be investigated individually.
Tidal power, thanks to its characteristics, can be a very valuable form of renewable energy source. Differently, to other clean energy resources, tidal energy can provide a minimum of base load and predicted firm power. These characteristics could give a particular community very low dependence on conventional resources. Nevertheless, various obstacles exist; these are mainly: technical; economical; consensus; and political issues.
Technically, the idea of storing tidal energy for neap days can be more feasible if consumption is reduced as much as possible and large enough HW volume is used. In order to accomplish this, relatively large volumes of HW are needed. Due to the fact that the cost per cubic meter of storage unit highly depends on HWT dimensions, the cost could decrease significantly if enough large HWTs are used [25]. Therefore, tidal energy storage could be feasible if large reservoirs of HW are chosen, and these used for satisfying the total demand of a certain number of households. In this circumstance, district heating schemes with tidal energy integration may definitely be more feasible. However, the efficiency of a wide pipe network and the performances of the HWT storage facility should be precisely assessed. In practice, if users are located too distant from the central HW reservoir the feasibility of such a possibility could be less.
Considering the case of applying the proposed idea in a community which is poorly connected to the electricity network, this would also bring other potential benefits. For example, in the case that multiple renewable energy intermittent generators exist, and these are combined with the thermal energy storage facility. Assuming that a number of remotely opportunely controlled HWTs are available, these could be used to absorb the extra power and directly stabilize the grid. In this way, expensive infrastructure can be avoided. Thus, community interests may be satisfied and large HWTs investment could be more realistic. In order to make this possible, a local incentive mechanism may be necessary.
On the other hand, day scale (short term) variability of tidal power can be highly reduced if HW storage is used in a large number of single houses. This will not require oversized HWTs but it will require merely specific smart timers or remote control systems to be implemented on commercially available electric boilers. This has already been done for stabilizing the grid and the technique is normally referred to as demand-side management or peak levelling methods. Nevertheless, if storage volume of traditional HWTs is not increased, the variability related to neap-spring tidal cycle cannot be locally reduced.
5.3. Economic Reflections
Energy storage with tidal energy could be applied in different circumstances and, depending on characteristics of the context, the scale of storage utility and logistical scenario, this could be economically viable or not. Economic advantages can be evaluated in terms of capability of tidal power and energy storage utilities to replace conventional generation resources. For instance, the idea may be practical in economic terms for those remote settlements where the price of diesel due to shipping costs is high.
Compared to other renewable energy technologies, the costs of tidal stream power plants are still greater [26]. In addition, due to the fact that tidal power is a relatively new form of technology, financial risks related to it are still not properly quantified yet. The trend in the industry is to go bigger. For large plans, the technology costs per installed Kilo-Watt of rated power are less. In addition, it has to be considered that the cost of a cubic meter of hot water storage facility rapidly decreases with the increment of the dimensions of the storage medium. For these reasons, the idea proposed would be more feasible in economic terms if large enough both, tidal power and thermal energy storage plants are developed.
If large HWTs are installed, SH and DHW demand could, in theory, be satisfied entirely by tidal power. Consequently, in cold regions where much of the domestic energy is spent on water heating purposes, a large amount of conventional power plants can be replaced. However, due to the costs of tidal power plants and large HWTs, this could be feasible only if large funds with low-interest rates are available for relatively long periods.
A tidal energy storage facility in domestic households could suit remote off-grid communities or in some cases settlements where transmission infrastructure to main electricity network (for instance grid connected islands) has reached its limit of capacity. In this latter case, the proposed idea would be multifunctional. Meaning that on one hand such a system would allow a community to be more self-sufficient for energy production and, on the other hand, the system would help to balance the electrical network. In this way, other expensive systems may not be required.
Indeed, one of the main functionalities of large HWT facilities integrated with tidal energy could concern local electricity network stability and providing community-wide economic benefits. As in the case of particular islands or coastal communities, by remotely controlling HWTs, local electricity networks could be stabilized. The method, known as peak shaving, is used with other forms of renewable energy resources such as wind power. The system could be also systematically extended so to be used for stabilizing the output of other form of renewable energy resources. For instance, considering a scenario where tidal power is highly exploited, taking into account predicted variability of local tidal power resource, a methodology for maximizing the peak shaving functionality of HWT facilities, could be created.
Consequently, by installing HWTs and by implementing adequate control systems the electricity network could be greatly balanced and community-wide compensations may occur. Depending on which percentage of other renewable energy sources exist in a local community energy portfolio, the proposed idea may become more profitable. Indeed, in the case that a properly planned large HW reservoir could be constructed; this could be fed by peak power outputs of tidal and as well by other renewable energy resources such as wind or solar power. Thus, the high variable power output of also other renewable energy generators may be smoothed down by producing and storing hot water so that expensive other storage methods and system infrastructure may not need to be bought. Despite this, various economic factors, such as the one concerning to costs related to thermal and power losses must be weighed against the potential economic benefits that the idea could provide.
Given the predictability of tidal power and its type of variability, precise economic evaluations can be made years in advance and thus investors could have large advantages compared dealing with other renewable fed energy storage plans. Indeed, a company managing a large HW reservoir integrated with tidal energy for domestic use purposes could precisely plan firm power output, which will feed the storage utility. Assuming that the company manages both, the tidal power station and other energy sources, can appropriately decide (considering time-varying costs of electricity and depending on other renewable energy input) to sell or store tidal energy output.
The proposed idea before being applied to a particular community should be carefully assessed also considering local characteristics. A detailed technical and economic study would be required, which should include an extensive cost-benefit analysis. Depending on the local actual cost of energy, on the grid connection availability and on building layout, the idea could be moulded accordingly. For each particular case, the system proposed should be tailored so that the overall system cost can be somehow justified. Given the finding of this study, for economic viability issues, it is indicated that thermal energy losses are an important aspect on which particular focus is required. For instance, considering single houses the system proposed may be more convenient in economic terms if multiple hot water reservoirs, having different insulation characteristics and costs, are installed. The hot water stored in the most insulated tank would be used only during critical days when tidal energy availability is at its lowest. In this way, part of the energy losses may be further reduced. In general, evaluating various options is essential; considering the case of applying the concept to a few isolated buildings, different storing technologies such as conventional large batteries may be more economically viable. Nevertheless, in order to implement the proposed concept, a series of other possibilities exist. These may also concern mixed type of design, which could incorporate classical sources of energy for heating water such as electricity from the grid, from diesel generators, or electricity obtained from other local renewable energy generators as wind turbines or solar panels. Likewise, similar systems including multiple types of energy storage technologies may also be investigated. In any circumstance, a specific technical and economic study, which includes as many as possible details and characteristics of the buildings and the location considered, is essential. Thus, in this way it is possible to identify a specific system design and to optimize and estimate the overall system cost.
6. Conclusions
In this paper, the concept of utilizing and storing tidal energy for domestic use was investigated. A generic system was hypothesized and through a numerical study, this was assessed. For this purpose, time domain simplified SIMULINK models were produced and considerations about possible issues, implementation circumstances, designs, economics and control strategies were discussed.
The simulations of idealized configurations for a year period were run and consequently, it was found that, for using stored energy during low energy output days, relatively larger HWTs rather than the traditional ones are needed. It was found that even solely for domestic hot water (DHW) demand, due to the dimension of the hot water tank (HWT) needed for what concerns single household, the system is less convenient. However, by looking at the performance of a case concerning ten families, it was found that economies of scale could be advantageous. In particular, for the case concerning a single household, HWT losses are high compared to demand and thus the efficiency of the system can be low. On the other hand, depending on the dimensions of the storage utility, the system efficiency can be much higher. Besides, to reduce HWT volume and thus increase efficiency, demand should be reduced as much as possible. As a consequence, it is advised that energy-saving designs and solutions should be implemented to improve the effectiveness of the proposed system.
Concerning the third case related to applying the idea for providing both DHW and space heating demand to a single household, it was found that even for a low-energy house the volume of HWT should be relatively large, i.e., 5 m3. Considering that an oversized HWT is needed for only about 6 months, year-average HWT losses make the solution challenging to be implemented, both in technical and economic terms. However, figures were found that indicated that possible HWT control strategies could slightly reduce losses. In this way, to some extent, the viability of the system could be incremented.
The study indicated that even if the proposed idea may be relatively expensive to implement, this is technically feasible. In addition, considering remote communities, possible potential economic advantages may in some cases exist. Without bearing in mind financial and technical challenges that must be overcome, the most suitable circumstances in which the idea could be reasonably applied are: The one concerning relatively large implementations, such as district heating schemes and for buildings compounds; and the one concerning absorbing local short-time power surplus locally generated.
Funding
This research received no external funding.
Acknowledgments
The author would like to acknowledge Sandy Day of the University of Strathclyde for the supervision on the work carried out and presented in this paper. Besides, the author would further like to acknowledge: David Clelland, Andy Grant and Paul Strachan of the University of Strathclyde; David Palmer of the Campbell Palmer Partnership Ltd.; Gary Connor of Nova Innovation Ltd.; for the advice and support provided during the time of the project.
Conflicts of Interest
The author declares no conflict of interest.
References
- Environmental Change Institute, University of Oxford. Variability of UK Marine Resources. July 2005. Available online: https://www.carbontrust.com/media/174017/eci-variability-uk-marine-energy-resources.pdf (accessed on 14 December 2018).
- University of Edinburgh. Matching Renewable Electricity Generation with Demand. 24 April 2006. Available online: www.scotland.gov.uk/Publications/2006/04/24110728/1 (accessed on 10 July 2018).
- Iyer, A.; Couch, S.; Harrison, G.; Wallace, R. Developing Methodologies for Quantifying the Impact of Tidal Current Energy Variability. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6 October 2010. [Google Scholar]
- Davidson, R. A Feasibility Study: Tidal Power Generation for a Remote, off-Grid Community on the British Columbia Coast. Unpublished manuscript. 21 February 2007. [Google Scholar]
- Salequzzaman, M.; Newman, P.; Ellery, M.E.; Corry, B. Prospects of Electricity from Tidal Power in Coastal Regions of Bangladesh. 2018. Available online: https://www.researchgate.net/publication/237297146_PROSPECTS_OF_ELECTRICITY_FROM_TIDAL_POWER_IN_COASTAL_REGIONS_OF_BANGLADESH (accessed on 24 January 2019).
- Bryden, I.; Macfarlane, D. The utilization of short term energy storage with tidal current generation systems. Energy 2000, 25, 893–907. [Google Scholar] [CrossRef]
- Shaw, T.; Thorpe, G. Integration of Pumped-Storage with Tidal Power. J. Power Div. 1971, 97, 159–180. [Google Scholar]
- Vennell, R.; Adcock, T. Energy storage inherent in large tidal turbine farms. Proc. R. Soc. 2014, 470, 20130580. [Google Scholar] [CrossRef] [PubMed]
- Manchester, S.; Swan, B.B.L.; Groulx, D. Energy storage requirements for in-stream tidal generation on a limited capacity electricity grid. Energy 2013, 61, 283–290. [Google Scholar] [CrossRef]
- Markillie, R. £1.79M Electrolizer sale to EMEC; ITM Power: Orkneys Islands, UK, 2015. [Google Scholar]
- Ross, K. Tesla Batteries Integrated with Tidal Array; Power Engineering International: Shetland Islands, UK, 2018. [Google Scholar]
- How to Use Solar Energy at Night. Scientific American, 18 February 2009.
- Schmidt, T.; Mangold, D.; Müller-Steinhagen, H. Seasonal thermal energy storage in Germany. In Proceedings of the ISES Solar World Congress, Göteborg, Schweden, 14–19 June 2003. [Google Scholar]
- EMEC Assessment of Tidal Energy Resource; Charlesworth Group: Wakefield, UK, 2009.
- ABP mer. Atlas of UK Marine Renewable Energy Resources—WEBvision—Renewables (Tide), 2007. Available online: http://vision.abpmer.net/renewables/map_default.phtml?config=tide&resetsession=groups,resultlayers (accessed on 10 July 2011).
- Lee, M.; Lu, C.; Huang, H. Reliability and cost analyses of electricity collection systems of a marine current farm—A Taiwanese case study. Renew. Sustain. Energy Rev. 2009, 13, 2012–2021. [Google Scholar] [CrossRef]
- Electric Power Research Institute Inc. Economic Assessment Methodology for Tidal In-Stream Power Plants. 10 June 2006. Available online: http://oceanenergy.epri.com/attachments/streamenergy/reports/002_TP_Econ_Methodology_06-10-06.pdf (accessed on 15 August 2011).
- Runming, Y.; Koen, S. A method of formulating energy load profile for domestic buildings in the UK. Energy Build. 2004, 663–671. [Google Scholar] [CrossRef]
- Ulrike, J.; Klaus, V. DHWcalc: Program to generate domestic hot water profiles with statistical means for user defined conditions. In Proceedings of the ISES Solar World Congress, Orlando, FL, USA, 8–12 August 2005. [Google Scholar]
- BRE, SAP 2009. The Government’s Standard Assessment Procedure for Energy Rating of Dwellings, March 2010. Available online: www.bre.co.uk/sap2009/page.jsp?id=1642 (accessed on 10 July 2018).
- Audenaerta, A.; De Cleynb, S.; Vankerckhoveb, B. Economic analysis of passive houses and low-energy houses compared with standard houses. Energy Policy 2008, 47–55. [Google Scholar] [CrossRef]
- Ally, M.R.; Tomlinson, J.J.; Ward, B.T. Water and Energy Savings using Demand Hot Water,2002, pp. 33–77. Technical report for U.S. Department of Energy, Palo Alto, California. Available online: https://info.ornl.gov/sites/publications/Files/Pub57428.pdf (accessed on 24 January 2019).
- Suter, J.M. Heat losses from storage tanks: Up to 5 times higher than calculated! Available online: https://www.scribd.com/document/98530195/Heat-Losses-From-Storage-Tanks-by-Jm-Suter (accessed on 10 July 2011).
- Energy Management and Research Associates. Energy Use and Domestic Hot Water Consumption; Report for the New York State Energy Research and Development Authority; New York State Energy Research and Development Authority: New York, NY, USA, 1994. [Google Scholar]
- Wit, J.D. Heat storage for CHP plants - adding flexibility, improving performance, n.d. Available online: http://www.cospp.com/articles/print/volume-8/issue-6/features/heat-storage-for-chp-plants-adding-flexibility-improving-performance.html. (accessed on 10 July 2011).
- Ernst & Young LLP; Black & Veatch, Cost of and financial support for wave, tidal stream and tidal range generation in the UK, 02 November 2010. Available online: http://www.decc.gov.uk/assets/decc/What%20we%20do/UK%20energy%20supply/Energy%20mix/Renewable%20energy/explained/wave_tidal/798-cost-of-and-finacial-support-for-wave-tidal-strea.pdf. (accessed on 02 July 2011).
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).