Designing a Thermal Radiation Oven for Smart Phone Panels
Abstract
1. Introduction
2. Design Strategy
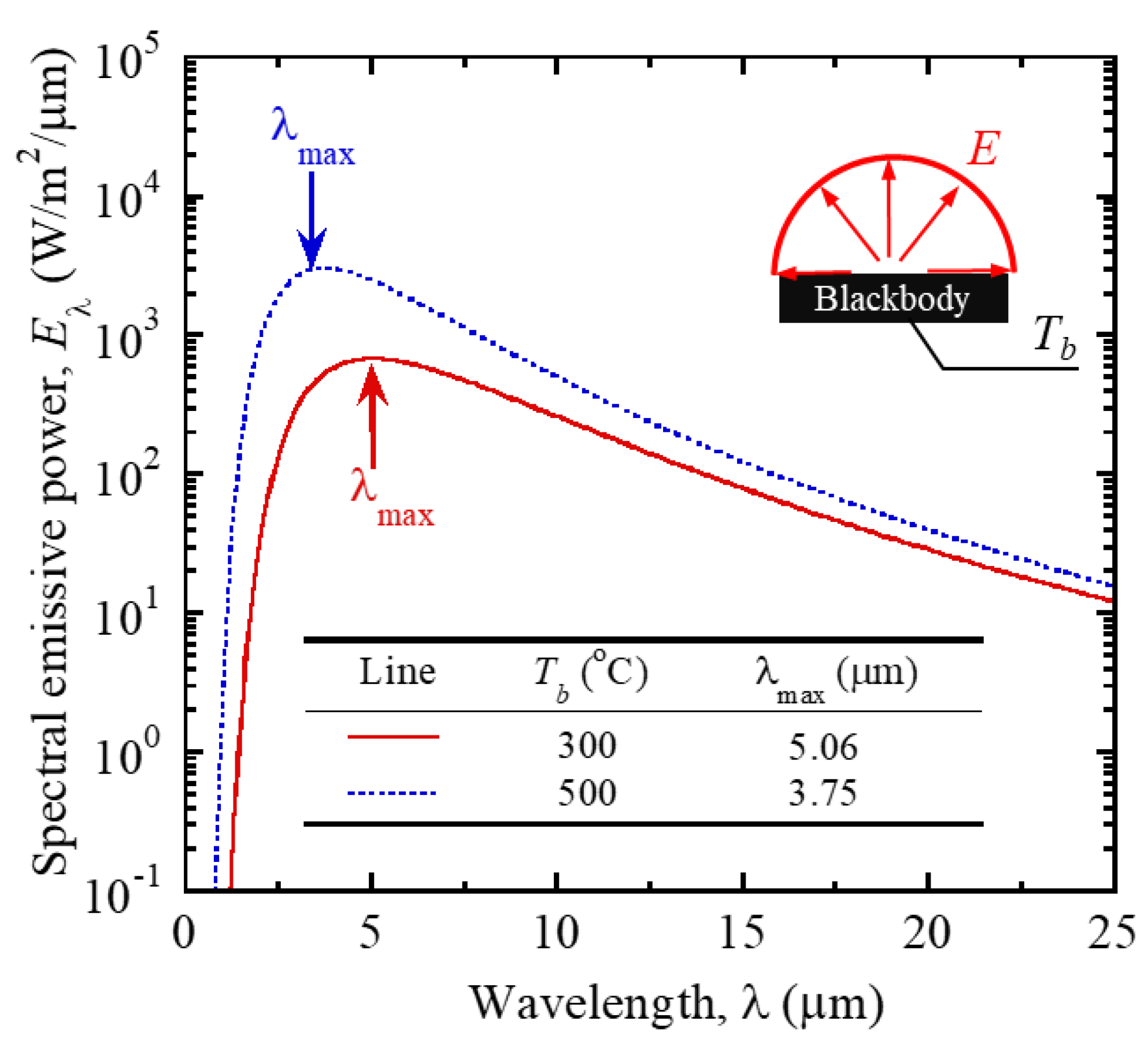
3. Numerical Model
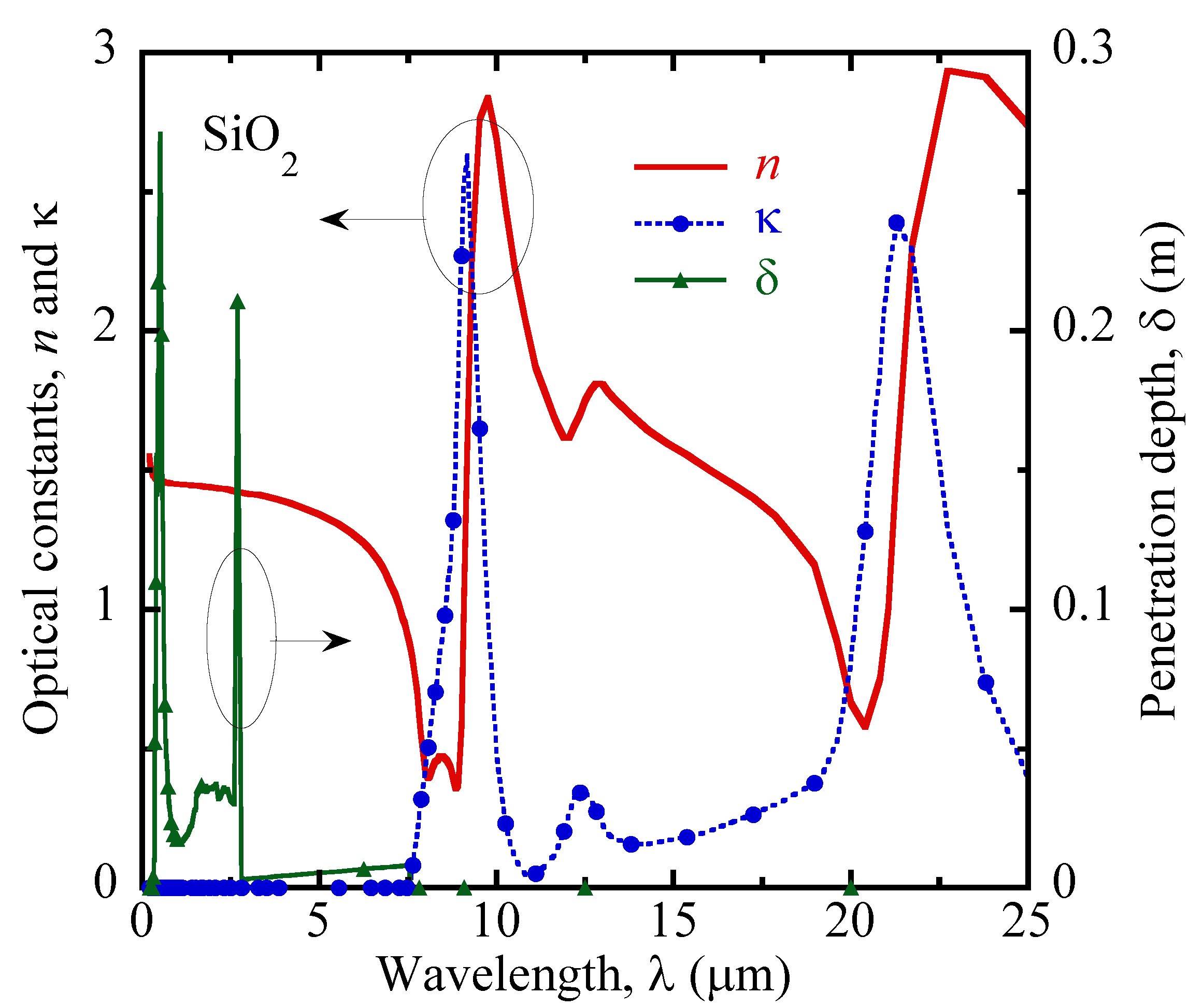
3.1. Thermophysical Properties
3.2. Finite-Difference Method
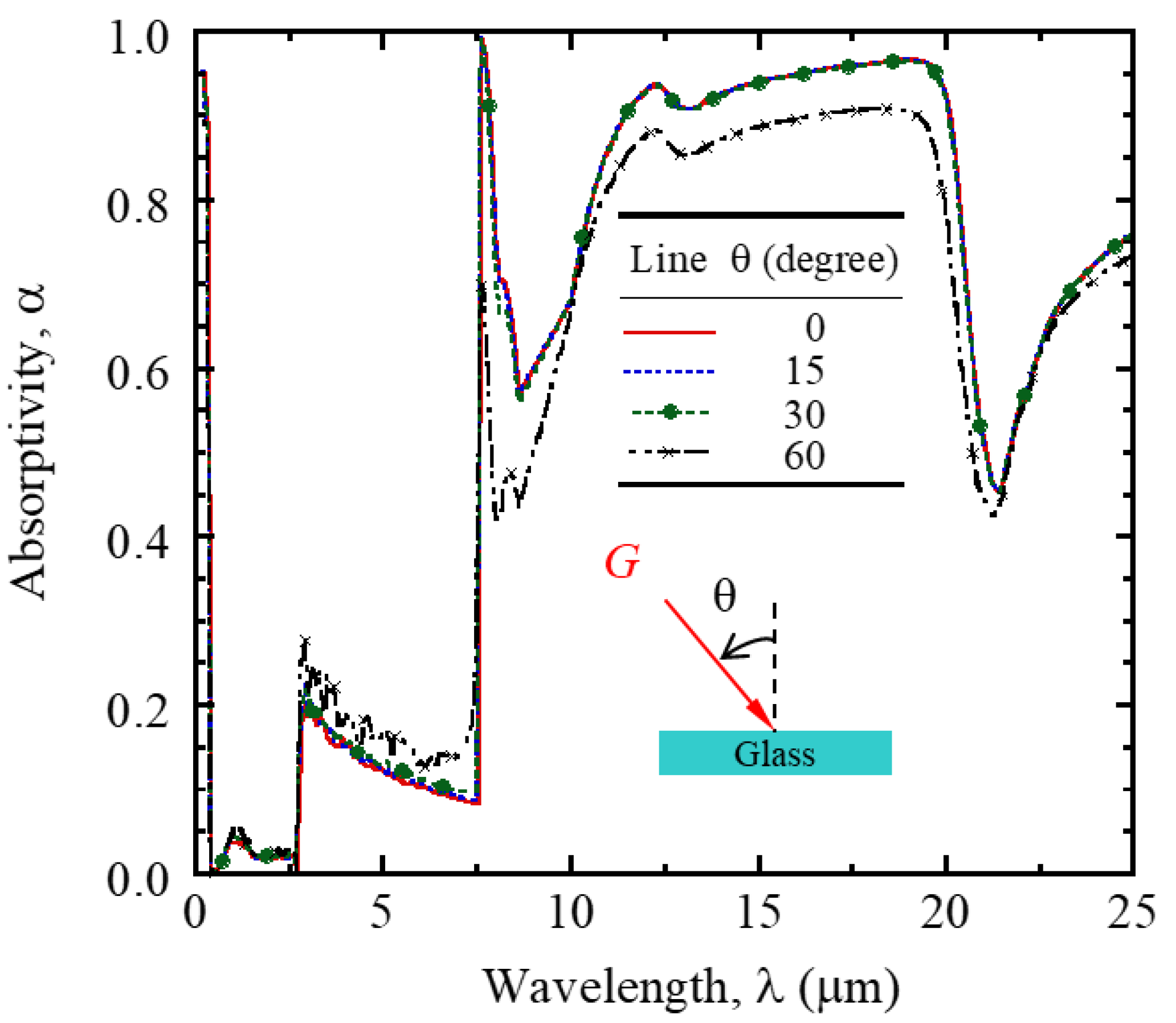
4. Results and Discussion
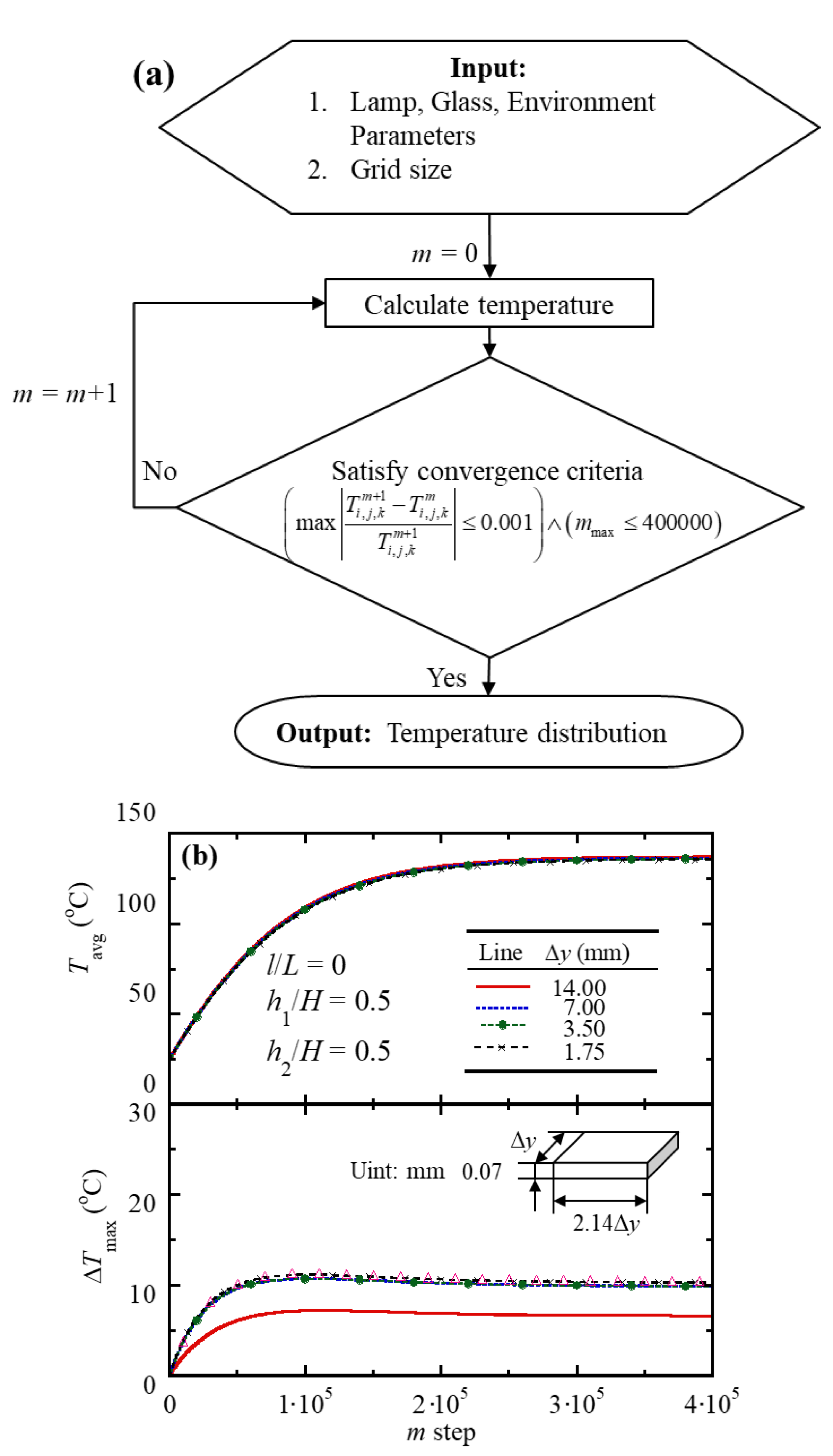
4.1. Program Convergence
4.2. Temperature Distribution
4.3. Main Effects and Fitness Function
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | thermal diffusivity, m/s2 |
| C1 | first radiation constant, 3.742 × 108 W μm4/m2 |
| C2 | second radiation constant, 1.439 × 104 μm·K |
| D | diameter of infrared lamp, m |
| E | emissive power, W/m2 |
| fraction of the total emission in a wavelength interval λ1 ≦ λ ≦ λ2 | |
| G | irradiation, W/m2 |
| H | height, m |
| h1 | vertical distance between the upper/lower side of oven wall and panel top/bottom surface, m |
| h2 | vertical distance between center of the middle lamp and panel, m |
| k | thermal conductivity, W/m·K |
| L | length of glass panel |
| l | lateral distance between center of a side lamp and the closest edge of glass panel, m |
| Q | fitness function |
| T | temperature, K |
| W | width of panel, m |
| x, y, z | Cartesian coordinate system |
| Superscript | |
| m | number of iterations |
| Subscripts | |
| avg | average |
| b | blackbody |
| down | bottom surface of panel |
| ini | initial temperature |
| i,j,k | incidence dummy index for x, y, and z |
| L | heating lamp |
| max | maximum |
| min | minimum |
| surr | surrounding |
| total | total radiative property |
| up | top surface of panel |
| Greek symbols | |
| α | absorptivity |
| Δ | difference |
| δ | penetration depth, m |
| ε | emissivity |
| θ | incident angle, degree |
| κ | extinction coefficient |
| λ | wavelength, m |
| σ | Stefan–Boltzmann constant, 5.67×10-8 W/m2·K4 |
| Abbreviations | |
| CFD | computational fluid dynamics |
References
- Blundell, S.; Blundell, K. Concepts in Thermal Physics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Rabl, A.; Nielsen, C.E. Solar ponds for space heating. Sol. Energy 1975, 17, 1–12. [Google Scholar] [CrossRef]
- Mayo, E.I.; Kilså, K.; Tirrell, T. Cyclometalated iridium(III)-sensitized titanium dioxide solar cells. Photochem. Photobiol. Sci. 2006, 10, 1039. [Google Scholar] [CrossRef] [PubMed]
- Rabi, A.; Sevcik, V.J.; Giugler, R.M.; Winston, R. Use of Compound Parabolic Concentrator for Solar Energy Collection; United States Press: Las Vegas, NV, USA, 1974. [Google Scholar]
- Lewis, N.S.; Nocera, D.G. Powering the planet: Chemical challenges in solar energy utilization. Proc. Natl. Acad. Sci. USA 2006, 103, 15729–15735. [Google Scholar] [CrossRef] [PubMed]
- Reisfeld, R. New developments in luminescence for solar energy utilization. Opt. Mater. 2010, 32, 850–856. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, F.Q.; Xia, X.L.; Tan, H.P.; Liang, Y.C. Radiative properties of a solar cavity receiver/reactor with quartz window. Int. J. Hydrogen Energy 2011, 36, 12148–12158. [Google Scholar]
- Huang, X.; Chen, X.; Shuai, Y.; Yuan, Y.; Zhang, T.; Li, B.X.; Tan, H.P. Heat transfer analysis of solar-thermal dissociation of NiFe2O4 by coupling MCRTM and FVM method. Energy Convers. Manag. 2015, 106, 676–686. [Google Scholar] [CrossRef]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washomc, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared thermography for temperature measurement and non-destructive testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef] [PubMed]
- Kylili, A.; Fokaides, P.A.; Christou, P.; Kalogirou, S.A. Infrared thermography (IRT) applications for building diagnostics: A review. Appl. Energy 2014, 134, 531–549. [Google Scholar] [CrossRef]
- Sorour, H.; Mesery, H.E. Eeffect of microwave and infrared radiation on drying of onion slices. Impact J. 2014, 2, 119–130. [Google Scholar]
- Shibukawa, S.; Sugiyama, K.; Yano, T. Effects of heat transfer by radiation and convection on browning of cookies at baking. J. Food Sci. 1989, 54, 621–624. [Google Scholar] [CrossRef]
- Forrer, W.O. Infrared Cooking Oven. U.S. Patent No. 2864932, 16 December 1958. [Google Scholar]
- Bergendal, L.R.G. Domestic Infrared Radiation Oven. U.S. Patent No. 4575616, 11 March 1986. [Google Scholar]
- Wassman, D. Convectively-Enhanced Radiant Heat Oven. U.S. Patent No. 5676870, 14 October 1997. [Google Scholar]
- Lee, D.R. Gas Radiation Oven Range. U.S. Patent No. 7690374 B2, 6 April 2010. [Google Scholar]
- James, L.P. Radiant Convection Oven. U.S. patent No. 9513057 B2, 6 December 2016. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; DeWitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons Press: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pallik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Chen, Y.-B.; Zhang, Z.M.; Timans, P.J. Radiative properties of patterned wafers with nanoscale linewidth. J. Heat Transf. Trans. ASME 2007, 129, 79–90. [Google Scholar] [CrossRef]
- Gu, M.J.; Chen, Y.-B. Modeling bidirectional reflectance distribution function of one-dimensional random rough surfaces with the finite difference time domain method. Smart Sci. 2014, 2, 101–106. [Google Scholar] [CrossRef]

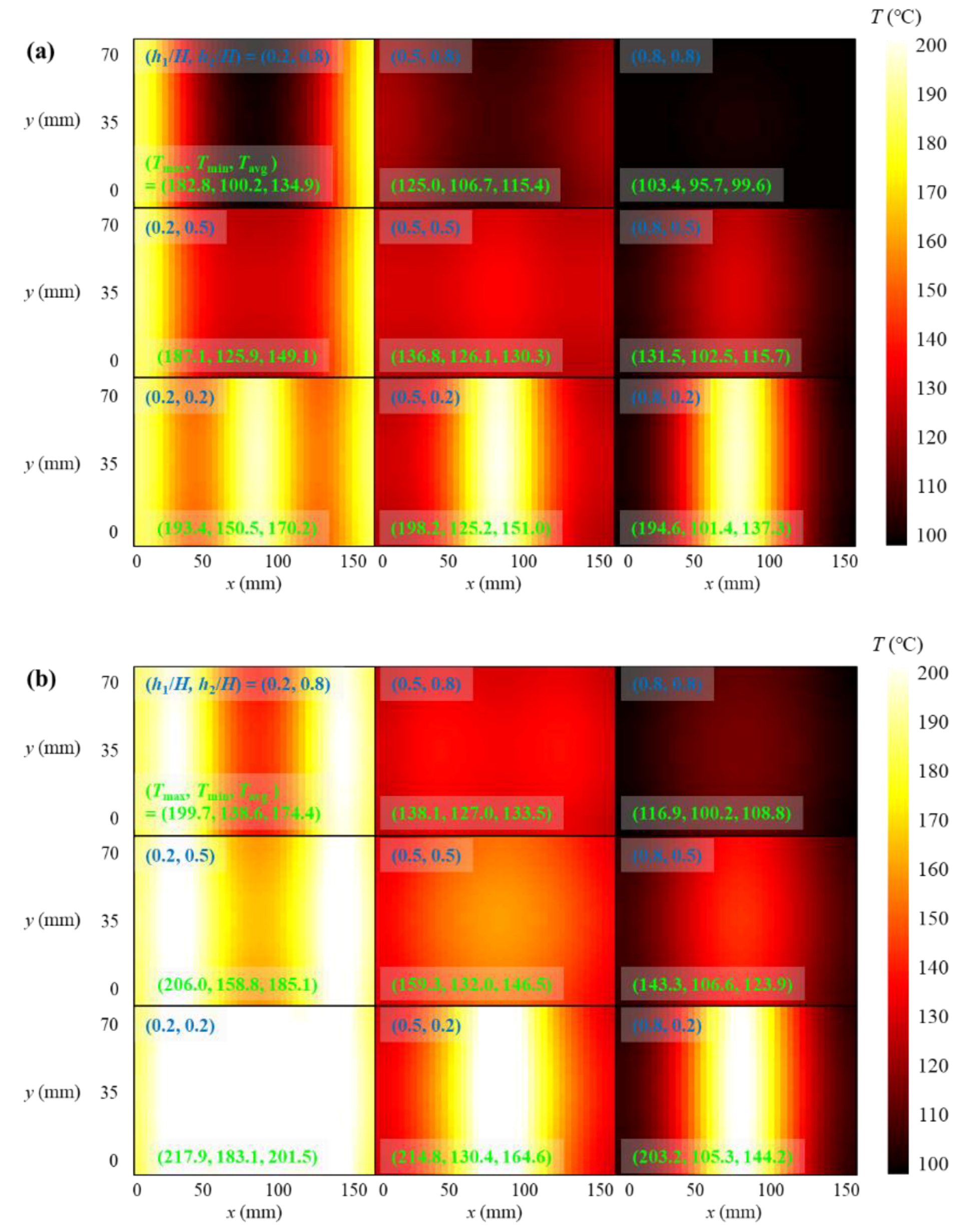
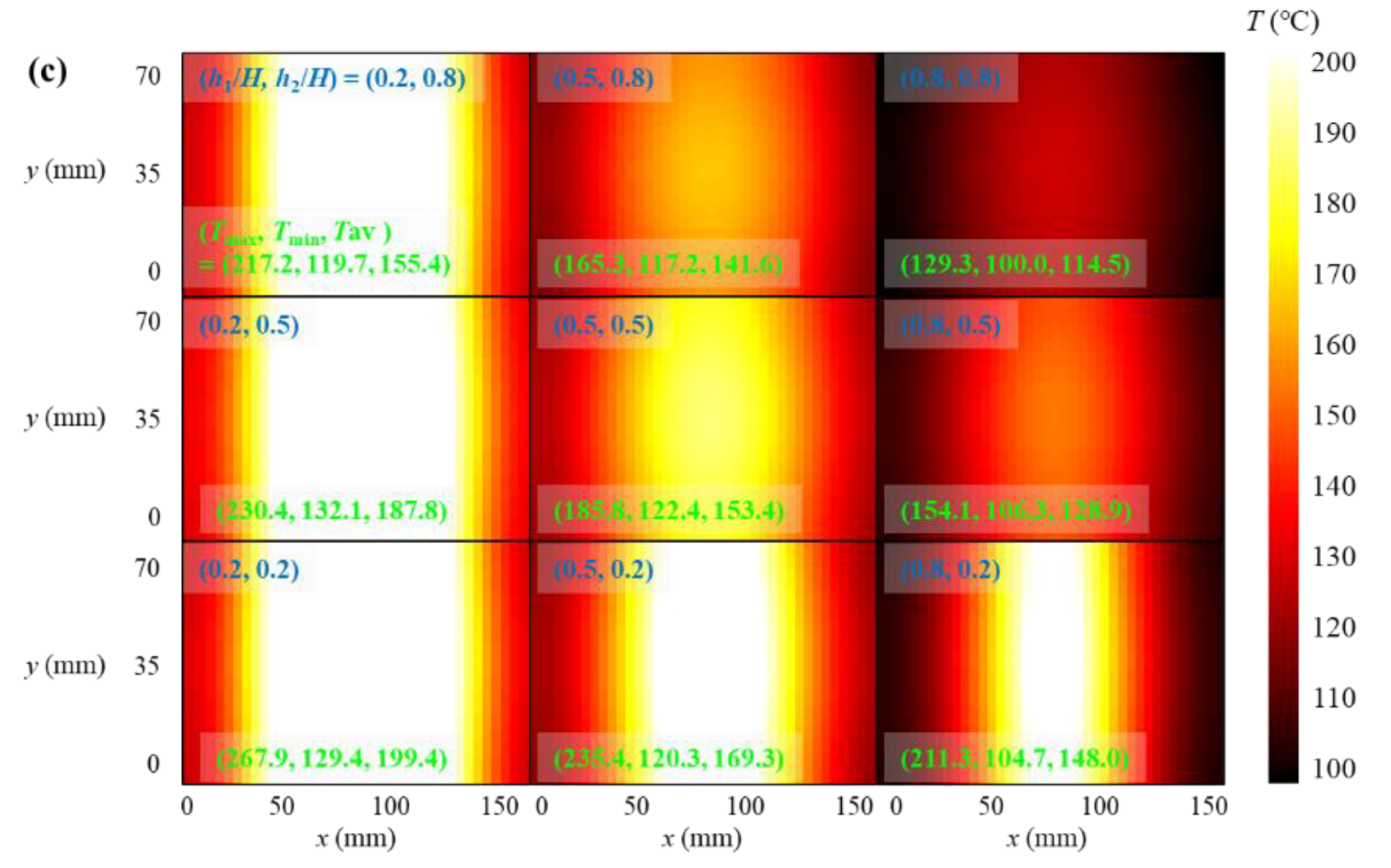
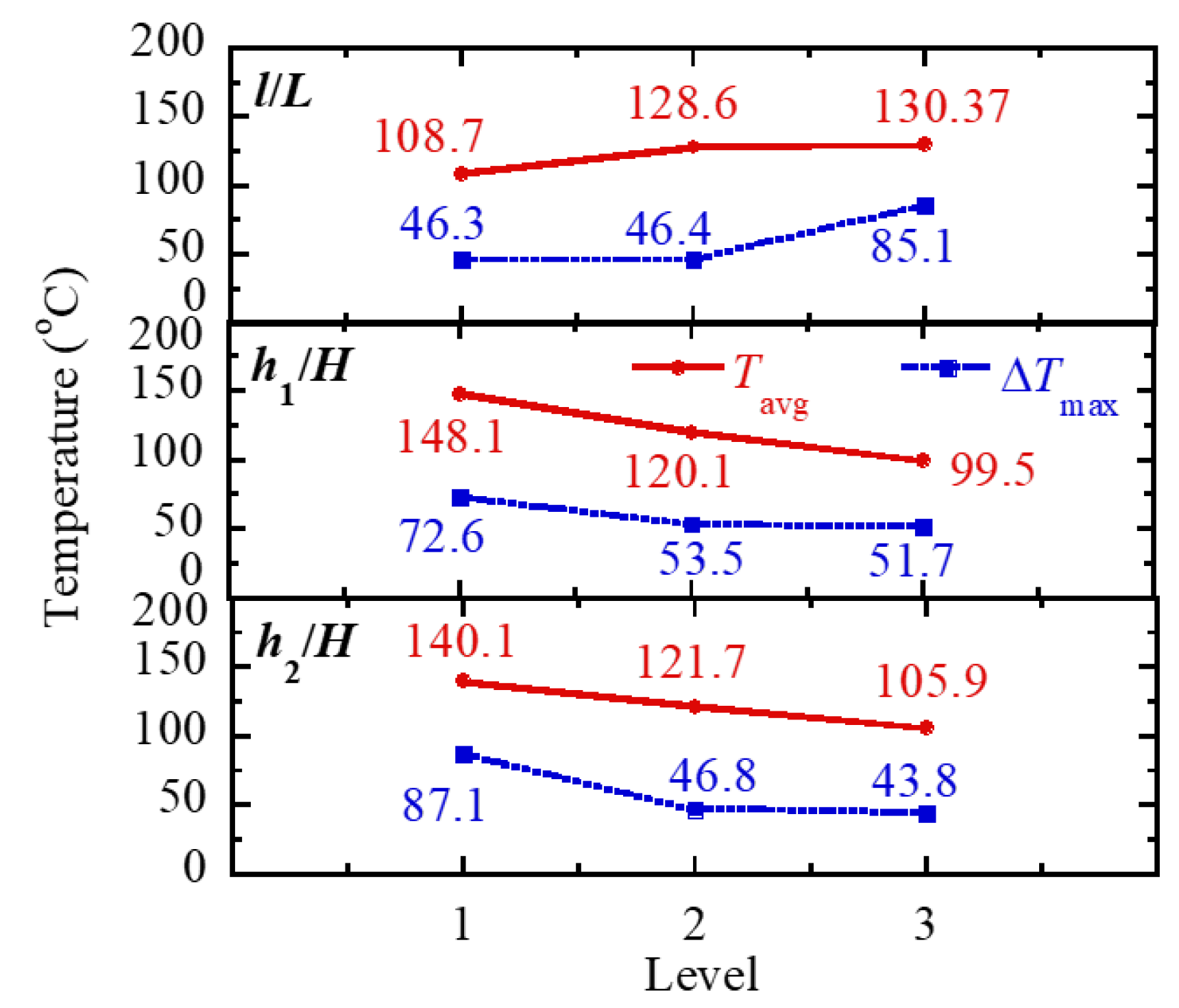
| Factor | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| l/L | 0 | 1/6 | 1/3 |
| h1/H | 0.2 | 0.5 | 0.8 |
| h2/H | 0.2 | 0.5 | 0.8 |
| Test | l/L (Level) | h1/H (Level) | h2/H (Level) | Tavg | ΔTmax | Q |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 170.2 | 40.9 | 0 |
| 2 | 1 | 1 | 2 | 149.1 | 61.2 | 0 |
| 3 | 1 | 1 | 3 | 134.9 | 82.5 | 0 |
| 4 | 1 | 2 | 1 | 151.0 | 73.0 | 0 |
| 5 | 1 | 2 | 2 | 130.3 | 10.6 | 9.93 |
| 6 | 1 | 2 | 3 | 115.4 | 18.4 | 4.91 |
| 7 | 1 | 3 | 1 | 137.3 | 93.2 | 0 |
| 8 | 1 | 3 | 2 | 115.7 | 29.1 | 0 |
| 9 | 1 | 3 | 3 | 99.6 | 7.7 | 9.69 |
| 10 | 2 | 1 | 1 | 201.5 | 34.8 | 0 |
| 11 | 2 | 1 | 2 | 185.1 | 47.2 | 0 |
| 12 | 2 | 1 | 3 | 174.4 | 61.1 | 0 |
| 13 | 2 | 2 | 1 | 164.6 | 84.4 | 0 |
| 14 | 2 | 2 | 2 | 146.5 | 27.3 | 0 |
| 15 | 2 | 2 | 3 | 133.5 | 11.2 | 9.69 |
| 16 | 2 | 3 | 1 | 144.2 | 97.9 | 0 |
| 17 | 2 | 3 | 2 | 123.9 | 36.7 | 0 |
| 18 | 2 | 3 | 3 | 108.8 | 16.7 | 5.02 |
| 19 | 3 | 1 | 1 | 199.4 | 138.5 | 0 |
| 20 | 3 | 1 | 2 | 187.8 | 98.3 | 0 |
| 21 | 3 | 1 | 3 | 155.4 | 89.2 | 0 |
| 22 | 3 | 2 | 1 | 169.3 | 115.0 | 0 |
| 23 | 3 | 2 | 2 | 153.4 | 63.4 | 0 |
| 24 | 3 | 2 | 3 | 141.6 | 78.0 | 0 |
| 25 | 3 | 3 | 1 | 148.0 | 106.5 | 0 |
| 26 | 3 | 3 | 2 | 128.9 | 47.8 | 0 |
| 27 | 3 | 3 | 3 | 114.5 | 29.3 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, M.-J.; Yang, S.; Wu, Y.-C.; Chiu, C.-J.; Chen, Y.-B. Designing a Thermal Radiation Oven for Smart Phone Panels. Inventions 2018, 3, 36. https://doi.org/10.3390/inventions3020036
Gu M-J, Yang S, Wu Y-C, Chiu C-J, Chen Y-B. Designing a Thermal Radiation Oven for Smart Phone Panels. Inventions. 2018; 3(2):36. https://doi.org/10.3390/inventions3020036
Chicago/Turabian StyleGu, Min-Jhong, Shuai Yang, Yen-Cheng Wu, Chien-Jui Chiu, and Yu-Bin Chen. 2018. "Designing a Thermal Radiation Oven for Smart Phone Panels" Inventions 3, no. 2: 36. https://doi.org/10.3390/inventions3020036
APA StyleGu, M.-J., Yang, S., Wu, Y.-C., Chiu, C.-J., & Chen, Y.-B. (2018). Designing a Thermal Radiation Oven for Smart Phone Panels. Inventions, 3(2), 36. https://doi.org/10.3390/inventions3020036






