An Embeddable Strain Sensor with 30 Nano-Strain Resolution Based on Optical Interferometry
Abstract
:1. Introduction
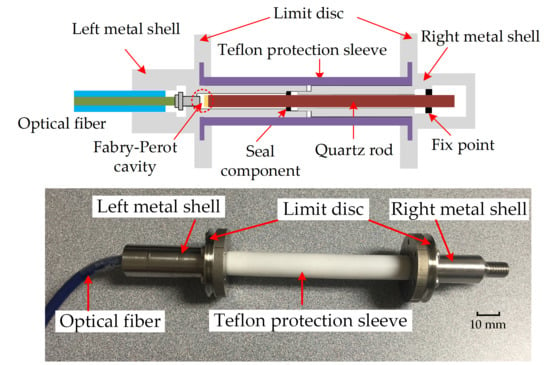
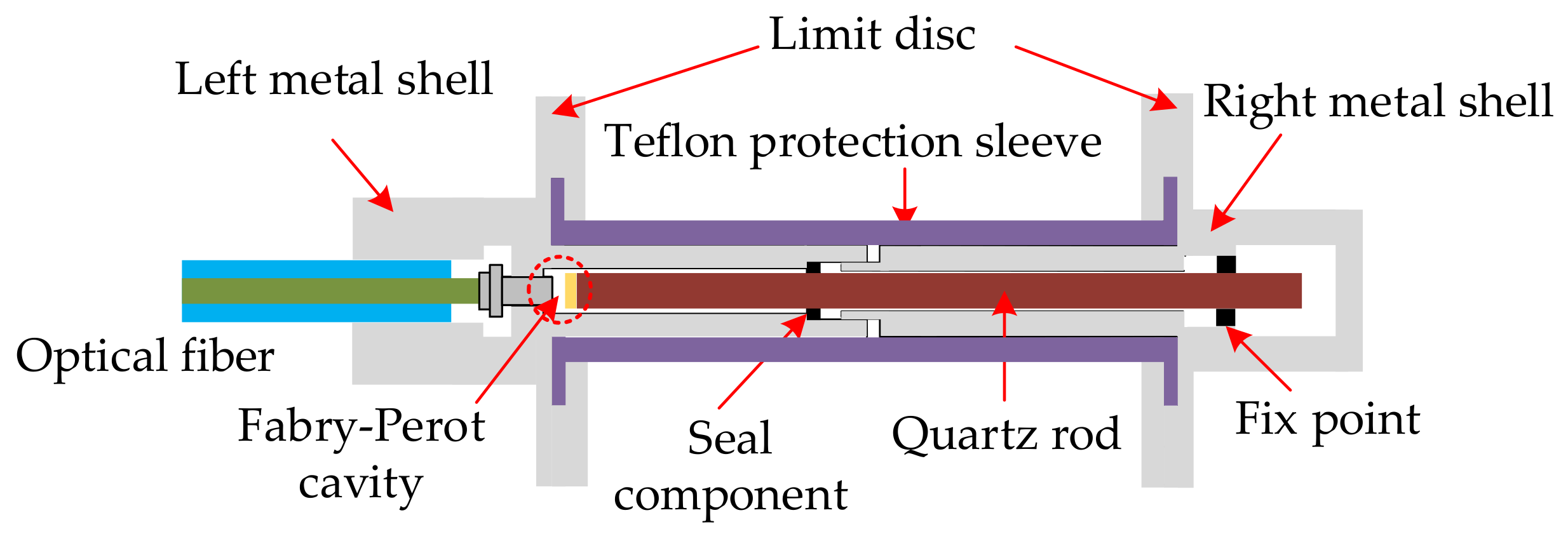
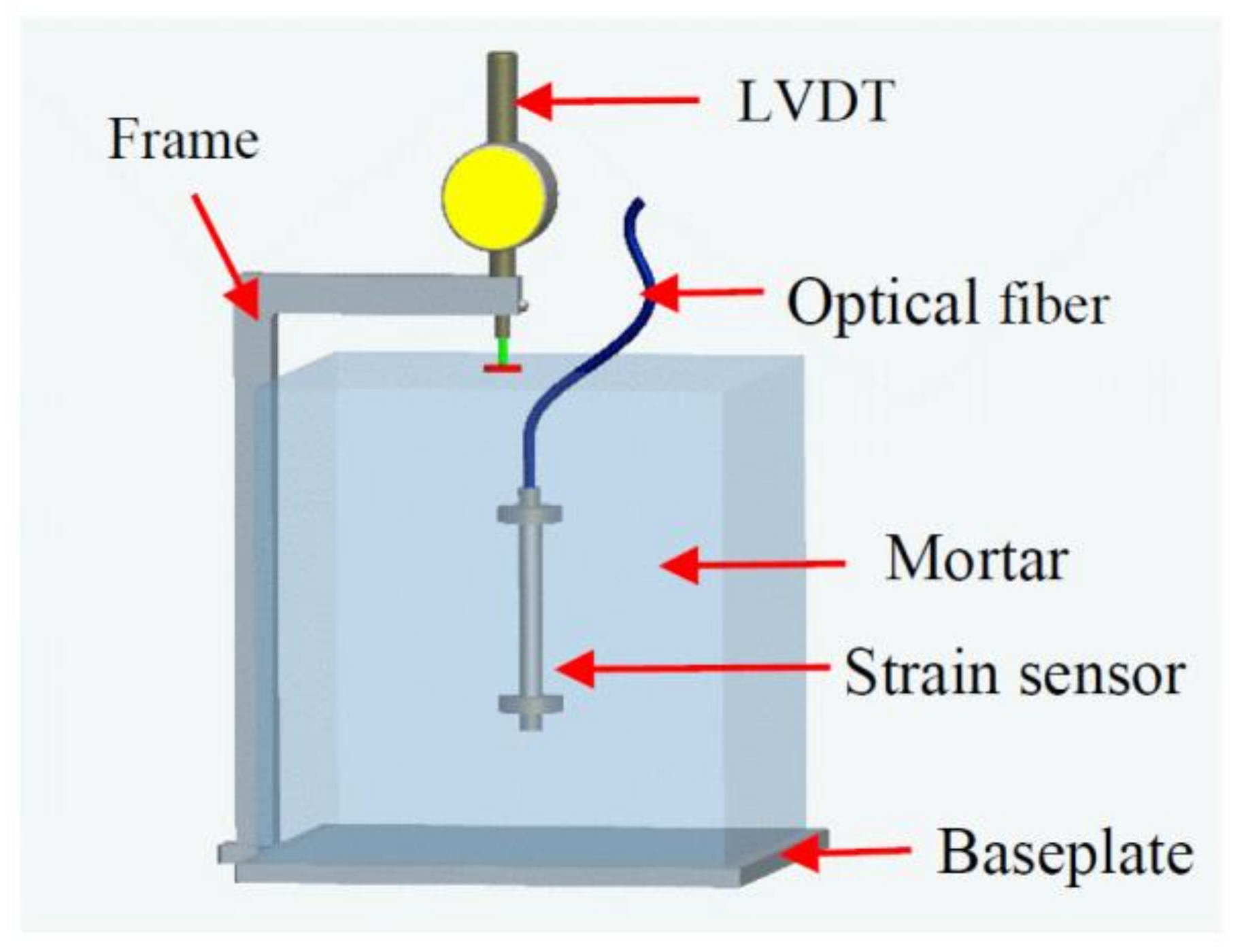
2. Sensor Structure and Principle
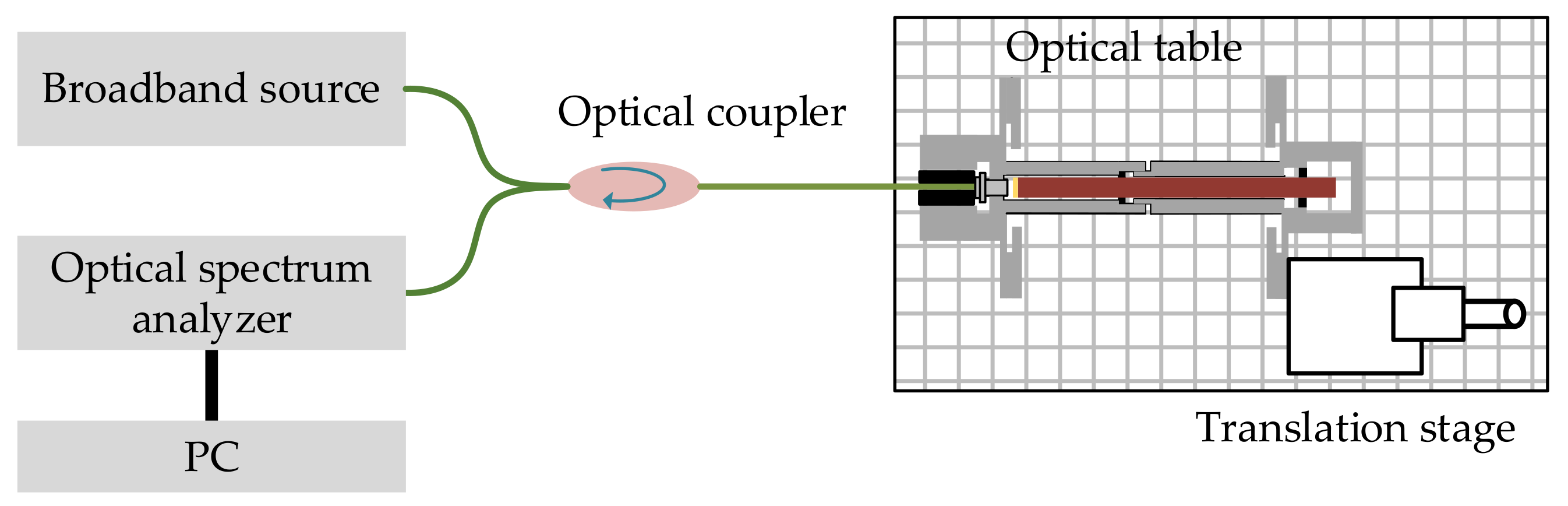
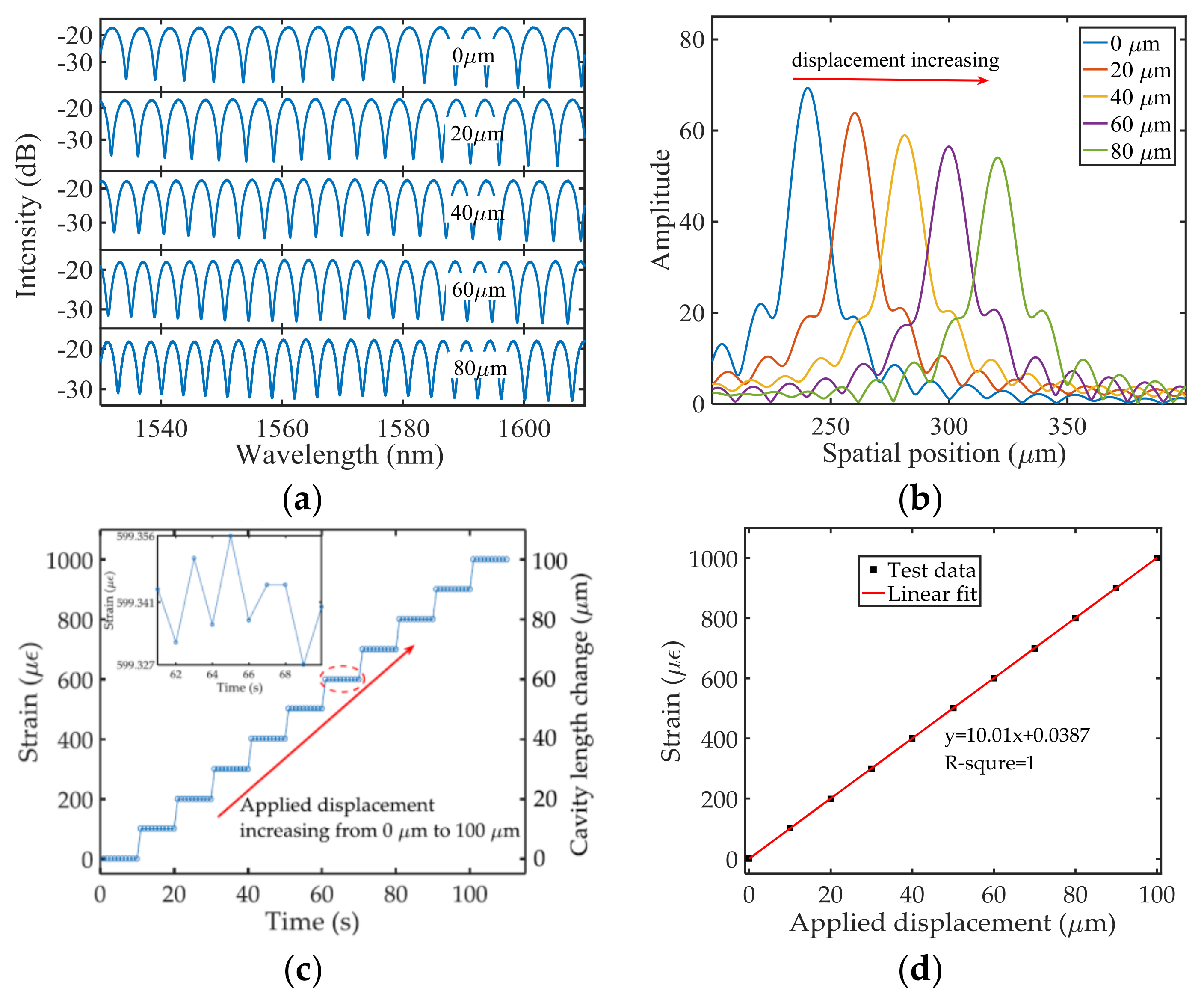
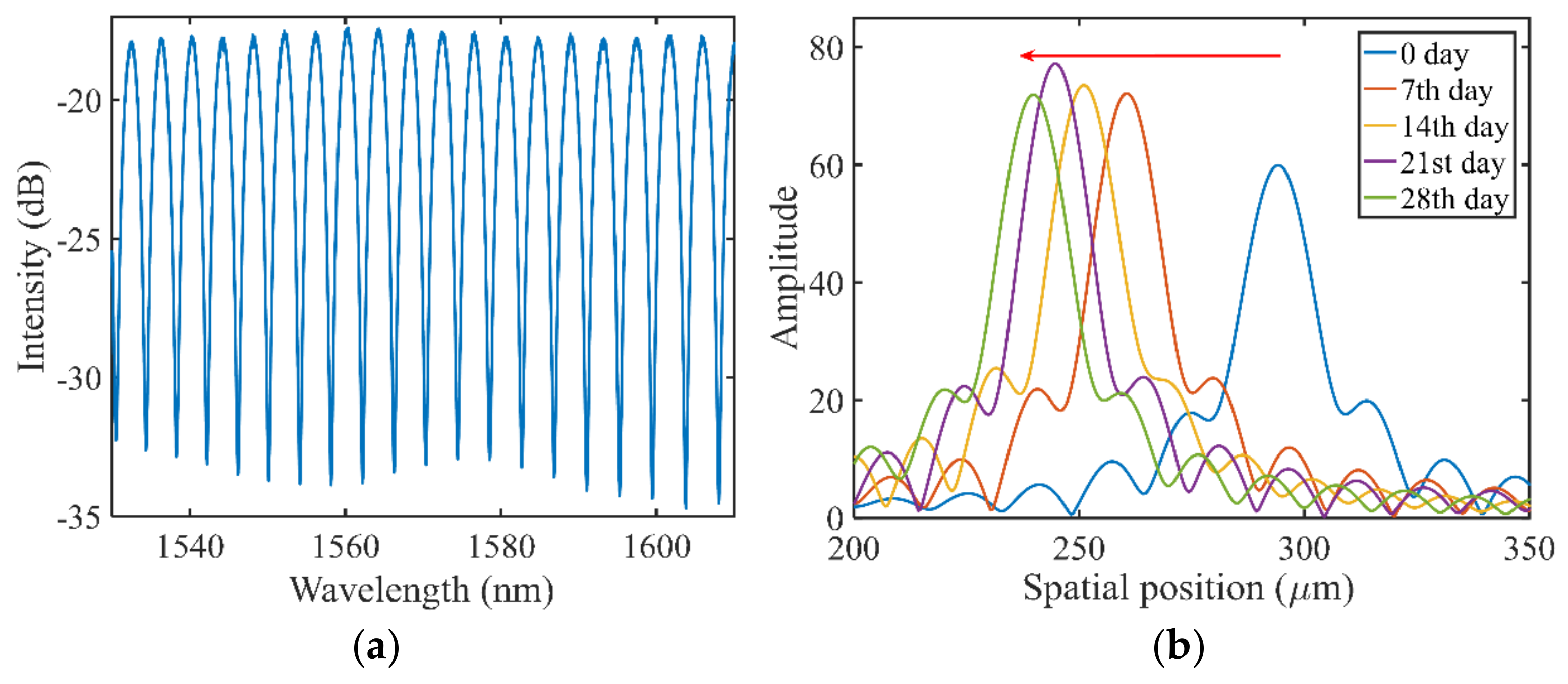
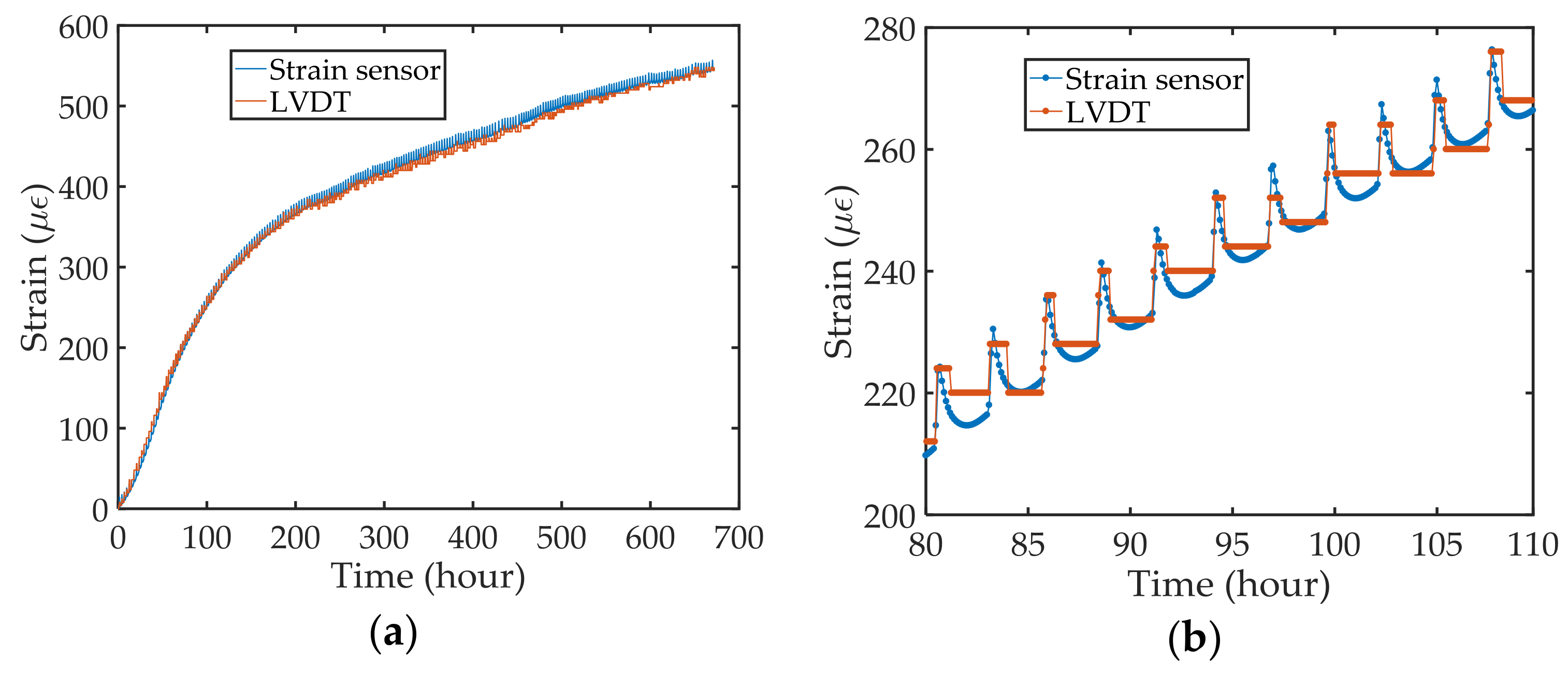
3. Experimental Results and Discussions
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gagliardi, G.; Salza, M.; Avino, S.; Ferraro, P.; De Natale, P. Probing the ultimate limit of fiber-optic strain sensing. Science 2010, 330, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Lan, X.; Wang, H.; Yuan, L.; Wei, T.; Gao, Z.; Xiao, H. Polymer optical fiber for large strain measurement based on multimode interference. Opt. Lett. 2012, 37, 4308–4310. [Google Scholar] [CrossRef] [PubMed]
- Dong, B.; Hao, J.; Liaw, C.Y.; Lin, B.; Tjin, S.C. Simultaneous strain and temperature measurement using a compact photonic crystal fiber inter-modal interferometer and a fiber Bragg grating. Appl. Opt. 2010, 49, 6232–6235. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yuan, L.; Hefferman, G.; Wei, T. Ultraweak intrinsic Fabry-Perot cavity array for distributed sensing. Opt. Lett. 2015, 40, 320–323. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Liang, X.; Galedar, S.A.; Azarmi, F. Integrated Fiber Optic Sensing System for Pipeline Corrosion Monitoring. Pipelines 2015, 1667–1676. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Bao, X. Sensitive acoustic vibration sensor using single-mode fiber tapers. Appl. Opt. 2010, 50, 1873–1878. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.D.; Morey, W.W.; Berkoff, T.A. Fiber-optic Bragg grating strain sensor with drift-compensated high-resolution interferometric wavelength-shift detection. Opt. Lett. 1993, 18, 72–74. [Google Scholar] [CrossRef] [PubMed]
- Chow, J.H.; Littler, I.C.; De Vine, G.; McClelland, D.E.; Gray, M.B. Phase-sensitive interrogation of fiber Bragg grating resonators for sensing applications. J. Lightw. Technol. 2005, 23, 1881–1889. [Google Scholar] [CrossRef]
- Chow, J.H.; McClelland, D.E.; Gray, M.B.; Littler, I.C. Demonstration of a passive subpicostrain fiber strain sensor. Opt. Lett. 2005, 30, 1923–1925. [Google Scholar] [CrossRef] [PubMed]
- Gatti, D.; Galzerano, G.; Janner, D.; Longhi, S.; Laporta, P. Fiber strain sensor based on a π-phase-shifted Bragg grating and the Pound-Drever-Hall technique. Opt. Express 2008, 16, 1945–1950. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Zhang, W.; Zhen, T.; Zhang, F.; Li, F. π-Phase-Shifted FBG for High-Resolution Static-Strain Measurement Based on Wavelet Threshold Denoising Algorithm. J. Lightw. Technol. 2014, 32, 3692–3698. [Google Scholar]
- Gillooly, A.M.; Dobb, H.; Zhang, L.; Bennion, I. Distributed load sensor by use of a chirped Moiré fiber Bragg grating. Appl. Opt. 2004, 43, 6454–6457. [Google Scholar] [CrossRef] [PubMed]
- Shu, X.; Chisholm, K.; Felmeri, I.; Sugden, K.; Gillooly, A.; Zhang, L.; Bennion, I. Highly sensitive transverse load sensing with reversible sampled fiber Bragg gratings. Appl. Phys. Lett. 2003, 83, 3003–3005. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Fang, G.; Liu, X.; Huang, J. Optical Interferometric Pressure Sensor Based on a Buckled Beam With Low-Temperature Cross-Sensitivity. IEEE Trans. Instrum. Meas. 2018, 67, 950–955. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, Y.; Zhu, C.; Gerald, R.E.; Huang, J. Probing changes in tilt angle with 20 nanoradian resolution using an extrinsic Fabry-Perot interferometer-based optical fiber inclinometer. Opt. Express 2018, 26, 2546–2558. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Du, Y.; Gerald, R.E.; Tang, Y.; Huang, J. An Optical Interferometric Triaxial Displacement Sensor for Structural Health Monitoring: Characterization of Sliding and Debonding for a Delamination Process. Sensors 2017, 17, 2696. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Chen, Y.; Zhu, C.; Zhuang, Y.; Huang, J. An embeddable optical strain gauge based on a buckled beam. Rev. Sci. Instrum. 2017, 88, 115002. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Chen, Y.; Du, Y.; Zhuang, Y.; Liu, F.; Gerald, R.E.; Huang, J. A displacement sensor with centimeter dynamic range and submicrometer resolution based on an optical interferometer. IEEE Sensors J. 2017, 17, 5523–5528. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, G.D.; Yuan, L.; Sun, W. Composite-cavity-based Fabry-Perot interferometric strain sensors. Opt. Lett. 2007, 32, 1833–1835. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Yu, Q. Wide-range displacement sensor based on fiber-optic Fabry–Perot interferometer for subnanometer measurement. IEEE Sens. J. 2011, 11, 1602–1606. [Google Scholar] [CrossRef]
- Xiao, G.Z.; Adnet, A.; Zhang, Z.; Sun, F.G.; Grover, C.P. Monitoring changes in the refractive index of gases by means of a fiber optic Fabry-Perot interferometer sensor. Sens. Actuators A Phys. 2005, 118, 77–182. [Google Scholar] [CrossRef]
- Huang, Y.; Wei, T.; Zhou, Z.; Zhang, Y.; Chen, G.; Xiao, H. An extrinsic Fabry–Perot interferometer-based large strain sensor with high resolution. Meas. Sci. Technol. 2010, 21, 105308. [Google Scholar] [CrossRef]
- Al-Saleh, S.A.; Al-Zaid, R.Z. Effects of drying conditions, admixtures and specimen size on shrinkage strains. Cem. Concr. Res. 2006, 36, 1985–1991. [Google Scholar] [CrossRef]
- Schmidt, M.; Fürstenau, N. Fiber-optic extrinsic Fabry–Perot interferometer sensors with three-wavelength digital phase demodulation. Opt. Lett. 1999, 24, 599–601. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Chen, Y.; Zhuang, Y.; Tang, F.; Huang, J. An Embeddable Strain Sensor with 30 Nano-Strain Resolution Based on Optical Interferometry. Inventions 2018, 3, 20. https://doi.org/10.3390/inventions3020020
Zhu C, Chen Y, Zhuang Y, Tang F, Huang J. An Embeddable Strain Sensor with 30 Nano-Strain Resolution Based on Optical Interferometry. Inventions. 2018; 3(2):20. https://doi.org/10.3390/inventions3020020
Chicago/Turabian StyleZhu, Chen, Yizheng Chen, Yiyang Zhuang, Fujian Tang, and Jie Huang. 2018. "An Embeddable Strain Sensor with 30 Nano-Strain Resolution Based on Optical Interferometry" Inventions 3, no. 2: 20. https://doi.org/10.3390/inventions3020020
APA StyleZhu, C., Chen, Y., Zhuang, Y., Tang, F., & Huang, J. (2018). An Embeddable Strain Sensor with 30 Nano-Strain Resolution Based on Optical Interferometry. Inventions, 3(2), 20. https://doi.org/10.3390/inventions3020020