1. Introduction
Demand-side management (DSM) usually refers to the control of energy consumption by the utility company at the customer side. It relies on the two-way communication and energy transmission capabilities of the future smart grid [
1]. For a thorough review of game-theoretic approaches to DSM, please refer to [
2]. Furthermore, Pilz et al. [
3] comprises recent advances based on local energy-trading scenarios. In general, the main objective of such programs is to decrease the consumption during peak times and thus reduce the costs that are associated with peak loads [
4]. On the one hand, the practical implementation can be direct (i.e., through smart meters that shift high-power household appliances based on signals from the utility company). On the other hand, the utility company can indirectly incentivise the users to shift these loads themselves by time-of-use tariffs. Within these tariff schemes, the price per energy unit changes depending on the aggregated load of all users (cf. [
5,
6,
7]). Both ways can lead to a reduction of the peak-to-average ratio (PAR) in load, which in turn increases the stability and power quality of the grid [
4].
Several such scenarios have been studied in the past and show great potential [
5,
8,
9,
10]. However, there remains one issue: all of them interfere with the routines of users, who might not want to give away the freedom to run their appliances whenever they want. The tradeoff between comfort and energy costs has been addressed, for instance, in [
11]. In their study, they show that the amount of savings from the energy bill reduces by more than half of the optimum when acceptable comfort levels are preserved.
In this paper, we investigate a scenario that does not interrupt the habits of the customers. Instead of shifting the loads directly, autonomously managed battery storage systems can be employed to achieve the same net effect. The idea is not new, but has been pushed forward, for instance, in [
12,
13,
14]. Within the idea of using the battery system as a load-shifting tool, it is essential to have a high-quality battery model. This is what was so-far lacking in the literature, but is now provided in our manuscript. In this sense, our work can be seen as an extension to [
12], where a more realistic battery model replaces the one used in [
12]. Only when all inherent characteristics of the whole system are incorporated can an insightful analysis be done. In fact, we will see that with an advanced battery model the outcome of the game changes drastically. Thus, our contributions are the following:
introduction of a detailed model for lithium-ion batteries, including the specific charging, discharging, and self-discharging characteristics,
analysis of the influence of the efficiency parameters of the battery on the PAR value and the resulting savings for each household, and
analysis of the participation behaviour in the proposed battery scheduling game.
The paper is organised as follows. In
Section 2, we introduce the models that constitute the scenario. This includes a detailed description of the battery characteristics, definitions of demand and load of a household, and an overview of the time-of-use tariff that determines the energy costs. For details on the scheduling game and an analysis of the existence of a solution, please refer to
Section 3. This also includes the algorithm employed throughout our simulations. Results are shown and discussed in
Section 4. The final section concludes the paper and reveals directions of future research.
2. The System Model
Consider a smart grid neighbourhood of households who take part in a DSM program. They are equipped with individual energy storage systems in the form of lithium-ion batteries. The model introduced in this section may also be used to represent lead–acid battery systems, but is not suitable for nickel-based batteries due to their different charging behaviour. Nevertheless, in the following we will only refer to lithium-ion batteries as they generally show better specific energy and cycle efficiency compared to lead–acid batteries [
15]. This makes them the superior battery system for the purpose of a DSM program.
In this section, we will detail the specific characteristics of such batteries, clarify the terms ‘demand’ and ‘load’, and introduce the pricing model.
2.1. Battery Model
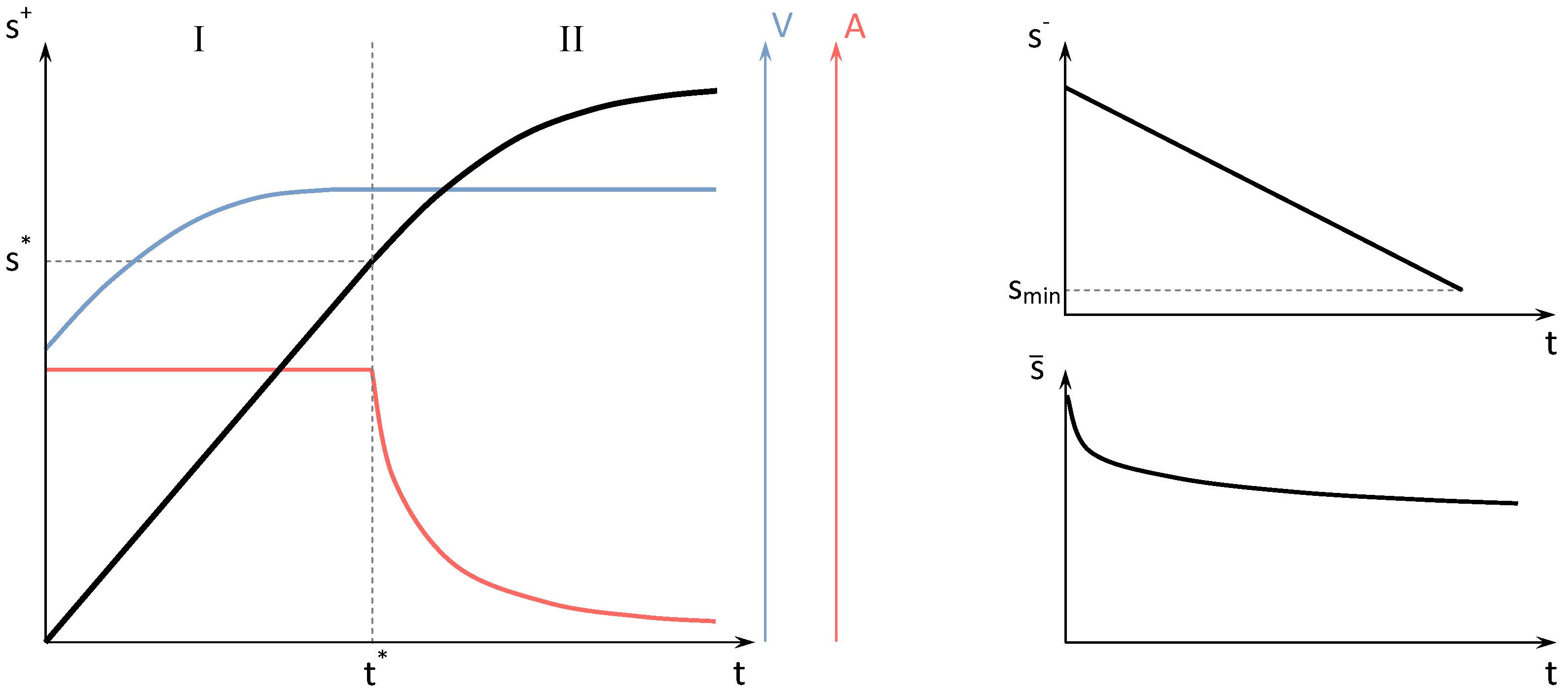
Charging a lithium-ion battery is a two stage process [
16] (cf.
Figure 1).
The first stage is characterised by a “constant current” process, whereas the second stage applies “constant voltage”. Within the constant current stage we have a constant charging rate
, and thus linearly increase the amount of stored energy in the battery. The cell voltage is following this trend, but tapers off towards its terminal cell voltage. Let the capacity at this point be denoted by
. Once this value is reached, the second stage is initiated, where the voltage is kept constant. As a result, the charging current drops off exponentially. The battery is fully charged when the charging current reaches a pre-defined value of approximately ten percent of the charging current in stage I. For the charging rate
this implies that it also levels off exponentially. We summarise the change of stored energy
during the two stages of the charging process by:
where
is the charging efficiency with
and
is the maximum capacity. The parameters
and
are chosen such that the capacity curve and its derivatives are continuous at
.
When discharging a lithium-ion battery, the operating voltage (given a fixed current) behaves as shown in [
16,
17]; i.e., with an almost constant value for a wide range until it drops off sharply at low capacities. According to this, we consider a constant discharging rate
until a lower limit
is reached
where
is the discharging efficiency with
. Discharging the battery below
is prohibited for the user within our model (cf.
Figure 1).
If the battery is neither charged nor discharged, it will still lose capacity due to self-discharging. We model the effect with an exponential decrease of the capacity
where
is the self-discharging rate.
2.2. Household Demand and Load
The set of households who participate in the DSM program is denoted by . The total number of participants is . We define the energy demand of a household as the amount of energy that is needed to run all its appliances at time interval . The total daily schedule of unshiftable demand is then . This demand does not include any action of the battery.
Let
denote the load, which is defined by the amount of energy that is drawn from the grid by household
n at at time interval
. It combines the energy demand with the amount of energy that is charged or discharged by the battery; i.e.,
where
is obtained from suitable integrals of the charging and discharging curves (
1) and (
2). Note that
for all intervals, as the amount discharged from the battery cannot be larger than the demand in the respective interval. We write
for the schedule of loads and can calculate the total load on the grid at time interval
by
2.3. Cost Model
We model one utility company that serves all the households in the neighbourhood. In order to incentivise the users to avoid consumption during peak hours, a time-of-use tariff is employed. The costs per energy unit is calculated separately for each interval and depends on the aggregated load of all users. Similar to [
8,
11,
18], we want to employ a quadratic cost function
; i.e.,
where
y is the aggregated load at time
t given by
and the coefficients
,
, and
.
3. The Battery Scheduling Game
In this section we formulate the non-cooperative game between the households. To be more precise, we describe a battery scheduling game in which players want to minimise their energy bill by shifting loads through their respective battery usage. Here, we detail the possible actions for each participant and clarify the relation between the cost function and the utility function of the game. This is followed by an analysis of the existence of a solution. We also present the iterative algorithm that is employed to find this solution.
3.1. Game Formulation and Equilibrium Analysis
In this day-ahead scheduling game, an action of player
is described by schedule
of battery activities
. In particular there are four options
can represent per interval:
Based on (
4), we can calculate a corresponding load schedule
for each action
. Actions are deemed unplayable if they lead to invalid battery states; i.e., charge states that do not fulfil the requirements given in
Section 2. The fact that there are two possibilities to charge the battery gives more flexibility for the user.
The utility function
reflects the bill player
n has to pay for the upcoming day, given that they chose action
, while their opponents chose the actions
. Similar to [
5,
8], we employ a proportional billing scheme, where every player pays for the share of their consumption:
with
To sum up, we define the non-cooperative battery scheduling game , with
One can show that there exists a pure Nash equilibrium (NE) for this game. The proof can be done similarly to the one in [
12] (Theorem 1), due to the similarity of the structure of the utility functions, the properties of the actions sets, and the fact that the demand
is bounded.
3.2. Numerical Solution
The solution to the game (i.e., a NE) is computed by a best-response algorithm (cf. Algorithm 1). Through empirical studies, we found that there are usually many different NEs for each daily configuration. This is why the algorithm contains the additional
do-loop in comparison to the “myopic best-response” algorithm [
19].
| Algorithm 1: Best-response algorithm for finding a pure NE based on [19] |
![Inventions 02 00030 i001]() |
Choosing the best NE is done by comparing the sum of the utility functions for every player. Please note that even when the existence of a pure NE is guaranteed, the algorithm might not converge to it. An additional counter variable prevents getting stuck in an infinite while-loop. Nevertheless, this exit condition was not triggered in any of our simulation runs.
4. Simulation Results and Discussion
In this section, the data set and system variables that constitute the DSM scheme with a battery scheduling game are presented. The simulation results based on these are subsequently shown and discussed.
4.1. Data and Variables
The household consumption data for all our simulations stem from the openei dataset [
20]. This dataset contains 365 days of simulated hourly demand data for all TMY3-locations in the USA [
21]. Details on the building models can be found in [
22]. Additionally, the “Residential Energy Consumption Survey” was used to associate suitable building types with each location. There are three categories: BASE, HIGH, and LOW based on the specific attributes of the respective household [
23].
For our simulations, we picked
households (i.e., nine BASE, nine HIGH, and seven LOW) that are all within close vicinity to represent a small neighbourhood. In order to gain insight into seasonal effects, we chose four equally separated weeks from the data set—in particular weeks 12, 25, 38 and 51—and used it to represent the individual household demand. Nevertheless, the scheduling is done on a day-ahead basis as described in
Section 3.1. To this end, we set
; i.e., consider two-hour intervals, and initialise the battery at the beginning of the week with a small random capacity. From the NE, the battery states at the end of the day can be calculated and are used as initial data for the following day.
The parameters of the battery are inspired by the
Tesla Powerwall 2 [
24] data sheet, and can be found in
Table 1.
The efficiency variables
and
are calculated under the assumption that charging and discharging contribute to equal amounts towards the given round-trip efficiency of
. We denote this type of battery by the “realistic” battery (RB) model. For comparisons, we also run all the simulations with an “ideal” battery (IB) model; i.e., the same storage system but with
. We want to highlight that the IB still follows the proposed charging and discharging curves shown in
Figure 1 and is also subject to self-discharging. Within the cost function (
6), we use the coefficients
$/MW
,
$/MW, and
[
25].
4.2. Results
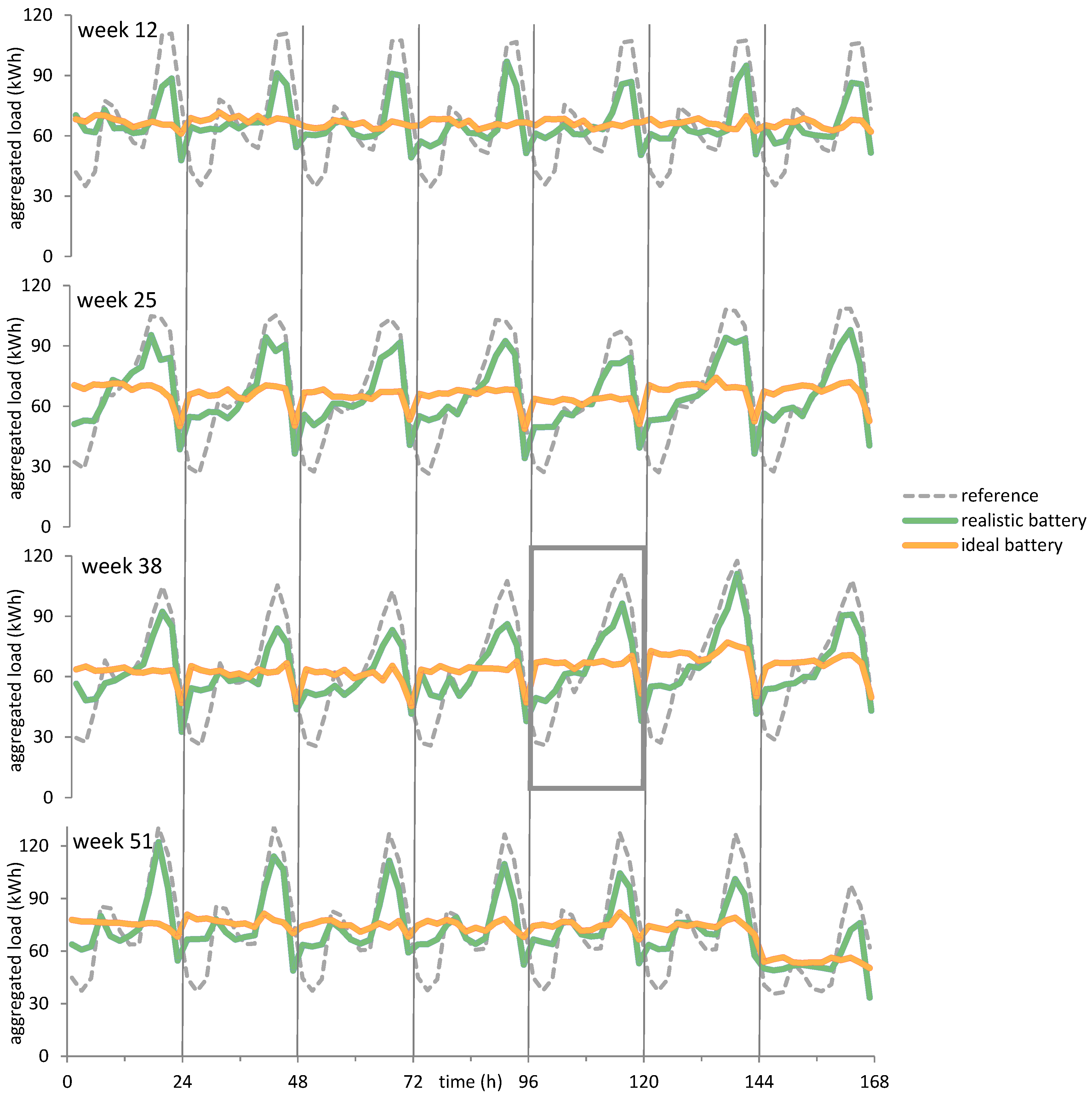
In
Figure 2, the aggregated load curves resulting from playing the game with different battery models are shown—one of them with realistic parameters and the other with ideal 100% efficiency (see
Section 4.1). The reference curve represents the aggregated load of the system without the battery scheduling game.
For a quantitative analysis of the load-shifting phenomenon, and since our aim is to reduce consumption during peak times, we look at the peak-to-average ratio (PAR) of the aggregated load for each individual day; i.e.,
The averages over the seven days of the respective weeks are shown in
Table 2.
On average, a 14% and a 36% decrease of the PAR value was achieved by employing a game with an RB and IB model, respectively.
When considering the participation behaviour of the households, we look at two things: (i) the rate at which players choose to play any action other than the
zero-schedule
in the Nash equilibrium (cf. (
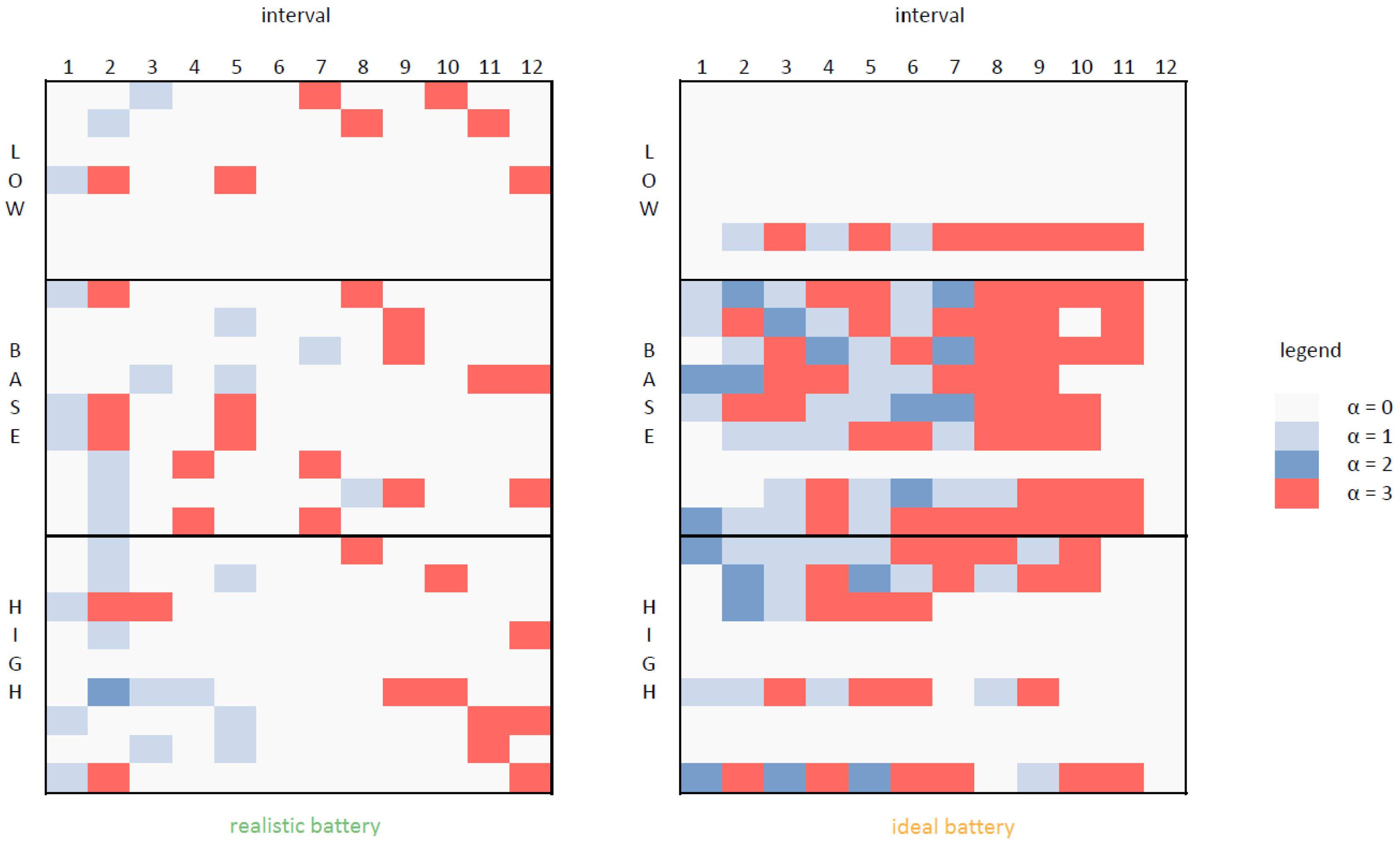
7)); and (ii) the distribution of activities chosen for each individual interval. A visualisation of the schedules of a randomly chosen day (week 38, day 5) is shown in
Figure 3 for both battery models. It can be seen as a representative example of the schedules for all other days. A summary for the different user classes of the participation rate and the activity distribution can be found in
Table 3 and
Table 4, respectively.
Table 5 shows by how much the utility function of the consumers, i.e. the energy costs for each of them, was reduced. The results for each of the four different weeks are averaged over the consumer categories for both battery models.
4.3. Discussion
4.3.1. Peak-to-Average Ratio
By playing the game the usual evening peaks of each individual day were decreased. This effect was stronger for simulation runs that apply an IB model, where an almost flat load profile was produced. Troughs are visible at the end of several days (e.g., in weeks 25 and 38) due to a finite-horizon effect that occurs when the aggregated demand during the final interval is lower than the average load in the previous intervals. This results in the players choosing to play
in the respective interval, see
Figure 3. As the load can only be increased by charging the battery, this would have caused an increase in costs (for this day) and thus would not have been beneficial for the players.
From our results we see the importance of the battery efficiency for reducing the PAR value. In fact, our research has shown that the cycling efficiency is the most sensitive parameter of all parameters introduced in
Section 2.1 [
26]. With state-of-the-art technology such as the
Tesla Powerwall 2 [
24], the PAR value was reduced by
to
. Under the assumption of an IB, PAR values close to the optimum were achieved (i.e., a reduction of
). It is worth highlighting that these results do not seem to depend on seasonal effects, as fluctuations of PAR values between the four simulated weeks were less than
.
4.3.2. Participation in the Game
We observe that the participation rate was higher overall for the RB model. Nevertheless, the players who did participate in the IB scheduling game were more active; i.e., chose more activities
. It becomes apparent that the lack of efficiency causes a disincentive to charge the battery for many users. While charging for shorter time periods (i.e.,
) was still occasionally done during low-demand intervals, charging throughout the whole interval (i.e.,
) was almost non-present in the NE schedules. None of the LOW households with an RB made use of this activity within any of the 28 simulated days (cf.
Figure 3 and
Table 4).
4.3.3. Utility Function
In direct relation to the smaller PAR value reduction of the game with RB model is the smaller reduction in energy costs (see
Table 5). Similar to results regarding the PAR value, we observe that there seems to be no seasonal dependency. Furthermore, within each separate week, the differences between the three consumer classes is negligible. This was anticipated and intentionally pushed forward by the introduction of the proportionality factor
in the utility function (
8). It should be noted that the pricing scheme benefits all users whether they participate in the DSM scheme or not. A tariff that gives a higher share of savings towards the contributors might be a fairer approach.
5. Conclusions
In this paper, we proposed an advanced battery model for a DSM program: residential customers play a battery scheduling game to decrease their own costs which eventually reduce the PAR value of the aggregated neighbourhood load. The advantage of this approach is that every household can make its own decision, thereby addressing concerns of individual freedom.
It turns out that the round-trip efficiency of the storage system has an impact on the participation behaviour. In fact, it lowers the PAR reduction by more than half of what can be achieved by a system with perfect efficiency. This is accompanied by a lower reduction in energy bills for all participants. Thus, our studies underline the importance of further advancements in battery technology. One way of compensating for the imperfect efficiency of the storage system might be the introduction of a more advanced billing scheme. In the current framework, participants react to a given pricing policy, which causes a PAR reduction. In a reverse scheme, participants could be incentivised to reduce the PAR value directly and are granted cost reductions based on their respective success.
Other future research directions may include the incorporation of on-site renewable energy generation for individual participants and a thorough analysis of the life-cycle costs of the proposed system.