1. Introduction
The first sustained nuclear chain reaction was conducted within the Chicago Pile (CP-1), located underneath the University of Chicago’s Stagg Field in 1942. Since then, the scientific value of the subcritical pile grew significantly during the first era of nuclear energy research but now appears to have dwindled from the nuclear community [
1].
There are three known subcritical piles located at universities throughout the United States, which strictly act as an educational tool or have limited research use [
2]. In late 2023, the pile located at Purdue University was rearranged to accommodate a testbed to explore how thermal neutrons could affect the performance of microelectronics. Prior to the inclusion of the testbed, the pile was well categorized by students and professors; however, the construction of the pile originally prevented any appreciable size of testing material from being placed within the pile. The inclusion of the testbed establishes a testing volume of approximately 1.5 × 10
5 cm
3, which exceeds that of any pile in the United States and of many test reactors that also exist in the university setting.
While the testbed was originally designed and constructed with the goal of testing the performance of commercial off-the-shelf microelectronics under neutron and gamma irradiation, the potential research uses extend beyond this topic of interest. An example that has received much attention within the nuclear community is the potential for limited isotope production via neutron activation under 1 Ci for research and educational purposes [
3,
4], both of which could have significant commercial and military applications.
Before the testbed can be used in any experimental capacity, it is important to quantify the spatial and energy distribution of neutrons and gammas, internal and external to the testbed. These values allow for the identification of maxima and minima that may justify an experimental setup and optimization. The subcritical pile neutron flux can be obtained using metallic foils that are activated and then measured for subsequent gamma decay. A secondary approach is the use of open-source Monte Carlo (MC) simulations to model the geometries of the pile to a high degree of fidelity [
5]. One advantage of the MC methods is the production of large data sets that can be used for educational purposes or training and testing machine learning and artificial intelligence algorithms [
6].
This article discusses the testbed design and construction, test methods, and data used to conduct metal foil neutron analysis to quantify the total flux within the pile and thermal/epithermal neutrons within the volume of the testbed. Two high-fidelity Monte Carlo models of the subcritical pile were produced using MIT’s OpenMC and MCNP6.3 software and then benchmarked using the obtained experimental metal foil measurements. The overall purpose is to classify the modified Purdue subcritical pile in the current testbed configuration to support its role as a scientific instrument for the future testing and modeling of radiation environments.
2. Literature Review
Perhaps one of the most comprehensive resources for subcritical assemblies within the United States can be found in the 1961 Proceedings of the University Subcritical Assembly Conference. In this document, there are works from several universities across the nation covering the then-ongoing research. The fundamentals of subcritical multiplication, nuclear diffusion theory, and construction details are discussed. The dimensions of the Purdue subcritical pile in its original configuration are listed in the Proceedings. One important detail that can be derived from the graphite-moderated pile section is the analytical solution to the diffusion theory for thermal neutrons. The cosine function is used as a baseline for the experimental methods presented in this article [
7].
While subcritical piles have been largely written off as only a tool to teach undergraduate students about basic neutrons, a team at MIT recently made use of their graphite pile to produce a data-driven control system. This project was sparked by the interest of the NRC and other nuclear regulators seeking the ability of artificial intelligence to control reactors. The research team highlighted the inherent safety of subcritical multiplication in the design system for training their algorithm and ultimately developing a digital twin. They reported that their artificial neural network could accurately predict the position of their initiating control rod within 2.5 cm with a 95% confidence interval [
8].
Another recent study made use of a subcritical pile in Japan to conduct material testing on a fuel plate consisting of U-7Mo, a depleted uranium and molybdenum fuel that has caught the attention of non-proliferation advocates for possible refueling efforts in research reactors. The paper provides neutron flux measurements but highlights the need for additional reactor physics studies [
9]. However, the significance of this work is the use of subcritical piles to evaluate new reactor fuel sources and structural materials without the need for building large testing facilities [
9].
The Purdue subcritical pile has also recently been used to evaluate the performance of the Defense Threat Reduction Agency’s Scatterable Radiation Monitor (SCRAM) while under a gamma and neutron flux. The purpose of the SCRAM is to act as a Department of Defense tool for real-time environmental dose readout. The inspiration for placing the SCRAM into the pile was to determine if the environment in which the electronics are subjected to would cause a degradation of the accuracy of the data. While it was ultimately determined that the neutron flux was not significant enough to damage the SCRAM to any substantial degree, the rearranged pile was determined to be a useful tool in conducting microelectronic tests under low-to-medium thermal neutron flux [
10].
In addition to experimental measurements, Monte Carlo numerical methods are often used to model the radiation environments that electronics are subjected to. One such example is the use of the Monte Carlo Neutron Particle transport (MCNP) to model the fast neutron environment of the University of Texas at Austin’s TRIGA reactor for testing analog–digital converters. Similarly to the experiment outlined in this article, the thesis compares the results of activated foil measurements to the output of the MCNP for the validation of the environment. This is then used to classify the mechanism of damage to microelectronics. The author argues for the use of both experimental and numerical methods to reinforce the results of one another [
11].
While the MCNP is often regarded as an industry standard for modeling Monte Carlo methods, it is also an export-controlled software, which hinders the ability of some users to apply for a license. With this problem in mind, a team at MIT produced OpenMC [
12]. An open-source, Python 3.13.0-based program for rivaling the MCNP. There are several advantages to OpenMC over MCNP, but OpenMC has yet to receive the same widespread industry use as its counterpart. Several comparison studies have been conducted, many of which provide evidence that OpenMC can be used as a replacement for the MCNP. However, this statement should receive some scrutiny in that these studies consider the one nuclear scenario of many possible scenarios that can be modeled, where one software may outperform the other. At least for common applications, OpenMC may offer a reliable substitute [
5,
13,
14].
3. Modified Subcritical Pile Testbed
Pile Geometry
The subcritical pile is a repeating matrix of rectangular prism graphite and fuel. Natural uranium fuel rods in aluminum cladding are placed inside graphite blocks, combining a total of 90 fuel–graphite joint blocks. Another 247 blocks of only graphite are placed inside as well. Together, they form the subcritical pile, measuring 179 cm in length, 260 cm in height, and 179 cm in depth. A cadmium sheath surrounds the whole pile to reduce thermal neutron flux in the worker space. One Americium-Berylium (AmBe) source of ten Ci and four Plutonium-Berylium (PuBe) sources of 1 Ci each are placed in the pile. These sources are used to emit neutrons inside the pile, initiating and later controlling the fission reaction in the subcritical pile. The AmBe source has a neutron yield of 2.0–2.4 × 10
6 n/(s × Ci), while each PuBe source has a neutron yield of 1.5–2.0 × 10
6 n/(s × Ci) [
7].
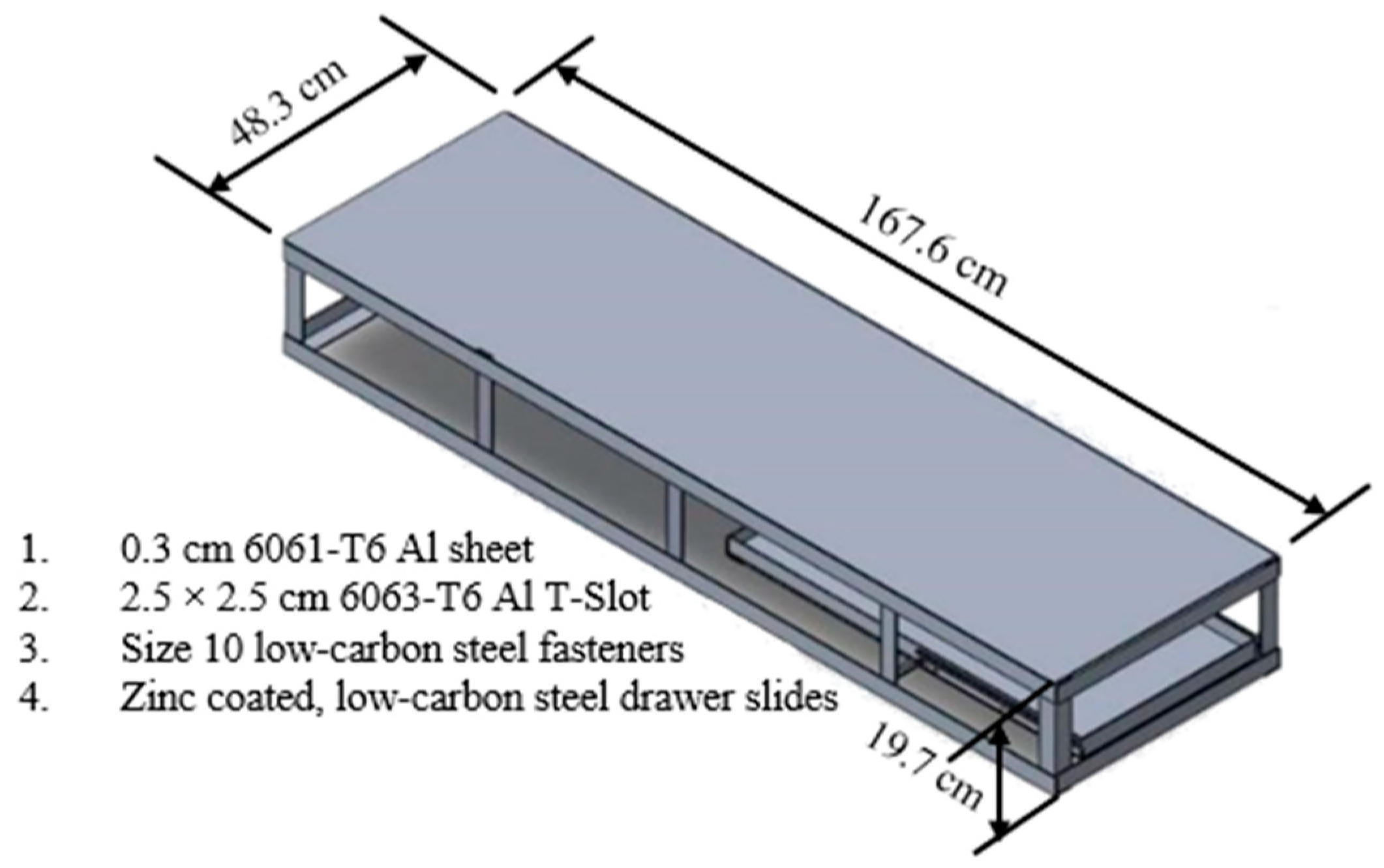
The chief addition to the pile is the rectangular testbed near the upper center of the Z and X planes. This feature was added to the pile in late 2023 and is the focal point of what differentiates the Purdue subcritical pile from others. The testbed dimensions are 45 cm × 20 cm × 162 cm, and the limiting constraint was set to ensure minimal disruption to the original pile configuration. In addition to the testbed volume, there is a removable platform on drawer slides to allow for the easy placement of test materials. The platform minimizes the potential for contamination from test materials and minimizes the dose to technicians while conducting measurements. The platform is roughly the same width as the testbed but has half of the depth into the pile. This design feature was selected due to the placement of the neutron sources near the front face of the pile relative to the personnel working space.
Figure 1 displays the front and isometric views of the pile.
In addition to volume consideration for the testbed, the secondary concern was the potential for creating long-lived radioactive material. To prevent undesired waste, aluminum was selected as the structural material. While the potential for the activation of Al-27 is not low (0.231 b), the half-life of Al-28 is 2.3 min, classifying the material as a short-lived isotope. The hardware of the testbed, to a reasonable degree, is low-cobalt steel. Construction materials were selected for metals that had a low cross-section for absorption and subsequent activation; as a result, the bulk of the testbed is aluminum, thus minimizing the production of long-lived waste. A 3D SolidWorks rendering of the testbed is shown in
Figure 2. The testbed integrated into the pile from the working face is shown in
Figure 3.
4. Methods
4.1. Neutron Interactions
Neutrons interact with the nuclei of target materials via scattering or absorption reactions. The methods outlined in the ASTM Standard E262-17 are the basis of the analysis techniques presented in this work [
15,
16].
The specific isotopes being activated for neutron flux measurements are indium-115 and gold-197. The specific neutron activation reactions are given by reactions (1) and (2).
The gold reaction is straightforward, as it only has one naturally occurring isotope (Au-197), and it only activates to a single isotope (Au-198) with a singular photopeak of 411 keV. The cross-section for this reaction is 98.65 barns, assuming a complete thermal flux. The indium reaction is more complicated, as naturally occurring indium contains more than one isotope. Indium-113 is present in natural indium at 4.28% abundance, and indium-115 makes up the remaining 95.72% [
17]. Indium-113 activates to indium-114. With a half-life of 49.51 days, indium-114 is often not activated enough to be taken into consideration during neutron activation analysis. The final consideration to take into account is that indium-115 can activate into a metastable isotope. 79% of the time, indium-115 activates to indium-116 m with a half-life of 54.29 min, so the neutron absorption cross-section (202 barns) must be multiplied by 0.79 to yield the appropriate cross-section for this specific reaction (159.58 barns). The other isotope, indium-115, is activated into indium-116 and indium-116 m
2, which have half-lives of less than 15 s; therefore, it is important for those isotopes to decay before measuring the activities of any indium foils during neutron activation analysis [
16].
In a similar manner, neutrons are also captured by cadmium-113. This isotope has a large capture cross-section at 0.55 eV (2233 barns) when compared to surrounding energies. This makes it convenient to block thermal neutrons from reaching an activation foil by covering the foil with cadmium. The method of cadmium-covered activation foils is discussed extensively later in this work. Reaction (3) displays cadmium absorption [
16].
4.2. Metal Foil Neutron Activation
Au-197 (1.5 cm and 0.1 mm) and In-115 foils (2.5 cm in diameter and 0.25 mm) were activated in the subcritical pile to determine the neutron flux at different locations throughout, with an emphasis on the testbed region. Once activated, the gamma activity could be measured to determine the neutron flux at that location. Two regions of interest were considered, inside the testbed and throughout the pile.
Foils measured throughout the pile were placed in an aluminum tray. The tray extends the whole length of the pile and has 17 slots to place foils. Each slot has an aluminum covering and a label to ensure consistent placement and the safety of the handler. Due to having only nine indium-115 foils, they were placed in every other slot. Each foil was labeled with a letter that corresponded to the numbered slot they were placed in.
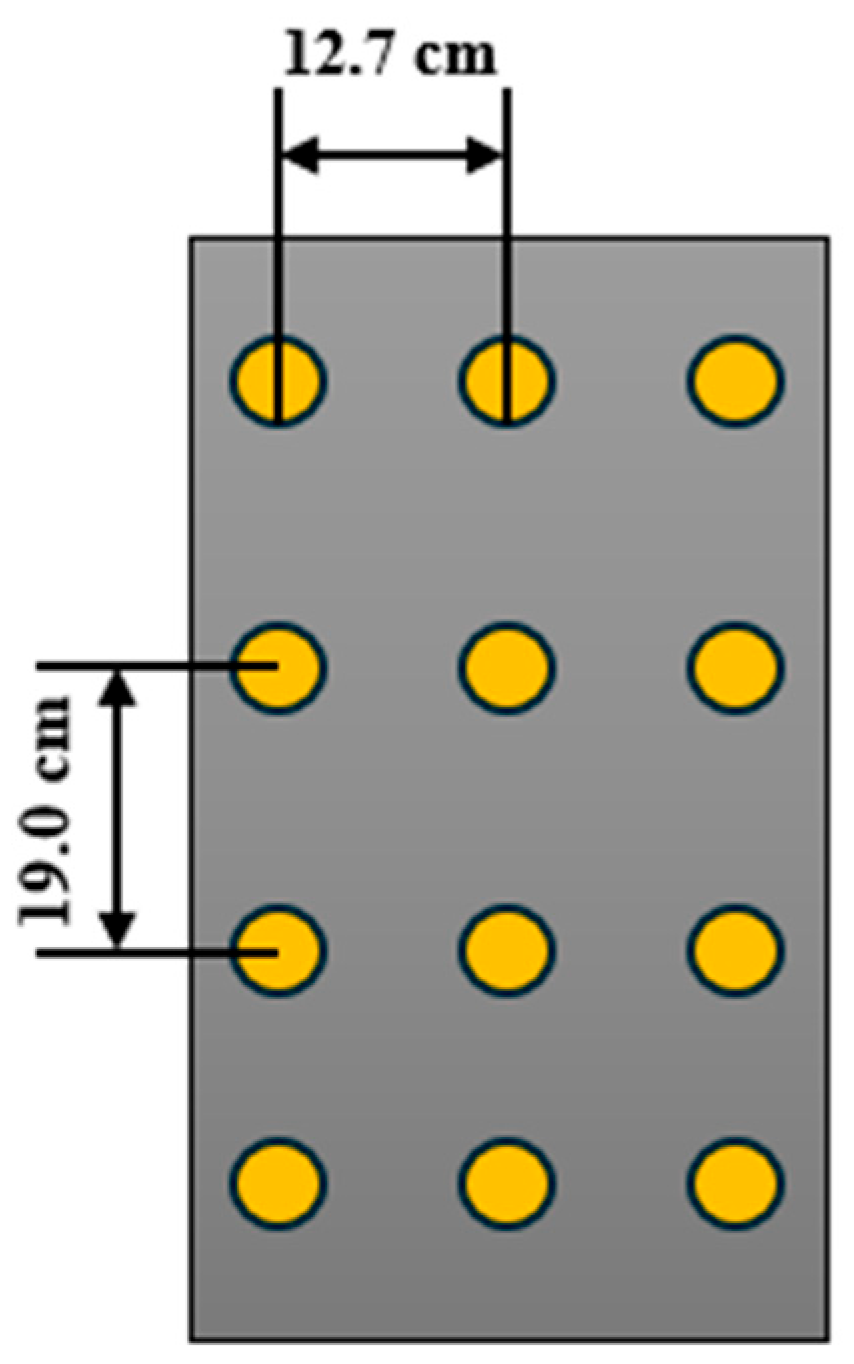
Foils for testbed measurement were set in various measured locations on the platform to be activated. There were several orientations, and the placement location was determined by taking the width and the length and then dividing by the number of foils in each respective dimension. For example, a layout of 3 wide by 4 deep was placed on the testbed described in
Figure 4.
All indium foils were activated in the pile overnight to ensure they approached saturation. Gold foils were activated for 14 days to approach the saturation condition. When being placed in the pile and removed, proper safety precautions were taken. The handlers wore a dosimeter to track their radiation exposure, as well as gloves to prevent contamination. When removing the foils from the pile, the long trays were taken out and moved to a separate room with the germanium detector. They were set on a desk on the opposite side of the room from the handler and the detector, still in the tray. When removing the foils from the testbed, tweezers were used to pick up and transport the foils to the detector. For indium, only one foil at a time was removed from the flux to prevent decay. However, the decay time of gold is sufficiently long, so this was not a factor.
4.3. Two-Group Neutron Profile
The measurement and subsequent calculation of two energy groups of neutrons require a two-foil approach. This is typically conducted through a cadmium–gold combination due to the neutron absorption cross-sections of the metals. In the thermal neutron energies (considered less than 1 eV for Cd), the neutron cross-section is at least two orders of magnitude larger than gold. A 1 mm thick 1 cm diameter cadmium cover over gold will attenuate 99% of the thermal neutrons [
18]. Thus, any gold activation is the result of epithermal neutrons.
Figure 5 displays the neutron cross-section for the absorption of the two metal foils and the cadmium covers.
The neutron flux calculation process requires the use of both cadmium-covered and bare foils. The measured activities of the bare foils (
Ab) and covered foils (
Ac), normalized for mass, are used to develop the cadmium ratio (
RCd), shown in Equation (4). The gamma-decay constant (
λ), activation time (
ta), cooling time (
tw), averaged neutron cross-section for absorption for thermal neutrons (σ
th), resonance integral of cadmium energy cross-section (
I0), thermal self-shielding (
Gth), and resonance self-shielding (
Gepi) are all required to calculate the thermal flux and epithermal flux, respectively, from Equations (5) and (7) [
16].
FCd is a convenience variable that is calculated in Equation (6).
There is a fast neutron flux present in the pile due to the fission sources, but for experimental measurements, it is assumed to be less than 1%. Subsequently, the energy range of epithermal neutrons is assumed to be between 2.5 MeV and 0.5 eV. All energies below the cadmium cutoff are assumed to be thermal. The resonance integral, thermal self-shielding factor, and resonance self-shielding factor were determined using the ASTM standard [
16]. These values are displayed in
Table 1.
4.4. Monte Carlo Pile Modeling
The entire subcritical pile was modeled using the Python language-based OpenMC software and the industry standard Fortran-based MCNP6.3. The geometry was measured and replicated in the software using the respective languages. Material assignments were conducted by referencing technical manuals from the pile construction. The source strength was defined by the known fission rate of the Am-Be and Pu-Be sources placed within the graphite channels of the pile [
22]. The geometry of the models is defined using constructive solid geometry (CSG), also sometimes referred to as combinational geometry. This is conducted by defining the regions of space where the neutron is either counted or discarded. It is important to note for this particular model that any physical void space within the pile was assigned to air at standard temperature and pressure. All regions outside the cadmium shield set the neutron importance to null and discarded the counts. Though each graphite cell and the testbed were modeled, the placement of count tallies hides these features in the model when displaying the neutron count for any given location.
While the inputs between the two codes vary slightly, all efforts were made to replicate the same input between the codes.
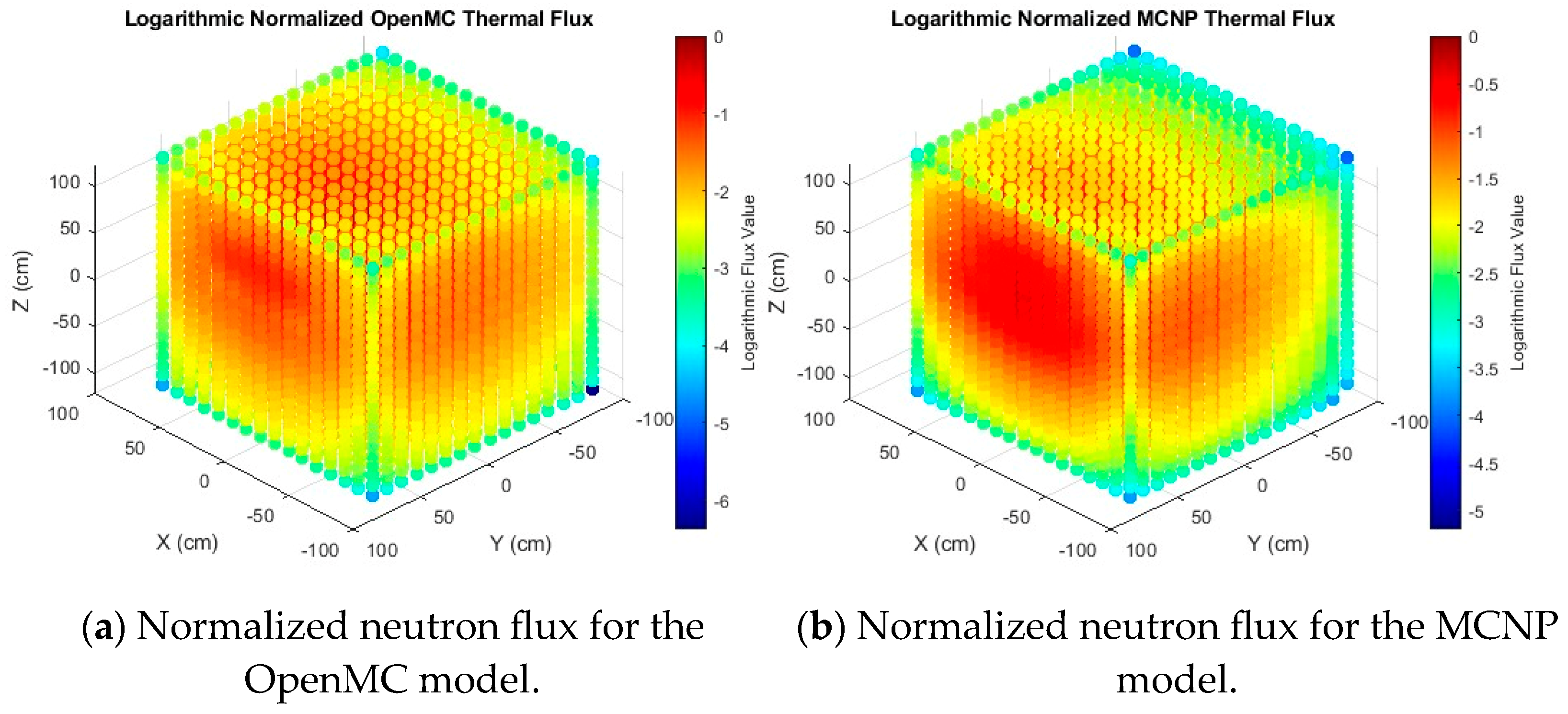
Figure 6 provides the output of the MCNP and OpenMC tallies for the pile as viewed from the working space of the testbed. The tallies were normalized to one for each respective model; then, the logarithmic value was plotted. It is important to note that tallies for the two models do not output the neutron flux directly, and their comparison to the experimental results cannot be made without considering the source strength. However, they are proportional to flux, and a normalization of both models and experimental results offers a convenient means of comparing the foils to a corresponding tally. Taking the logarithm aids in generating the visual comparison of only two Monte Carlo methods.
At first glance, it is evident that the OpenMC model is slightly cooler than the MCNP model. Evidence supports that while this effect is minimal, the AmBe and PuBe sources are handled differently between the two codes. This is more apparent when peering at the X-Y plane at Z = 30.48 cm, where the three sources are defined. This is displayed in
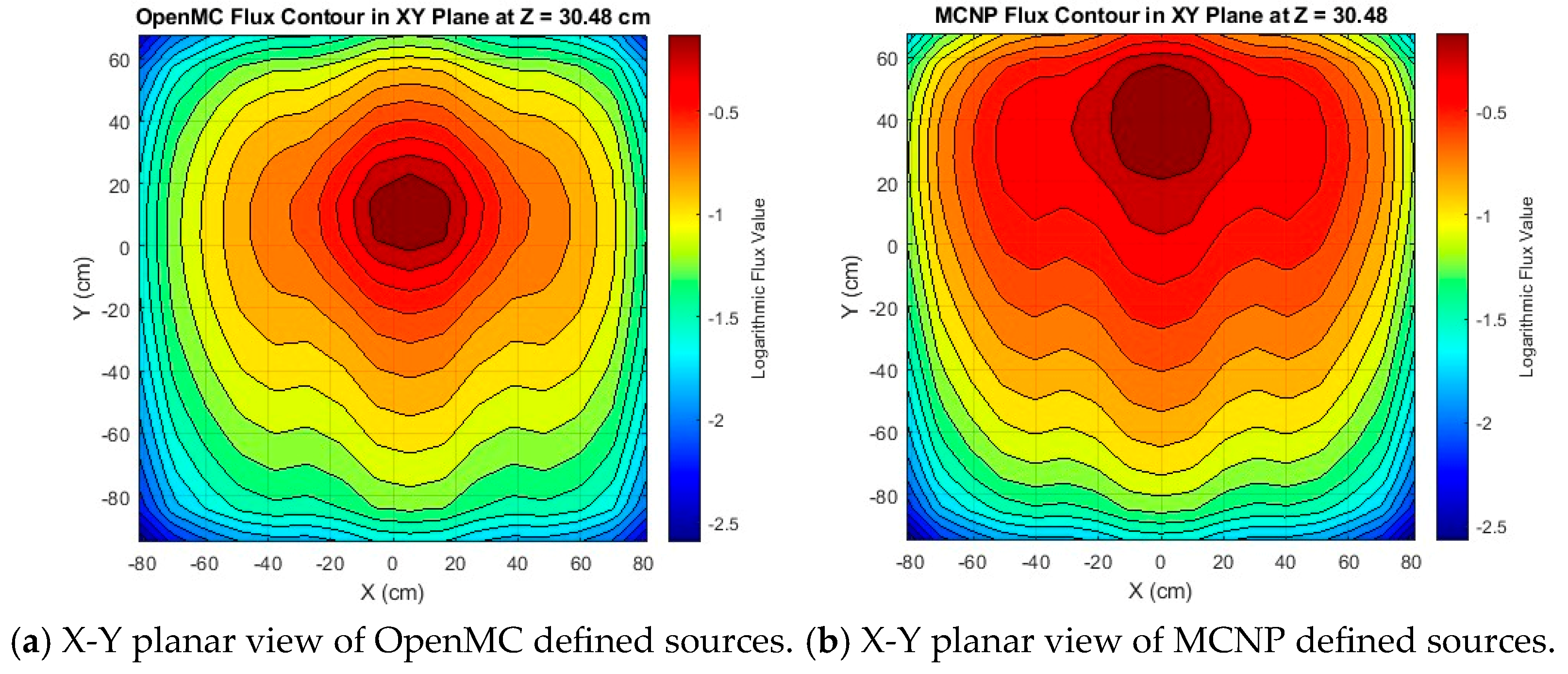
Figure 7, where the general flux profile is similar, but the OpenMC is slightly lower and concentrated about 15 cm offset from the MCNP.
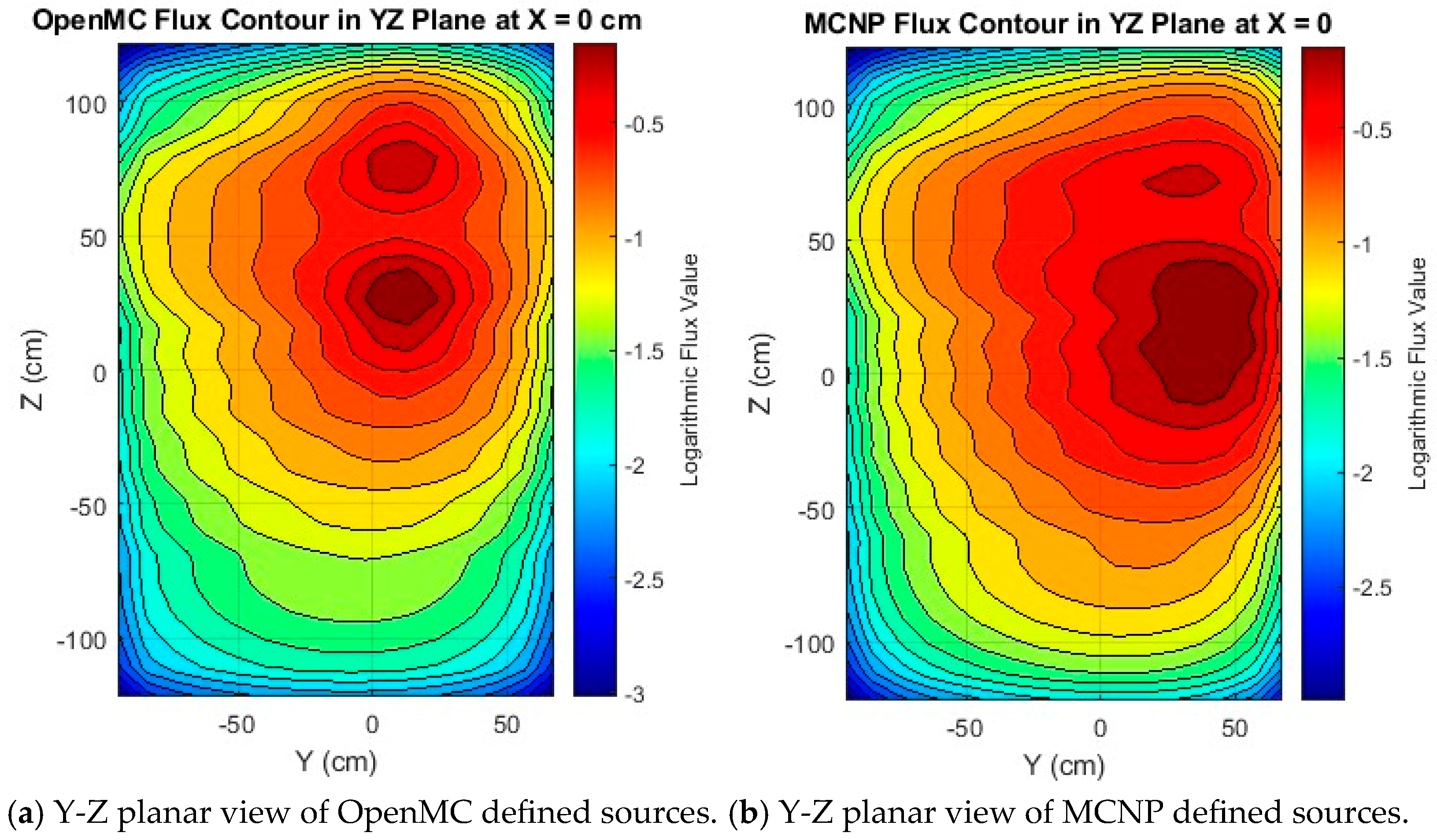
However, the flux contour in the Y-Z plane at X = 0 shows a slightly different perspective, where the upper set of sources, which is only PuBe, agrees better than the lower set. This suggests that OpenMC’s handling of the AmBe source is the basis for the difference in the models. These observations are displayed in
Figure 8.
Despite the slight deviation between the two Monte Carlo methods near the defined AmBe source, the general neutron flux profile is consistent. Because the testbed region exists between the two sets of defined sources in the Y-Z plane and has fair agreement between the two data sets, the models are taken as comparable. However, because the MCNP has a more historical use in the industry, it is taken as the more accurate model of the two. When analyzing neutron cross-sections and the energy profile, the MCNP model is considered.
5. Results
5.1. Detector Energy Calibration
The use of the Ametek Ortec HPGe (Oakridge, TN, USA) is standard among radiation detection experiments for its high energy resolution. Equation (8) displays the method for calculating energy resolution, where FWHM is the full width at half maximum. The ideal energy resolution as a function of energy follows the proportional relationship (9). Data produced from the HPGe measurements are found in
Table 2.
An energy calibration is conducted through the use of known gamma-emitting test sources. The HPGe in the following experiments made use of Na-22, Ba-133, Co-60, and Cs-137 to establish the near-linear channel-to-energy relationship. An ABS 3D-printed stand (10.8 cm above the endcap) was built for the general use of the HPGe to minimize the potential for endcap contamination. The gold experiments were conducted before the use of the stand.
Figure 9 displays the stand and measurement setup for indium and the placement of gold on the endcap.
Table 2 presents the measured resolution, and
Figure 10 displays the resolution graphed against the photopeak energy, where the measured values are in agreement with the expected values calculated through relationship (9).
The resolution is not particularly interesting in the scope of the measuring flux. However, it is an indicator that the HPGe detector is working properly. As a result, only the resolution at the stand is reported. It is important to note that placement does not affect the neutron flux results so long as the counts and absolute photopeak efficiency are considered from the same location.
5.2. Absolute Photopeak Efficiency
As is the case with all instruments, the HPGe detectors are not capable of detecting all of the radiation emitted from a source. Geometry, distance, energy, and imperfections in electronics make for a less-than-ideal counting space. The counting error is minimized by investigating the detector’s absolute photopeak efficiency as a function of gamma energy. Again, test sources are used for this calculation. However, the activity of the source must be brought to the current date. In these experiments, the activity of the sources was verified on 1 July 2003. Using the exponential decay Equation (10) and the half-life of the isotope of interest, the activity in decays/second could be determined for the date of the measurement.
The ratio of the activity measured by the detector and the current date activity at the particular photopeak is the absolute photopeak efficiency. These values must be calculated at the location where subsequent measurements are intended to be taken. The distance from the source to the detector face has a strong dependence on absolute efficiency. If there is a deviation from this practice, it is important to consider the distance of the source relative to the detector face to determine if the source should be treated as a point source or a planar source. A general rule is that any source greater than 10 cm is considered a point source.
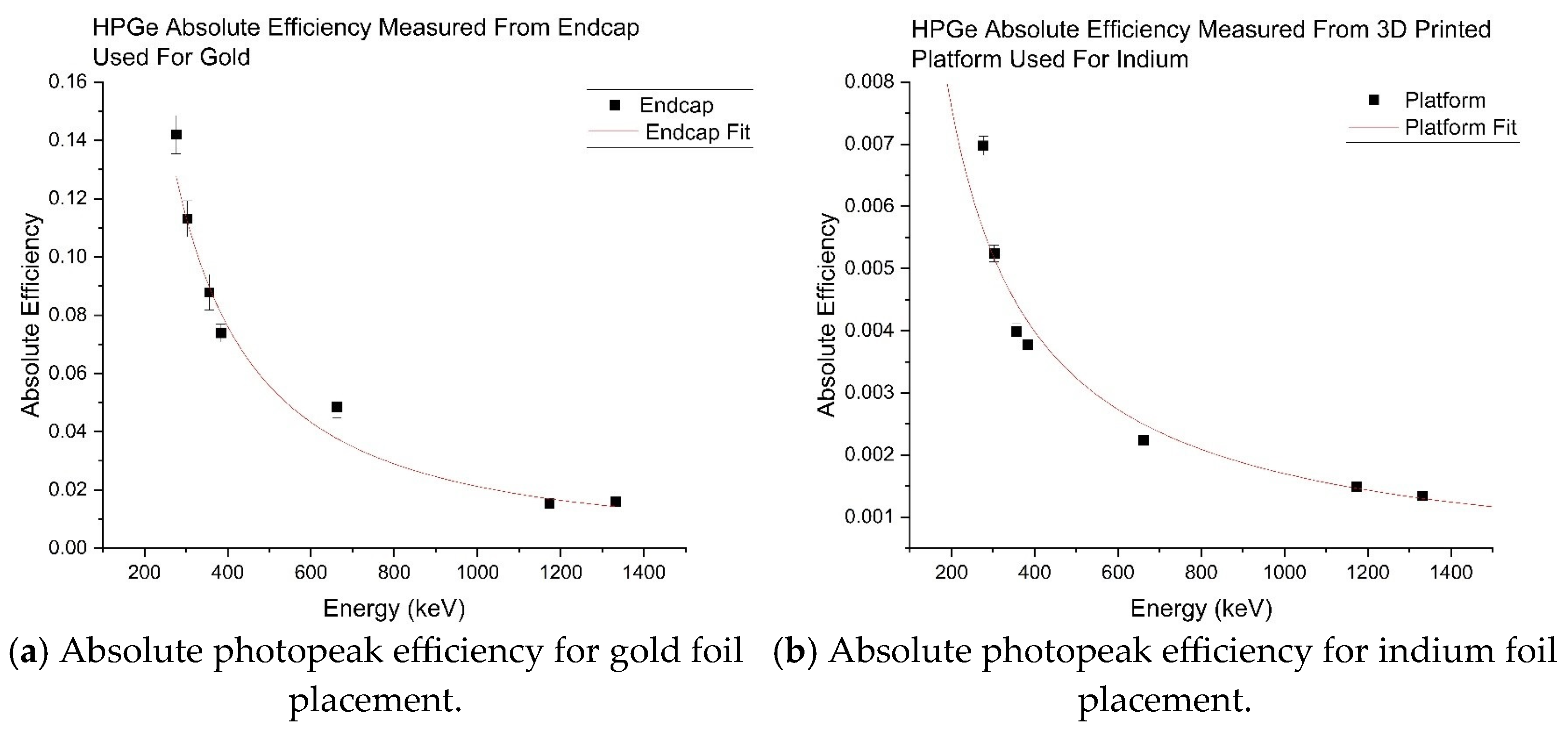
Figure 11 provides the measured absolute photopeak efficiency for the HPGe detector at the endcap and on the platform where the indium foils were measured. A curve was fitted that follows Equation (11) for the endcap and Equation (12) for the platform, where
ε is the absolute efficiency and
E is the gamma energy in keV.
It is common practice to curve fit the photopeak efficiency using a fifth-order polynomial per the ASTM E181 standard. However, this standard typically considers the low-energy gamma peaks below 300 keV. The analysis conducted in the report was not concerned with energies this low, so they were discarded. As a result, an exponential curve fit was more applicable. The curve used for gold has a bit more uncertainty due to the Cs-137 peak compared to the curve fit used for indium [
23].
5.3. Testbed Region Neutron Flux Measured by Indium and Gold
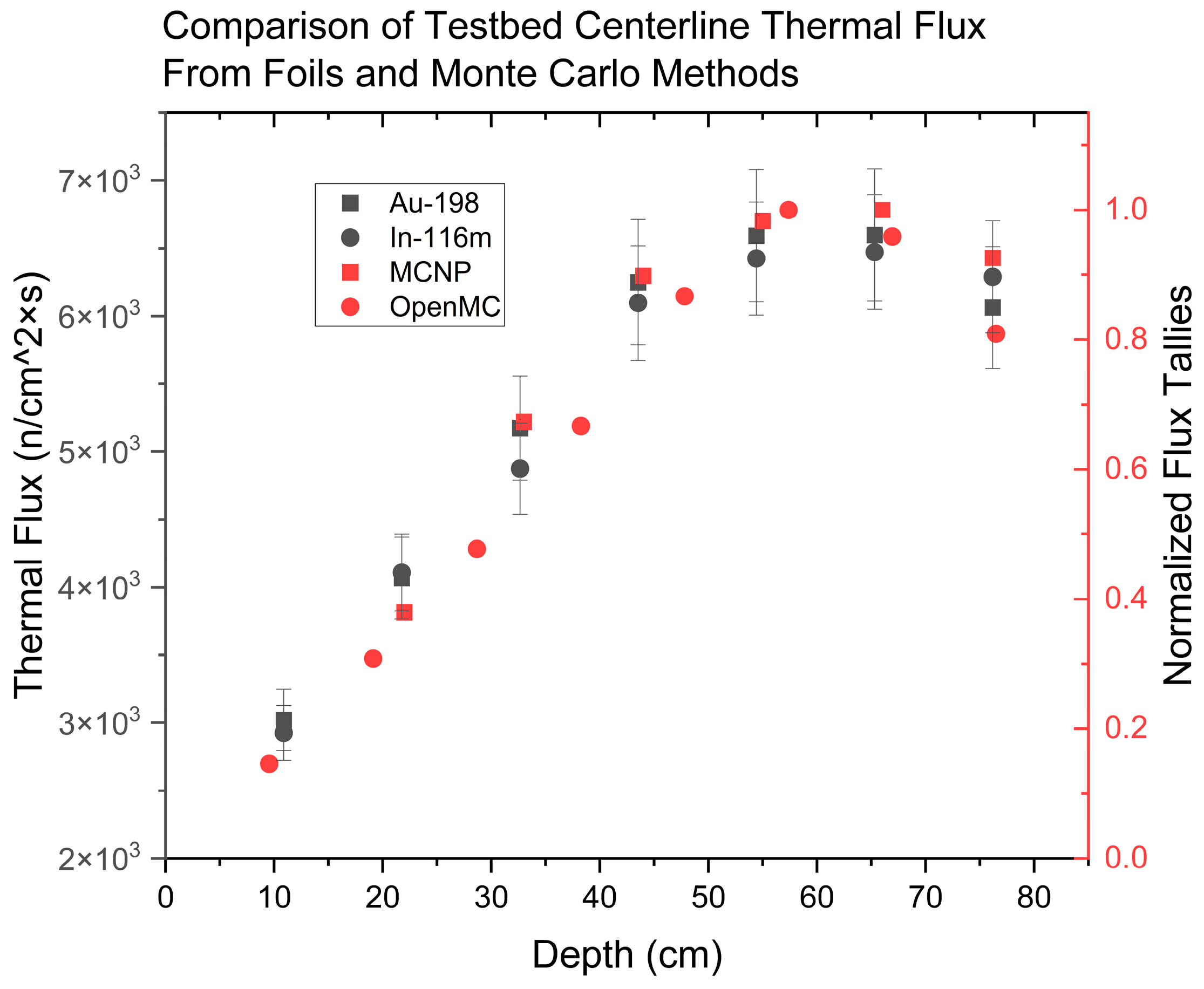
The neutron flux within the volume of the testbed was measured using gold foils in a 4-wide by 7-deep configuration. The HPGe photopeak efficiency of gold was determined to be approximately 0.073 at the 411.0 keV photopeak through curve fitting. Using this value, the neutron flux as a function of location was determined for the 28 foils. To determine the average value of the flux, the mean of the four foils at each depth position was considered to determine the testbed centerline flux. The averaged flux along the depth (Y) dimension of the testbed is shown in
Figure 12. The dimensions of the profile are in the X-Z plane relative to the OpenMC model. However, the origin of the testbed is set at the front face of the pile.
A similar analysis was conducted to verify the results of the gold foil experiments by using indium foils as the activation target. When using indium, multiple photopeaks can be used for calculation. Similarly to gold, each of the absolute photopeak efficiencies and branching ratios must be considered.
Table 3 displays the values for the activated indium photopeaks determined.
Figure 12 also displays the calculated neutron flux for the approximately same testbed region as displayed above for both the gold-197 and indium-115 foils. It is important to note that there were 4 by 12 foils in the indium trial. The centerline average is considered because the length dimension for each depth position has a relatively flat neutron flux, as indicated by
Figure 13 with the gold foils. However, the same occurrence was observed with indium. The uncertainty in the calculated flux values propagates the uncertainties from the counts, absolute photopeak efficiency, and cross-section from the ASTM standard.
5.4. Two-Energy Neutron Testbed Profile
Following the measurement of the bare and cadmium-covered foils from the pile, mass-normalized activity was considered to determine the
RCd value as a function of depth. The cadmium ratio, on average, was determined to be 3.8 for gold and 4.2 for indium. These values were assumed to be the
RCd for the further calculations of epithermal and thermal neutrons. Making use of the equations presented in
Section 4.3, along with the activity and estimated
RCd, the thermal and epithermal neutrons can be calculated as a function of the depth of the testbed. The results of the calculated two-energy group neutron flux are also presented in
Figure 14. The uncertainty in the calculated thermal and epithermal flux values propagates the uncertainties from the counts, absolute photopeak efficiency foil cross-section, and cadmium cover cross-section from the ASTM standard.
5.5. Complete Pile Volume Neutron Flux via Indium Foils
The neutron flux across the full volume of the subcritical pile was measured using indium foils. In total, 271 foils were placed in various locations throughout the pile in place of graphite rods. The HPGe photopeak efficiency of indium was measured at 2.24 × 10
−2 at the 1293 keV peak. Using this value, along with the other necessary parameters from Equation (7), the radiation counts measured from the HPGe detector were converted into flux values for this photopeak. The total flux, averaged from the 417 keV, 1097 keV, and 1293 keV photopeaks of In-116m throughout the volume of the pile, is displayed in
Figure 15. This figure omits the testbed region, as these measurements were conducted separately.
5.6. Gamma Profile of Subcritical Pile
Though neutrons were the primary concern during this study, a gamma measurement was conducted with a sodium iodide detector. The premise of this measurement is to establish a sense of the energy profile of the gammas, while the gamma flux at any point within the pile is not considered. The use of foils to measure neutron flux allows for an indirect measurement without damage to electronic equipment. The direct measurement of gammas within the pile could potentially damage the detector. As a result, the sodium iodide detector was placed 30 cm away from the front face of the pile for 10 min. The energy spectra collected were primarily low-energy gammas, indicative of uranium fission. However, two additional photopeaks and a 511 peak were identified.
Figure 16 contains the collected gamma energy spectrum and detector energy calibration.
It is speculated that the additional photopeaks displayed in the gamma spectrum are from the activation of the aluminum and other trace elements in the testbed. The use of a sodium iodide detector in gamma analysis is difficult, as the energy resolution is poor compared to an HPGe detector. However, due to the neutrons in the facility, it is problematic to design an experiment while preventing damage to the germanium detector. The further analysis of the gamma spectra may be warranted to include an experimental setup of an HPGe detector, minimizing potential damage to the sensitive components.
5.7. MCNP and OpenMC Modeled Pile
The experiments within the testbed and of the entire pile were conducted separately. Subsequently, the normalization for the two regions of interest is handled differently to portray the best results. For the region within the testbed, the centerline flux was calculated by averaging the results from the foils in the same manner as discussed earlier. However, the Monte Carlo results were exclusively taken from tallies along the centerline. Because the testbed region is small, relative to the entire pile volume, these tallies were normalized to one within the data set, corresponding to the centerline of the testbed. It should be noted that simulated data are a function of the defined source strength. Therefore, the shape of the plots as a function of depth is of interest. Shown below in
Figure 17 are the Monte Carlo data from both models overlayed with the values of the flux measured from gold and indium within the testbed.
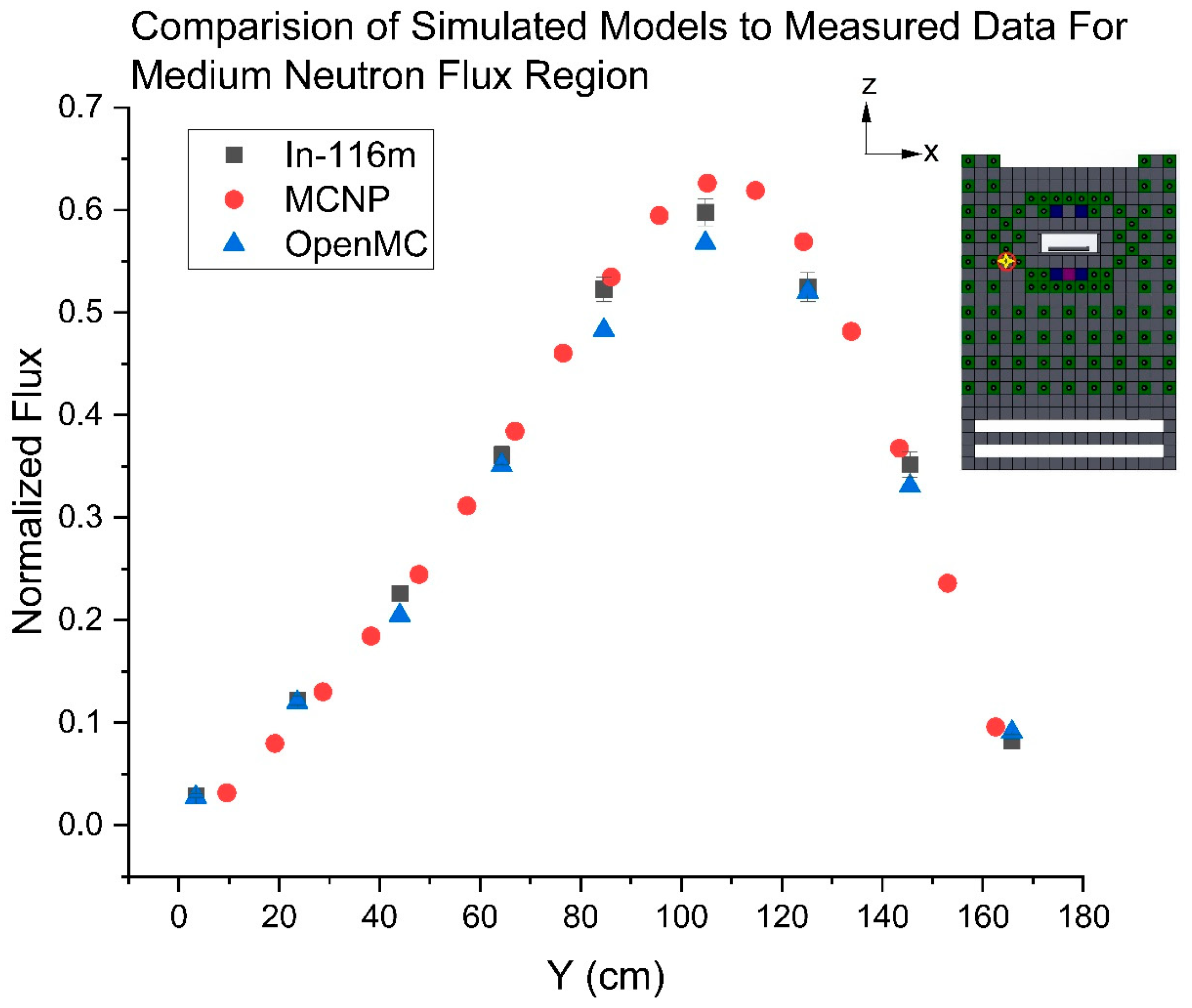
Conversely, the remainder of the pile volume is normalized to one, considering the largest tally or measured indium flux from the respective data sets. This process allows for a better representation of the overall volumetric flux shape than normalizing each depth as conducted within the testbed. To display the agreement between the simulated data and measured data, three regions, designated as low, medium, and high flux, were selected from the indium data set in
Figure 15 and plotted against the simulated data as a function of depth into the pile. The flux designation was subjectively chosen relative to the distance from the source. However, all of the data plotted in one designator are representative of the same region within the pile volume, excluding the testbed volume or physical AmBe/PuBe sources.
Figure 18,
Figure 19, and
Figure 20 correspond to low, medium, and high flux, respectively. Note that the error for the Monte Carlo data is smaller than the symbol.
It is important to note that the neutron tallies in both Monte Carlo programs were defined as 64 cm3 blocks. These values align with the graphite blocks, which are 10.1 cm by 10.1 cm. The volume definition did not necessarily line up with the placement of the indium foils. When selecting the three regions above, it was dependent upon the foil placement cavities. A Monte Carlo data point was used if the foil location intersected the tally volume. The center point of the tally volume is plotted. This results in the offset discrepancy between the foils and the Monte Carlo results.
6. Discussion
6.1. Subcritical Pile Error Analysis
The advantage of using Monte Carlo methods in conjunction with the experimental data allows for an exploration into the experimental uncertainties generated through measurements. It is believed that the largest source of error for the flux calculations in the experimental setup is the assumption of a constant microscopic cross-section for absorption as a function of depth into the testbed and the consistent energy profile throughout the pile. The ASTM attempts to correct for this by providing integrated cross-section data, but this is based upon experiments that have a different neutron energy profile than this experiment. The neutron energy profile generated by the Monte Carlo method indicates that the energy profile varies as a function of location within the testbed. This occurrence, in turn, affects the probability of absorption for each foil within any given testbed location. The average microscopic cross-section for absorption was calculated for gold and indium. These values are presented in
Table 4 and
Table 5. If accurate, this would indicate an underestimate of the gold calculated flux and an overestimate of the indium calculated flux compared to the nominal values selected from the ASTM standard.
The neutron cross-section values were calculated by defining the diameter of the foils and the respective material. An initial run was conducted where the foil thickness was as thin as allowable for the MCNP to define. A second run with the same foils, but defined at their true thickness, was conducted. Tallies were defined as the edge of materials, effectively counting the neutrons that passed through the disk. The ratio between the simulated infinitely thin foil tallies and the true thickness tallies was taken to be the neutron absorption cross-section value for all neutron energies.
It is worth mentioning that the methods by which the cross-section values were derived are typically conducted through a manipulation of the density rather than the thickness, though the setup of the method is based on the definition of the neutron section, as it considers the numerical probability of interaction between an infinitely thin material and the thickness used in the experiments. Of course, the error introduced into the method is a result of the MCNP not allowing for a thickness of 0 to be applied to a material. An additional source of error is the potential for neutrons to be scattered outside of the sides of the defined material, but this was considered negligible.
Evidence in support of the Monte Carlo-generated cross-section data may also be drawn from two other assumptions that were made. The first is that there is no fast flux in the pile. This is simply not true; fission neutrons are generated at energies considered fast, and upscattering does occur. The second assumption is that the cadmium-covered foils remove all the thermal flux. Including these effects will vary the average cross-section value. This is supported by plotting a spectrum of the generated neutron energy as a function of location within the testbed.
Figure 19 shows the neutron energy spectra as a function of testbed depth, and
Figure 21 shows the percent difference among locations relative to the testbed drawer.
The MCNP results suggest that the largest number of fast neutrons relative to the testbed exists above the AmBe source. This is intuitive given the large source strength of the AmBe source compared to the PuBe sources and the birth energies of neutrons from both AmBe and PuBe. These results are further supported by the cadmium-covered gold experiment, where the epithermal neutron flux from foils placed at a 22 cm depth extends above the expected cosine distribution by approximately 20%.
The experimental methods in this article aim to validate the results in the Monte Carlo output. Efforts were made to maintain consistency among all foil measurements. However, it should be noted that the sources of uncertainty in this data set are a result of conducting a detector calibration for each foil set and taking the centerline average of the testbed. Ultimately, the testbed and the whole pile measurements were independent experiments aligned with a common coordinate system to establish characterization through the subcritical volume. Ultimately, the combined foil data sets, aligned with the normalized flux profiles of each numerical model, provide support for the characterization of the Purdue subcritical pile.
6.2. Monte Carlo Discrepancies
Upon comparing the two Monte Carlo data sets, it is clear that the OpenMC software underreports neutron flux for the same input parameters. However, this is most prominent in the high-flux region. The flux cross-sections in
Figure 7 and
Figure 8 show a similar profile, but each contour line for OpenMC is smaller than the respective line in the MCNP. This suggests that the source definition may be the source of the difference as opposed to the multiplication effect from fissions. Even more specifically, the AmBe source appears to be significantly smaller in the OpenMC model when compared to the PuBe sources. It is difficult to isolate the cause of the reduced neutron flux or even apply it generally to the OpenMC source definition, as we do not have access to the source code. What can be stated is that for the same input conditions, modeling the subcritical pile, OpenMC underperforms compared to the MCNP and experimental data. A brief study of increasing OpenMC tally mesh sizes was conducted with positive results, aligning it closer to the MCNP results. However, it was deemed beyond the scope of this project. Further analysis is warranted to determine why the AmBe source is handled differently between the codes.
6.3. Data Bias
Despite efforts to remove any predisposition from the two foil experiments, there still exists a clear bias in the indium data. The cross-section analysis discussed above is believed to be the source of the bias. The ASTM thermal neutron standard assumes a fully thermal source near 2.5 × 10
−8 MeV. It is not clear what neutron energy spectrum was used to integrate the neutron cross-section data. Intuition suggests it was most likely the Watt fission spectrum. However, this is not the same spectrum that exists in the pile. As a result, using the standard for deriving the cross-sectional data for gold and indium introduces uncertainty.
Figure 21 shows that while the vast majority of the neutrons in the pile are in thermal energies, this is also a function of location relative to the AmBe source. This article proposes that the ASTM standard is a sufficient first approach, but the reliance on the standard for cross-section may over- or underestimate the foil cross-section, given the test volume’s true neutron energy spectrum or location within the volume.
The gold foil flux within the testbed at approximately 65 cm of depth is much lower than expected, given the trend and compared to the indium foils at the same location. This effect is more prominent for the cadmium-covered gold. Upon further analysis, it was found that this foil location exists underneath one of the aluminum T-slot support bars for the testbed. While there is a low thermal neutron cross-section for interaction with aluminum, the cross-section increases with increased neutron energy. The added aluminum from the support may slightly affect the neutron energy profile reaching the foils. The total neutrons reaching the foils are most likely the same; otherwise, a similar effect would be observed at this location for the indium foils as well.
7. Conclusions
Purdue University is home to one of three subcritical piles at universities in the United States. It features a testbed located between neutron sources. The testbed was added in 2023, allowing enough volume for devices and objects to be placed and tested. The inclusion of the testbed separates the pile at Purdue University from those at other universities.
To use the subcritical pile and testbed for experiments, the neutron flux present at various locations must be determined. Multiple experiments were conducted to establish these values, including measuring the gamma decay of metallic foils after being activated in the neutron flux and Monte Carlo simulations.
The Au-197 and In-115 foils were placed throughout the pile and on the testbed in the neutron flux for a time duration to reach saturation. Once removed, the foils were placed in a high-purity germanium detector to determine a neutron flux proportional to decay gammas. The MCNP and OpenMC programs were used to replicate the pile geometry and materials to validate the measurements from foil activation. While there was general agreement among the experimental and computational methods, it was determined that OpenMC, given the same input, underperforms in handling the AmBe source. This resulted in a decreased neutron flux profile when compared to the experimental and MCNP results. However, this difference remains minimal in regions of the pile that are greater than 4 cm radially from the AmBe source.
Furthermore, the use of the ASTM standard for measuring neutron flux with foil activation presents an acceptable means of classifying neutron flux. However, the tabulated variables for the calculations are often a result of integrating the neutron energy-dependent variable over relevant energies. The use of an indefinite integral neglects to take into consideration the birth energies of any particular source. As a result, this method could over- or underestimate the values. Due to the use of graphite in the pile, it was assumed that the ratio of thermal to epithermal neutrons was the same throughout. As such, the same neutron cross-sections were applied to all of the foils. An energy profile generated from the MCNP suggested that the fast/epithermal flux above the AmBe source was upwards of 350% compared to the testbed volume average. This was further validated in the cadmium-covered foil experiments. This finding invalidates the assumption of a constant cross-section value applied to all foils.
Without the individual cross-section correction, the indium-116m and gold-198 foil experiments indicate that the maximum testbed region exhibits a thermal and epithermal neutron flux of 6.5 × 103 n/cm2 × s and 1.1 × 103 n/cm2 × s, respectively, for a total neutron flux of 9.5 × 103 n/cm2 × s, where the discrepancy is due to fast neutrons. Excluding the sources, the maximum measured total neutron flux in the entire pile was determined to be 1.1 × 104 n/cm2 × s. The maximum total was located directly above the AmBe source, where foils could be placed. It is possible, and indicated by the MC data, that the flux in the fuel rods between the closest foil measurement and the source is slightly higher. However, the measurements are limited by physical design. Efforts were not specifically conducted to separate energies at this location, but it can be assumed that the majority of these neutrons are fast and epithermal due to the proximity to the sources. However, it should be mentioned that the testbed remains the area of interest, as this is where radiation tests would be conducted.
Future work related to this project may include methods that aim to experimentally measure the gamma flux within the subcritical pile and the testbed region. This can then be used to validate the Monte Carlo-generated gamma energy spectra and flux maps. Given the correlation between the experimental and MC-generated neutron data, it can reasonably be assumed that the gamma data generated have some validity when compared to the subcritical pile. The gamma production results presented should be viewed as, at the very least, a numerical approximation based on a partially characterized MCNP and OpenMC model.
Author Contributions
Conceptualization, B.J., M.N., T.M., and S.C.; methodology, all; software, V.T.; validation, M.N., R.M., H.P., and V.T.; resources, B.J., T.M., and S.C.; data curation, R.M.; writing—original draft preparation, M.N., R.M., H.P., and V.T.; Editing, S.C.; supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This project did not receive external funding.
Data Availability Statement
Data are available upon request.
Acknowledgments
An additional thank you to the Purdue Military Research Institute for their support in higher education for the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Manhattan Project: CP-1 Goes Critical, Met Lab. 2 December 1942. Available online: https://www.osti.gov/opennet/manhattan-project-history/Events/1942-1944_pu/cp-1_critical.htm (accessed on 16 December 2024).
- RRDB. Available online: https://nucleus.iaea.org/rrdb/#/home (accessed on 16 December 2024).
- Beck, J.N.; Lamberty, C.M. Thermal Neutron Activation Analysis—An Important Analytical Tool. Appl. Spectrosc. Rev. 2002, 37, 19–55. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron Imaging in Materials Science. Mater. Today 2011, 14, 248–256. [Google Scholar] [CrossRef]
- Lababsa, D.; Mazrou, H.; Belgaid, M. Performance Evaluation and Validation of OpenMC Code for Criticality Analysis of an MTR-Type Research Reactor. Ann. Nucl. Energy 2024, 206, 110617. [Google Scholar] [CrossRef]
- Vasili, K.; Yilmaz, S.; Niichel, M.M.; Lau, J.; Revankar, S.; Tsoukalas, L.; Chatzidakis, S. Exploring Quantitative and Qualitative Machine Learning Methods for Predicting Neutron Flux Values from a Simulated Molten Salt Reactor; Transactions: Las Vegas, NV, USA, 2024. [Google Scholar]
- Babb, A.L. The Graphite Moderated Subcritical Assembly. In Proceedings of the University Subcritical Assemblies Conference, Gatlinburg, TN, USA, 28–30 August 1961; United States Atomic Energy Commission, Technical Information Service Extension: Germantown, MD, USA, 1961. [Google Scholar]
- Yu, J.; Wilson, J.C.; Dave, A.J.; Sun, K.; Forget, B.; Phillips, B. Experimental Demonstration of a Data-Driven Control System for Subcritical Nuclear Facility. Prog. Nucl. Energy 2024, 168, 104977. [Google Scholar] [CrossRef]
- Takahashi, Y.; Wakabayashi, K.; Kitamura, Y.; Unesaki, H.; Misawa, T. Subcritical Experiment Using U-7Mo LEU at KUCA Facility. In Proceedings of the RERTR 2022—42nd International Meeting on Reduced Enrichment for Research and Test Reactors, Virtual, 2–5 October 2022. [Google Scholar]
- Niichel, M. Development of an Electronics Testbed for Radiation Testing in Gamma and Neutron Environments; Purdue University: West Lafayette, IN, USA, 2024. [Google Scholar]
- Aghara, S. Characterization of an In-Core Irradiator for Testing of Microelectronics in a Mixed Radiation Environment; The University of Texas: Austin, TX, USA, 2003. [Google Scholar]
- Romano, P.; Horelik, N.; Herman, B.; Nelson, A.; Forget, B.; Smith, K. OpenMC: A State-of-the-Art Monte Carlo Code for Research and Development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Raflis, H.; Ilham, M.; Su’ud, Z.; Waris, A.; Irwanto, D. Comparative Study on Fuel Assembly of Modular Gas-Cooled Fast Reactor Using MCNP and OpenMC Code. J. Phys. Conf. Ser. 2021, 1772, 012031. [Google Scholar] [CrossRef]
- Eade, T.; Colling, B.; Naish, J.; Packer, L.W.; Valentine, A. Shutdown Dose Rate Benchmarking Using Modern Particle Transport Codes. Nucl. Fusion 2020, 60, 056024. [Google Scholar] [CrossRef]
- Lewis, E.E. Fundamentals of Nuclear Reactor Physics; Academic Press: Boston, MA, USA, 2008; ISBN 978-0-12-370631-7. [Google Scholar]
- ASTM E262-17; Test Method for Determining Thermal Neutron Reaction Rates and Thermal Neutron Fluence Rates by Radioactivation Techniques. ASTM: West Conshohocken, PA, USA, 2024. [CrossRef]
- De Laeter, J.R.; Böhlke, J.K.; De Bièvre, P.; Hidaka, H.; Peiser, H.S.; Rosman, K.J.R.; Taylor, P.D.P. Atomic Weights of the Elements. Review 2000 (IUPAC Technical Report). Pure Appl. Chem. 2003, 75, 683–800. [Google Scholar] [CrossRef]
- Thomas, D.J.; Kolkowski, P.; Roberts, N.J.; D’Mellow, B.; Joyce, M.J. Investigation of a Possible Replacement for Cadmium as a Thermal Neutron Absorbing Material in Neutron Instruments; National Physical Laboratory: Teddington, UK, 2006. [Google Scholar]
- Sirakov, I.; Kopecky, S.; Young, P.G. Evaluation of Neutron Data for Au-197; ENDF/B-VIII.0, Report NDS 148, 1; International Atomic Energy Agency, Nuclear Data Section: Vienna, Austria, 2018; Available online: https://www-nds.iaea.org/exfor/servlet/E4sGetIntSection?SectID=9017283&req=56972 (accessed on 30 May 2025).
- Mughabghab, S.F. Evaluated Nuclear Data File for 48-Cd-113; ENDF/B-VII.1; National Nuclear Data Center, Brookhaven National Laboratory: Upton, NY, USA; Available online: https://www-nds.iaea.org/exfor/servlet/E4sGetIntSection?SectID=8976985&req=56963 (accessed on 30 May 2025).
- Mughabghab, S.F. Evaluated Nuclear Data File for 49-In-115; ENDF/B-VIII.0, Report NDS 148, 1, Evaluated March 2005, Distributed February 2018; National Nuclear Data Center, Brookhaven National Laboratory: Upton, NY, USA, 2018; Available online: https://www-nds.iaea.org/exfor/servlet/E4sGetIntSection?SectID=8977875&req=56966 (accessed on 30 May 2025).
- 0751-H122-Basic Health Physics-2-Neutron Sources. US NRC, 2011. Available online: https://www.nrc.gov/docs/ML1122/ML11229A619.html (accessed on 30 May 2025).
- ASTM E181-17; Standard Test Methods for Detector Calibration and Analysis of Radionuclides. ASTM: West Conshohocken, PA, USA, 2023.
Figure 1.
Three-dimensional SolidWorks 2024 of subcritical pile with testbed integration.
Figure 1.
Three-dimensional SolidWorks 2024 of subcritical pile with testbed integration.
Figure 2.
Three-dimensional SolidWorks rendering of the electronics testbed drawer placed within the Purdue subcritical drawer [
10].
Figure 2.
Three-dimensional SolidWorks rendering of the electronics testbed drawer placed within the Purdue subcritical drawer [
10].
Figure 3.
Reconfigured Purdue subcritical pile shown with and without experimental setup.
Figure 3.
Reconfigured Purdue subcritical pile shown with and without experimental setup.
Figure 4.
Example testbed foil placement for a 3 × 4 configuration.
Figure 4.
Example testbed foil placement for a 3 × 4 configuration.
Figure 5.
Neutron capture cross-section data for Au-197, In-115, and Cd-113 [
19,
20,
21].
Figure 5.
Neutron capture cross-section data for Au-197, In-115, and Cd-113 [
19,
20,
21].
Figure 6.
Subcritical normalized neutron flux map comparing OpenMC and MCNP generated data.
Figure 6.
Subcritical normalized neutron flux map comparing OpenMC and MCNP generated data.
Figure 7.
X-Y cross-sectional comparison of OpenMC and MCNP neutron flux for the subcritical pile.
Figure 7.
X-Y cross-sectional comparison of OpenMC and MCNP neutron flux for the subcritical pile.
Figure 8.
Y-Z cross-sectional comparison of OpenMC and MCNP neutron flux for the subcritical pile.
Figure 8.
Y-Z cross-sectional comparison of OpenMC and MCNP neutron flux for the subcritical pile.
Figure 9.
Measurement setup in the HPGe detector for the gold-197 and indium-115 foils.
Figure 9.
Measurement setup in the HPGe detector for the gold-197 and indium-115 foils.
Figure 10.
Comparison of HPGe energy resolution to ideal resolution. Fit: y = 13.6(x)−0.6.
Figure 10.
Comparison of HPGe energy resolution to ideal resolution. Fit: y = 13.6(x)−0.6.
Figure 11.
Absolute photopeak efficiency for the HPGE detector used for gold and indium experiments using Ba-133, Co-60, and Cs-137.
Figure 11.
Absolute photopeak efficiency for the HPGE detector used for gold and indium experiments using Ba-133, Co-60, and Cs-137.
Figure 12.
Testbed centerline average of experimental neutron flux determined by gold and indium foils. Error bars represent 1σ uncertainty.
Figure 12.
Testbed centerline average of experimental neutron flux determined by gold and indium foils. Error bars represent 1σ uncertainty.
Figure 13.
Refined 7 by 4 gold foil neutron flux along the length of the drawer.
Figure 13.
Refined 7 by 4 gold foil neutron flux along the length of the drawer.
Figure 14.
Comparison of the experimentally determined thermal and epithermal neutron flux profiles in the testbed region.
Figure 14.
Comparison of the experimentally determined thermal and epithermal neutron flux profiles in the testbed region.
Figure 15.
Flux map of the entire pile as measured by indium foils.
Figure 15.
Flux map of the entire pile as measured by indium foils.
Figure 16.
(a) The gamma energy spectrum measured at 90 cm from the front face of the pile. (b) Energy calibration for the sodium iodide detector.
Figure 16.
(a) The gamma energy spectrum measured at 90 cm from the front face of the pile. (b) Energy calibration for the sodium iodide detector.
Figure 17.
Comparison of measured thermal flux to normalized OpenMC and MCNP tallies within the testbed region.
Figure 17.
Comparison of measured thermal flux to normalized OpenMC and MCNP tallies within the testbed region.
Figure 18.
Normalized In-116m foils compared to MCNP and OpenMC at the low neutron flux region within the pile.
Figure 18.
Normalized In-116m foils compared to MCNP and OpenMC at the low neutron flux region within the pile.
Figure 19.
Normalized In-116m foils compared to MCNP and OpenMC at the medium neutron flux region within the pile.
Figure 19.
Normalized In-116m foils compared to MCNP and OpenMC at the medium neutron flux region within the pile.
Figure 20.
Normalized In-116m foils compared to MCNP and OpenMC at the high neutron flux region within the pile.
Figure 20.
Normalized In-116m foils compared to MCNP and OpenMC at the high neutron flux region within the pile.
Figure 21.
Neutron energy comparison within the testbed region relative to the AmBe Source.
Figure 21.
Neutron energy comparison within the testbed region relative to the AmBe Source.
Table 1.
ASTM standard E262-17 calculated flux variables.
Table 1.
ASTM standard E262-17 calculated flux variables.
| Characteristic | Gold-198 | Indium-116 m |
|---|
| Rcd | 3.80 | 4.18 |
| Gth | 0.97 | 0.77 |
| Gepi | 0.13 | 0.14 |
| I0 [b] | 628.00 | 1557.00 |
| σth [b] | 98.70 | 159.60 |
| Cd Cutoff | N/A | 0.91 |
Table 2.
Measured energy resolution of the HPGe detector.
Table 2.
Measured energy resolution of the HPGe detector.
| Energy (keV) | Resolution | Error | Net Counts |
|---|
| 276 (Ba-133) | 7.2 × 10−3 | 5.2 × 10−4 | 3.7 × 106 |
| 302 (Ba-133) | 6.8 × 10−3 | 3.8 × 10−4 | 7.0 × 106 |
| 356 (Ba-133) | 6.0 × 10−3 | 2.3 × 10−4 | 1.9 × 107 |
| 383 (Ba-133) | 5.3 × 10−3 | 6.2 × 10−4 | 2.6 × 106 |
| 662 (Cs-137) | 4.8 × 10−3 | 1.6 × 10−4 | 3.9 × 107 |
| 1173 (Co-60) | 2.6 × 10−3 | 6.5 × 10−4 | 2.4 × 106 |
| 1332 (Co-60) | 2.4 × 10−3 | 7.4 × 10−4 | 1.9 × 106 |
Table 3.
Absolute photopeak efficiencies and branching ratios used for indium and gold.
Table 3.
Absolute photopeak efficiencies and branching ratios used for indium and gold.
| Energy (keV) | Efficiency (ε) | Branching Ratio |
|---|
| 416.9 | 3.84 × 10−3 | 0.272 |
| 411.8 | 7.31 × 10−2 | 0.956 |
| 1097.2 | 1.56 × 10−3 | 0.585 |
| 1293.6 | 1.33 × 10−3 | 0.848 |
Table 4.
MCNP calculated the microscopic cross-section for absorption for gold-197 foils 1.
Table 4.
MCNP calculated the microscopic cross-section for absorption for gold-197 foils 1.
| Row 1 (b) | Row 2 (b) | Row 3 (b) | Row 4 (b) |
|---|
| 73.34 | 74.20 | 72.83 | 73.03 |
| 81.52 | 77.27 | 77.27 | 77.99 |
| 88.79 | 85.68 | 85.68 | 87.37 |
| 89.01 | 90.94 | 90.94 | 89.97 |
Table 5.
MCNP calculated the microscopic cross-section for absorption for indium-115 foils 2.
Table 5.
MCNP calculated the microscopic cross-section for absorption for indium-115 foils 2.
| Row 1 (b) | Row 2 (b) | Row 3 (b) | Row 4 (b) |
|---|
| 147.58 | 142.21 | 144.50 | 145.57 |
| 162.48 | 157.71 | 165.16 | 159.03 |
| 178.52 | 174.62 | 170.70 | 167.97 |
| 167.42 | 178.22 | 169.14 | 170.11 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).