Planar Bragg Reflectors for Frequency-Tunable Sub-Terahertz Gyrotrons

Abstract

A novel concept of a frequency-tuned sub-terahertz gyrotron based on a combination of an irregular low-frequency resonator and an external reflector has been proposed recently. A simulation was carried out for a fundamental-cyclotron-harmonic gyrotron that demonstrates the possibility of achieving high (10–30%) efficiencies in a wide (~10%) frequency range. A possible solution to the problem of narrow-band frequency-tunable external reflectors in the form of so-called modified planar Bragg structures is discussed. The manufacturing of such structures on the basis of a novel additive technology based on photopolymer 3D printing, as well as the results of “cold” experiments of the manufactured samples, are described in the paper.

1. Introduction

For various important spectroscopic applications, compact and relatively high-power sub-terahertz (sub-THz) sources of the coherent narrow frequency band radiation are needed. The possibility of broadband tuning of the radiation frequency could be a very attractive advantage of such sources from the point of view of a number of applications, namely, high-resolution spectroscopy and, in particular, nuclear magnetic resonance spectroscopy, as well as radio-acoustic detection and terahertz spectroscopy of large biological molecules [1,2,3,4,5,6,7,8,9,10,11].

From the point of view of such characteristics as high generation frequency and output power, compactness, the ability to provide long-pulse and continuous generation modes, narrow-band output signal, and sub-THz gyrotrons [12,13,14,15,16,17,18,19,20,21,22,23,24,25] are the most attractive for such applications. However, a principal disadvantage of traditional gyrotrons is that the use of high-Q, close to the cut-off value in axial modes with open cavities present as operating waves, which makes broadband frequency tuning difficult. At the same time, the spectroscopy applications mentioned above require sources that ensure a narrow-band output signal, along with the possibility of smoothly adjusting the operating frequency in the band by a few percent, which would allow us to obtain a complete spectrum in a wide range.

Recently, a scheme was proposed for implementing sub-THz gyrotrons with frequency tuning based on the excitation of the low-Q eigenmodes of irregular cavities. A simulation was carried out for a fundamental-cyclotron-harmonic sub-THz gyrotron, demonstrating the possibility of achieving a high (10–30%) efficiency in a wide (~10%, 125–137 GHz) frequency range [26]. It is important that the selective excitation of such a cavity at a given frequency is provided via the reflection of a part of the output wave beam from a narrow-band mirror located outside the output window of the gyrotron. In such an auto-oscillator, the frequency of the excited wave is determined via the frequency of reflection of the external mirror. Correspondingly, the broadband frequency adjustment in this scheme is provided via either changing the operating frequency of the output mirror or replacing one mirror with another. Such a scheme allows us to perform any mechanical actions with the mirror because it is placed outside the vacuum space of the gyrotron.

To implement the gyrotron scheme proposed in the framework of the project, mirrors operating in the sub-terahertz frequency range and possessing special properties are needed. First, such a mirror should provide an effective reflection of the Gaussian wave beam coming from the output gyrotron window in a narrow (less than 1%) frequency band. Second, a continuous mechanical tuning of the operating frequency (the central frequency of the reflection band) within a 2–3% band should be possible. In this case, a set of several such tunable mirrors could smoothly cover the 10–12 GHz frequency band mentioned above.

As a possible solution of this problem, we consider the use of so-called modified planar Bragg structures as effective frequency-tunable reflectors [27]. Their important advantages are a greater selectivity compared to “traditional” Bgarr-type reflectors, as well as a possibility for tuning their operating frequencies [28]. At the same time, these reflectors represent planar structures with small-scale corrugations; the corrugation period should be of the order of the operating wavelength. In the sub-THz frequency range, this can be a serious problem from the point of view of manufacturing such structures.

Thus, new technologies ensuring a quick and inexpensive manufacturing of experimental samples of sets of these sub-THz mirrors are required. The IAP RAS actively implements a novel additive technology based on photopolymer 3D printing together with the chemical metallization of photopolymer-based structures (CMPS) [29,30]. The use of this technology allows us to create components of complex forms with small-scale elements. On the operating surfaces of such components, thin (several microns) copper layers are applied.

In the present paper, we describe our activity in the design, manufacturing, and testing of the frequency-tunable Bragg-type mirrors for the sub-THz gyrotron with a broadband frequency tuning. Section 2 of this paper briefly describes the design and typical parameters of the frequency-tunable sub-THz gyrotron with external mirrors. In Section 3, we present a design and the simulations of a prototype of the Bragg-type mirror to be used in this gyrotron. Section 4 describes the use of additive CMPS technologies in manufacturing such Bragg-type mirrors, as well as the results of the first “cold” test of the manufactured samples.

2. Frequency Tunable Sub-THz Gyrotron

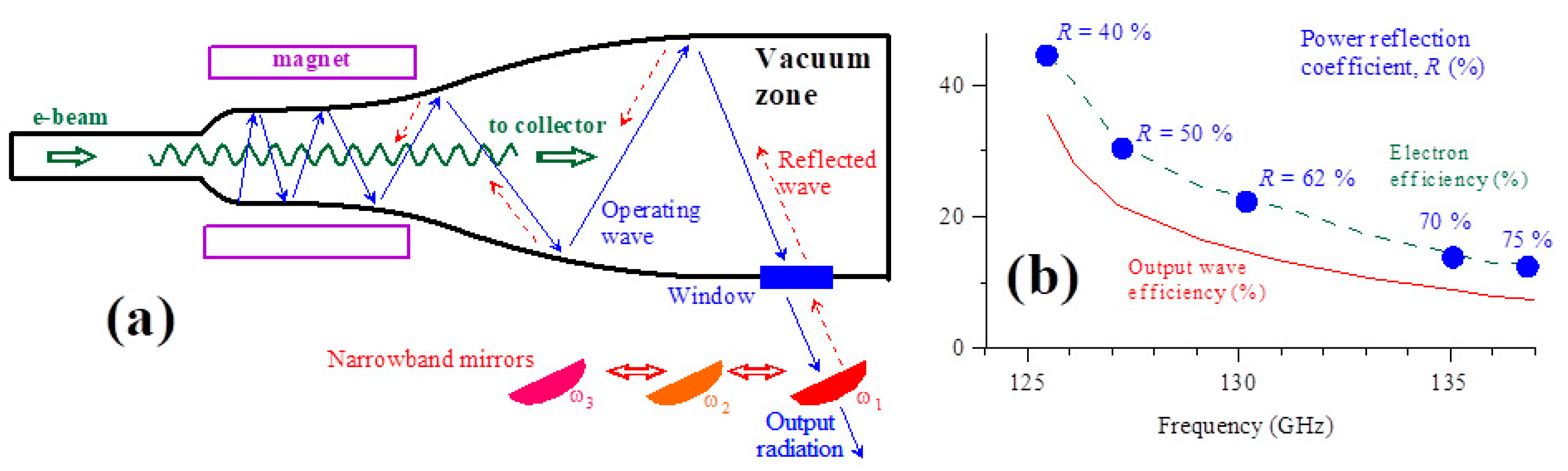
The idea of a frequency-tunable gyrotron [26] (Figure 1a) can be formulated as follows. First, a cavity with an inhomogeneous axial profile should be used. At the same time, the cavity should be so strongly irregular as to prevent excitations of any wave if there are no external reflections. Second, to ensure the start and establishment of stable oscillations at a required frequency, we use a partial reflection of the output wave beam from an external narrow-band reflector back into the cavity. In such a system, the frequency of the wave excited in this gyrotron is fixed via the operating frequency of the external narrow-band mirror. Correspondingly, the change in the gyrotron frequency can be provided by changing the operating frequency of the external reflector. The latter can be ensured either by replacing one mirror with another (as shown in Figure 1a), or by using narrow-band mirrors with a smooth mechanical adjustment of the reflection frequency. Since the reflector is placed outside the vacuum space of the gyro-oscillator, any mechanical manipulations can be provided.

The idea of such a scheme came from an experiment with a 0.39 THz continuous-wave third cyclotron harmonic gyro-oscillator based on the use of a 30 keV/0.7 A electron beam [24]. In one of experiments [31], the output wave beam was fed to a focusing quasi-optical system. To visualize the distribution of the wave field according to the breakdown scheme, a gas flow injected into the compression point was used. In this experiment, the reflection of the wave from the gas supply system resulted in the stable generation of the TE1,3 mode at the fundamental cyclotron resonance instead of the third cyclotron harmonic operation. As the subsequent analysis showed, the conditions for the excitation of such a wave were provided not in the regular part of the operating cavity but in its output conical section. Thus, this experiment and the corresponding modeling have shown that the stable single-frequency excitation of a complex wave structure in an irregular low-Q cavity can be achieved by reflecting part of the wave signal back into the cavity, and the efficiency of such generation can be high (tens of percent).

We consider the experiment described above as the basis for a future experiment to implement a frequency-tunable gyrotron on the fundamental cyclotron resonance. Reproducing the experimental parameters [31], we investigate the excitation of the transverse mode TE1,3 via an axis-encircling electron beam (30 keV, 0.5 A, and pitch factor 1.4) in the frequency range of 125–137 GHz.

Figure 1b illustrates the calculated [26] dependence of the electronic efficiency (the fraction of the power of the electron beam given to the microwave field) and the output wave efficiency (the output power of the wave divided by the power of the electron beam) on the frequency of the excited wave “imposed” via an external reflector, at the optimal (at each of the generation frequencies) values of the reflection factor and the operating magnetic field. The difference in the wave and electronic efficiency describes the ohmic losses in this system. In addition, the optimal reflection power coefficients of the external mirror are shown in Figure 1b. We see that the typical reflection coefficient required to ensure the optimal modes of the electron–wave interaction is 50–70%. The calculations predict generation with an output wave efficiency of 40–10% in the frequency band of the order of 10% (125–137 GHz). This corresponds to a power of 2–6 kW in the continuous-wave regime.

3. Planar Bragg-Type Reflectors

Thus, according to the results of the simulations given in Section 2, we should provide a set of mirrors which should operate in the sub-THz frequency range (~120–140 GHz) with relatively high reflection factors (40–80%) and which continuously covers the frequency band of 12 GHz. Note that at any frequency from the 12 GHz frequency-tuning band, the mirrors should have narrow reflection frequency bands (at least less than 1 GHz); this is needed to avoid the competition between different axial modes excited in a long irregular cavity at slightly different frequencies.

Our idea is to use several narrow-band mirrors possessing 2–3 GHz frequency-tuning bands and having different “central” frequencies. If the distance between these “central” frequencies is about of 2–3 GHz, then 4–5 replaceable mirrors continuously cover the required 12 GHz band of the frequency tuning of our gyrotron.

As the concrete variant of such effective frequency-tunable mirrors, we plan to use the modified Bragg structures of planar geometry (Figure 2a); the distinctive feature of which is the inclusion of quasi-critical waves in the feedback circuit [27]. In this scheme of the reflection, the corrugated Bragg structure provides coupling between the incident wave 1 and the quasi-critical wave 4, as well as between the reflected wave 2 and the quasi-critical wave 4 (Figure 2a). This is in contrast to the traditional Bragg reflector, where a corrugated structure provides the “direct” coupling between two counter-propagating traveling waves 1 and 2 without involving the auxiliary quasi-critical wave 4. To realize such scattering, the corrugation period should be approximately twice as long as in the “traditional” structures. The advantage of the new type of structures is significantly greater selectivity compared to “traditional” analogues in the conditions of significant super-dimensionality. At the same time, structures of this type allow for a frequency shift of the Bragg reflection band when the gap width a₀ changes [28].

The analysis of the electrodynamic properties of modified Bragg reflectors was carried out using FDTD modeling using three-dimensional commercial code CST Microwave Studio. For the first “cold” test experiments, we design a mirror operating within the frequency band of 117–120 GHz; naturally, in the case of positive results of this experiment, it could be easy to reproduce a set of such mirrors operating in the whole frequency band of the future gyrotron experiment.

A layout of the structure was developed with the following parameters: length l_z = 20 cm, width l_x = 5 cm, corrugation period 2.5 mm, and corrugation depth 0.1 mm. The feedback duty cycle of the structure was designed for the connection of two counter-propagating waves of the type via the excitation of a quasi-critical wave TM₈ in the specified frequency range. The gap between the plates a₀ varied from 9.8 to 10.2 mm.

In the simulation carried out, a non-stationary method of the S-parameters' determination was used. The structure was excited via an external initial electromagnetic pulse incident from the end having the structure of a TEM wave of a planar waveguide. The duration of the incident pulse was Δt ≈ 0.05 ns, which corresponded to the spectral width of the signal Δf ≈ 20 GHz. To determine the S-parameters, the temporal evolution of the fields was analyzed. The simulation results are shown in Figure 2b and demonstrate the high reflective properties of the developed structures with a significant super-dimensionality parameter a₀/λ~4, as well as the possibility of implementing a mechanical adjustment of the Bragg band of about 2–3% in the operating frequency range. At the same time, for each fixed value of a₀, the structure provides a sufficiently narrow-band reflection in the ~0.1–0.3 GHz band, which is achieved via a small coupling coefficient (corrugation depth) and a relatively long structure length. The maximum amplitude reflection coefficients of the structure, taking into account the ohmic losses in the walls (in the simulation, it was assumed that the structure is made of copper) and the diffraction losses in the sidewalls in the frequency range ranges from 70 to 95% (the corresponding power reflection coefficients are 65–90%). The typical ohmic losses in these simulations are under 10% of the power, whereas the diffractions losses are as small as a few percent. Note that the reflection coefficients mentioned above are enough from the point of view of the future gyrotron experiment described in Section 2, as the maximal (at frequencies of 135–137 GHz, see Figure 1b) required reflection factors amount to 70–75% (in the power). As for the smaller reflection factors that are required at relatively low frequencies (40–60% at 125–130 GHz, see Figure 1b), they can obviously be implemented in similar Bragg systems by reducing the lengths of the reflectors. Figure 3 illustrates the typical structures of the near-cutoff and the partial travelling components of the wave field inside the mirror.

4. Manufacturing and “Cold” Tests

A new additive technology based on photopolymer 3D printing, which is currently being actively applied at the IAP RAS, was used to produce a model of a modified Bragg reflector [29,30]. Within the framework of this technology, plastic is polymerized in layers via UV radiation passing through a liquid crystal LCD screen, while the high resolution of LCD matrices allows us to achieve a minimum size of roughness in all coordinates of no more than 20 microns. If the MultiJet Printing (MJP) technology is used in the printing process, then the surface roughness can be significantly lower and is determined mainly via the discretization of the surface curves by the layers of printing. In the case of surfaces lying in the printing plane, the roughness is minimal, since each layer is polished with special blades at the end of each printed layer. Next, the surface is chemically metalized with a copper layer, about 5–7 microns thick. The advantage of the new technology is the possibility of the high-precision manufacturing of the electrodynamic components of complex shapes for an operation up to the THz frequency range with an order of magnitude, and less time and costs.

The length of the manufactured resonator (consisting of the upper and lower sections) was 27 cm, and the additional system of waveguides and horns was about 40 cm, which in total makes up a line about 1 m long. Therefore, these elements were printed as separate parts and subsequently copper-plated. The final set of elements is shown in Figure 4.

In the “cold” experiments conducted, we use an input wave signal formed by the lowest wave TE_1,0 of a standard G-band rectangular waveguide having a cross section of 1.6 × 0.8 mm². The formation system consisting of two horns was designed to supply an incident signal to the reflector, where a similar system was used at the resonator output when measuring the transmittance (see Figure 4g). The first horn (Figure 4f) has a length of 100 mm and provides expansion along the “narrow” wall of a rectangular waveguide to a cross-section of 3.9 × 7.4 mm². According to the simulation, with the specified geometry, this horn ensures the almost complete (more than 99%) preservation of the structure of the input TE_1,0—type wave beam, and the transformation into any other “parasitic” propagating wave does not exceed the 30 dB level. The geometry of the second horn was elaborated so as to provide expansion along the “wide” wall with a centrally concentrated distribution of the amplitude of the rf-field and a close to uniform distribution of the phase at its output. For this purpose, the parabolic shape of the horn was chosen (see Figure 4c–e), in which, as a result of the optimization, the output cross-section of the horn was 65 × 7.4 mm² and a length of 312 mm, with the focal length of the parabola being 0.85 mm. At the design parameters, the rf-field structure at the output of this horn was close to a TEM-type wave, and the width of the constant phase region in the center was about 50 mm.

Naturally, an important difference between this cold experiment and the future gyrotron experiment mentioned in Section 2 is the transverse structure of the input wave signal coming to the reflector system. As mentioned above, in the cold experiment, the lowest mode TE_1,0 of a standard G-band rectangular waveguide was used, whereas the wave signal passing through the gyrotron window (Figure 1) has a close-to-Gaussian transverse structure. Therefore, the horn system forming the input signal for the Bragg reflector should be modified accordingly. This means that the input wave system described above (transforming the rectangular waveguide mode TE_1,0 into the TEM-type wave which is scattered inside the planar Bragg-type system) should be supplemented with an additional system transforming a circularly-polarized Gaussian wave beam going from the gyrotron into the rectangular waveguide mode TE_1,0. As for the horn system forming the output signal (passed through the planar Bragg reflector and leaving the system), in the first proof-of-principle gyrotron experiment, it can be left in the same form (the rectangular waveguide mode TE_1,0) as in the “cold” electrodynamic experiment described above.

A possible variant of such a system can be a set of three elements. First, the circularly-polarized Gaussian wave is transformed into the circularly-polarized mode TE_1,1 of a circular waveguide in a multimode horn [32]. Second, the circularly-polarized mode TE_1,1 is transformed inside a polarization converter [33] into the same wave of the circular waveguide, but with the plane polarization. Finally, a standard smooth waveguide transition transforms the mode TE_1,0 of the circular waveguide into the mode TE_1,0 of the rectangular waveguide. The types of mode transformations described above are well studied, and the corresponding high-efficiency mode converters are well known. Naturally, the TEM-type wave coming out from the Bragg-type reflector in the opposite direction (that is, in the direction corresponding to the return of the wave back to the gyrotron window) undergoes an inverse transformation and is transformed into a Gaussian wave beam of the “correct” circular polarization.

Further assembly was carried out on a flat section of a metal profile, then this electrodynamic system was connected to a vector panorama (Figure 5). As primary experiments, the base level of the signal passing through the microwave line without the resonator part was obtained. Then, by correctly setting the gap between the upper and lower parts of the resonator, it was tested by measuring the reflection and transmission coefficients. The result of these “cold” tests is presented in Figure 6 for two various gap values. The Bragg resonance was observed under the design parameters at a frequency of~117 GHz with a gap a₀ = 10.2 mm and at ~ 118.5 GHz with a₀ = 10.1 mm. Transmission up to −25 dB and −27 dB was measured in these cases, respectively, at a base signal level of about −3 dB. These measurements are in good agreement with the results of the simulations (compare Figure 6 and Figure 2b). However, we should note that this system is very sensitive to possible distortions of the planes, which requires extreme caution when assembling and adjusting the resonator. Thus, a special system must be constructed to properly tune the gap. Due to some inaccuracy in setting the distance between the plates, a slight discrepancy between the calculated and measured values of resonant frequencies can be explained. Nevertheless, the experiments conducted demonstrate high prospects of both the considered scientific idea for the frequency tuning and the method used for the implementation of electrodynamic elements.

5. Conclusions

The paper illustrates the use of CMPS technology to create electrodynamic elements of a frequency-tunable sub-THz gyrotron. While the creation of such elements on CNC machines is a long and expensive task, the proof-of-principle experiments, which can be easily performed using additive technology, are extremely effective in testing various scientific theoretical ideas and calculations. In the present work, Bragg reflectors have been successfully implemented via the CMPS method, as well as all auxiliary elements of the microwave line. The total length of the electrodynamic system is about 1 m, while the characteristic size of the small-scale inhomogeneities (cavity corrugation) is 100 μm.

An experimental study of the electrodynamic characteristics of the developed model of a frequency-tunable modified Bragg reflector was carried out at a specialized stand on the basis of a vector panoramic source of the milliwatt power level. The conducted “cold” tests confirmed the operability of the new type of reflectors and a good compliance with the calculation both via the frequency positions of the Bragg reflection zones and via the measured values of the reflection amplitude in these zones. Currently, a system is being designed to place the developed reflectors on a gyrotron stand and prepare for the experiments to control the frequency of its radiation.