Abstract
The state-of-the-art research at the intensity frontier of particle physics aims to find evidence for new physics beyond the Standard Model by searching for faint signals in a vast amount of background. To this end, detectors with excellent resolution in all kinematic variables are required. For future calorimeters, a very promising material is LYSO, due to its short radiation length, fast decay time and good light yield. In this article, the simulation of a calorimeter assembled from multiple large LYSO crystals is presented. Although there is still a long way to go before crystals of that size can be produced, the results suggest an energy resolution of 1%, a position resolution around 5 mm and a time resolution of about 30 ps for photons and positrons with an energy of 55 MeV. These results would put such a calorimeter at the technology forefront in precision particle physics.
1. Introduction
Research at the intensity frontier in particle physics aims to find evidence for physics beyond the Standard Model (SM) by comparing its high-precision predictions with equally precise experimental measurements. This requires a detector system capable of measuring low signals in a large amount of background with unprecedented accuracy.
One of the main investigations in this field is the search for charged Lepton Flavour Violation (cLFV) in processes that are forbidden or highly suppressed in the SM [1]. In this regard, muons are a very sensitive probe, as they are fairly simple to produce and can be transported at low energies from the production target to the experiment, without receiving significant contamination from other particles.
Some of these processes, such as , contain one or more photons in the final state with an energy scale of 0 MeV–100 MeV. The state-of-the-art method to detect such particles are calorimeters based on a high-density scintillating material coupled to photosensors of various kind, such as Silicon Photomultipliers (SiPMs). The same method can be applied to electrons and positrons, eventually in combination with a more accurate tracking system.
The photon detection in the MEG II experiment relies on a calorimeter based on a single large volume of liquid Xenon, which has been estimated to provide an energy resolution of 1.7%, a time resolution of about 40 ps and a position resolution of about mm for signal photons at 53 MeV [2].
Other experiments at the precision frontier rely on calorimeters built from large crystals. As an example, the PIENU experiment uses a single NaI crystal and reports a detector resolution of 2.2% FWHM for 70 MeV/c positrons [3].
The importance of the calorimeter in this kind of experiments can be easily understood by looking at its requirements. In MEG II one of the limiting factor is the accidental background rate, which is estimated to be
where only the muon beam rate and the positron momentum resolution do not depend on the calorimeter performance. The photon energy resolution enters directly, while position and time resolutions enter through the relative angle resolution the relative timing resolution , respectively.
For experiments such as PIENU, the situation is different. Here, the importance of the energy resolution is crucial to reliably separate the different decay channels and suppress the low energy tail of the decay channel, while in this situation the time resolution does not directly affect the result, a fast detector allows to take data at higher rate and thus acquire the required statistics in shorter time.
The development towards future calorimeters for the next generation of precision experiments is currently ongoing. Thanks to its high density, good light yield and fast decay time, LYSO is promising material. A comparison with other commonly used scintillators is given in Table 1.

Table 1.
Properties of commonly used scintillators.
LYSO was first used in medical applications but soon attracted attention from the HEP community. In the past decade, multiple tests using thin crystals with a front area up to and a length between 10 and 20 cm have been made [9,10,11,12]. Limited by the crystal size, these experimental tests found resolutions on the order of 4% for particles below 100 MeV. In particular, the size of the used crystals was comparable to the Moliere radius of LYSO, which is approximately 2 cm.
In addition, LaBr(Ce) is a very promising material as well. However, earlier studies [13] found that the higher light yield and faster decay time cannot compensate for the worse energy containment due to the longer radiation length of LaBr(Ce) compared to LYSO.
Both materials are currently limited by the single crystal size. However, the constant progress in the crystal growing process suggests that larger crystals will be available in the future. This perspective makes LYSO a viable choice of material for the precision frontier in particle physics. In this regard, a prototype made of a single LYSO crystal of 10 cm length and cm diameter is currently under construction.
Focusing on future developments, larger crystals are assumed in this study. Improving the crystal size is crucial to counteract the energy leakage and improve the containment of the shower. Given the larger surface of these crystals, it is crucial to provide a bulk SiPM readout to have an appreciable light collection. The high granularity also provides a handle for position reconstruction, improving the spatial resolution.
2. Materials and Methods
Motivated by the construction of the prototype, a large scale calorimeter built of several LYSO crystals is simulated using Geant4 [14] and analysed with ROOT [15]. Each crystal has a size of .
A representation of the simulated detector geometry is shown in Figure 1. Eight crystals are arranged in an octagonal structure with the surfaces oriented perpendicular to the radial direction. Three of these octagonal structures are stacked next to each other to obtain a cylindrical structure of 24 crystals in total. This geometry results in a calorimeter with approximately 12 depth and an inner volume with about 60 cm diameter for further instrumentation, such as stopping targets or trackers.
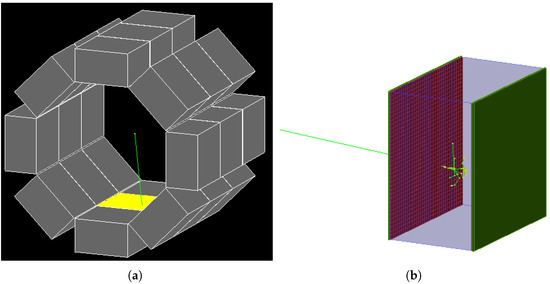
Figure 1.
Representation of the simulated calorimeter. A set of 24 large crystals are arranged around the vertex. Inner and outer surface of each crystal are covered with SiPMs. (a) Total View. (b) Single Crystal.
Every crystal features its independent readout on the inner (facing the centre of the octagon) and outer surface. The lateral surfaces are sealed with a thin sub-millimetre aluminum layer to protect the crystal itself and avoid optical cross-talk.
The readout consists of a matrix of SiPMs with an active area of and a slightly larger support structure, mounted on PCBs. A carbon fibre layer is also used to close the system on both sides. Given the small thickness of the readout system, its effect on incoming photons is negligible. Hence, the inner readout does not significantly affect the energy deposited in the crystal.
The LYSO crystals are simulated almost fully transparent with an order of magnitude estimate of the bulk absorption length of 1 m. The refractive index of LYSO is assumed to be 1.81. The aluminum coated surfaces are considered to be polished with a reflectivity of 95%. The SiPM entrance window is simulated with a refractive index of and a dielectric boundary towards the LYSO crystal. The active area of the SiPM is simulated with a high refractive index (4) and a ultra-short absorption length.
The small size of the SiPMs results in a huge number of channels, which is on the order of a thousand per crystal, while this produces a massive amount of data, it also provides a high granularity that can be used for the geometrical reconstruction of the event.
For this study, photon or positron events at the centre of the geometry with an energy of 55 MeV and an isotropic angular distribution in the detector acceptance are simulated. The energy has been chosen to resemble a signal, as in the previous studies [13]. It also corresponds to the energy at which the prototype will be tested.
The standard Geant4 algorithms are used to simulate the shower inside the crystals and propagate optical photons from production through scintillation to absorption in the SiPM active area. For a photon absorbed inside the active area of a SiPM, the position is used to determine the SiPM pixel if any, thus accounting for the fill factor. If a photon is absorbed within a pixel, a hit is generated with a probability corresponding to the quantum efficiency of the SiPM.
The simulation is also complemented with measurements performed to characterise the SiPMs to be used for the prototype. Namely, the digitised waveforms obtained for the Hamamatsu SiPM S13360-6025PE are used to simulate the detector and electronics response to a single photon hit in the post-processing. This is done by iterating over all hits in each SiPM, sorted by pixel and time, and accumulating the single photon responses. A second hit in the same pixel is only considered if the time separation is larger than the dead time of 40 ns of the SiPM, thus accounting for saturation effects.
After distorting the obtained waveform with gaussian noise for each channel, charge integration and constant fraction timing is performed for each obtained waveform. This information is then used along with the position of each SiPM to reconstruct the events in terms of energy, time and three-dimensional position.
In addition to the analysis of each individual channel, the waveforms for all channels on the inner readout of each crystal are summed up and the constant fraction method is applied to obtain an averaged time for the inner readout of the crystal. The same procedures is applied to the channels on the outer readout to obtain the outer time .
These parameters are used to estimate the entrance time t of the original particle as
where stands for the thickness of the crystal, for its refractive index and c for the speed of light. This formula is obtained by assuming in a one dimensional geometry that the incident particle propagates at the speed of light c and the optical photons propagate at a reduced velocity . In order to extract the intrinsic time of the event, the estimated entrance time has to be corrected with the time of flight between the vertex and the crystal entrance point.
The depth (z-coordinate) of the first interaction between the incoming particle and the crystal is reconstructed as
where again the solution of the one dimensional problem is used. The position in the other two dimensions is estimated by analysing the distribution of the charge collected by each SiPM and using the high granularity to fit it with a Gaussian. The coordinates are then used to estimate the distance between the centre of the setup and entrance location on the crystal.
In first approximation, the total energy is assumed to be proportional to the charge collected by all SiPMs of one crystal, i.e.,
To account for the position dependence, an approximate correction was introduced to modify the charge depending on the hit position
where a is a geometry-dependent coefficient to be determined and are obtained from the reconstructed position of the event. Note that this correction corresponds to the simplest term that respects the symmetry of the geometry, while a more sophisticated correction could be considered, this form was found to be sufficient for the current application.
3. Results
For each simulated event, the waveform of every channel is analysed to extract its charge and time. An example of charge distribution obtained at the inner readout for one crystal is shown in Figure 2. This is the starting point for all further reconstructions.
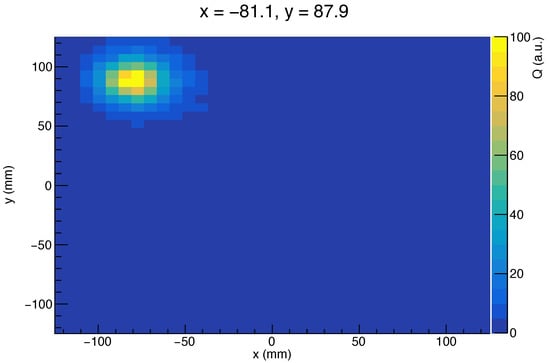
Figure 2.
Charge distribution on the inner readout for one event. The initial photon entered at (Monte Carlo truth value). The charge is arbitrarily scaled.
3.1. Time Reconstruction
Using the time reconstruction described in Section 2, the distribution shown in Figure 3 is obtained for photons and positrons, respectively. The result includes the time of flight correction due to the distance between the event vertex and the calorimeter hit.
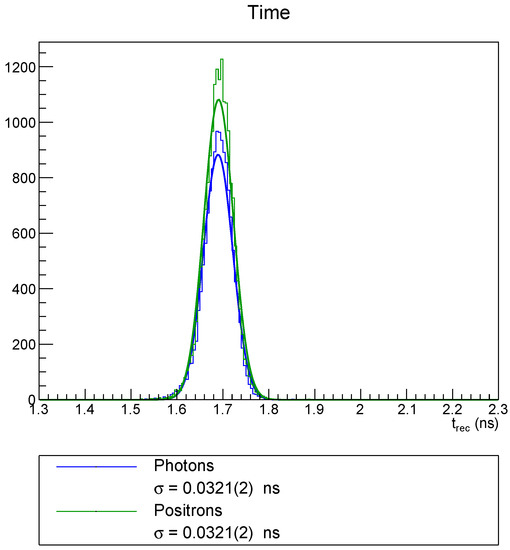
Figure 3.
Time reconstruction for photons and positrons of 55 MeV. The correction accounting for the particle time of flight is applied. The resolution is obtained from a Gaussian fit.
In addition, a Gaussian fit is shown for each distribution and a standard deviation of about 30 ps is obtained. This value can be compared to the reported time resolution of 40 ps of the MEG II calorimeter [2].
Both particles behave fairly similar with respect to time reconstruction. The time offset is due to the fact that the reconstruction does not account for the time delay between the energy deposit and the light emission, as well as the time required to build up the readout waveforms. However, since this is a constant offset, it can be neglected for this simulation and canceled by adequate calibrations in an actual experiment.
3.2. Position Reconstruction
The position of first interaction in the directions x and y are reconstructed from a Gaussian fit of the charge distribution as observed by the inner readout plane. The distribution of the deviation between the reconstructed position and the Monte Carlo truth value is shown in Figure 4.
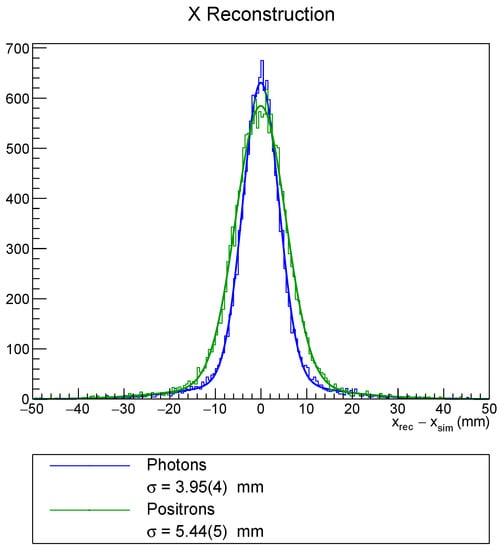
Figure 4.
Position reconstruction in the x-direction for photons and positrons of 55 MeV. The resolution is obtained from a Gaussian fit.
These distributions are fitted with the sum of two Gaussians, one for the core distribution and one to account for the tail. The standard deviations for the core fit are reported in the legend of Figure 4. One can observe that the reconstruction for photons is more precise than for positrons. An excellent resolution below 5 mm is observed for photons and a resolution around 5 mm for positrons. For the chosen geometry a spatial resolution of 5 mm corresponds to an angular resolution below 20 mrad.
These numbers compare unfavourably to the resolutions obtained by the MEG II calorimeter of about mm for the vertex position and below 10 mrad for the angle between photon and positron [2]. In the context of the angular resolution, it has to be considered that the MEG II calorimeter is located further away from the vertex. Moreover, it consists of only one singular volume, thus reducing the effects of the boundaries.
Due to the symmetric nature of the crystals, a very similar behaviour along the y-direction is observed. Applying the same methods for the z-direction yields to depth resolutions for the point of first interaction on the same scale.
3.3. Energy Reconstruction
The effect of correcting the charge collected based on the hit position reconstructed is shown in Figure 5. Note that for this visualisation, the geometrical position (Pos) on the x-axis is a relative value that describes how centred the event was. It is computed as
with , being the position of the crystal edges, i.e., half the crystal length in the corresponding direction. Thus, a value of 0 represents a perfectly central hit and a value of 1 is a hit at the very edge of the crystal.
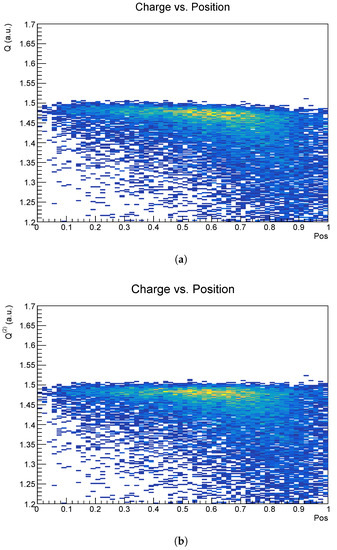
Figure 5.
Charge versus reconstructed position of the hit. The position is chosen such that 0 refers to the centre of the crystal and 1 to the edge. See (6) for details. (a) Uncorrected. (b) Corrected.
While for corrected and uncorrected charge it is clearly visible that the distribution widens up for more lateral hits, the uncorrected charge distribution is slightly tilted. This effect is mostly removed by applying the correction to the charge.
The distribution of the corrected charge without any geometrical selection is shown in Figure 6 for both photons and positrons. There is a main peak at around , corresponding to the 55 MeV particle energy. The secondary peak at is due to energy leakage from neighbouring crystals.
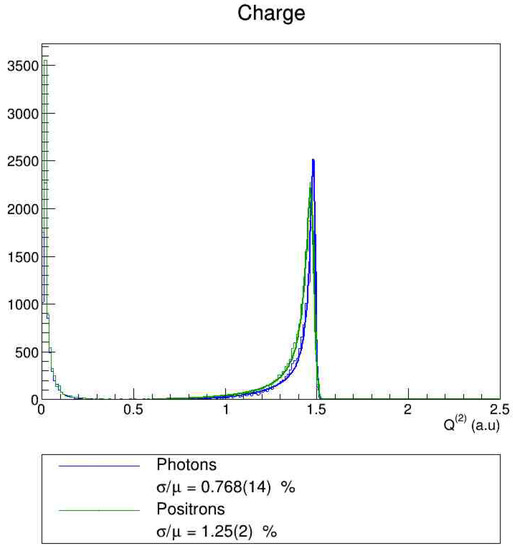
Figure 6.
Corrected charge reconstruction for photons and positrons of 55 MeV. The relative resolution is obtained from a fit with a tailed Gaussian function, defined in (7).
The main peak at 55 MeV is fitted with a tailed Gaussian function
where stands for the peak position, for the Gaussian standard deviation and are parameters to model the tail. The relative resolution is estimated as .
Doing so for 55 MeV photons yields an energy resolution below 1%. For 55 MeV positrons, the resolution estimated is just above 1%. One can further notice that the positron peak is slightly shifted to lower charges compared to the photon peak. This is due to energy losses in the readout layer for the positron, whereas the photon passes straight through to the scintillating crystal.
This resolution can be compared to the MC simulation of the MEG II calorimeter, which suggests a resolution of about 1.1% for MeV photons, or the recently measured value of 1.7% [2]. This suggests that a LYSO calorimeter is likely to provide a better energy resolution compared to this kind of currently running calorimeters.
As can be seen from Figure 5, events further out contribute more prominently to the tail of the distribution and thus affect the overall resolution adversely. Hence, it can be considered to remove the worst of those events by applying a geometrical cut based on the reconstructed position.
This possibility is studied systematically and the key findings are shown in Figure 7. The more stringent the cut, the more events get rejected and the overall efficiency gets reduced. One can see that the resolution tends to improve at the expense of reconstruction efficiency. This effect is enhanced for the uncorrected charge, while it is shown as well that the correction applied does not cancel all geometrical effects. However, it is clear that the correction is more effective for the most lateral events, that are cut first.
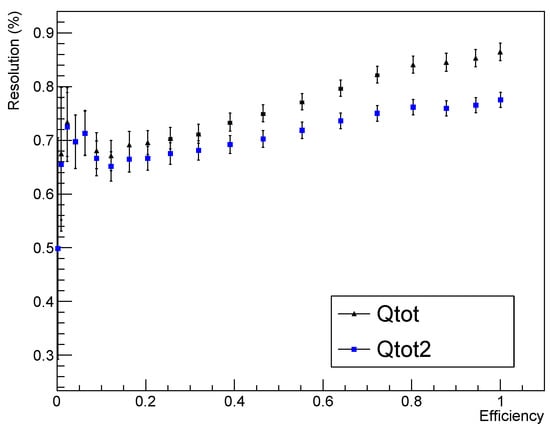
Figure 7.
Application of a geometrical cut for photons to reject events close to the edge, based on the position reconstruction.
4. Discussion
In this study, simulation results for a large calorimeter based on multiple LYSO crystals are presented. Unfortunately, such crystals cannot yet be produced with the required uniformity, but the constant progress in the crystal growing process suggests that this might be possible in the future. Until then, LYSO remains an interesting candidate for high-precision measurements by assembling a calorimeter from a multitude of smaller tapered crystals, as proposed for the PIONEER experiment [16].
The readout is based on a matrix of closely packed SiPM, covering both the inner and outer surface of each crystal. This allows a high-precision reconstruction of energy, time and position for each individual particle hit. For 55 MeV photons, an energy resolution below 1%, a time resolution around 30 ps and a position resolution of 5 mm was obtained. For positrons of the same energy, similar values for time and position were found, while the energy resolution resulted slightly worse.
Comparing these numbers to the performance of the MEG II calorimeter, which operates at very similar energies, it shows that this calorimeter offers slightly better timing resolution (32 ps this study, 40 ps for MEG II) and clearly improved energy resolution up to a factor two (clearly below 1% for 55 MeV photons compared to 1.7% for MEG II) at the cost of position resolution (4 mm compared to mm for MEG II). However, the position reconstruction used in this study is still to be optimised and thus offers opportunities for improvements.
In addition, the geometrical reconstruction was found to be good enough to allow an event selection that rejects lateral events, characterised by a broader charge distribution which worsens the overall energy resolution. This cut has to be tuned on the experimental context in which the calorimeter is used, in order to balance the improvement in energy resolution with the consequent efficiency loss.
In conclusion, the energy resolution obtained for the studied crystal size is clearly improved for 55 MeV photons compared to state-of-the-art detectors and it appears to be slightly better when it comes to timing. With the current position reconstruction algorithms, one may not yet be able to match the position resolutions of the MEG II calorimeter which has been used as comparison here. However, it has to be considered that the geometry of the detector can be adapted to the specific situation. For example, placing the crystals further away, would improve the angular resolutions at the cost of detector acceptance. Moreover, one must not forget about the other advantages such as these crystals do not require a cryogenic environment opposed to liquid Xenon and the fact that the events will distribute over all crystals instead of only one Xenon volume, thus reducing pileup. These results would put such a calorimeter at the technology forefront in precision particle physics.
Author Contributions
Conceptualization, P.S. and A.P.; methodology, P.S., A.G. and A.P.; software, P.S.; validation, P.S. and A.G.; formal analysis, P.S.; investigation, P.S., A.G. and A.P.; resources, A.P.; writing—original draft preparation, P.S.; writing—review and editing, P.S., A.G. and A.P.; supervision, A.P.; project administration, A.P.; funding acquisition, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by SNF n. 200020_172706 and MIUR Montalcini D.M. 2014 n. 975.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the Paul Scherrer Institute in Villigen for hosting the research facilities.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this article:
| cLFV | charged Lepton Flavour Violation |
| HEP | High Energy Physics |
| LYSO | Lutetium Yttrium Oxyorthosilicate |
| PCB | Printed Circuit Board |
| PDG | Particle Data Group |
| SiPM | Silicon Photomultiplier |
| SM | Standard Model |
References
- Calibbi, L.; Signorelli, G. Charged Lepton Flavour Violation: An Experimental and Theoretical Introduction. La Riv. Nuovo Cim. 2018, 41, 71–174. [Google Scholar]
- Baldini, A.M.; Baranov, V.; Biasotti, M.; Boca, G.; Cattaneo, P.W.; Cavoto, G.; Cei, F.; Chiappini, M.; Chiarello, G.; Corvaglia, A.; et al. The Search for μ+→e+γ with 10-14 Sensitivity: The Upgrade of the MEG Experiment. Symmetry 2021, 13, 1591. [Google Scholar] [CrossRef]
- Aguilar-Arevalo, A.A.; Aoki, M.; Blecher, M.; Vom Bruch, D.; Bryman, D.; Comfort, J.; Cuen-Rochin, S.; Doria, L.; Gumplinger, P.; Hussein, A.; et al. Detector for measuring the π+→e+νe branching fraction. Nucl. Instrum. Methods Phys. Res. Sect. A 2015, 791, 38–46. [Google Scholar] [CrossRef]
- Particle Data Group. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar] [CrossRef]
- Saint-Gobain Ceramics & Plastics Inc. Lanthanum Bromide and Enhanced Lanthanum Bromide Scintillation Materials; Saint-Gobain Ceramics & Plastics Inc.: Malvern, PA, USA, 2017. [Google Scholar]
- Papa, A. (Paul Scherrer Institute, 5232 Villigen, Switzerland); Saint-Gobain (02410 Paris, France). Private communication, 2018.
- EPIC-Crystal. LYSO(Ce) Scintillator. Available online: https://www.epic-crystal.com/oxide-scintillators/lyso-ce-scintillator.html (accessed on 8 June 2021).
- Groom, D. Atomic and Nuclear Properties of Materials. Available online: https://pdg.lbl.gov/2021/AtomicNuclearProperties/index.html (accessed on 8 June 2021).
- Eigen, G.; Zhou, Z.; Chao, D.; Cheng, C.H.; Echenard, B.; Flood, K.T.; Hitlin, D.G.; Porter, F.C.; Zhu, R.Y.; De Nardo, G.; et al. A LYSO calorimeter for the SuperB factory. Nucl. Instrum. Methods Phys. Res. Sect. A 2013, 718, 107–109. [Google Scholar] [CrossRef]
- Cordelli, M.; Happacher, F.; Martini, M.; Miscetti, S.; Sarra, I.; Schioppa, M.; Stucci, S. CCALT: A crystal calorimeter for the KLOE-2 experiment. J. Phys. Conf. Ser. 2011, 293, 012010. [Google Scholar] [CrossRef]
- Pezzullo, G.; Budagov, J.; Carosi, R.; Cervelli, F.; Cheng, C.; Cordelli, M.; Corradi, G.; Davydov, Y.; Echenard, B.; Giovannella, S.; et al. The LYSO crystal calorimeter for the Mu2e experiment. J. Instrum. 2014, 9, C03018. [Google Scholar] [CrossRef]
- Oishi, K. Development of Electromagnetic Calorimeter Using LYSO Crystals for the COMET Experiment at J-PARC. Proc. Sci. 2018, 314, 800. [Google Scholar]
- Schwendimann, P.; Papa, A. Study of 3D calorimetry based on LYSO or LaBr3:Ce crystals for future high energy precision physics. J. Instrum. 2020, 15, C06018. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. ROOT: An object oriented data analysis framework. Nucl. Instrum.Methods Phys. Res. Sect. A 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Binney, H.; Blucher, E.; Bryman, D.; Caminada, L.; Chen, S.; Cirigliano, V.; Corrodi, S.; Crivellin, A.; Cuen-Rochin, S.; et al. PSI Ring Cyclotron Proposal R-22-01.1. arXiv 2022, arXiv:2203.01981. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).