Tracker-in-Calorimeter (TIC) Project: A Calorimetric New Solution for Space Experiments †
Abstract
1. Introduction
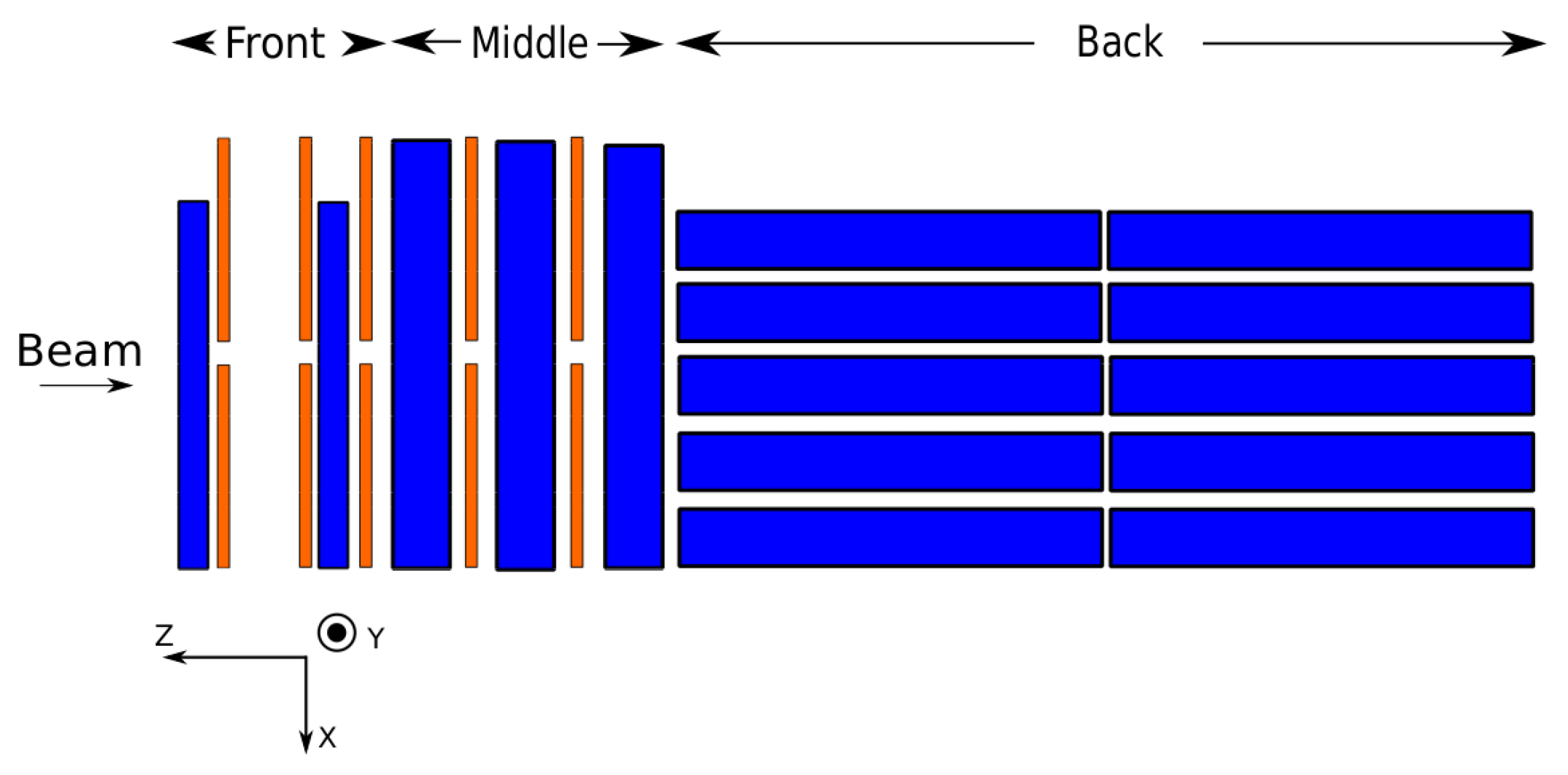
2. Problems and Proposed Solution
3. Monte Carlo Simulations
4. Track Reconstruction Method
5. Prototype and Beam Test Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct measurement of the cosmic-ray proton spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 122, 181102. [Google Scholar] [CrossRef] [PubMed]
- An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; Chen, J.L.; et al. Measurement of the cosmic-ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [PubMed]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the cosmic ray helium energy spectrum from 70 GeV to 80 TeV with the DAMPE space mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.N.; Adriani, O.; Consortium, H.; Albergo, S.; Ambrosi, G.; An, Q.; Azzarello, P.; Bai, Y.; Bao, T.; Bernardini, P.; et al. Introduction to the High Energy cosmic-Radiation Detection (HERD) Facility onboard China’s FutureSpace Station. Proc. Sci. 2017, 301, 1077. [Google Scholar]
- Atwood, W.B.; Bagagli, R.; Baldini, L.; Bellazzini, R.; Barbiellini, G.; Belli, F.; Borden, T.; Brez, A.; Brigida, M.; Caliandro, G.A.; et al. Design and initial tests of the Tracker-converter of the Gamma-ray Large Area Space Telescope. Astropart. Phys. 2007, 28, 422–434. [Google Scholar] [CrossRef]
- Bulgarelli, A.; Argan, A.; Barbiellini, G.; Basset, M.; Chen, A.; Di Cocco, G.; Foggetta, L.; Gianotti, F.; Giuliani, A.; Longo, F.; et al. The AGILE silicon tracker: Pre-launch and in-flight configuration. Nucl. Instruments Methods Phys. Res. Sect. 2010, 95, 213–226. [Google Scholar] [CrossRef]
- Adriani, O.; Ambrosi, G.; Azzarello, P.; Basti, A.; Berti, E.; Bertucci, B.; Bigongiari, G.; Bonechi, L.; Bongi, M.; Bottai, S.; et al. Tracker-In-Calorimeter (TIC): A calorimetric approach to tracking gamma rays in space experiments. J. Instrum. 2020, 15, P09034. [Google Scholar] [CrossRef]
- Starodubtsev, O.; Adriani, O.; Bongi, M.; Bottai, S.; D’Alessandro, R.; Detti, S.; Lenzi, P.; Mori, N.; Papini, P.; Vannuccini, E.; et al. Development of a homogeneous, isotropic and high dynamic range calorimeter for the study of primary cosmic rays in space experiments. Proc. Sci. 2015, 189, 1–9. [Google Scholar]
- Adriani, O.; Albergo, S.; Auditore, L.; Basti, A.; Berti, E.; Bigongiari, G.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Bottai, S.; et al. The CaloCube project for a space based cosmic ray experiment: Design, construction, and first performance of a high granularity calorimeter prototype. J. Instrum. 2019, 14, P11004. [Google Scholar] [CrossRef]
- Adriani, O.; Bonechi, L.; Bongi, M.; Castellini, G.; Ciaranfi, R.; D’Alessandro, R.; Grandi, M.; Papini, P.; Ricciarini, S.; Tricomi, A.; et al. The construction and testing of the silicon position sensitive modules for the LHCf experiment at CERN. J. Instrum. 2010, 5, P01012. [Google Scholar] [CrossRef]
- Battistoni, G.; Boehlen, T.; Cerutti, F.; Chin, P.W.; Esposito, L.S.; Fassò, A.; Ferrari, A.; Lechner, A.; Empl, A.; Mairani, A.; et al. Overview of the FLUKA code. Ann. Nucl. Energy 2015, 82, 10–18. [Google Scholar] [CrossRef]
- Fermi Collaboration, Fermi LAT Performance. Available online: https://www.slac.stanford.edu/exp/glast/groups/canda/lat_Performance.htm (accessed on 19 September 2022).
- Chang, J.; Ambrosi, G.; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bertucci, B.; Cai, M.S.; Caragiulo, M.; Chen, D.Y.; et al. The DArk Matter Particle Explorer mission. Astropart. Phys. 2017, 95, 6–24. [Google Scholar] [CrossRef]
- Azzarello, P.; Ambrosi, G.; Asfandiyarov, R.; Bernardini, P.; Bertucci, B.; Bolognini, A.; Cadoux, F.; Caprai, M.; De Mitri, I.; Domenjoz, M.; et al. The DAMPE silicon-tungsten tracker. Nucl. Instruments Methods Phys. Res. Sect. 2016, 831, 378–384. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Asano, K.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; et al. Determination of the Point-Spread Function for the Fermi Large Area Telescope from On-Orbit Data and Limits on Pair Halos of Active Galactic Nuclei. Astrophys. J. 2013, 54, 765. [Google Scholar]






| Energy (GeV) | Angle (Deg) | Res. 68% (Deg)—TB | Res. 68% (Deg)—MC |
|---|---|---|---|
| 1 | 0 | 3.72 ± 0.11 | 3.87 ± 0.12 |
| 5 | 0 | 0.985 ± 0.016 | 0.955 ± 0.014 |
| 10 | 0 | 0.4095 ± 0.0087 | 0.3971 ± 0.0050 |
| 50 | 0 | 0.1205 ± 0.0023 | 0.0995 ± 0.0050 |
| 100 | 0 | 0.0897 ± 0.0010 | 0.0680 ± 0.0008 |
| 100 | 10 | 0.0884 ± 0.0013 | 0.0646 ± 0.0004 |
| Energy (GeV) | Angle (Deg) | Res. 95% (Deg)—TB | Res. 95% (Deg)—MC |
|---|---|---|---|
| 1 | 0 | 10.63 ± 0.15 | 11.44 ± 0.33 |
| 5 | 0 | 3.300 ± 0.063 | 3.282 ± 0.054 |
| 10 | 0 | 1.946 ± 0.062 | 1.790 ± 0.068 |
| 50 | 0 | 0.921 ± 0.029 | 0.710 ± 0.058 |
| 100 | 0 | 0.678 ± 0.033 | 0.308 ± 0.010 |
| 100 | 10 | 0.662 ± 0.036 | 0.259 ± 0.019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bigongiari, G.; Adriani, O.; Ambrosi, G.; Azzarello, P.; Basti, A.; Berti, E.; Bertucci, B.; Bonechi, L.; Bongi, M.; Bottai, S.; et al. Tracker-in-Calorimeter (TIC) Project: A Calorimetric New Solution for Space Experiments. Instruments 2022, 6, 52. https://doi.org/10.3390/instruments6040052
Bigongiari G, Adriani O, Ambrosi G, Azzarello P, Basti A, Berti E, Bertucci B, Bonechi L, Bongi M, Bottai S, et al. Tracker-in-Calorimeter (TIC) Project: A Calorimetric New Solution for Space Experiments. Instruments. 2022; 6(4):52. https://doi.org/10.3390/instruments6040052
Chicago/Turabian StyleBigongiari, Gabriele, Oscar Adriani, Giovanni Ambrosi, Philipp Azzarello, Andrea Basti, Eugenio Berti, Bruna Bertucci, Lorenzo Bonechi, Massimo Bongi, Sergio Bottai, and et al. 2022. "Tracker-in-Calorimeter (TIC) Project: A Calorimetric New Solution for Space Experiments" Instruments 6, no. 4: 52. https://doi.org/10.3390/instruments6040052
APA StyleBigongiari, G., Adriani, O., Ambrosi, G., Azzarello, P., Basti, A., Berti, E., Bertucci, B., Bonechi, L., Bongi, M., Bottai, S., Brianzi, M., Brogi, P., Castellini, G., Catanzani, E., Checchia, C., D’Alessandro, R., Detti, S., Duranti, M., Finetti, N., ... Vannuccini, E. (2022). Tracker-in-Calorimeter (TIC) Project: A Calorimetric New Solution for Space Experiments. Instruments, 6(4), 52. https://doi.org/10.3390/instruments6040052








