Monte Carlo Modeling and Design of Photon Energy Attenuation Layers for >10× Quantum Yield Enhancement in Si-Based Hard X-ray Detectors
Abstract
1. Introduction
2. Concept of Photon Attenuation Layer (PAL)
3. Monte Carlo Simulations & Results
3.1. Verification of Photon Energy Attenuation in High-Z PAL
- (1)
- A nearly continuous low energy spectrum at 1–5 keV, where Si has large mass attenuation coefficients for efficient absorption. This regime is induced by multiple inelastic scattering of incident photons;
- (2)
- Sharp and discrete energy peaks corresponding either to the characteristic X-ray emissions of Pb or Te atoms [48,49,50], or transition energies corresponding to energy losses from incident energies, otherwise known as edges. The characteristic X-ray emissions of Pb or Te atoms also correspond with X-ray fluorescence (XRF) spectrum of Pb and Te [50,51]. Full tables that list the origins of a majority of the significant peaks are provided in Appendix A and Appendix B. This regime is induced by photons that have only experienced from one to a few inelastic scattering events.
3.2. Quantum Yield Enhancement in Si
3.3. Impact Ionization Process
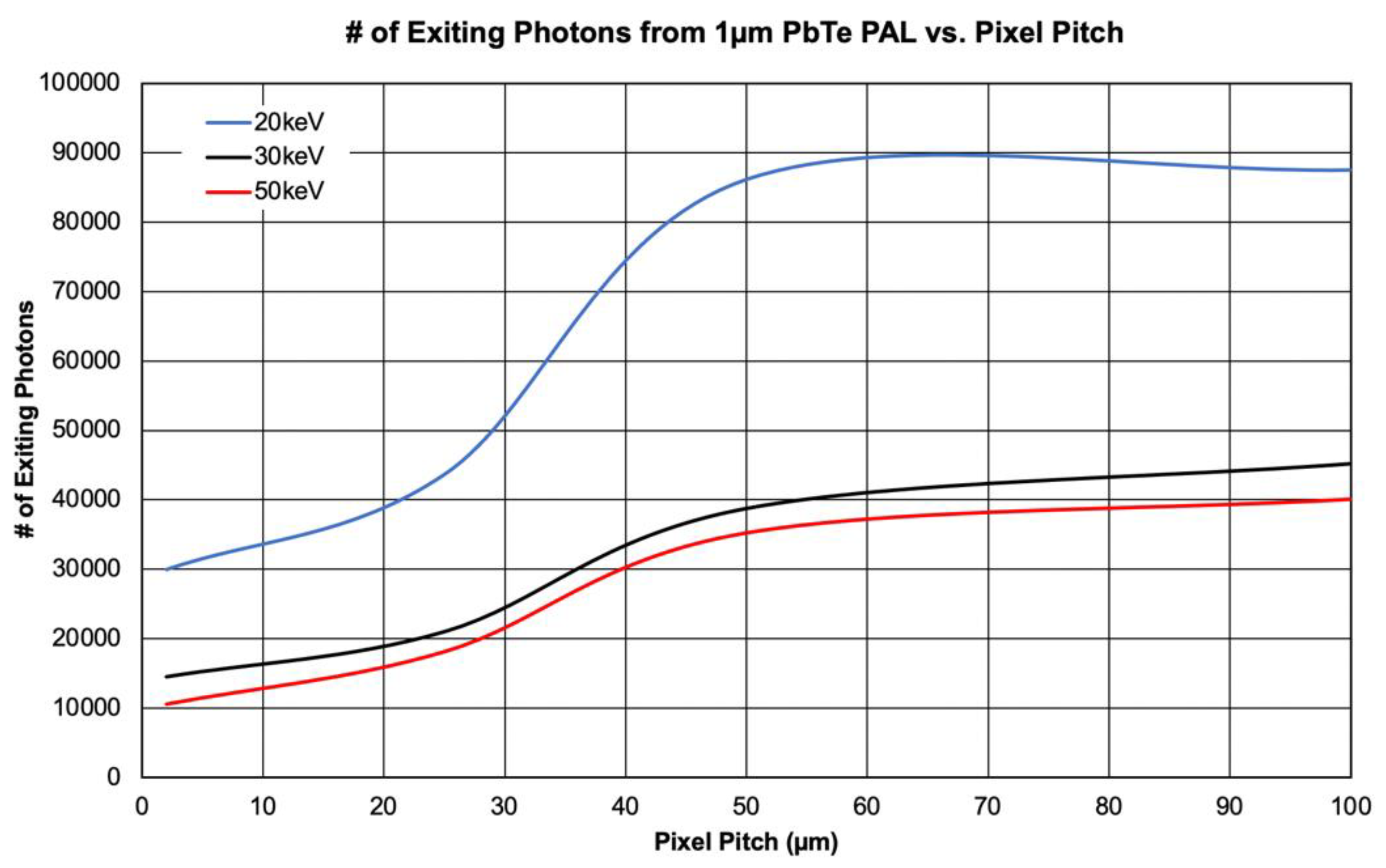
3.4. PAL Thickness Optimization
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
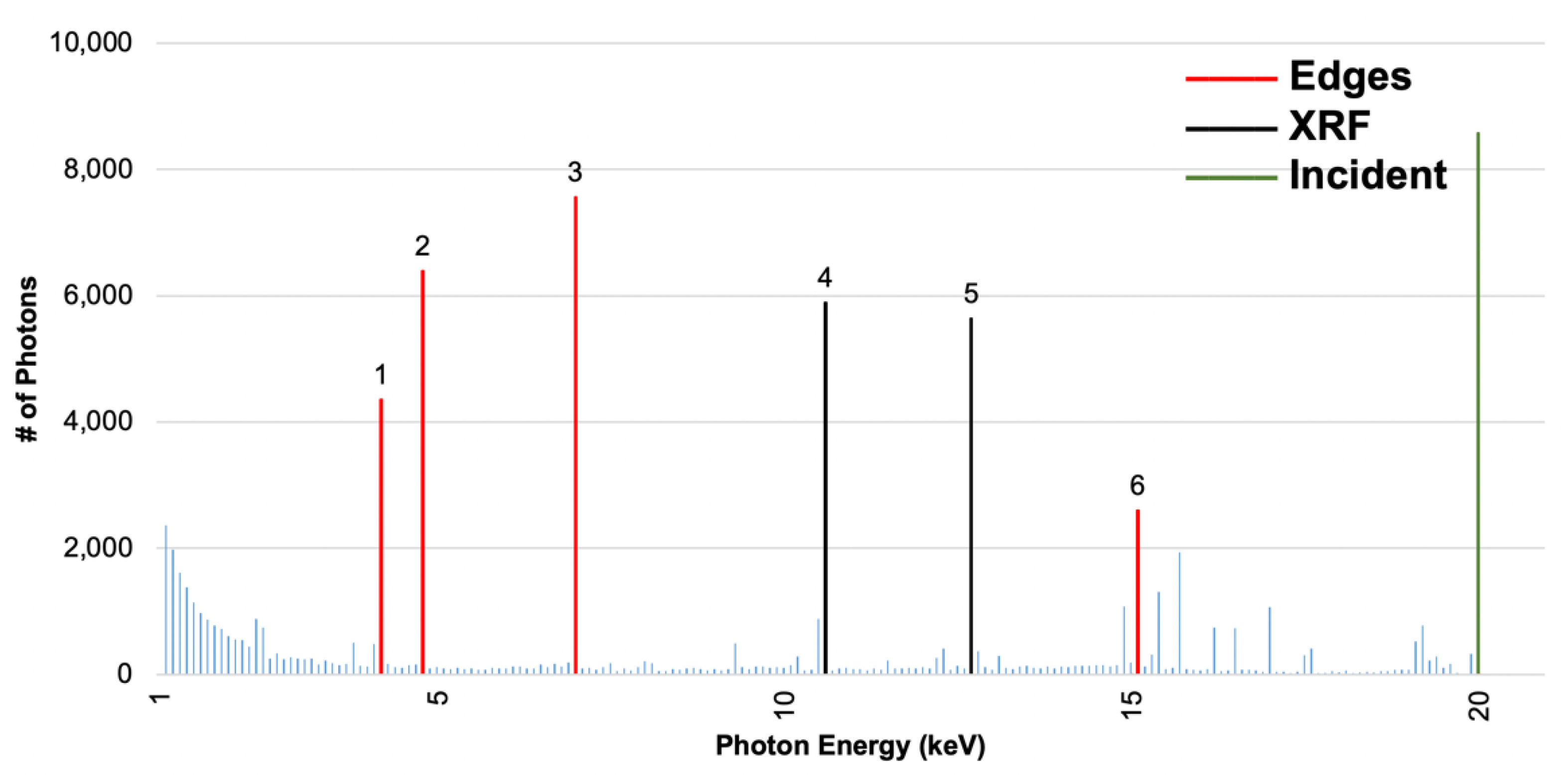
| Peak # | Peak Energy (keV) | Energy Loss from Incident (keV) | Transition Corresponding to Loss | XRF Peak |
|---|---|---|---|---|
| 6 | 15.1 | 4.9 | L1 edge (Te) or M (Pb) | - |
| 5 | 12.7 | 7.3 | - | Lβ1 or Lβ2 (Pb) |
| 4 | 10.6 | 9.4 | - | Lα1 (Pb) |
| 3 | 7.0 | 13.0 | L3 edge (Pb) | - |
| 2 | 4.8 | 15.2 | L2 edge (Pb) | - |
| 1 | 4.2 | 15.8 | L1 edge (Pb) | - |
Appendix B

| Peak # | Peak Energy (keV) | Energy Loss from Incident (keV) | Transition Corresponding to Loss | XRF Peak |
|---|---|---|---|---|
| 10 | 25.1 | 4.9 | L1 edge (Te) or M (Pb) | -- |
| 9 | 17.0 | 13.0 | L3 edge (Pb) | -- |
| 8 | 14.8 | 15.2 | L2 edge (Pb) | -- |
| 7 | 14.2 | 15.8 | L1 edge (Pb) | -- |
| 6 | 12.7 | 17.3 | -- | Lβ1 or Lβ2 (Pb) |
| 5 | 12.3 | 17.7 | -- | Lβ4 (Pb) |
| 4 | 10.6 | 19.4 | -- | Lα1 (Pb) |
| 3 | 9.3 | 20.7 | -- | L or L (Pb) |
| 2 | 4.1 | 25.9 | -- | Lβ3 (Te) |
| 1 | 3.8 | 26.2 | -- | Lα1 (Te) |
Appendix C

Appendix D


Appendix E


Appendix F
Appendix G

References
- Li, X.; Chu, P.; Wang, Z.; O’Shaughnessy, C.M.; Morris, C.; Demarteau, M.; Wagner, R.; Xie, J.; Xia, L.; Zhu, R.-Y.; et al. Initial assessment of multilayer silicon detectors for hard X-ray imaging. Nucl. Instrum. Methods Phys. Res. A 2019, 942, 162414. [Google Scholar] [CrossRef]
- Hu, C.; Zhang, L.; Zhu, R.-Y.; Demarteau, M.; Wagner, R.; Xia, L.; Xie, J.; Li, X.; Wang, Z.; Shih, Y.; et al. Ultrafast inorganic scintillator-based front imager for gigahertz hard X-ray imaging. Nucl. Instrum. Methods. Phys. Res. A 2019, 940, 223–229. [Google Scholar] [CrossRef]
- Wang, Z. On the Single-Photon-Counting (SPC) modes of imaging using an XFEL source. J. Instrum. 2015, 10, C12013. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Barnes, C.W.; Dattelbaum, D.M.; Fossum, E.R.; Lee, E.; Liu, J.; Ma, J.J.; Pokharel, R.; Sechrest, Y.H.; Sweeney, C.M.; et al. Los Alamos National Laboratory Report No. LA-UR-19-27804; Los Alamos National Laboratory: Los Alamos, NM, USA, 2019. [Google Scholar]
- Lee, E.; James, M.R.; Wang, Z.; Liu, J. Monte Carlo simulation and design of high-energy X-ray detection concept with enhanced efficiency using high-Z semiconductor photon attenuation materials. OSA Tech. Dig. 2020, NoTu2F.3. [Google Scholar] [CrossRef]
- Derenzo, S.E.; Choong, W.; Moses, W.W. Fundamental limits of scintillation detector timing precision. Phys. Med. Biol. 2014, 59, 3261–3286. [Google Scholar] [CrossRef] [PubMed]
- Lynch, F.J. Basic limitation of scintillation counters in time measurements. IEEE Trans. Nucl. Sci. 1975, 22, 58–64. [Google Scholar] [CrossRef][Green Version]
- Huber, M.C.E.; Pauluhn, A.; Timothy, J.G. Observing Photons in Space; Springer: New York, NY, USA, 2013; pp. 409–418. [Google Scholar]
- X-ray Detectors, Hamamatsu Photonics. Available online: https://www.hamamatsu.com/resources/pdf/ssd/e09_handbook_xray_detectors.pdf (accessed on 23 March 2020).
- Parsai, E.I.; Shvydka, D.; Kang, J. Design and optimization of large area thin-film CdTe detector for radiation therapy imaging applications. Med. Phys. 2010, 37, 3980. [Google Scholar] [CrossRef] [PubMed]
- Shvydka, D.; Parsai, E.I. Performance of large area thin-film CdTe detector in diagnostic x-ray imaging. Int. J. Med. Phys. Clin. Eng. Radiat. Oncol. 2013, 2, 98–109. [Google Scholar] [CrossRef]
- Hondongwa, D.B.; Fossum, E.R. Temporally over sampled CMOS X-ray photon counting sensor for low dose fluoroscopy. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1101–1104. [Google Scholar]
- Thompson, A.C.; Attwood, D.; Gullikson, E.M.; Howells, M.R.; Kim, K.-J.; Kirz, J.; Kortright, J.B.; Lindau, I.; Liu, Y.; Pianetta, P.; et al. Lawrence Berkeley National Laboratory Report No. LBNL/PUB-490 Rev. 3; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Miyai, H.; Kitaguchi, H.; Kawasaki, S.; Izumi, S. Response of silicon detector for high energy X-ray computed tomography. IEEE Trans. Nucl. Sci. 1994, 41, 999–1003. [Google Scholar] [CrossRef]
- Nikzad, S.; Cunningham, T.J.; Hoenk, M.E.; Ruiz, R.P.; Soules, D.M.; Holland, S.E. Direct detection of 0.1-20 keV electrons with delta doped, fully depleted, high purity silicon p-i-n diode arrays. Appl. Phys. Lett. 2006, 89, 182114. [Google Scholar] [CrossRef]
- Fraser, G.W.; Abbey, A.F.; Holland, A.; McCarthy, K.; Owens, A.; Wells, A. The X-ray energy response of silicon Part A. Theory. Nucl. Instrum. Methods Phys. Res. A 1994, 350, 368–378. [Google Scholar] [CrossRef]
- Opachich, Y.P.; Bell, P.M.; Bradley, D.K.; Chen, N.; Feng, J.; Gopal, A.; Hatch, B.; Hilsabeck, T.J.; Huffman, E.; Koch, J.A.; et al. Structured photocathodes for improved high-energy X-ray efficiency in streak cameras. Rev. Sci. Instrum. 2016, 87, 11E331. [Google Scholar] [CrossRef] [PubMed]
- Henke, B.; Knauer, J.; Premaratne, K. The characterization of x-ray photocathodes in the 0.1-10-keV photon energy region. J. Appl. Phys. 1981, 52, 1509. [Google Scholar] [CrossRef]
- Reinhardt, K.; Kern, W. Handbook of Silicon Wafer Cleaning Technology; William Andrew Publishing: New York, NY, USA, 2018; p. 634. [Google Scholar]
- Leitz, C.; Rabe, S.; Prigozhin, I.; Burke, B.; Zhu, M.; Ryu, K.; Cooper, M.; Reich, R.; Johnson, K.; Hu, W.; et al. Germanium CCDs for large-format SWIR and X-ray imaging. J. Instrum. 2017, 12, C05014. [Google Scholar] [CrossRef]
- Rumaiz, A.; Kuczewski, A.; Mead, J.; Vernon, E.; Pinelli, D.; Dooryhee, E.; Ghose, S.; Caswell, T.; Siddons, D.; Miceli, A.; et al. Multi-element germanium detectors for synchrotron applications. J. Instrum. 2018, 13, C04030. [Google Scholar] [CrossRef]
- Veale, M.C.; Bell, S.J.; Duarte, D.D.; French, M.J.; Schneider, A.; Seller, P.; Wilson, M.D.; Lozinskaya, A.D.; Novikov, V.A.; Tolbanov, O.P.; et al. Chromium compensated gallium arsenide detectors for X-ray and gamma-ray spectroscopic imaging, Nuc. Instrum. Methods Phys. Res. A 2014, 752, 6–14. [Google Scholar]
- Miyajima, S. Thin CdTe detector in diagnostic X-ray spectroscopy. Med Phys. 2003, 30, 771–777. [Google Scholar] [CrossRef]
- Amsterdam Scientific Instruments. LynX Hybrid Pixel Detectors for X-ray. 2017. Available online: https://www.amscins.com/products/lynx/ (accessed on 18 March 2021).
- Brient, J.-C.; Rusack, R.; Sefkow, F. Silicon calorimeters. Ann. Rev. Nucl. Part. Sci. 2018, 68, 271–290. [Google Scholar] [CrossRef]
- Compagnie de Saint-Gobain, S.A. Efficiency Calculations for Selected Scintillators. Available online: https://www.crystals.saint-gobain.com/sites/imdf.crystals.com/files/documents/efficiency-calculations.pdf (accessed on 18 March 2021).
- Compagnie de Saint-Gobain, S.A. NaI(TI) and Polyscin NaI(TI) Sodium Iodide Scintillation Material. Compagnie de Saint-Gobain, S.A. Available online: https://www.crystals.saint-gobain.com/sites/imdf.crystals.com/files/documents/sodium-iodide-material-data-sheet_0.pdf (accessed on 18 March 2021).
- Chen, X.; Liu, B.; Zhu, J.; Gu, M.; Chen, H.; Liu, J.; Chen, L.; Ouyang, X. Light extraction enhancement and directional control of scintillator by using microlens arrays. Opt. Express 2018, 26, 23132–23141. [Google Scholar] [CrossRef]
- Wang, Z.; Morris, C.; Kapustinsky, J.S.; Kwiatkowski, K.; Luo, S.-N. Towards hard X-ray imaging at GHz frame rate. Rev. Sci. Instrum. 2012, 83, 10E510. [Google Scholar] [CrossRef]
- Hubbell, J.H.; Grimm, H.A.; Overbo, I. Pair, triplet, and total atomic cross sections (and mass attenuation coefficients) for 1 MeV–100 GeV photons in elements Z = 1 to 100. J. Phys. Chem. Ref. Data 1980, 9, 1023–1148. [Google Scholar] [CrossRef]
- Gierga, D.P. Electron Photon Calculations Using MCNP. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]
- Durini, D. High Performance Silicon Imaging: Fundamentals and Applications of CMOS and CCD Sensors; William Andrew Publishing: Cambridge, UK, 2019; p. 476. [Google Scholar]
- Lutz, G. Silicon drift and pixel devices for X-ray imaging and spectroscopy. J. Synchrotron Radiat. 2006, 13, 2. [Google Scholar] [CrossRef] [PubMed]
- Kitchin, C.R. Astrophysical Techniques; CRC Press: Boca Raton, FL, USA, 2013; p. 159. [Google Scholar]
- Ismail, M.P.b.; Ssni, S.b.; Masenwat, N.A.b.; Mohd, S.; Sayuti, S.; Ahmad, M.R.B.; Mahud, M.H.b.; Isa, N.b. Radiation attenuation on labyrinth design bunker using Iridium-192 source. AIP Conf. Proc. 2017, 1799, 050011. [Google Scholar]
- Owens, A. Semiconductor Radiation Detectors; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Singh, V.K.; Lin, P.T.; Patel, N.; Lin, H.; Li, L.; Zou, Y.; Deng, F.; Ni, C.; Hu, J.; Giammarco, J.; et al. Mid-infrared materials and devices on a Si platform for optical sensing. Sci. Technol. Adv. Mater. 2014, 15, 014603. [Google Scholar] [CrossRef]
- Piccioni, G.; Formisano, V.; Bellucci, G. Evaluation of aPbTe detector for infrared imaging purposes. Nuovo Cimento C 1992, 15, 1121–1128. [Google Scholar] [CrossRef]
- Corsi, C. PbTe rf-sputtered infrared detectors. Appl. Phys. Lett. 1974, 24, 137. [Google Scholar] [CrossRef]
- Schulman, T. Si, CdTe, and CdZnTe Radiation Detectors for Imaging Applications. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2006. [Google Scholar]
- Piccioni, G.; Formisano, V.; Bellucci, G. Polarization of Bi2Te3 thin film in a floating-gate capacitor structure. Appl. Phys. Lett. 2014, 105, 233505. [Google Scholar]
- Lin, P.T.; Singh, V.; Wang, J.; Lin, H.; Hu, J.; Richardson, K.; Musgraves, J.D.; Luzinov, I.; Hensley, J.M.; Kimerling, L.C.; et al. Si-CMOS compatible materials and devices for mid-IR microphotonics. Opt. Mater. Express 2013, 3, 1474–1487. [Google Scholar] [CrossRef]
- Del Sordo, S.; Abbene, L.; Caroli, E.; Mancini, A.M.; Zappettini, A.; Ubertini, P. Progress in the Development of CdTe and CdZnTe Semiconductor Radiation Detectors for Astrophysical and Medical Applications. Sensors 2009, 9, 3491–3526. [Google Scholar] [CrossRef] [PubMed]
- Islamian, J.P.; Abbaspour, S.; Mahmoudian, B. Cadmium telluride semiconductor detector for improved spatial and energy resolution radioisotopic imaging. World J. Nucl. Med. 2017, 16, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Yoriyaz, H.; Moralles, M.; Siqueira, P.d.T.D.; Guimaeaes, C.d.C.; Cintra, F.B.; Santos, A.d. Physical models, cross sections, and numerical approximations used in MCNP and GEANT4 Monte Carlo codes for photon and electron absorbed fraction calculation. Med. Phys. 2009, 36, 11. [Google Scholar] [CrossRef] [PubMed]
- Werner, C.J. Los Alamos National Laboratory Report No. LA-UR-17-29981; Los Alamos National Laboratory: Los Alamos, NM, USA, 2017. [Google Scholar]
- Hubbell, J.H.; Seltzer, S.M. National Institute of Standards and Technology Standard Reference Database 126. Available online: https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients (accessed on 2 April 2020).
- Berhardt, L.V. Advances in Medicine and Biology; Nova Science Publishers: New York, NY, USA, 2019; pp. 2–44. [Google Scholar]
- Deslattes, R.D.; Kessler, E.G., Jr.; Indelocato, P.; de Billy, L.; Anton, J.; Coursey, J.S.; Schwab, D.J.; Chang, J.; Sukumar, R.; Olsen, K.; et al. National Institute of Standards and Technology Standard Reference Database 128. Available online: https://www.nist.gov/pml/x-ray-transition-energies-database (accessed on 2 April 2020).
- Ahmed, T. IUPAC vs. Siegbahn Notation of X-ray Transitions. 2014. Available online: https://figshare.com/articles/dataset/IUPAC_vs_Siegbahn_notation_of_x_ray_transitions/1168938 (accessed on 2 April 2020).
- XRF Research, Inc. XRF Spectra. Available online: http://www.xrfresearch.com/xrf-spectra/ (accessed on 18 March 2021).
- Gong, K.; Berg, E.; Cherry, S.R.; Qi, J. Machine Learning in PET: From Photon Detection to Quantitative Image Reconstruction. Proc. IEEE 2020, 108, 51–68. [Google Scholar] [CrossRef]
- Arabi, H.; Zaidi, H. Applications of artificial intelligence and deep learning in molecular imaging and radiotherapy. Eur. J. Hybrid Imaging 2020, 4, 1–23. [Google Scholar] [CrossRef]




| IncidentEnergy (keV) | Si Thickness (µm) | Avg. Electron Energy in Si (keV) | # of Primary Photoelectrons Pre-Impact Ionization (Figure 3a Solid Lines) | Approx. Ultimate # of Electrons Post- Impact Ionization |
|---|---|---|---|---|
| 20 | 5 | 4.83 | 6535 | 8.65 × 106 |
| 30 | 5 | 6.79 | 2373 | 4.41 × 106 |
| 50 | 5 | 11.00 | 805 | 2.43 × 106 |
| 20 | 50 | 4.39 | 21,123 | 2.54 × 107 |
| 30 | 50 | 5.75 | 8799 | 1.39 × 107 |
| 50 | 50 | 8.45 | 4162 | 9.64 × 106 |
| 20 | 200 | 4.24 | 33,478 | 3.89 × 107 |
| 30 | 200 | 5.43 | 14,260 | 2.12 × 107 |
| 50 | 200 | 7.73 | 6156 | 1.30 × 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.; Anagnost, K.M.; Wang, Z.; James, M.R.; Fossum, E.R.; Liu, J. Monte Carlo Modeling and Design of Photon Energy Attenuation Layers for >10× Quantum Yield Enhancement in Si-Based Hard X-ray Detectors. Instruments 2021, 5, 17. https://doi.org/10.3390/instruments5020017
Lee E, Anagnost KM, Wang Z, James MR, Fossum ER, Liu J. Monte Carlo Modeling and Design of Photon Energy Attenuation Layers for >10× Quantum Yield Enhancement in Si-Based Hard X-ray Detectors. Instruments. 2021; 5(2):17. https://doi.org/10.3390/instruments5020017
Chicago/Turabian StyleLee, Eldred, Kaitlin M. Anagnost, Zhehui Wang, Michael R. James, Eric R. Fossum, and Jifeng Liu. 2021. "Monte Carlo Modeling and Design of Photon Energy Attenuation Layers for >10× Quantum Yield Enhancement in Si-Based Hard X-ray Detectors" Instruments 5, no. 2: 17. https://doi.org/10.3390/instruments5020017
APA StyleLee, E., Anagnost, K. M., Wang, Z., James, M. R., Fossum, E. R., & Liu, J. (2021). Monte Carlo Modeling and Design of Photon Energy Attenuation Layers for >10× Quantum Yield Enhancement in Si-Based Hard X-ray Detectors. Instruments, 5(2), 17. https://doi.org/10.3390/instruments5020017







