Study of the Extracted Beam Energy as a Function of Operational Parameters of a Medical Cyclotron

Abstract

The medical cyclotron at the Bern University Hospital (Inselspital) is used for both routine ${}^{18}$F production for Positron Emission Tomography (PET) and multidisciplinary research. It provides proton beams of variable intensity at a nominal fixed energy of 18 MeV. Several scientific activities, such as the measurement of nuclear reaction cross-sections or the production of non-conventional radioisotopes for medical applications, require a precise knowledge of the energy of the beam extracted from the accelerator. For this purpose, a study of the beam energy was performed as a function of cyclotron operational parameters, such as the magnetic field in the dipole magnet or the position of the extraction foil. The beam energy was measured at the end of the 6 m long Beam Transfer Line (BTL) by deflecting the accelerated protons by means of a dipole electromagnet and by assessing the deflection angle with a beam profile detector.

1. Introduction

The accurate knowledge of the energy of a particle beam extracted from an accelerator is fundamental for several scientific activities. In particular, it is crucial for the research program focused on the measurement of nuclear reaction cross-sections or the production of radioisotopes of medical interest ongoing at the compact medical cyclotron in operation at the Bern University Hospital (Inselspital). The beam transfer line of the medical cyclotron in Bern is used for the measurement of cross-sections of nuclear reactions as a function of the proton energy. A precise knowledge of the beam energy is needed to improve nuclear data. Considering that lower energies are obtained by absorbers, an accuracy of about 250 keV on the pristine beam is required. Several methods have already been used for measuring the proton beam energy in medical cyclotrons. Some of these techniques are based on the use of passive absorbers and simulations of stopping power processes [1,2] or the determination of the Bragg peak to calculate the penetration range in water [3]. At the Bern cyclotron, the beam energy was measured using absorbers of different thickness [4] or a segmented Faraday cup [5]. A further measurement was performed based on Rutherford backscattering (RBS) [6]. These studies suggested a dependence of the extracted beam energy with respect to the magnetic field in the cyclotron main coil, which determines the resonance conditions. The position of the extraction foil also has an influence.

To investigate these effects without relying on energy loss simulations, a direct assessment of the beam energy was pursued by means of magnetic deflection. This method has been used in many different kinds of particle accelerators and has proved to be fast and accurate [7,8]. In this paper, we report on the use of this technique to study the extracted beam energy as a function of two operational parameters of the cyclotron: the strength of the dipole magnetic field and the position of the extraction foil.

2. Materials and Methods

The medical cyclotron at the Bern University Hospital (Inselspital) is used for commercial production of ${}^{18}$F for Positron Emission Tomography (PET) imaging and for multidisciplinary research activities running in parallel [9]. For the latter aim, a 6 m long Beam Transfer Line (BTL) transports the beam into a separate bunker with independent access. The cyclotron (IBA Cyclone 18/18 HC) provides proton beams at a nominal energy of 18 MeV. The beam current may vary from a few pA to 150 $\mathsf{\mu }$A. Currents below 1 $\mathsf{\mu }$A are a special feature and are obtained by means of a method developed by our group [10] based on the variation of the magnetic field produced by the main coil and the peak voltage of the Radio Frequency (RF). The RF operates at the constant frequency of 42 MHz. The RF peak voltage can be tuned from 27 to 40 kV. For the present experiment, the peak voltage was set to 32 kV. 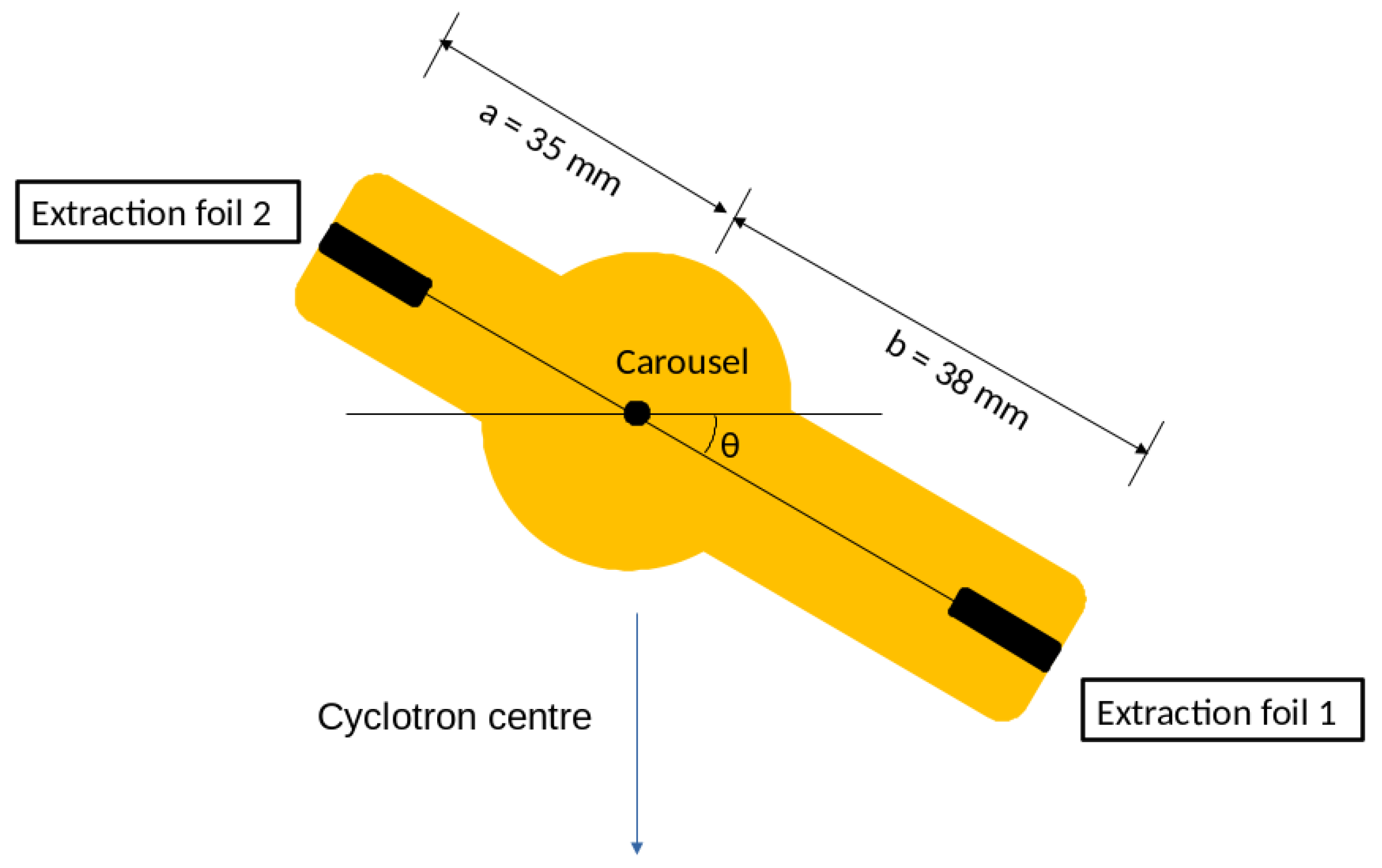The cyclotron accelerates H${}^{-}$ ions which are extracted by stripping. For each of the eight out-ports, two extraction foils are mounted on a carousel to allow for fast replacement, as depicted in Figure 1. To optimise extraction, the carousel can be rotated around its axis which is perpendicular with respect to the horizontal acceleration plane. In this way, the selected extraction foil might intercept different proton orbits producing potential changes in the extracted beam energy. Carousels are usually symmetric with a single value for the arm length. For the out-port corresponding to the BTL, specific carousels are used to optimise extraction [11]. To study the effect of the arm length on the beam energy, we constructed the asymmetric carousel shown in Figure 1.

The experimental set-up is shown in Figure 2. To deflect the proton beam trajectory, a dipole electromagnet was located at the end of the BTL. The magnetic field produced by this electromagnet was accurately simulated and measured at CERN [12] and verified for this measurement campaign using a Hall probe. The magnetic field as a function of the applied current and the position along the beam path are shown in Figure 3. The magnetic field was verified by increasing and by decreasing the current in the dipole to investigate possible hysteresis effects. An important feature of the magnet is its Good Field Region (GFR) covering the entire cross-section of the vacuum chamber. The obtained results are hence valid also for off-centred beams. Furthermore, the beam can enter the dipole magnet with a non-zero angle. Calculations show that if the angle is smaller than 20 mrad, as is the case for our measurement, the effect is negligible. To assess the deflection angle, a beam profile detector was located downstream the dipole at 63 cm from the centre of the magnet. A specific detector named UniBEaM [13] was designed and constructed to fit an ISO-K 100 flange. It is based on a Ce-doped silica fibre that is moved across the beam by means of a high-precision motor. The collected scintillation light is used to reconstruct the beam profile. The position of the centre of the beam can be assessed with an accuracy of 0.1 mm. The UniBEaM is commercialised under licence by the Canadian company D-Pace [14].

The relation between the kinetic energy of the accelerated protons, the magnetic field of the bending dipole and the deflection angle is given by the relativistic formula:

$$\begin{array}{ccc}\hfill E_{kin}& =& -m{c}^2+\sqrt{m^2{c}^4+{\left(\frac{q\Gamma c}{sin\phi }\right)}^2},\hfill \end{array}$$

(1)

where m is the mass of the proton, c the speed of light, $\phi$ the deflection angle, and q the electric charge of the proton. The contribution of the magnetic field is given by the integral magnetic strength $\Gamma =\int B\left(l\right)dl$, where $B\left(l\right)$ is the magnetic field along the path inside the magnet. The factor $\Gamma$ was determined at CERN by measuring the current induced in a single stretched wire put across the magnet [12]. The deflection angle was obtained from the beam profiles as $\phi =\mathrm{atan}\left(\frac{\Delta x}{d}\right)$, where $\Delta x$ is the difference between the position of the centre of the beam profile with and without the magnetic field. For small deflection angles, as in the work presented in this paper, d can be identified with the distance between the centre of the magnet and the scintillating fibre. It should be noted that the non-relativistic approximation of Equation (1) would provide a systematic error which is of the order of the accuracy of this experiment. The main contribution to the uncertainty of the beam energy is due to the determination of $\Delta x$, which is measured with an accuracy of 0.2 mm. The uncertainty propagation can be derived from the non-relativistic approximation [16]:

$$\frac{\Delta E_{kin}}{E_{kin}}=-2\frac{d^2}{d^2+{(\Delta x)}^2}\frac{\Delta (\Delta x)}{\Delta x}.$$

(2)

An analysis prior to the experiment using Equation (2) confirmed that the required accuracy can be obtained.

3. Results and Discussion

Beam profiles were measured with and without applying the magnetic field to evaluate the deflection angle. A typical situation is shown in Figure 4. The two profiles are well separated, and the distance between the two centroids can be assessed with good accuracy.

The field strength of the cyclotron dipole magnet was changed to study the behaviour of the extracted beam energy around the resonance conditions. It has to be noted that these conditions slowly vary during the cyclotron operation due to the warming-up of the machine. As shown in Figure 5, the resonance plateau may shift of a few per mille to higher values of the current in the main coil. The beam intensity was evaluated by the integral of the beam profile measured by the UniBEaM [13]. The carousel for the beam extraction was set at an angle of $\theta$ = 97.08${}^{\circ }$ and the extraction foil 2 was used. This angle was chosen to obtain the maximum resolution in the separation of the profiles. The measured beam energy as a function of the current in the cyclotron main coil is reported in Figure 6. The energy variation in resonance condition due to the change of the cyclotron magnetic field can be estimated to be of the order of 160 keV, under the assumption of linearity between main coil current and cyclotron magnetic field. When the resonance condition is fulfilled, the energy as a function of the main coil current is consistent with the expected $B^2$ dependency. Outside the resonance condition, the non-optimal accordance between the RF signal phase and the phase of the particle revolution induces an off-centring of the beam. This has an effect on the extracted beam orbit and hence on the beam energy, which does not scale with $B^2$ anymore.

The beam energy was measured as a function of the angle of the carousel holding the extraction foils for both foils with the cyclotron in the resonance regime. The results are shown in Figure 7. The energy of the beam extracted with foil 2 is found to be systematically higher of about 300 keV, consistent with the difference of 3 mm in the radial extraction position. The beam energy is found to increase almost linearly with the $\theta$ angle for both foils. This increase is due to the fact that the extraction foil intercepts orbits with higher energy by increasing $\theta$. It has to be remarked that the orbits are not circular due to structure of the cyclotron dipole magnet that presents hills with high magnetic field (1.9 T) and valleys with low field (0.35 T). This peculiar magnetic configuration has an influence on the energy variation shown in Figure 7.

As already stated in the previous section, the main uncertainty is associated to the accuracy on $\Delta x$. Using Equation (2), we obtain for the example shown in Figure 4 a contribution of 170 keV. Other sources of uncertainty are due to the magnetic field of the bending dipole (1%) and to geometrical factors (0.5%). The total uncertainty in the beam energy ranges from 140 to 230 keV.

4. Conclusions

An apparatus for measuring the energy of the beam produced by a medical cyclotron was constructed. It is based on the deflection of the accelerated protons by a known magnetic field and on the measurement of the deflection angle using an optical fibre beam monitoring detector. Our apparatus achieved accuracies comparable to other techniques and has the advantage of being capable of measuring a broad range of beam currents (pA −$\mathsf{\mu }$A), as well as assessing the beam energy almost in real time and in a non-destructive manner.

The energy of the beam extracted in the 6 m long beam transfer line of the Bern medical cyclotron was measured as a function of the current in the main coil of the accelerator and of the angle of the carousel holding the extraction foils. In resonance conditions, the beam energy was found to be constant with respect to small variations of the main coil current for a given position of the carousel. For $\theta$ = 97.08${}^{\circ }$, which corresponds to a typical operational condition, it was measured to be E${}_{kin}$ = (18.59 ± 0.14) MeV. This result is in agreement with our previously published values obtained with independent methods. For a given angle of the extraction carousel, the beam energy is found to increase by shortening the arm of the carousel, as expected. For a given arm, the beam energy is found to increase almost linearly with respect to the angle.

The methodology described in this paper allows for a fast assessment of the beam energy as a function of cyclotron operational parameters. It can be applied to any H${}^{-}$ cyclotron, i.e. with stripping foils for beam extraction, if enough space for installing our apparatus is available. In particular, this technique can be used to optimise processes in which accurate knowledge of the beam energy is crucial, such as radioisotope production with solid target stations.