1D Quantum Simulations of Electron Rescattering with Metallic Nanoblades
Abstract
1. Introduction
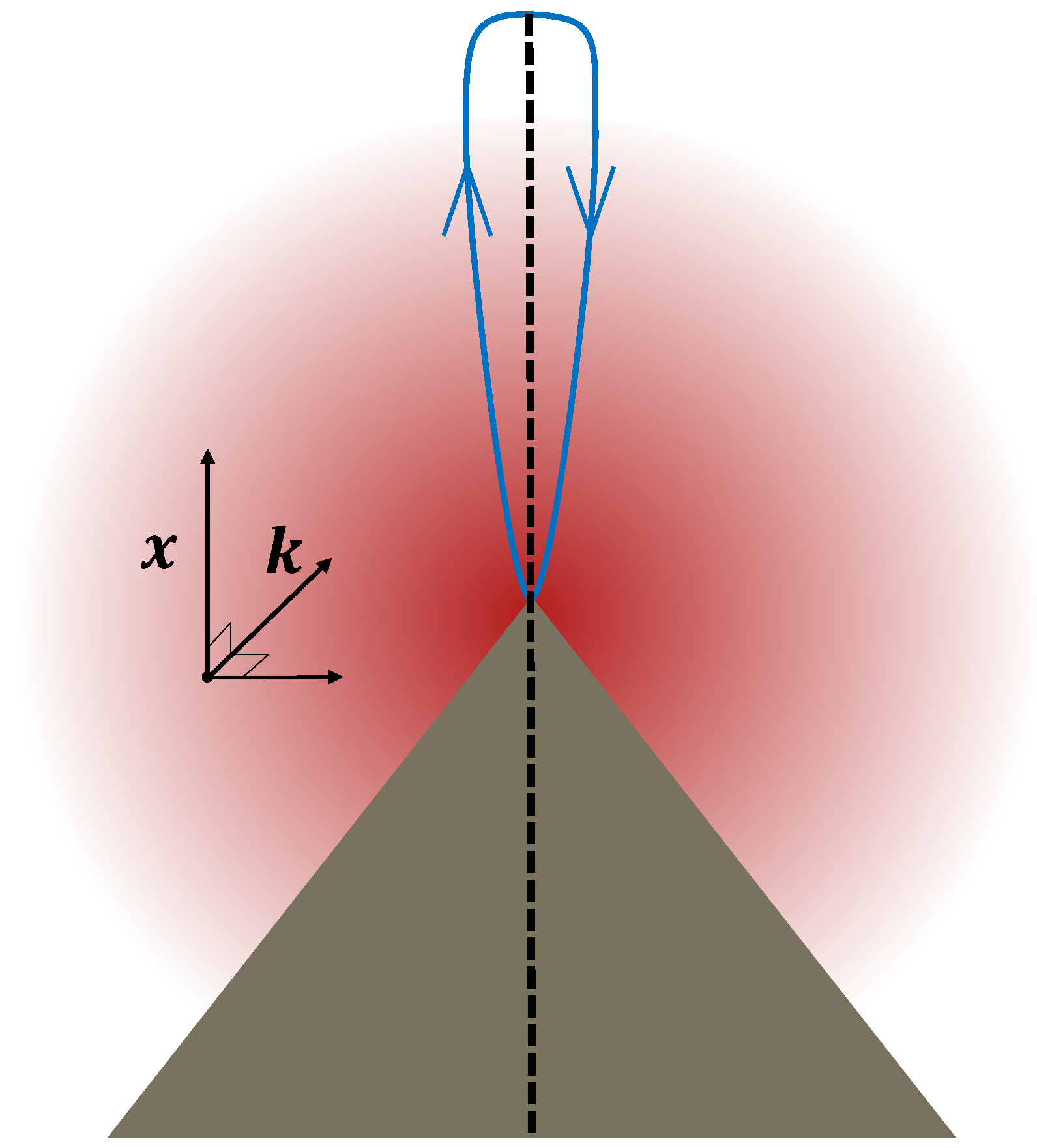
2. Methods
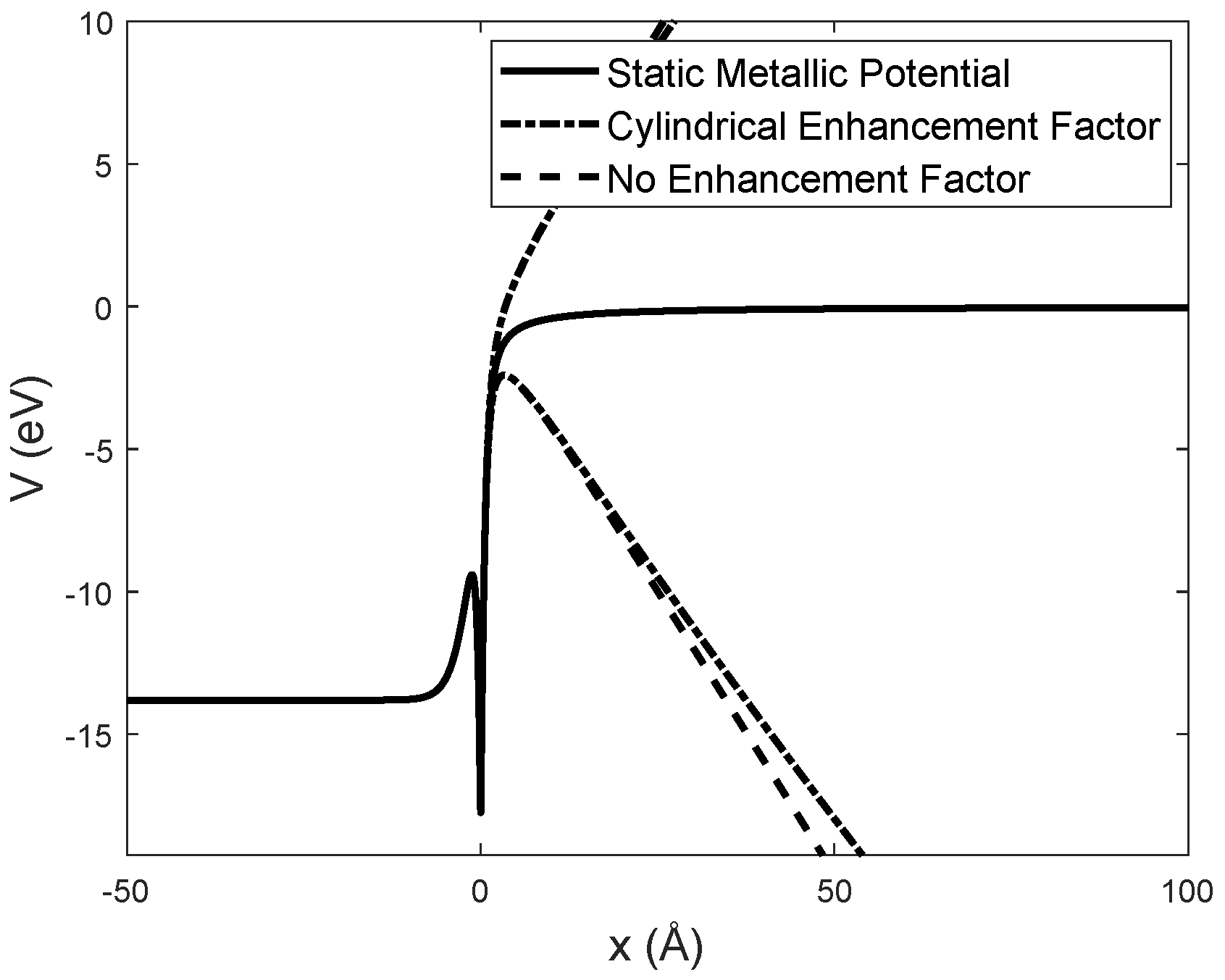
2.1. Electrostatic Potentials
2.2. Simple Light Field Model
2.3. FDTD-Based Light Field Model
2.4. The Virtual Detector Method for Measuring Emitted Electron Spectra
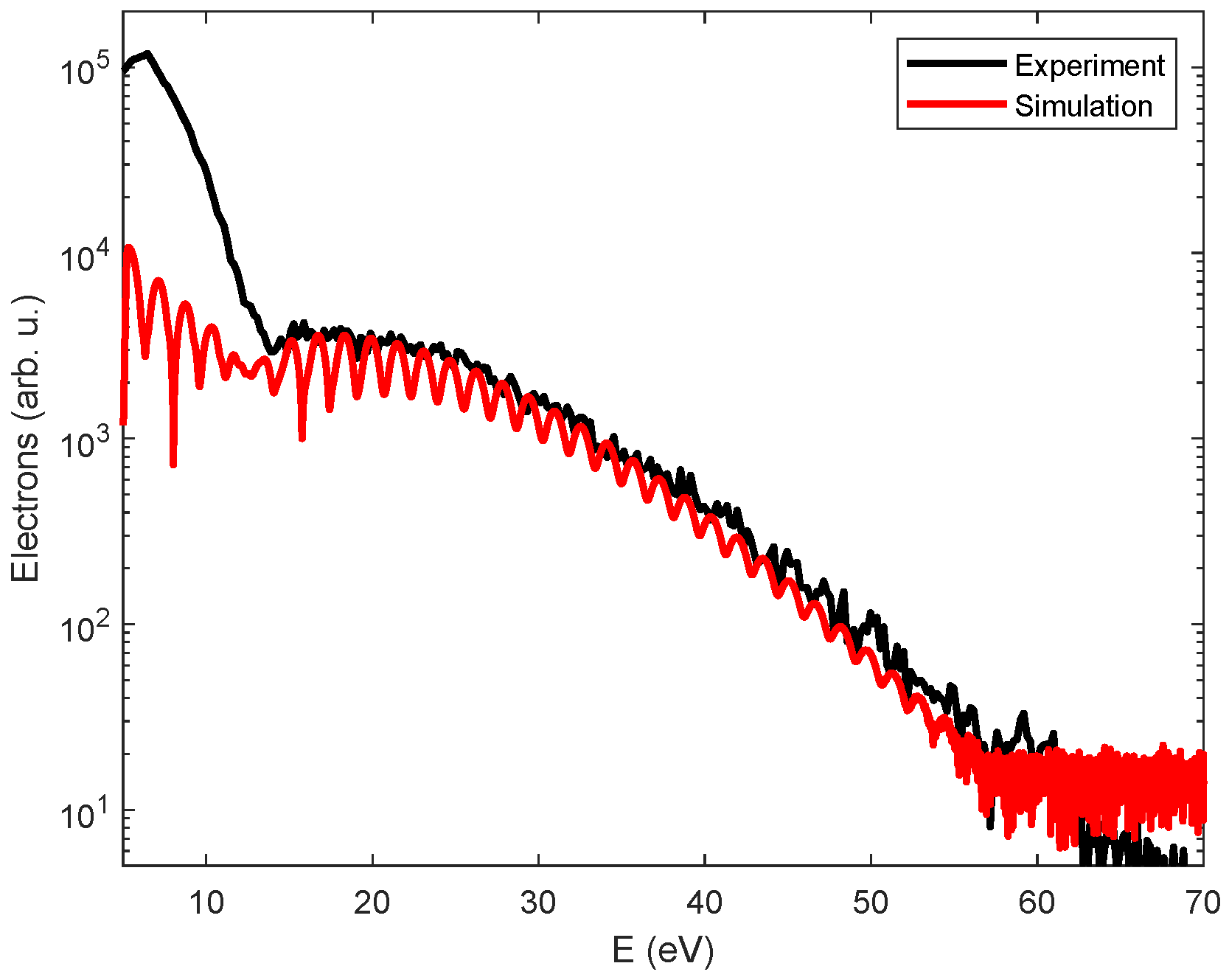
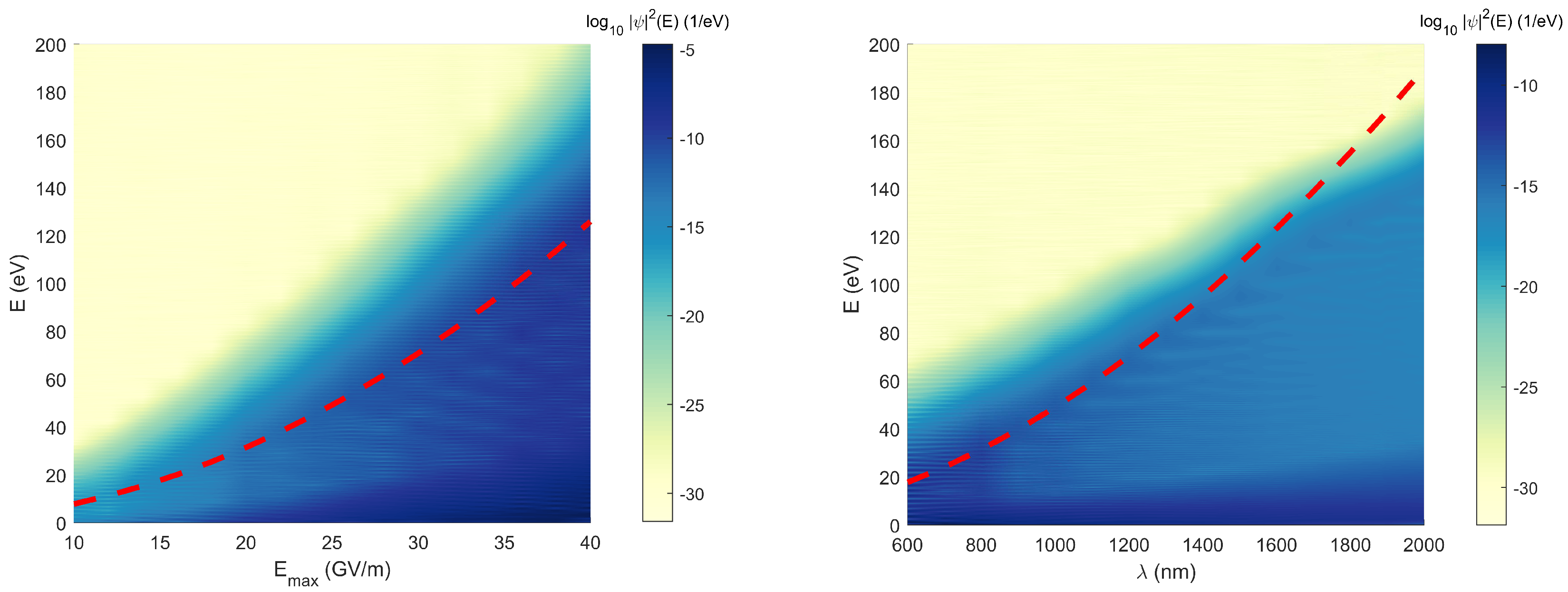
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ATI | Above Threshold Ionization |
| DFT | Density Functional Theory |
| FDTD | Finite-Difference Time-Domain |
| FFT | Fast Fourier Transform |
| FWHM | Full-Width at Half-Max |
| HHG | High Harmonic Generation |
| TD-DFT | Time-Dependent Density Functional Theory |
| TDSE | Time-Dependent Schrödinger Equation |
| UCLA | University of California at Los Angeles |
| VD | Virtual Detector |
| WO | Window Operator |
References
- Tsujino, S.; Beaud, P.; Kirk, E.; Vogel, T.; Sehr, H.; Gobrecht, J.; Wrulich, A. Ultrafast electron emission from metallic nanotip arrays induced by near infrared femtosecond laser pulses. Appl. Phys. Lett. 2008, 92, 193501. [Google Scholar] [CrossRef]
- Schenk, M.; Krüger, M.; Hommelhoff, P. Strong-field above-threshold photoemission from sharp metal tips. Phys. Rev. Lett. 2010, 105, 257601. [Google Scholar] [CrossRef] [PubMed]
- Krüger, M.; Schenk, M.; Hommelhoff, P. Attosecond control of electrons emitted from a nanoscale metal tip. Nature 2011, 475, 78. [Google Scholar] [CrossRef] [PubMed]
- Freeman, R.; Bucksbaum, P.; Milchberg, H.; Darack, S.; Schumacher, D.; Geusic, M. Above-Threshold Ionization with Subpicosecond Laser Pulses. Phys. Rev. Lett. 1987, 59, 1092. [Google Scholar] [CrossRef] [PubMed]
- Paulus, G.; Nicklich, W.; Xu, H.; Lambropoulos, P.; Walther, H. Plateau in Above Threshold Ionization Spectra. Phys. Rev. Lett. 1994, 72, 2851. [Google Scholar] [CrossRef] [PubMed]
- Kruger, M.; Lemell, C.; Wachter, G.; Burgdörfer, J.; Hommelhoff, P. Attosecond physics phenomena at nanometric tips. J. Phys. B 2018, 51, 172001. [Google Scholar] [CrossRef]
- Li, S.; Champenois, E.; Cryan, J.; Marinelli, A. Coherent Space-Charge to X-ray Up-Conversion in Gas. arXiv 2018, arXiv:1806.09650v1. Available online: https://arxiv.org/abs/1806.09650 (accessed on 1 November 2019).
- Hermann, R.; Gordon, M. Quantitative comparison of plasmon resonances and field enhancements of near-field optical antennae using FDTD simulations. Opt. Express 2018, 26, 27668–27682. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Wachter, G.; Lemell, C.; Burgdorfer, J.; Hommelhoff, P. Large optical field enhancement for nanotips with large opening angles. New J. Phys. 2015, 17, 063010. [Google Scholar] [CrossRef]
- Lennart, S.; Paschen, T.; Hommelhoff, P.; Fennel, T. High-order above-threshold photoemission from nanotips controlled with two-colored laser fields. J. Phys. B. 2018, 51, 134001. [Google Scholar]
- Parker, N. Numerical Studies of Vortices and Dark Solitons in Atomic Bose-Einstein Condensates. Ph.D. Thesis, University of Durham, Durham, UK, 7 October 2004. [Google Scholar]
- Lang, N.; Kohn, W. Theory of metal surfaces: Charge density and surface energy. Phys. Rev. B 1970, 1, 4555. [Google Scholar] [CrossRef]
- Jennings, P.; Jones, R.; Weinert, M. Surface barrier for electrons in metals. Phys. Rev. B 1988, 37, 6113. [Google Scholar] [CrossRef] [PubMed]
- Wachter, G. Simulation of Condensed Matter Dynamics in Strong Femtosecond Laser Pulses. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, October 2014. [Google Scholar]
- Paschen, T.; Roussel, R.; Heide, C.; Seiffert, L.; Mann, J.; Kruse, B.; Dienstbier, P.; Fennel, T.; Rosenzweig, J.; Hommelhoff, P. Observation of rescattering and space-charge trapping in strong-field photoemission from a macroscopically extruded nanoblade. PRX 2019. submitted. [Google Scholar]
- Wang, X.; Tian, J.; Eberly, J.H. Virtual detector theory for strong-field atomic ionization. J. Phys. B 2018, 51, 084002. [Google Scholar] [CrossRef]
- Wang, X.; Tian, J.; Eberly, J.H. Extended Virtual Detector Theory for Strong-Field Atomic Ionization. PRL 2013, 110, 243001. [Google Scholar] [CrossRef] [PubMed]
- Schafer, K.; Kulander, K. Energy analysis of time-dependent wave functions: Application to above-threshold ionization. Phys. Rev. A 1990, 42, 5794. [Google Scholar] [CrossRef] [PubMed]
- Paulus, G.; Grasbon, F.; Walther, H.; Kopold, R.; Becker, W. Channel-closing-induced resonances in the above-threshold ionization plateau. Phys. Rev. A 2001, 64, 021401(R). [Google Scholar] [CrossRef]
- Muller, H.; Linden van den Heuvell, H.; Wiel, M. Experiments on “above-threshold ionization” of atomic hydrogen. Phys. Rev. A 1986, 34, 236. [Google Scholar] [CrossRef] [PubMed]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mann, J.; Lawler, G.; Rosenzweig, J. 1D Quantum Simulations of Electron Rescattering with Metallic Nanoblades. Instruments 2019, 3, 59. https://doi.org/10.3390/instruments3040059
Mann J, Lawler G, Rosenzweig J. 1D Quantum Simulations of Electron Rescattering with Metallic Nanoblades. Instruments. 2019; 3(4):59. https://doi.org/10.3390/instruments3040059
Chicago/Turabian StyleMann, Joshua, Gerard Lawler, and James Rosenzweig. 2019. "1D Quantum Simulations of Electron Rescattering with Metallic Nanoblades" Instruments 3, no. 4: 59. https://doi.org/10.3390/instruments3040059
APA StyleMann, J., Lawler, G., & Rosenzweig, J. (2019). 1D Quantum Simulations of Electron Rescattering with Metallic Nanoblades. Instruments, 3(4), 59. https://doi.org/10.3390/instruments3040059





