1. Introduction
Accurate knowledge of the incident beam energy is fundamental for the production of medical radioisotopes; either to optimize production yields or to prevent the co-production of undesired radioimpurities. However, since biomedical cyclotrons are not properly equipped for energy measurements, several indirect measurement techniques have been studied and reported over the years. These methods are commonly based on activity measurements of radioisotopes produced via well-documented and recommended monitor-reactions, requiring both beam current and activity measurements. In order to avoid the difficulty arising from beam current measurements, several authors measured activity ratios from distinct radioisotopes produced simultaneously, either in a single monitor foil or in a stack of target foils, and compared the results to calculated ratios from the recommended cross-sections in the published data [
1,
2,
3,
4]. However, as these methods rely on the determination of absolute activities for two distinct radioisotopes through γ-spectrometry, the results are highly influenced by uncertainties in the absolute efficiency calibration. In order to surmount this drawback, Burrage et al. [
5] suggested the determination of activity ratios for a single radioisotope. Because a unique photopeak is characterized, the technique presents the advantage of requiring neither direct beam-current measurement nor problematic γ-spectroscopy absolute efficiency calibration. Burrage et al. [
5] implemented the method by characterizing the production of
65Zn in a stack of copper foils; with the technique later improved by Asad et al. [
6]. Gagnon et al. [
7] also made use of this technique with only two foils of copper separated by an energy degrader of adequate thickness. These latter methods make use of the fact that each monitor excitation function presents a unique shape so that the activity profile vs. depth, i.e., vs. foil, is specific of the monitor reaction but also dependent on the incident energy. Since the cross-sections and the stopping-power can be estimated for each foil, it is possible to compute and predict the activity ratios between foils for several distinct initial energies and to determine which computed energy best fits the experimental data. As previously pointed out by Gagnon et al. [
7], uncertainties in the cross-sections do not influence the ratio of activities between foils because it is the profile of the excitation function that determines the activity ratio.
The present work describes an improved method based on the stacked-foils technique, in an experimental configuration similar to the useful work of Burrage et al. [
5] and Asad et al. [
6]. The use of several foils in a stack configuration enables to experimentally determine several activity ratios instead of elaborating the result of an entire experiment on a single ratio as is the case in the work developed by Gagnon et al. [
7]. The developed method was used to determine the proton beam energy in a IBA Cyclone 18/9 cyclotron [
8], accelerating protons to 18 MeV. The beam energy was measured at several exit ports and for distinct high-voltages for the radio-frequency. Both the materials used and the experimental arrangement were chosen so that the technique can be immediately performed, exploiting only materials from routine productions, therefore available on-site and later reusable, and without any set-up amendment.
2. Materials and Methods
For proton energies up to about 20 MeV the well established
natCu(p,x)
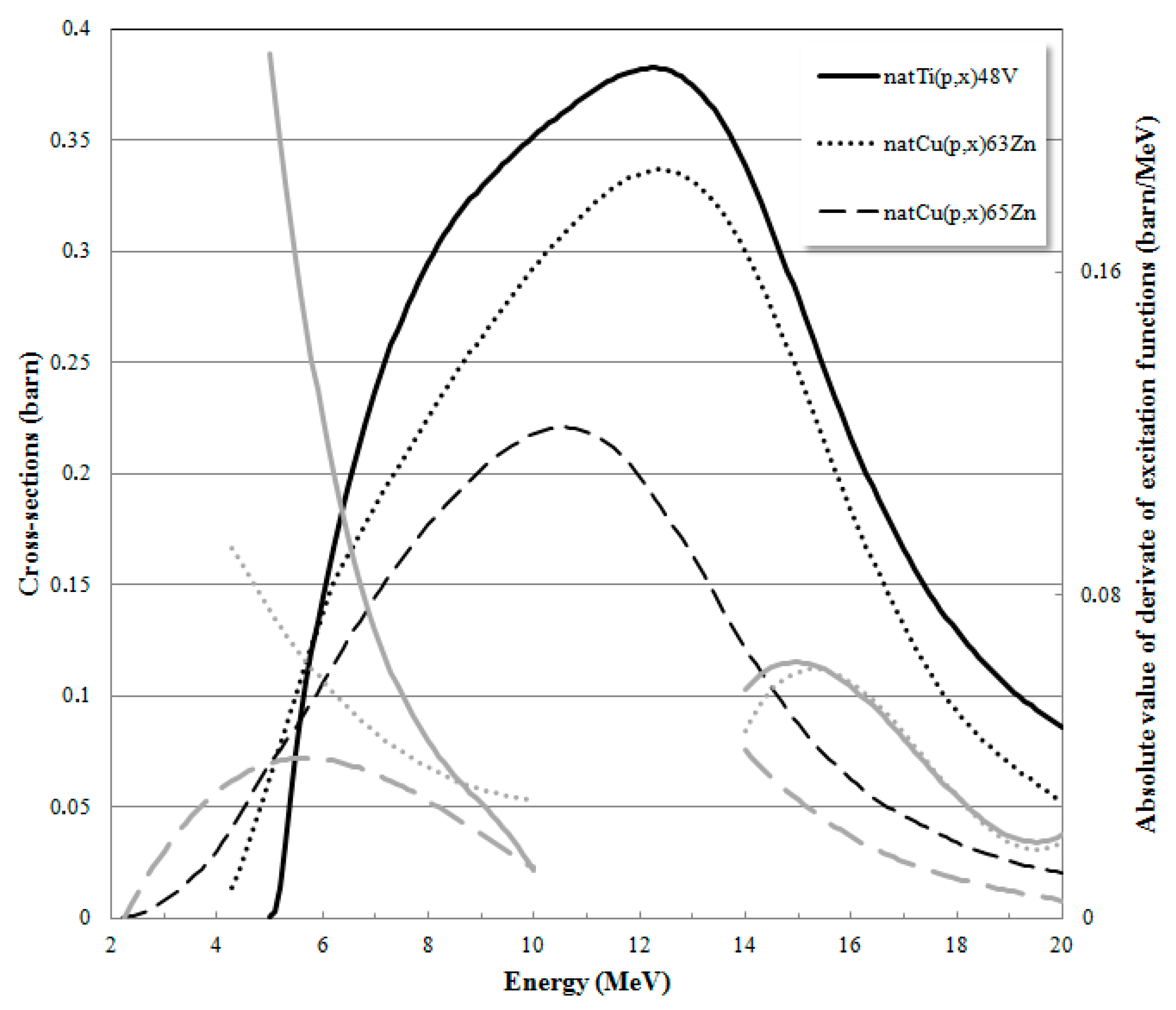
63,65Zn reactions represented in
Figure 1 have been commonly used as monitor reactions [
9].
Figure 1 also shows that the shapes of these monitor reactions only show significant variations in the 5–10 and 14–20 MeV energy ranges. As a result, when a stack is used in the overall energy range as in the work of Asad et al. [
6], part of the experiment contains little information because several foils present similar activities. In the present work, two stacks were exclusively distributed in the two energy ranges showing significant variations, whereas a beam degrader was used around the inadequate 10–14 MeV energy range, following the strategy adopted in the work reported by Gagnon et al. [
7]. Moreover, in order to achieve more significant activity differences between foils so that the “method signal” is more significant, we ought to exploit monitor reactions providing more pronounced variations in the energy ranges of interest. As illustrated in
Figure 1, where the absolute of the derivates of the monitor reactions considered are also represented in the energy ranges of interest, the
natTi(p,x)
48V monitor reaction presents more accentuate absolute variations, in particular in the low-energy region, and was thus chosen as monitor reaction for the present study. This advantageous characteristic is combined with the practicality arising from the fact that 12.5 µm titanium foils are commonly used as vacuum windows in commercial liquid target arrangements in IBA cyclotrons; so that these foils are not only immediately and easily available on site but can also be reused in routine production afterwards. Besides,
48V presents an adequate long half-life of 16 days enabling measurements several days after bombardment. As the stacks were meant for narrower energy ranges, thinner and/or fewer foils are more suitable. Thinner foils present the advantage of providing a smaller and thus more defined energy loss in each foil; an improvement also due to the choice of titanium instead of copper because of its smaller atomic number. Such improved characteristic over the 25–100 µm thick foils of copper used in previous methods is also achieved by using the 12.5 µm thick titanium foils.
The thickness of each of the 99.6% pure and 12.5 µm thick titanium circular foils used was determined by weight determination. Thickness differences between foils are of no concern as the expected activity of each foil are determined, taking into account the experimentally determined thicknesses. The degrader used in the present work was also made from material available from routine productions; namely two 250 µm thick niobium disks commonly used as target windows for the production of radiometals in liquid targets [
10,
11,
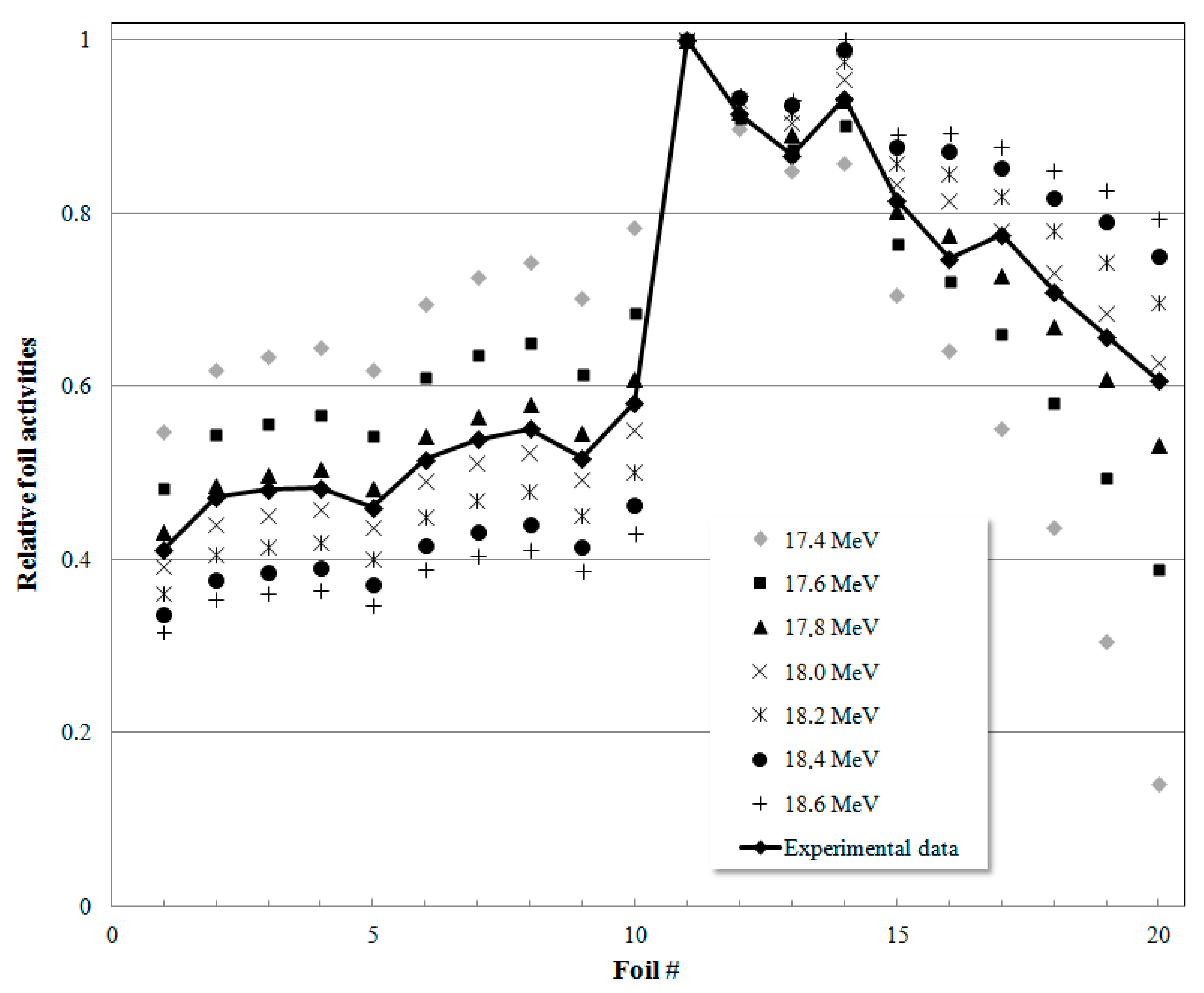
12]. The stack foil arrangement consists of two stacks of ten titanium foils each separated by the niobium degrader. The total thickness, i.e., the number of titanium foils in each stack, was calculated so that the exit beam energy remains slightly higher than the 5.0 MeV threshold of the excitation function. Such consideration also enables one to avoid the larger uncertainties in the proton stopping-power, and therefore in energy, at lower energies. The stack arrangement was mounted in a standard liquid target system with no modifications, precisely at the place where a 12.5 µm titanium foil is usually placed as vacuum window. The rest of the target assembly remained as for routine productions, with the liquid target filled with ultra-pure water. Such an arrangement means that the experimental set-up can be immediately used in any cyclotron target and at any exit port with no additional material and/or modification required; while also benefiting from the continuous helium cooling flux available at the end side of the stack. Irradiations of the liquid target containing the stack were performed at 1 µA and during 5–10 min so that the foil activities remain inferior to about 100 kBq at End-Of-Bombardment (EOB). The first foil of the second stack crossed, i.e., the foil just after the Nb energy degrader, is the foil expected to present the higher activity as illustrated in
Figure 2. Such maximum activity, and thus the maximum irradiation time, was determined so that the foil activities could be determined immediately after proper cooling time taking into account the particular geometry of the HPGe set-up used. The irradiated stack was allowed to cool down for at least one day to minimize the presence of numerous undesired radionuclide in the spectra. Activity measurements were carried out using a high purity germanium (HPGe) spectrometer (model GEM30P4-70 from Canberra) with a dead-time inferior to 4%. The relevant 944.1, 983.5 and 1312.1 keV characteristic γ-lines can all be used to identify and quantify
48V. Although the 983.5 and 1312.1 keV γ-lines are also characteristic of
48Sc, the
natTi(p,x)
48Sc reaction is relevant only for proton energies higher than 18 MeV [
13]. Even if unnecessary, as only relative activities were necessary, the HPGe spectrometer was calibrated in absolute efficiency. Activity measurements can alternatively be performed using a dose calibrator, as considered by Gagnon et al. [
7].
Stopping power for protons in
natTi and
natNb were obtained using the SRIM software [
14] and used to determine continuous polynomial function fits. The IAEA recommended cross-sections for the
natTi(p,x)
48V reaction [
9] were also fitted to two distinct continuous polynomial functions, for the high 14–20 and low 5–10 MeV energy ranges. These continuous functions enable the computation of the activities of each foil taking into account the experimentally deduced thicknesses, using small increments of 0.5 µm. The procedure was repeated for several initial impinging energies in the 17.4–18.6 MeV energy range as the nominal energy is 18 MeV. Although the beam current and the irradiation time considered in the calculations match the ones used in typical irradiations; these are not important because the calculated activities are only used to determine relative intensities.
Figure 2 presents typical calculated relative activity profiles, determined for different impinging energies, together with an activity profile determined experimentally.
Figure 2 illustrates the fact that the activity profile vs. depth depends on the initial beam energy.
In order to determine the computed activity profile that best matches the experimental data, the experimentally obtained relative activities were compared to the computed relative activities by calculating their residual for each foil. The residuals were then squared and summed for the several initial energies considered in the calculations to be used in an iterative least-squares minimization technique to adjust the experimental data, as described in Asad et al. [
6].
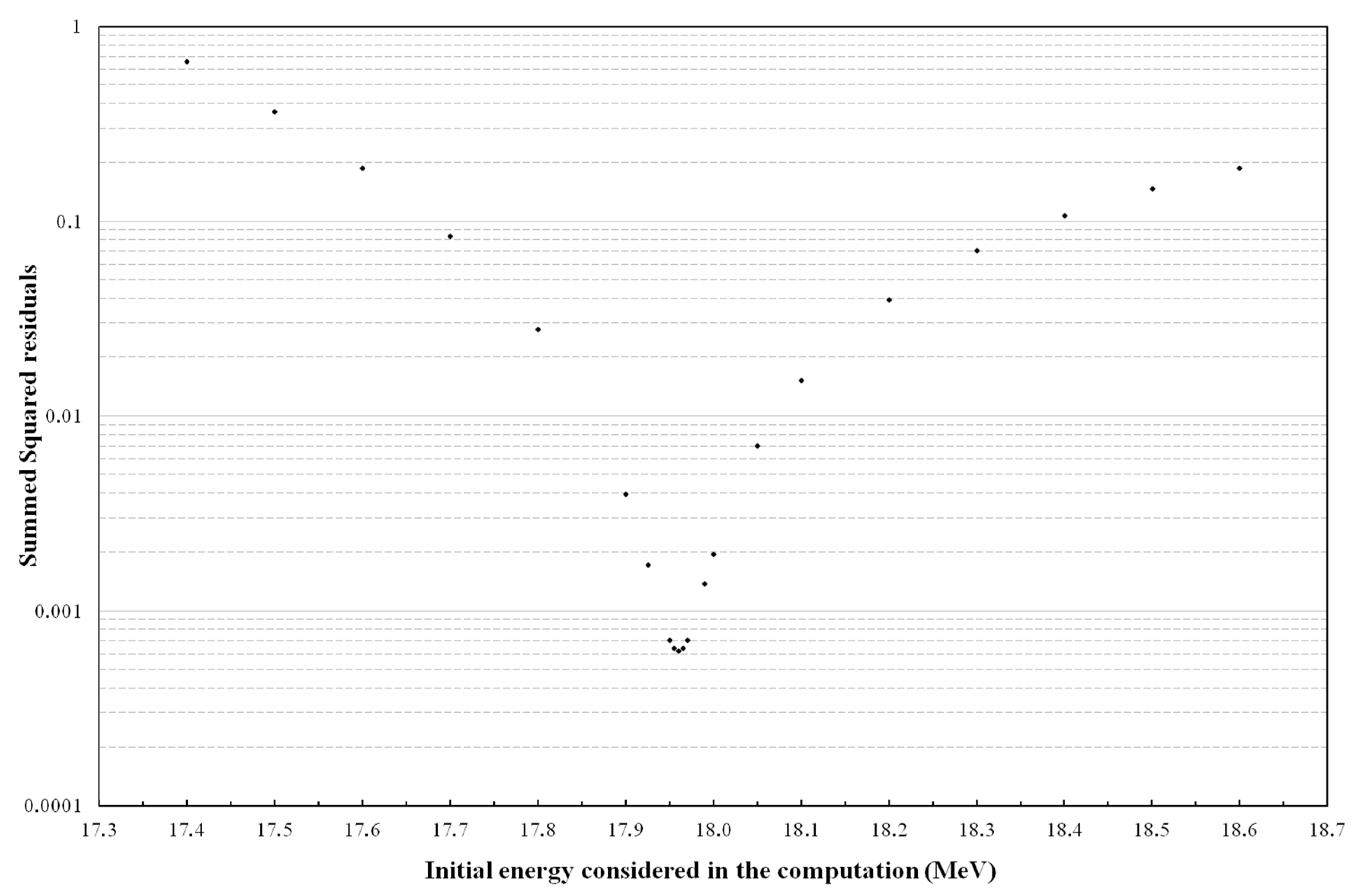
Figure 3 presents a typical example of the sum of squared residuals as a function of the initial energy considered in the computation; illustrating the fact that there is a matching computed initial energy providing minimized squared residuals.
The procedure described was repeated for distinct high-voltages in the radiofrequency system and using a same exit port and also at different exit ports while maintaining constant 32 kV in the radio-frequency system.
Table 1 shows that the radio-frequency voltage affects the beam energy on target; an expected result as the voltage alters the condition of acceleration. Two of the distinct exit ports used were also intentionally chosen as diametrically opposed in order to evaluate the influence of the last acceleration stage between exit ports. The experimentally obtained beam energy for these two diametrically opposed exits were 17.900 ± 11.6% MeV and 17.960 ± 11.6% MeV; a result in agreement with the fact that the maximum energy gain is 32 kV between the two exits considered.
The technique provides precise results as the matching computed energy is experimentally determined considering the combined activities in 20 foils. As illustrated in
Figure 3, slightly different computed energies indeed result in distinct sums of residuals. Such consistency is in agreement with the fact that, given a set of computed foil activity, the result is only determined by the experimentally measured foil activities for which the counting statistical error was determined to be not superior to 1% (as the efficiency calibration is not relevant because only activity ratios are considered, the accuracy in the determination of the foil activities is only governed by the statistic in counting events in the Gaussian peak).
One has to point out that the results are obtained bearing in mind that the incident beam energy is not fully monoenergetic. Indeed, as the particles are not all exactly centered with the geometrical center of the cyclotron during the accelerating revolutions, the beam shape alters in between accelerations and results in a certain beam width with consequent energy spread. Additionally, the stripping process at the end of acceleration of the H− ions also slightly increases the final energy spread. The present method only determines average incident beam energies.
Even if identical experiments lead to precise consistency in the computed results, this characteristic is unfortunately not related to the accuracy of the technique. As several aspects, external to the computing technique, are inevitably involved in the method, a discussion concerning the accuracy of the method must arise. For instance, the beam also suffers beam straggling when crossing the stack, leading to an energy spread influencing the results, which was previously evaluated to be of 2.7% [
6] In addition, besides the referred counting statistical error, the calculations of the foil activities are based on the knowledge of the thickness of each foil and inevitably rely on recommended excitation functions and stopping powers from databases. As the errors of these parameters were estimated to be of 1, 10 and 5%, respectively, the uncertainty of the technique was estimated to be of 11.6%; a typical limitation for energy determination techniques based on stacks.