Instrumentation for Simultaneous Non-Destructive Profiling of Refractive Index and Rare-Earth-Ion Distributions in Optical Fiber Preforms
Abstract
1. Introduction
2. Materials and Methods
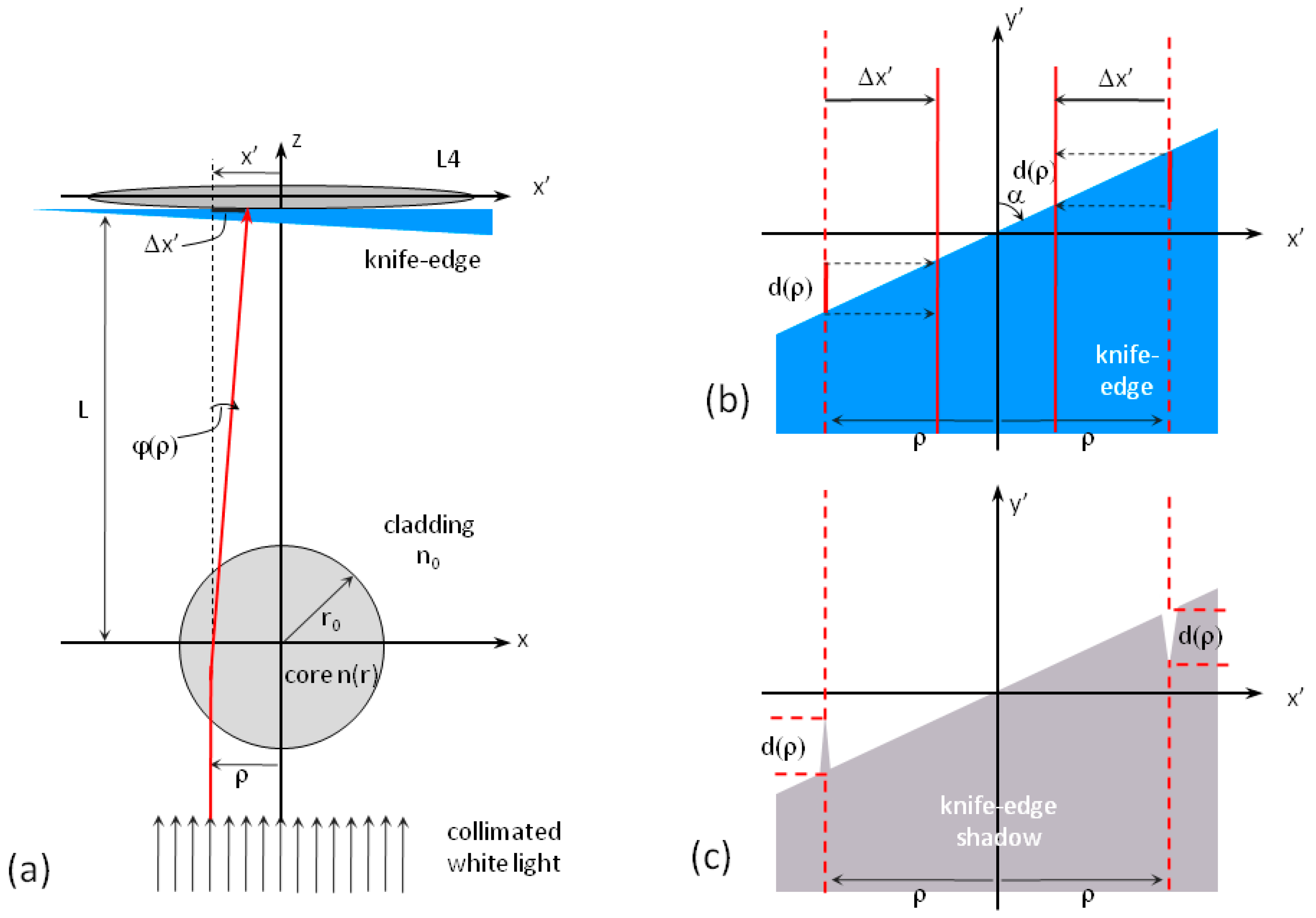
2.1. Refractive Index Profiling: Principle of Operation
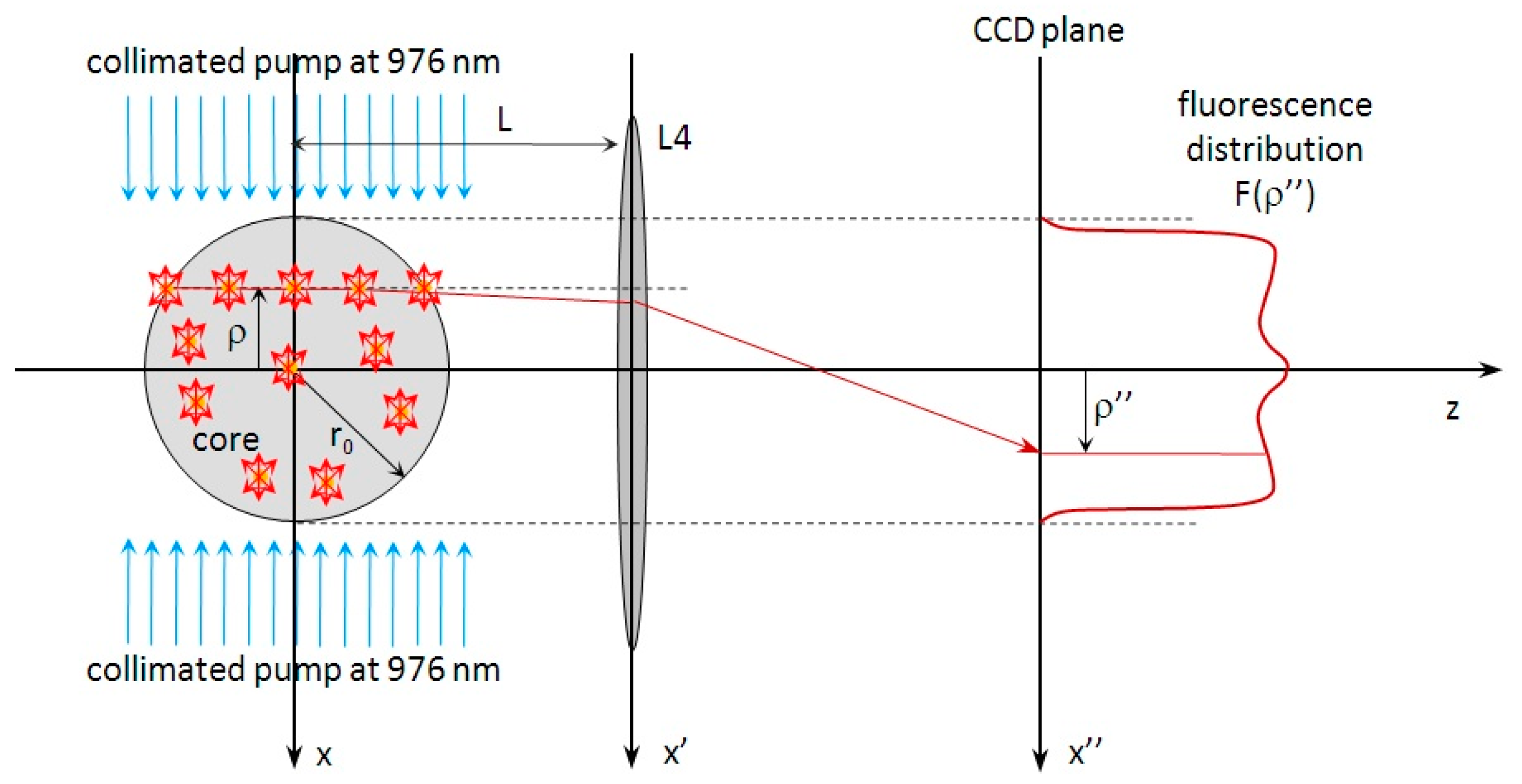
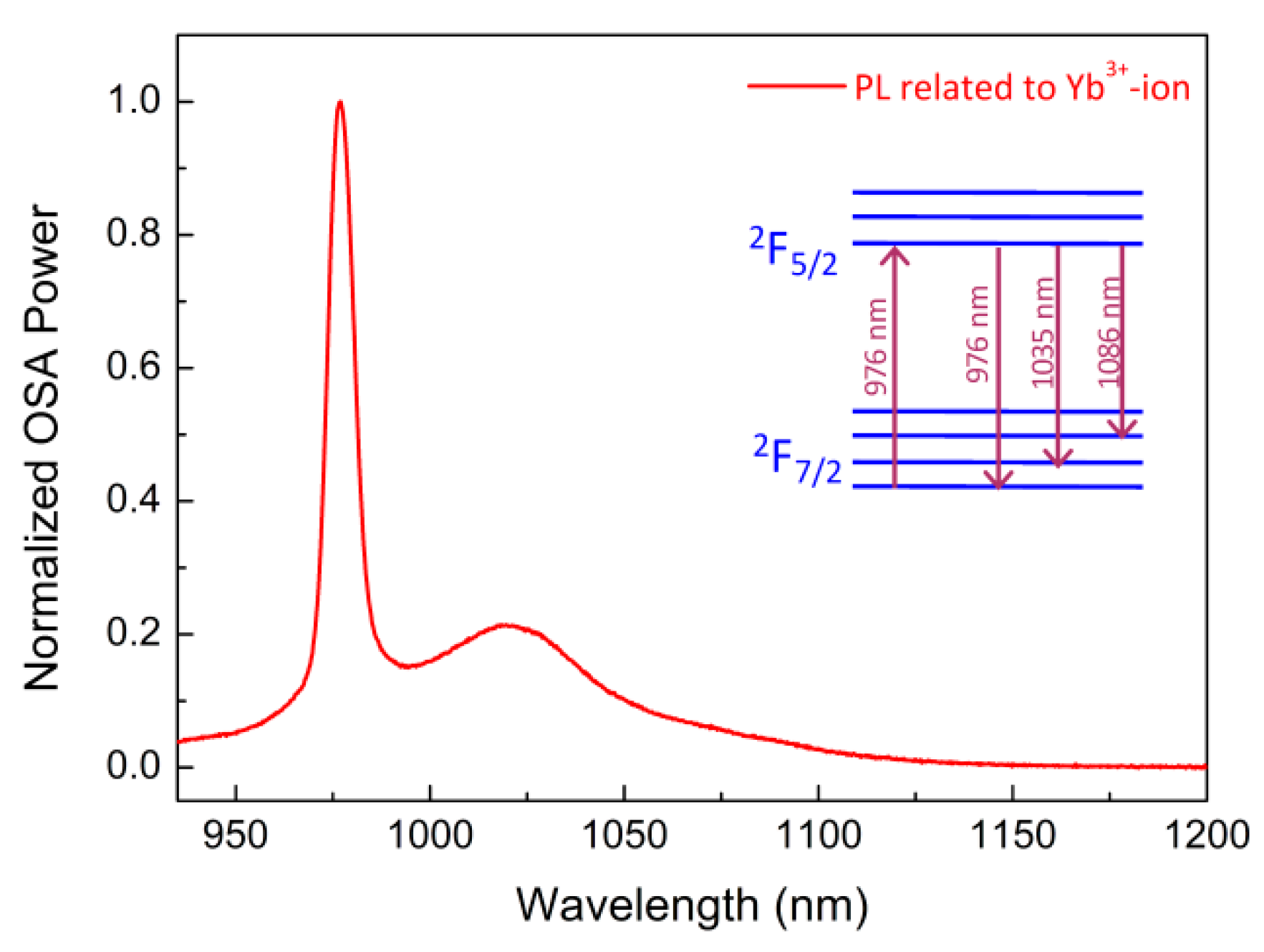
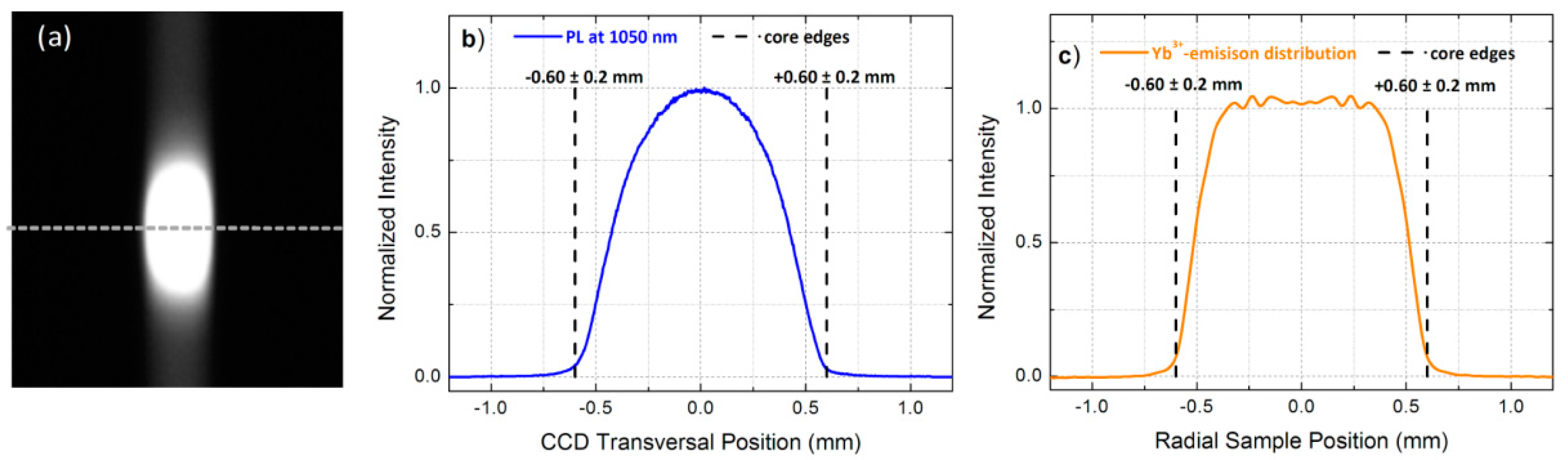
2.2. Active Dopant Distribution Profiling: Principle of Operation
3. Results
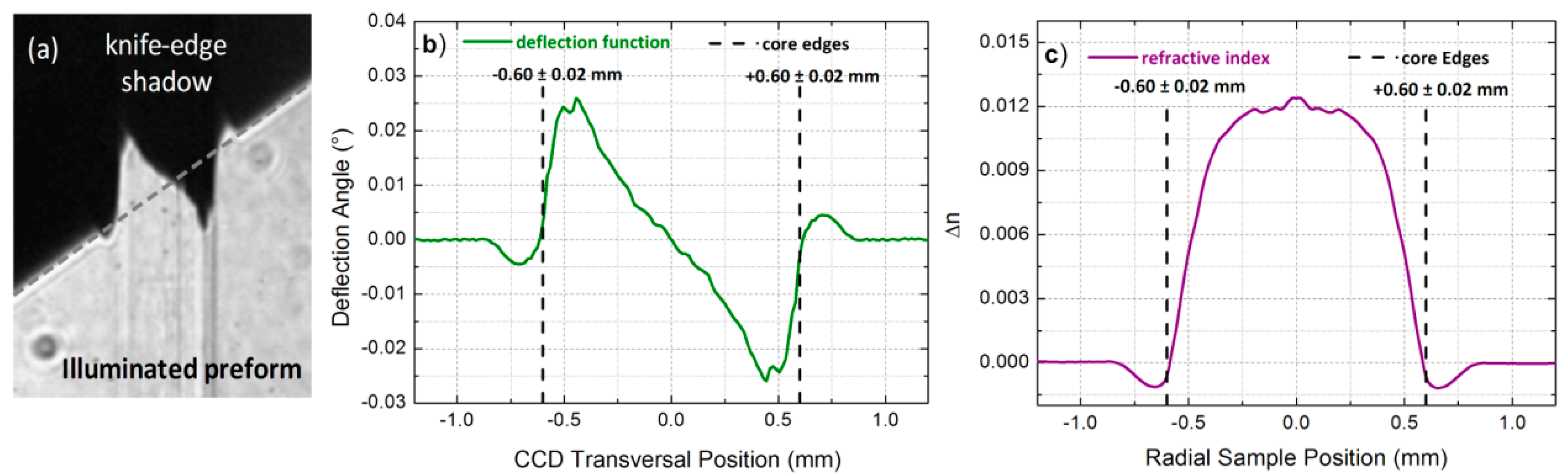
3.1. Refractive Index Profiling
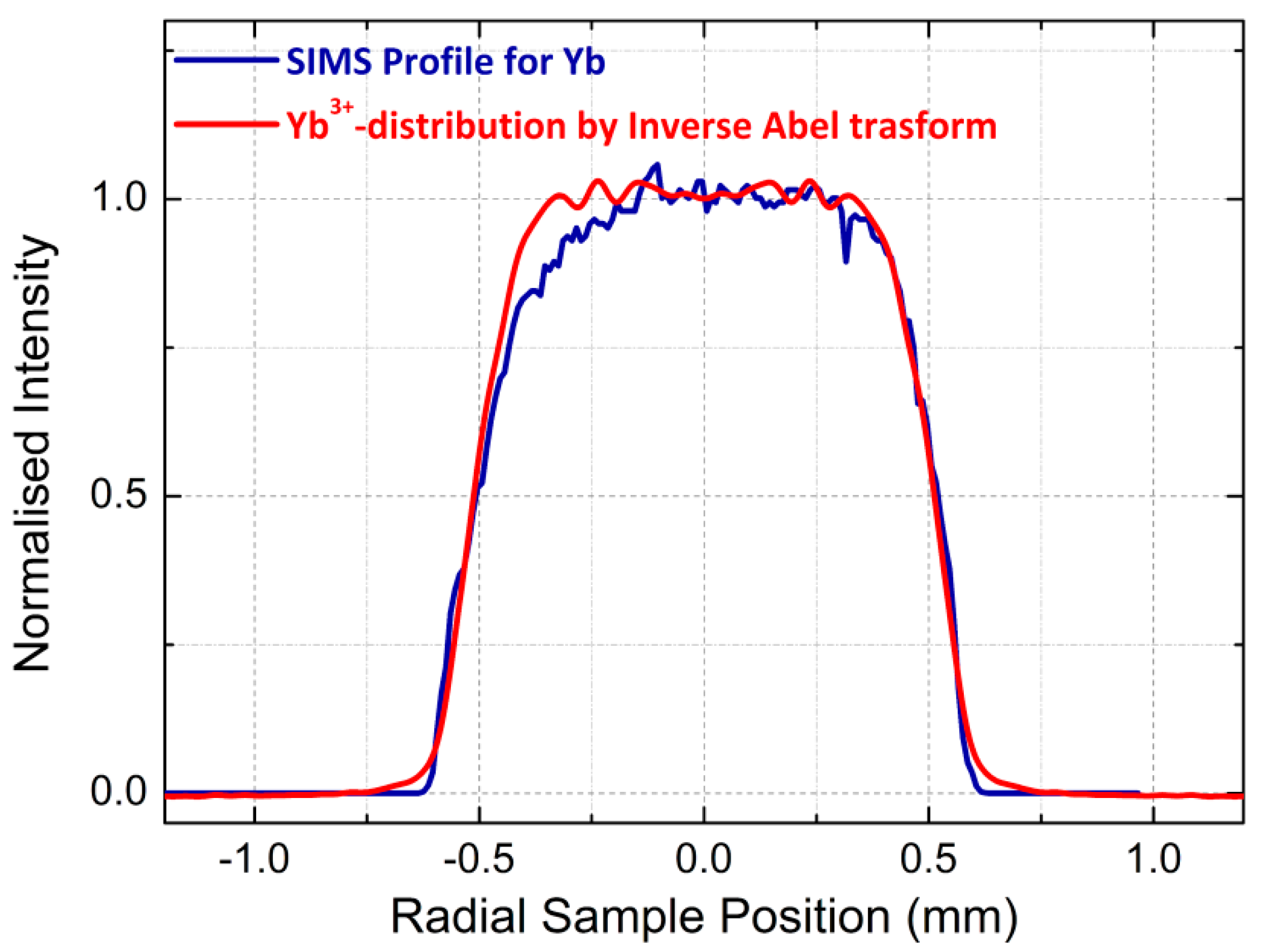
3.2. Active-Dopant Distribution Profiling
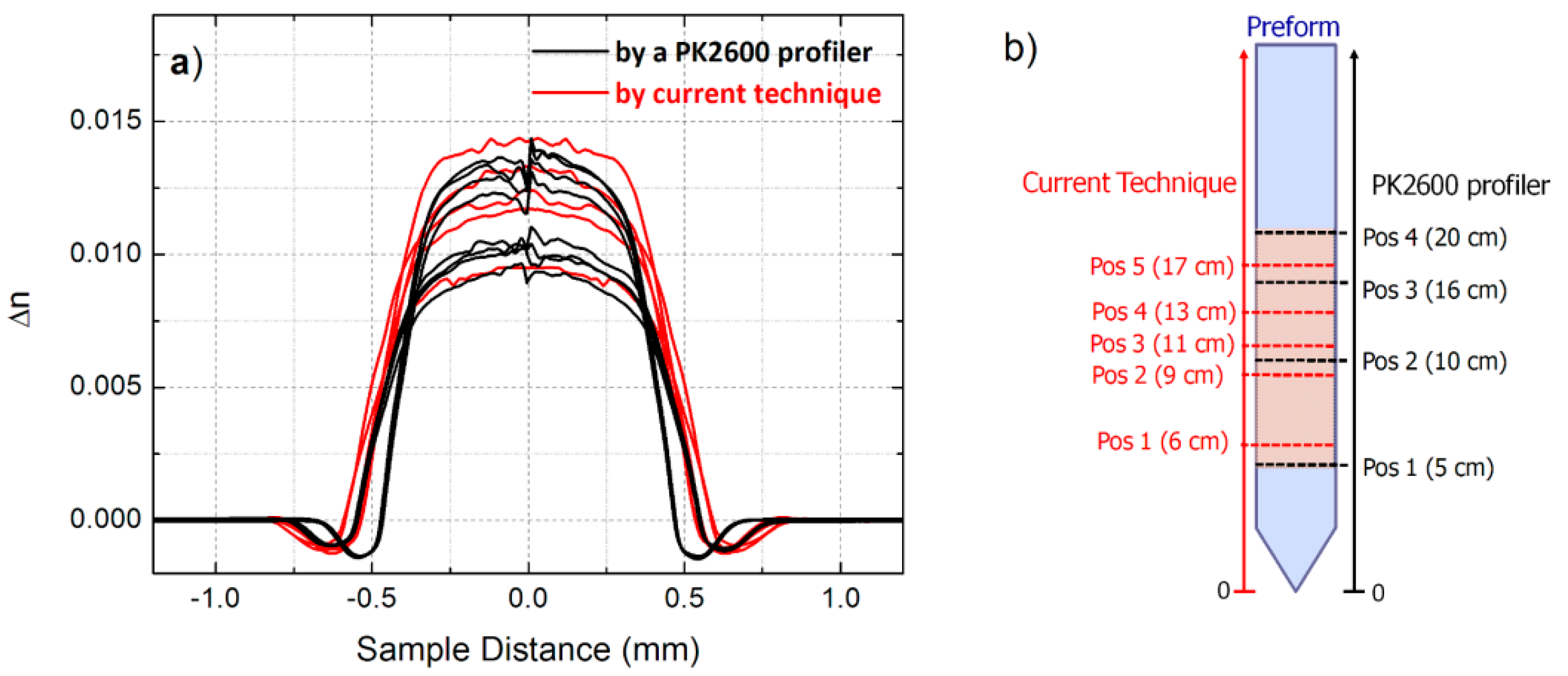
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- SPI Lasers. Available online: https://www.spilasers.com/ (accessed on 4 November 2018).
- Willner, A.E.; Byer, R.L.; Chang-Hasnain, C.J.; Forrest, S.R.; Kressel, H.; Kogelnik, H.; Tearney, G.J.; Townes, C.H.; Zervas, M.N. Optics and Photonics: Key Enabling Technologies. Proc. IEEE 2012, 100, 1604–1643. [Google Scholar] [CrossRef]
- Baek, S.; Jeong, Y.; Nilsson, J.; Sahu, J.K.; Lee, B. Temperature-dependent fluorescence characteristics of an ytterbium-sensitized erbium-doped silica fiber for sensor applications. Opt. Fiber Technol. 2006, 12, 10–19. [Google Scholar] [CrossRef]
- Vedda, A.; Chiodini, N.; Di Martino, D.; Fasoli, M.; Keffer, S.; Lauria, A.; Martini, M.; Moretti, F.; Spinolo, G.; Nikl, M.; et al. Ce3+-doped fibers for remote radiation dosimetry. Appl. Phys. Lett. 2004, 85, 6356–6358. [Google Scholar] [CrossRef]
- Yu, A.W.; Krainak, M.A.; Stephen, M.A.; Chen, J.R.; Coyle, B.; Numatam, K.; Camp, J.; Abshire, J.B.; Allan, G.R.; Li, S.X.; et al. Fiber lasers and amplifiers for space-based science and exploration. Proc. SPIE 2012, 8237, 823713. [Google Scholar] [CrossRef]
- Girard, S.; Vivona, M.; Laurent, A.; Cadier, B.; Marcandella, C.; Robin, T.; Pinsard, E.; Boukenter, A.; Ouerdane, Y. Radiation hardening techniques for Er/Yb-doped optical fibers and amplifiers for space application. Opt. Express 2012, 20, 8457–8465. [Google Scholar] [CrossRef] [PubMed]
- Zervas, M.N.; Codemard, C.A. High Power Fiber Lasers: A Review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 0904123. [Google Scholar] [CrossRef]
- Nagel, S.R.; Mac Chesney, J.B.; Walker, K.L. An overview of the modified chemical vapor deposition (MCVD) process and performance. IEEE J. Quantum Electron. 1982, 18, 459–476. [Google Scholar] [CrossRef]
- Townsend, J.E.; PooleS, B.; Payne, D.N. Solution-doping technique for fabrication of Rare Earth-doped optical fibres. Electron. Lett. 1987, 23, 329–331. [Google Scholar] [CrossRef]
- Schuster, K.; Unger, S.; Aichele, C.; Lindner, F.; Grimm, S.; Litzkendorf, D.; Kobelke, J.; Bierlich, J.; Wondraczek, K.; Bartelt, H. Material and technology trends in fiber optics. Adv. Opt. Technol. 2014, 3, 447–468. [Google Scholar] [CrossRef]
- Krummrich, P.M. Spatial multiplexing for high capacity transport. Opt. Fiber Technol. 2011, 17, 480–489. [Google Scholar] [CrossRef]
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef]
- Stewart, W.J. Optical fiber and preform profiling technology. IEEE Trans. Microw. Theory Technol. 1982, 30, 1439–1454. [Google Scholar] [CrossRef]
- Sidiroglou, F.; Roberts, A.; Baxter, G. Contributed Review: A review of the investigation of rare-earth dopant profiles in optical fibers. Rev. Sci. Instrum. 2016, 87, 041501. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, I.; Payne, D.N.; Adams, M.J. Measurement of refractive-index profiles in optical-fibre preforms by spatial-filtering technique. Electron. Lett. 1980, 6, 219–221. [Google Scholar] [CrossRef]
- Okoshi, T.; Nishimura, M.; Kosuge, M. Non-destructive measurement of axially non-symmetric refractive-index distribution of optical fibre preforms. Electron. Lett. 1980, 16, 722–723. [Google Scholar] [CrossRef]
- Saekeang, C.; Chu, P.L.; Whitbread, T.W. Nondestructive measurement of refractive index profile and cross-sectional geometry of optical fiber preforms. Appl. Opt. 1980, 19, 2025–2030. [Google Scholar] [CrossRef] [PubMed]
- Roberts, A.; Ampem-Lassen, E.; Barty, A.; Nugent, K.A.; Baxter, G.W.; Dragomir, N.M.; Huntington, S.T. Refractive-index profiling of optical fibers with axial symmetry by use of quantitative phase microscopy. Opt. Lett. 2002, 27, 2061–2063. [Google Scholar] [CrossRef] [PubMed]
- Kagi, N.; Oyobe, A.; Nakamura, K. Gain Characteristics of E3+ doped fiber with a quasi-confined structure. J. Lightwave Technol. 1990, 8, 1319–1322. [Google Scholar] [CrossRef]
- Bowron, D.T.; Newport, R.J.; Rigden, J.S.; Tarbox, E.J.; Oversluizen, M. An X-ray absorption study of doped silicate glass, fibre optic preforms. J. Mater. Sci. 1996, 32, 485–490. [Google Scholar] [CrossRef]
- Aljamimi, S.M.; Yusoff, Z.; Abdul-Rashid, H.A.; KhairulAnuar, M.S.; Muhamad-Yasin, S.Z.; Zulkifli, M.I.; Hanif, S.; Tamchek, N. A fabrication of aluminum doped silica preform using MCVD and solution doping technique: Soot analyses and solution concentration effect. Adv. Mater. Res. 2014, 896, 197–202. [Google Scholar] [CrossRef]
- Perry, I.R.; Tropper, A.C.; Barr, J.R.M. Micro-fluorescence profiling of erbium-doped fibre preforms. J. Lumin. 1994, 59, 39–49. [Google Scholar] [CrossRef]
- Hino, M.; Aono, T.; Nakajima, M.; Yuta, S. Light emission computed tomography system for plasma diagnostics. Appl. Opt. 1987, 26, 4742–4746. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, H.; Nakajima, M.; Yuta, S. Measurement of flame temperature distribution by IR emission computed tomography. Appl. Opt. 1985, 24, 4111–4116. [Google Scholar] [CrossRef] [PubMed]
- Yablon, A.D. New transverse techniques for characterizing high-power optical fibers. Opt. Eng. 2011, 50, 111603. [Google Scholar] [CrossRef]
- Marcuse, D. Refractive Index determination by focusing method. Appl. Opt. 1979, 18, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Deans, S.R. Radon and Abel Transforms. In The Transforms and Applications Handbook, 2nd ed.; Alexander, D.P., Ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Nilsson, J.; Paschotta, R.; Caplen, J.E.; Hanna, D.C. Yb3+-ring-doped fiber for high-energy pulse amplification. Opt. Lett. 1997, 22, 1092–1094. [Google Scholar] [CrossRef] [PubMed]
- Quimby, R.S.; Morse, T.F.; Shubochkin, R.L.; Ramachandran, S. Yb3+ Ring Doping in High-Order-Mode fiber for High-Power 977-nm Lasers and Amplifiers. IEEE J. Quantum Electron. 2009, 15, 12–19. [Google Scholar] [CrossRef]
- Kokki, T.; Koponen, J.; Laurila, M.; Ye, C. Fiber amplifier utilizing an Yb-doped large-mode-area fiber with confined doping and tailored refractive index profile. Proc. SPIE 2010, 7580, 758016. [Google Scholar] [CrossRef]
- Kang, Q.; Lim, E.-L.; Jung, Y.; Sahu, J.K.; Poletti, F.; Baskiotis, C.; Alam, S.; Richardson, D.J. Accurate modal gain control in a multimode erbium doped fiber amplifier incorporating ring doping and a simple LP01 pump configuration. Opt. Express 2012, 20, 20835–20843. [Google Scholar] [CrossRef] [PubMed]
- Ip, E. Gain equalization for few-mode fiber amplifiers beyond two propagating mode groups. IEEE Photonics Technol. Lett. 2012, 24, 1933–1936. [Google Scholar] [CrossRef]
- Hansen, K.R.; Alkeskjold, T.T.; Broeng, J.; Lægsgaard, J. Thermally induced mode coupling in rare-earth doped fiber amplifiers. Opt. Lett. 2013, 37, 2382–2384. [Google Scholar] [CrossRef] [PubMed]
- Robin, C.; Dajani, I.; Pulford, B. Modal instability-suppressing, single-frequency photonic crystal fiber amplifier with 811 W output power. Opt. Lett. 2014, 39, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Vest, C.M. Interferometry of strongly refracting axisymmetric phase objects. Appl. Opt. 1975, 14, 1601–1606. [Google Scholar] [CrossRef] [PubMed]
- Vivona, M.; Kim, J.; Zervas, M.N. Non-destructive characterization of rare-earth-doped optical fiber preforms. Opt. Lett. 2018, 37, 2382–2384. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivona, M.; Zervas, M.N. Instrumentation for Simultaneous Non-Destructive Profiling of Refractive Index and Rare-Earth-Ion Distributions in Optical Fiber Preforms. Instruments 2018, 2, 23. https://doi.org/10.3390/instruments2040023
Vivona M, Zervas MN. Instrumentation for Simultaneous Non-Destructive Profiling of Refractive Index and Rare-Earth-Ion Distributions in Optical Fiber Preforms. Instruments. 2018; 2(4):23. https://doi.org/10.3390/instruments2040023
Chicago/Turabian StyleVivona, Marilena, and Michalis N. Zervas. 2018. "Instrumentation for Simultaneous Non-Destructive Profiling of Refractive Index and Rare-Earth-Ion Distributions in Optical Fiber Preforms" Instruments 2, no. 4: 23. https://doi.org/10.3390/instruments2040023
APA StyleVivona, M., & Zervas, M. N. (2018). Instrumentation for Simultaneous Non-Destructive Profiling of Refractive Index and Rare-Earth-Ion Distributions in Optical Fiber Preforms. Instruments, 2(4), 23. https://doi.org/10.3390/instruments2040023





