Optimizing Momentum Resolution with a New Fitting Method for Silicon-Strip Detectors
Abstract
1. Introduction
2. Details of the Method
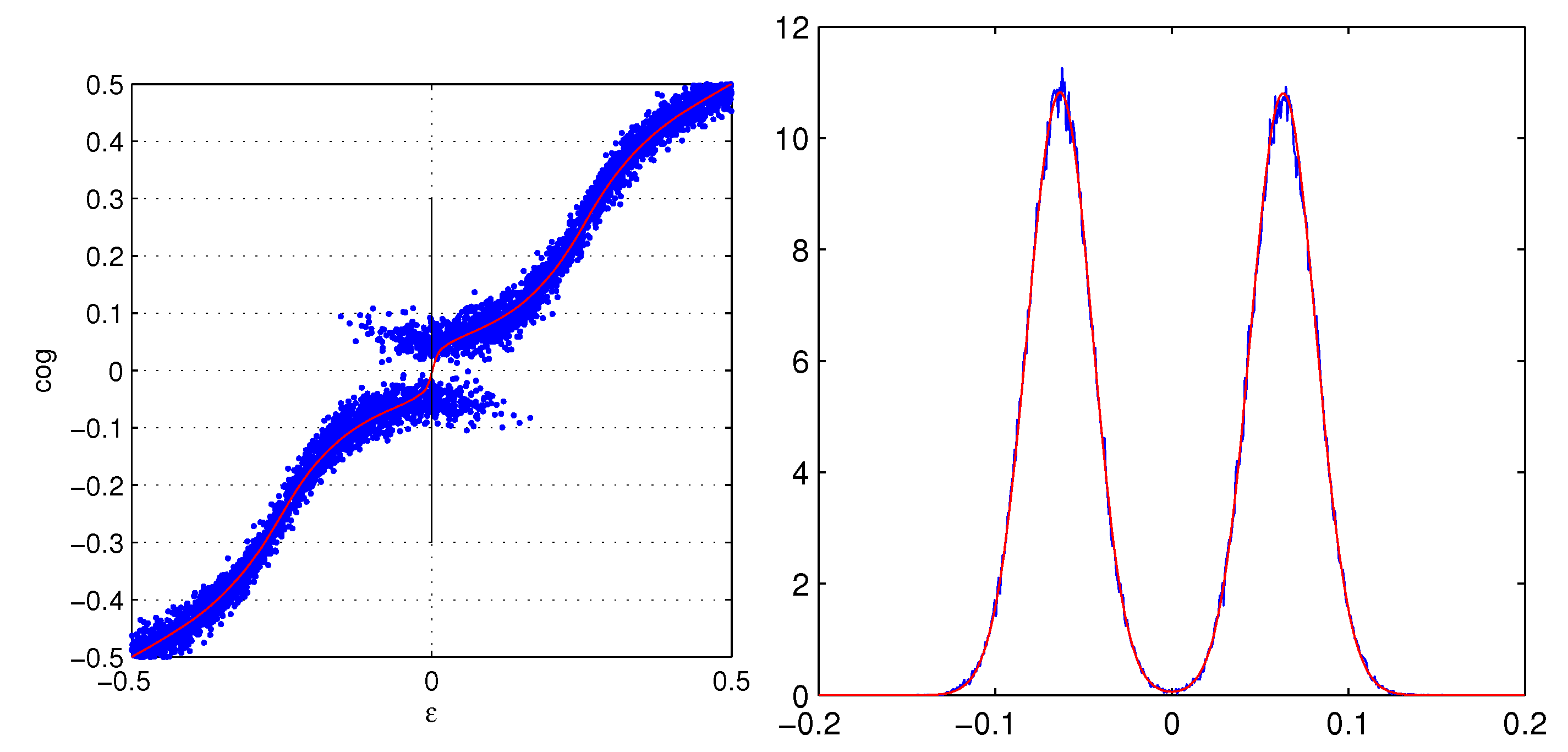
2.1. A Short Derivation of the PDF for the COG Algorithm
2.2. The Probability for Small x
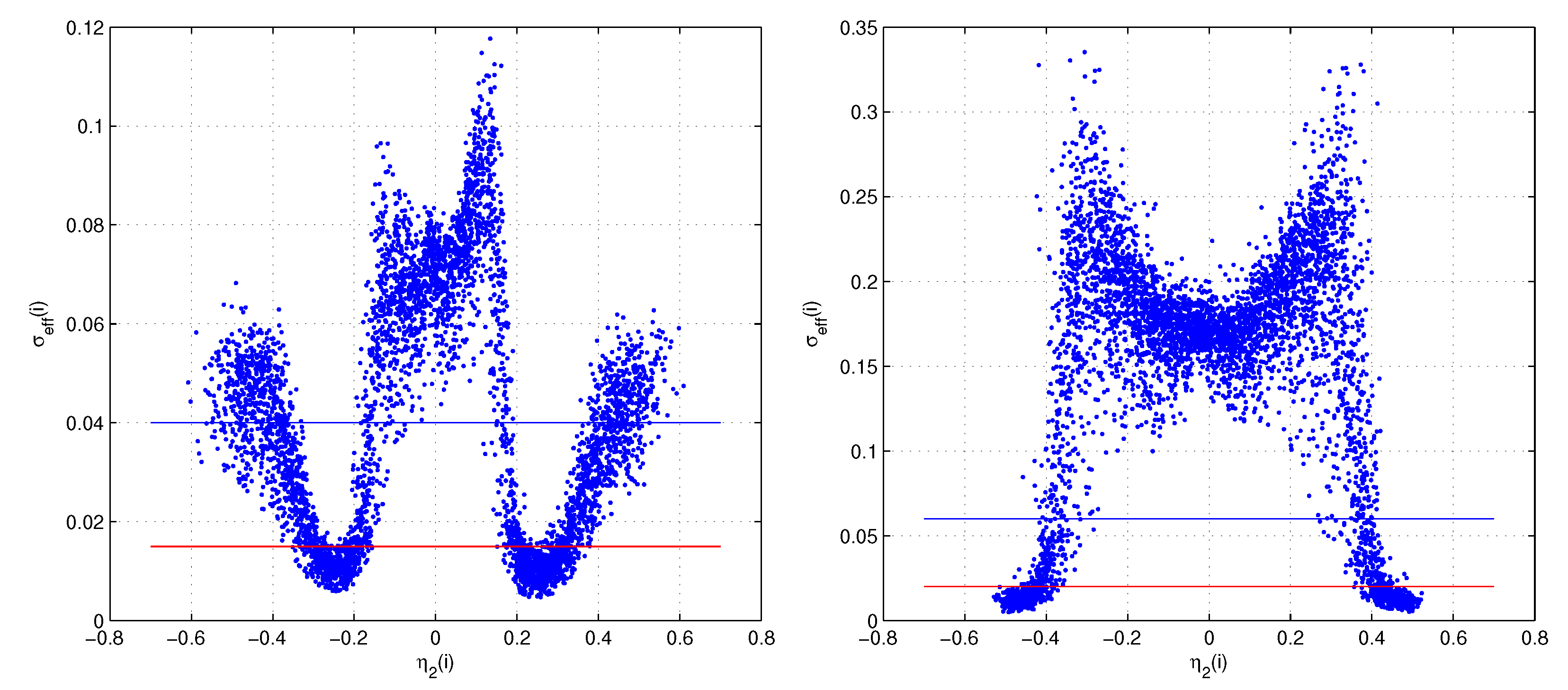
2.3. The Functional Dependence from the Impact Point
2.4. The Position Algorithms
2.5. Track Definition
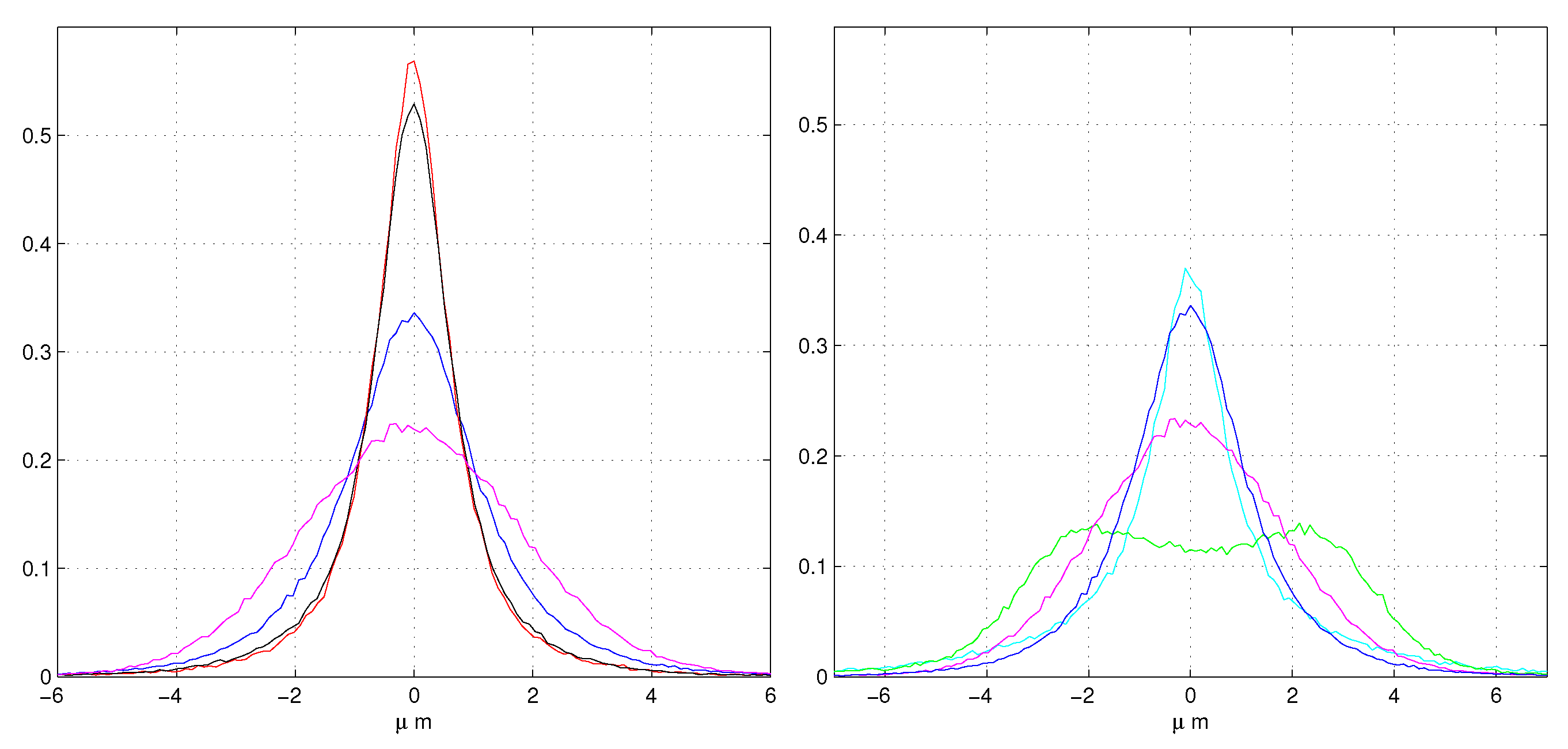
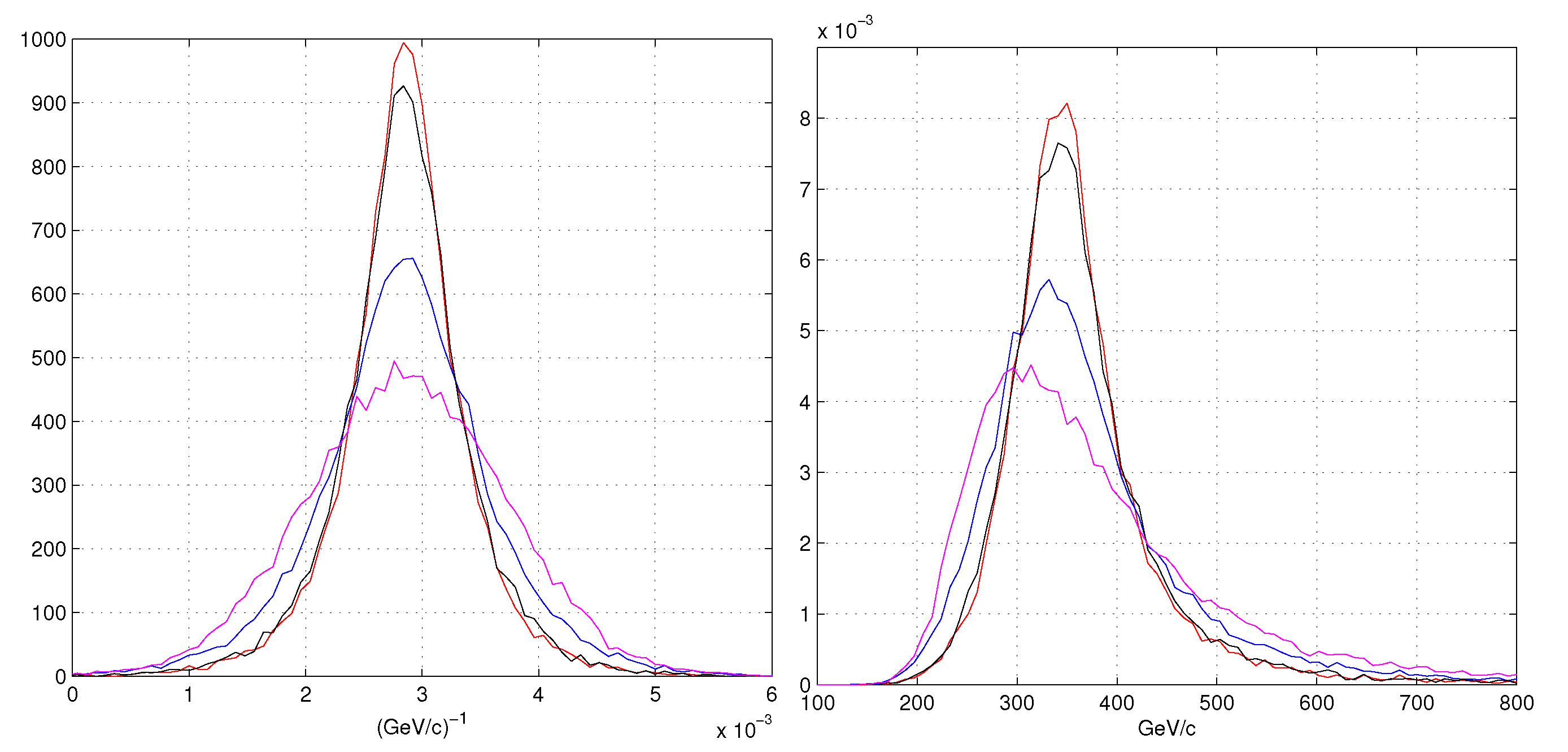
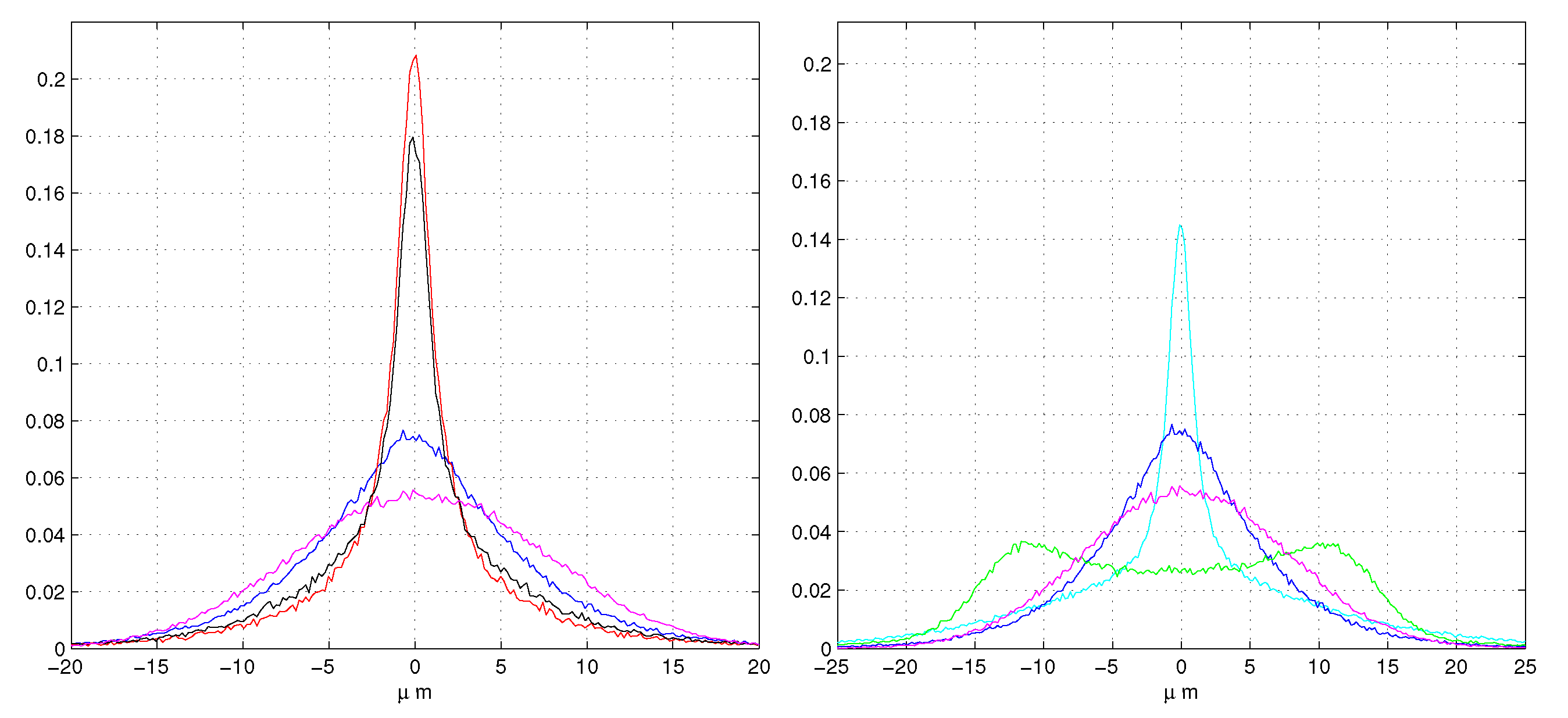
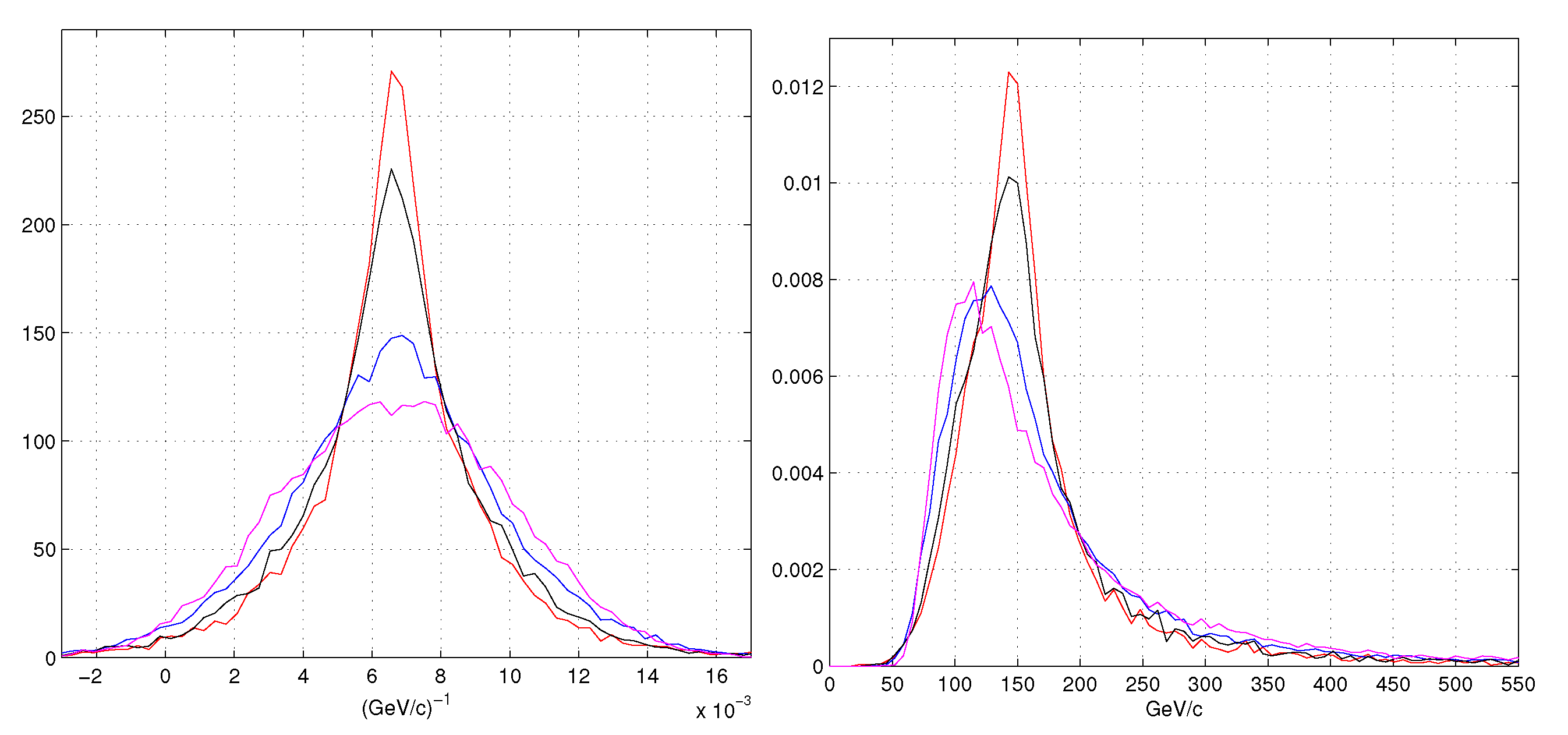
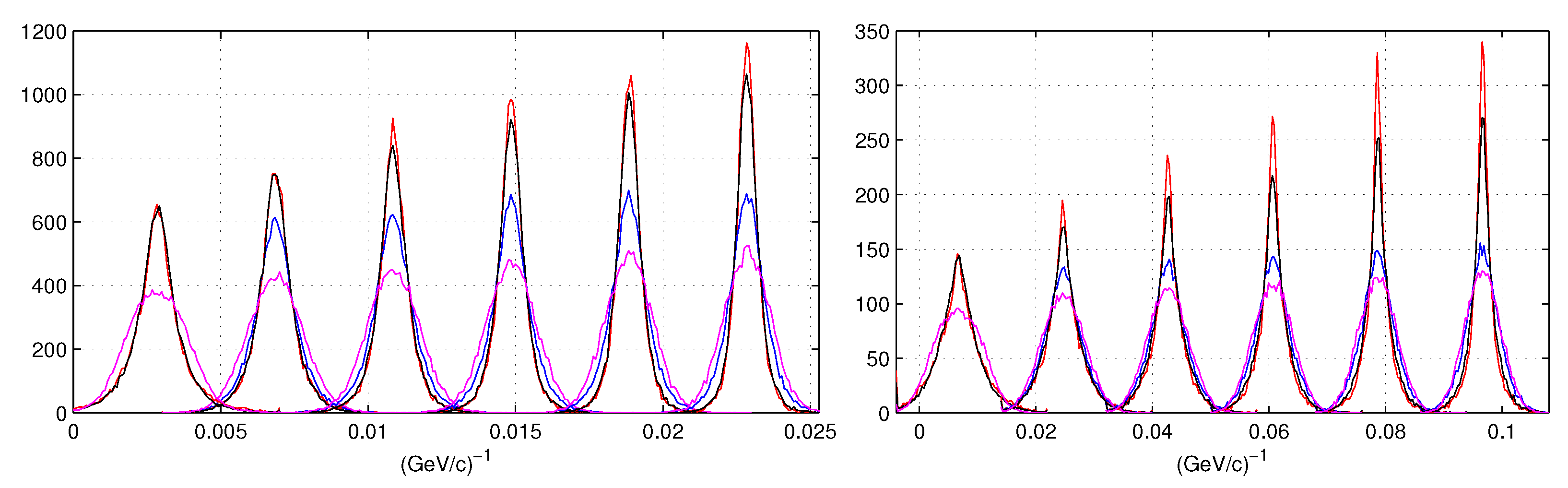
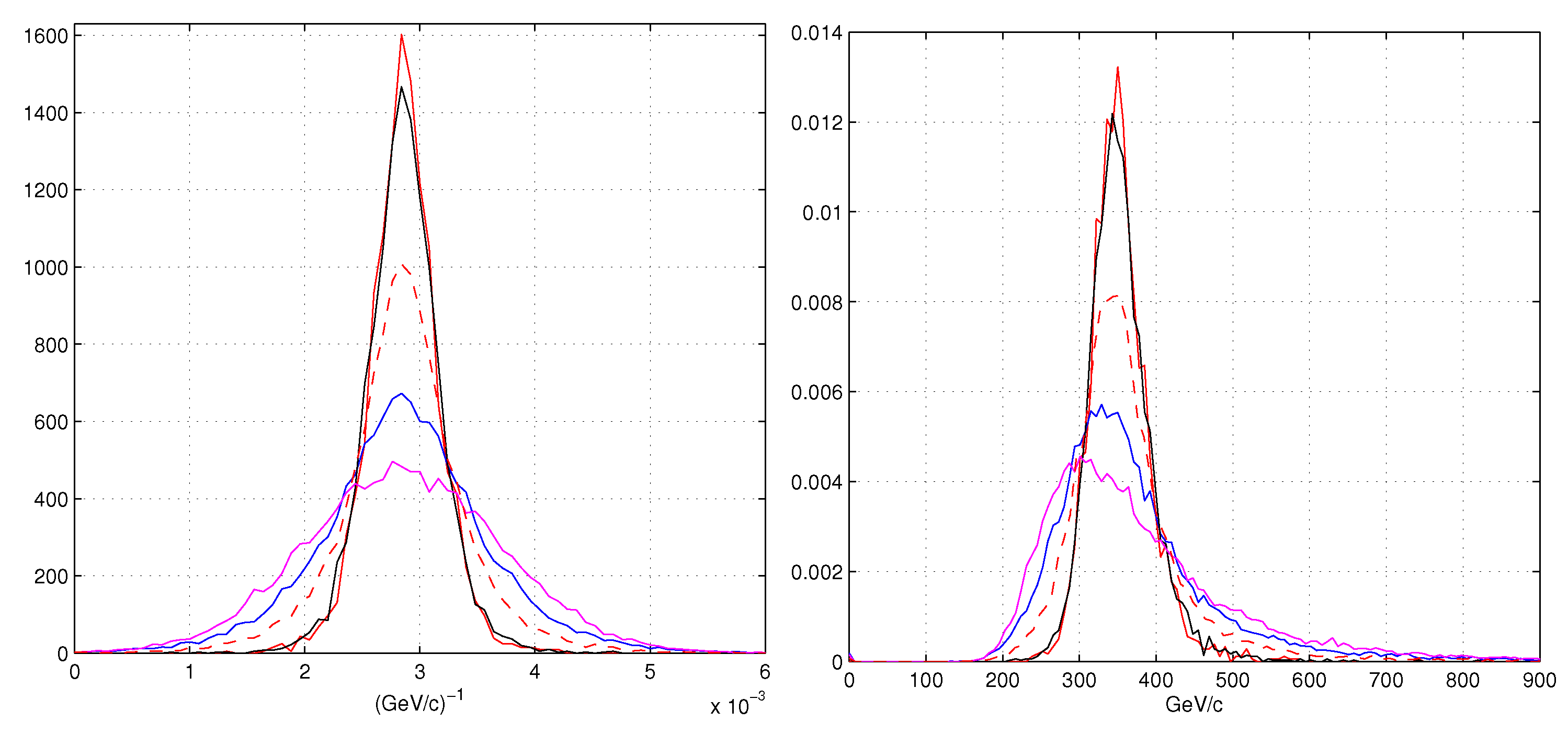
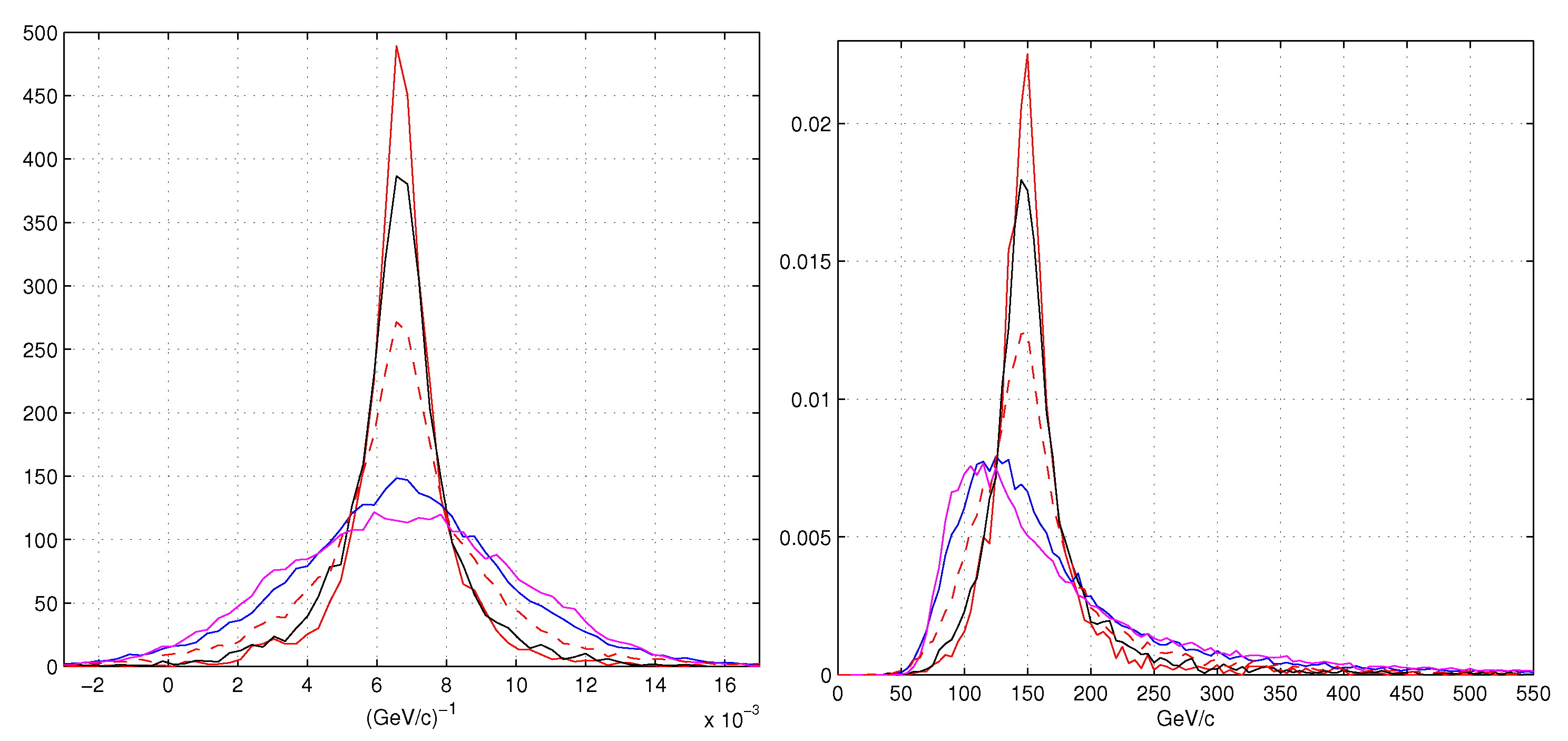
- red lines: refer to our MLE (Equation (10)),
- black lines are the weighted least squares with weight and position,
- blue lines for the least squares with the position algorithm
- magenta lines for the least squares with the COG position algorithm.
3. Low Noise, High Resolution, Floating Strip Side
3.1. Other Track Parameters
4. High Noise, Low Resolution, Normal Strip Side
5. Discussion
5.1. Increasing the Magnetic Field
5.2. Increasing the Signal-to-Noise Ratio
5.3. Momentum Resolution for a Track Selection
5.4. Momentum Resolution for a Track Selection
5.5. A “Gift” from Heteroscedasticity
6. Conclusions
Funding
Conflicts of Interest
Abbreviations
| MIP | Minimum Ionizing Particle |
| Probability Distribution Function | |
| COG | Center of Gravity |
| COG | Center of Gravity algorithm with n-strips |
| MLE | Maximum Likelihood Evaluation. |
References
- Berger, N.; Kozlinskiy, A.; Kiehn, M.; Schõning, A. A new three-dimensional fit with multiple scattering. Nucl. Instrum. Methods Phys. Res. A 2017, 844, 135–140. [Google Scholar] [CrossRef]
- Blobel, V. A new fast track-fit algorithm based on broken lines. Nucl. Instrum. Methods Phys. Res. A 2006, 566, 14–17. [Google Scholar] [CrossRef]
- Karimäki, V. Effective circle fitting for particle trajectories. Nucl. Instrum. Methods Phys. Res. A 1991, 305, 187–191. [Google Scholar] [CrossRef]
- Landi, G. Properties of the center of gravity as an algorithm for position measurements. Nucl. Instrum. Methods Phys. Res. A 2002, 485, 698–719. [Google Scholar] [CrossRef]
- Landi, G. Properties of the center of gravity as an algorithm for position measurements: Two-dimensional geometry. Nucl. Instrum. Methods Phys. Res. A 2003, 497, 511–534. [Google Scholar] [CrossRef]
- Gauss, C.F. Methode de Moindre Carre. Memoires sur la Conbination des Observation; French translation by Bertrand, J.; Revised by the author; Mallet-Bachelier: Paris, France, 1855; Available online: https://books.google.it/books?id=_qzpB3QqQkQC (accessed on 1 September 2018).
- Belau, E.; Klanner, R.; Lutz, G.; Neugebauer, E.; Seebrunner, H.J.; Wylie, A. Charge collection in silicon strip detector. Nucl. Instrum. Methods Phys. Res. A 1983, 214, 253–260. [Google Scholar] [CrossRef]
- Landi, G. Problems of position reconstruction in silicon microstrip detectors. Nucl. Instrum. Methods Phys. Res. A 2005, 554, 226–246. [Google Scholar] [CrossRef]
- Landi, G.; Landi, G.E. Improvement of track reconstruction with well tuned probability distributions. JINST 2014, 9, P10006. [Google Scholar] [CrossRef]
- Adriani, O.; Bongi, M.; Bonechi, L.; Bottai, S.; Castellini, G.; Fedele, D.; Grandi, M.; Papini, P.; Vannuccini, E.; Taddei, E.; et al. In-flight performance of the PAMELA magnetic spectrometer. In Proceedings of the 16th International Workshop on Vertex Detectors, Lake Placid, NY, USA, 23–28 September 2007. [Google Scholar]
- Batignani, G.; Bosi, F.; Bosisio, L.; Conti, A.; Focardi, E.; Forti, F.; Giorgi, M.A.; Parrini, G.; Scarlini, E.; Tempesta, P.; et al. Double sided read out silicon strip detectors for the ALEPH minivertex. Nucl. Instrum. Methods Phys. Res. A 1989, 277, 147–153. [Google Scholar] [CrossRef]
- Adriani, O.; Alcaraz, J.; Ahlen, S.; Ambrosi, G.; Basçhirotto, A.; Battiston, R.; Bay, A.; Bencze, G.; Bertucci, B.; Biasini, M.; et al. The New double sided silicon microvertex detector for the L3 experiment. Nucl. Instrum. Methods Phys. Res. A 1994, 348, 431–435. [Google Scholar] [CrossRef]
- Picozza, P.; Galper, A.M.; Castellini, G.; Adriani, O.; Altamura, F.; Ambriola, M.; Barbarino, G.C.; Basili, A.; Bazilevskaja, G.A.; Bencardino, R.; et al. PAMELA-A Payload for Matter Antmatter Exploration and Light-nuclei Astrophysics. Astropart. Phys. 2007, 27, 296–315. [Google Scholar] [CrossRef]
- Frühwirth, R. Track fitting with non-Gaussian noise. Comput. Phys. Commun. 1997, 100, 1–16. [Google Scholar] [CrossRef]
- Frühwirth, R.; Speer, T. A Gaussian-sum filter for vertex reconstruction. Nucl. Instrum. Methods Phys. Res. A 2004, 534, 217–221. [Google Scholar] [CrossRef]
- ALICE Collaboration. The ALICE experiment at the CERN LHC. JINST 2008, 3, S08002. [Google Scholar] [CrossRef]
- ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider. JINST 2008, 3, S08003. [Google Scholar] [CrossRef]
- CMS Collaboration. The CMS experiment at the CERN Large Hadron Collider. JINST 2008, 3, S08004. [Google Scholar] [CrossRef]
- CMS Collaboration. The performance of the CMS muon detector in proton-proton collision at = 7 TeV at the LHC. JINST 2013, 8, P11002. [Google Scholar] [CrossRef]
- The CMS Collaboration. Description and performance of track and primary-vertex reconstruction with the CMS tracker. JINST 2014, 9, P10009. [Google Scholar] [CrossRef]
- Landi, G.; Landi, G.E. Asymmetries in Silicon Microstrip Response Function and Lorentz Angle. arXiv, 2014; arXiv:1403.4273. [Google Scholar]
- Olive, K.A.; Agashe, K.; Amsler, C.; Antonelli, M.; Arguin, J.-F.; Asner, D.M.; Baer, H.; Band, H.R.; Barnett, R.M.; Basaglia, T.; et al. Particle Data Group. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- MATLAB 8, The MathWorks Inc.: Natick, MA, USA.

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landi, G.; Landi, G.E. Optimizing Momentum Resolution with a New Fitting Method for Silicon-Strip Detectors. Instruments 2018, 2, 22. https://doi.org/10.3390/instruments2040022
Landi G, Landi GE. Optimizing Momentum Resolution with a New Fitting Method for Silicon-Strip Detectors. Instruments. 2018; 2(4):22. https://doi.org/10.3390/instruments2040022
Chicago/Turabian StyleLandi, Gregorio, and Giovanni E. Landi. 2018. "Optimizing Momentum Resolution with a New Fitting Method for Silicon-Strip Detectors" Instruments 2, no. 4: 22. https://doi.org/10.3390/instruments2040022
APA StyleLandi, G., & Landi, G. E. (2018). Optimizing Momentum Resolution with a New Fitting Method for Silicon-Strip Detectors. Instruments, 2(4), 22. https://doi.org/10.3390/instruments2040022



