Abstract
This work introduces an algorithm designed to solve the Bogoliubov–de Gennes equations of superconductivity theory. What sets this algorithm apart is its remarkable ability to precisely and consistently consider the impact of an external magnetic field, all within the microscopic approach. The computation scheme’s convergence is guaranteed by addressing the Biot–Savart equation for the field where the vector potential appears on both of its sides. To showcase the capabilities of this approach, we provide several key examples: the Abrikosov lattice, vortex core states, and the vortex structure in the intermediate mixed state of a superconductor. This method promises to offer valuable insights into the microscopic physics of intertype superconductivity.
1. Introduction
In the realm of superconductivity, the presence of a magnetic field is known to exert adverse effects on the superconducting state. Two distinct factors contribute to this phenomenon. Firstly, the Zeeman term, arising from the intrinsic spin degrees of freedom of electrons, induces a tendency for the alignment of the spins of paired electrons forming a Cooper pair. Secondly, the Lorentz force, originating from the orbital degrees of freedom of electrons, exerts a force that endeavors to separate the two electrons within the pair. Consequently, in general, the magnetic field disrupts these electron pairs. The mechanism responsible for shielding the external magnetic field involves the generation of surface currents, which precisely counteract the external field beyond a certain depth known as the penetration depth denoted as . Another crucial length scale to consider is the coherence length, represented as , which quantifies the extent to which the superconducting order parameter is established within the superconducting region. The ratio of these two lengths, denoted as , plays a pivotal role in defining distinct regimes of superconducting materials [1].
When is small (), characteristic of type-I superconductors, the magnetic field is completely expelled from the interior of the superconductor, resulting in perfect diamagnetism. For large values (), characteristic of type-II superconductors, the magnetic field penetrates the superconducting region in the form of flux tubes enclosed by superconducting regions, creating a mixed phase. These flux lines exhibit quantization in units of the flux quantum . At low magnetic fields, the superconducting material efficiently expels the magnetic field, and the system resides in the Meissner phase. As the magnetic field strength increases, the system permits the penetration of flux tubes, commencing at a critical field strength denoted as , marking the transition into the mixed phase.
The investigation of a single vortex line within an s-wave superconductor in this regime was initiated through seminal work by Caroli, de Gennes, and Matricon [2], followed by Bardeen et al. [3], employing various approximations of the Bogoliubov–de Gennes (BdG) formalism. Subsequently, Shore et al. [4] and Gygi and Schlueter [5] obtained numerical solutions for quasiparticle amplitudes within a vortex core, employing approximate forms for the pair potential. Notably, these early numerical calculations utilized a pair potential derived from experimentally inferred coherence lengths, while neglecting the spatial variation of the magnetic field, an assumption justified for large values. More rigorous solutions to the BdG equations are attainable solely through numerical methods, allowing for the self-consistent determination of the pair potential. Gygi et al. [6,7] demonstrated within this BdG formalism that, as the temperature decreases, the vortex core size diminishes, aligning with predictions originally posited by Kramer and Pesch [8]. Furthermore, at very low temperatures, the pair potential exhibits Friedel-like oscillations, primarily arising from the vortex core states [7,9]. It is worth noting that, in these analyses, the spatial dependence of the magnetic field was omitted, a valid simplification for systems with . Similar outcomes have been observed in nanostructures, such as nanowires aligned with a magnetic field [10], etc.
In the low field limit, the quasiparticle states within a superconductor can be adequately described by considering a single isolated vortex. Conversely, in the high field limit, where still , a lattice of vortices forms, known as an Abrikosov lattice, with closely packed vortices [11]. In this regime, the description of a single isolated vortex becomes inadequate. The quasiparticle spectrum in this scenario is influenced by the combined effects of bound states within the vortex cores and states in the continuum, arising from propagation within the superconducting region between the vortex cores. In contrast to the single isolated vortex case, the vector potential must be explicitly accounted for in the BdG equations. In most calculations, it is assumed that extreme type-II superconductors () apply, where the vector potential is primarily determined by the external magnetic field. In such cases, the critical field , marking the transition to the normal phase, greatly exceeds the lower critical field .
Nevertheless, there exists a category of superconducting materials characterized by values (low-kappa materials), which do not conform neatly to the conventions of type-I or type-II superconductors. Experimental evidence has unveiled the existence of an intermediate mixed state (IMS) within these crossover or intertype (IT) materials. In this unique state, the magnetic field infiltrates the superconductor while giving rise to diverse spatial configurations, including Meissner domains coexisting with vortex lattice islands, vortex clusters, and chains, among others [12].
When modeling the magnetic response of such superconductors, , it is imperative to no longer disregard the spatial dependence of the magnetic field. Under these circumstances, the shielding of the external magnetic field becomes a critical factor for accurately describing and comprehending the phenomena occurring in these superconductors.
The primary objective of this work is to present a fast and tractable method for calculating the Bogoliubov–de Gennes equations alongside the Ampère–Maxwell equation for the magnetic field that can be used to investigate strongly inhomogeneous superconducting states in any material, including those with . The task requires developing a numerical algorithm that is self-consistent over the magnetic field as well as over the gap function. A fully self-consistent method would offer a significant edge over earlier calculations where the magnetic field was obtained in the first iteration of the self-consistency procedure [13] which is not adequate for the low-kappa superconductors. The proposed approach offers a decisive improvement also of the Ginzburg–Landau (GL) theory, which is commonly employed to investigate the magnetic properties of superconductors [14] but can describe neither a fine structure of the vortex core nor the mixed state in the low-kappa materials correctly.
In this work, we introduce a scheme of double self-consistency and conduct initial self-consistent calculations on typical inhomogeneous superconducting systems featuring values near 1, with a specific focus on s-wave superconductivity to illustrate the method’s efficiency. It is worth noting that our approach holds promise for addressing more general scenarios, including d-wave superconductivity in magnetic fields and multi-orbital superconductivity with spin–orbit coupling, as well as those with disorder [15,16].
2. Method
2.1. Formalism
In this work, we present a numerical procedure for solving the Bogoliubov–de Gennes equations for the highly inhomogeneous mixed state of a superconductor without any particular symmetry. The equations are solved self-consistently with the conditions for the superconducting gap function, as well as with the Ampère–Maxwell equation for the magnetic field. We consider an effectively 2D problem, so that the quantities of interest do not depend on one of the coordinates (z), and the magnetic field is directed along the z axis .
In the 2D plane, , the equations are formulated on a discrete lattice and are solved using the free boundary conditions. For simplicity, we assume a zero temperature and also that the lattice is placed in an external perpendicular magnetic field . This field is described by the vector potential, , attributed to each of the discrete lattice sites. For simplicity, the external field is taken to be uniform, with the corresponding vector potential being .
The discretized BCS model is defined by the tight-binding Hamiltonian with the s-wave pairing symmetry that reads as
where is the electron operator at site i of the lattice, is the electron spin, is the hopping amplitude between sites i and j, which is non-zero only for the nearest neighbors, and is the on-site BCS coupling constant. The magnetic field is taken into account via the Peierl’s phase factor for the hopping matrix elements,
where is the vector potential of the total magnetic field at a point .
Within the BdG approach, one has to solve the eigenvalue problem of the mean-field Hamiltonian
where the single-particle Hamiltonian is
is the chemical potential, is the gap function, and is the Hartree potential. This mean field model is solved together with the self-consistency conditions for the gap and the Hartree potential
The eigenvalue problem of the mean-field Hamiltonian is reduced to solving the BdG matrix equation
where . Using solutions u and v to the BdG equations, one finds both normal and anomalous averages in Equation (5), so that Equations (5) and (6) can be solved self-consistently [17].
The self-consistency cycle, involving the order parameter and Hartree potential, is a standard well-established procedure. Its description can be found in numerous works (see, e.g., [18]). In this work, we use the same procedure, which yields a converging solution for the problem.
However, the presence of the magnetic field brings additional complexity to the problem. Equations (5) and (6) are to be amended by the Ampère–Maxwell equation
An applied external magnetic field generates supercurrents which, in turn, create an additional magnetic field. Clearly, this screening Meissner “self-action” must also be taken into account when solving the BdG equations. Therefore, the solution requires two self-consistency cycles: one for the order parameter, hereafter referred to as the inner convergence cycle (ICC), and another for the magnetic field, referred to as the outer convergence cycle (OCC).
A complete scheme for solving the BdG equations in the presence of a magnetic field is illustrated in Figure 1. A detailed description is given in the following sections.
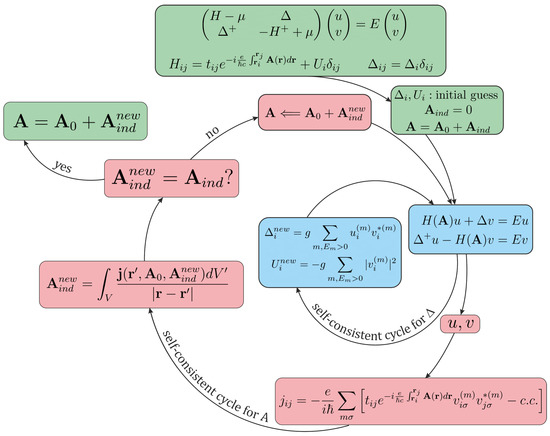
Figure 1.
A scheme for the self-consistent solution of BdG equations in the presence of the magnetic field. ICC (blue frames) solves the system of a BdG Equation (6) with the fixed external field. The solution is then fed as an input of OCC (red frames). The outer cycle calculates the total field in the superconductor, which is the sum of the external and current generated fields. The cycles repeat sequentially until the convergence is reached in both the field and gap function.
2.2. Inner Convergence Cycle—ICC
The ICC is the calculation scheme that finds the solution of the BdG equation with the gap function and the Hartree potential self-consistently. The magnetic field is fixed (taken from the previous step). The ICC follows a standard procedure where one first solves the BdG Equation (6) for the gap function . The solution gives a set of eigenfunctions and eigenvalues . Due to the symmetry of the problem, only half of the eigenfunctions from this set, with positive eigenvalues , are needed to compute the next iteration for the order parameter and Hartree potential as
The obtained quantities are then used to solve the BdG Equation (6). The cycle repeats itself until the convergence criterium is reached. It is important that this procedure converges without employing special convergence enhancement methods.
The ICC can be easily generalized to the case of disordered superconductors [18,19,20]. In a recent work [21], it was used to study the influence of correlations in the impurity potential on the superconducting characteristics of materials.
2.3. Outer Convergence Cycle—OCC
The OCC is needed to find the solution of the BdG equations together with the Ampère–Maxwell equation for the field. As with the ICC, the equations are solved sequentially.
As a first step, one solves the BdG, the gap, and the Hartree equations self-consistently using the ICC, as discussed in the previous subsection. The magnetic field that enters the BdG equations via the Peierl’s factor in Equation (2) is taken from the previous step and is assumed to be fixed throughout the ICC procedure.
Once the convergence in the ICC is achieved, one takes eigenfunctions of the BdG equations to find the superconducting current. In the discrete tight-binding model, the current along the link is found using the expression
The vector potential is discretized on the lattice sites as well. Using this descretization scheme, we approximate
where a is the lattice constant, and and are obtained as the projection of the vector potential onto the vector connecting the lattice sites i and j, so that is the projection of the averaged vector potential which is assigned to the link between these lattice points (see Figure 2). The discretization scheme is consistent with the gauge invariance of the vector potential.
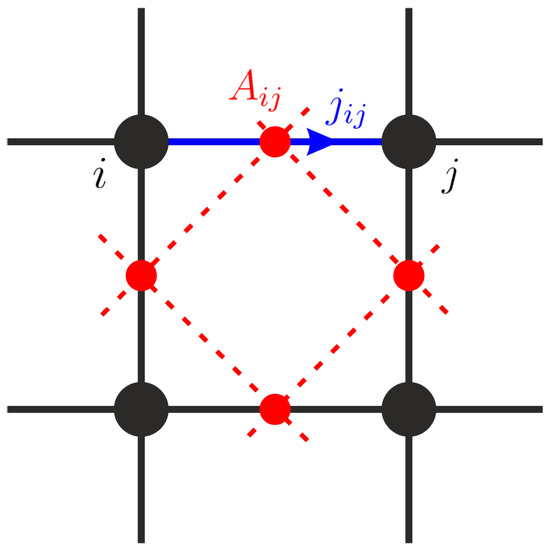
Figure 2.
Two grids used in the algorithm. Black circles are the sites of the square lattice, and red circles form the grid of links.
We now need to find the magnetic field for the next step of the OCC. The field is related to the supercurrent via the Ampère–Maxwell Equation (10). Formally, one can write the solution for the field in the form of the Biot–Savart law,
so that the total field is a sum of the applied and induced fields
where one notes that .
It is tempting to regard the left-hand side of Equation (12) as the field for the next step in the OCC. However, when one takes this result for the next step, the OCC algorithm would not converge. The reason is that the current in Equation (10) depends on the field explicitly via the Peierl’s factor entering in Equation (2). It is responsible for the diamagnetism of the superconducting state.
To circumvent this problem, one needs to regard Equation (12) as an equation where the current is an explicit function of . The vector potential for the next step of the OCC will be obtained by regarding Equation (12) as an equation, where enters both the right-hand side and left-hand side. Note that we take and , needed to calculate the current in Equation (10) and obtained by solving the BdG equation, as fixed inputs, calculated using the field in the previous step of the OCC. Equation (12) is solved using the method proposed by Krylov, which is generalized to solve non-linear equations as well [22].
The solution of Equation (12) summed with the external gives the field in the next iteration of the OCC. It is then used to solve the BdG equations consistently in the ICC. The combination of the ICC and OCC, as described above, ensures the convergence of the entire procedure of solving the microscopic mean field BCS equations self-consistently with the equations for the superconductive gap, Hartree potential, and the magnetic field. We note that one can also include the self-consistency for the number of electrons. The corresponding equation is added to the ICC, where the procedure also involves changes in the value of the chemical potential.
3. Illustrative Examples
In this section, we discuss the results of the microscopic solution of the problem with three illustrative examples of the interaction between the superconductivity and magnetic field. These examples are the Abrikosov vortex lattice in type II superconductors, a detailed structure of a single vortex, and multiple vortices in inter-type (IT) superconductors. The last two examples are most interesting as they demonstrate the regime where the proposed method is indispensable in describing the profile of the magnetic flux penetrating a superconducting state.
The calculations are performed on a lattice with sites assuming free boundary conditions. The hopping constant is regarded as the energy scale of the model.
3.1. Abrikosov Lattice
In the deep type-II regime, the ratio of the magnetic penetration length to the coherence length is significantly larger than one, . It is then expected that the magnetic field penetrates a superconductor in the form of Abrikosov vortices arranged in a triangular lattice.
The results of our calculations for the spatial profile of the magnetic field and the order parameter are shown in Figure 3a,b, respectively. The parameters of the model t and t are chosen such that the system is in the Type-II regime, so that the GL parameter satisfies . This can be seen easily by comparing the characteristic lengths of a vortex for the condensate (Figure 3a) and for the magnetic field (Figure 3b).
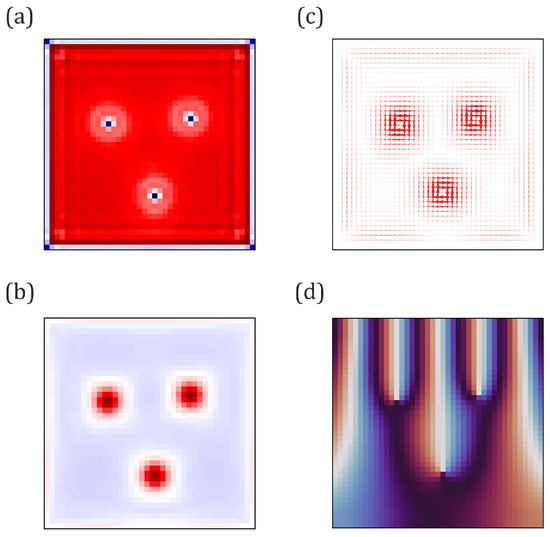
Figure 3.
A triangle of Abrikosov vortices in a Type-II superconductor. (a) The absolute value of the order parameter (blue is normal state, red is superconducting state). (b) The distribution of the magnetic field (blue is ). (c) The distribution of superconducting currents. Arrows point in the direction of the current. Arrow thickness is proportional to the current value. (d) Phase of the order parameter, changing in the interval .
Figure 3c plots the distribution of the superconducting currents. The normal regions in the vortex cores are surrounded by currents. The Meissner currents flowing along the border screen the superconducting field, preventing it from entering the sample. Figure 3d shows the phase of the order parameter. It changes by around each of the vortex cores.
Figure 3 demonstrates three vortices forming a triangle. This is expected for a Type-II superconductor, when vortrices are repulsive. Furthermore, the Bio–Savart Equation (12) already gives a correct result for the field after the first iteration of the OCC.
The accuracy of the solutions, obtained after the first iteration and after the full OCC procedure with many cycles (defined by the convergence criterium), is demonstrated in Figure 4, which plots the radial cross-section of the absolute value of the gap function. Red dots demonstrate the result calculated for the full OCC, while blue dots are the result obtained after the first step. One can see that the difference between the results is only marginal. This demonstrates that, in the limit of Type II superconductors, a single OCC iteration is sufficient to obtain both the condensate and field profiles with a very good accuracy. The first iteration reproduces even the fine structures in the Friedel-like oscillations in the vicinity of the vortex core, which is clearly visible in Figure 4. These were first noted in numerical solutions of the Eilenberger equations [8], and later obtained analytically for a single vortex solution of the BdG equations [9]. We note, in passing, that their origin lies in the oscillating contributions with the period of in both components u and v of the eigenfunction of the BdG Hamiltonian.
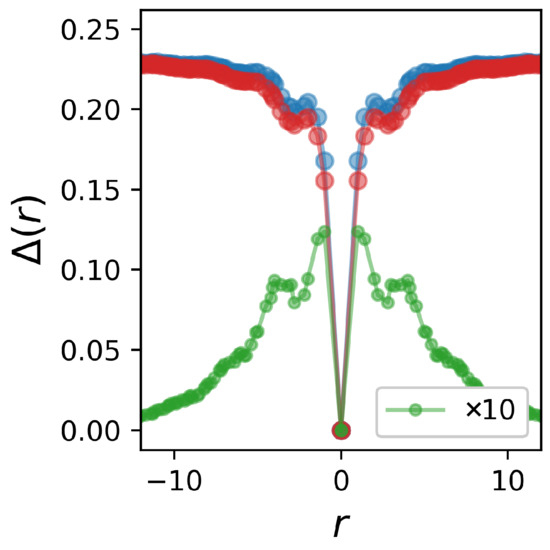
Figure 4.
Radial profile of the vortex order parameter extracted from Figure 3a. Red dots are the results after the first iteration of the OCC; blue dots are obtained after the OCC is converged. The difference between the first and last iterations is shown in green and magnified by a factor of 10.
3.2. Vortex Core States
We now consider single-electron states inside of the vortex core obtained from the full solution of the BdG equations. These Andreev states are bound to the core and exhibit a quantization of the energy levels.
Figure 5 gives the spectrum and the spatial distribution of the vortex core states for a system with the same model parameters as taken above to calculate results in Figure 3 and Figure 4; however, this is assuming the value of the external field, which allows only one flux quantum to penetrate the sample.
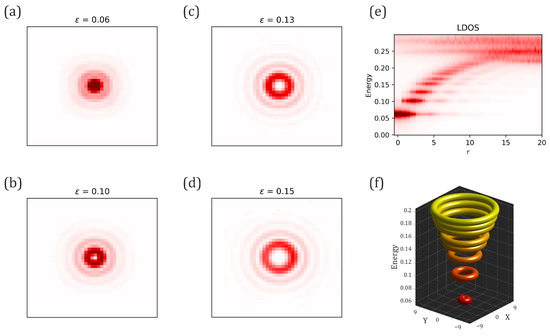
Figure 5.
Single particle states in the vortex core. (a–d) Spatial profile of the absolute value of the bound core states corresponding to the four lowest energy levels. The intensity of the red color is proportional to the amplitude of the wave function. The energy spectrum lies in the interval with . (e) The colour density plot showing the local density of states (LDOS) near the vortex as a function of the distance from the vortex core and of the energy. (f) 3D sketch of the localization of the eigenfunctions in the 3D space.
The first four bound states are shown in Figure 5a–d. The absolute values form concentric circles around the vortex core, meaning the states are localized at a specific distance from the vortex centre, which grows with the energy of the state. Figure 5e shows the map of the local density of electronic states depending on the distance from the center. Separate energy levels are clearly visible. At low energy levels, the LDOS increases towards the vortex center. At , the spectrum is continuous. A 3D sketch of the level structure in the space is shown in Figure 5f. The spatial profile of the LDOS can be experimentally observed using the scanning tunneling microscopy technique (see, e.g., [23], the pioneering work in this area).
3.3. Intermediate Mixed State
When the coherence length and penetration depth are comparable and , a material becomes an inter-type (IT) superconductor demonstrating the intermediate mixed state (IMS). It is defined by a special type of vortex–vortex interaction which is non-monotonic, and also has a significant multi-vortex component. The IMS vortex matter is characterized by clustering and vortex liquid, which gives rise to complex vortex patterns [24,25].
In the regime of IT superconductivity with the IMS, the first cycle of the OCC gives totally inadequate results for both the condensate and the field profiles. This is illustrated in Figure 6, which shows the results obtained for model parameter t and t that correspond to the IT superconductivity regime.
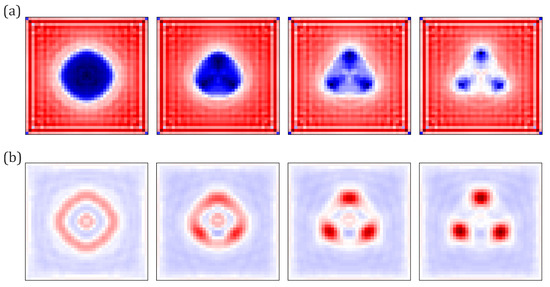
Figure 6.
Evolution of the solution with the number of OCC cycles, for (a) order parameter and (b) magnetic field profiles. The model parameters t and correspond to the regime of IT superconductivity. From the left to the right, the panels correspond to OCC cycles. is sufficient to reach convergence.
In the IT regime, the material still admits the mixed state with vortices. This is illustrated in the rightmost panels in Figure 6, panel (a) for the order parameter and (b) for the field. The vortices, however, form a cluster with a distance corresponding to a minimum intervortex interaction energy. This result is achieved after 40 steps of the OCC, which are required to reach the convergence. The other panels, on the left, show the results for a fewer number of steps. The leftmost panels show the result after the first step, the second panels are obtained after the fifth step, and the third panels are the results after the ninth step.
The panel sequence from left to right demonstrates that a system undergoes a very deep transformation with the number of OCC steps. It proves the importance of the back action of the field on the profile of the order parameter. After the first OCC step, one obtains a single large area of suppressed superconductivity (giant vortex), whereas, after 40 OCC steps, the calculation converges to a state with a cluster of three separate vortices.
4. Discussion
This work presents an efficient method to solve Bogoliubov–de Gennes equations self-consistently with the equations for the gap and the magnetic field as well. The method runs two consecutive consistency cycles: an inner cycle over the gap, assuming the field does not change, and an outer one over the field. An important ingredient of the approach is the solution of the Bio–Savart equation for the field, in which the explicit field dependence of the current is taken into account to find the solution.
The proposed method offers reasonably fast convergence and accurate results. It overcomes the limitations of the frequently used approximation where the field was obtained using the first iteration of the outer consistency cycle. In this approximation, the induced field is calculated using the solution of the BdG equation with the uniform external field as an input [13]. It has been demonstrated above that the first iteration gives reasonably accurate results for superconductors in the deep Type-II regime with the large GL parameter . However, the first iteration approximation becomes inaccurate when departing from the deep Type-II regime, and it is totally inadequate for low-kappa materials with . In this regime, the back action of the field onto the condensate is very significant and cannot be neglected. It leads to the considerable rearrangement of both the condensate and the field profiles.
The proposed method yields results that cannot be obtained employing the popular Ginzburg–Landau theory [14]. In particular, the latter cannot adequately describe the inner fine structure of a vortex and cannot be used to study the magnetic properties of the low-kappa materials and the phenomen of inter-type superconductivity [12]. In contrast, the approach discussed in this work can take all these effects into account, thereby offering a considerable advantage over the other methods.
With minimal alternations, the approach can also be used to investigate various more general situations, including a non-uniform applied magnetic field, d-wave superconductivity in magnetic fields, multi-orbital superconductivity with spin-orbit coupling, and systems with disordered arbitrary strength. The versatility of our method allows for its application to a wide range of inhomogeneous superconducting systems, including films and wires, facilitating further investigations into their unique properties. Finally, we note that it is also feasible to construct the extension of this method into the time domain for use in investigating dynamic effects [26,27] in intertype superconductors. This extension will allow us to study the coherent quantum evolution of the system, in contrast to the approach based on the time-dependent Ginzburg–Landau equations where dynamical quantum coherent effects are neglected [28].
Author Contributions
Conceptualization, A.V. and M.D.C.; methodology, A.V.K. and V.D.N.; software, V.D.N., A.E.L. and A.K.; writing—original draft preparation, A.V.K. and V.D.N.; writing—review and editing, A.V. and M.D.C.; visualization, V.D.N. All authors have read and agreed to the published version of the manuscript.
Funding
V.D.N., A.E.L. and A.V.K. acknowledge support from the Ministry of Science and Higher Education of the Russian Federation (state task project No. FSWU-2023-0031). The calculations were performed with the support of the MEPhI Program Priority 2030. Analysis of single vortex states has been funded within the framework of the HSE University Basic Research Program. A.V. acknowledges support by the Ministry of Science and Higher Education of the Russian Federation (No. FSMG-2023-0014) and the RSF grant 23-72-30004 (https://rscf.ru/project/23-72-30004/ accessed on 1 November 2023) that were used for analytical derivations.
Data Availability Statement
The software used in the work is available at gitlab.com/center-quantum-metamaterials/bdg, accessed on 1 November 2023.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abrikosov, A.A. Nobel Lecture: Type-II superconductors and the vortex lattice. Rev. Mod. Phys. 2004, 76, 975–979. [Google Scholar] [CrossRef]
- Caroli, C.; Gennes, P.D.; Matricon, J. Bound Fermion states on a vortex line in a type II superconductor. Phys. Lett. 1964, 9, 307–309. [Google Scholar] [CrossRef]
- Bardeen, J.; Kümmel, R.; Jacobs, A.E.; Tewordt, L. Structure of Vortex Lines in Pure Superconductors. Phys. Rev. 1969, 187, 556–569. [Google Scholar] [CrossRef]
- Shore, J.D.; Huang, M.; Dorsey, A.T.; Sethna, J.P. Density of states in a vortex core and the zero-bias tunneling peak. Phys. Rev. Lett. 1989, 62, 3089–3092. [Google Scholar] [CrossRef] [PubMed]
- Gygi, F.; Schluter, M. Electronic tunneling into an isolated vortex in a clean type-II superconductor. Phys. Rev. B 1990, 41, 822–825. [Google Scholar] [CrossRef]
- Gygi, F.; Schluter, M. Angular band structure of a vortex line in a type-II superconductor. Phys. Rev. Lett. 1990, 65, 1820–1823. [Google Scholar] [CrossRef] [PubMed]
- Gygi, F.; Schlüter, M. Self-consistent electronic structure of a vortex line in a type-II superconductor. Phys. Rev. B 1991, 43, 7609–7621. [Google Scholar] [CrossRef]
- Kramer, L.; Pesch, W. Core structure and low-energy spectrum of isolated vortex lines in clean superconductors atT ≪T c. Z. Phys. 1974, 269, 59–64. [Google Scholar] [CrossRef]
- Hayashi, N.; Isoshima, T.; Ichioka, M.; Machida, K. Low-Lying Quasiparticle Excitations around a Vortex Core in Quantum Limit. Phys. Rev. Lett. 1998, 80, 2921–2924. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Croitoru, M.D.; Peeters, F.M. Magnetic-field induced quantum-size cascades in superconducting nanowires. Phys. Rev. B 2008, 78, 024505. [Google Scholar] [CrossRef]
- Abrikosov, A. The magnetic properties of superconducting alloys. J. Phys. Chem. Solids 1957, 2, 199–208. [Google Scholar] [CrossRef]
- Vagov, A.; Wolf, S.; Croitoru, M.D.; Shanenko, A.A. Universal flux patterns and their interchange in superconductors between types I and II. Commun. Phys. 2020, 3, 58. [Google Scholar] [CrossRef]
- Han, Q. A method of studying the Bogoliubov–de Gennes equations for the superconducting vortex lattice state. J. Phys. Condens. Matter 2009, 22, 035702. [Google Scholar] [CrossRef] [PubMed]
- Berdiyorov, G.R.; Hernandez, A.D.; Peeters, F.M. Confinement Effects on Intermediate-State Flux Patterns in Mesoscopic Type-I Superconductors. Phys. Rev. Lett. 2009, 103, 267002. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Banerjee, A.; Trivedi, N.; Ghosal, A. New paradigm for a disordered superconductor in a magnetic field. arXiv 2021, arXiv:2101.00220. [Google Scholar] [CrossRef]
- Fan, B.; García-García, A.M. Exploring the vortex phase diagram of Bogoliubov-de Gennes disordered superconductors. arXiv 2022, arXiv:2205.12347. [Google Scholar] [CrossRef]
- de Braganca, R.H.; Croitoru, M.D.; Shanenko, A.A.; Aguiar, J.A. Effect of Material-Dependent Boundaries on the Interference Induced Enhancement of the Surface Superconductivity Temperature. J. Phys. Chem. Lett. 2023, 14, 5657–5664. [Google Scholar] [CrossRef]
- Ghosal, A.; Randeria, M.; Trivedi, N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 2001, 65, 014501. [Google Scholar] [CrossRef]
- Bouadim, K.; Loh, Y.L.; Randeria, M.; Trivedi, N. Single- and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 2011, 7, 884–889. [Google Scholar] [CrossRef]
- Gastiasoro, M.N.; Andersen, B.M. Enhancing superconductivity by disorder. Phys. Rev. B 2018, 98, 184510. [Google Scholar] [CrossRef]
- Neverov, V.D.; Lukyanov, A.E.; Krasavin, A.V.; Vagov, A.; Croitoru, M.D. Correlated disorder as a way towards robust superconductivity. Commun. Phys. 2022, 5, 177. [Google Scholar] [CrossRef]
- Liesen, J.; Strakos, Z. Krylov Subspace Methods: Principles and Analysis; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Maggio-Aprile, I.; Renner, C.; Erb, A.; Walker, E.; Fischer, O. Direct Vortex Lattice Imaging and Tunneling Spectroscopy of Flux Lines on YBa2Cu3O7-δ. Phys. Rev. Lett. 1995, 75, 2754–2757. [Google Scholar] [CrossRef] [PubMed]
- Vagov, A.; Shanenko, A.A.; Milošević, M.V.; Axt, V.M.; Vinokur, V.M.; Aguiar, J.A.; Peeters, F.M. Superconductivity between standard types: Multiband versus single-band materials. Phys. Rev. B 2016, 93, 174503. [Google Scholar] [CrossRef]
- Córdoba-Camacho, W.Y.; da Silva, R.M.; Vagov, A.; Shanenko, A.A.; Aguiar, J.A. Between types I and II: Intertype flux exotic states in thin superconductors. Phys. Rev. B 2016, 94, 054511. [Google Scholar] [CrossRef]
- Volkov, A.F.; Kogan, S.M. Collisionless relaxation of the energy gap in superconductors. Sov. J. Exp. Theor. Phys. 1974, 38, 1018–1021. [Google Scholar]
- Hannibal, S.; Kettmann, P.; Croitoru, M.D.; Axt, V.M.; Kuhn, T. Persistent oscillations of the order parameter and interaction quench phase diagram for a confined Bardeen-Cooper-Schrieffer Fermi gas. Phys. Rev. A 2018, 98, 053605. [Google Scholar] [CrossRef]
- Berdiyorov, G.R.; Hernández-Nieves, A.D.; Milošević, M.V.; Peeters, F.M.; Domínguez, D. Flux-quantum-discretized dynamics of magnetic flux entry, exit, and annihilation in current-driven mesoscopic type-I superconductors. Phys. Rev. B 2012, 85, 092502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).