Enhancing Performances of the VOXES Bragg Spectrometer for XES Investigations
Abstract
1. Introduction
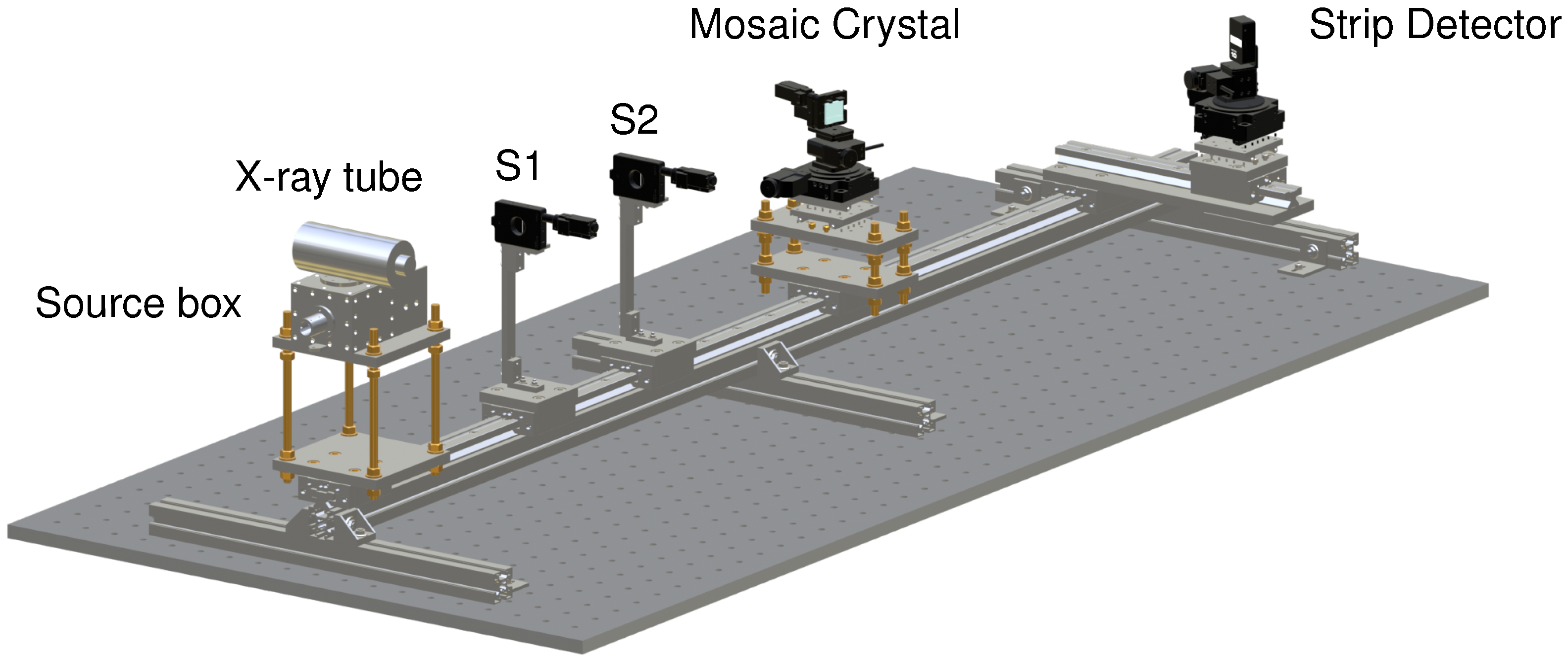
2. Setup and Methods
3. Results and Discussion
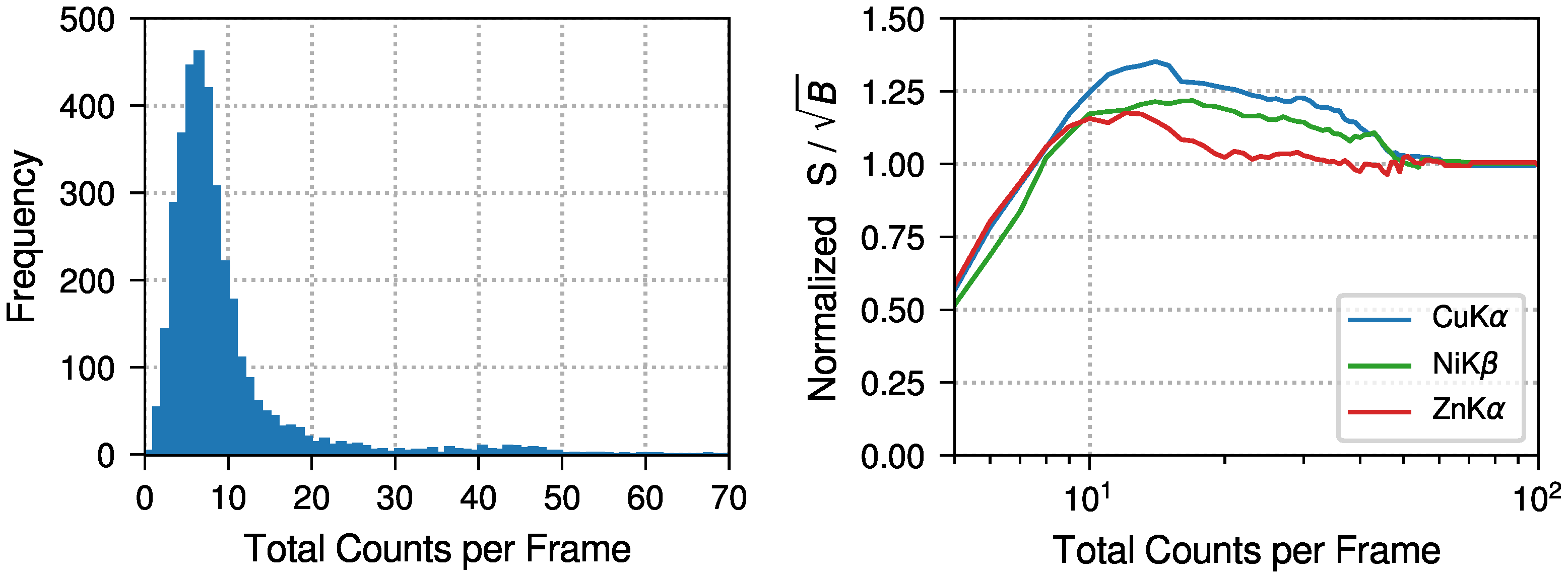
3.1. Background Reduction
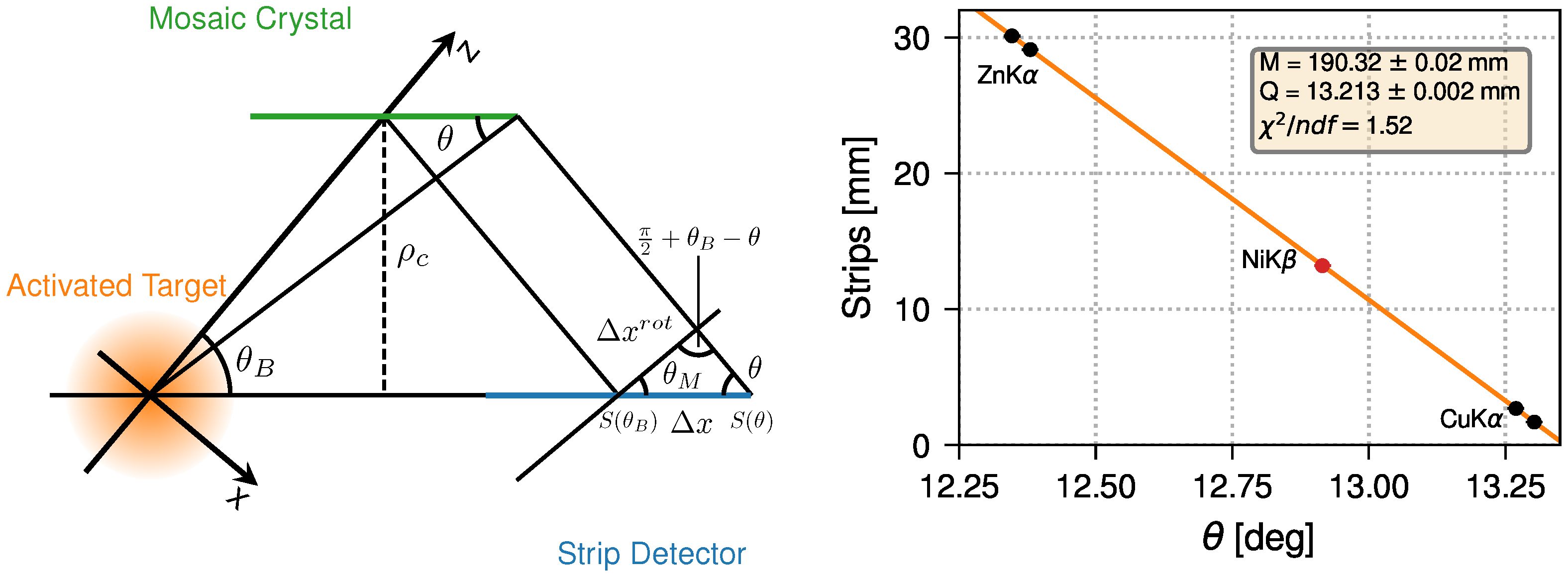
3.2. Energy Calibration
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Groot, F. High-Resolution X-ray Emission and X-ray Absorption Spectroscopy. Chem. Rev. 2001, 101, 1779–1808. [Google Scholar] [CrossRef] [PubMed]
- Rovezzi, M.; Glatzel, P. Hard X-ray emission spectroscopy: A powerful tool for the characterization of magnetic semiconductors. Semicond. Sci. Technol. 2014, 29, 023002. [Google Scholar] [CrossRef]
- Gamblin, S.D.; Urch, D.S. Metal Kβ X-ray emission spectra of first row transition metal compounds. J. Electron Spectrosc. Relat. Phenom. 2001, 113, 179–192. [Google Scholar] [CrossRef]
- Lafuerza, S.; Carlantuono, A.; Retegan, M.; Glatzel, P. Chemical Sensitivity of Kβ and Kα X-ray Emission from a Systematic Investigation of Iron Compounds. Inorg. Chem. 2020, 59, 12518–12535. [Google Scholar] [CrossRef]
- Beckwith, M.A.; Roemelt, M.; Collomb, M.N.; DuBoc, C.; Weng, T.C.; Bergmann, U.; Glatzel, P.; Neese, F.; DeBeer, S. Manganese Kβ X-ray Emission Spectroscopy As a Probe of Metal–Ligand Interactions. Inorg. Chem. 2011, 50, 8397–8409. [Google Scholar] [CrossRef]
- Kawai, J.; Suzuki, C.; Adachi, H.; Konishi, T.; Gohshi, Y. Charge-transfer effect on the linewidth of Fe Kα X-ray fluorescence spectra. Phys. Rev. B 1994, 50, 11347–11354. [Google Scholar] [CrossRef] [PubMed]
- Glatzel, P.; Smolentsev, G.; Bunker, G. The electronic structure in 3d transition metal complexes: Can we measure oxidation states? J. Phys. Conf. Ser. 2009, 190, 012046. [Google Scholar] [CrossRef]
- Pollock, C.J.; Delgado-Jaime, M.U.; Atanasov, M.; Neese, F.; DeBeer, S. Kβ Mainline X-ray Emission Spectroscopy as an Experimental Probe of Metal–Ligand Covalency. J. Am. Chem. Soc. 2014, 136, 9453–9463. [Google Scholar] [CrossRef] [PubMed]
- Malzer, W.; Grötzsch, D.; Gnewkow, R.; Schlesiger, C.; Kowalewski, F.; Van Kuiken, B.; DeBeer, S.; Kanngießer, B. A laboratory spectrometer for high throughput X-ray emission spectroscopy in catalysis research. Rev. Sci. Instrum. 2018, 89, 113111. [Google Scholar] [CrossRef] [PubMed]
- Haschke, M.; Flock, J.; Haller, M. X-ray Fluorescence Spectroscopy for Laboratory Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Miliucci, M.; Scordo, A.; Sirghi, D.; Amirkhani, A.; Baniahmad, A.; Bazzi, M.; Bosnar, D.; Bragadireanu, M.; Carminati, M.; Cargnelli, M.; et al. Silicon drift detectors system for high-precision light kaonic atoms spectroscopy. Meas. Sci. Technol. 2021, 32, 095501. [Google Scholar] [CrossRef]
- Doriese, W.B.; Abbamonte, P.; Alpert, B.K.; Bennett, D.A.; Denison, E.V.; Fang, Y.; Fischer, D.A.; Fitzgerald, C.P.; Fowler, J.W.; Gard, J.D.; et al. A practical superconducting-microcalorimeter X-ray spectrometer for beamline and laboratory science. Rev. Sci. Instrum. 2017, 88, 053108. [Google Scholar] [CrossRef] [PubMed]
- Uhlig, J.; Doriese, W.B.; Fowler, J.W.; Swetz, D.S.; Jaye, C.; Fischer, D.A.; Reintsema, C.D.; Bennett, D.A.; Vale, L.R.; Mandal, U.; et al. High-resolution X-ray emission spectroscopy with transition-edge sensors: Present performance and future potential. J. Synchrotron Radiat. 2015, 22, 766–775. [Google Scholar] [CrossRef] [PubMed]
- Von Hámos, L. Röntgenspektroskopie und Abbildung mittels gekrümmter Kristallreflektoren. I. Geometrisch-optische Betrachtungen. Ann. Phys. 1933, 409, 716–724. [Google Scholar] [CrossRef]
- Zimmermann, P.; Peredkov, S.; Abdala, P.M.; DeBeer, S.; Tromp, M.; Müller, C.; van Bokhoven, J.A. Modern X-ray spectroscopy: XAS and XES in the laboratory. Coord. Chem. Rev. 2020, 423, 213466. [Google Scholar] [CrossRef]
- Grigorieva, I.; Antonov, A.; Gudi, G. Graphite Optics—Current Opportunities, Properties and Limits. Condens. Matter 2019, 4, 18. [Google Scholar] [CrossRef]
- Wansleben, M.; Kayser, Y.; Hönicke, P.; Holfelder, I.; Wählisch, A.; Unterumsberger, R.; Beckhoff, B. Experimental determination of line energies, line widths and relative transition probabilities of the Gadolinium L X-ray emission spectrum. Metrologia 2019, 56, 065007. [Google Scholar] [CrossRef]
- Scordo, A.; Curceanu, C.; Miliucci, M.; Sirghi, F.; Zmeskal, J. Pyrolitic Graphite Mosaic Crystal Thickness and Mosaicity Optimization for an Extended Source Von Hamos X-ray Spectrometer. Condens. Matter 2019, 4, 38. [Google Scholar] [CrossRef]
- Scordo, A.; Breschi, L.; Curceanu, C.; Miliucci, M.; Sirghi, F.; Zmeskal, J. High resolution multielement XRF spectroscopy of extended and diffused sources with a graphite mosaic crystal based Von Hamos spectrometer. J. Anal. At. Spectrom. 2020, 35, 155–168. [Google Scholar] [CrossRef]
- Scordo, A.; De Leo, V.; Curceanu, C.; Miliucci, M.; Sirghi, F. Efficiency measurements and simulations of a HAPG based Von Hamos spectrometer for large sources. J. Anal. At. Spectrom. 2021, 36, 2485–2491. [Google Scholar] [CrossRef]
- Schoonjans, T.; Brunetti, A.; Golosio, B.; Sanchez del Rio, M.; Solé, V.A.; Ferrero, C.; Vincze, L. The xraylib library for X-ray–matter interactions. Recent developments. Spectrochim. Acta Part B At. Spectrosc. 2011, 66, 776–784. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manti, S.; Napolitano, F.; Clozza, A.; Curceanu, C.; Moskal, G.; Piscicchia, K.; Sirghi, D.; Scordo, A. Enhancing Performances of the VOXES Bragg Spectrometer for XES Investigations. Condens. Matter 2024, 9, 19. https://doi.org/10.3390/condmat9010019
Manti S, Napolitano F, Clozza A, Curceanu C, Moskal G, Piscicchia K, Sirghi D, Scordo A. Enhancing Performances of the VOXES Bragg Spectrometer for XES Investigations. Condensed Matter. 2024; 9(1):19. https://doi.org/10.3390/condmat9010019
Chicago/Turabian StyleManti, Simone, Fabrizio Napolitano, Alberto Clozza, Catalina Curceanu, Gabriel Moskal, Kristian Piscicchia, Diana Sirghi, and Alessandro Scordo. 2024. "Enhancing Performances of the VOXES Bragg Spectrometer for XES Investigations" Condensed Matter 9, no. 1: 19. https://doi.org/10.3390/condmat9010019
APA StyleManti, S., Napolitano, F., Clozza, A., Curceanu, C., Moskal, G., Piscicchia, K., Sirghi, D., & Scordo, A. (2024). Enhancing Performances of the VOXES Bragg Spectrometer for XES Investigations. Condensed Matter, 9(1), 19. https://doi.org/10.3390/condmat9010019






