Abstract
In 1T-TaSSe, the charge density wave (CDW) state features a star of David lattice that expands across layers as the system becomes commensurate upon cooling. The layers can also order along the c-axis, and different stacking orders have been proposed. Using neutron scattering on powder samples, we compared the stacking order previously observed in 1T-TaS when the system is doped with Se. While at low temperature, a 13c layer sequence stacking was observed in TaS; this type of ordering was not evident with doping. Doping with Se results in a metallic state in which the Mott transition is suppressed, which may be linked to the absence of layer stacking.
1. Introduction
Quasi-two-dimensional (2D) in nature, transition metal dichalcogenides (TMDs) such as 1T-MX (M = Ti, Ta and X = S, Se, Te) are prone to electronic instabilities [1]. 1T-Ta(S/Se) exhibits an incredibly rich phase diagram with multiple charge density wave (CDW) transitions emerging as a function of temperature and upon doping. In 1T-TaSSe, macroscopic behaviors such as CDW and superconductivity [2,3,4,5] have been observed, and more recently, a quantum spin liquid (QSL) has been proposed in 1T-TaS as well [6]. In the typical Peierls model for CDW order [7], the instability of the coupled electron–lattice system results in a structural phase transition that is driven by strong electron–phonon coupling [8,9,10,11]. CDW formation can result in electron localization, where displacements along phonon modes lower the total electronic energy by opening up a gap at the Fermi level, E [12,13]. This scenario, although applicable to simple one-dimensional systems, does not fully describe the case of 1T-TaSSe, in which the CDW behavior is intertwined with the opening of a Mott gap [14]. The origin of the CDW has been highly debated in TMDs [15,16,17]. The Fermi surface nesting scenario most often does not apply. Existing models of the CDW order are broadly classified into three types: in one, it involves an excitonic condensation mechanism; in another, it involves a Jahn–Teller-like distortion mechanism; and in the third type, it involves a hybrid model, a combination of Jahn–Teller and exciton condensation [17].
1T-TaS exhibits a strong CDW instability and electronic localization that leads to several interesting effects. Upon cooling from high temperatures, three main phases form: the high-temperature incommensurate CDW (ICDW), the intermediate-temperature nearly commensurate CDW (NCCDW), and the low-temperature commensurate CDW (CCDW) [18]. The ICDW appears below 540 K upon cooling from the high-temperature metallic state, with a transition from the crystal symmetry shown in Figure 1a to the structure shown in Figure 1b. This transition leads to displacements of Ta ions that give rise to the well-known star of David motifs. Upon cooling from the normal, high-temperature metallic state, systematic displacements of the transition metal Ta leads to a star of David formation consisting of 13 Ta ions, in-plane. Domains of these formations expand to a commensurate CDW phase on cooling. Distinct from other CDW systems, in 1T-TaS, the commensurate CDW state is accompanied by a metal–insulator (MI) transition that has been proposed to arise either from Mott localization or from disorder-induced Anderson localization. Important to the MI behavior are the orbital ordering and out-of-plane correlations, as well as layer stacking order.
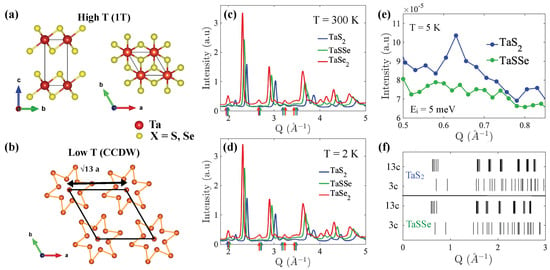
Figure 1.
(a) The high−temperature and (b) low−temperature crystal structures of 1T-TaX. The lattice symmetry is the trigonal at high temperatures, and becomes at low temperatures. The star lattice shown is the result of the Ta displacements. (c) A plot of the neutron diffraction data at 300 K for the three samples measured. Indicated with arrows are the calculated positions of possible superlattice peaks. (d) The neutron diffraction data collected at 2 K. All data are fitted well using symmetry. The diffraction peaks shift to the left with doping because Se is a nominally larger ion than S. (e) The diffraction data plotted at very low Q indicate a superlattice peak corresponding to the 13c stacking order present in 1T-TaS. The reflection is absent in TaSSe. (f) A plot of the expected positions of 13c and 3c stacking order.
In the ICDW, the stars are formed but have limited ordering in-plane. Further cooling leads to the ICDW becoming NCCDW at T = 350 K, where the structural modulation first appears with a 12° tilt relative to the original ab-plane. An expansion of the star of David motifs occurs in-plane [19]. Below 180 K, the structural modulation persists with a rotation of 13.9° relative to the plane while the CDW becomes commensurate. The steps in the CDW transitions coincide with the kinks observed in the transport [20] as the system goes from the metallic to the insulating state. On the other end of the phase diagram, in 1T-TaSe, the CCDW sets in at T ≈ 430 K, and the system shows no MI transition. It remains metallic down to the lowest temperature according to transport data [21]. Between these two ends, superconductivity emerges upon doping that coexists with a broad NCCDW region in the phase diagram [18]. The coexistence of superconductivity with CDW domains has been observed in other TMDs such as in the 2H polytype and in other systems such as cuprates [22,23,24,25].
The electronic bands appear to undergo a continuous change with decreasing temperature in going though the many transition steps [26,27,28]. In the absence of high-temperature angle-resolved photoemission spectroscopy (ARPES) due to resolution, there is no apparent nesting of the Fermi surface, and a CDW gap is not necessarily located at the point. Measurements suggest that the gap appears elsewhere in k-space [7,29]. The domain-like CDW structures of the NCCDW and ICDW states in 1T-TaS are discommensurate and semi-metallic, but when the CDW becomes commensurate, the Fermi surface disappears and either a Mott–Hubbard localization or a disorder-induced Anderson localization sets in [29]. Across the NCCDW-CCDW boundary, the Fermi surface is continuously reduced. This effect is convoluted by d-electron localization that opens up an energy gap. In the CCDW phase, the gap is fully present, leading to a semiconducting state with about a 200 meV bandgap [7].
In the normal phase above 540 K, the Ta 5d band at the point should be above E [30]. As the system goes through the NCCDW phase, this band becomes visible using ARPES. Upon further cooling to the CCDW state, band folding is observed because of the smaller Brillouin zone between 180 and 160 K, and an abrupt energy shift occurs due to opening of the energy gap [4]. The loss of the Fermi surface continues with further cooling, while the CDW gap continues to grow. The first-order transition seen in the transport at 180 K upon cooling is most likely due to a Mott–Hubbard localization [31,32]. On warming, a different behavior is observed where the resistivity exhibits a hysteresis, with its value dropping at 280 K, marking the CCDW-NCCDW transition. This has been attributed to be due to changes in the c-axis stacking order [4,33].
We report on the nature of the layer stacking order with temperature and doping. Earlier, we observed that the c-axis expands in the CCDW phase of 1T-TaS on warming but drops at the crossover between the CCDW-NCCDW transition [34]. It has been suggested that the localization of the d-electrons that results in the gap in the electronic structure depends on the expansion of the c-axis [31,32]. This in turn is related to the c-axis stacking order, where changes in the interlayer coupling might drive the Mott transition. Neutron diffraction measurements confirmed the presence of a 13c stacking order that disappears on warming across the CCDW-NCDW transition in 1T-TaS. The appearance of the 13c layer sequence is expected to drive the Mott localization. The 13c stacking sequence was previously suggested in Ref. [35] from X-ray diffraction data down to 80 K. This study extends the data down to 2 K. Moreover, from single crystal measurements, we previously identified a 3c layer stacking as well that commences in the ICDW state and continues to grow through the NCCDW to CCDW crossover. It is possible that both the 3c and 13c stacking coexist at low temperatures in 1T-TaS. Our single-crystal data only reached 150 K. With doping, the neutron diffraction data clearly indicate that the 13c structure is suppressed. Its signature diffraction peak around 0.6 Å is not observed with doping. At the same time, it is not clear what happens to the 3c stacking with doping. Further experiments using single crystals are underway to elucidate the doping dependence of the 3c order.
2. Results and Discussion
Figure 1a shows the hexagonal crystal structure of the high-temperature, undistorted lattice. Layers of the transition metal are separated by the chalcogen ion, creating a quasi-2D lattice where weak interlayer interactions are expected due to the van der Waals nature of the forces holding the layers together. However, orbitals play an important role in this TMD, and out-of-plane electron correlations lead to layer ordering and a gap in the density of states. The out-of-plane coupling is important to understand the electronic characteristics of these materials where band structure calculations suggested that opening a gap at the point depends on the orbital order and out-of-plane stacking [31,32]. Also shown in Figure 1a is the low-temperature crystal structure in the CCDW phase, where the high-temperature cell has undergone a structural expansion and a rotation of 13.9° relative to the primary axis. The star formation is the result of Ta displacements towards the middle Ta ion. The extent to which the star lattice spreads in the ab-plane depends on temperature. The star clusters expand on cooling, giving rise to large domains in the CCDW state that are highly ordered, but become disordered on warming, breaking up into domains with star formations separated by regions of undistorted lattice. Three samples were measured using neutron scattering, and the diffraction data are shown in Figure 1c,d. Powder samples of TaS, TaSSe, and TaSe were measured as a function of temperature. At 300 K, several superlattice reflections are indicated that might be due to 3c stacking structure. Similarly, at 2 K, the same superlattice reflections are observed as indicated. However, the intensity of the peaks is too small to be discerned from the powder diffraction data, and single-crystal experiments will help elucidate their presence.
The reciprocal lattice vector was calculated using , following the formalism introduced in [19]. The modulation wave vectors and for the CCDW phase were obtained based on the commensurate wave vector parameters and . The reciprocal lattice commensurate wave vector can be described as , and for the in-plane translation, the and values are 0.2308 and 0.0769, respectively. In the NCCDW phase, the and values are 0.2448 and 0.0681, respectively. Shown in Figure 1e is a plot of the diffraction pattern at very small momentum transfers, Q. At 5 K, a superlattice reflection belonging to 13c ordering is observed in 1T-TaS at low temperatures. This reflection only appears from the 13c stacking order and not from the 3c order, even though most of the higher-order reflections overlap between the two stacking models, as shown in Figure 1f. The calculated positions of the satellite peaks corresponding to the stacking order () and the stacking order () are shown. Also shown in Figure 1e are data for TaSSe in the same region of momentum transfer. In the TaSSe data, the reflection ∼0.6 Å is notably absent which indicates that there is no 13c ordering in the superconducting state. A similar measurement was carried out for 1T-TaSe and even though the sample was not a single phase of 1T, no evidence for the 0.6 Å was observed. This indicates that stacking order might only be present in 1T-TaS.
The temperature and composition dependence of the Ta and S/Se thermal factors, <U>, lattice constants, and unit cell volume are plotted in Figure 2. As a function of composition, superconducting TaSSe has the largest thermal factor for the Ta ion that continues to increase on warming. Shown in Figure 2c are the thermal factors for S and Se. Figure 2b is a plot of the c/a ratio. In the case of TaSSe and TaSe, the c/a ratio is almost constant as a function of temperature which indicates that the unit cell expands uniformly in the a- and c-direction. However, in TaS, the ratio drops between 200 and 300 K because of the contraction of the c-lattice constant, as previously observed in our earlier study [34] and by others [36]. The contraction of the c-axis corresponds to the transition from the commensurate to the nearly commensurate state. We observed that this transition is coupled to the disappearance of the 13c ordering. Shown in Figure 2d is the unit cell volume for the three compositions as a function of temperature.
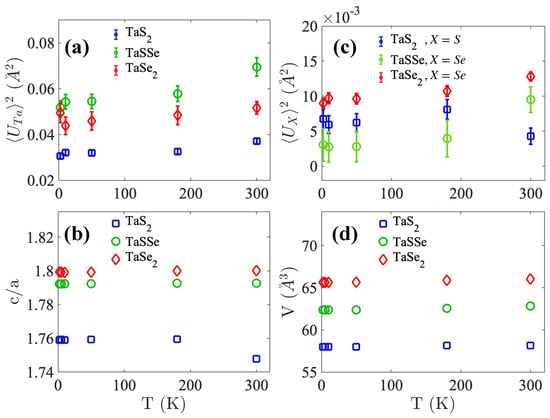
Figure 2.
(a) The Ta−displacements <U> are shown as a function of temperature for the three compositions. Of the three, superconducting TaSSe shows the largest thermal factors. Shown in (c) are the S and Se thermal factors for the three compositions. In (b) is a plot of the c/a ratio for the three compositions, and in (d) is a plot of the unit cell volume. The c/a ratio in 1T-TaS shows a decline upon warming past 200 K.
Figure 3 is a plot of the results from the pair density function (PDF) analysis of the Ta displacements from the local structure at 2 K. The local structure is obtained by Fourier transforming the diffraction data shown in Figure 1, to obtain the pair correlation function, G(r). Fitting the G(r) with a local model results in the distortions shown in the table of Figure 3a. Local Ta distortions are listed for the 12 Ta ions shown in Figure 3b. The 13th center Ta ion does not move by symmetry. This indicates that even after the transition from the to the symmetry, locally, the stars are distorted due to displacements of Ta in the directions shown with the arrows in the star lattice on the right. Moreover, the Ta ions are not all displaced in a symmetric way. This implies that the local trigonal symmetry is broken but that there is, nonetheless, a long-range order of the star of David motifs in-plane. Similar distortions were observed in all three compositions with the results listed for 1T-TaS.

Figure 3.
A list of the Ta atoms and their distortions obtained from fitting the local atomic structure. The Ta atoms make up the star of David. The center Ta ion does not move by symmetry. The Ta atoms are labeled on the star lattice on the right. Also shown are the displacement directions.
3. Materials and Methods
Powder samples were prepared using solid-state reactions. The neutron powder diffraction measurements were performed to investigate the structure through the multiple CDW steps. The time-of-flight (TOF) neutron measurements were carried out using the Nanoscale Ordered Materials Diffractometer (NOMAD/BL-1B) and at SEQUOIA (BL-17), a direct geometry spectrometer, at the Spallation Neutron Source (SNS) of Oak Ridge National Laboratory (ORNL) at temperatures ranging from 1.8 to 500 K. The aluminum can was used for SEQUOIA measurements, and the empty can data were subtracted from the data. The reason SEQUOIA was used is that it reaches very small momentum transfers, not accessible to NOMAD. The diffraction data from NOMAD were analyzed using the Rietveld refinement to obtain the unit cell parameters characterizing the crystal structure [37], resulting in what is referred to as the average model. The pair density function (PDF) analysis [24,38] provides information on the local arrangement of atoms in real space without the assumption of periodicity. It was performed on the same neutron diffraction data as the ones used for the Rietveld refinement. NOMAD is a diffractometer with a large bandwidth of momentum transfer Q, and it provides the total structure function . The was Fourier transformed into real-space to obtain the [39,40]. The instrument background and empty sample container were subtracted from the , and the data were normalized by a vanadium rod. A maximum Q of 40 Å−1 was used.
4. Conclusions
The control of heterostructure stacking can be engineered to enable new behaviors and new properties. For instance, it has been theoretically proposed that stacking of the honeycomb ferromagnet CrI has the potential to give rise to ferroelectricity [41]. Moreover, stacking in moiré superlattices can create polar domains because of local spontaneous polarization [42]. Hexagonal boron nitride was shown to exhibit ferroelectric switching in bilayers, leading to new concepts for functional heterostructures [43]. Similarly, ferromagnetic heterostructures were demonstrated by stacking non-magnetic WS with antiferromagnetic FePS. At the interface, the FePS shows ferromagnetism [44].
Layer stacking in homostructure TMDs may be similarly linked to the transport behavior. 1T-TaS has an insulating CDW in contrast to other CDW dichalcogenides that have metallic CDW’s. The reason for this is linked to Mott–Hubbard electron–electron correlations. Every star of David contributes one electron to a half-filled narrow conduction band. In the 13c layer stacking, there is an odd number of electrons and in the presence of large Coulomb repulsion acting on the layers, the Mott–Hubbard transition occurs [29]. Density functional theory (DFT) calculations [33] have shown that the insulating phase and the MI transition originate not from the 2D order of the stars of David but by the vertical order. Our results confirm the significance of interlayer coupling and the insulating property. Interlayer stacking order in the CCDW phase has been verified to be a 13c repeat unit cell. This result contradicts the notion that the stacking is partially disordered in the CCDW state. Hence, it is less likely that Anderson localization drives the MI transition. This result also contradicts the bilayer stacking model.
Author Contributions
Conceptualization, D.L.; Data curation, S.S.P.; Neutron scattering experiment, M.B.S. and A.I.K.; Formal analysis, S.S.P.; Funding acquisition, D.L.; Investigation, S.S.P.; Methodology, S.S.P.; Resources, D.L.; Supervision, D.L.; Writing—original draft, D.L.; Writing—review and editing, S.S.P. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. National Science Foundation, Grant No. 2219493.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are readily available upon request from any of the authors.
Acknowledgments
A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by Oak Ridge National Laboratory. We thank John Schneeloch (University of Virginia) for the valuable inputs on the sample growth and Utpal Chatterjee for the valuable discussions about the ARPES data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilson, J.A.; Di Salvo, F.; Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 1975, 24, 117–201. [Google Scholar] [CrossRef]
- Liu, Y.; Ang, R.; Lu, W.J.; Song, W.H.; Li, L.J.; Sun, Y.P. Superconductivity induced by Se-doping in layered charge density-wave system 1T-TaS2−xSex. Appl. Phys. Lett. 2013, 102, 192602. [Google Scholar] [CrossRef]
- Liu, Y.; Shao, D.F.; Li, L.J.; Lu, W.J.; Zhu, X.D.; Tong, P.; Xiao, R.C.; Ling, L.S.; Xi, C.Y.; Pi, L. Nature of charge density waves and superconductivity in 1 T-TaSe2- x Te x. Phys. Rev. B 2016, 94, 045131. [Google Scholar] [CrossRef]
- Wang, Y.D.; Yao, W.L.; Xin, Z.M.; Han, T.T.; Wang, Z.G.; Chen, L.; Cai, C.; Li, Y.; Zhang, Y. Band insulator to Mott insulator transition in 1T-TaS2. Nat. Commun. 2020, 11, 4215. [Google Scholar] [CrossRef]
- Sipos, B.; Kusmartseva, A.F.; Akrap, A.; Berger, H.; Forro, L.; Tutis, E. From Mott state to superconductivity in 1T-TaS2. Nat. Mater. 2008, 7, 960–965. [Google Scholar] [CrossRef]
- Law, K.T.; Lee, P.A. 1T-TaS2 as a quantum spin liquid. Proc. Natl. Acad. Sci. USA 2017, 114, 6996–7000. [Google Scholar] [CrossRef]
- Rossnagel, K. On the origin of charge-density waves in select layered transition-metal dichalcogenides. J. Phys. Condens. Matter 2011, 23, 213001. [Google Scholar] [CrossRef]
- Chen, V.; Lee, H.R.; Koroglu, C.; McClellan, C.J.; Daus, A.; Pop, E. Ambipolar Thickness-Dependent Thermoelectric Measurements of WSe2. Nano Lett. 2023, 23, 4095–4100. [Google Scholar]
- Sun, K.; Sun, S.; Zhu, C.; Tian, H.; Yang, H.; Li, J. Hidden CDW states and insulator-to-metal transition after a pulsed femtosecond laser excitation in layered chalcogenide 1T-TaS2−x Se x. Sci. Adv. 2018, 4, eaas9660. [Google Scholar] [CrossRef]
- Butler, C.J.; Yoshida, M.; Hanaguri, T.; Iwasa, Y. Mottness versus unit-cell doubling as the driver of the insulating state in 1T-TaS2. Nat. Commun. 2020, 11, 2477. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, J. Stacking order and driving forces in the layered charge density wave phase of 1T-MX2 (M = Nb, Ta and X = S, Se). Mater. Res. Express 2023, 10, 046302. [Google Scholar] [CrossRef]
- Warawa, K.; Christophel, N.; Sobolev, S.; Demsar, J.; Roskos, H.G.; Thomson, M.D. Combined investigation of collective amplitude and phase modes in a quasi-one-dimensional charge-density-wave system over a wide spectral range. arXiv 2023, arXiv:2303.08558. [Google Scholar] [CrossRef]
- Hansen, M.O.; Palan, Y.; Hahn, V.; Thomson, M.D.; Warawa, K.; Roskos, H.G.; Demsar, J.; Pientka, F.; Tsyplyatyev, O.; Kopietz, P. Collective modes in the charge-density wave state of K0.3MoO3: The role of long-range Coulomb interactions revisited. Phys. Rev. B 2023, 108, 045148. [Google Scholar] [CrossRef]
- Manzke, R.; Buslaps, T.; Pfalzgraf, B.; Skibowksi, M.; Anderson, O. On the Phase Transitions in 1T-TaS2. Europhys. Lett. 1989, 8, 195–200. [Google Scholar] [CrossRef]
- Wegner, A.; Zhao, J.; Li, J.; Yang, J.; Anikin, A.A.; Karapetrov, G.; Esfarjani, K.; Louca, D.; Chatterjee, U. Evidence for pseudo–Jahn-Teller distortions in the charge density wave phase of 1T-TiSe2. Phys. Rev. B 2020, 101, 195145. [Google Scholar] [CrossRef]
- Chatterjee, U.; Zhao, J.; Iavarone, M.; Di Capua, R.; Castellan, J.; Karapetrov, G.; Malliakas, C.; Kanatzidis, M.G.; Claus, H.; Ruff, J.; et al. Emergence of coherence in the charge-density wave state of 2 H-NbSe2. Nat. Commun. 2015, 6, 6313. [Google Scholar] [CrossRef]
- van Wezel, J.; Nahai-Williamson, P.; Saxena, S.S. An alternative interpretation of recent ARPES measurements on TiSe2. Europhys. Lett. 2010, 89, 47004. [Google Scholar] [CrossRef]
- Ang, R.; Wang, Z.C.; Chen, C.L.; Tang, J.; Liu, N.; Liu, Y.; Lu, W.J.; Sun, Y.P.; Mori, T.; Ikuhara, Y. Atomistic origin of an ordered superstructure induced superconductivity in layered chalcogenides. Nat. Commun. 2015, 6, 6091. [Google Scholar] [CrossRef]
- Spijkerman, A.; de Boer, J.L.; Meetsma, A.; Wiegers, G.A.; van Smaalen, S. X-ray crystal-structure refinement of the nearly commensurate phase of 1 T-TaS2 in (3+2)-dimensional superspace. Phys. Rev. B 1997, 56, 13757. [Google Scholar] [CrossRef]
- Fazekas, P.; Tosatti, E. Electrical, structural and magnetic properties of pure and doped 1T-TaS2. Philos. Mag. B 1979, 39, 229–244. [Google Scholar] [CrossRef]
- Wilson, J.A.; Di Salvo, F.J.; Mahajan, S. Charge-Density Waves in Metallic, Layered, Transition-Metal Dichalcogenides. Phys. Rev. Lett. 1974, 32, 882–885. [Google Scholar] [CrossRef]
- Canfield, P.C.; Gammel, P.L.; Bishop, D.J. New Magnetic Superconductors: A Toy Box for Solid State Physicists. Phys. Today 1998, 51, 40–46. [Google Scholar] [CrossRef]
- Kvashnin, Y.; VanGennep, D.; Mito, M.; Medvedev, S.A.; Thiyagarajan, R.; Karis, O.; Vasiliev, A.N.; Eriksson, O.; Abdel-Hafiez, M. Coexistence of Superconductivity and Charge Density Waves in Tantalum Disulfide: Experiment and Theory. Phys. Rev. Lett. 2020, 125, 186401. [Google Scholar] [CrossRef] [PubMed]
- Egami, T.; Billinge, S.J. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Lee, J.; Demura, S.; Stone, M.B.; Iida, K.; Ehlers, G.; Dela Cruz, C.R.; Matsuda, M.; Deguchi, K.; Takano, Y.; Mizuguchi, Y.; et al. Coexistence of ferromagnetism and superconductivity in CeO 0.3 F 0.7 BiS 2. Phys. Rev. B 2014, 90, 224410. [Google Scholar] [CrossRef]
- Smith, N.V.; Kevan, S.D.; Disalvo, F.J. Band structures of the layer compounds 1T-TaS, and 2H-TaSe, in the presence of commensurate charge-density waves. J. Phys. C Solid State Phys. 1985, 18, 3175–3189. [Google Scholar] [CrossRef]
- Aiura, Y.; Hase, I.; Yagi-Watanabe, K.; Bando, H.; Ozawa, K.; Tanaka, K.; Kitagawa, R.; Maruyama, S.; Iwase, T.; Nishihara, Y.; et al. Increase in charge-density-wave potential of 1T-TaSxSe2−x. Phys. Rev. B 2004, 69, 245123. [Google Scholar] [CrossRef]
- Zwick, F.; Berger, H.; Vobornik, I.; Margaritondo, G.; Forró, L.; Beeli, C.; Onellion, M.; Panaccione, G.; Taleb-Ibrahimi, A.; Grioni, M. Spectral Consequences of Broken Phase Coherence in 1T-TaS2. Phys. Rev. Lett. 1998, 81, 1058–1061. [Google Scholar] [CrossRef]
- Fei, Y.; Wu, Z.; Zhang, W.; Yin, Y. Understanding the Mott insulating state in 1 T-TaS2 and 1 T-TaSe2. AAPPS Bull. 2022, 32, 20. [Google Scholar] [CrossRef]
- Bovet, M.; Popović, D.; Clerc, F.; Koitzsch, C.; Probst, U.; Bucher, E.; Berger, H.; Naumović, D.; Aebi, P. Pseudogapped Fermi surfaces of 1T-TaS2 and 1T-TaSe2: A charge density wave effect. Phys. Rev. B 2004, 69, 125117. [Google Scholar] [CrossRef]
- Ritschel, T.; Trinckauf, J.; Koepernik, K.; Büchner, B.; Zimmermann, M.v.; Berger, H.; Joe, Y.; Abbamonte, P.; Geck, J. Orbital textures and charge density waves in transition metal dichalcogenides. Nat. Phys. 2015, 11, 328–331. [Google Scholar] [CrossRef]
- Ritschel, T.; Berger, H.; Geck, J. Stacking-driven gap formation in layered 1T-TaS 2. Phys. Rev. B 2018, 98, 195134. [Google Scholar] [CrossRef]
- Lee, S.H.; Goh, J.S.; Cho, D. Origin of the Insulating Phase and First-Order Metal-Insulator Transition in 1 T-TaS2. Phys. Rev. Lett. 2019, 122, 106404. [Google Scholar] [CrossRef] [PubMed]
- Philip, S.S.; Neuefeind, J.C.; Stone, M.B.; Louca, D. Local structure anomaly with the charge ordering transition of 1T-TaS2. Phys. Rev. B 2023, 107, 184109. [Google Scholar] [CrossRef]
- Scruby, C.B.; Williams, P.M.; Parry, G. The role of charge density waves in structural transformations of 1T TaS2. Philos. Mag. 1975, 31, 255–274. [Google Scholar] [CrossRef]
- Petkov, V.; Peralta, J.; Aoun, B.; Ren, Y. Atomic structure and Mott nature of the insulating charge density wave phase of 1T-TaS2. J. Phys. Condens. Matter 2022, 34, 345401. [Google Scholar] [CrossRef]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Proffen, T.; Billinge, S.; Egami, T.; Louca, D. Structural analysis of complex materials using the atomic pair distribution function—A practical guide. Z. FÜR-Krist.-Cryst. Mater. 2003, 218, 132–143. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Courier Corporation: North Chelmsford, MA, USA, 1990. [Google Scholar]
- Peterson, P.; Gutmann, M.; Proffen, T.; Billinge, S. PDFgetN: A user-friendly program to extract the total scattering structure factor and the pair distribution function from neutron powder diffraction data. J. Appl. Crystallogr. 2000, 33, 1192. [Google Scholar] [CrossRef]
- Ji, J.; Yu, G.; Xu, C.; Xiang, H. General Theory for Bilayer Stacking Ferroelectricity. Phys. Rev. Lett. 2023, 130, 146801. [Google Scholar] [CrossRef]
- Bennett, D.; Remez, B. On electrically tunable stacking domains and ferroelectricity in moiré superlattices. npj 2D Mater. Appl. 2022, 6, 7. [Google Scholar] [CrossRef]
- Yasuda, K.; Wang, X.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P. Stacking-engineered ferroelectricity in bilayer boron nitride. Science 2021, 372, 1458–1462. [Google Scholar]
- Gong, C.; Zhang, P.; Norden, T.; Li, Q.; Guo, Z.; Chaturvedi, A.; Najafi, A.; Lan, S.; Liu, X.; Wang, Y.; et al. Ferromagnetism emerged from non-ferromagnetic atomic crystals. Nat. Commun. 2023, 14, 3839. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).