Abstract
In this study, we investigated, for the first time, the effects of the spatially varying effective mass, asymmetry parameter, and well width on the electronic and optical properties of a quantum well which has an improved Rosen–Morse potential. Calculations were made within the framework of the effective mass and parabolic band approximations. We have used the diagonalization method by choosing a wave function based on the trigonometric orthonormal functions to find eigenvalues and eigenfunctions of the electron confined within the improved Rosen–Morse potential. Our results show that the position dependence mass, asymmetry, and confinement parameters cause significant changes in the electronic and optical properties of the structure we focus on since these effects create a significant increase in electron energies and a blue shift in the absorption spectrum. The increase in energy levels enables the development of optoelectronic devices that can operate at wider wavelengths and absorb higher-energy photons. Through an appropriate choice of parameters, the Rosen–Morse potential offers, among many advantages, the possibility of simulating heterostructures close to surfaces exposed to air or vacuum, thus giving the possibility of substantially enriching the allowed optical transitions given the breaking of the system´s symmetries. Similarly, the one-dimensional Rosen–Morse potential model proposed here can be extended to one- and zero-dimensional structures such as core/shell quantum well wires and quantum dots. This offers potential advancements in fields such as optical communication, imaging technology, and solar cells.
1. Introduction
Constructing a universal empirical potential energy function for diatomic and/or polyatomic molecules holds significant importance. The fitting quality between the function and experimental data improves with an increased number of parameters in the analytical potential energy function. To illustrate, Morse proposed the first simple empirical analytical potential function in 1929 [1], which found utility in studying transition frequencies and intensities in diatomic and polyatomic molecules [2]. Several potential-energy functions, namely the Manning–Rosen, Schiöberg, Tietz, and Rosen–Morse potential functions, have been derived for diatomic molecules by explicitly incorporating the dissociation energy and equilibrium bond length as parameters [3,4,5].
The improved Rosen–Morse potential (IRMP) or exponential Rosen–Morse potential has more independent fitting parameters for experimental data than the trigonometric Rosen–Morse potential. Quantum well potentials are often used in combination with other materials to create heterostructures. By stacking different layers of materials with varying bandgaps and compositions, researchers can create quantum wells with different geometries. These heterostructures can provide additional degrees of freedom to control the electronic properties, enabling the design of advanced devices like high-electron-mobility transistors (HEMTs) [6,7] and quantum cascade lasers. The significance of quantum well potentials with different geometries lies in their ability to manipulate electron energies, confinement effects, quantum tunneling, optical properties, and the creation of complex heterostructures.
By tailoring the geometry, researchers can engineer the desired electronic and optical characteristics for various applications in semiconductor devices and quantum technologies. Low-dimensional semiconductor heterostructures in which position-dependent mass (PDM) or spatially variable mass effects are taken into account are of interest to researchers because of their importance in many branches of physics, especially in the study of electronic and optical properties of semiconductors [8,9,10,11,12,13,14,15]. The IRMP, or eRMP, serves as a reliable model for describing the interaction between particles in various physical systems. By including more appropriate parameters, it provides a more flexible framework than trigonometric RM potential to accurately represent experimental data.
This study capitalizes on these advantages to explore the behavior of electrons in a quantum well, where the effective mass varies spatially. As known, understanding the electronic properties of confined electrons is crucial for developing advanced electronic devices and optoelectronic applications. Although there are a limited number of studies on the optical properties of quantum wells and quantum dots with trigonometric RM potential under external fields and without PDM [16,17,18], we have not found any studies on the optical properties of quantum well (QW) with IRMP. Therefore, in this study, which had never been studied except for the calculation of rotational-vibration energies of some diatomic molecules, we investigated, for the first time, the electronic and optical properties of an electron with spatially varying effective mass, confined in a QW which has IRMP.
2. Theoretical Framework
In the effective mass approximation, the Hamiltonian for the electron is given by
where is the position-dependent electron effective mass along the heterostructure growth direction, and it is as defined below:
where the d-parameter describes the effective length of position dependence mass (PDM) distribution and is the effective mass at ( is the free electron mass). At sufficiently large d-values, the variable mass approaches the value of the electron mass in the bulk material of interest, and the uniform behavior, stability, and spatial extension of the effective mass also increase. is the IRMQW potential, and its functional form is given as follows [19]
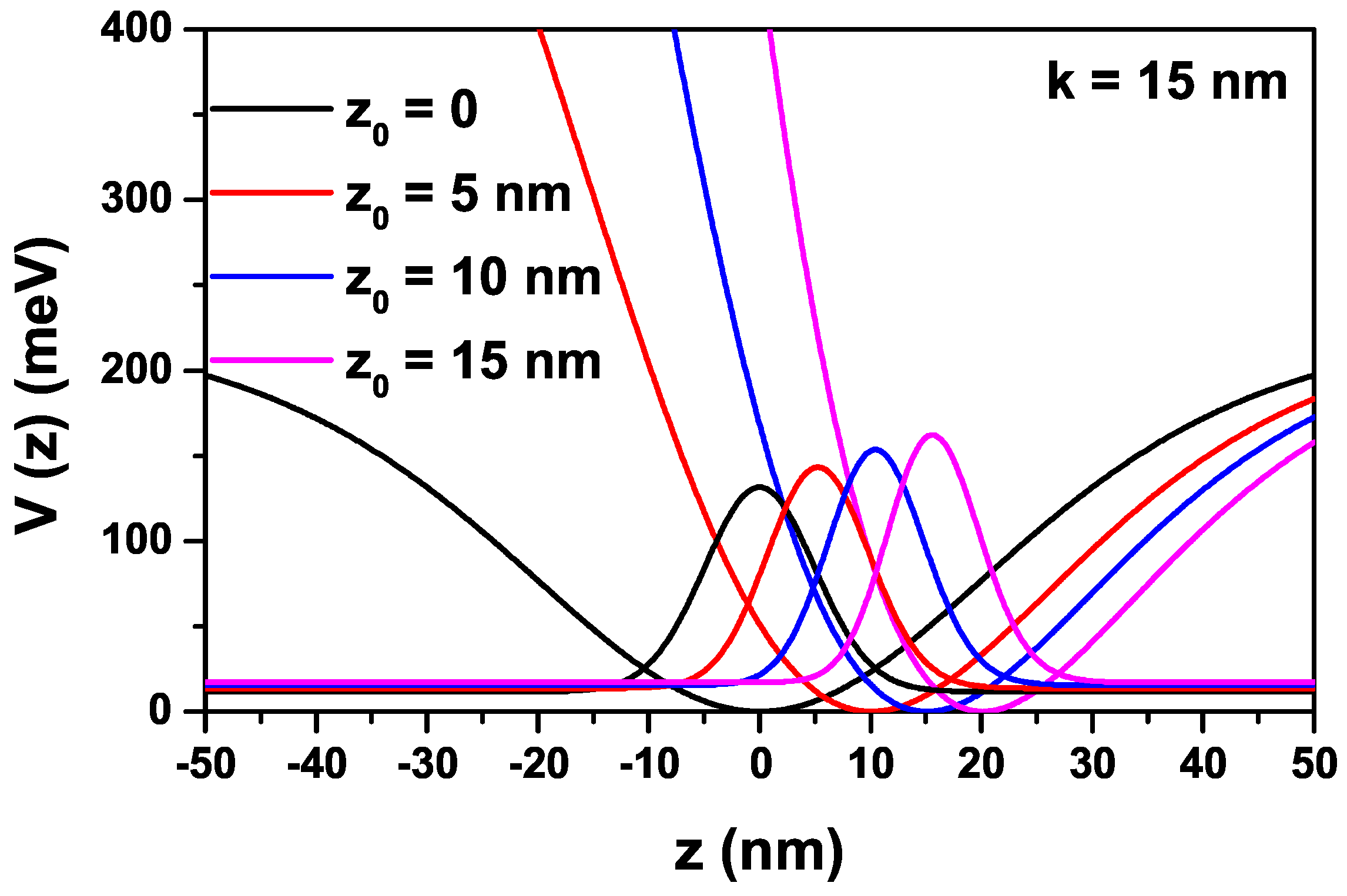
where is the depth of the quantum well and the k-parameter is related to the well width. As seen in Figure 1, as increases, the minimum point of the potential shifts and barrier height on the right side slowly decreases, while the left side becomes sharper and rises to infinity. So, we defined as an asymmetry parameter since it causes the IRMQW to turn into an asymmetrical structure. It should also be noted that the IRMQW used in the literature to obtain the molecular energy spectrum of diatomic molecules (see, for instance, Ref. [19] and the references therein) has been modified by us to investigate the electronic and optical properties of an electron confined within this potential.
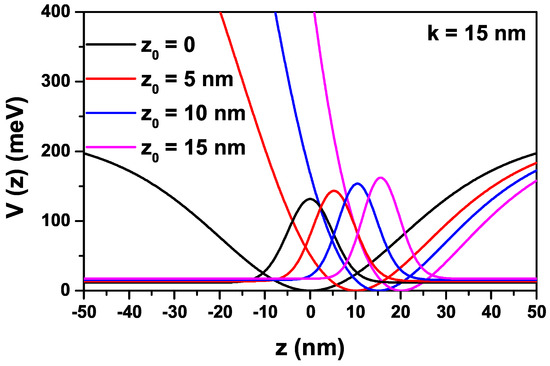
Figure 1.
For nm and different -values, quantum well with the improved Rosen–Morse confinement potential, and squared wave function corresponding to the ground state of the electron localized in this well.
At this point, before continuing, we want to emphasize that the potential profiles shown in Figure 1 can be obtained experimentally and without any difficulty given the technological advances of recent years, considering an epitaxial growth of AlGaAs where the aluminum concentration is varied in a controlled manner as the layers of semiconductor material are deposited. It starts from , which corresponds to the bottom of the potential wells, and its value is increased in line with the value of the desired potential. The structures with divergent potential on one of the faces correspond to an interface with air or a vacuum. Among the advantages of the proposed model is that using non-abrupt variations of the potential, the effects of interdiffusion in two-dimensional heterostructures such as quantum wells can be simulated.
Regarding the effective mass distribution that we use in this investigation and that is given by Equation (2), we have to state that the model is suitable to represent a solitonic profile found in condensed matter and low-energy nuclear physics [20,21,22,23]. It is important to highlight that among the reasons that have motivated us to choose this model of effective mass that decreases with the absolute value of the z-coordinate and that presents the same GaAs effective mass at point are the following: (i) it is a model where the spatial dependence of the effective mass adapts very well to the profile of the probability density for the ground state, and (ii) it is an effective mass model that gives a very good account of the presence of singularities in the confinement potential. Sari et al. have used a model with Gaussian mass distribution in quantum wells and quantum dots with Gaussian-like confinement potential [24,25]. It is well known that in a model of effective mass theory, a direct connection can be established between the electron effective mass and the gap energy of the respective semiconductor. For example, in AlGaAs, the energy gap, in turn, has a direct dependence on the aluminum concentration. Then, another functional distribution of effective mass along the structure growth direction is the one obtained by connecting the spatial dependence of the effective mass with the spatial dependence of the aluminum concentration and then this dependence, in turn, with the spatial dependence of the confinement potential, which in turn is ultimately connected to the semiconductor energy gap. Work in that direction has been reported in Ref. [26] for cylindrical quantum dots with hyperbolic-type axial potential. Finally, we emphasize that achieving similar outcomes could be possible through precise spatial control of both the confinement potential and effective mass within other emerging opto-electronics materials. Remarkably, recent advances in this field have opened up an entirely new spectrum of opportunities.
Immediately after the energies and related wave functions are acquired, for transitions between any two electronic states, the linear and non-linear absorption coefficients are found by using perturbation expansion and density matrix methods. Using the relevant approaches mentioned before, expressions of the linear, third-order nonlinear, and total absorption coefficients (ACs) for the optical transitions are found, respectively, as follows [27,28,29,30]:
and
where is the real part of the permittivity, is the carrier density in the system, is the vacuum permeability, is the energy difference between two energy levels, , is the transition matrix element between the eigenstates and for incident radiation polarized in the z-direction, (=1/Tij) is the relaxation rate, is the relaxation time, c is the speed of light in free space, and I is the intensity of an incident photon with an -angular frequency that leads to the intersubband optical transitions. It should be noted that diagonal (non-diagonal) matrix elements are zero (different zero) , in the symmetric case for .
3. Results and Discussion
The parameter values in our numerical calculations are , (where is the free electron mass), meV, , ps, H m, and m. Two values of the incident radiation intensity are used: W/m2 and W/m2. These parameters are suitable for GaAs/GaAlAs heterostructures [8].
The changes in the shape of the IRM-type QW according to the -asymmetry parameter as a function of the z-coordinate are given in Figure 1. When the -parameter is zero, the structure has a symmetrical character; if is nonzero, it becomes an asymmetrical character; and the -parameter also has a dominant effect on geometric confinement.
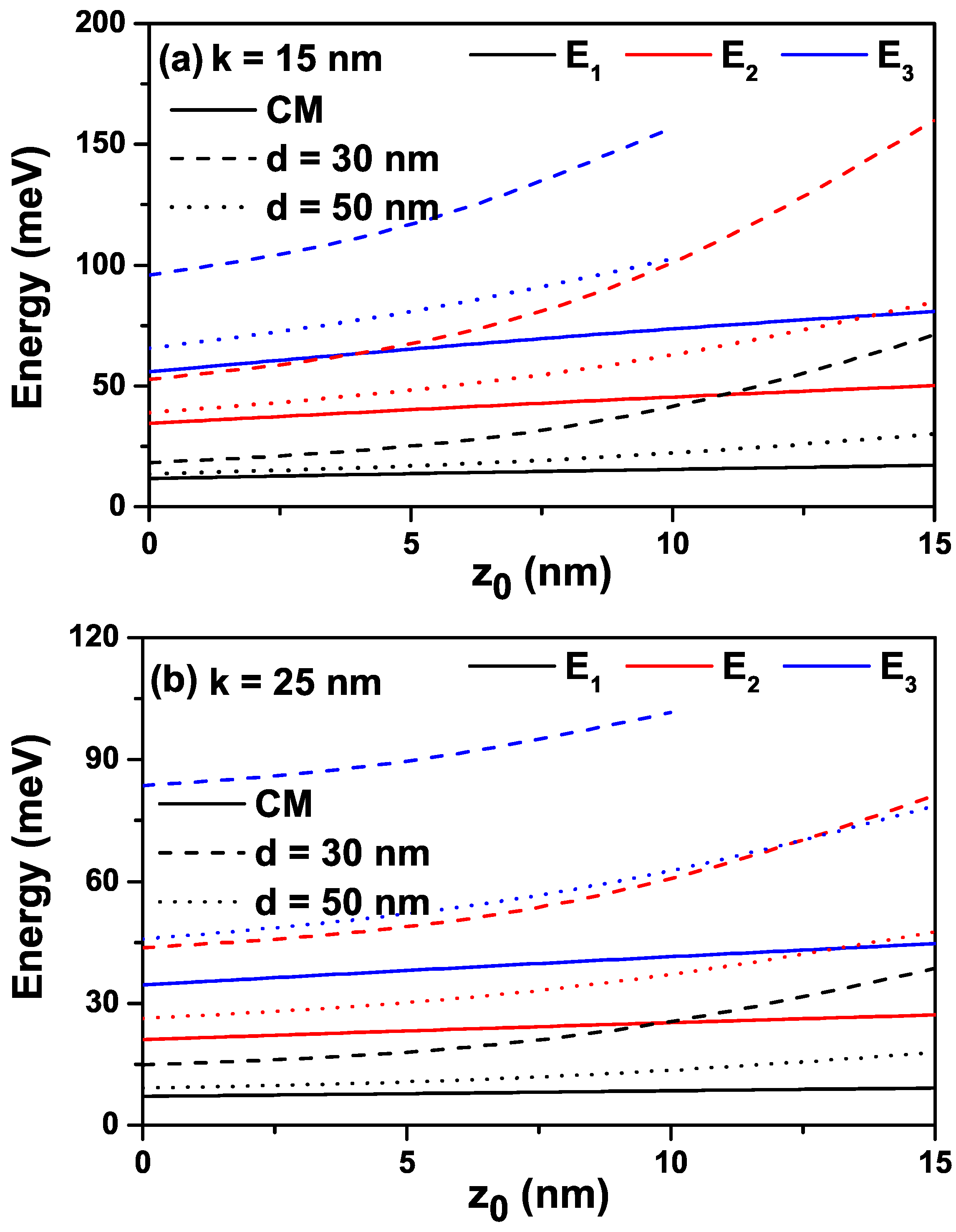
The variations in the energies corresponding to the first three levels of a confined electron within the IRMQW as a function of the -parameter in the absence and presence of position dependence mass for the nm and nm values are given in Figure 2a,b. In the absence and presence of PDM, energies are an increasing function of the -parameter. As explained above, the energies increase since the increase in the -parameter causes an increase in the geometric confinement. As seen in Equation (2), for small values of the d-parameter, the PDM of the electron is lower than that of the constant mass (CM), i.e., . So, the energy values of the electron become larger since the energy levels are always inversely proportional to the electron’s effective mass. However, for larger values of the d-parameter, the energy values of the electron also approach the CM results since approaches the -value. Furthermore, the electron that has -energy becomes unbound at nm due to the increase in energies following the combined effects of the PDM and -parameter. The increase in the k-width parameter weakens the geometric confinement. Therefore, the energies decrease, and the electron with -energy becomes bound in the well at the same value for a large d.
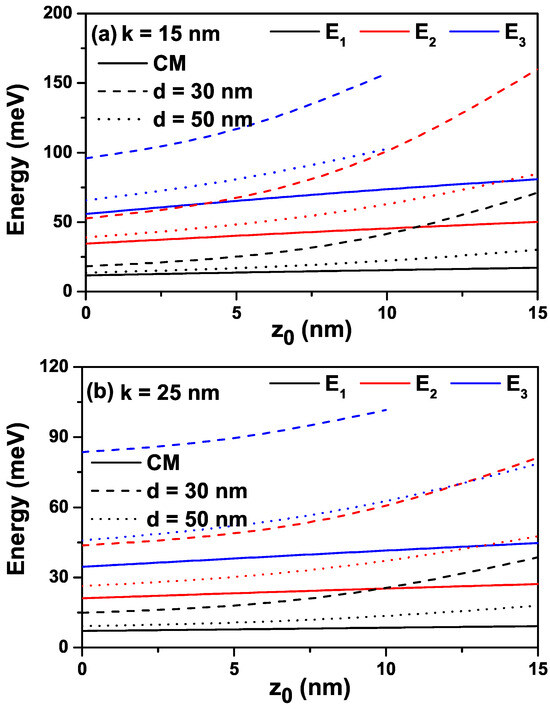
Figure 2.
The variation in the energies corresponding to the first three energy levels of a confined electron within the improved Rosen–Morse confinement potential as a function of the -parameter in the absence and presence of position dependence mass nm (a), and nm (b). Solid lines are for electrons with constant mass (CM), and dashed lines are for position dependence mass (PDM).
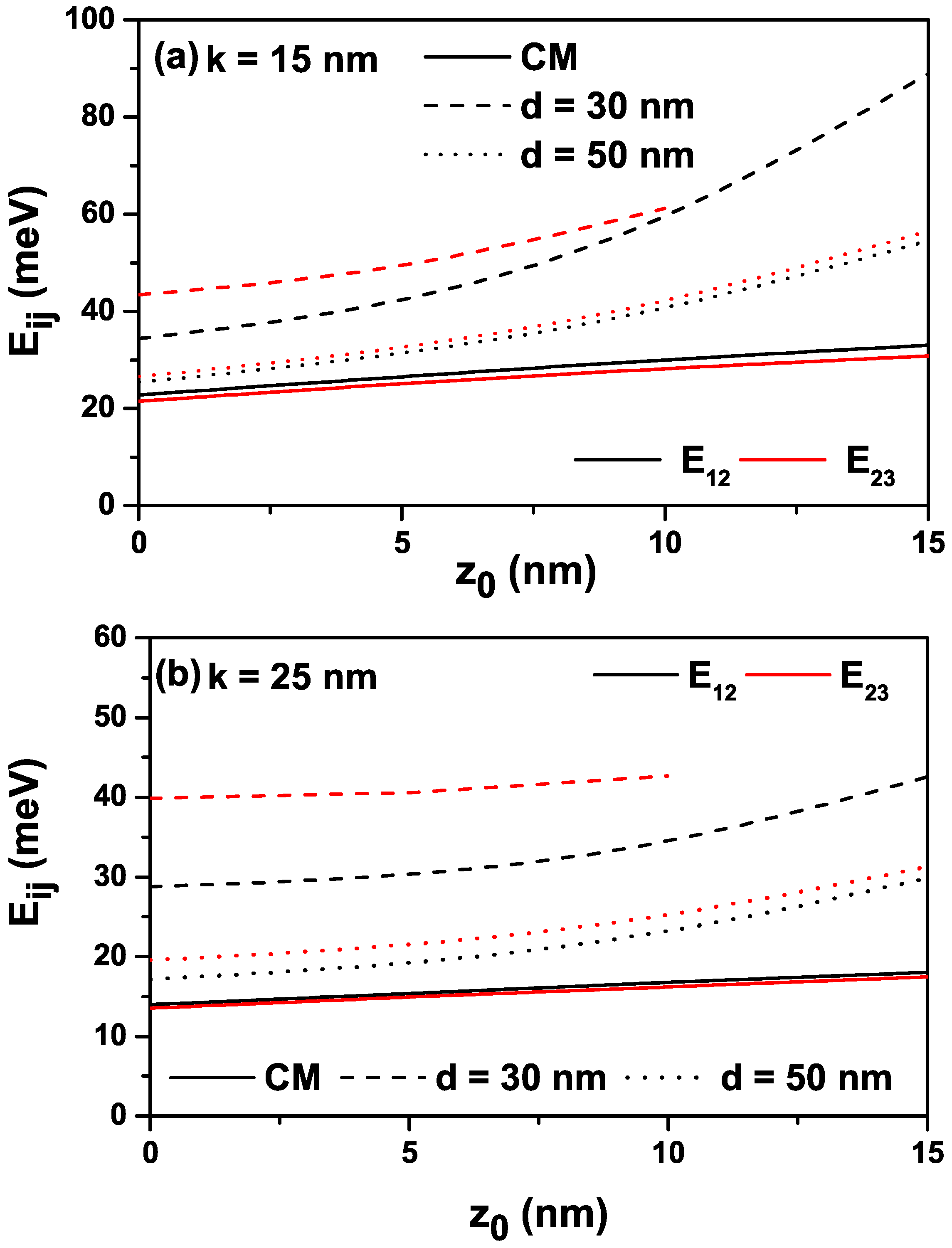
The variations in the energy differences between some energy levels of interest as a function of the -parameter for the values of nm and nm are given in Figure 3a,b. As a natural consequence of the increase in energies as a function of , the energy differences between the two levels indicated at the inset of the figures also increase.
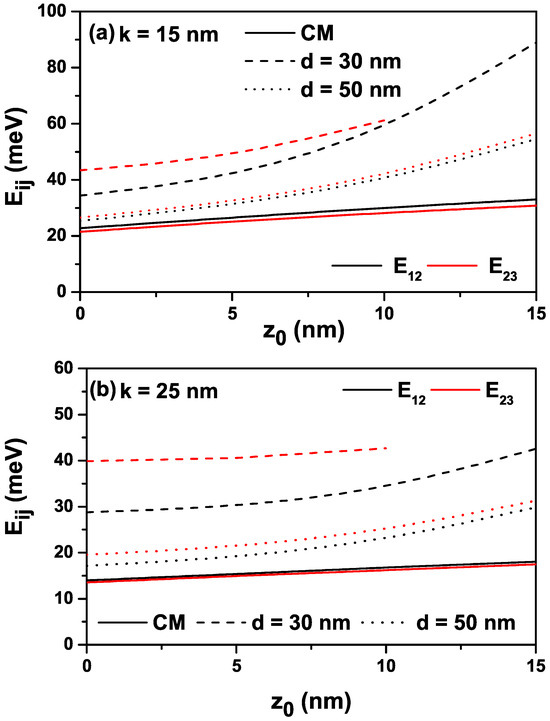
Figure 3.
The variation in the energy differences between some energy levels of interest as a function of the -parameter: nm (a) and nm (b).
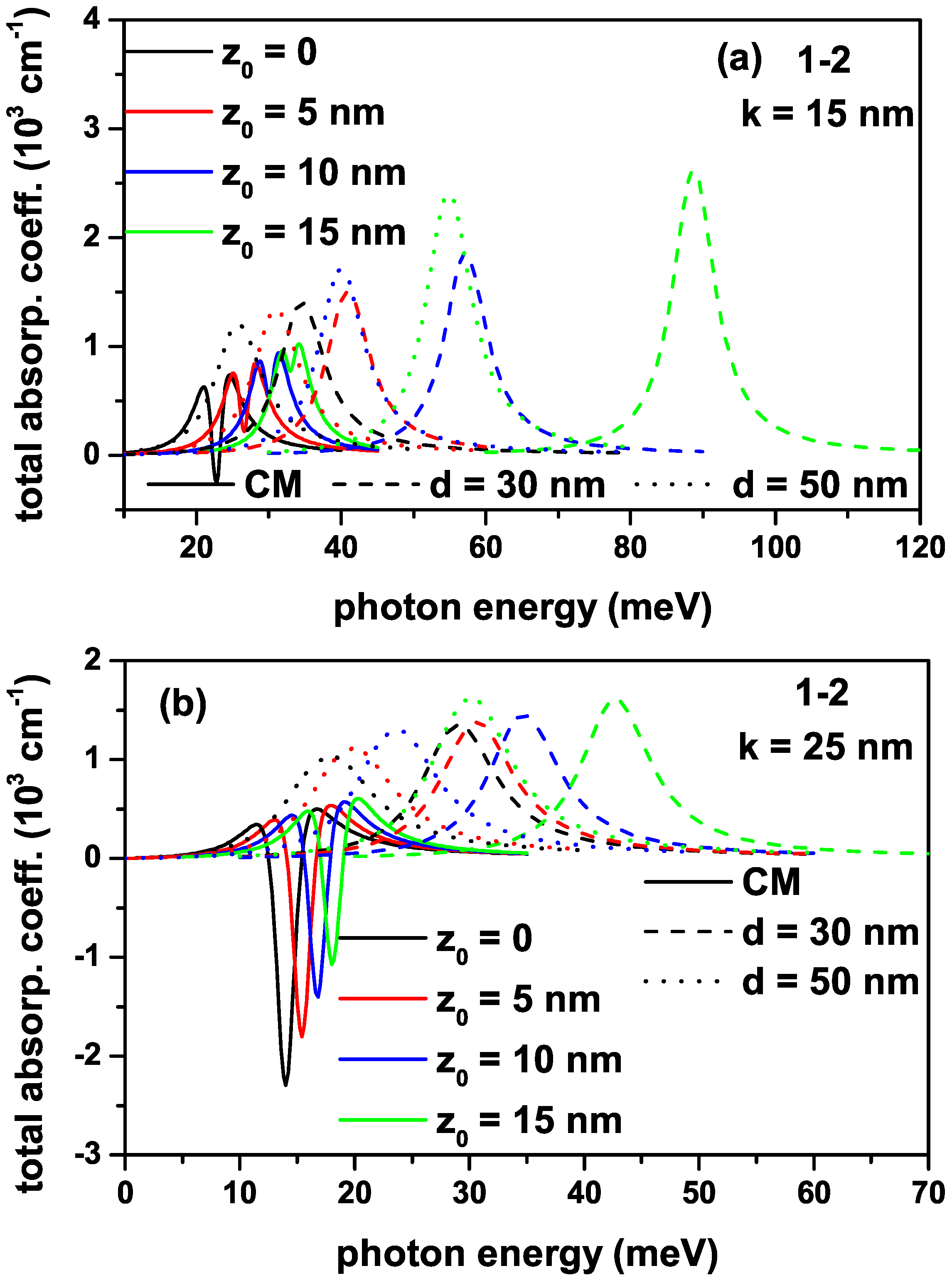
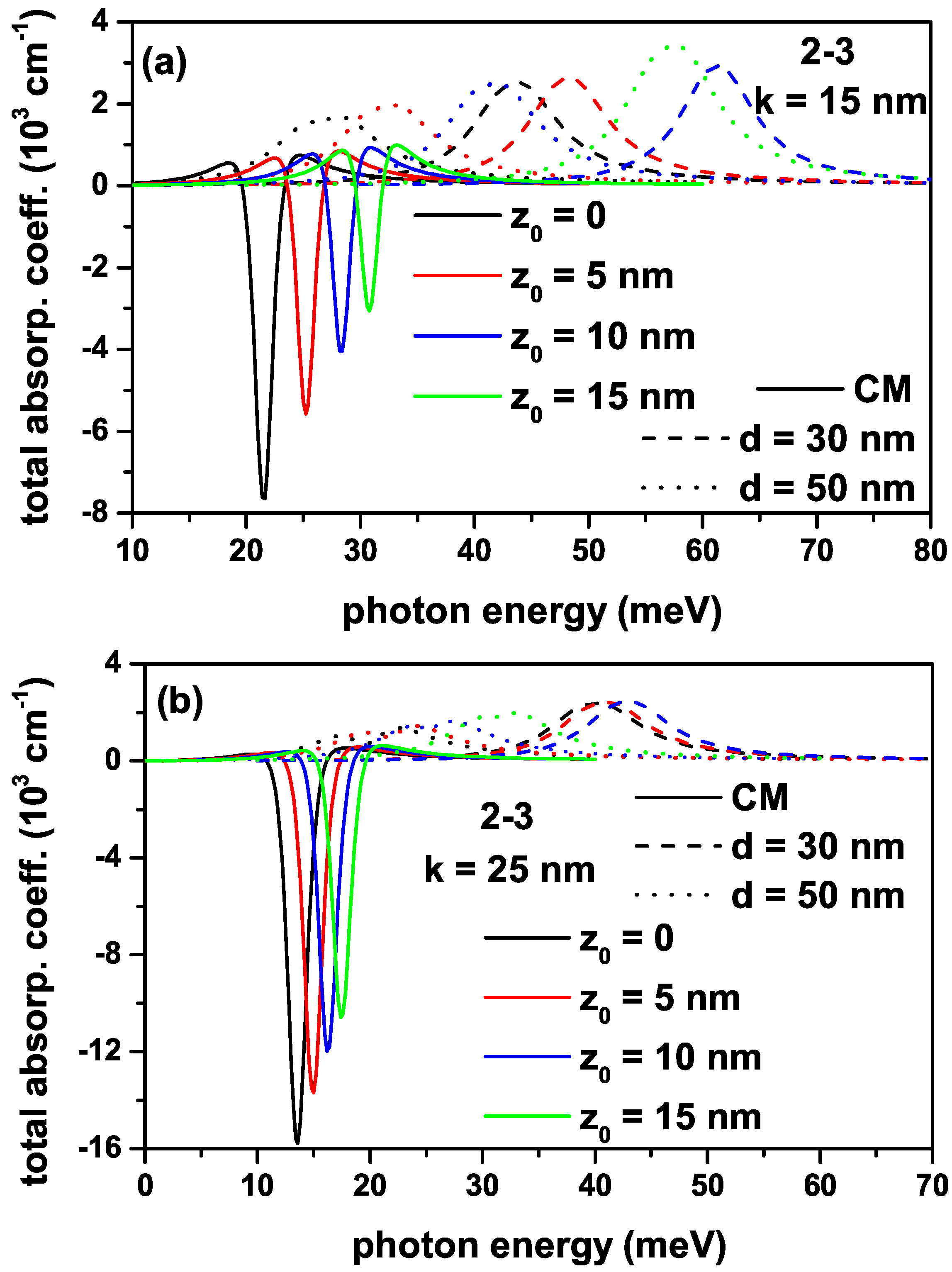
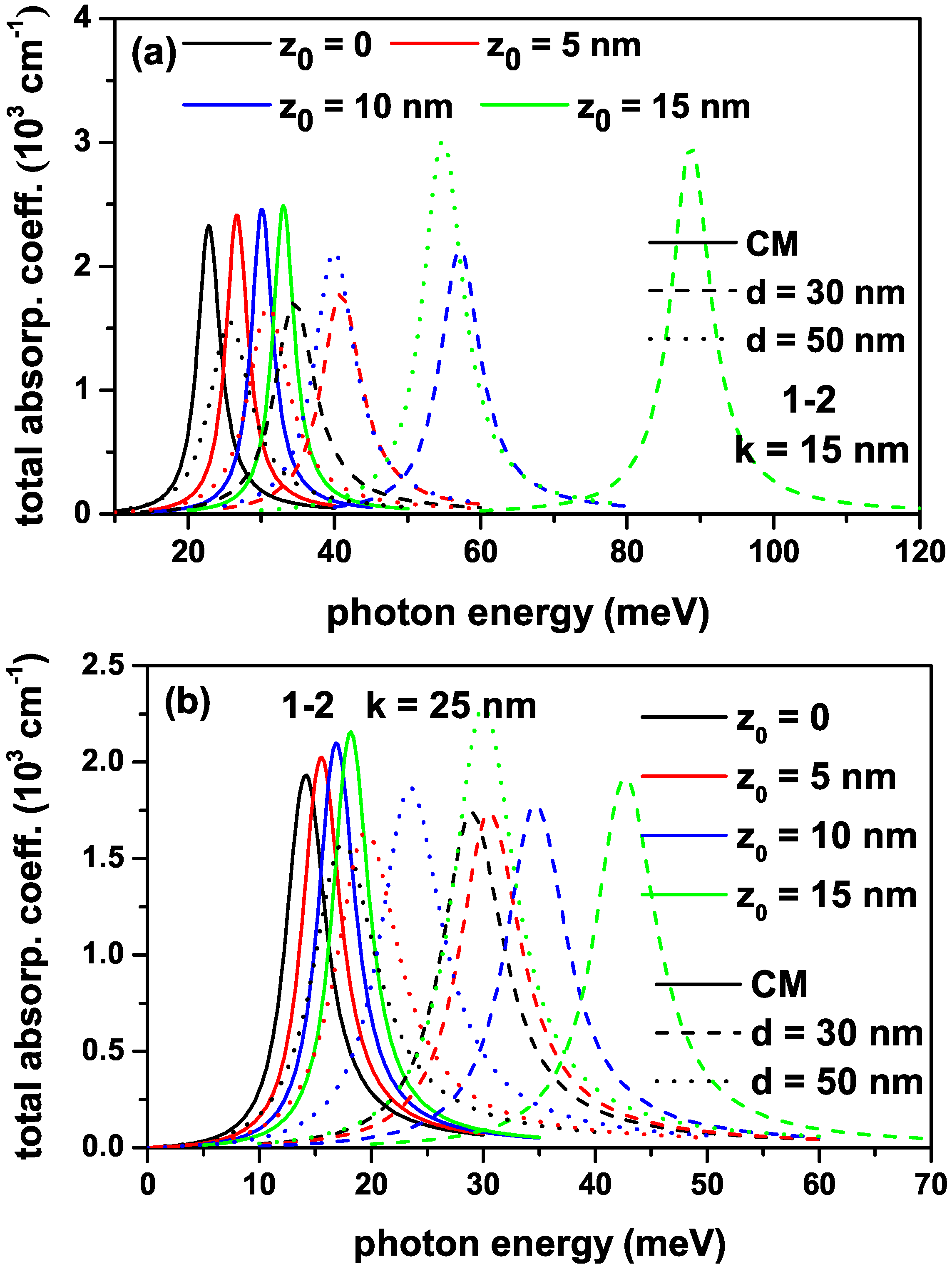
Figure 4a,b show the variation in total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen–Morse confinement potential as a function of the incident photon energy for different -values for nm and nm, respectively.
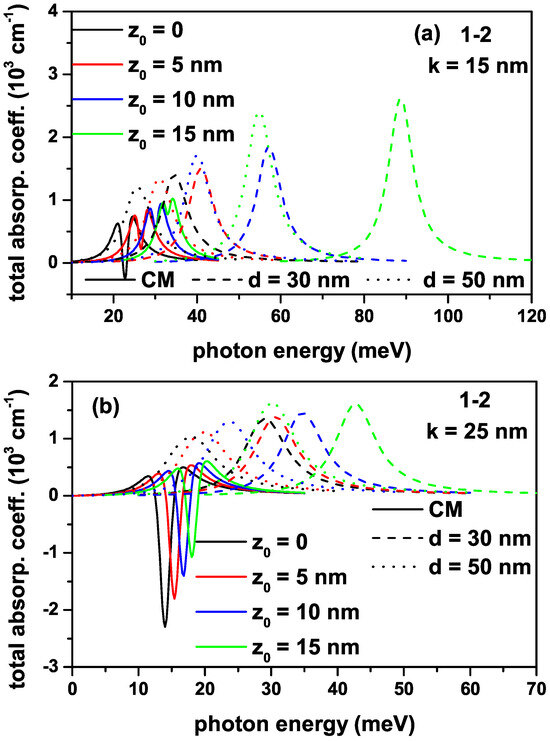
Figure 4.
The variation in total absorption coefficients for a transition that is called the (1-2) transition between the ground and first excited states of an electron confined within the quantum well with the improved Rosen–Morse confinement potential as a function of the incident photon energy with intensity W/m2 for different -values: nm (a) and nm (b).
First of all, it should be noted that for , the IRMQW is symmetrical and the (1-3) transition between the ground state and the second excited level is forbidden; other than that for all -values, all transitions are allowed since the structure is asymmetrical. Due to the delocalization of the electron with -energy by the spatially varying mass and asymmetry effects, the (1-3) transition is not shown in the figures. The amplitude of the absorption peak corresponding to this transition is already tiny due to the transition matrix element. For nm, the total absorption peak positions corresponding to the (1-2) transition shift towards blue with increasing -values. The peak positions shift first to blue with the effect of PDM and, for larger d-values, towards the peak positions corresponding to the results of the CM case, that is, to red. For the CM case, the bleaching effect is observed in absorption peaks due to the increasing importance of the nonlinear contribution; the contribution of the nonlinear absorption coefficient decreases with increasing -value. The negative values of the total AC depend entirely on the increasing values of the negative nonlinear term. As can be seen from Equations (4) and (5), the linear AC term (third-order non-linear AC term) is proportional to , and it is independent of I-light intensity ( and also I-intensity). In this context, the non-linear term is larger than the linear term since the diagonal matrix elements are zero (), and therefore, the total AC takes negative values. Since the diagonal matrix elements are no longer zero and increase with increasing -values, the nonlinear term takes on smaller negative values and the total AC gradually takes positive values. In addition, by using lower light intensities or smaller well widths, the negative contribution of nonlinear AC is reduced so that the total AC takes positive values. In the case of PDM, the bleaching effect disappears, indicating that the nonlinear optical coefficient is negligible compared with the linear one. For nm, all peaks shift to red with decreasing magnitudes, and the contribution of the nonlinear term is more significant compared with the nm.
Figure 5a,b have the same regulations as in Figure 4a,b, but the results given are for the (2-3) transition. It should be noted that the incident photon intensity for all the transitions in Figure 4 and Figure 5 is W/m2. The bleaching effect is quite pronounced in the total absorption peaks corresponding to the (2-3) transition since the nonlinear term is greater than the linear term, and absorption peaks localize in lower photon energies than the (1-2) transition. Furthermore, the total absorption peaks for the (2-3) transition are not observed since the electron with the -energy is unbound within the IRMQW for nm.
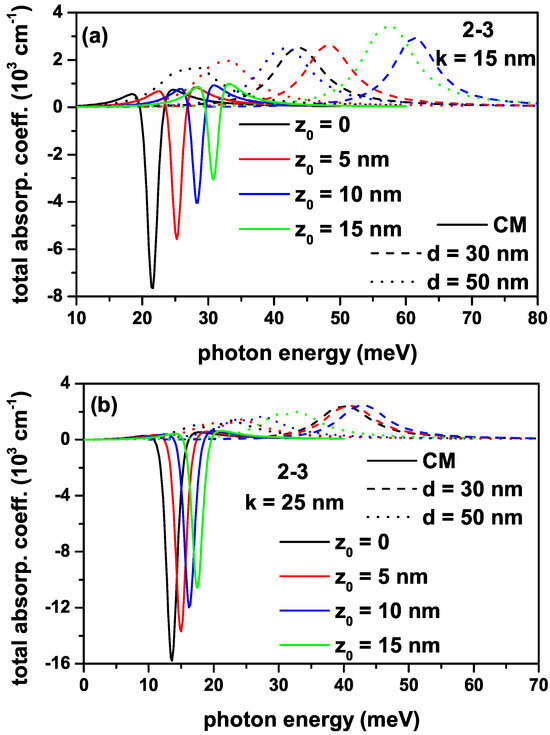
Figure 5.
The variation in total absorption coefficients for a transition that is called the (2-3) between the first and second excited states of an electron confined within the quantum well with the improved Rosen–Morse confinement potential as a function of the incident photon energy for different -values: nm (a) and nm (b).
As known, in linear absorption, the absorption properties of the material are independent of the light intensity. When the nonlinear absorption coefficient, which depends on the intensity of the incident light, is much larger than the linear absorption coefficient, the material exhibits a significantly stronger light absorption at high intensities compared with low intensities. This phenomenon is often observed in nonlinear optics. The material may exhibit strong absorption or even saturation effects at higher light intensities, leading to a higher light attenuation rate. This behavior can be exploited in applications such as optical limiting, optical switching, and nonlinear imaging, where controlling the intensity-dependent absorption is crucial. It is worth noting that the specific mechanisms behind nonlinear absorption can vary depending on the material and the physical processes involved. Common examples include two-photon absorption, multiphoton absorption, and saturable absorption, each having a different dependence on the light intensity.
It is also well known that when the energy difference between any two states is sufficiently small and the optical intensity which leads to the intersubband optical transitions is sufficiently high, the bleaching effect is observed. It is already known that the bleaching effect disappears using a smaller optic intensity than the one used here when the energy difference between the two energy levels is small. To show this, we used a lower intensity for the photon causing the intersubband transitions. Figure 6a,b have the same regulation as in Figure 4a,b, but the results are for the photon intensity W/m2 and include only the (1-2) transition. There is already no bleaching effect in the presence of PDM. Still, as can be seen from the figures, when lower light intensity is used, the amplitude of all total ACs increases as the contribution of the third-order nonlinear term is reduced. Thus, the bleaching effect observed in ACs without PDM disappears.
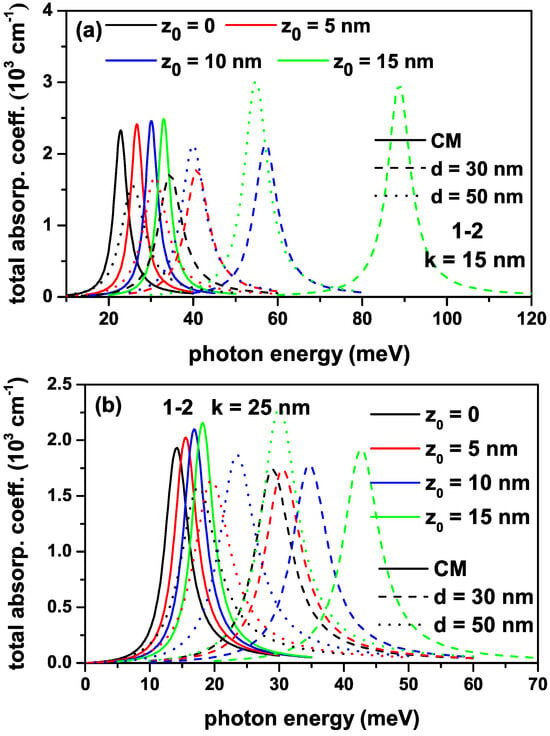
Figure 6.
The variation in total absorption coefficients for a transition that is called the (1-2) between the ground and first excited states of an electron confined within the quantum well with the improved Rosen–Morse confinement potential as a function of the incident photon energy with intensity W/m2 for different -values: nm (a) and nm (b).
As previously stated, the negative absorption coefficient obtained for some energies of the incident resonate radiation can be controlled by considering lower intensities, as seen when comparing the results in Figure 4 and Figure 6. Using a form of the rotating wave approximation for asymmetric quantum systems, Paspalakis et al. solved the relevant density matrix equations under steady-state conditions and derived the formulae for nonlinear optical absorption under the interaction with a strong probe field [31]. Among the most relevant characteristics of their research is that regardless of the intensity of the incident resonant radiation, they never observe the bleaching effect. In the case of low intensities, their results are the same as those obtained with the model that we present here through Equations (4)–(6).
The physical foundations for the negative absorption phenomenon are rooted in quantum mechanics and the behavior of electrons in confined systems. By carefully engineering the energy levels, the carrier dynamics, and the relaxation mechanisms, researchers can create conditions where population inversion can be achieved, leading to gain and negative absorption. It is worth noting that while this phenomenon is fascinating and has potential applications in optoelectronics, it also requires precise control and optimization of the quantum well structure, carrier lifetimes, and other parameters. The actual realization of negative absorption and gain in intersubband transitions can be quite complex and dependent on the specific details of the system being studied. An excellent discussion about the concept of negative absorption, or gain, was discussed by Eli Yablonovich in his work titled Light emission in photonic crystal micro-cavities [32]. In that work, the author shows that the transparency condition at which the gain occurs (negative absorption condition) is when the internal chemical potential exceeds the photon energy. This is the famous Bernard–Duraffoug condition and also applies well to dye molecules.
Finally, it is important to note that the present study is reported at low temperatures, K. In this sense, in the absence of the resonant radiation that excites the intersubband transitions, only the band corresponding to the ground state is occupied. The other subbands, associated with states 2 and 3, are unoccupied. Considering that we have assumed a fixed electron density (see the first paragraph in Section 3), the difference in occupancies between the ground state and the first excited state corresponds to the value presented there. The density difference between the first and second excited states, corresponding to the (2-3) transition, would be zero. At a finite temperature, close, for example, to room temperature, occupation appears in the first excited subband, which implies a reduction in the corresponding density for the ground subband. This benefits the (2-3) transition since the difference in densities acquires a finite value, to the detriment of the difference in densities between the ground subband and the first excited one, which disfavors the intensity of the optical absorption coefficient for the (1-2) transition. Under these considerations, only Figure 4 and Figure 6 are adjusted to finite absorption coefficient values, and their intensities reported here correspond to the chosen carrier density. Figure 5 should then have, at low temperatures, a zero absorption coefficient given the zero character of the difference in densities between the subbands involved. The results of Figure 5 allow us to show the position of the resonant structures and their red or blue shifts depending on external factors. This figure also allows us to establish relationships between the absorption coefficients for the (2-3) transition under different external factors.
4. Conclusions
In this work, the position-dependent effective mass, structure, and asymmetry parameter effects on the electronic and optical properties of an electron confined in symmetric and asymmetric quantum wells that have improved or exponential Rosen–Morse potential are investigated for the first time. The position-dependent effective mass, asymmetry, and confinement parameters significantly increase electron energies, energy differences between the confined electron states, and the blue shift in the absorption spectrum. These results enable the development of optoelectronic devices that can operate at wider wavelengths and absorb higher-energy photons. In the presence of the position-dependent mass, the bleaching effect disappears, which is observed in the case of constant mass. This behavior can be exploited in applications such as optical limiting, optical switching, and nonlinear imaging, where controlling the intensity-dependent absorption is crucial.
It is important to highlight that in this article, we have presented two issues that may generate controversy: (i) the use of an effective mass that decreases with the distance to the zero of coordinates and that is contrary to what has traditionally been considered in the literature for an effective mass that adapts to the gap of the semiconductor, and (ii) the appearance of negative absorption for high intensities of the incident radiation; this phenomenon contradicts the well-known principle according to which it is impossible to implement population investment in a two-level system. It is important to highlight that a pulsed laser system can achieve population inversion considering only two energy levels. A study expanding these considerations is in progress and will be published elsewhere.
Author Contributions
E.K.: conceptualization, methodology, software, formal analysis, investigation, supervision, writing; M.B.Y.: conceptualization, methodology, software, formal analysis, writing; C.A.D.: formal analysis, writing. All authors have read and agreed to the published version of the manuscript.
Funding
C.A.D. is grateful to Colombian agencies CODI-Universidad de Antioquia (Estrategia de Sostenibilidad de la Universidad de Antioquia and projects “Propiedades magneto-ópticas y óptica no lineal en superredes de Grafeno”, “Estudio de propiedades ópticas en sistemas semiconductores de dimensiones nanoscópicas”, “Propiedades de transporte, espintrónicas y térmicas en el sistema molecular ZincPorfirina”, and “Complejos excitónicos y propiedades de transporte en sistemas nanométricos de semiconductores con simetría axial”) and Facultad de Ciencias Exactas y Naturales-Universidad de Antioquia (C.A.D. exclusive dedication project 2022–2023).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morse, P.M. Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels. Phys. Rev. 1929, 34, 57. [Google Scholar] [CrossRef]
- Rong, Z.; Kjaergaard, H.G.; Sage, M.L. Comparison of the Morse and Deng-Fan potentials for X-H bonds in small molecules. Mol. Phys. 2003, 101, 2285. [Google Scholar] [CrossRef]
- Jia, C.S.; Diao, Y.F.; Liu, X.J.; Wang, P.Q.; Liu, J.Y.; Zhang, G.D. Equivalence of the Wei potential model and Tietz potential model for diatomic molecules. J. Chem. Phys. 2012, 137, 014101. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.Q.; Zhang, L.H.; Jia, C.S.; Liu, J.Y. Equivalence of the three empirical potential energy models for diatomic molecules. J. Mol. Spectrosc. 2012, 274, 5. [Google Scholar] [CrossRef]
- Wang, P.Q.; Liu, J.Y.; Zhang, L.H.; Cao, S.Y.; Jia, C.S. Improved expressions for the Schiöberg potential energy models for diatomic molecules. J. Mol. Spectrosc. 2012, 278, 23. [Google Scholar] [CrossRef]
- Kaneriya, R.K.; Rastogi, G.; Basu, P.K.; Upadhyay, R.B.; Bhattacharya, A.N. Intersubband device modeling of gallium nitride high electron mobility transistor for terahertz applications. Radio Sci. 2019, 54, 1172–1180. [Google Scholar] [CrossRef]
- Miller, D.A.B. Quantum well optoelectronic switching devices. Int. J. High Speed Electron. Syst. 1991, 1, 19–46. [Google Scholar] [CrossRef]
- Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sökmen, I. Position-dependent mass effects on the optical responses of the quantum well with Tietz–Hua potential. Optik 2019, 178, 1280–1284. [Google Scholar] [CrossRef]
- Panahi, H.; Golshani, S.; Doostdar, M. Influence of position dependent effective mass on donor binding energy in square and V-shaped quantum wells in the presence of a magnetic field. Physica B 2013, 418, 47–51. [Google Scholar] [CrossRef]
- Peter, A.J.; Navaneethakrishnan, K. Effects of position-dependent effective mass and dielectric function of a hydrogenic donor in a quantum dot. Physica E 2008, 40, 2747–2751. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Belhadj, W.; Kasapoglu, E.; Ungan, F. Position-dependent-mass and laser field impact on the optical characteristics of Manning-like double quantum well. Physica E 2023, 151, 115737. [Google Scholar] [CrossRef]
- Kasapoglu, E.; Duque, C.A. Position dependent effective mass effect on the quantum wells with three-parameter modified Manning potential. Optik 2021, 243, 166840. [Google Scholar] [CrossRef]
- Li, K.; Guo, K.; Jiang, X.; Hu, M. Effect of position dependent effective mass on nonlinear optical properties in a quantum well. Optik 2017, 132, 375–381. [Google Scholar] [CrossRef]
- Keshavarz, A.; Zamani, N. Optical properties of spherical quantum dot with position-dependent effective mass. Superlattices Microst. 2013, 58, 191–197. [Google Scholar] [CrossRef]
- Khordad, R. Effect of position-dependent effective mass on linear and nonlinear optical properties of a cubic quantum dot. Physica B 2011, 406, 3911–3916. [Google Scholar] [CrossRef]
- Durmuslar, A.S.; Turkoglu, A.; Mora-Ramos, M.E.; Ungan, F. The non-resonant intense laser field effects on the binding energies and the nonlinear optical properties of a donor impurity in Rosen–Morse quantum well. Indian J. Phys. 2022, 96, 3485–3492. [Google Scholar] [CrossRef]
- Ungan, F.; Bahar, M.K. The laser field controlling on the nonlinear optical specifications of the electric field-triggered Rosen-Morse quantum well. Phys. Lett. A 2020, 384, 126400. [Google Scholar] [CrossRef]
- Khordad, R.; Mirhosseini, B. Linear and nonlinear optical properties in spherical quantum dots: Rosen-Morse potential. Opt. Spectrosc. 2014, 117, 434–440. [Google Scholar] [CrossRef]
- Zhang, G.-D.; Liu, J.-Y.; Zhang, L.-H.; Zhou, W.; Jia, C.-S. Modified Rosen-Morse potential-energy model for diatomic molecules. Phys. Rev. A 2012, 86, 062510. [Google Scholar] [CrossRef]
- Cunha, M.S.; Christiansen, H.R. Analytic results in the position-dependent mass Schrödinger problem. Commun. Theor. Phys. 2013, 60, 642–650. [Google Scholar] [CrossRef]
- Panahi, H.; Bakhshi, Z. Solvable potentials with position-dependent effective mass and constant mass Schrödinger equation. Acta Phys. Pol. B 2010, 41, 11–21. [Google Scholar]
- Bagchi, B.; Gorain, P.; Quesne, C.; Roychoudhury, R. A general scheme for the effective-mass Schrödinger equation and the generation of the associated potentials. Mod. Phys. Lett. A 2004, 19, 2765–2775. [Google Scholar] [CrossRef]
- Kasapoglu, E.; Sari, H.; Sokmen, I.; Vinasco, J.A.; Laroze, D.; Duque, C.A. Effects of intense laser field and position dependent effective mass in Razavy quantum wells and quantum dots. Physica E 2021, 126, 114461. [Google Scholar] [CrossRef]
- Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sokmen, I.; Duque, C.A. Effect of intense laser field in Gaussian quantum well with position dependent effective mass. Phys. Status Solidi B 2019, 256, 1800758. [Google Scholar] [CrossRef]
- Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sökmen, I.; Duque, C.A. Effect of position-dependent effective mass on donor impurity- and exciton-related electronic and optical properties of 2D Gaussian quantum dots. Eur. Phys. J. Plus 2022, 137, 341. [Google Scholar] [CrossRef]
- Kasapoglu, E.; Yucel, M.B.; Sakiroglu, S.; Sari, H.; Duque, C.A. Optical properties of cylindrical quantum dots with hyperbolic-type axial potential under applied electric field. Nanomaterials 2022, 12, 3367. [Google Scholar] [CrossRef]
- Zeiri, N.; Sfina, N.; Abdi-BenNasrallah, S.; Said, M. Linear and non-linear optical properties in symmetric and asymmetric double quantum wells. Optik 2013, 124, 7044–7048. [Google Scholar] [CrossRef]
- Dinh Hien, N. Comparison of the nonlinear optical properties of asymmetrical and symmetrical quantum wells. Eur. Phys. J. B 2022, 95, 192. [Google Scholar] [CrossRef]
- AL-Naghmaish, A.; Dakhlaoui, H.; Ghrib, T.; Wong, B.M. Effects of magnetic, electric, and intense laser fields on the optical properties of AlGaAs/GaAs quantum wells for terahertz photodetectors. Physica B 2022, 635, 413838. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Nefzi, M. Tuning the linear and nonlinear optical properties in double and triple δ doped GaAs semiconductor: Impact of electric and magnetic field. Superlattices Microst. 2019, 136, 106292. [Google Scholar] [CrossRef]
- Paspalakis, E.; Boviatsis, J.; Baskoutas, S. Effects of probe field intensity in nonlinear optical processes in asymmetric semiconductor quantum dots. J. Appl. Phys. 2013, 114, 153107. [Google Scholar] [CrossRef]
- Yablonovitch, E. Light emission in photonic crystal micro-cavities. In Confined Electrons and Photons; Burstein, E., Weisbuch, C., Eds.; Springer: Berlin, Germany, 2012; Volume 340, pp. 635–646. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).