Composed Effects of Electron-Hole Exchange and Near-Field Interaction in Quantum-Dot-Confined Radiative Dipoles
Abstract
1. Introduction
2. Hamiltonian and Theoretical Model
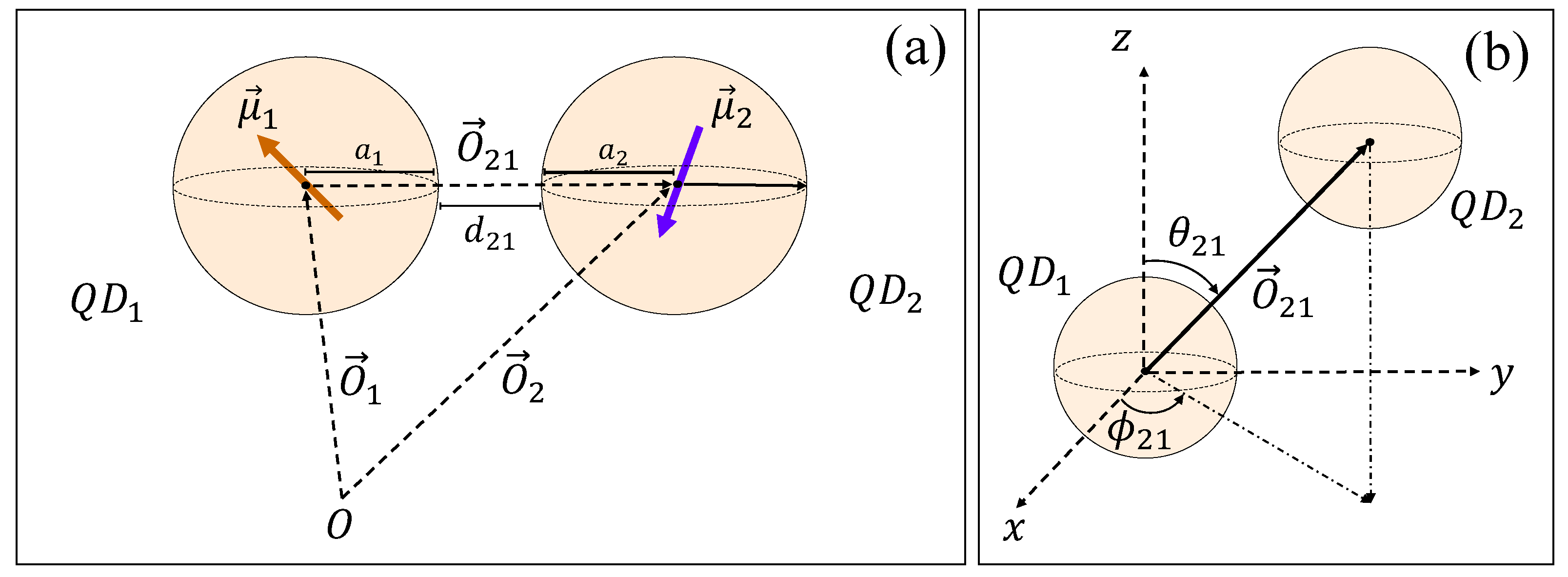
2.1. Quantum Dot Model
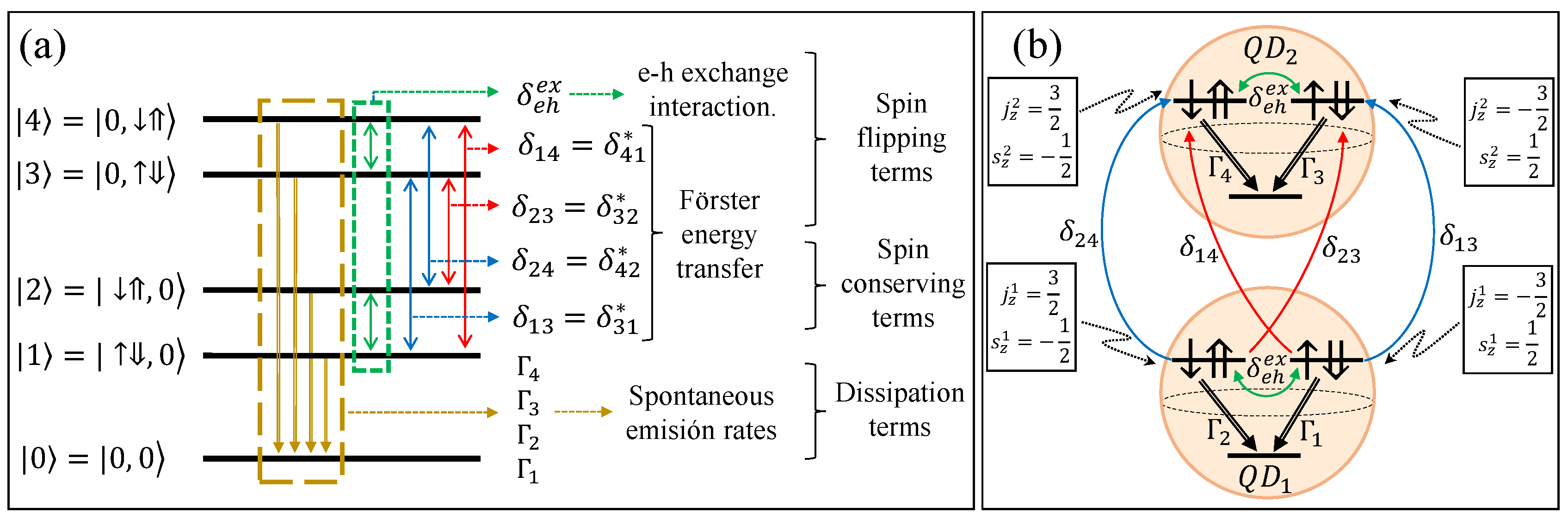
2.2. Electron-Hole Exchange
2.3. Förster Resonance Energy Transfer
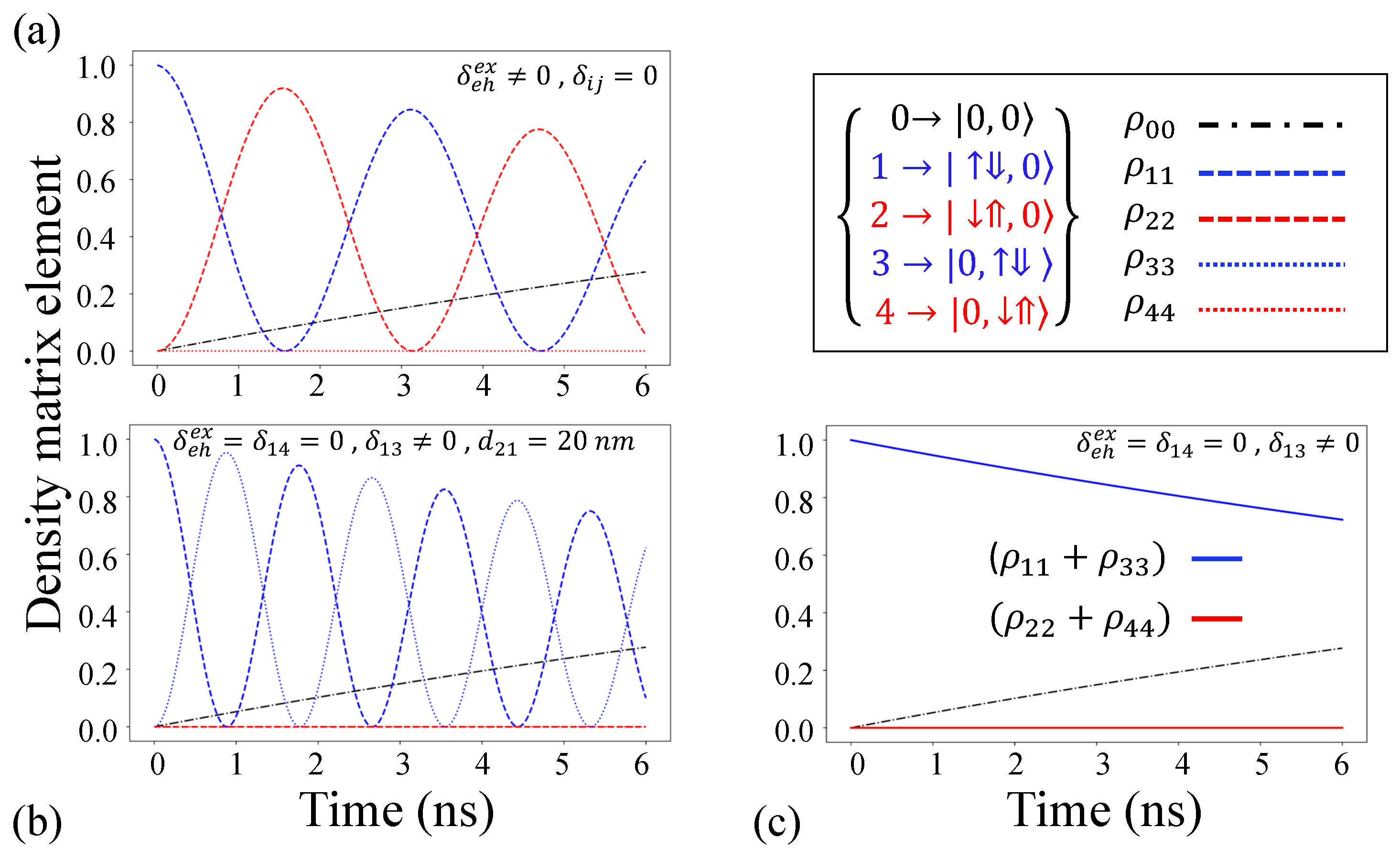
3. Time Dependence
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- O’Brien, J.L.; Furusawa, A.; Vučković, J. Photonic quantum technologies. Nat. Photonics 2009, 3, 687–695. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Zopf, M.; Jung, K.; Zhang, Y.; Keil, R.; Ding, F.; Schmidt, O.G. Wavelength-tunable entangled photons from silicon-integrated III–V quantum dots. Nat. Commun. 2016, 7, 10387. [Google Scholar] [CrossRef] [PubMed]
- Huber, D.; Reindl, M.; Covre da Silva, S.F.; Schimpf, C.; Martín-Sánchez, J.; Huang, H.; Piredda, G.; Edlinger, J.; Rastelli, A.; Trotta, R. Strain-Tunable GaAs Quantum Dot: A Nearly Dephasing-Free Source of Entangled Photon Pairs on Demand. Phys. Rev. Lett. 2018, 121, 033902. [Google Scholar] [CrossRef]
- Ramírez, H.Y.; Chou, Y.L.; Cheng, S.J. Effects of electrostatic environment on the electrically triggered production of entangled photon pairs from droplet epitaxial quantum dots. Sci. Rep. 2019, 9, 1547. [Google Scholar] [CrossRef]
- Htoon, H.; Furis, M.; Crooker, S.A.; Jeong, S.; Klimov, V.I. Linearly polarized ‘fine structure’ of the bright exciton state in individual CdSe nanocrystal quantum dots. Phys. Rev. B 2008, 77, 035328. [Google Scholar] [CrossRef]
- Htoon, H.; Crooker, S.A.; Furis, M.; Jeong, S.; Efros, A.L.; Klimov, V.I. Anomalous Circular Polarization of Photoluminescence Spectra of Individual CdSe Nanocrystals in an Applied Magnetic Field. Phys. Rev. Lett. 2009, 102, 017402. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, W.; Guo, G.C.; He, L. Exciton Polarization, Fine-Structure Splitting, and the Asymmetry of Quantum Dots under Uniaxial Stress. Phys. Rev. Lett. 2011, 106, 227401. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.; Chen, L.; Song, N.; Lv, Y.; Hu, F.; Sun, C.; Yu, W.W.; Zhang, C.; Wang, X.; Zhang, Y.; et al. Bright-Exciton Fine-Structure Splittings in Single Perovskite Nanocrystals. Phys. Rev. Lett. 2017, 119, 026401. [Google Scholar] [CrossRef] [PubMed]
- Prin, E.; Xia, C.; Won, Y.H.; Jang, E.; Goupalov, S.V.; Tamarat, P.; Lounis, B. Revealing the Band-Edge Exciton Fine Structure of Single InP Nanocrystals. Nano Lett. 2023, 23, 6067–6072. [Google Scholar] [CrossRef]
- Kuroda, T.; Mano, T.; Ha, N.; Nakajima, H.; Kumano, H.; Urbaszek, B.; Jo, M.; Abbarchi, M.; Sakuma, Y.; Sakoda, K.; et al. Symmetric quantum dots as efficient sources of highly entangled photons: Violation of Bell’s inequality without spectral and temporal filtering. Phys. Rev. B 2013, 88, 041306. [Google Scholar] [CrossRef]
- Gurioli, M.; Wang, Z.; Rastelli, A.; Kuroda, T.; Sanguinetti, S. Droplet epitaxy of semiconductor nanostructures for quantum photonic devices. Nat. Mater. 2019, 18, 799–810. [Google Scholar] [CrossRef]
- Juska, G.; Dimastrodonato, V.; Mereni, L.O.; Gocalinska, A.; Pelucchi, E. Towards quantum-dot arrays of entangled photon emitters. Nat. Photonics 2013, 7, 527–531. [Google Scholar] [CrossRef]
- Thoma, A.; Schnauber, P.; Böhm, J.; Gschrey, M.; Schulze, J.H.; Strittmatter, A.; Rodt, S.; Heindel, T.; Reitzenstein, S. Two-photon interference from remote deterministic quantum dot microlenses. Appl. Phys. Lett. 2017, 110, 011104. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Cheng, S.J.; Chang, C.P. Theory of electron–hole exchange interaction in double quantum dots. Phys. Status Solidi B 2009, 246, 837–841. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Lin, C.H.; You, W.T.; Huang, S.Y.; Chang, W.H.; Lin, S.D.; Cheng, S.J. Electron–hole symmetry breakings in optical fine structures of single self-assembled quantum dots. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1155–1158. [Google Scholar] [CrossRef]
- Cheng, S.J.; Liao, Y.H.; Lin, P.Y. Mechanically encoded single-photon sources: Stress-controlled excitonic fine structures of droplet epitaxial quantum dots. Phys. Rev. B 2015, 91, 115310. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Camacho, A.S.; Lew Yan Voon, L.C. DC electric field effects on the electron dynamics in double rectangular quantum dots. Braz. J. Phys. 2006, 36, 869. [Google Scholar] [CrossRef]
- Evans, R.E.; Bhaskar, M.K.; Sukachev, D.D.; Nguyen, C.T.; Sipahigil, A.; Burek, M.J.; Machielse, B.; Zhang, G.H.; Zibrov, A.S.; Bielejec, E.; et al. Photon-mediated interactions between quantum emitters in a diamond nanocavity. Science 2018, 362, 662–665. [Google Scholar] [CrossRef]
- Reindl, M.; Jöns, K.D.; Huber, D.; Schimpf, C.; Huo, Y.; Zwiller, V.; Rastelli, A.; Trotta, R. Phonon-Assisted Two-Photon Interference from Remote Quantum Emitters. Nano Lett. 2017, 17, 4090–4095. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Camacho, A.S.; Voon, L.C.L.Y. Influence of shape and electric field on electron relaxation and coherent response in quantum-dot molecules. J. Phys. Condens. Matter 2007, 19, 346216. [Google Scholar] [CrossRef]
- Bermúdez-Ureña, E.; Gonzalez-Ballestero, C.; Geiselmann, M.; Marty, R.; Radko, I.P.; Holmgaard, T.; Alaverdyan, Y.; Moreno, E.; García-Vidal, F.J.; Bozhevolnyi, S.I.; et al. Coupling of individual quantum emitters to channel plasmons. Nat. Commun. 2015, 6, 7883. [Google Scholar] [CrossRef]
- Kim, H.; Kim, I.; Kyhm, K.; Taylor, R.A.; Kim, J.S.; Song, J.D.; Je, K.C.; Dang, L.S. Exciton Dipole–Dipole Interaction in a Single Coupled-Quantum-Dot Structure via Polarized Excitation. Nano Lett. 2016, 16, 7755–7760. [Google Scholar] [CrossRef]
- Rolon, J.E.; Ulloa, S.E. Förster energy-transfer signatures in optically driven quantum dot molecules. Phys. Rev. B 2009, 79, 245309. [Google Scholar] [CrossRef]
- Rolon, J.E.; Ulloa, S.E. Coherent control of indirect excitonic qubits in optically driven quantum dot molecules. Phys. Rev. B 2010, 82, 115307. [Google Scholar] [CrossRef]
- Ramirez, H.Y.; Lin, C.H.; Chao, C.C.; Hsu, Y.; You, W.T.; Huang, S.Y.; Chen, Y.T.; Tseng, H.C.; Chang, W.H.; Lin, S.D.; et al. Optical fine structures of highly quantized InGaAs/GaAs self-assembled quantum dots. Phys. Rev. B 2010, 81, 245324. [Google Scholar] [CrossRef]
- Kim, D.; Okahara, S.; Nakayama, M.; Shim, Y. Experimental verification of Förster energy transfer between semiconductor quantum dots. Phys. Rev. B 2008, 78, 153301. [Google Scholar] [CrossRef]
- Unold, T.; Mueller, K.; Lienau, C.; Elsaesser, T.; Wieck, A.D. Optical Control of Excitons in a Pair of Quantum Dots Coupled by the Dipole-Dipole Interaction. Phys. Rev. Lett. 2005, 94, 137404. [Google Scholar] [CrossRef]
- Govorov, A.O. Spin and energy transfer in nanocrystals without tunneling. Phys. Rev. B 2003, 68, 075315. [Google Scholar] [CrossRef]
- Govorov, A.O. Spin-Förster transfer in optically excited quantum dots. Phys. Rev. B 2005, 71, 155323. [Google Scholar] [CrossRef]
- Kuno, M. Introductory nanoscience: Physical and chemical concepts. MRS Bull. 2012, 37, 169–170. [Google Scholar] [CrossRef][Green Version]
- Zapata-Herrera, M.; Flórez, J.; Camacho, A.S.; Ramírez, H.Y. Quantum Confinement Effects on the Near Field Enhancement in Metallic Nanoparticles. Plasmonics 2018, 13, 1–7. [Google Scholar] [CrossRef]
- Zapata-Herrera, M.; Camacho, A.S.; Ramírez, H.Y. Influence of the confinement potential on the size-dependent optical response of metallic nanometric particles. Comput. Phys. Commun. 2018, 227, 1–7. [Google Scholar] [CrossRef]
- Huber, D.; Reindl, M.; Aberl, J.; Rastelli, A.; Trotta, R. Semiconductor quantum dots as an ideal source of polarization-entangled photon pairs on-demand: A review. J. Opt. 2018, 20, 073002. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Optoelectronic Devices; Wiley: New York, NY, USA, 1995; pp. 124–195. [Google Scholar]
- Gywat, O.; Krenner, H.J.; Berezovsky, J. Spins in Optically Active Quantum Dots: Concepts and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Carmichael, H. Statistical Methods in Quantum Optics 1: Master Equations and Fokker-Planck Equations; Springer Science & Business Media: Berlin, Germany, 1999; Volume 1. [Google Scholar]
- Al-Ahmadi, A.N.; Ulloa, S.E. Coherent state monitoring in quantum dots. Phys. Rev. B 2004, 70, 201302. [Google Scholar] [CrossRef]
- Woggon, U.; Gindele, F.; Wind, O.; Klingshirn, C. Exchange interaction and phonon confinement in CdSe quantum dots. Phys. Rev. B 1996, 54, 1506–1509. [Google Scholar] [CrossRef] [PubMed]
- Shiang-Yu Huang, S.J.C. Theoretical Studies of Energy Transfer between Coupled Semiconductor Nanocrystals. Master’s Thesis, National Chiao Tung University, HsinChu, Taiwan, China, 2015. [Google Scholar]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- Reiss, P.; Bleuse, J.; Pron, A. Highly Luminescent CdSe/ZnSe Core/Shell Nanocrystals of Low Size Dispersion. Nano Lett. 2002, 2, 781–784. [Google Scholar] [CrossRef]
- Heyn, C.; Stemmann, A.; Schramm, A.; Welsch, H.; Hansen, W.; Nemcsics, A. Regimes of GaAs quantum dot self-assembly by droplet epitaxy. Phys. Rev. B 2007, 76, 075317. [Google Scholar] [CrossRef]
- Jo, M.; Mano, T.; Sakuma, Y.; Sakoda, K. Extremely high-density GaAs quantum dots grown by droplet epitaxy. Appl. Phys. Lett. 2012, 100, 212113. [Google Scholar] [CrossRef]
- Won, Y.H.; Cho, O.; Kim, T.; Chung, D.Y.; Kim, T.; Chung, H.; Jang, H.; Lee, J.; Kim, D.; Jang, E. Highly efficient and stable InP/ZnSe/ZnS quantum dot light-emitting diodes. Nature 2019, 575, 634–638. [Google Scholar] [CrossRef]
- Du, J.S.; Shin, D.; Stanev, T.K.; Musumeci, C.; Xie, Z.; Huang, Z.; Lai, M.; Sun, L.; Zhou, W.; Stern, N.P.; et al. Halide perovskite nanocrystal arrays: Multiplexed synthesis and size-dependent emission. Sci. Adv. 2020, 6, eabc4959. [Google Scholar] [CrossRef] [PubMed]
- Jastrzebska-Perfect, P.; Zhu, W.; Saravanapavanantham, M.; Li, Z.; Spector, S.O.; Brenes, R.; Satterthwaite, P.F.; Ram, R.J.; Niroui, F. On-site growth of perovskite nanocrystal arrays for integrated nanodevices. Nat. Commun. 2023, 14, 3883. [Google Scholar] [CrossRef] [PubMed]

| Relevant Parameters for CdSe QDs | |
|---|---|
| QD radius () | 3 nm |
| Bulk energy gap () | eV |
| QD energy gap, | eV |
| Kane energy parameter | eV |
| Electron effective mass | |
| Hole effective mass | |
| Relative permittivity | 10 |
| Electron-hole exchange | 1 ns |
| Spontaneous emission rate () | ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Ramírez, J.D.; Huang, S.-Y.; Cheng, B.-L.; Lo, P.-Y.; Cheng, S.-J.; Ramírez-Gómez, H.Y. Composed Effects of Electron-Hole Exchange and Near-Field Interaction in Quantum-Dot-Confined Radiative Dipoles. Condens. Matter 2023, 8, 84. https://doi.org/10.3390/condmat8030084
Díaz-Ramírez JD, Huang S-Y, Cheng B-L, Lo P-Y, Cheng S-J, Ramírez-Gómez HY. Composed Effects of Electron-Hole Exchange and Near-Field Interaction in Quantum-Dot-Confined Radiative Dipoles. Condensed Matter. 2023; 8(3):84. https://doi.org/10.3390/condmat8030084
Chicago/Turabian StyleDíaz-Ramírez, Jaime David, Shiang-Yu Huang, Bo-Long Cheng, Ping-Yuan Lo, Shun-Jen Cheng, and Hanz Yecid Ramírez-Gómez. 2023. "Composed Effects of Electron-Hole Exchange and Near-Field Interaction in Quantum-Dot-Confined Radiative Dipoles" Condensed Matter 8, no. 3: 84. https://doi.org/10.3390/condmat8030084
APA StyleDíaz-Ramírez, J. D., Huang, S.-Y., Cheng, B.-L., Lo, P.-Y., Cheng, S.-J., & Ramírez-Gómez, H. Y. (2023). Composed Effects of Electron-Hole Exchange and Near-Field Interaction in Quantum-Dot-Confined Radiative Dipoles. Condensed Matter, 8(3), 84. https://doi.org/10.3390/condmat8030084







