Elliptical Quantum Rings with Variable Heights and under Spin–Orbit Interactions

Abstract

We investigate the electronic properties of a semiconductor quantum ring with an elliptical shape and non-uniform height, allowing for distributed quantum-dot-like bulges along its perimeter. The adiabatic approximation and the finite element method are combined to calculate the allowed electron states in the structure under the effective mass approximation, considering the contributions from Rashba and Dresselahaus spin–orbit interactions and the Zeeman effect in the presence of an applied magnetic field. We discuss the features of the calculated spectra for two different ring geometries: a symmetric one with four dot-like bulges, and an asymmetric one with three hilled protuberances. The information about those states allows us to evaluate the linear optical absorption response associated with interlevel transitions between the ground and lowest excited states. This phenomenon takes place at resonant energies of only a few milielectronvolts. It is observed that spin–orbit interactions tend to quench this response under zero-field conditions in the case of symmetric confinement.

1. Introduction

Semiconductor quantum rings (QRs) are low-dimensional structures that—ideally—exhibit total confinement for the movement of charge carriers and display peculiar electronic and optical properties [1], particularly in the presence of magnetic fields, such as the Aharonov–Bohm effect [2,3,4]. Among the practical methods for obtaining these systems, droplet epitaxy has enabled the formation of annular nanostructures using various materials, including Group IV elements and III-V compounds [5,6,7,8,9,10,11,12,13]. These reports show that, in general, the fabricated structures exhibit certain deformations in terms of the height of the ring walls, and often, along the perimeter, bulging regions in the form of quantum dots can be observed. In particular, the report of Ref. [7] reveals the presence of multiple such bulges in the case of InP-based systems, to the extent that the obtained structures are referred to as annular quantum dot molecules.

Some previous attempts have theoretically modeled the confinement profiles of such deformed QRs by proposing specific mathematical functions [14,15]. The model in [15] embodies a simple expression that allows tuning the position, number, and height of those dot-like bulges in the multi-hilled structure. However, once the confining design of the deformed QR is analytically described or somehow reproduced from experimental data, the mathematical task of solving the effective mass differential equations in 3D remains. Then, numerical schemes such as finite difference [16] and finite elements [17] are tools of choice.

The effect of spin–orbit interaction (SOI) is relevant to a III-V semiconductor electronic structure, as was shown by Kane 66 years ago [18]. Specific contributions to this interaction appear when there is no centrosymmetry in the system. In this sense, there are two of them: One is related to structure-induced asymmetry (Rashba interaction, RI), and the other is associated with bulk-induced asymmetry (Dresselhaus interaction, DI) (see details in [19] and references therein). The particular subject of low-dimensional semiconductor structures entails one or both of mentioned situations, so it becomes relevant to explore their possible influences on charge carrier states in those systems as, for instance, was performed in the case of QRs by Nowak and Szafran [20]. Several works that incorporate the study of these SOI mechanisms in QRs have been published in recent years. For instance, Khordad [21], Zamani et al. [22,23,24], and Pourmand and Rezaei [25] investigated the influence of SOI on different nonlinear optical responses of QRs, considering contributions from RI and DI. More recently, Bejan and Stan studied electron spin and donor impurity effects on light absorption in QRs under magnetic fields [26], while Lia and Tamborenea reported on general RI and DI in narrow QRs [27].

With all that in mind, the purpose of the present work is to theoretically investigate the features of electronic states in structurally non-uniform GaAs/AlGaAs QRs in the presence of externally applied magnetic fields, taking into account the combined effects of RI and DI SOIs as well as the Zeeman effect. In particular, we use the adiabatic approximation to deal with the 3D problem of determining the energy spectrum. Ultimately, this approach leads to a 2D numerical procedure within the Finite Element Method (FEM). The information about allowed states is then taken as starting point to evaluate the linear optical absorption related to transitions between the lowest confined energy levels. In Section 2, we explain the theoretical environment. Section 3 is devoted to presenting and discussing the obtained results, and, finally, conclusions will be given in Section 4.

2. Theoretical Model

This work considers an elliptical QR with variable height, consisting of GaAs in an AlGaAs matrix. An ellipse delimits the elliptical QR. The equation for the geometry of an elliptical QR is:

$$g(x,y,R{x}_2,R{y}_2)<1<f(x,y,R{x}_1,R{y}_1).$$

(1)

Here, f and g are the outer and the inner borders of the QR and are defined by:

$$f(x,y,R{x}_1,R{y}_1)={\left(\frac{x}{R{x}_1}\right)}^2+{\left(\frac{y}{R{y}_1}\right)}^2$$

(2)

and

$$g(x,y,R{x}_2,R{y}_2)={\left(\frac{x}{R{x}_2}\right)}^2+{\left(\frac{y}{R{y}_2}\right)}^2,$$

(3)

where $R{x}_1$ and $R{x}_2$ are the semiaxes on x-direction of the inner and outer ellipses, respectively, and $R{y}_1$ and $R{y}_2$ are the semiaxes on the y-direction.

The equation of the height as a function of x, y is given by:

$$z(x,y)=h(x,y)\left[1-{\left(\frac{\left|2-f^{-1/2}-g^{-1/2}\right|}{f^{-1/2}-g^{-1/2}}\right)}^2\right],$$

(4)

where the height corresponds to a parabolic profile. Additionally, h represents the angularly modulated height of the quantum ring in z-direction and is given by

$$h(x,y)=H+\mathcal{A}cos\left[narccos\left(\frac{x}{\sqrt{x^2+y^2}}\right)\right],$$

(5)

where H denotes the average height of the quantum structure, $\mathcal{A}$ represents the amplitude of the harmonic modulation, and $n=3,4$ is the number of height maxima.

Considering the effective mass as a function of position (with constant values on each QR region) in the form:

$$m^{*}\left(\overrightarrow{r}\right)=\left\{\begin{array}{cc}{m}_i^{*},\hfill & \mathrm{inner}\mathrm{of}\mathrm{the}\mathrm{QR}\left(\mathrm{GaAs}\right)\hfill \\ m_o^{*},\hfill & \mathrm{outer}\mathrm{of}\mathrm{the}\mathrm{QR}\left(\mathrm{AlGaAs}\right)\hfill \end{array}\right.$$

(6)

and a Coulomb gauge for the magnetic vector potential $\overrightarrow{A}=\frac{B}{2}(-y,x,0)$ ($\nabla ·\overrightarrow{A}=0$, B is the magnetic field strength), we write the 2D Hamiltonian for an electron in the QR confining potential

$$V(x,y)=\left\{\begin{array}{cc}0,\hfill & \mathrm{inner}\mathrm{of}\mathrm{the}\mathrm{QR}\hfill \\ V_0,\hfill & \mathrm{outer}\mathrm{of}\mathrm{the}\mathrm{QR},\hfill \end{array}\right.$$

(7)

in the form

$${\widehat{H}}_{2D}=\frac{1}{2}\left(-i\hslash \nabla +\frac{e}{c}\overrightarrow{A}\right)\frac{1}{m^{*}\left(\overrightarrow{r}\right)}·\left(-i\hslash \nabla +\frac{e}{c}\overrightarrow{A}\right)+V(x,y).$$

(8)

Now, with the inclusion of Zeeman and SOI terms, we have the total energy operator,

$$\widehat{H}={\widehat{H}}_{2D}{I}_2+\frac{1}{2}gB{\mu }_B{\sigma }_z+{\widehat{H}}_R+{\widehat{H}}_D,$$

(9)

where $I_2$ represents the identity matrix of order $2\times 2$, g is the Landé factor, and ${\mu }_B$ labels the Bohr magneton. Besides, ${\sigma }_z$ is the z-component of the Pauli matrices. ${\widehat{H}}_R$ and ${\widehat{H}}_D$ are the Rashba and Dresselhaus terms, respectively, which contain the contribution from SOI. These SOI terms are given by [26]:

$${\widehat{H}}_R=\alpha \left(k_y{\sigma }_x-k_x{\sigma }_y\right)$$

(10)

and

$${\widehat{H}}_D=\beta \left(k_x{\sigma }_x-k_y{\sigma }_y\right),$$

(11)

where $\alpha$ and $\beta$ are the coupling constants for the Rashba and Dresselhaus interactions, respectively, ${\sigma }_i(i=x,y,z)$ are Pauli matrices, and $k_x$ and $k_y$ are the components of the 2D wavevector operator. According to the matrix nature of such a model, solutions for the system will be two-component wavefunctions that incorporate information on both spin orientations, up and down.

To consider the finite QR height (z-direction), we shall use the adiabatic approximation (AA). In our case, this is justified by the very geometry of the system, where the height of the ring is always much smaller than the semi-axes of the ellipse. Ref. [28] provides a detailed explanation of the procedure. This approach leaves the problem to solve in the form of a 2D effective differential equation, which needs to be solved to determine the eigenenergies and eigenfunctions of the corresponding effective-mass problem. This task is addressed in numerical form, using FEM, as implemented in the COMSOL-Multiphysics environment [29].

The information on electron states obtained through the procedure mentioned above will be used to evaluate the light absorption coefficient, considering transitions between the ground and the first two excited states in the system. Details of the expressions used for this purpose are found in Ref. [30].

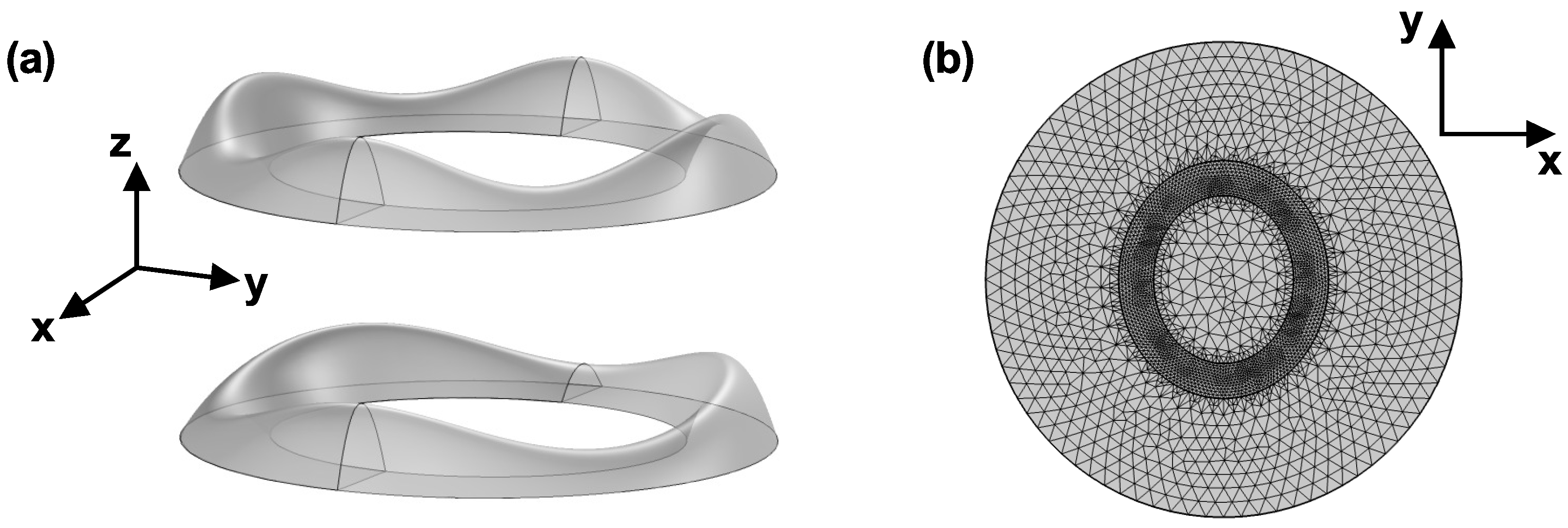
Figure 1a depicts the scheme of GaAs-Al${}_{0.3}$Ga${}_{0.7}$As QRs with non-uniform height, showing three and four dot-like hills. For the FEM calculation, the particular meshes chosen for the inner and outer QR regions are shown in Figure 1b. Before proceeding with the specific subject of the present work, we would like to provide additional validation to the essential approximation made to obtain the allowed electronic states.

In that sense, we leave aside, for the moment, the influence of any external field and switch off SOI in the system, and focus on an alternative—a simpler—system, which is a circular GaAs/AlGaAs QR of rectangular cross-section and a height of $3.5$nm. A FEM calculation, in this situation, implies enclosing the QR region in a cylindrical cage with a height equal to $20$nm and a radius of $60$nm. The potential energy within the ring is assumed to be equal to zero, and, outside, it has a constant barrier value of $262$meV.

Three different numerical approaches are applied to calculate the lowest electron energy levels: A 2D axisymmetric scheme that implies separating variables in cylindrical coordinates, with angular contribution $exp\left(il\phi \right)$ to the wavefunction, and a $(\rho ,z)$-dependent part is numerically determined. A second approach is the 3D complete numerical solution via FEM, whereas the third method employs AA and separates $(x,y)$ motion from the strongly confined z one, as discussed in [28], leaving the contribution to the wavefunction in the $xy$-plane to be calculated via FEM.

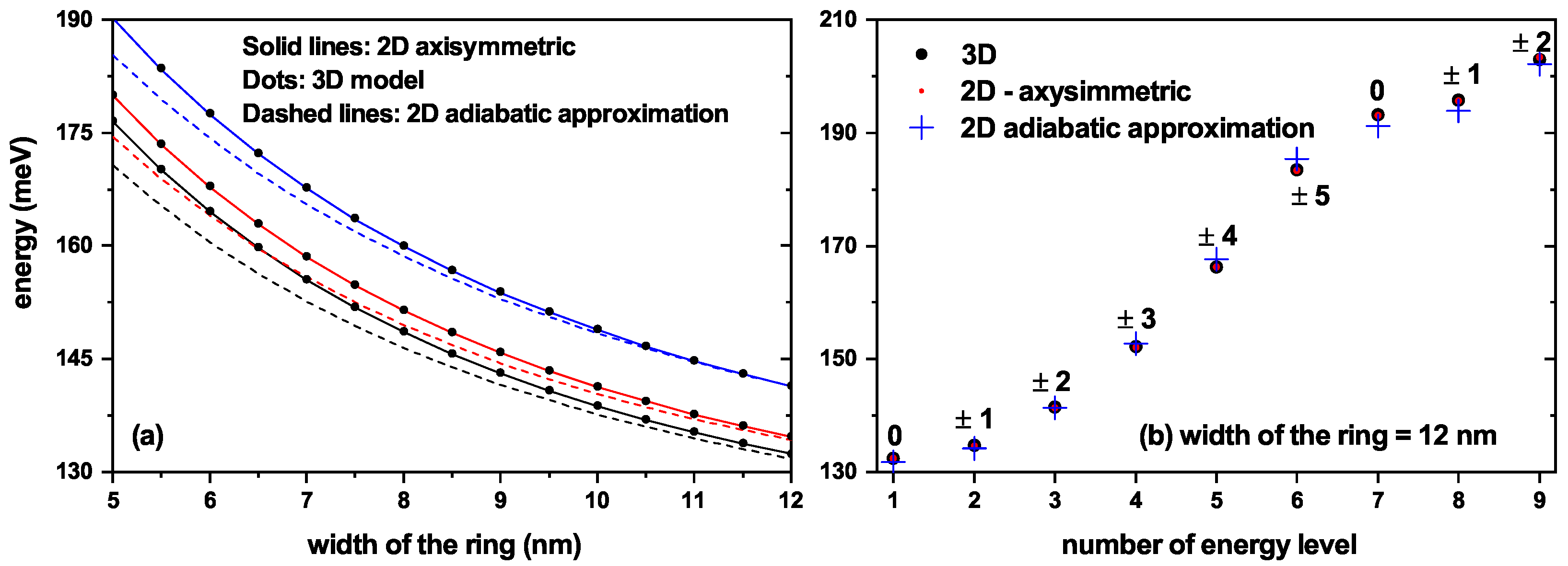
Let us now discuss the outcome of such a comparison. For that purpose, we plot in Figure 2 the spectrum of lowest energies depending on the radial size of the circular QR. In Figure 2a, the energy value as a function of the increase of the ring’s width indicates a decrease in all used approaches due to the loss of spatial carrier confinement. It can be readily noticed that the 2D axisymmetric and the complete 3D numerical solutions coincide all along the range of ring sizes considered given, precisely, the symmetry of the structure.

The results obtained with the AA remain slightly below (just a few meV) the numerically determined in the “exact” cases. However, such a difference tends to disappear when the ring size augments, and this happens more rapidly for the upper levels. Actually, for the larger value of QR width analyzed, the AA-obtained second excited state coincides with the value resulting from the non-adiabatic approaches. Nonetheless, the energy separation for the lowest two levels is, at that value of QR width, about $1$meV. This fact is verified by observing the plot in Figure 2b. There, the first energy levels for the widest QR considered in Figure 2a are represented, indicating the associated values of the “orbital” quantum number l in each case. One may notice the very good coincidence of the levels determined via the three described approaches. All this serves us as means for justifying the use of the AA in calculating the allowed energy states in the non-uniform elliptic QR of our interest here. Then, the 2D numerical FEM procedure employs the mesh partition depicted in Figure 1b.

To support that in the case of symmetry loss, an elliptical ring with variable height is working properly.

Table 1. Comparison between the adiabatic approximation method and the 3D model for an elliptical quantum ring with variable height. The geometrical parameter values are: $H=3$ nm, $\mathcal{A}=0.3$ nm, $R{x}_1=10$ nm, $R{x}_2=22$ nm, $R{y}_1=12$ nm, and $R{y}_2=24$ nm, and, for the external parallelepiped of sides, $R{x}_{\mathbf{out}}=2R{x}_2$, and height = $9.9$ nm (for the 3D model).

Magnetic Field (T)	Energy Level	2D AA (meV)	3D (meV)	Relat. Error (%)
0	Ground state	170.8	169.6	0.7
	First excited	172.0	170.6	0.8
	Second excited	172.9	171.5	0.8
10	Ground state	171.6	170.2	0.8
	First excited	172.8	171.2	0.9
	Second excited	173.7	172.1	0.9
20	Ground state	174.0	172.1	1.1
	First excited	174.9	172.8	1.2
	Second excited	175.9	173.8	1.2

compares the results for four quantum dots on the elliptical ring under the adiabatic approximation method and the 3D model. Note that the last column presents the relative error, around 1%. It is also important to highlight that when the two excited states are compared, the energy difference between the ground state and the first two excited states only differs by $0.2$ meV. The geometrical parameter values are: $H=3$ nm, $\mathcal{A}=0.3$ nm, $R{x}_1=10$ nm, $R{x}_2=22$ nm, $R{y}_1=12$ nm, and $R{y}_2=24$ nm and, for the external parallelepiped of sides, $R{x}_{out}=2R{x}_2$, and height = $9.9$ nm (for the 3D model). This calculation was carried out without both the SOI and Zeeman effect. This result comparison allows us to establish that the adiabatic approximation is adequate in this study even with the loss of symmetry and has the advantage that the calculation times are significantly reduced. For example, to calculate the solutions for zero magnetic field, the AA method takes 5 s, in contrast to the 3D model, in which, for the same case, it takes 106 seconds on a computer with an AMD Ryzen 5 3550H processor, 16 GB of RAM, and frequency 4.0 GHz.

On the other hand, in reference [31], a study on the adiabatic approximation is carried out. In particular, in that work, an asymmetric three-dimensional case is analyzed, and the authors conclude on the method’s effectiveness even in the absence of cylindrical symmetry.

To evaluate the optical response of the system, the following expression for the linear absorption coefficient between the ground state and the first excited state was used

$${\mathsf{\Omega }}_{1j}=\omega \sqrt{\frac{{\mu }_0}{{\epsilon }_0\epsilon }}\frac{{\left|M_{1j}\right|}^2{e}^2{\rho }_{1j}\hslash {\Gamma }_{1j}}{{(E_{1j}-\hslash \omega )}^2+{(\hslash {\Gamma }_{1j})}^2},$$

(12)

where $\omega$ is the frequency of incident laser, ${\mu }_0=4\pi {10}^{-7}$ is the magnetic permeability of free space, ${\epsilon }_0$ is the vacuum permittivity, $\epsilon$ the relative permittivity, e elementary charge, ${\rho }_{1j}$ is the population difference between the ground state and the j-th state per unit volume, and ${\Gamma }_{1j}$ the inter-level broadening [32]. The specific values of these optical parameters are presented in the section of the results.

In this article, the expression for calculating the matrix elements is given by

$$M_{1j}=\frac{1}{\sqrt{2}}\int \int \left[{\left({\varphi }_{\uparrow }^{*}\right)}_2(x+iy){\left({\varphi }_{\uparrow }\right)}_1+{\left({\varphi }_{\downarrow }^{*}\right)}_j(x+iy){\left({\varphi }_{\downarrow }\right)}_1\right]dxdy.$$

(13)

These transition elements between the 1- to j-states were calculated for right circular polarization. Note that in Equation (12), each spinor has a real and imaginary component; For example, ${\left({\varphi }_{\uparrow }\right)}_1=\mathfrak{Re}\left({\left({\varphi }_{\uparrow }\right)}_1\right)+i\mathfrak{Im}\left({\left({\varphi }_{\uparrow }\right)}_1\right)$. Consequently, Equation (13) can be expanded in the following form

$$\begin{array}{c}\hfill M_{1j}=\frac{1}{\sqrt{2}}\int \int \left[(\mathfrak{Re}\left({\left({\varphi }_{\uparrow }\right)}_j\right)-i\mathfrak{Im}\left({\left({\varphi }_{\uparrow }\right)}_j\right))(x+iy)(\mathfrak{Re}\left({\left({\varphi }_{\uparrow }\right)}_1\right)+i\mathfrak{Im}\left({\left({\varphi }_{\uparrow }\right)}_1\right))\right]dxdy\\ \hfill +\frac{1}{\sqrt{2}}\int \int \left[(\mathfrak{Re}\left({\left({\varphi }_{\downarrow }\right)}_j\right)-i\mathfrak{Im}\left({\left({\varphi }_{\downarrow }\right)}_j\right))(x+iy)(\mathfrak{Re}\left({\left({\varphi }_{\downarrow }\right)}_1\right)+i\mathfrak{Im}\left({\left({\varphi }_{\downarrow }\right)}_1\right))\right]dxdy.\end{array}$$

(14)

In general, Equation (14) shows that it is not intuitive to predict the behavior of dipole moments, which definitely involves the symmetries of the real and imaginary parts of each spinor in each of the two wave functions involved in the matrix element. Let us analyze a particular case that corresponds to the study system with $n=4$, where two hills are located along the x-axis (at $\theta =0$, dot 1, and at $\theta =\pi$, dot 3) and two along the y-axis (at $\theta =\pi /2$, dot 2, and at $\theta =3\pi /2$, dot 4). Taking the case of $B=0$, although it is not shown in the figures, the real and imaginary parts of the spinors of the ground state and the first excited state exhibit the following symmetries: (i) for the ground state, the spinors that spin up and spin down their real and imaginary parts are even functions along both the x-axis and the y-axis (ii) for the first excited state, the spin-up and spin-down spinors, their real and imaginary parts, are even functions along both the x-axis and the y-axis. Considering that the polarization introduces odd linear functions, then, clearly, at zero magnetic field, the $M_{12}$ dipole element is null since it involves the product of even functions by odd functions, which finally leads to integrals of odd functions in both x and y. A similar analysis must be performed for finite magnetic fields and for the case $n=3$.

3. Results and Discussion

Figure 3 contains the density plots of the lowest three electron states in the GaAs/ Al${}_{0.3}$Ga${}_{0.7}$As QRs with non-uniform height, for the two particular examples here considered: the one with four quantum dot (QD)-like hills (upper row), and that with three QD-like hills (lower row). The depicted cases correspond to the solutions of the energy operator ${\widehat{H}}_{2D}$, with $B=0$. It is observed that states have well-defined parities in the symmetric four-QD design, while no symmetry appears in the three-hilled one.

The following input data have been used to generate the numerical results in the work: The band parameters for the GaAs/AlGaAs are: $m_i^{*}=0.067m_0$, $m_o^{*}=0.093m_0$, where $m_0$ is the free electron mass. The geometrical parameter values are $H=3$ nm, $\mathcal{A}=0.3$ nm, $R{x}_1=10$ nm, $R{x}_2=22$ nm, $R{y}_1=12$ nm, and $R{y}_2=24$ nm, and, for a external parallelepiped of sides, $R{x}_{\mathbf{out}}=2R{x}_2$, $R{y}_{\mathbf{out}}=2R{y}_2$, and height = $9.9$ nm. Landé factor, $g=-2.15$.

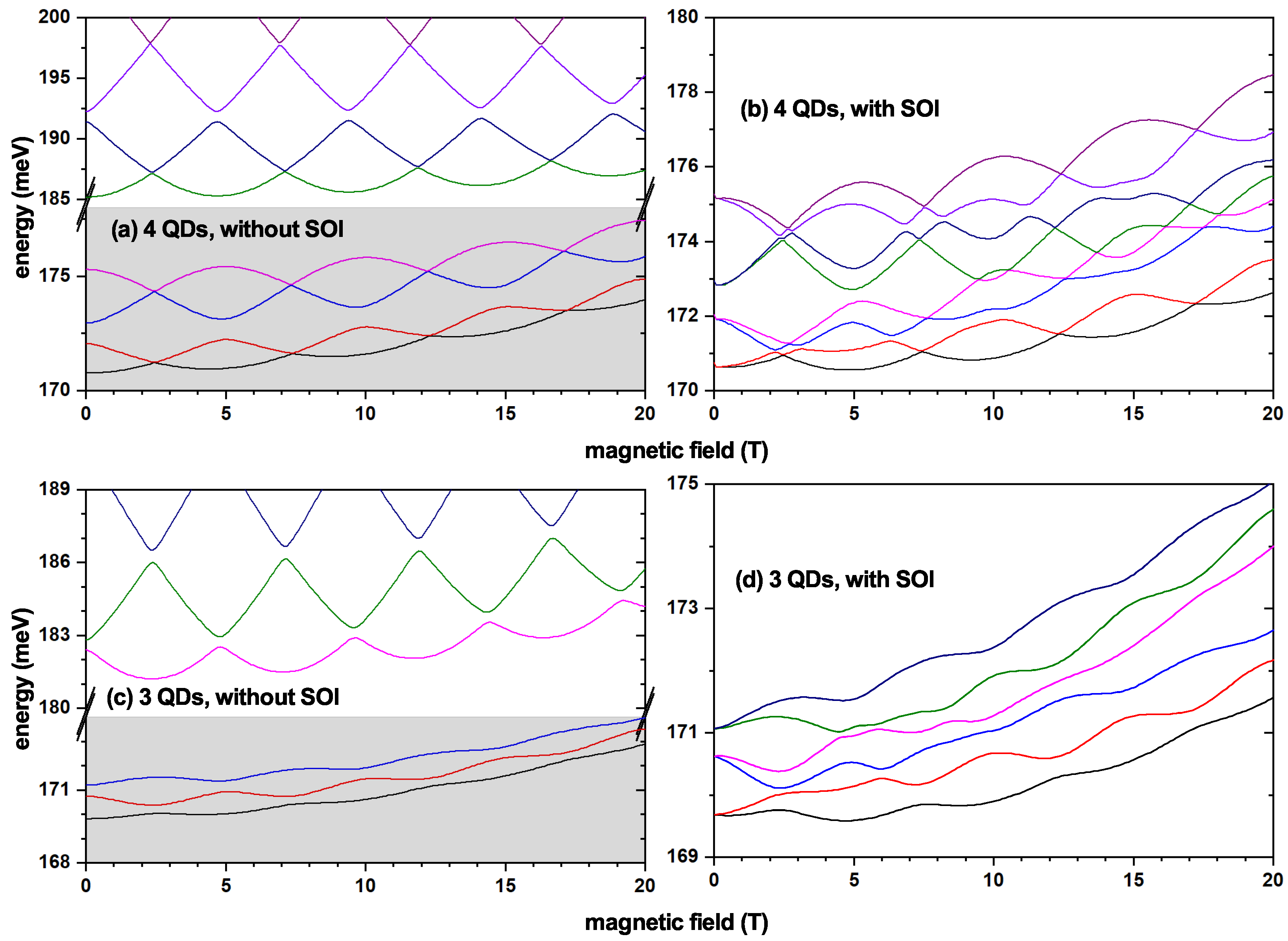
Figure 4 shows the calculated lowest electron energy levels corresponding to the two different non-uniform elliptic QRs as functions of the intensity of the applied magnetic field. Results are shown for two cases without Zeeman and SOI and considering those two contributions. Analyzing the first of those cases, corresponding to (Figure 4a,c), one may notice that the zero-field condition produces no degeneracies in the allowed electron states by having a non-complete symmetry in the elliptic structure. However, when $B\ne 0$, the number of QD-like bulges in the structure plays a determining role. When there are four symmetrically arranged hill structures, the spectrum shows typical Aharonov–Bohm oscillations. At specific field intensity values, there are crossings between the ground and first excited states, with the known exchange in wavefunction symmetry. Crossings are present as well for higher excited states. When only three dot-like structures are in the ring profile, energy oscillations for lower states are practically extinguished, mainly noticed for upper excited states without crossings. The overall tendency of increasing energy values when the field strength augments have to do with the increment in the degree of spatial confinement introduced by the magnetic field. Considering the second of the mentioned cases (Figure 4b,d), in which Zeeman and SOI terms are switched on, the zero-field case reveals the levels disposed of in doubly degenerate states in the four-hilled geometric setup. Such a degeneracy is immediately broken under nonzero magnetic field conditions for the three-hill QR. Still, crossings remain at specific B values in the four-hilled one, with the feature of occurring at different field intensities for each pair of degenerate states. Furthermore, it can be noticed that the influence of the linear term in B, associated with the Zeeman operator, reflects in the trend of variation for intense enough applied fields, mainly affecting the upper levels, which exhibit a nearly linear increment. In addition, the presence of the SOI is responsible for a redshift of the entire spectrum, independently of the geometry considered.

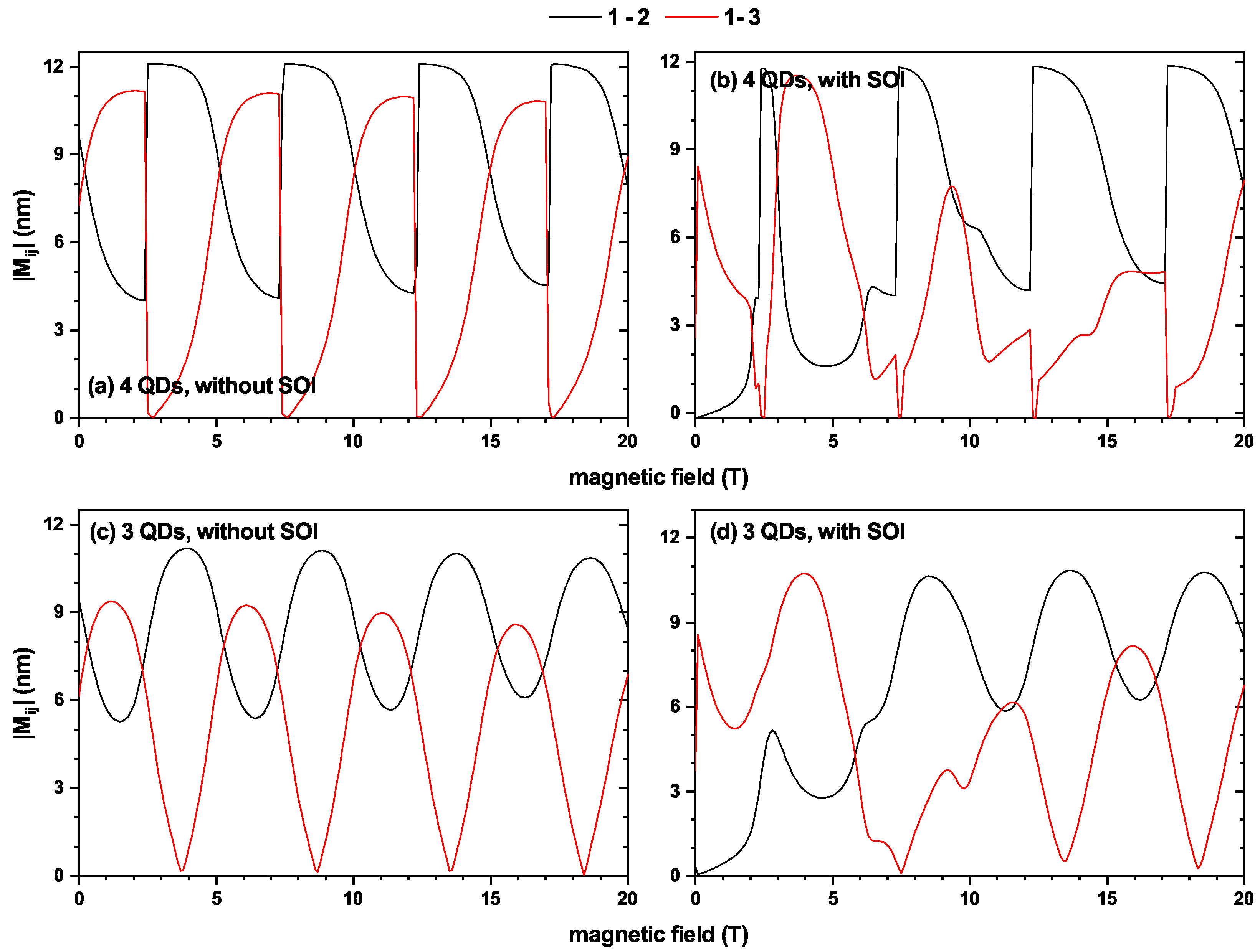
As our interest is to analyze the interlevel optical absorption in the QRs under consideration, it is convenient to determine the values of the corresponding electric dipole moment matrix elements $M_{ij}$. For this purpose, we assume the right circular polarization ($p=(x+iy)/\sqrt{2}$) of the incident light and limit ourselves to evaluate the off-diagonal elements associated with transitions from the ground ($i=1)$ to the first and second excited ($j=2,3$) states in each case.

Figure 5 contains the plots of calculated absolute values of electric dipole moment matrix elements as functions of the applied magnetic field intensity. It is seen that, in the absence of Zeeman and SOI effects, there is a kind of alternating behavior between these quantities in which a maximum of $M_{12}$ coincides in B-position with a minimum of $M_{13}$ and vice versa. Minima of $M_{13}$ are zero in the four-dots case due to the symmetry of involved states and nearly zero in the three-dot one (becoming zero at high enough field strengths). This indicates that a stronger magnetic field induces a kind of spatial symmetry in the wavefunctions, so their products acquire parity and nullify the contribution to the spatial integrals, thus turning the given transition into a forbidden one. Furthermore, when the magnetic field strengthens, there is a decrease in the absolute values of the off-diagonal matrix elements. The increment in B implies an increase in the degree of spatial confinement, and, therefore, the effective integrating region over $(x,y)$ reduces, with a smaller contribution from the linear terms in the polarization dipole vector.

The inclusion of Zeeman and SOI effects causes a change in the shape of the $|M_{ij}|$ curves as functions of the magnetic field, and there is also a reduction in their values. For the QR with a four-QD configuration, such a reduction is not so pronounced, and there is a tendency to keep the alternate behavior above described, with the main deformation of the curves associated with the smaller values of B. However, Zeeman and SOI terms strongly affect the size and shape of the $|M_{ij}|$ curves in the spatially nonsymmetric three-QD ring. In this case, the increase in magnetic field intensity greatly reduces the absolute values of the off-diagonal matrix elements. Some alternations between respective maxima and minima are preserved for larger B values, and, significantly—at least within the range of field strength considered—no zero values of dipole matrix elements appear for the three-hilled QR.

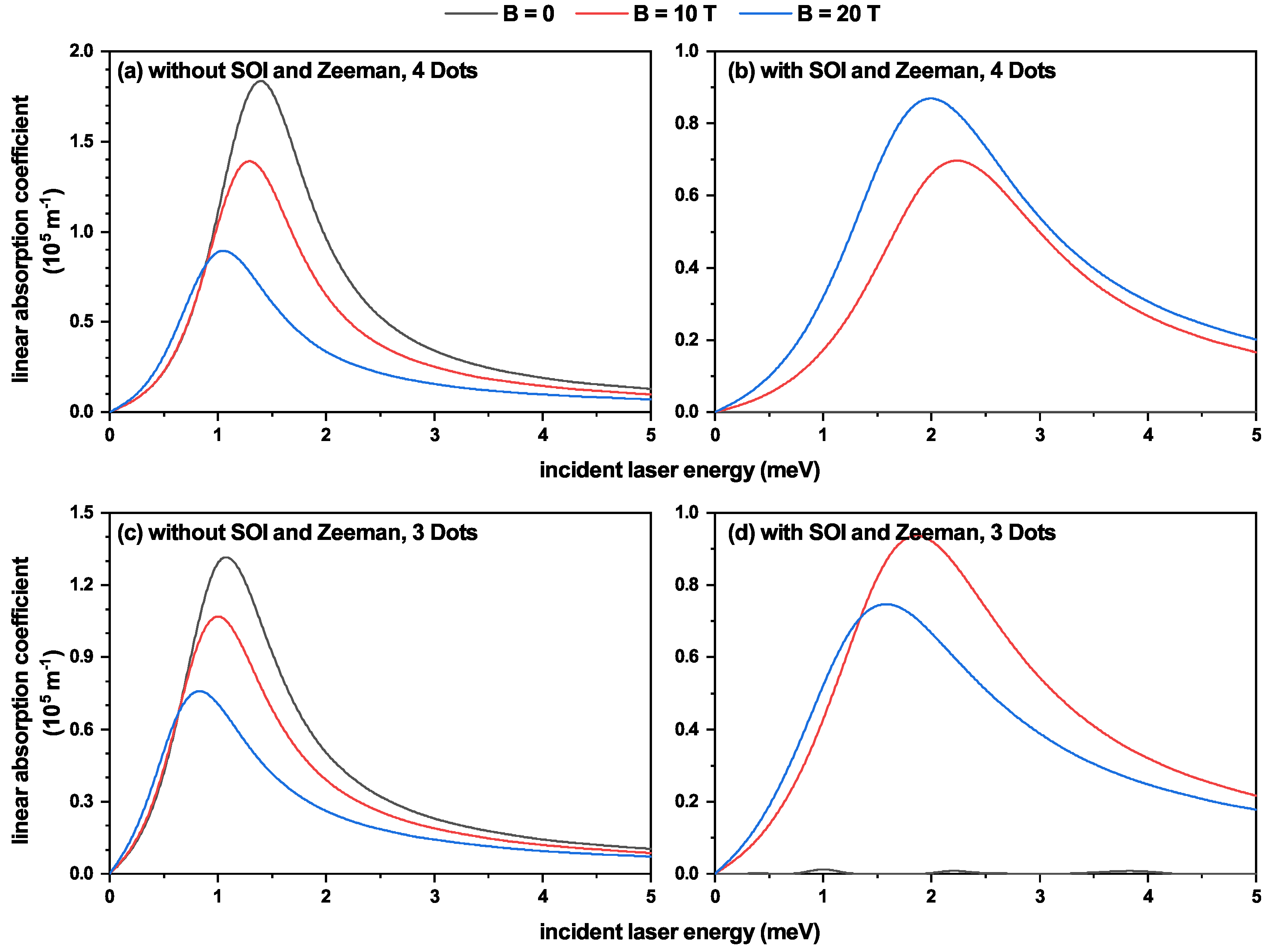
Figure 6 shows the calculated linear absorption coefficient. In this case, we have used a value ${\epsilon }_r=12.58$ for the static dielectric constant of GaAs. In addition, the electron volume density in the system is homogeneously taken as $\rho =3.0\times {10}^{22}$m${}^{-3}$, and the spread of the Lorentzian-type response is associated with a phenomenological damping rate $\Gamma =1/\tau$, with $\tau =8.27$ps ($\hslash \Gamma =0.5$meV). Results in the figure correspond to the sum of contributions from the $1\to 2$ and $1\to 3$ transitions.

The amplitude of light absorption resonant peaks is proportional to the product $\omega |M_{ij}{|}^2$, for $\hslash \omega =E_j-E_i$, which determines the peak’s energy position. By analyzing, in the first place, the situation without the influence of Zeeman and SO effects, one notices that the increase in the magnetic field causes the redshift of the absorption response as well as the reduction in peak amplitude, in which the decrease in the resonant frequencies has something to do. By observing Figure 5a,c, it is found that the chosen values of B correspond to situations in which both involved transitions have nonzero contributions through their $M_{ij}$. The magnitudes of the absolute values of these quantities are very similar for the three field intensities chosen. Therefore, we mainly ascribe the reduction in the light absorption signal to its redshift. It is important to notice that in these systems, the interstate transitions entail energy differences of only a few meV. At this point, it can be said that, from the quantitative point of view, these light absorption responses are similar to those investigated in Ref. [30] for double QRs with inversely quadratic confinement.

The plots in Figure 6b,d correspond to the calculated optical absorption coefficient in four-QD and three-QD elliptic QR with non-uniform height, incorporating Zeeman and SOI effects. In all cases, peak amplitudes are smaller than those achieved without such additional effects. There is no response (or almost zero) at zero magnetic fields in three- and four-hilled systems. From Figure 5b,d, it is seen that the $1\to 2$ transition is forbidden since the corresponding electric dipole matrix element is zero for such degenerate energies. Furthermore, note that for the $1\to 3$ transition, the corresponding dipole matrix elements are relatively small for $B\to 0$. The absorption response presents differences in the three- and four-hilled cases for the two nonzero field values. The increase in the magnetic field implies, in both cases, a small redshift. When resonant energies are approximately of the same value for each magnetic field strength, the variations in the amplitude of the resonant peaks are controlled by the changes in the dipole matrix elements. In the four-dot geometry, $|M_{12}|$ has a higher value at $B=20$T, compared with those achieved when the field is of $10$T. In the three-hilled QR, higher values of $|M_{12}|$ appear. This and the difference in resonant energies lead to greater absorption amplitude for the lower two field strengths.

Finally, we want to make some reflections on the system of elliptical QRs of variable height that we have studied in this article. From the multiple experimental reports that appear in Fomin’s book on quantum rings [1] and the references included therein, it is concluded that, generally, the QR systems obtained by different growth techniques are structures of variable height along the axial coordinate of the system. Despite the excellent control in the growth processes, obtaining homogeneous annular systems in height is not easy. However, this, which is apparently a problem, is actually an advantage or strength. Systems with variable heights give rise to regions where the probability density of finding the confined charge carrier increases. These regions, corresponding to maximum heights, are connected through regions of minimum height. This, finally, translates into the presence of coupled QDs located along the system’s axial coordinate. In our model of variable-height QRs, we can control for the presence of one, two, three, or more QDs along the ellipse that defines the ring. Furthermore, with appropriate variations of the function that controls these distributions, we can vary the dimensions of the QDs. By means of electric, magnetic, and intense non-resonant laser radiation fields applied to the structure, the coupling can be generated between these zero-dimensional regions, giving rise to, for example, spatially direct and indirect excitonic states with considerable variations in the exciton lifetime. Such coupled QD systems can be technologically used in multiple optoelectronic devices, see Ref. [1]. Additionally, it is important to note that the presence of these zero-dimensional structures along the angular coordinate gives rise to azimuthal symmetry breaking, which means an enrichment in the allowed optical transitions between electronic, excitonic, and impurity states for different polarizations of the incident resonant radiation. In the same way, there is a rupture of degeneracies between different states, which can be recovered or controlled by external fields.

4. Conclusions

In this work, we have investigated the features of the electronic states in the presence of magnetic fields for elliptic quantum rings with nonuniform height in the form of multi-hilled profiles that resemble inserted quantum dot structures. Three and four cases of such protuberances are considered, and the influence of Zeeman and spin–orbit interaction effects are discussed. The use of the adiabatic approximation in determining the allowed states is suitably justified and complemented with the finite element calculation—within COMSOL MUltiphysics—of two-dimensional contributions to electron wavefunctions. The obtained electron states are then used in evaluating the coefficient of linear light absorption associated with transitions from the ground to the lowest excited levels in the structures.

The interstate transitions have energy differences of only very few meV, but, under such circumstances, there is a non-negligible optical response in general. Despite the presence of a magnetic field that provides for a symmetric confining potential in the system, the influence of the mentioned additional effects provokes a significant change in the symmetry of electronic states in the investigated GaAs/AlGaAs elliptic quantum rings, with the arising of double degeneracies at zero fields and the redshift of the entire spectrum such a phenomenon. The modification in the electronic structure affects the light absorption response, with a notorious quenching of the signal in the zero-field case.