A DFT + U Study on the Stability of Small Cu_N Clusters (N = 3–6 Atoms): Calculation of Phonon Frequencies

Abstract

Despite the interest in copper clusters, a consensus on their atomic structure is still lacking. The experimental observation of isolated clusters is difficult, and theoretical predictions vary widely. The latter is because one must adequately describe the closed shell of d electrons both in its short- and long-range effects. Herein, we investigate the stability of small copper clusters (Cu${}_N$, N = 3–6 atoms) using spin-polarized DFT calculations under the GGA approximation, the Hubbard U correction, and the van der Waals forces. We found that the spin-polarized and vdW contributions have little effect on the binding energies of the isomers. The inclusion of U represents the most relevant contribution to the ordering of the Cu${}_N$ isomers, and our calculated binding energies for the clusters agreed with the experimental values. We also found that atomic relaxations alone are not enough to determine the stability of small copper clusters. It is also necessary to build the energy landscape or calculate the vibrational frequencies of the isomers. We found that the vibrational frequencies of the isomers were in the THz range and the normal modes of vibration were discrete. This approach is relevant to future studies involving isolated or supported copper clusters.

1. Introduction

Many studies have shown that copper clusters (Cu${}_N$) can be used for CO${}_2$ reduction, for photocatalysis processes [1,2,3,4,5,6], and as dopants to improve the photocatalytic activity of other photocatalysts [7,8,9,10,11,12,13,14,15]. Due to the importance of copper clusters, there are many theoretical works that have studied these structures. For example, the structure and stability of small copper clusters were studied using DFT by Jug et al. in 2002 [16]. The energy and structure of copper clusters were studied using the Monte Carlo method by Zhang et al. in 2007 [17]. The structures and electronic properties of copper clusters were studied using DFT by Cui-Ju et al. in 2009 [18]. A study of the structure and an analysis of the atomic vibrations of copper clusters were carried out by Rusina et al. in 2013 [19], whereas a density functional study on the stability and structural properties of Cu${}_N$ clusters was presented by Ketabi et al. in 2013 [20]. The atomic structures of small Cu clusters with 3–6 atoms were investigated using density functional theory and a random search algorithm by Cogollo-Olivo in 2015 [21]. Recently (2020), Ahmed reported a study in which the structural properties of Cu${}_N$ clusters (N = 1–7) were determined [22]. Experimental studies have also been reported [23,24,25,26,27]. Finally, studies can be found in which the properties of small copper clusters are compared with those of copper surfaces [28,29].

At this point, it is clear that copper clusters have great relevance and very promising applications. This is reason enough to review their current research status. We have found that small copper clusters are frequently added to surfaces to improve their properties. The interaction of Cu${}_N$ cluster (N = 1–4) nanoparticles with ChCl:Urea deep eutectic solvent was studied by Ghenaatian and coworkers in 2021 [12], whereas the stability of Cu${}_N$ clusters (N = 1–4) adsorbed on CuAlO${}_2$ surfaces was studied using atomic thermodynamics by Wang and coworkers in 2022 [14]. The frequent use of these sizes of Cu${}_N$ clusters motivated us to review the structures reported as stable for small copper clusters in vacuum, finding large differences between the results reported in previous works, despite the fact that some of them used the same level of theory [16,21,22,30,31,32,33,34,35,36,37,38,39,40,41]. These differences further motivated us to carry out a study on the stability of small copper clusters, considering the frequently used cluster sizes (3–6 atoms), where the greatest discrepancies occur. With this work, we hope to provide a better understanding of the structural properties of small copper clusters, as well as clarify the differences between the results previously reported in other works.

Also, from a fundamental standpoint, by revisiting the structural properties of small isolated Cu${}_N$ clusters with a more accurate level of theory compared to most previous works, our results provide a stronger foundation for future studies that require good knowledge of the systematic reasons that can explain the relative stabilities of these forms. Here, an improved description of the clusters is achieved, for instance, by sampling a wide range of values of the Hubbard U and gradually observing their effects. On the other hand, although the impact of the van der Waals interactions on the structural properties of copper clusters seems to be minor, judging from our results, we observe that it still may become important in future studies and does not negatively affect the description of these structures obtained using DFT + U.

After this section, the rest of this work is organized as follows. In Section 2, we present the computational details necessary to reproduce all the results in this work. A discussion is also provided in the framework of DFT on the different levels of theory that we consider necessary to study the stability of small copper clusters. Section 3 is divided into four main parts. First, we present the Cu${}_N$ clusters (N = 3–6) that were optimized in this work using DFT + GGA (ground states and other metastable isomers), and we discuss the differences between our results and others reported in the literature. Binding energies are then calculated for all structures using different levels of theory, including spin-polarized, Hubbard U correction, and van der Waals dispersion forces. In this part, we can see how the energy ordering of the isomers changes with the inclusion of the U term and also how the energy landscape of Cu${}_3$ changes with the inclusion of this term. Binding energies are also calculated using the HSE hybrid functional, and all results are compared with those of other experimental and theoretical works. Since it is not easy to build the energy landscape for Cu${}_4$, Cu${}_5$, and Cu${}_6$ to identify points of minimum energy, maximum energy, and saddle points for these structures, we calculate the densities of the state of phonons so that we can determine which of the structures found for Cu${}_4$, Cu${}_5$, and Cu${}_6$ are really stable. In the last part of Section 3, the structural and electronic properties of Cu${}_N$ copper clusters are shown. Finally, we present the conclusions of this work in Section 4.

2. Materials and Methods

We started by reproducing a complete set of the most stable copper-cluster isomers (Cu${}_N$ for N = 3–6 atoms) that have been reported in the literature [21,36], while also performing a heuristic structural search. After this, ab initio atomic relaxations were performed for each of the studied cases independently, using three different levels of theory (SGGA, SGGA + U, and SGGA + U + vdW). The Hubbard term correction was applied using the simplified version of Dudarev et al. [42], and the vdW dispersion forces were included using Grimme’s DFT + D2 approach [43].

All the DFT calculations were performed with the Quantum ESPRESSO [44,45] package, using the Perdew–Burke–Ernzerhof (PBE) generalized gradient (GGA) exchange-correlation functionals [46], which was generated using a scalar-relativistic calculation and the nonlinear core correction. Vanderbilt ultra-soft pseudopotentials were employed [47], and a plane-wave basis set was used. LSDA spin-polarized calculations were taken into account. The tested values of U ranged from 0 to 9 eV. The convergence of the total energy for the clusters was achieved using cutoffs of 60 and 600 Ry for the kinetic energy of the wavefunctions and the charge density, respectively. A grid of $2\times 2\times 2$ k-points was generated using the method of Monkhorst and Pack [48], which was selected based on the convergence of the total energy with respect to the k-points.

To avoid interactions between neighboring periodic images, copper clusters were placed inside a large cubic cell with an edge of 14 Å. The converged cell size was determined by analyzing the stabilization within 5 meV/atom of the total energy with respect to the cell parameters for the largest isomer included in this study (Cu${}_6$), taken as the worst-case scenario. Atomic relaxations were performed for each increase in cell size using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the forces and energies converged within $1\times {10}^{-4}$ and $1\times {10}^{-6}$ a.u., respectively. The average binding energy was defined as

$$B_E=\left[n\times E\left(Cu\right)-E\left(C{u}_n\right)\right]/n$$

(1)

where $E(Cu)$ is the electronic energy of a Cu atom and $E(C{u}_n)$ is the electronic energy of the cluster of n atoms.

We now discuss why it is important to take into account the Hubbard U correction when studying the stability of small copper clusters. The peculiar electronic structure $(3s^{2}3p^{6}3d^{10}4s^1)$ of copper leads to a subtle interplay between the one s electron and the closed d shell, resulting in complex behavior, which is difficult to capture using theoretical methods. On the other hand, Density Functional Theory (DFT) is a convenient theoretical tool that is frequently used to characterize the properties of photocatalysts with impurities. It is well-known that basic descriptions of the exchange-correlation functionals, such as the local density and generalized gradient approximations (LDA and GGA, respectively), fail to predict the presence of some states in the electronic structure of the supported Cu${}_N$/photocatalyst system and also overestimate the binding energies for molecules and clusters [8,49,50,51,52]. This failure is due to the self-interaction error inherent in these exchange-correlation functionals, leading to small energy differences between the atomic s and d levels and strong hybridization effects [53]. To correct this error, post-DFT methods, such as DFT + U and hybrid functionals, have been employed [8,49,50,51,52,54,55,56,57,58,59,60,61,62,63]. However, hybrid approaches result in greater computational costs, which turns out to be critical for calculations such as those involving supported clusters via the supercell method to describe rare events. On the other hand, the Strongly Constrained and Appropriately Normed (SCAN) semilocal density functional has been shown to be a great alternative in the DFT framework [64]; however, Tameh and coworkers [65] showed that the Gibbs energies and the binding energies for the hydrogenation of CO and CO${}_2$ on Cu(211) calculated using the SCAN functional are worse than those obtained using PBE and HSE. Moreover, Long and coworkers recently evaluated the optimal U value for $3d$ transition-metal oxides within the SCAN + U framework [66] and found that using DFT-SCAN, the variation of the oxidation reaction enthalpy overestimates the experimental enthalpy by ∼0.7 eV, and when the U term is included, it monotonically worsens the error between theoretical (SCAN + U) and experimental enthalpies.

We also provide an explanation of the inclusion of the van der Waals dispersion forces in this work. It is known that vdW is a long-range interaction, and, therefore, this force is really important in adsorption studies, such as contaminant adsorption on copper clusters or copper clusters’ adsorption on surfaces. Therefore, we have included this interaction to provide information on the minor effects of it on the stability of isolated copper clusters that can be used in future studies. Additionally, the presence of a full d shell not only affects the short-range electron–electron interaction but also influences long-range electronic correlations (van der Waals interactions). It is then clear that performing calculations accurately in both ranges is extremely important. However, although several theoretical works based on DFT have studied the structure of small copper clusters [16,21,22,30,31,32,33,34,35,36,37,38,39,40,41], to the best of our knowledge, no previous work has included the Hubbard U correction and van der Waals (vdW) dispersion forces simultaneously within a spin-polarized treatment (SGGA + vdW + U for short). By the end, we hope to convey the message that this level of treatment is indeed relevant, with important implications for future studies involving interactions between supported Cu clusters and molecules, where adsorbate-metal hybridization interaction, as well as physisorption governed by dispersion forces, are frequently present.

3. Results and Discussion

This section begins with the presentation of the Cu${}_N$ clusters (N = 3–6 atoms), which were obtained in this work using DFT-GGA and atomic relaxations. These isomers are shown in Table 1, which shows two structures for Cu${}_3$, four for Cu${}_4$, five for Cu${}_5$, and seven for Cu${}_6$.

Table 1. Cu${}_N$ clusters that were optimized in this work using atomic relaxations.

GS Cu${}_3$ (A)	Cu${}_3$ (B)	GS Cu${}_4$ (C)	Cu${}_4$ (D)	Cu${}_4$ (E)	Cu${}_4$ (F)
GS Cu${}_5$ (G)	Cu${}_5$ (H)	Cu${}_5$ (I)	Cu${}_5$ (J)	Cu${}_5$ (K)	GS Cu${}_6$ (L)
Cu${}_6$ (M)	Cu${}_6$ (N)	Cu${}_6$ (O)	Cu${}_6$ (P)	Cu${}_6$ (Q)	Cu${}_6$ (R)

GS: Ground state.

Although the atomic relaxations suggest that all the structures in Table 1 are stable, we will demonstrate that some of them are not, thereby showing that DFT-GGA alone is not sufficient to predict the correct structures of small copper clusters. On the other hand, based on our current knowledge, previous theoretical studies by other authors have only considered the GGA approach in the DFT framework to study the structures of small copper clusters, and, therefore, we can find different results among similar works. For example, Cogollo-Olivo et al. [21] and Ahmed et al. [22] reported two stable isomers for Cu${}_3$, one of them being an isosceles triangle (GS) and the other a bent-type isomer. Moreover, Guvelioglu et al. [36] also used DFT-GGA and reported two stable triangular isomers for Cu${}_3$, whereas Lammers and Borstel [67] used the tight-binding method and instead reported four. In our case, the DFT-GGA atomic relaxations suggest an equilateral triangle as the GS of Cu${}_3$ (A isomer in Table 1) and a linear isomer as the stable structure (B isomer in Table 1). An equilateral triangle was also proposed as the GS for Cu${}_3$ in [18,19], and a linear isomer was also proposed as the stable GS for Cu${}_3$ in [18]. In the same way, for Cu${}_4$, Guvelioglu et al. [36] and Cui-Ju et al. [18] suggested the possibility of a metastable tetrahedral structure (using DFT-GGA), but Cogollo-Olivo et al. [21], using the same level of theory, showed that this isomer is not stable, whereas our DFT-GGA atomic relaxations also predict the possibility of a tetrahedral structure (F isomer in Table 1), Furthermore, this tetrahedral isomer was proposed as the GS for Cu${}_4$ in [17,19] who used the Monte Carlo and tight-binding methods, respectively. Structures C and D in Table 1 are in agreement with those reported in [21,22,36], whereas the E isomer for Cu${}_4$ was also reported in [36]. Our atomic relaxations do not predict the other Cu${}_4$ isomers reported in [21]. Regarding Cu${}_5$ (clusters with this particular size have been already synthesized and proposed as promising catalysts [1,5]), the G and H isomers in Table 1 were also reported by Cogollo-Olivo et al. [21], Ahmed et al. [22], and Guvelioglu et al. [36], whereas our DFT-GGA atomic relaxations also predict the I, J, and K structures for Cu${}_5$. Moreover, the J isomer was also suggested as stable by the authors of [18], and the H structure was proposed as the GS for Cu${}_5$ in [17]. Finally, for Cu${}_6$, the L, M, N, and O structures in Table 1 were also reported by Cogollo-Olivo et al. [21], whereas the P and Q isomers were reported in [36], and the last structure (R) for Cu${}_6$ was obtained by our DFT-GGA atomic relaxations. In addition, the L isomer was also proposed by the authors of [18,20,22], the M, N, and P isomers were also proposed by the authors of [18], and the P isomer was also proposed as the GS for Cu${}_6$ by the authors of [17,19], who used the Monte Carlo and tight-binding methods, respectively. To clarify why there are some different results in the works mentioned above and identify which structures in Table 1 are really stable, we use other approaches in the next subsections of this work.

3.1. Binding Energies of Cu${}_N$ Clusters

Binding energies ($B_E$) are usually used to determine the ground state (GS) of each group of isomers. The isomer with the highest binding energy is the GS, and the isomers with negative binding energies are not stable. In this work, the binding energies were calculated for all the isomers in Table 1 using DFT + SGGA + vdW + U (DFT with GGA, spin-polarized calculations, van der Waals (vdW) dispersion forces, and Hubbard-U correction), the values of U term were varied from 0 to 9 eV, and the results are shown in Table 2, Table 3 and Table 4. In these tables, the isomers A, C, G, and L are the GS of each group of copper clusters with 3–6 atoms, respectively. In Table 2, Table 3 and Table 4, $\Delta B_E$ are the relative binding energies and the binding energy differences between each isomer and the corresponding GS.

Table 2. Binding energies ($B_E$) of Cu${}_N$ (N = 3–4 atoms) isomers and their energy differences per atom ($\Delta B_E$) with respect to the GS as a function of the U parameter.

U
	GS Cu${}_{\mathbf{3}}$ (A)		Cu${}_{\mathbf{3}}$ (B)		GS Cu${}_{\mathbf{4}}$ (C)		Cu${}_{\mathbf{4}}$ (D)		Cu${}_{\mathbf{4}}$ (E)		Cu${}_{\mathbf{4}}$ (F)
	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$
(eV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)
0	1.361	0	1.254	107	1.718	0	1.622	96	1.544	174	1.502	217
1	1.278	0	1.162	116	1.632	0	1.536	96	1.448	184	1.407	225
2	1.209	0	1.110	99	1.559	0	1.465	94	1.369	190	1.327	232
3	1.184	0	1.101	83	1.530	0	1.438	92	1.336	194	1.293	237
4	1.162	0	1.087	75	1.504	0	1.414	90	1.308	197	1.262	242
5	1.143	0	1.074	68	1.482	0	1.394	88	1.283	199	1.236	246
6	1.125	0	1.063	62	1.461	0	1.376	85	1.261	200	1.212	249
7	1.110	0	1.053	57	1.443	0	1.359	83	1.242	200	1.190	252
8	1.096	0	1.044	51	1.426	0	1.345	81	1.225	200	1.171	255
9	1.083	0	1.035	47	1.410	0	1.331	79	1.209	201	1.153	257
HSE	0.995	0	NC	NC	1.322	0	1.234	88	1.141	182	NC	NC
DFT + PBE [21]	1.433${}^{IT}$	0	- -	- -	1.851	0	1.755	96	- -	- -	- -	- -
DFT + PW [36]	1.129${}^{IT}$	0	- -	- -	1.505	0	- -	- -	1.329	176	1.269	236
DFT + BLYP [18]	1.030${}^{ET}$	0	0.962	68	1.307	0	- -	- -	- -	- -	1.077	230
Tight binding [19]	1.660${}^{ET}$	0	- -	- -	- -	- -	- -	- -	- -	- -	1.93${}^{GS}$	0
DFT + B3LYP [20]	1.001${}^{IT}$	0	- -	- -	1.300	0	- -	- -	- -	- -	- -	- -
DFT + PW91 [22]	1.164${}^{IT}$	0	- -	- -	1.515	0	1.429	86	- -	- -	- -	- -
Monte Carlo, $T=300$ K [17]	1.137	0	- -	- -	- -	- -	- -	- -	- -	- -	1.460${}^{GS}$	0
Exp. [23]	1.063	0	- -	- -	1.478	0	- -	- -	- -	- -	- -	- -

NC: The isomer does not converge. - -: Not reported. $GS$: Ground state. $IT$: isosceles triangle. $ET$: Equilateral triangle.

Table 3. Binding energies ($B_E$) of Cu${}_N$ (N = 5–6) isomers and their energy differences per atom ($\Delta B_E$) with respect to the GS as a function of the U parameter.

U
	GS Cu${}_{\mathbf{5}}$ (G)		Cu${}_{\mathbf{5}}$ (H)		Cu${}_{\mathbf{5}}$ (I)		Cu${}_{\mathbf{5}}$ (J)		Cu${}_{\mathbf{5}}$ (K)		GS Cu${}_{\mathbf{6}}$ (L)
	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$
(eV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)
0	1.859	0	1.816	43	1.813	46	1.779	80	1.751	108	2.051	0
1	1.769	0	1.718	50	1.722	47	1.678	90	1.664	105	1.965	0
2	1.693	0	1.637	57	1.647	47	1.595	99	1.591	102	1.891	0
3	1.662	0	1.600	63	1.615	47	1.557	105	1.563	99	1.859	0
4	1.635	0	1.567	68	1.588	47	1.524	111	1.538	97	1.831	0
5	1.611	0	1.538	73	1.564	47	1.495	115	1.516	95	1.806	0
6	1.588	0	1.511	77	1.542	46	1.470	119	1.496	93	1.783	0
7	1.569	0	1.488	81	1.523	46	1.446	122	1.478	91	1.765	0
8	1.550	0	1.466	85	1.505	46	1.426	125	1.461	89	1.746	0
9	1.533	0	1.446	88	1.488	45	1.407	127	1.446	87	1.726	0
HSE	1.449	0	1.382	67	1.399	51	NC	NC	1.356	93	1.633	0
DFT + PBE [21]	1.963	0	1.913	50	- -	- -	- -	- -	- -	- -	2.178	0
DFT + PW [36]	1.634	0	1.580	54	- -	- -	- -	- -	- -	- -	1.834	0
DFT + BLYP [18]	1.428	0	1.342	86	- -	- -	1.318	110	- -	- -	1.589	0
Tight binding [19]	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -
DFT + B3LYP [20]	1.273	0	- -	- -	- -	- -	- -	- -	- -	- -	1.594	0
DFT + PW91 [22]	1.643	0	1.585	58	- -	- -	- -	- -	- -	- -	1.834	0
Monte Carlo, $T=300$ K [17]	- -	- -	1.646${}^{GS}$	0	- -	- -	- -	- -	- -	- -	- -	- -
Exp. [23]	1.552	0	- -	- -	- -	- -	- -	- -	- -	- -	1.720	0

NC: The isomer does not converge. - -: Not reported. $GS$: Ground state.

Table 4. Binding energies ($B_E$) of Cu${}_6$ isomers and their energy differences per atom ($\Delta B_E$) with respect to the GS as a function of the U parameter.

U
	Cu${}_{\mathbf{6}}$ (M)		Cu${}_{\mathbf{6}}$ (N)		Cu${}_{\mathbf{6}}$ (O)		Cu${}_{\mathbf{6}}$ (P)		Cu${}_{\mathbf{6}}$ (Q)		Cu${}_{\mathbf{6}}$ (R)
	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$	${\mathit{B}}_{\mathit{E}}$	$\Delta {\mathit{B}}_{\mathit{E}}$
(eV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)	(eV)	(meV)
0	2.033	19	2.014	37	2.010	42	1.973	78	1.905	146	1.873	179
1	1.949	15	1.917	47	1.923	42	1.866	99	1.803	162	1.777	188
2	1.876	15	1.836	55	1.849	41	1.776	115	1.718	173	1.698	193
3	1.845	14	1.798	61	1.819	40	1.732	127	1.678	181	1.663	196
4	1.817	14	1.765	66	1.793	39	1.693	138	1.644	187	1.633	198
5	1.792	14	1.735	71	1.768	38	1.659	147	1.614	192	1.607	199
6	1.770	14	1.708	75	1.746	37	1.629	155	1.587	197	1.583	200
7	1.751	14	1.683	82	1.726	38	1.601	163	1.563	202	1.566	203
8	1.732	14	1.661	85	1.708	38	1.577	169	1.541	205	1.542	204
9	1.714	11	NC	NC	1.691	35	1.554	172	1.521	205	1.524	202
HSE	1.617	16	1.573	59	1.593	39	NC	NC	1.460	172	1.447	185
DFT + PBE [21]	2.153	24	2.136	42	2.128	50	- -	- -	- -	- -	- -	- -
DFT + PW [36]	1.797	37	1.757	77	- -	- -	1.685	149	1.637	197	- -	- -
DFT + BLYP [18]	1.548	41	1.497	92	- -	- -	1.456	133	- -	- -	- -	- -
Tight binding [19]	- -	- -	- -	- -	- -	- -	2.200${}^{GS}$	0	- -	- -	- -	- -
DFT + B3LYP [20]	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -	- -
DFT + PW91 [22]	1.812	22	- -	- -	1.785	49	- -	- -	- -	- -	- -	- -
Monte Carlo, $T=300$ K [17]	- -	- -	- -	- -	- -	- -	1.835${}^{GS}$	0	- -	- -	- -	- -

NC: The isomer does not converge. - -: Not reported. $GS$: Ground state.

In this study, spin-polarized calculations and vdW forces have minor relevance in determining the binding energies’ values, whereas the U term produces larger changes in the $B_E$ values (see Table 2, Table 3 and Table 4). $B_E$ decreases for all structures in Table 1 when the value of U increases. This is the first effect we can observe due to the inclusion of U. The second is that the decrease in $B_E$ is not in the same proportion for all isomers. In some, the decrease is greater than in others, which can be observed in the data for $\Delta B_E$ in Table 2, Table 3 and Table 4. For some structures, $\Delta B_E$ increases, and for others, it decreases when the U term enhances. Therefore the U term produces an energetic rearrangement in the structures. Note that when $U=0$, the energetic arrangement of the isomers is as shown in Table 5.

Table 5. Binding energy ordering of Cu${}_N$ clusters for $U=0$.

Cu${}_3$

$B_E$(A)

>

$B_E$(B)

Cu${}_4$

$B_E$(C)

>

$B_E$(D)

>

$B_E$(E)

>

$B_E$(F)

Cu${}_5$

$B_E$(G)

>

$B_E$(H)

>

$B_E$(I)

>

$B_E$(J)

>

$B_E$(K)

Cu${}_6$

$B_E$(L)

>

$B_E$(M)

>

$B_E$(N)

>

$B_E$(O)

>

$B_E$(P)

>

$B_E$(Q)

>

$B_E$(R)

For $U=8$ eV, the energetic arrangement of the isomers is as shown in Table 6. In Table 5 and Table 6, it can be seen that the GS of the structures is the same for $U=0$ and $U=8$ eV, but for Cu${}_5$ and Cu${}_6$, there are changes in the order of some isomers. For example, when $U=0$, the second isomer of Cu${}_5$ is (H), the third is (I), the fourth is (J), and the fifth is (K). But when $U=8$ eV, the (I) isomer becomes the second, the (K) isomer is now the third, and H and J become the fourth and fifth, respectively. Therefore, we can say that the U term favors 2D structures because the $\Delta B_E$ of the 3D structures (H and J) increases more than the $\Delta B_E$ of the planar isomers (I and K). A similar analysis can be made for Cu${}_6$, where for $U=8$ eV, the O, N, P, R, and Q isomers become the third, fourth, fifth, sixth, and seventh, respectively. In addition, for $U=9$ eV, the N isomer of Cu${}_6$ does not converge. But for $U<9$ eV, that structure does converge. So the following question can be asked: What is the correct value of U for copper clusters? We provide a response to that question later.

Table 6. Binding energy ordering of Cu${}_N$ clusters for $U=8$ eV.

Cu${}_3$

$B_E$(A)

>

$B_E$(B)

Cu${}_4$

$B_E$(C)

>

$B_E$(D)

>

$B_E$(E)

>

$B_E$(F)

Cu${}_5$

$B_E$(G)

>

$B_E$(I)

>

$B_E$(K)

>

$B_E$(H)

>

$B_E$(J)

Cu${}_6$

$B_E$(L)

>

$B_E$(M)

>

$B_E$(O)

>

$B_E$(N)

>

$B_E$(P)

>

$B_E$(R)

>

$B_E$(Q)

On the other hand, recalling the main objective of this work, it can be observed in Table 2, Table 3 and Table 4 that the atomic relaxations with the U term can still predict stable copper clusters. We proceed to carry out another type of analysis. For this, we start with Cu${}_3$ clusters.

3.1.1. Energy Landscape for Cu${}_3$ Copper Clusters

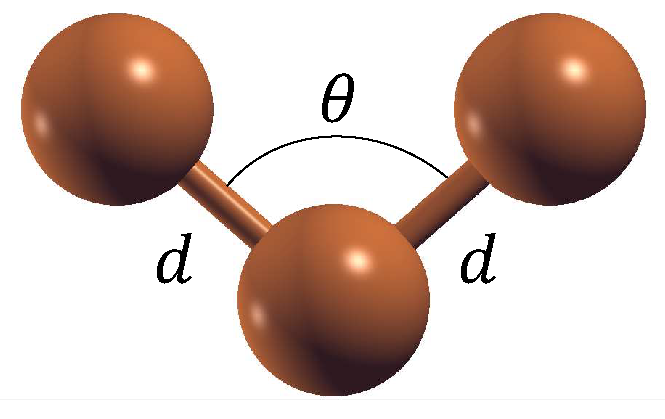
Figure 1 shows a general Cu${}_3$ copper cluster. It is possible to find all the isomers for Cu${}_3$ by varying the angle ($\theta$) and calculating the optimal interatomic distance (d).

Figure 1. Variation of angle and interatomic distance for Cu${}_3$ copper clusters.

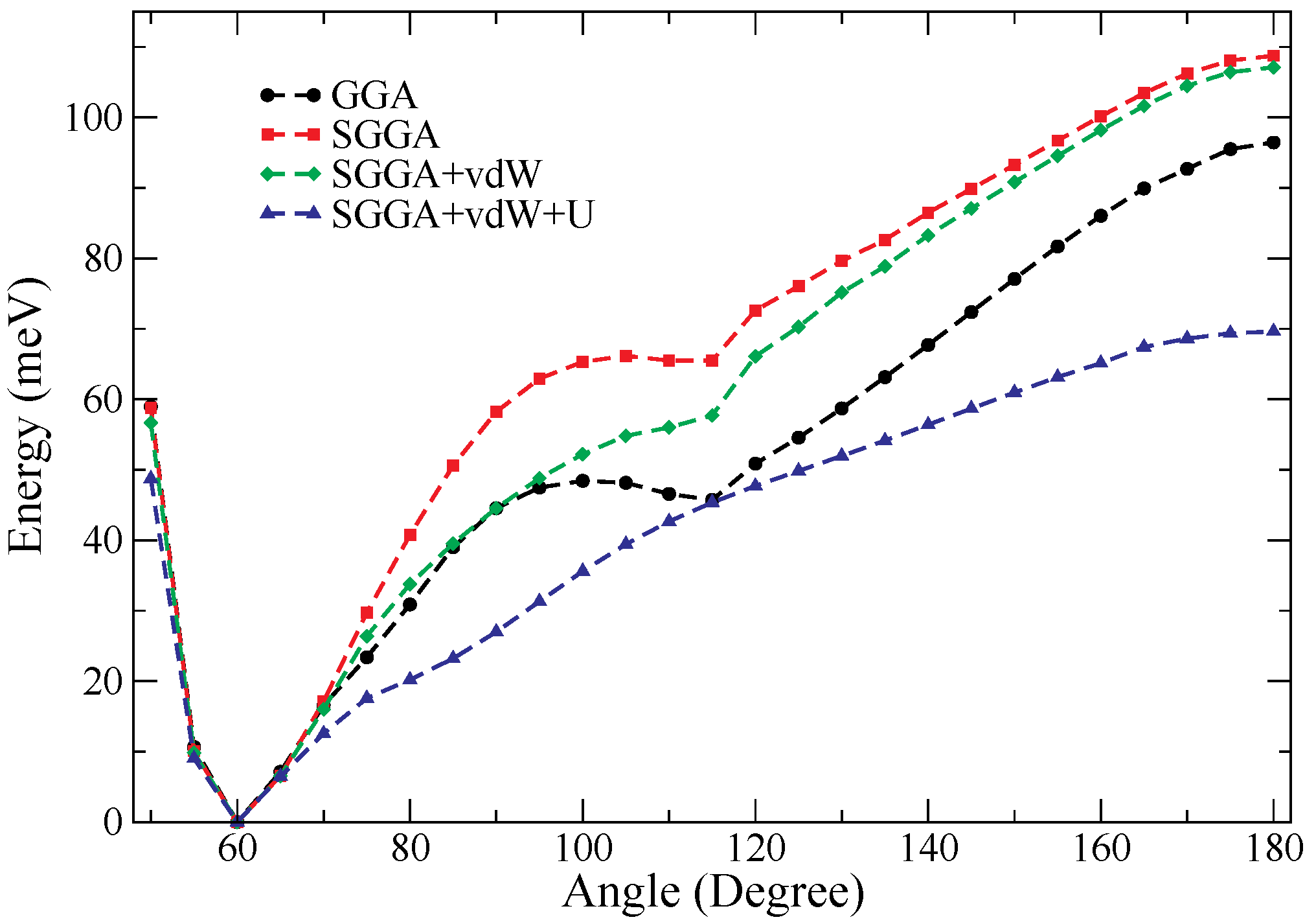
In Figure 2, the energy landscape of Cu${}_3$ is shown. To make this graph, we fixed several angles (from 0 to 180 degrees in steps of 5 degrees) and identified the optimal d distance, which minimizes the energy for each of them. We see that using just GGA (black curve), it predicts two minimum energy points ($\theta =60°,118°$), representing two stable isomers, as reported in [21,22]. The minimum energy point (near $118$) tends to disappear when the spin-polarized calculations (red curve) and vdW dispersion forces (green curve) are introduced (here, the first effect due to spin-polarized calculations and vdW forces is observed). Finally, when the Hubbard U term is taken into account (blue curve), there is only one minimum energy point on the energy landscape of Cu${}_3$, corresponding to one stable isomer for Cu${}_3$, which is an equilateral triangle ($\theta =60°$). The inclusion of the term U rules out the possibility of finding the metastable isosceles triangle reported in previous DFT studies [21,22,36]. On the other hand, in Figure 2, it can be seen that the linear isomer for Cu${}_3$ corresponds to a maximum energy point ($\theta =180°$); therefore, the linear isomer Cu${}_3$(B) in Table 1 is unstable. By analyzing the behavior of the Cu${}_3$(B) isomer, we can see that the atomic relaxations could converge on structures that correspond to points of maximum energy in the energy landscape. However, the point of maximum energy seen in Figure 2 at $\theta =180°$ is really a saddle point. In other words, at this point, the energy is a function of two variables E($\theta$, d). Therefore, for variations of $\theta$, the behavior of the energy is as shown in Figure 2, whereas for a fixed $\theta$ value ($\theta =180°$) and variations of the interatomic distance (d), E($180°$, d) has a minimum at $\theta =180°$. So we can ask: Which of the structures in Table 1 are also unstable (saddle points for the energy)? Building the energy landscape for Cu${}_4$, Cu${}_5$, and Cu${}_6$ is not easy, so we must find other ways to determine the stability of copper clusters.

Figure 2. Energy as a function of the $\theta$ angle for the Cu${}_3$ cluster for optimized values of the interatomic distance d. The Hubbard parameter is set to $U=5$ eV.

3.1.2. Binding Energies Calculated Using the HSE Hybrid Functional

Using the HSE hybrid functional, atomic relaxations were also performed for all structures in Table 1, and the values of the binding energies are shown in Table 2, Table 3 and Table 4. It can be seen that the $B_E$ values calculated using the HSE are lower than those found using SGGA + vdW + U. On the other hand, it can be observed that the HSE indicates that the isomers Cu${}_4$(F), Cu${}_5$(J), and Cu${}_6$(P) are not stable, in contrast to the predictions using SGGA + vdW + U. Table 2, Table 3 and Table 4 also show that the HSE indicates a stable configuration for Cu${}_6$(N) in accordance with the SGGA + vdW + U predictions for this structure for $U<9$ eV. The latter is very interesting because SGGA + vdW + U predicts that Cu${}_6$(N) is unstable for $U=9$ eV, so we may think that there should be a limit for taking a correct value of U for copper clusters. 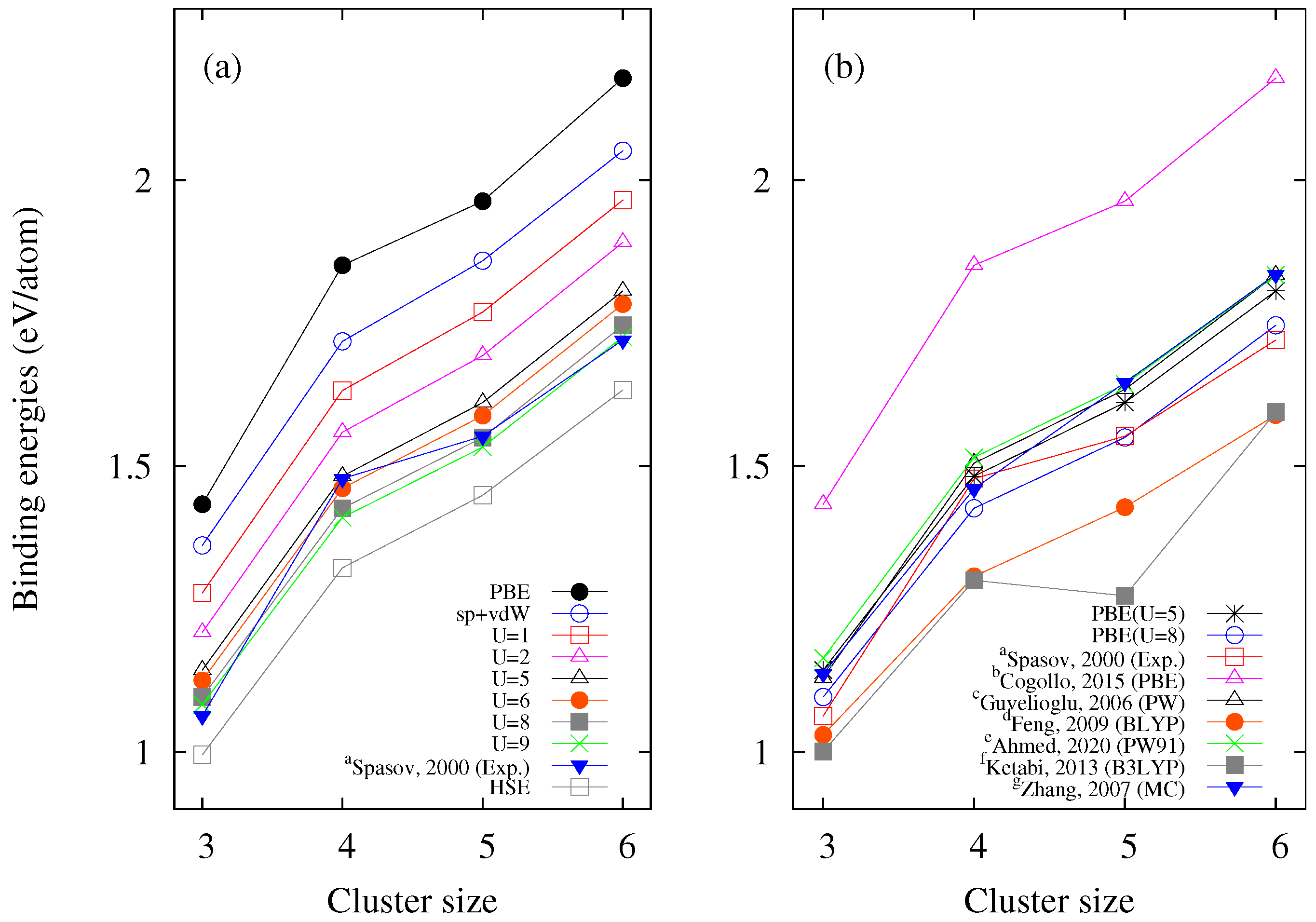In fact, this is confirmed by looking at Figure 3a, where graphs of the $B_E$ values are shown as a function of the size of the copper cluster (for the GS) for different levels of theory.

Figure 3. (a) Binding energies of the GS isomers vs. cluster size for the different levels of theory in this work. (b) Previous theoretical and experimental results for comparison, ${}^{\mathrm{a}}$ Ref. [23], ${}^{\mathrm{b}}$ Ref. [21], ${}^{\mathrm{c}}$ Ref. [36], ${}^{\mathrm{d}}$ Ref. [18], ${}^{\mathrm{e}}$ Ref. [22], ${}^{\mathrm{f}}$ Ref. [20] and ${}^{\mathrm{g}}$ Ref. [17]. The U values are in eV.

In Figure 3a, it can be seen that when the value of U increases, the $B_E$ values tend to approach the experimental values reported by Spasov et al. (2000) [23]. It can also be observed that the $B_E$ values calculated using the HSE hybrid functional are further from the experimental data than those calculated using SGGA + vdW + U. On the other hand, Table 2, Table 3 and Table 4 also show the values of the binding energies reported by other authors [17,18,19,20,21,22,23,36], and Figure 3b shows a comparison of the binding energies calculated in this work for $U=5$ and $U=8$ eV with those reported in other works. It can be seen that our results are closer to the experimental values than those previously calculated, even for $U=5$ eV. Therefore, we can suggest any value of U in the interval ($5\le U\le 8$) eV as a suitable choice to work with copper atoms. These values of U are, in any case, in line with those of previous works that have used values for U between 4 and 8 eV for copper and copper oxides [8,68,69,70,71,72]. In addition, in Figure 3a, it can be seen that the values of the binding energies calculated using only spin polarization and vdW (sp-vdW) are closer to the experimental data compared to those found using only PBE. This shows the importance of including these interactions in this work.

Remembering again that the main objective of this work is to study the stability of the structures in Table 1, the only thing we can say up until now is that for Cu${}_3$, there is only one stable isomer. For Cu${}_4$, Cu${}_5$, and Cu${}_6$, we still cannot ensure that these isomers are stable because we did not build their energy landscapes, and as we mentioned before, this is not easy. Therefore, we choose to calculate the vibration frequencies of these structures to investigate which of them are really stable.

3.2. Density of States of Phonons of Cu${}_N$ Copper Clusters

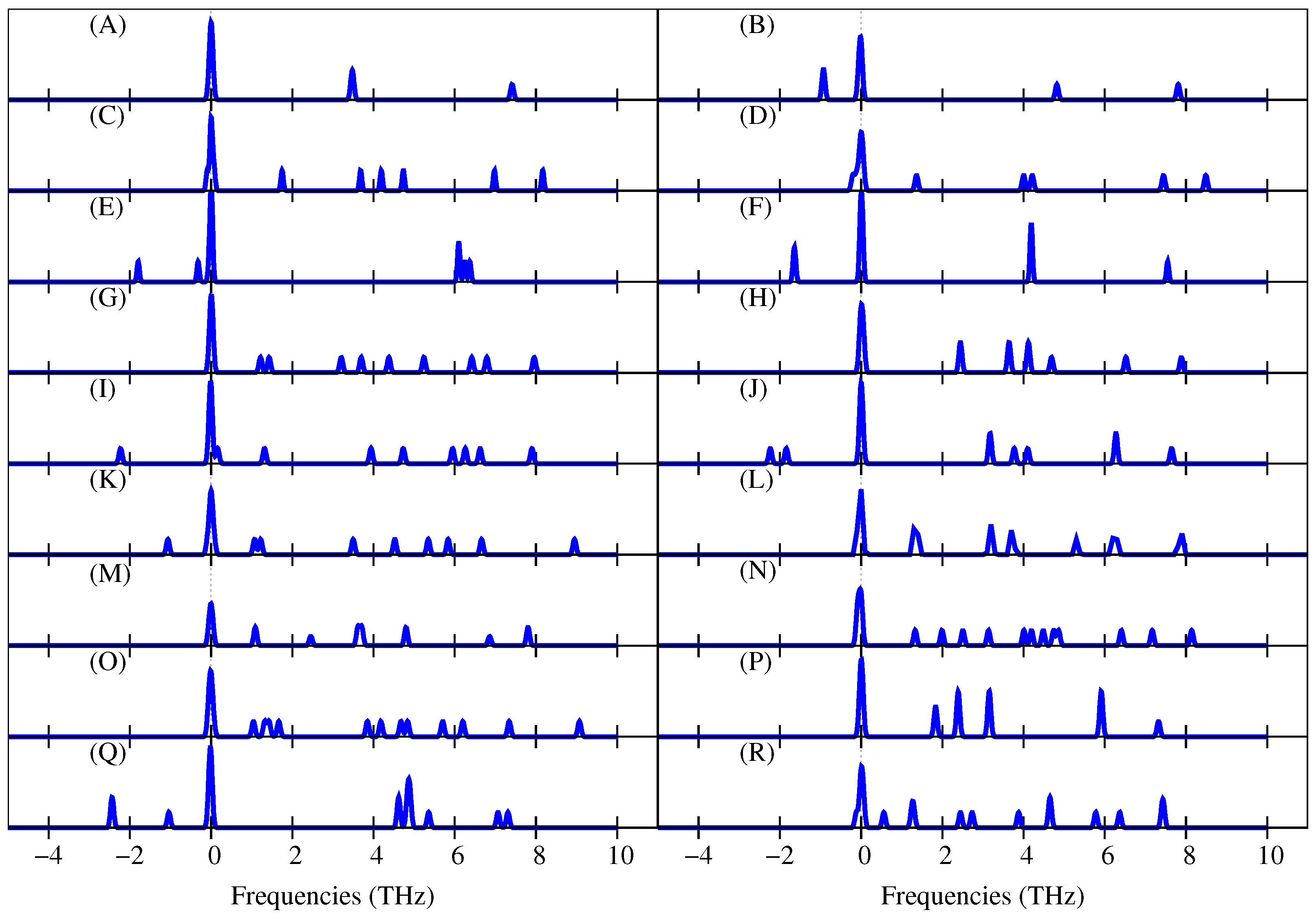
To finish the investigation on the stability of the copper clusters in Table 1, we calculated the vibration frequencies of these isomers using SGGA + vdW + U. At this point, we know from the previous subsection what values of U we can use, so we used $U=8$ eV to continue. In Figure 4, the phonon state densities for $U=8$ eV are presented. Note that Cu${}_3$(B) has negative frequencies, confirming that this isomer is unstable. It can also be seen that the phonon state densities of the isomers Cu${}_4$(D), Cu${}_4$(F), Cu${}_5$(I), Cu${}_5$(J), Cu${}_5$(K), and Cu${}_6$(Q) also have negative frequencies; therefore, those isomers are also unstable. Remember that the HSE hybrid functional also predicted that Cu${}_4$(F) and Cu${}_5$(J) were unstable. Furthermore, the HSE suggested that Cu${}_6$(P) was unstable, but the atomic relaxation using SGGA + vdW + U and the phonon state density predicted that Cu${}_6$(P) was stable. In this case, we think that Cu${}_6$(P) is really stable, considering that the results of the $B_E$ values using SGGA + vdW + U were closer to the experimental data compared to those obtained using the HSE (see Figure 3a).

Figure 4. Density of states of phonons for Cu${}_N$ copper clusters. $U=8$ eV was used. Each letter i in the figure corresponds to the letter i of each cluster Cu${}_N$(i).

Of the 18 initial structures in Table 1, only 11 are stable: one for Cu${}_3$, two for Cu${}_4$, two for Cu${}_5$, and six for Cu${}_6$. We have seen that only the atomic relaxations using SGGA + vdW + U or the HSE hybrid functional were not enough to determine the stability of the small copper clusters in this study. We also needed to calculate the energy landscape (as for Cu${}_3$) or the vibrational frequencies of the isomers to determine their stability.

As an additional result, in Figure 4, it can be seen that the vibrational frequencies of the copper clusters are between 0 and 10 THz.

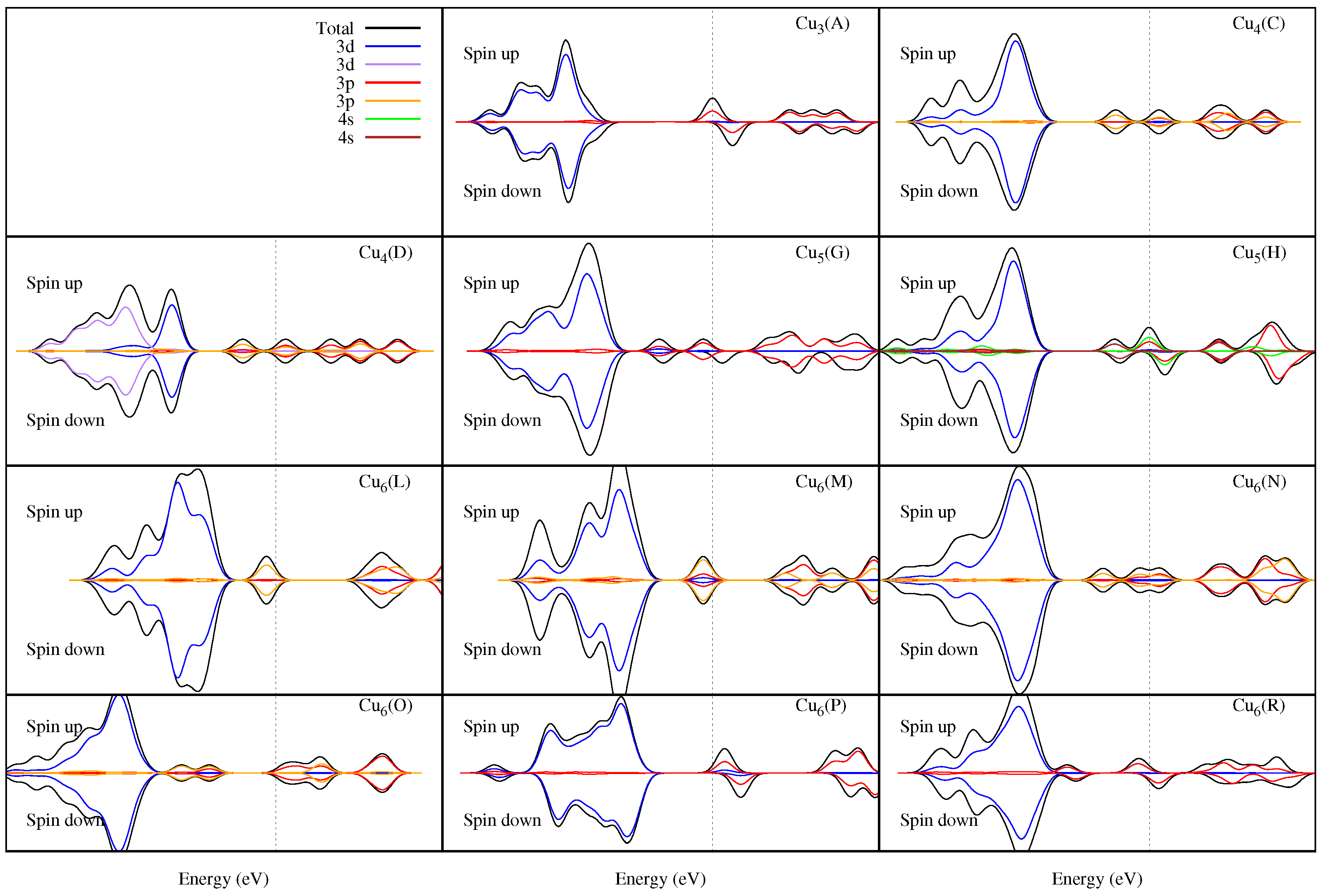
3.3. Structural and Electronic Properties of Cu${}_N$ Copper Clusters

In this subsection, the main structural and electronic properties of the eleven stable copper clusters are presented. Table 7, Table 8 and Table 9 show the bond lengths of the isomers for three different values of the U term. It can be seen that when the U term increases, all the bond lengths of the isomers also increase. This helps to explain why the binding energies of the isomers decrease when the U term increases. We also calculated de density of states (DOS) of these isomers (see Figure 5) and found that when the U term increases, an intragap appears within the valence band (see the intragap values in Table 7 and Table 9). The latter is also associated with the decrease in the binding energies of the isomers when the U term increases. The greatest intragaps occur for 3D structures such as Cu${}_5$(H), Cu${}_6$(N), and Cu${}_6$(P), so by increasing the U term, they have a greater decrease in the binding energies (see Table 2, Table 3 and Table 4).

Table 7. Values of the bond lengths ($B_L$), magnetization (${\mu }_B$), polarization (P), and intragaps within the valence band ($\Delta g$) of the copper clusters ($C{u}_N,N=3–5$) for $U=$ 0, 5, and 8 eV.

	Cu${}_{\mathbf{3}}$ (A)	Cu${}_{\mathbf{4}}$ (C)	Cu${}_{\mathbf{4}}$ (D)	Cu${}_{\mathbf{5}}$ (G)	Cu${}_{\mathbf{5}}$ (H)
	(1–2) = 2.333	(1–2) = 2.368	(1–2) = 2.241	(1–2) = 2.376	(1–2) = 2.414
	(1–3) = 2.333	(1–3) = 2.368	(2–3) = 2.374	(1–3) = 2.349	(1–3) = 2.414
	(2–3) = 2.333	(2–3) = 2.272	(2–4) = 2.374	(1–4) = 2.386	(1–4) = 2.414
		(2–4) = 2.368	(3–4) = 2.259	(2–4) = 2.386	(2–3) = 2.380
$B_L$ (Å)		(3–4) = 2.368		(2–5) = 2.349	(2–4) = 2.380
$U=0$				(3–4) = 2.324	(2–5) = 2.414
				(4–5) = 2.324	(3–4) = 2.380
					(3–5) = 2.414
					(4–5) = 2.414
	(1–2) = 2.350	(1–2) = 2.391	(1–2) = 2.256	(1–2) = 2.403	(1–2) = 2.435
	(1–3) = 2.350	(1–3) = 2.391	(2–3) = 2.409	(1–3) = 2.361	(1–3) = 2.435
	(2–3) = 2.350	(2–3) = 2.260	(2–4) = 2.409	(1–4) = 2.392	(1–4) = 2.435
		(2–4) = 2.391	(3–4) = 2.257	(2–4) = 2.392	(2–3) = 2.384
$B_L$ (Å)		(3–4) = 2.391		(2–5) = 2.361	(2–4) = 2.383
$U=5$				(3–4) = 2.347	(2–5) = 2.435
				(4–5) = 2.347	(3–4) = 2.383
					(3–5) = 2.435
					(4–5) = 2.435
	(1–2) = 2.360	(1–2) = 2.402	(1–2) = 2.267	(1–2) = 2.416	(1–2) = 2.447
	(1–3) = 2.360	(1–3) = 2.402	(2–3) = 2.427	(1–3) = 2.369	(1–3) = 2.447
	(2–3) = 2.360	(2–3) = 2.261	(2–4) = 2.427	(1–4) = 2.399	(1–4) = 2.447
		(2–4) = 2.402	(3–4) = 2.261	(2–4) = 2.399	(2–3) = 2.389
$B_L$ (Å)		(3–4) = 2.402		(2–5) = 2.369	(2–4) = 2.389
$U=8$				(3–4) = 2.358	(2–5) = 2.447
				(4–5) = 2.358	(3–4) = 2.389
					(3–5) = 2.447
					(4–5) = 2.447
${\mu }_B$ (a.u.), $U=0$	1.06	0.00	0.00	0.93	1.13
${\mu }_B$ (a.u.), $U=5$	1.07	0.00	0.00	1.00	1.13
${\mu }_B$ (a.u.), $U=8$	1.07	0.00	0.00	1.01	1.13
	(1) = 0.351	(1) = 0.000	(1) = 0.000	(1) = 0.229	(1) = 0.131
	(2) = 0.352	(2) = 0.000	(2) = 0.000	(2) = 0.229	(2) = 0.286
P (a.u.), $U=0$	(3) = 0.352	(3) = 0.000	(3) = 0.000	(3) = 0.128	(3) = 0.286
		(4) = 0.000	(4) = 0.000	(4) = 0.212	(4) = 0.286
				(5) = 0.128	(5) = 0.131
	(1) = 0.352	(1) = 0.000	(1) = 0.000	(1) = 0.246	(1) = 0.129
	(2) = 0.352	(2) = 0.000	(2) = 0.000	(2) = 0.246	(2) = 0.286
P (a.u.), $U=5$	(3) = 0.352	(3) = 0.000	(3) = 0.000	(3) = 0.136	(3) = 0.286
		(4) = 0.000	(4) = 0.000	(4) = 0.226	(4) = 0.286
				(5) = 0.136	(5) = 0.129
	(1) = 0.353	(1) = 0.000	(1) = 0.000	(1) = 0.247	(1) = 0.127
	(2) = 0.353	(2) = 0.000	(2) = 0.000	(2) = 0.247	(2) = 0.287
P (a.u.), $U=8$	(3) = 0.352	(3) = 0.000	(3) = 0.000	(3) = 0.137	(3) = 0.287
		(4) = 0.000	(4) = 0.000	(4) = 0.227	(4) = 0.287
				(5) = 0.137	(5) = 0.127
$\Delta g$ (eV), $U=0$	0.00	0.00	0.00	0.00	0.00
$\Delta g$ (eV), $U=5$	1.60	0.90	0.60	0.14	1.00
$\Delta g$ (eV), $U=8$	1.80	1.20	1.10	0.60	1.90

Table 8. Values of the bond lengths ($B_L$) of the copper clusters (Cu${}_6$) for $U=$ 0, 5, and 8 eV.

	Cu${}_{\mathbf{6}}$ (L)	Cu${}_{\mathbf{6}}$ (M)	Cu${}_{\mathbf{6}}$ (N)	Cu${}_{\mathbf{6}}$ (O)	Cu${}_{\mathbf{6}}$ (P)	Cu${}_{\mathbf{6}}$ (R)
	(1–2) = 2.320	(1–2) = 2.417	(1–2) = 2.370	(1–2) = 2.376	(1–2) = 2.413	(1–2) = 2.344
	(1–3) = 2.320	(1–3) = 2.342	(1–3) = 2.480	(1–3) = 2.403	(1–3) = 2.413	(1–4) = 2.362
	(2–3) = 2.411	(1–4) = 2.417	(1–4) = 2.458	(1–4) = 2.312	(1–4) = 2.413	(1–5) = 2.429
	(2–4) = 2.322	(2–3) = 2.342	(1–6) = 2.458	(2–4) = 2.305	(1–5) = 2.413	(2–3) = 2.324
$B_L$ (Å)	(2–5) = 2.411	(2–5) = 2.417	(2–4) = 2.458	(3–4) = 2.414	(2–3) = 2.413	(2–5) = 2.375
$U=0$	(3–5) = 2.411	(3–4) = 2.342	(2–5) = 2.480	(3–5) = 2.403	(2–5) = 2.413	(2–6) = 2.429
	(3–6) = 2.322	(3–5) = 2.342	(2–6) = 2.458	(4–5) = 2.312	(2–6) = 2.413	(3–6) = 2.362
	(4–5) = 2.321	(3–6) = 2.342	(3–4) = 2.378	(4–6) = 2.305	(3–4) = 2.413	(4–5) = 2.324
	(5–6) = 2.321	(4–6) = 2.417	(3–6) = 2.378	(5–7) = 2.376	(3–6) = 2.413	(5–6) = 2.344
		(5–6) = 2.417	(4–5) = 2.378		(4–5) = 2.413
			(4–6) = 2.320		(4–6) = 2.413
			(5–6) = 2.378		(5–6) = 2.413
	(1–2) = 2.349	(1–2) = 2.457	(1–2) = 2.375	(1–2) = 2.410	(1–2) = 2.427	(1–2) = 2.383
	(1–3) = 2.349	(1–3) = 2.338	(1–3) = 2.523	(1–3) = 2.438	(1–3) = 2.427	(1–4) = 2.370
	(2–3) = 2.420	(1–4) = 2.457	(1–4) = 2.483	(1–4) = 2.315	(1–4) = 2.427	(1–5) = 2.394
	(2–4) = 2.349	(2–3) = 2.338	(1–6) = 2.484	(2–4) = 2.310	(1–5) = 2.427	(2–3) = 2.366
$B_L$ (Å)	(2–5) = 2.420	(2–5) = 2.457	(2–4) = 2.483	(3–4) = 2.403	(2–3) = 2.428	(2–5) = 2.430
$U=5$	(3–5) = 2.420	(3–4) = 2.338	(2–5) = 2.523	(3–5) = 2.438	(2–5) = 2.428	(2–6) = 2.394
	(3–6) = 2.349	(3–5) = 2.338	(2–6) = 2.484	(4–5) = 2.315	(2–6) = 2.428	(3–6) = 2.370
	(4–5) = 2.349	(3–6) = 2.338	(3–4) = 2.392	(4–6) = 2.310	(3–4) = 2.428	(4–5) = 2.366
	(5–6) = 2.349	(4–6) = 2.457	(3–6) = 2.392	(5–7) = 2.410	(3–6) = 2.428	(5–6) = 2.283
		(5–6) = 2.457	(4–5) = 2.392		(4–5) = 2.428
			(4–6) = 2.292		(4–6) = 2.428
			(5–6) = 2.392		(5–6) = 2.428
	(1–2) = 2.359	(1–2) = 2.472	(1–2) = 2.380	(1–2) = 2.426	(1–2) = 2.439	(1–2) = 2.395
	(1–3) = 2.359	(1–3) = 2.342	(1–3) = 2.545	(1–3) = 2.458	(1–3) = 2.439	(1–4) = 2.379
	(2–3) = 2.427	(1–4) = 2.472	(1–4) = 2.497	(1–4) = 2.312	(1–4) = 2.439	(1–5) = 2.396
	(2–4) = 2.359	(2–3) = 2.342	(1–6) = 2.499	(2–4) = 2.313	(1–5) = 2.439	(2–3) = 2.381
$B_L$ (Å)	(2–5) = 2.427	(2–5) = 2.472	(2–4) = 2.497	(3–4) = 2.401	(2–3) = 2.439	(2–5) = 2.448
$U=8$	(3–5) = 2.427	(3–4) = 2.342	(2–5) = 2.545	(3–5) = 2.458	(2–5) = 2.439	(2–6) = 2.528
	(3–6) = 2.359	(3–5) = 2.342	(2–6) = 2.499	(4–5) = 2.319	(2–6) = 2.439	(3–6) = 2.379
	(4–5) = 2.359	(3–6) = 2.342	(3–4) = 2.400	(4–6) = 2.313	(3–4) = 2.439	(4–5) = 2.381
	(5–6) = 2.359	(4–6) = 2.472	(3–6) = 2.400	(5–7) = 2.426	(3–6) = 2.439	(5–6) = 2.395
		(5–6) = 2.472	(4–5) = 2.400		(4–5) = 2.439
			(4–6) = 2.289		(4–6) = 2.439
			(5–6) = 2.400		(5–6) = 2.439

Table 9. Values of the magnetization (${\mu }_B$), polarization (P), and intragaps within the valence band ($\Delta g$) of the copper clusters ($C{u}_N,N$ = 3–5) for $U=$ 0, 5, and 8 eV.

	Cu${}_6$ (L)	Cu${}_{\mathbf{6}}$ (M)	Cu${}_{\mathbf{6}}$ (N)	Cu${}_{\mathbf{6}}$ (O)	Cu${}_{\mathbf{6}}$ (P)	Cu${}_{\mathbf{6}}$ (R)
${\mu }_B$ (a.u.), $U=0$	0.00	0.00	0.00	0.00	2.12	1.42
${\mu }_B$ (a.u.), $U=5$	0.00	0.00	0.00	0.00	2.21	1.91
${\mu }_B$ (a.u.), $U=8$	0.00	0.00	0.00	0.00	2.21	1.95
	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.351	(1) = 0.228
	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.351	(2) = 0.235
P (a.u.), $U=0$	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.351	(3) = 0.239
	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.351	(4) = 0.239
	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.351	(5) = 0.235
	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.351	(6) = 0.228
	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.365	(1) = 0.304
	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.365	(2) = 0.321
P (a.u.), $U=5$	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.365	(3) = 0.320
	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.365	(4) = 0.320
	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.365	(5) = 0.321
	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.365	(6) = 0.304
	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.000	(1) = 0.365	(1) = 0.308
	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.000	(2) = 0.365	(2) = 0.330
P (a.u.), $U=8$	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.000	(3) = 0.365	(3) = 0.326
	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.000	(4) = 0.365	(4) = 0.326
	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.000	(5) = 0.365	(5) = 0.330
	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.000	(6) = 0.365	(6) = 0.308
$\Delta g$ (eV), $U=0$	0.00	0.00	0.00	0.60	0.00	0.00
$\Delta g$ (eV), $U=5$	1.20	0.60	0.60	1.00	1.10	0.50
$\Delta g$ (eV), $U=8$	0.90	1.40	1.60	0.70	2.20	0.70

Figure 5. Density of States (DOS) for Cu${}_N$ copper clusters. $U=5$ eV was used. The Fermi energy was placed at 0 eV and corresponds to the dotted vertical line.

On the other hand, regardless of the value of U, we found the following property for the isomers in our study: the binding energies increase with the cluster size. The ground state of the Cu${}_3$ and Cu${}_6$ isomers exhibit a $D_{3h}$ symmetry, whereas the GS for the Cu${}_4$ and Cu${}_5$ structures exhibit $D_{2h}$ and $C_{2v}$ symmetries, respectively. The Cu${}_3$ and Cu${}_5$ copper clusters exhibit a magnetization close to 1 a.u. due to the polarization of their atoms (see Table 7). Isomers with an even number of atoms exhibit no magnetization, but there is an interesting exception for the Cu${}_6$(P) and Cu${}_6$(R) isomers, which exhibit a magnetization of around 2 a.u., also due to the polarization of their atoms (see Table 9). In Figure 5, it can be seen that the isomers with magnetization do not exhibit a symmetric DOS around the Fermi level where the $3p$ and $4s$ orbitals of the copper atoms predominate.

4. Conclusions

We have carried out a study on the stability of small copper clusters (Cu${}_N$, N = 3–6 atoms) using DFT and have found that the GGA approximation alone is insufficient to predict the stability of these structures or the correct ordering of the binding energies of these isomers. The Hubbard U correction is absolutely necessary to predict the stability and correct ordering in the binding energies of small copper clusters. Based on our results, we think that this correction should always be taken into account in any study involving copper atoms. We recommend working with a value of U between 5 and 8 eV. We have also found that atomic relaxations alone are insufficient to determine the stability of clusters. Atomic relaxations based on hybrid functionals such as the HSE could rule out some structures, but they are insufficient since the isomers obtained after the relaxations could be associated with energy saddle points. To determine whether the isomers obtained with atomic relaxations are stable, it is necessary to build the energy landscape, as done for Cu${}_3$ in this study, or perform additional calculations. For this, we recommend calculating the frequencies of the phonons. On the other hand, the vibrational frequencies of small copper clusters are of the order of THz (0 to 10 THz), and the normal modes of vibration are discrete.