Next Article in Journal
Effect of the Spatially-Varied Electron Mean Free Path on Vortex Matter in a Superconducting Pb Island Grown on Si (111)
Previous Article in Journal
Hubbard Bands and Exotic States in Doped and Undoped Mott Systems: The Kotliar–Ruckenstein Representation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Condensed Matter
Volume 8
Issue 3
10.3390/condmat8030076
condensedmatter-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ab Initio Study of Structural, Electronic, and Thermal Properties of Pt/Pd-Based Alloys

by
Louise Magdalene Botha
1,*,
Cecil Naphtaly Moro Ouma
1,
Kingsley Onyebuchi Obodo
1,
Dmitri Georgievich Bessarabov
1,*,
Denis Lvovich Sharypin
2,
Pyotr Sergeevich Varyushin
2 and
Elizaveta Ivanovna Plastinina
2
1
HySA-Infrastructure, Faculty of Engineering, North-West University, Private Bag X6001, Potchefstroom 2520, South Africa
2
PJSC MMC Norilsk Nickel, 15, 1st Krasnogvardeysky Drive, 123100 Moscow, Russia
*
Authors to whom correspondence should be addressed.
Condens. Matter 2023, 8(3), 76; https://doi.org/10.3390/condmat8030076
Submission received: 23 June 2023 / Revised: 28 July 2023 / Accepted: 29 August 2023 / Published: 5 September 2023
Browse Figures
Review Reports Versions Notes

Abstract

:
Alloys are beneficial in numerous applications since they combine the desirable properties of different metals. In this regard, Pt/Pd alloys have been investigated as a replacement for Pt, which is the standard catalyst used in various catalytic processes. However, there are still gaps in our understanding of the structural, mechanical, and thermodynamic properties of Pt/Pd alloys. This study was conducted using density functional theory (DFT) calculations to investigate the electronic, elasticity, mechanical, and thermodynamic properties of Pt/Pd alloys and compared them to pristine Pt and Pd structures. The results indicate that the considered Pt/Pd alloy structures, PtPd3, PtPd, Pt3Pd, and Pt7Pd, are energetically favourable based on their formation energies. These structures also satisfy Born’s stability criteria and are elastically stable. The phonon density of states showed that the considered Pt/Pd alloy structures are dynamically stable, with no imaginary modes present. Additionally, the Pt atom dominates at lower frequencies, while the Pd atom dominates at higher frequencies, as seen in the phonon band structure. The electronic density of states revealed that the considered Pt/Pd alloy structures have a metallic character and are non-magnetic. These findings contribute to a better understanding of the properties and stability of Pt/Pd alloy structures that are relevant in various fields, including materials science and catalysis.

1. Introduction

In response to critical concerns, such as climate change, energy security, and decreasing dependency on fossil fuels, efforts have aimed towards the development of clean energy solutions/technologies that are sustainable and environmentally friendly [1,2]. PGMs (Platinum Group Metals) play a crucial role in several of these technologies, including fuel cells, which are highly efficient and environmentally friendly energy sources, among other clean energy applications, such as water electrolysis and hydrogen storage [3,4]. PGMs, which include Pt (platinum), Pd (palladium), Rh (rhodium), Ru (ruthenium), Os (osmium), and Ir (iridium), have unique properties, such as high melting point, resistance to corrosion, and excellent catalytic activity, which make them indispensable in many fields of industrial applications, particularly in catalysis, due to their outstanding physical and chemical properties [5]. Some of these applications include the catalytic combustion of methane [6,7], recombination catalysts for safety devices [8], oxidation reactions for catalytic converters in automobiles [9], and medical devices [10].
Although Pt is the standard catalyst in many catalytic reactions, other PGMs and PGM alloys have also proven useful in this regard [11,12]. Alloying Pt with other PGMs and non-PGMs has been considered [13,14,15,16,17]. For example, Pt/Pd alloys have been used in H2/O2 recombination reactions and have been found to provide enhanced catalytic activity, increased corrosion resistance, and improved mechanical strength [18]. Furthermore, Pt/Pd catalysts are used in numerous applications such as aromatic hydrogenation [7], methane combustion [6], NO oxidation over alumina support [19], and diesel oxidation catalysts (DOC) [20]. Due to the resistance of the alloy to poisons, catalyst deactivation, and wettability, Pt/Pd alloys are of particular interest as a potential recombination catalyst for nuclear safety [8,18,21,22,23]. Expanding the use of these catalysts for other applications requires a thorough understanding of their structural, mechanical, and thermodynamic properties.
Understanding the electronic, mechanical, and thermodynamic properties of alloys is crucial for the rational design of new catalysts. These properties provide a fundamental understanding of the stability, behaviour, and properties of materials under different conditions and enable accurate predictions of stable alloys. In manufacturing, the mechanical properties of materials, such as strength, ductility, hardness, toughness, elasticity, fatigue, and creep, are essential [24]. Of these, the elasticity of materials is particularly important, as it deals with the elastic stresses and strains, their relationship, and the external forces that cause them [25]. Therefore, predicting and controlling the mechanical properties of materials is crucial for creating structures that can withstand stresses and strains [26,27,28].
Although Pt/Pd alloys have been studied before [29], there are still gaps in understanding their thermodynamic properties. Therefore, the current study is necessary. Using density functional theory (DFT) calculations, the elastic, thermodynamic, electronic, and magnetic properties of Pt/Pd alloy structures were evaluated. The pristine Pt and Pd structures, as well as the Pt/Pd alloy structures, were found to be elastically and thermodynamically stable. It was observed that the percentage of Pt in the Pt/Pd alloy structures influenced the bulk modulus. As such, a higher bulk modulus and consequently increasing compression resistance, was observed in the Pt/Pd alloys, which consisted of higher Pt content. This paper is structured as follows: Section 2 presents the results and discussions, followed by a detailed description of the computational methodologies in Section 3. Finally, the conclusions are presented in Section 4.

2. Results and Discussion

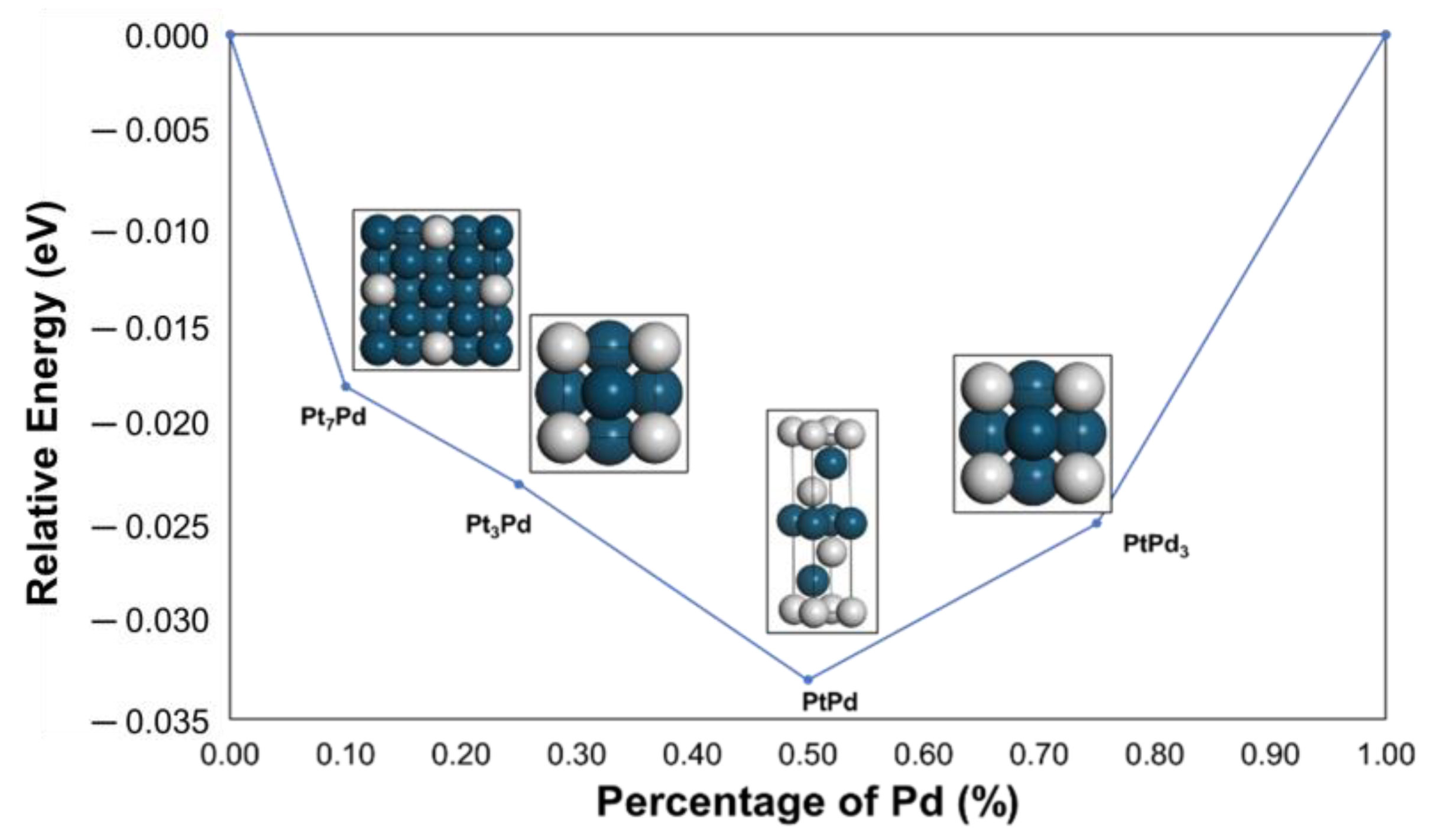
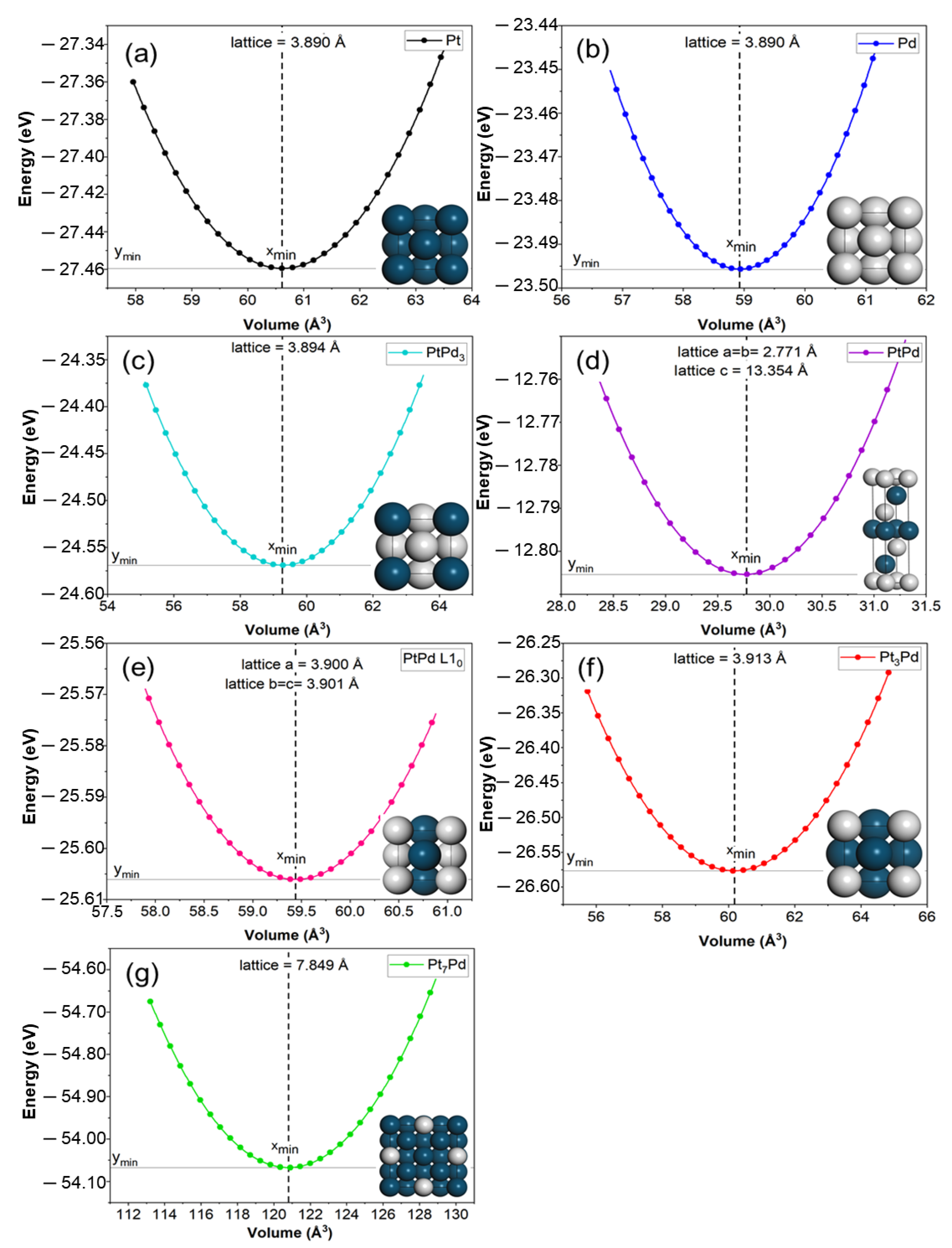
2.1. Structural Stability

The initial pristine Pt and Pd structures, as well as the Pt/Pd alloy structures, are depicted using the convex hull in Figure 1. The Pt3Pd and PtPd3 alloys are cubic structures with the 221 space group (Pm 3 ¯ m). The Pt7Pd alloy structure is also cubic with the 225 space group (Fm 3 ¯ m). However, the PtPd alloy structure is trigonal with the 166 space group (R 3 ¯ m). The equilibrium volume data, along with the space groups and unit cell parameters, can be found in the supplementary information (Table S1).
The respective equilibrium lattice constants for conventional cells, for the pristine Pt and Pd, as well as the alloy structures, as shown in Figure 2, were obtained by fitting the total energy versus volume to the Murnaghan equation of state [30]. Figure 2 illustrates the equilibrium volumes obtained for the pristine Pt and Pd structures, as well as the Pt/Pd alloy structures. The equilibrium volumes are as follows: 59 Å3 for pristine Pt and Pd, 59–60 Å3 for PtPd3 and Pt3Pd, 89 Å3 for PtPd, and 483 Å3 for Pt7Pd. The equilibrium volumes are consistent with the space groups and crystal structures considered as illustrated in the supplementary information (Figure S1). The equilibrium lattice constants were 3.93 Å (Pt), 3.89 Å (Pd), 3.90 Å (PtPd3), 2.771 Å (PtPd), 3.92 Å (PdPt3), and 7.849 Å (Pt7Pd), respectively. As shown in Table 1, the calculated lattice constants were consistent with those obtained in previous studies [31].
Previous experimental studies reported the existence of a PtPd alloy configuration [32,33,34]. In 1959, Raub et al., reported that the PtPd alloy can exist as a cubic structure with lattice constants of 3.90 Å, an observation that was also made by Darby et al. in 1972, who also reported that the cubic structure with lattice constant of 3.903 Å. In 2011, a computational study by Zhiyao et al. [35] reported that the cubic structure of PtPd belongs to the L10 phase with computed lattice constants of a = b = 3.964 Å and c = 3.966 Å. In the current study, the stable alloy configurations were predicted using the convex hull approach, which showed the existence of stable alloy configuration of PtPd in the hexagonal rhombohedral phase, characterised by the R3M space group with lattice constants of a = b = 2.771 Å and c = 13.354 Å.
Taking into account previous studies, the present study further investigated the possibility of the reported experimental structures. Using the structure observed by Raub et al. [33], the equilibrium lattice constant calculated using DFT is found to be a = 3.900 Å and b = c = 3.901 Å, which is consistent with the L10 phase reported by Zhiyao et al. [35] Upon the calculation of the formation energies, the formation energy of the L10 phase was −0.128 eV while that of the predicted hexagonal rhombohedral was −0.050 eV, indicating ease of formation of the latter rather than the former. Phonon calculations also indicated that this configuration was stable in both the L10 and hexagonal rhombohedral phases.
The lattice constants of alloys obey either Vegard’s law or Retger’s law, but cannot simultaneously satisfy both laws [36]. Vegard’s law states that the lattice parameters of a continuous substitutional solid solution vary linearly with concentration at constant temperature when the bonding nature is similar in the constituent phases. On the other hand, Retger’s law states that the mole fraction and cell volume of an alloy have a linear variation with each other. Consequently, alloys with higher mole fractions exhibit higher cell volumes [36].
In this study, the lattice constants of the Pt3Pd and PtPd3 alloy structures were found to deviate linearly from those of pristine Pt and Pd, thus adhering to Vegard’s law. However, it is important to note that Vegard’s law is an approximation, and binary alloys can deviate significantly from it in certain cases [37,38,39,40,41]. The Pt3Pd and PtPd3 alloy structures exhibit mole fractions and cell volume (14 atoms and volumes of 59–60 Å3) similar to the pristine Pt and Pd structures.
In contrast, the Pt7Pd and PtPd alloy structures, with different mole fractions and cell volumes, in contrast to the pristine Pt and Pd structures, follow Retger’s law. The Pt7Pd alloy has a mole fraction of 63 atoms and a cell volume of 483 Å3, while the PtPd alloy has a mole fraction of 16 atoms and a cell volume of 89 Å3.
Therefore, the differences in lattice constants and volumes observed in the Pt/Pd alloy structures are a consequence of the varying mole fraction. This indicates that the configuration of Pt/Pd alloys can be properly described by the convex hull method, taking into account the composition-dependent changes in lattice parameters and volume.
The formation energy (Ef) of the respective pristine Pt and Pd, as well as the Pt/Pd alloy structures, was calculated using Equation (1) [42].
E f PtPd = E tot PtPd − N × E Pt bulk − N × E Pd bulk
where E tot PtPd denotes the total energy of Pt/Pd alloy structures; E Pt bulk and E Pd bulk denote the total energies of bulk Pt and Pd, respectively; and N denotes the number of atoms of each species (Pt and Pd atoms) in the alloy structure. Formation energy determines the change in energy when an alloy structure is created from its constituent elements. Thus, the negative formation energies imply that the Pt/Pd alloy structures are energetically stable and likely to form spontaneously. The calculated formation energies for the alloy structures are also consistent with previous studies [43], as shown in Table 1. All calculated formation energies as shown in Table 1 were negative, indicating that the formation of Pt/Pd alloy structures from their constituent elements is favourable. As such, the Pt/Pd alloy structures are energetically stable. Note that the PtPd in the hexagonal rhombohedral phase and L10 phase are both energetically stable, with the latter being energetically more stable. However, both phases of PtPd have been used for further evaluation. In the next section, the elastic, phonon, and thermodynamic stability of these alloy structures are presented.
Table 1. Calculated equilibrium lattice constants for the conventional cells, in angstroms (Å), Volume in cubic angstroms (Å3), space groups, and formation energies of pristine Pt and Pd, as well as the Pt/Pd alloy structures in electron volt per formula unit (f.u).
Table 1. Calculated equilibrium lattice constants for the conventional cells, in angstroms (Å), Volume in cubic angstroms (Å3), space groups, and formation energies of pristine Pt and Pd, as well as the Pt/Pd alloy structures in electron volt per formula unit (f.u).
Unit Cell ParametersUnit Cell AnglesEquilibrium VolumeSpace GroupFormation Energy
(Å)(°)(Å3)(no)(eV/f.u)
abcαβγ
Pd3.8903.893.89090909058.86225
Pd ref3.89 a,b3.8903.89
PtPd33.8903.8903.89090909058.86221−0.023
PtPd3 ref3.88 c3.883.88909090
PtPd2.7712.77113.354909012088.80166−0.050
PtPd (L10)3.900 d3.901 d3.901 d90 d90 d90 d59.36123−0.128
Pt3Pd3.9203.9203.92090909060.24221−0.025
Pt3Pd ref3.91c3.913.91909090
Pt7Pd7.7897.7897.789909090483.53225−0.018
Pt3.9303.9303.93090909060.70225
Pt ref3.92 b,c3.923.92
Ptref, Pdref etc. refers to referenced papers. a Ref. [29], b Ref. [32], c Ref. [43], d Refs. [32,33,35].

2.2. Elastic, Phonon, and Thermodynamic Properties

The detailed mathematical equations and a comprehensive description of how to determine the bulk modulus (B), shear modulus (G), Young modulus (E), and Poisson’s ratio (v) from the elastic constants (Cij) can be found in the supplementary section.

2.2.1. Elastic Properties

Mechanical stability can be explored through the determination of elastic constants. The symmetry of the structure determines the elastic constants (Cij) needed to evaluate the mechanical properties. The elastic stability (at zero pressure) of the pristine Pt and Pd structures, as well as the alloys considered, was determined using the stress-strain method. The computed elastic constants are given in Table 2. The born stability criteria [44] for cubic (2) and trigonal (3) systems are as follows:
C11 − C12 > 0; C11 + 2C12 > 0; C44 > 0
C11 − C12 > 0; C132 < 0.5 × C33(C11 + C12); C142 < 0.5 × C44(C11 − C12); C44 > 0
Based on the cubic symmetry of the Pt, Pd, Pt3Pd, PtPd3, and Pt7Pd structures, three independent elastic constants (C11, C12, and C44) are required to analyse the mechanical behaviour of these alloy structures. Furthermore, the alloy structure of PtPd, which is trigonal, requires six independent elastic constants (C11, C12, C14, C33, and C44). The considered structures satisfied Born’s stability criteria as presented in Equations (2) and (3). Therefore, they are elastically stable.
Several elastic constants are related to the modulus of elasticity, depending on the applied strain direction, such as lateral, axial, torsional, and compression [24]. The bulk modulus of pristine Pt and Pd, and the considered Pt/Pd alloy structures determine their compression resistance, which is calculated using Murnaghan’s equation of state [30]. The values of the bulk modulus (B) and the shear modulus (G) represent the extreme limits of the elastic moduli [45] and are expressed differently depending on the crystal symmetry [46]. B is a measure of the resistance of a material to compression, while G is related to the applied shear strain or rigidity [47]. In Table 2, B and G are calculated from the elastic constants are shown. The calculated B for the pristine Pt and Pd, as well as the considered Pt/Pd alloy structures, are consistent with published values [31,48,49]. As shown in Table 2, the value of B increases with increasing Pt content in the alloy. The high values of B and G indicate that the pristine Pt and Pd, as well as the considered Pt/Pd alloys, are resistant to compression and shear deformation.
The Young modulus (E) is an important mechanical property of materials that refers to the behaviour of the material towards bending/twisting deformation (stiffness), whereas the Poisson’s ratio (v) relates to the absolute ratio of the lateral strain (stretching and compression) in response to longitudinal strain [24]. Therefore, stiffer materials are thus associated with high E values in the range of 150–550 GPa [24]. The E values, presented in Table 2, indicate that the pristine Pt and Pd, as well as the Pt/Pd alloys considered, are all high and therefore will resist deformation at low-stress loads. The calculated v ratios obtained for the pristine Pt and Pd, and the considered Pt/Pd alloy structures are in the range of 0.30–0.44 GPa [50,51], indicating that these considered structures are prone to some measure of lateral deformation when under compression. A v ratio of < 0.33 GPa implies that the system is metallic [52]. Therefore, from the ratios presented in Table 2, the pristine Pt and Pd, as well as the Pt/Pd alloy structures considered are metallic. Therefore, it is evident that the considered Pt/Pd alloy structures have a high resistance to compression and deformation while also exhibiting elasticity.
Table 2. The elastic constants (Cij), bulk modulus (B), shear modulus (G), Young modulus (E), and Poisson (v) for pristine Pt and Pd, as well as the Pt/Pd alloy structures. The table shows the minimum and maximum values for G, E and v.
Table 2. The elastic constants (Cij), bulk modulus (B), shear modulus (G), Young modulus (E), and Poisson (v) for pristine Pt and Pd, as well as the Pt/Pd alloy structures. The table shows the minimum and maximum values for G, E and v.
PhaseC11
GPa		C12
GPa		C13
GPa		C14
GPa		C33
GPa		C44
GPa		B
GPa		G
GPa		E
GPa		Ν
GPa
Pt327.76253.50 82.1927846–82107–2240.37–0.44
Pt ref 299 a, 238 b
250 c, 262 d		46–54 e132–164 e0.48–0.51 e
Pd232.90173.56 91.0619338–9185–2360.30–0.43
Pd ref 221 a 172 b 181 d
PtPd3256.55183.97 86.6721647–90107–2370.32–0.42
PtPd335.21190.62191.146.58323.8772.30227–24970–78189–2110.36–0.37
253 a
Pt3Pd327.20215.01 91.7221745–72108–1930.35–0.42
Pt7Pd372.38210.00 73.7626474–81202–2210.36–0.37
Ptref, Pdref etc refers to referenced papers. a Ref. [29], b Ref. [48], c Ref. [49], d Ref. [43], e Ref. [5].

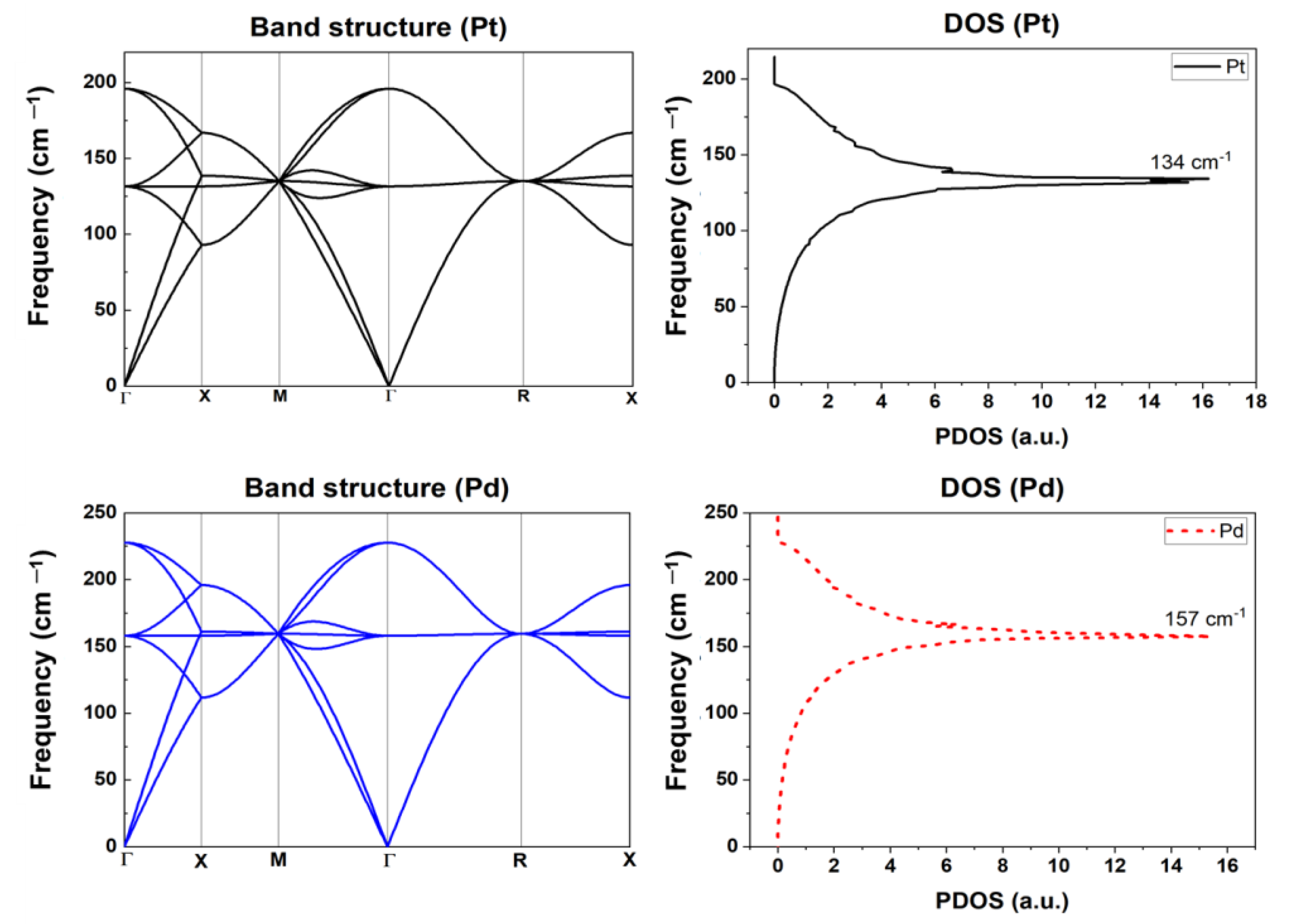
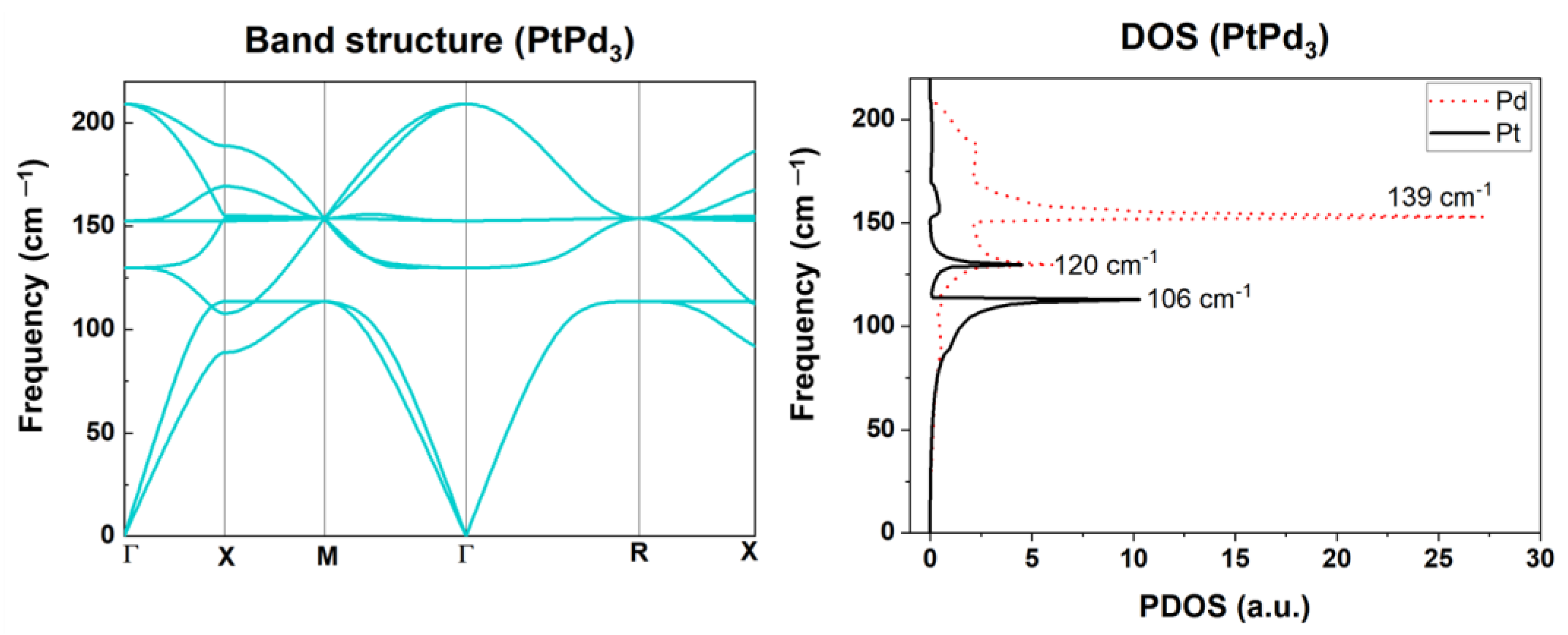
2.2.2. Phonon Properties

The calculated phonon band structures and DOS plotted along the high symmetry points of the respective Brillouin zones are shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. No imaginary modes (negative frequencies) were observed in the Pt/Pd alloy structures. Therefore, the P m 3 ¯ m (Pt3Pd, PtPd3), F m 3 ¯ m (Pt7Pd), and R 3 ¯ m (PtPd) phases of the considered Pt/Pd alloy structures are dynamically stable.
The dynamic stability of the alloys was further assessed by examining their pair distribution function (PDF) for a determined temperature range [53]. PDF is used as a descriptor of dynamic stability since it describes the short-range order between atoms in different materials [54]. In this study, molecular dynamics (MD) simulations were conducted to determine the PDF for both pristine Pt and Pd structures, as well as for Pt/Pd alloy structures, within a temperature range of 100 K to 2100 K. For dynamic stability structures, a decrease in temperature causes the pair correlation function to become more structured, reflecting the ordering of atoms in the crystalline lattice. For detailed information and results, refer to Figure S3 in the Supplementary Information. These results indicate a high degree of dynamical stability in the pristine Pt and Pd, as well as the Pt/Pd alloy structures, exhibit a high degree of dynamic stability and maintain their integrity as the temperature increases.
The phonon DOS for the pristine Pt and Pd, as shown in Figure 3, indicates peaks of the frequency spectrum at 134 cm−1 and 157 cm−1 respectively.
Figure 4 and Figure 5 show the calculated phonon band structures and DOS for the Pt3Pd, PtPd, and PtPd3 alloy structures. The DOS indicates that the Pt atom is dominant at lower frequencies (between the ranges of 113–134 cm−1) for the PtPd3 (Figure 4) and Pt3Pd (Figure 5) alloy structures, whereas the Pd atom is dominant at higher frequencies with peaks at 153 cm−1 for PtPd3, and 163 cm−1 for Pt3Pd alloys. Additional peaks were observed at 113 cm−1 (PtPd3), 119 cm−1 (Pt3Pd), 130 cm−1 (PtPd3), and 134 cm−1 (Pt3Pd).
Figure 6 shows the PtPd structures with an equal number of Pd and Pt atoms. In the hexagonal rhombohedral phase, the Pt and Pd atoms were observed to be dominant at lower frequencies (30–66 cm−1) and higher frequencies (84–110 cm−1 and 171–200 cm−1), respectively. Furthermore, several other peaks for the Pt and Pd atoms were observed in the DOS profile at 63 cm−1 (Pt), 87 cm−1(Pd), 126 cm−1 (Pt), and 173 cm−1 (Pd). On the other hand, in the L10 phase the Pd atoms were observed to be dominant at lower frequencies (76–121 cm−1) and Pt at higher frequencies (141–217 cm−1).
In Figure 7, the dominant frequency contribution is from the Pt atoms. This is due to the higher Pt content in the alloy, while the Pd frequency peak is observed around 176 cm−1.
Overall, the Pt and Pd frequency modes play a role in the dynamical stability of the considered Pt/Pd alloys. This observation is consistent with previous studies in which the mass of the elements determines the position of the phonon frequencies [55,56].

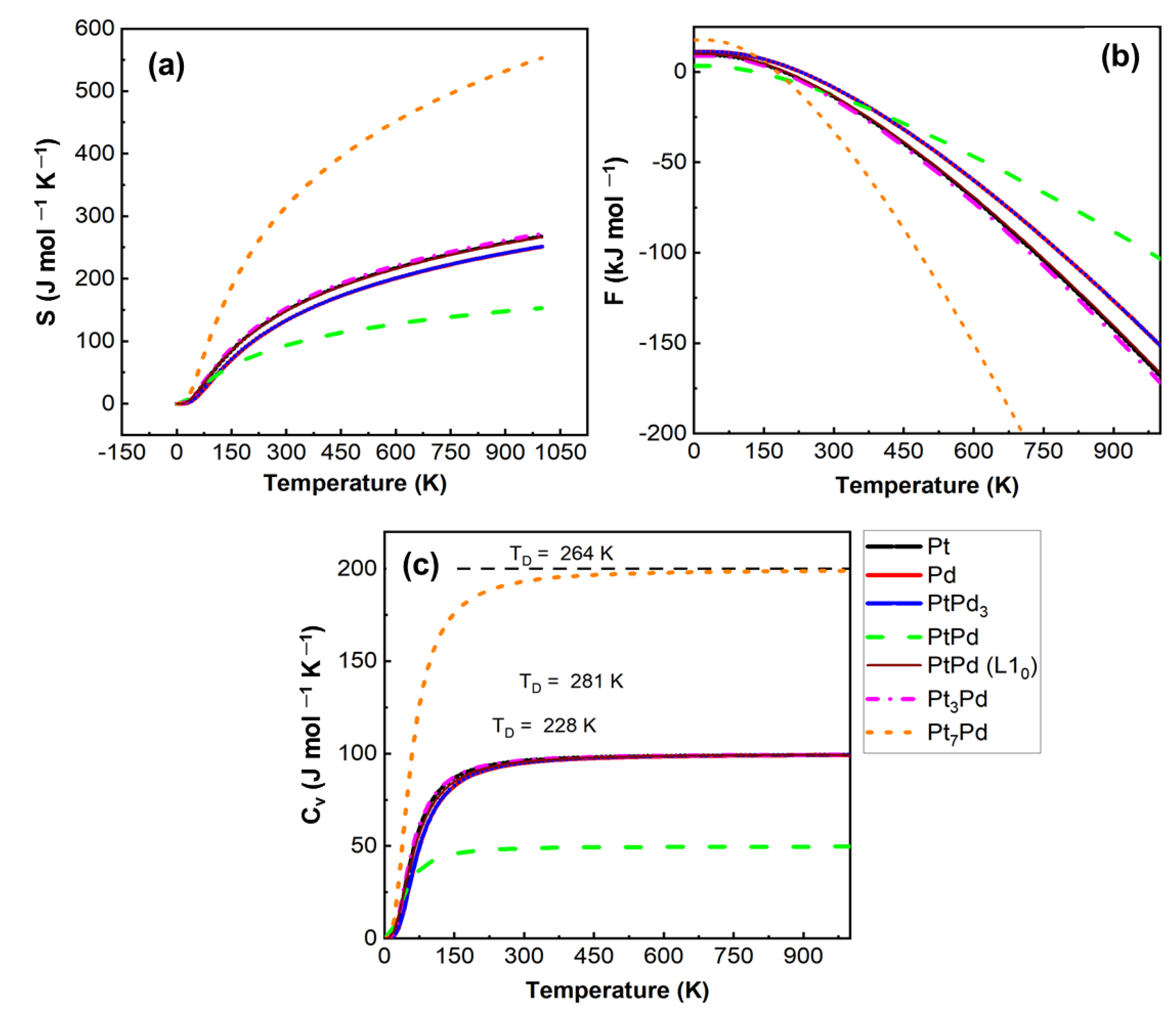
2.2.3. Thermodynamic Properties

A detailed mathematical equation and a comprehensive description of the thermodynamic properties are available in the Supplementary Information. The impact of temperature on alloy properties, such as crystal structure and thermal properties, is important [57,58,59]. Thus, the thermal properties were calculated in this study from the phonons. The relationship between temperature and Helmholtz free energy (F), entropy (S), and constant-volume specific heat (Cv) is shown in Figure 8. The relationship between these properties is given in Equations (4)–(6), respectively, for Helmholtz free energy (4), entropy (4) and constant-volume specific heat (5) [60]. In these equations, the Helmholtz free energy is related to entropy and temperature (4), whereas constant-volume specific heat is expressed in terms of the second derivative of Helmholtz free energy with respect to temperature at a constant volume (6) [60].
F = U − T S
C v = d U d T v
C v = − T   d 2 F d T 2
Entropy is an important thermodynamic property that affects a metal’s heat transfer and energy exchange. In Figure 8a, the calculated entropies for pristine Pt and Pt3Pd alloys are approximately similar in the considered temperature range, which indicates similar ordering of the structures. A similar observation was made in the case of pristine Pd and PtPd3 alloy structures. In comparison to the pristine Pt and Pd structures, the entropy of the Pt7Pd alloy increases rapidly at a temperature range of 0 to 300 K, while it increases slowly in the case of PtPd alloy in the same temperature range. The overall entropy for the considered structures is the highest for the Pt7Pd alloy structure and lowest for the PtPd alloy structure. Low entropy values indicate ordered structures, which allows for better thermal conductivity and reduces the likelihood of thermal expansion and deformation. Therefore, in comparison with the pristine Pt and Pd structures, the PtPd alloy will possess better thermal conductivity and reduced thermal expansion.
In Figure 8b, the calculated Helmholtz free energy shows an inverse relationship with the entropy, as shown in Figure 8a. The calculated constant-volume specific heat (Cv) increases exponentially as a function of temperature up to ~250 K and then flattens out (see Figure 8c) as it approaches the Dulong–Petit asymptote. The Cv at this asymptote is 200 J/mol K for Pt7Pd; 100 J/mol K for Pt3Pd, PtPd3, Pt; and Pd, and 50 J/mol K for PtPd. The Debye temperatures calculated from elastic constants were 301 K (Pd), 281 (PtPd3), 280 K (PtPd), 270 K (Pt3Pd), 264 K (Pt7Pd) and 228 K (Pt). We found that the Debye temperature decreased with increasing Pt content, similar to the observation of Tang et al. [43].
Overall, the pristine Pt and Pd structures, as well as the Pt/Pd alloy structures, exhibited similar trends for the investigated thermodynamic properties. Specifically, an increase in temperature resulted in an increase in entropy, a decrease in free energy, and an increase in the specific heat capacity for all structures considered. Although the trends are the same for all structures investigated, the thermodynamic properties vary. The entropy, Helmholtz free energy, and specific heat capacity of the Pt3Pd alloy structure is similar to those of the pristine Pt structure, whereas those of the PtPd3 alloy structure are similar to those of the pristine Pd structure.

2.3. Electronic Properties

The projected density of states (PDOS) for the d-electrons of the pristine Pt and Pd metals, as well as the Pt/Pd alloy structures, is shown in Figure 9. The calculated electronic structures indicate that the pristine Pt and Pd, as well as the Pt/Pd alloy structures, are metallic due to the absence of an electronic band gap at the Fermi level (EF = 0). There is an equal number of electrons in the up (majority) and down (minority) spin channels within the full d orbitals. As such the pristine Pt is non-magnetic with a symmetric PDOS, which is in agreement with previous work [61]. For the pristine Pd structure, a slight asymmetry is observed in the PDOS close to the Fermi level, which indicates a paramagnetic ground state. The atomic spin moment (μB atom−1) obtained from Bader analysis for the pristine Pd is 0.28. The Pt/Pd alloy structures considered in this study are non-magnetic, like pristine Pt.
The calculated atomic charges indicate that the Pt and Pd atoms were found to be charge-neutral, as shown in Table 3. In the case of the considered Pt/Pd alloys, the Pd atoms were negatively charged, while the Pt atoms were positively charged, resulting in a net charge of zero.

3. Computational Method

The pristine Pt and Pd as well as Pt/Pd alloy structures were investigated using spin-polarised density functional theory calculations (DFT) as implemented in the Vienna Ab Initio Simulation Package (VASP) code [62,63,64]. The generalised-gradient approximation (GGA) functional developed by Perdew, Burke, and Ernzernhof (PBE) [65] was applied. The interaction between core and valence electrons for Pd and Pt was described using the projected augmented-wave (PAW) method [66,67].
The structural optimisation was carried out using a kinetic energy cut-off fixed at 500 eV for the plane-wave basis set expansion of the Kohn–Sham (KS) valence states with an electronic convergence set at 10−6 eV. The Methfessel−Paxton approach was used with a smearing width of 0.2 eV. The alloy configurations (Pt3Pd, PtPd3, Pt7Pd, and PtPd) were obtained from the open quantum materials database (OQMD) [68]. The alloy structures of Pt3Pd, PtPd, PtPd3, and Pt7Pd with FCC and trigonal crystal structures were used, while the structure of the L10 phase of the alloy configuration of PtPd was obtained from the experimental work of Raub et al. [33] The Brillouin zones were sampled using Γ-centred Monkhorst-Pack grid [69] with a spacing width of 0.03 Å. Phonon frequencies were evaluated using PHONOPY [70]. A finite displacement amplitude of 0.01 Å was used, along with a Monkhorst sampling width of 0.04 Å for the phonon density of state calculations. The Monkhorst sampling width was set to 0.02 Å for the density of states (DOS) calculations, along with Blöchl corrections.
In this study, the equilibrium properties were estimated for each of the alloy configurations using Murnaghan’s equation of state. The bulk modulus, shear modulus, Young modulus, Poisson’s ratio, and elastic constants (stress-strain method) of these alloys were evaluated as implemented in the VASPKIT module [71]. Additionally, the thermodynamic properties were extracted from phonon calculations. For repeatability, the atomic coordinates and computational parameters utilised in this study have been included in the supplementary information.

4. Conclusions

This study has provided insights into the structural, elastic, mechanical, and thermal properties of pristine Pt and Pd, as well as various Pt/Pd alloy structures. The study found that pristine Pt and Pd, as well as the considered PtPd3, PtPd, Pt3Pd, and Pt7Pd alloy structures, are energetically stable and mechanically stable. The PtPd3, PtPd, Pt3Pd, and Pt7Pd alloy structures are energetically stable due to their negative formation energies of −0.023 eV, −0.033 eV, −0.025 eV, and −0.018 eV, respectively. Furthermore, the Pt/Pd alloy structures are mechanically stable, as they satisfy Born’s stability criteria. The phonon calculations indicate that the considered structures are dynamically stable due to the absence of imaginary modes. Moreover, the phonon DOS for the considered Pt/Pd alloy structures indicated that the Pt atom is the dominant contributor at low-frequency modes in the range of 80–133 cm−1, while the Pd atom is the dominant contributor at high-frequency modes at frequencies above 140 cm−1. The entropy, Helmholtz free energy, and constant-volume specific heat capacities were found to be similar to the considered temperature for both the pristine Pt and Pt3Pd alloy structures, as well as for the Pd and PtPd3 alloy structures. Additionally, the Debye temperature was found to decrease with increasing Pt content, hence the considered Pt/Pd alloy structures were found to be ordered thermodynamically stable structures. The considered Pt/Pd alloy structures were also found to exhibit metallic characteristics and to be non-magnetic. Overall, these findings contribute to a better understanding of the properties and stability of Pt/Pd alloy structures, which are relevant in various fields, including materials science and catalysis.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/condmat8030076/s1, Figure S1: Volume calculation for cubic Pt/Pd alloy structures, where α = β = γ = 90°. Figure S2: Volume calculation for non-cubic Pt/Pd alloy structure where α= β = γ≠ 90°. Figure S3: Temperature behaviour of the pair distribution function for the Pt-Pd bond distances, obtained from molecular dynamics (MD) simulations conducted over the range of 100 K to 2100 K. The plots represent the pristine structures of (a) Pt, (b) Pd, as well as the alloy structures for (c) PtPd3, (d) PtPd, (e) Pt3Pd and (f) Pt7Pd. Table S1: Atomic coordinates of the Pt/Pd alloy structures, as implemented in VASP. Table S2: INCAR file for Geometric optimisation of bulks. Table S3: INCAR file for density of States and work function calculations. Table S4: INCAR file for determining elastic constants. Table S5: Input file (VPKIT.in) for determining elastic constants. Table S6: CONTCAR file for Phonopy displacement 001 (PtPd3). Table S7: CONTCAR file for Phonopy displacement 002 (PtPd3). Table S8: INCAR file for Phonopy calculation of sets of forces. Table S9: mesh.conf file for Phonopy optimisation. Table S10: pdos.conf file for Phonopy optimisation. Table S11: Band.conf file for Phonopy. Table S12: INCAR file for MD simulations with changing temperature. Table S13: KPOINT file for MD simulations. The following citations was used in the supplementary section, Mathematical equations for the description of elastic properties [72,73,74] and temperature properties [75,76].

Author Contributions

L.M.B.: Investigation, Validation, Data curation, Visualization, Writing—original draft. C.N.M.O.: Writing—review & editing. K.O.O.: Writing—review & editing. D.G.B.: Conceptualisation, Resources, Writing—review & editing, Supervision, Project administration, Funding acquisition. D.L.S.: Conceptualisation and proofing. P.S.V.: Conceptualisation and proofing. E.I.P.: Conceptualisation and proofing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Department of Science and Innovation (DSI) and the HySA Infrastructure Center of Competence at the North-West University (NWU), South Africa; and Norilsk Nickel Asia Ltd. (Hong Kong); are acknowledged for financial support through the KP5 program.

Data Availability Statement

The data presented in this study are available in the supplementary material.

Acknowledgments

The computational resources were provided by South Africa’s Centre for High-Performance Computing (CHPC).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Peake, S. Renewable Energy-Power for a Sustainable Future; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
  2. Elliott, D. Renewable energy and sustainable futures. Futures 2000, 32, 261–274. [Google Scholar] [CrossRef]
  3. Chi, J.; Yu, H. Water electrolysis based on renewable energy for hydrogen production. Chin. J. Catal. 2018, 39, 390–394. [Google Scholar] [CrossRef]
  4. Hirscher, M.; Yartys, V.A.; Baricco, M.; von Colbe, J.B.; Blanchard, D.; Bowman, R.C., Jr.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P.; et al. Materials for hydrogen-based energy storage–Past, recent progress and future outlook. J. Alloys Compd. 2020, 827, 153548. [Google Scholar] [CrossRef]
  5. Merker, J.; Lupton, D.; Topfer, M.; Knake, H. High temperature mechanical properties of the platinum group metals. Platin. Met. Rev. 2001, 45, 74–82. [Google Scholar]
  6. Abbasi, R.; Wu, L.; Wanke, S.; Hayes, R. Kinetics of methane combustion over Pt and Pt–Pd catalysts. Chem. Eng. Res. Des. 2012, 90, 1930–1942. [Google Scholar] [CrossRef]
  7. Pawelec, B.; Mariscal, R.; Navarro, R.; van Bokhorst, S.; Rojas, S.; Fierro, J. Hydrogenation of aromatics over supported Pt-Pd catalysts. Appl. Catal. A Gen. 2002, 225, 223–237. [Google Scholar] [CrossRef]
  8. Payot, F.; Reinecke, E.-A.; Morfin, F.; Sabroux, J.-C.; Meynet, N.; Bentaib, A.; March, P.; Zeyen, R. Understanding of the operation behaviour of a Passive Autocatalytic Recombiner (PAR) for hydrogen mitigation in realistic containment conditions during a severe Light Water nuclear Reactor (LWR) accident. Nucl. Eng. Des. 2012, 248, 178–196. [Google Scholar] [CrossRef]
  9. Screen, B.T. Platinum Group Metal Perovskite Catalysts. Platin. Met. Rev. 2007, 51, 87–92. [Google Scholar] [CrossRef]
  10. Cowley, A.; Woodward, B. A Healthy Future: Platinum in Medical Applications. Platin. Met. Rev. 2011, 55, 98–107. [Google Scholar] [CrossRef]
  11. Cherevko, S.; Geiger, S.; Kasian, O.; Kulyk, N.; Grote, J.-P.; Savan, A.; Shrestha, B.R.; Merzlikin, S.; Breitbach, B.; Ludwig, A.; et al. Oxygen and hydrogen evolution reactions on Ru, RuO2, Ir, and IrO2 thin film electrodes in acidic and alkaline electrolytes: A comparative study on activity and stability. Catal. Today 2016, 262, 170–180. [Google Scholar] [CrossRef]
  12. Obodo, K.O.; Ouma, C.N.M.; Bessarabov, D. Modified Pt (2 1 1) and (3 1 1) surfaces towards the dehydrogenation of methylcyclohexane to toluene: A density functional theory study. Appl. Surf. Sci. 2022, 584, 152590. [Google Scholar] [CrossRef]
  13. Duan, H.; Xu, C. Nanoporous PtPd Alloy Electrocatalysts with High Activity and Stability toward Oxygen Reduction Reaction. Electrochimica Acta 2015, 152, 417–424. [Google Scholar] [CrossRef]
  14. Briguglio, N.; Pantò, F.; Siracusano, S.; Aricò, A. Enhanced performance of a PtCo recombination catalyst for reducing the H2 concentration in the O2 stream of a PEM electrolysis cell in the presence of a thin membrane and a high differential pressure. Electrochimica Acta 2020, 344, 136153. [Google Scholar] [CrossRef]
  15. Du, L.; Prabhakaran, V.; Xie, X.; Park, S.; Wang, Y.; Shao, Y. Low-PGM and PGM-Free Catalysts for Proton Exchange Membrane Fuel Cells: Stability Challenges and Material Solutions. Adv. Mater. 2020, 33, 1908232. [Google Scholar] [CrossRef]
  16. Shao, Y.; Dodelet, J.; Wu, G.; Zelenay, P. PGM-Free Cathode Catalysts for PEM Fuel Cells: A Mini-Review on Stability Challenges. Adv. Mater. 2019, 31, e1807615. [Google Scholar] [CrossRef]
  17. Obodo, K.O.; Ouma, C.N.M.; Modisha, P.M.; Bessarabov, D. Density functional theory calculation of Ti3C2 MXene monolayer as catalytic support for platinum towards the dehydrogenation of methylcyclohexane. Appl. Surf. Sci. 2020, 529, 147186. [Google Scholar] [CrossRef]
  18. Lalik, E.; Kosydar, R.; Tokarz-Sobieraj, R.; Witko, M.; Szumełda, T.; Kołodziej, M.; Rojek, W.; Machej, T.; Bielańska, E.; Drelinkiewicz, A. Humidity induced deactivation of Al2O3 and SiO2 supported Pd, Pt, Pd-Pt catalysts in H2+O2 recombination reaction: The catalytic, microcalorimetric and DFT studies. Appl. Catal. A Gen. 2015, 501, 27–40. [Google Scholar] [CrossRef]
  19. Graham, G.W.; Jen, H.-W.; Ezekoye, O.; Kudla, R.J.; Chun, W.; Pan, X.Q.; McCabe, R.W. Effect of alloy composition on dispersion stability and catalytic activity for NO oxidation over alumina-supported Pt–Pd catalysts. Catal. Lett. 2007, 116, 1–8. [Google Scholar] [CrossRef]
  20. Morlang, A.; Neuhausen, U.; Klementiev, K.; Schütze, F.-W.; Miehe, G.; Fuess, H.; Lox, E. Bimetallic Pt/Pd diesel oxidation catalysts. Appl. Catal. B Environ. 2005, 60, 191–199. [Google Scholar] [CrossRef]
  21. Sanap, K.K.; Varma, S.; Waghmode, S.B.; Bharadwaj, S.R. Supported Pt nanoparticles for the hydrogen mitigation application. Int. J. Hydrogen Energy 2014, 39, 15142–15155. [Google Scholar] [CrossRef]
  22. Morfin, F.; Sabroux, J.-C.; Renouprez, A. Catalytic combustion of hydrogen for mitigating hydrogen risk in case of a severe accident in a nuclear power plant: Study of catalysts poisoning in a representative atmosphere. Appl. Catal. B Environ. 2004, 47, 47–58. [Google Scholar] [CrossRef]
  23. Li, Z.; Tian, B.; Zhen, W.; Wu, Y.; Lu, G. Inhibition of hydrogen and oxygen recombination using oxygen transfer reagent hemin chloride in Pt/TiO2 dispersion for photocatalytic hydrogen generation. Appl. Catal. B Environ. 2017, 203, 408–415. [Google Scholar] [CrossRef]
  24. Kalpakjian, S.; Schmid, S. Manufacturing, Engineering and Technology Si 6th Edition-Serope Kalpakjian and Stephen Schmid: Manufacturing, Engineering and Technology; Digital Designs: Oklahoma City, OK, USA, 2006. [Google Scholar]
  25. Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
  26. Mellor, B.G. Surface Coatings for Protection against Wear; Woodhead Publishing: Sawston, UK, 2006. [Google Scholar] [CrossRef]
  27. Hoornaert, T.; Hua, Z.K.; Zhang, J.H. Hard Wear-Resistant Coatings: A Review. In Advanced Tribology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 774–779. [Google Scholar] [CrossRef]
  28. Boyer, R.R.; Briggs, R.D. The Use of β Titanium Alloys in the Aerospace Industry. J. Mater. Eng. Perform. 2005, 14, 681–685. [Google Scholar] [CrossRef]
  29. Ahmed, S.; Zafar, M.; Shakil, M.; A Choudhary, M. Density functional theory study of structural, electronic, and thermal properties of Pt, Pd, Rh, Ir, Os and PtPd X (X = Ir, Os, and Rh) alloys. Chin. Phys. B 2016, 25, 036501. [Google Scholar] [CrossRef]
  30. Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
  31. Ou, L.; Chen, S. Comparative Study of Oxygen Reduction Reaction Mechanisms on the Pd(111) and Pt(111) Surfaces in Acid Medium by DFT. J. Phys. Chem. C 2013, 117, 1342–1349. [Google Scholar] [CrossRef]
  32. Darby, J.B.; Myles, K.M. A thermodynamic study of solid Pd-Pt alloys. Met. Trans. 1972, 3, 653–657. [Google Scholar] [CrossRef]
  33. Raub, E. Metals and alloys of the platinum group. J. Less Common. Met. 1959, 1, 3–18. [Google Scholar] [CrossRef]
  34. Kidron, A. An X-ray diffuse scattering measurement of local order in a Pd Pt alloys. Phys. Lett. A 1967, 25, 112–113. [Google Scholar] [CrossRef]
  35. Duan, Z.; Wang, G. Monte Carlo simulation of surface segregation phenomena in extended and nanoparticle surfaces of Pt–Pd alloys. J. Physics Condens. Matter 2011, 23, 475301. [Google Scholar] [CrossRef]
  36. Jacob, K.T.; Raj, S.; Rannesh, L. Vegard’s law: A fundamental relation or an approximation? Int. J. Mater. Res. 2007, 98, 776–779. [Google Scholar] [CrossRef]
  37. Woolley, J.C.; Berolo, O. Phase studies of the Pb1−xSnxSe alloys. Mater. Res. Bull. 1968, 3, 445–450. [Google Scholar] [CrossRef]
  38. Bis, R.F.; Dixon, J.R. Applicability of Vegard’s Law to the PbxSn1−xTe Alloy System. J. Appl. Phys. 1969, 40, 1918–1921. [Google Scholar] [CrossRef]
  39. Friedel, J. LX. Deviations from Vegard’s law, London, Edinburgh, Dublin Philos. Mag. J. Sci. 1955, 46, 514–516. [Google Scholar] [CrossRef]
  40. Murphy, S.T.; Chroneos, A.; Jiang, C.; Schwingenschlögl, U.; Grimes, R.W. Deviations from Vegard’s law in ternary III-V alloys. Phys. Rev. B 2010, 82, 073201. [Google Scholar] [CrossRef]
  41. Magomedov, M. On the deviation from the Vegard’s law for the solid solutions. Solid State Commun. 2020, 322, 114060. [Google Scholar] [CrossRef]
  42. Beldi, L.; Bendaoud, H.; Obodo, K.; Abbar, B.; Bouhafs, B. Density functional theory studies of the SrC and SrN compounds. Mater. Chem. Phys. 2019, 237, 121875. [Google Scholar] [CrossRef]
  43. Tang, K.; Wang, T.; Qi, W.; Li, Y. Debye temperature for binary alloys and its relationship with cohesive energy. Phys. B Condens. Matter 2018, 531, 95–101. [Google Scholar] [CrossRef]
  44. Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
  45. Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954. [Google Scholar]
  46. Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
  47. Budinski, K.G.; Budinski, M.K. Engineering Materials; Pearson Education India: Noida, India, 1999. [Google Scholar]
  48. Bozzolo, G.; Mosca, H.O.; del Grosso, M.F. Energy of formation, lattice parameter and bulk modulus of (Ni,X)Ti alloys with X = Fe, Pd, Pt, Au, Al, Cu, Zr, Hf. Intermetallics 2008, 16, 668–675. [Google Scholar] [CrossRef]
  49. Bercegeay, C.; Bernard, S. First-principles equations of state and elastic properties of seven metals. Phys. Rev. B 2005, 72, 214101. [Google Scholar] [CrossRef]
  50. Dieter, G.E.; Bacon, D. Mechanical Metallurgy; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
  51. Köster, W.; Franz, H. Poisson’s ratio for metals and alloys. Metall. Rev. 1961, 6, 1–56. [Google Scholar] [CrossRef]
  52. Haines, J.; Léger, J.; Bocquillon, G. Synthesis and Design of Superhard Materials. Annu. Rev. Mater. Res. 2001, 31, 1–23. [Google Scholar] [CrossRef]
  53. Cao, D. Pair Distribution Functions. In Molecular Dynamics Simulations of Interfaces; West Virginia University: Morgantown, WV, USA, 2006. [Google Scholar]
  54. Toby, B.H.; Egami, T. Accuracy of pair distribution function analysis applied to crystalline and non-crystalline materials. Acta Crystallogr. Sect. A Found. Crystallogr. 1992, 48, 336–346. [Google Scholar] [CrossRef]
  55. Benaissa, H.; Benatmane, S.; Amari, S.; Obodo, K.O.; Beldi, L.; Bendaoud, H.; Bouhafs, B. Ferromagnetism in RaBi with Zinc-Blende and Wurtzite Structures: Ab-initio Prediction. SPIN 2018, 08, 1850008. [Google Scholar] [CrossRef]
  56. Beldi, L.; Bendaoud, H.; Obodo, K.O.; Abbar, B.; Bouhafs, B. Prediction of a Dynamically Stable New Half-Metallic Phase for the BaN and BaC Compounds. J. Supercond. Nov. Magn. 2018, 32, 2031–2044. [Google Scholar] [CrossRef]
  57. Cahn, R.W. Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Materials Park, OH, USA, 1991. [Google Scholar] [CrossRef]
  58. Bharadwaj, S.; Kerkar, A.; Tripathi, S.; Dharwadkar, S. The palladium-platinum phase diagram. J. Less Common Met. 1991, 169, 167–172. [Google Scholar] [CrossRef]
  59. Guisbiers, G.; Abudukelimu, G.; Hourlier, D. Size-dependent catalytic and melting properties of platinum-palladium nanoparticles. Nanoscale Res. Lett. 2011, 6, 396. [Google Scholar] [CrossRef]
  60. Atkins, P.; De Paula, J.; Keeler, J. Atkins’ Physical Chemistry International Edition, 11th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
  61. Botha, L.M.; Santos-Carballal, D.; Terranova, U.; Quesne, M.G.; Ungerer, M.J.; van Sittert, C.G.C.E.; de Leeuw, N.H. Mixing thermodynamics and electronic structure of the Pt1−xNix (0 ≤ x ≤ 1) bimetallic alloy. RSC Adv. 2019, 9, 16948–16954. [Google Scholar] [CrossRef]
  62. Kresse, G.; Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  63. Kresse, G.; Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
  64. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  65. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
  66. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  67. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  68. Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C.M. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
  69. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  70. Togo, A.; Tanaka, I. Spglib: A software library for crystal symmetry search. arXiv 2018, arXiv:1808.01590. [Google Scholar]
  71. Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
  72. Le Page, Y.; Saxe, P. Symmetry-General Least-Squares Extraction of Elastic Coefficients from Ab Initio Total Energy Calculations. Phys. Rev. B 2001, 63, 174103. [Google Scholar] [CrossRef]
  73. Le Page, Y.; Saxe, P. Symmetry-General Least-Squares Extraction of Elastic Data for Strained Materials from Ab Initio Calculations, of Stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
  74. Anderson, O.L. A Simplified Method for Calculating the Debye Temperature from Elastic Constants. J. Phys. Chem. Solids 1963, 24, 909. [Google Scholar] [CrossRef]
  75. Grüneisen’s, E. Zustand des festen Körpers. In Thermische Eigenschaften der Stoffe; Handbuch Der Physik; Springer: Berlin/Heidelberg, Germany, 1928. [Google Scholar]
  76. Mayer, B.; Anton, H.; Bott, E.; Methfessel, M.; Sticht, J.; Harris, J.; Schmidt, P.C. Ab-Initio Calculation of the Elastic Constants and Thermal Expansion Coefficients of Laves Phases. Intermetallics 2003, 11, 23–32. [Google Scholar] [CrossRef]
Condensedmatter 08 00076 g001
Figure 1. Relative energies of PtPd3, PtPd, Pt3Pd, and Pt7Pd alloy structures.
Figure 1. Relative energies of PtPd3, PtPd, Pt3Pd, and Pt7Pd alloy structures.
Condensedmatter 08 00076 g001
Condensedmatter 08 00076 g002
Figure 2. Murnaghan’s fit for the pristine (a) Pt and (b) Pd, as well as (c) PtPd3, (d) PtPd, (e) PtPd (L10), (f) Pt3Pd, and (g) Pt7Pd alloy structures (conventional unit cell structures).
Figure 2. Murnaghan’s fit for the pristine (a) Pt and (b) Pd, as well as (c) PtPd3, (d) PtPd, (e) PtPd (L10), (f) Pt3Pd, and (g) Pt7Pd alloy structures (conventional unit cell structures).
Condensedmatter 08 00076 g002
Condensedmatter 08 00076 g003
Figure 3. Comparison between calculated phonon band spectra and phonon DOS spectra for the pristine Pt and Pd structures.
Figure 3. Comparison between calculated phonon band spectra and phonon DOS spectra for the pristine Pt and Pd structures.
Condensedmatter 08 00076 g003
Condensedmatter 08 00076 g004
Figure 4. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered PtPd3 alloy structure.
Figure 4. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered PtPd3 alloy structure.
Condensedmatter 08 00076 g004
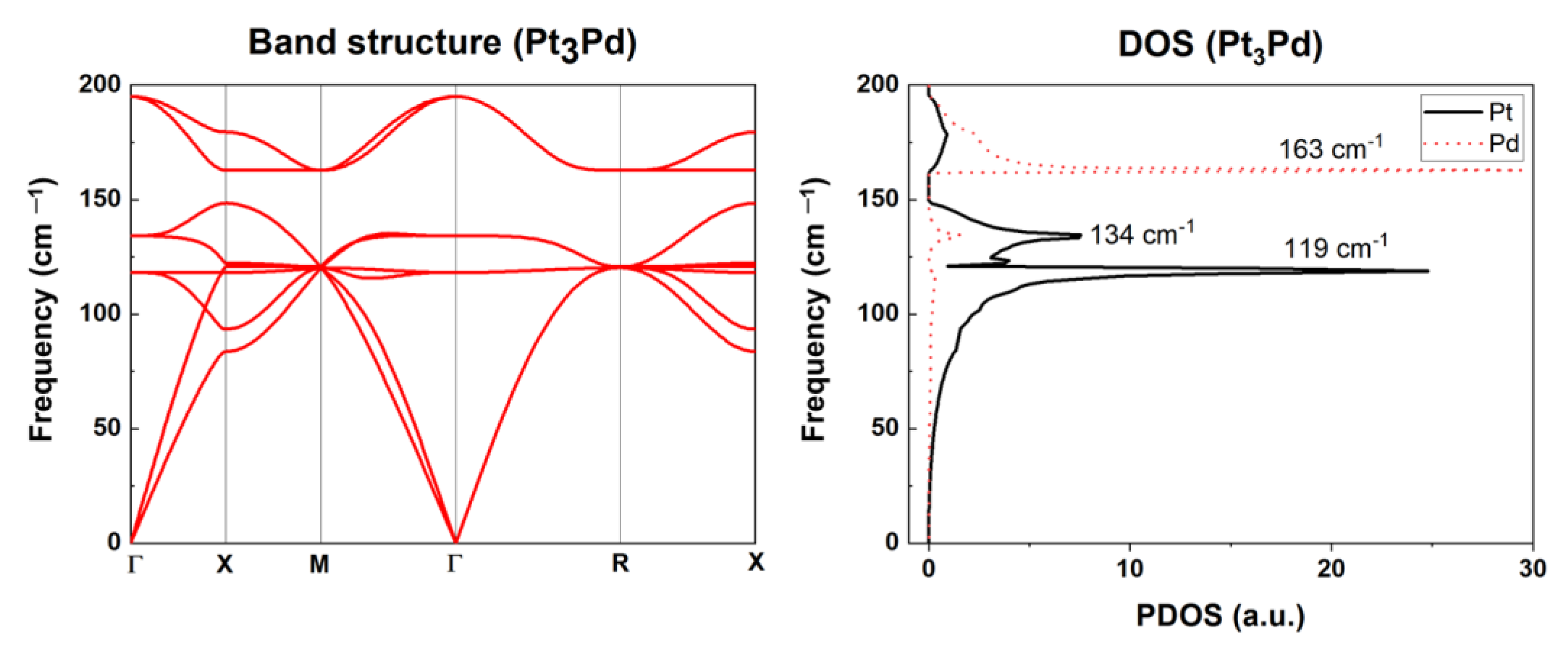
Condensedmatter 08 00076 g005
Figure 5. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered Pt3Pd alloy structure.
Figure 5. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered Pt3Pd alloy structure.
Condensedmatter 08 00076 g005
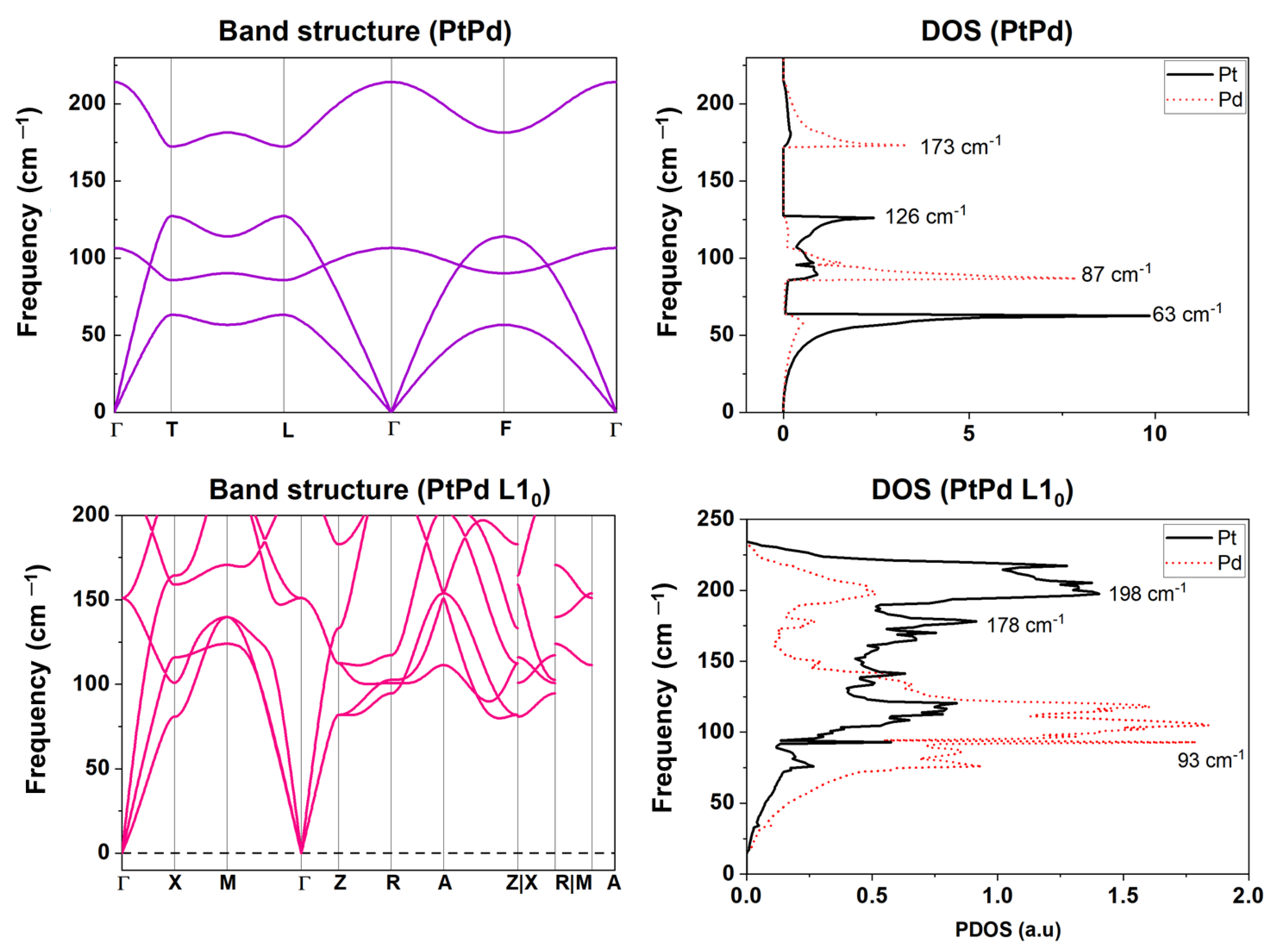
Condensedmatter 08 00076 g006
Figure 6. Comparison between the calculated phonon band spectra and phonon DOS spectra for the PtPd structures in the hexagonal rhombohedral and L10 phases.
Figure 6. Comparison between the calculated phonon band spectra and phonon DOS spectra for the PtPd structures in the hexagonal rhombohedral and L10 phases.
Condensedmatter 08 00076 g006
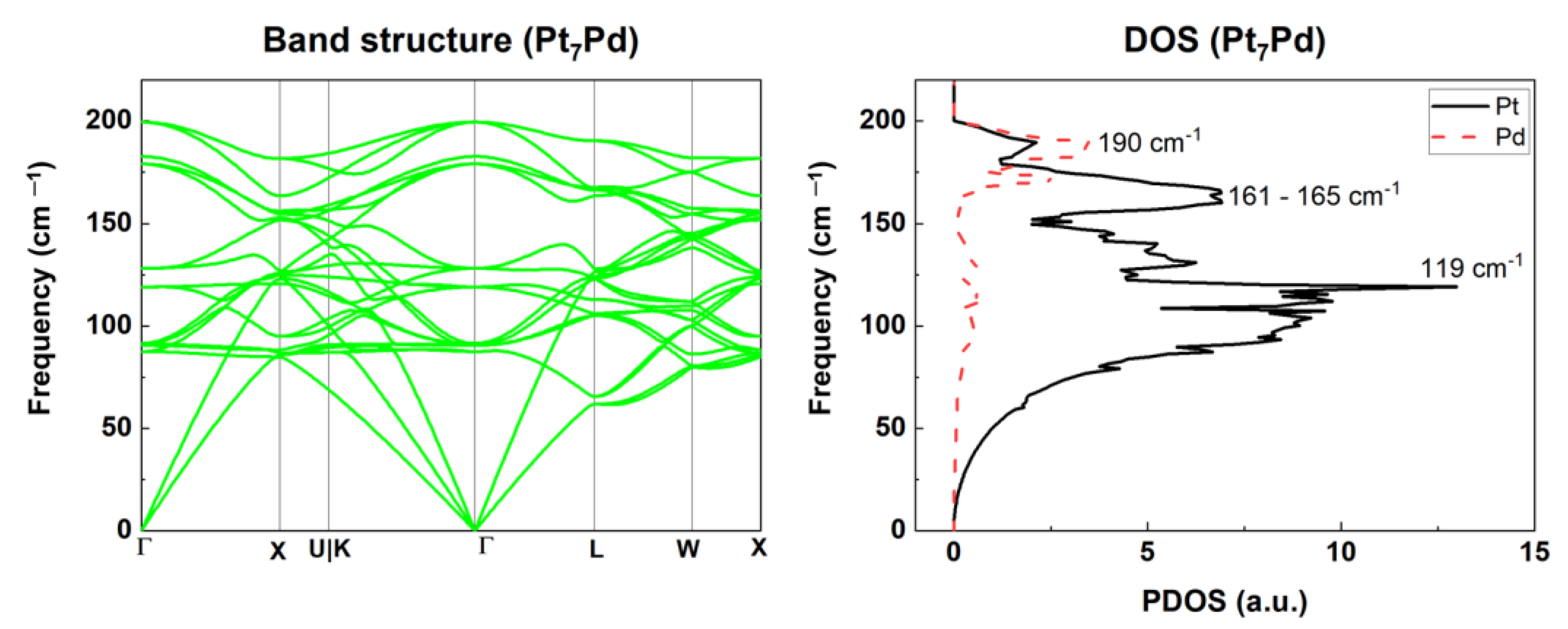
Condensedmatter 08 00076 g007
Figure 7. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered Pt7Pd alloy structure.
Figure 7. Comparison between the calculated phonon band spectra and phonon DOS spectra for the considered Pt7Pd alloy structure.
Condensedmatter 08 00076 g007
Condensedmatter 08 00076 g008
Figure 8. Calculated temperature dependence of the (a) entropy (S), (b) Helmholtz free energy (F), and (c) constant-volume specific heat capacity (Cv).
Figure 8. Calculated temperature dependence of the (a) entropy (S), (b) Helmholtz free energy (F), and (c) constant-volume specific heat capacity (Cv).
Condensedmatter 08 00076 g008
Condensedmatter 08 00076 g009
Figure 9. The calculated projected density of states (PDOS) for each atom in the pristine Pt and Pd, as well as the considered Pt/Pd alloy structures.
Figure 9. The calculated projected density of states (PDOS) for each atom in the pristine Pt and Pd, as well as the considered Pt/Pd alloy structures.
Condensedmatter 08 00076 g009
Table 3. Atomic charge (q) per atom for the pristine Pt and Pd, as well as for the Pt/Pd alloy structures.
Table 3. Atomic charge (q) per atom for the pristine Pt and Pd, as well as for the Pt/Pd alloy structures.
StructureAtomq (e/atom)
PtPt0.00
PdPd0.00
PtPd3Pt−0.10
Pd0.03
PtPdPt−0.11
Pd0.11
Pt3PdPt−0.03
Pd0.09
Pt7PdPt−0.03
Pd0.24
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Botha, L.M.; Ouma, C.N.M.; Obodo, K.O.; Bessarabov, D.G.; Sharypin, D.L.; Varyushin, P.S.; Plastinina, E.I. Ab Initio Study of Structural, Electronic, and Thermal Properties of Pt/Pd-Based Alloys. Condens. Matter 2023, 8, 76. https://doi.org/10.3390/condmat8030076

AMA Style

Botha LM, Ouma CNM, Obodo KO, Bessarabov DG, Sharypin DL, Varyushin PS, Plastinina EI. Ab Initio Study of Structural, Electronic, and Thermal Properties of Pt/Pd-Based Alloys. Condensed Matter. 2023; 8(3):76. https://doi.org/10.3390/condmat8030076

Chicago/Turabian Style

Botha, Louise Magdalene, Cecil Naphtaly Moro Ouma, Kingsley Onyebuchi Obodo, Dmitri Georgievich Bessarabov, Denis Lvovich Sharypin, Pyotr Sergeevich Varyushin, and Elizaveta Ivanovna Plastinina. 2023. "Ab Initio Study of Structural, Electronic, and Thermal Properties of Pt/Pd-Based Alloys" Condensed Matter 8, no. 3: 76. https://doi.org/10.3390/condmat8030076

APA Style

Botha, L. M., Ouma, C. N. M., Obodo, K. O., Bessarabov, D. G., Sharypin, D. L., Varyushin, P. S., & Plastinina, E. I. (2023). Ab Initio Study of Structural, Electronic, and Thermal Properties of Pt/Pd-Based Alloys. Condensed Matter, 8(3), 76. https://doi.org/10.3390/condmat8030076

Article Metrics

Back to TopTop