Properties of Blue Phosphorene Nanoribbon-P3HT Polymer Heterostructures: DFT First Principles Calculations
Abstract
:1. Introduction
2. Computational Methodology
3. Results and Discussion
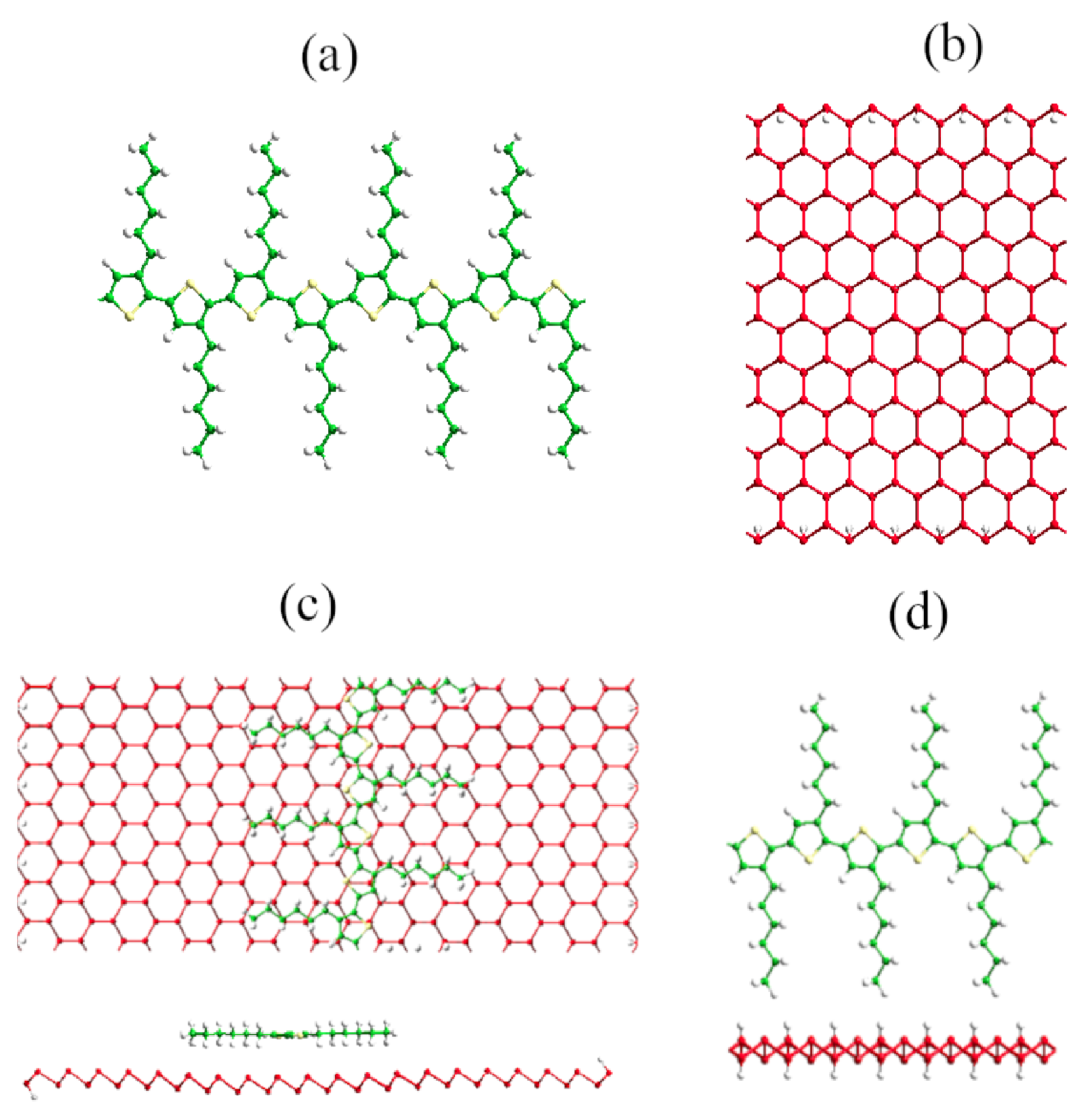
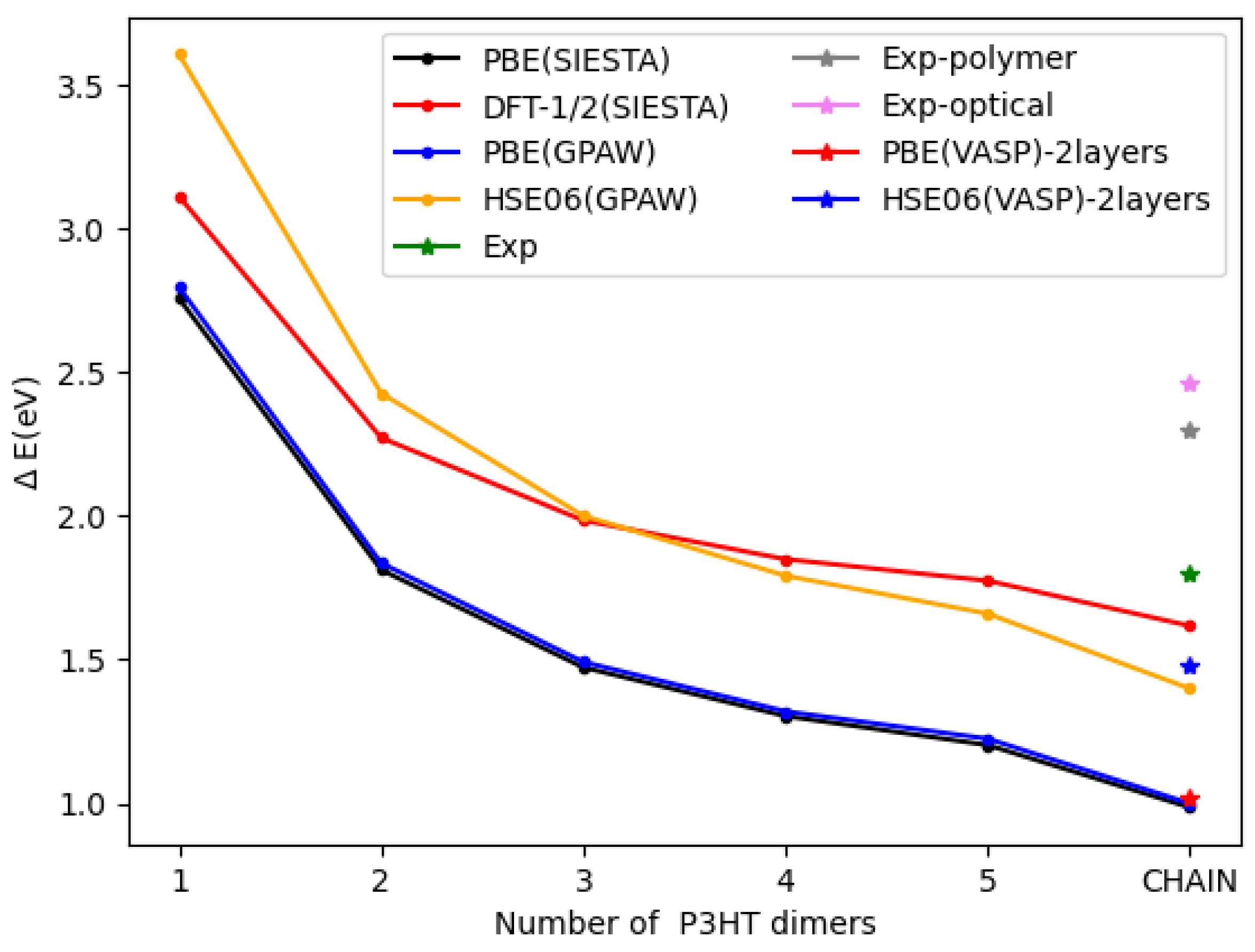
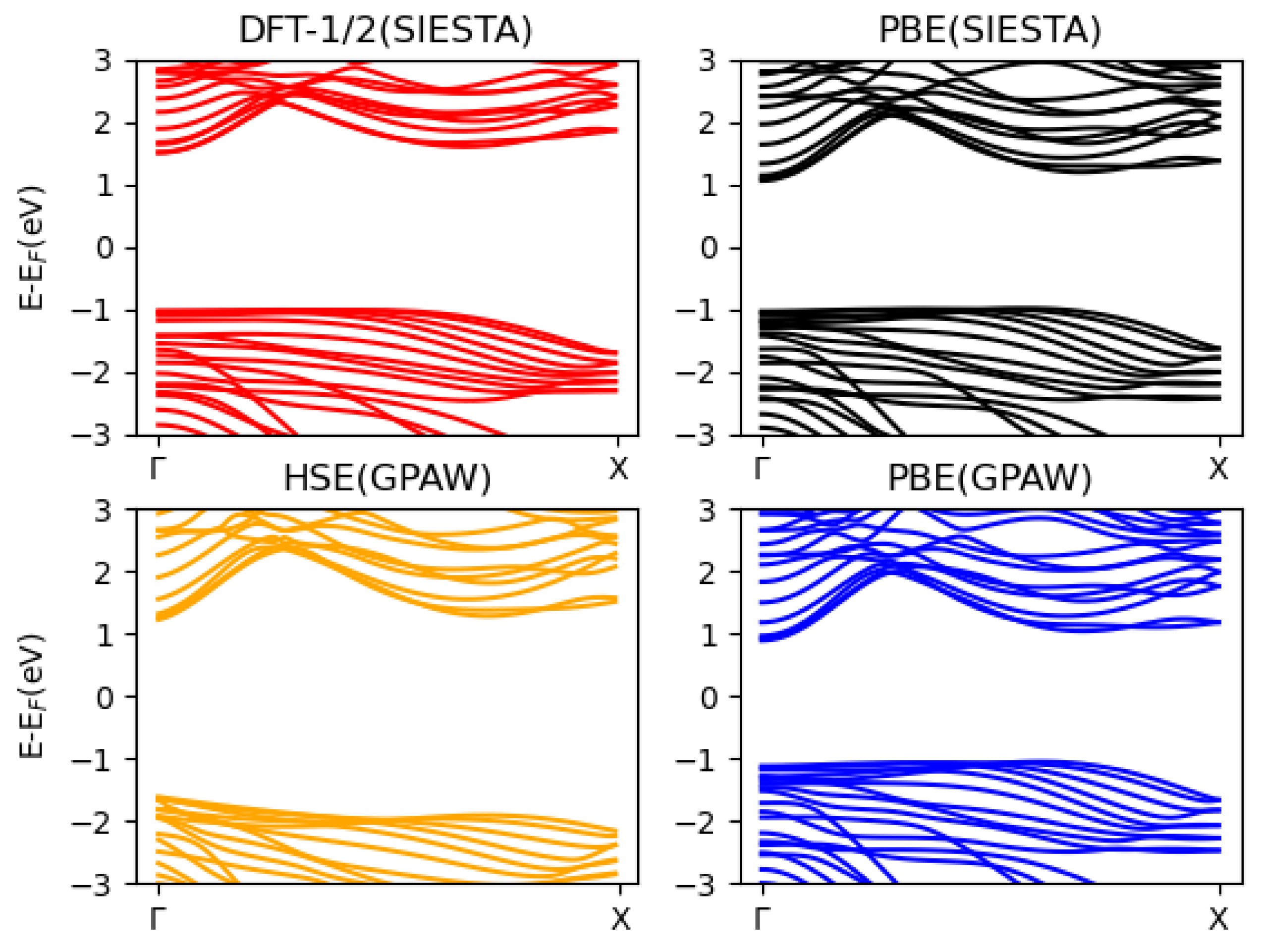
3.1. P3HT Oligomers and Periodic Chain
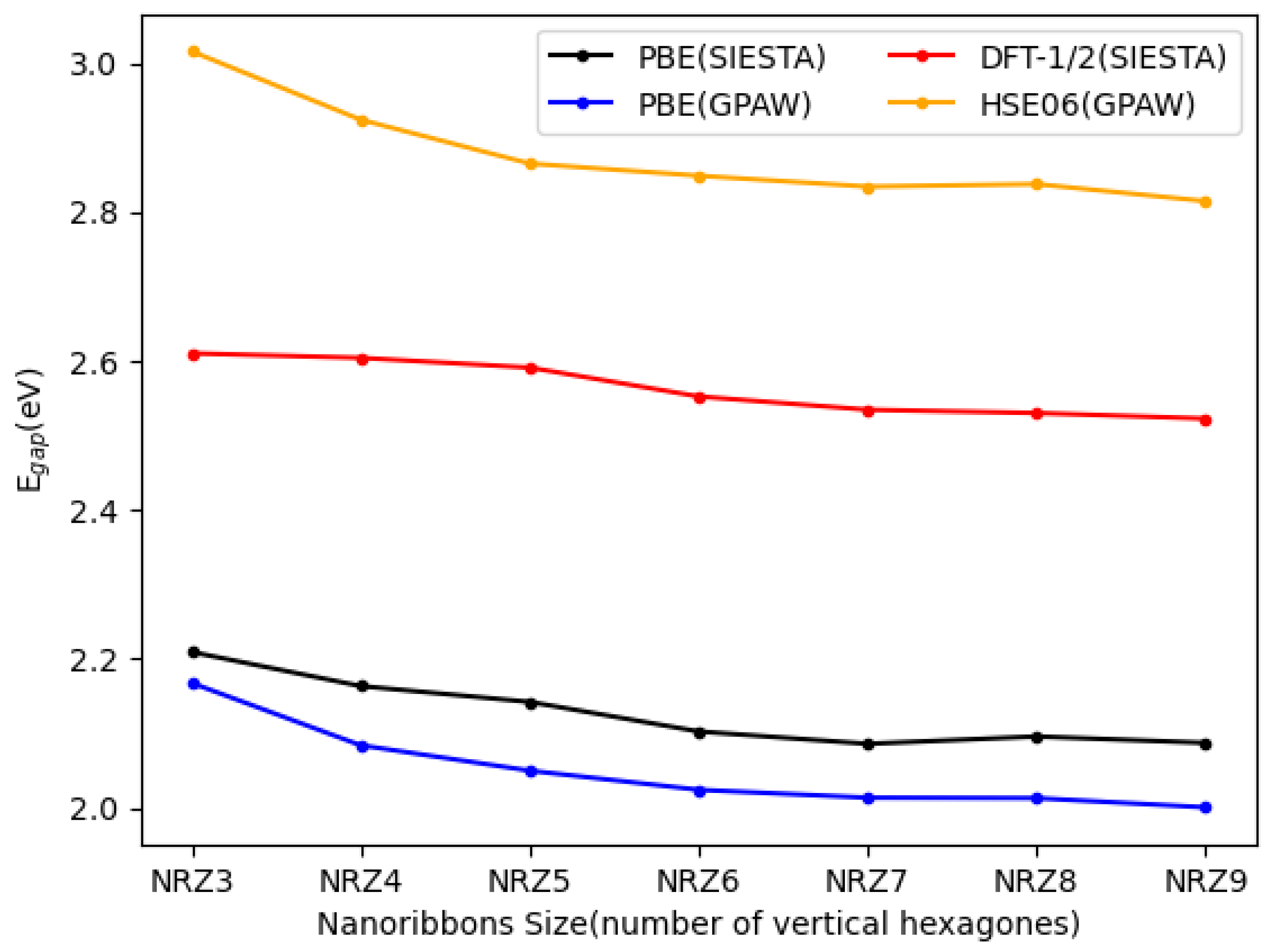
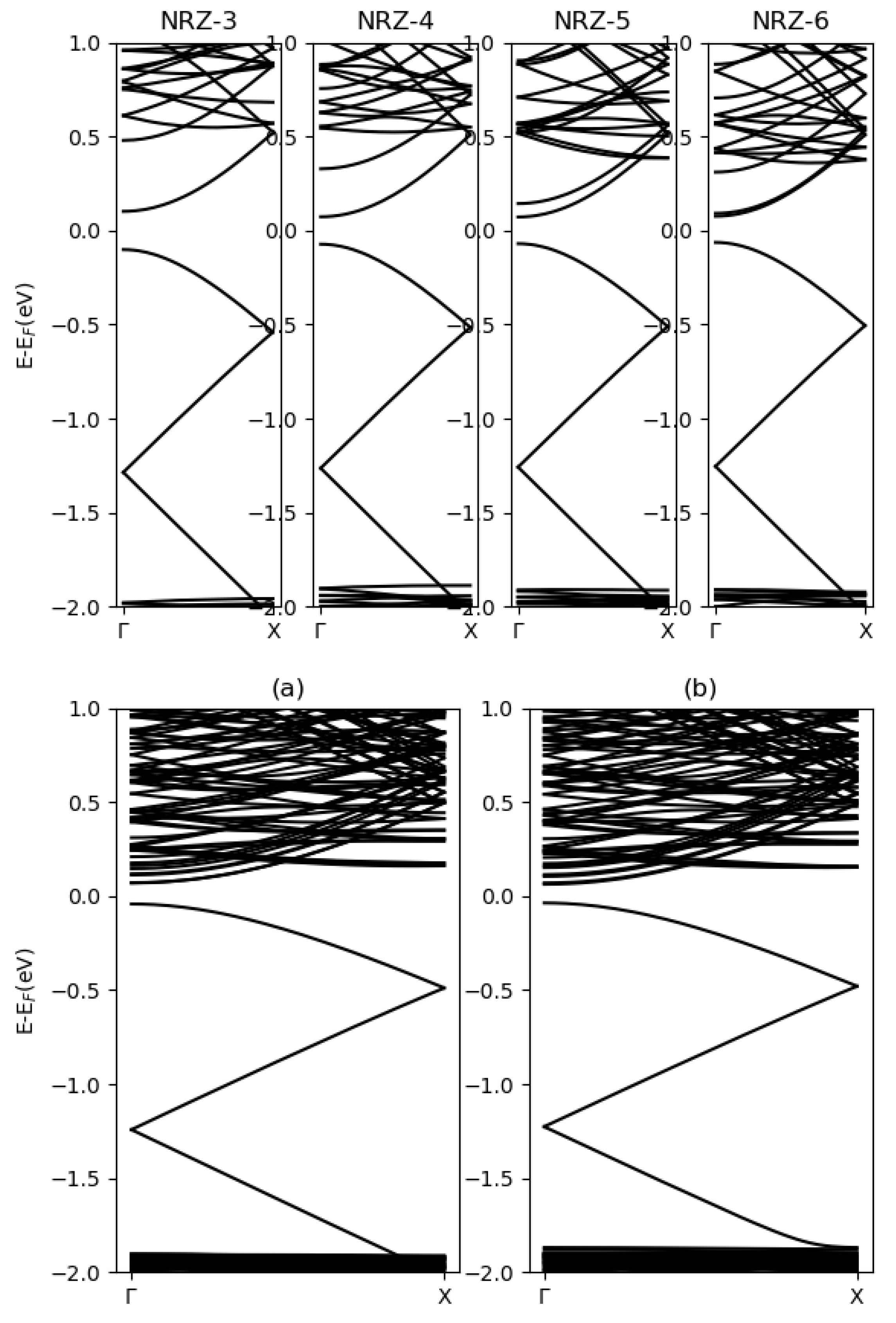
3.2. Blue Phosphorene Nanoribbons
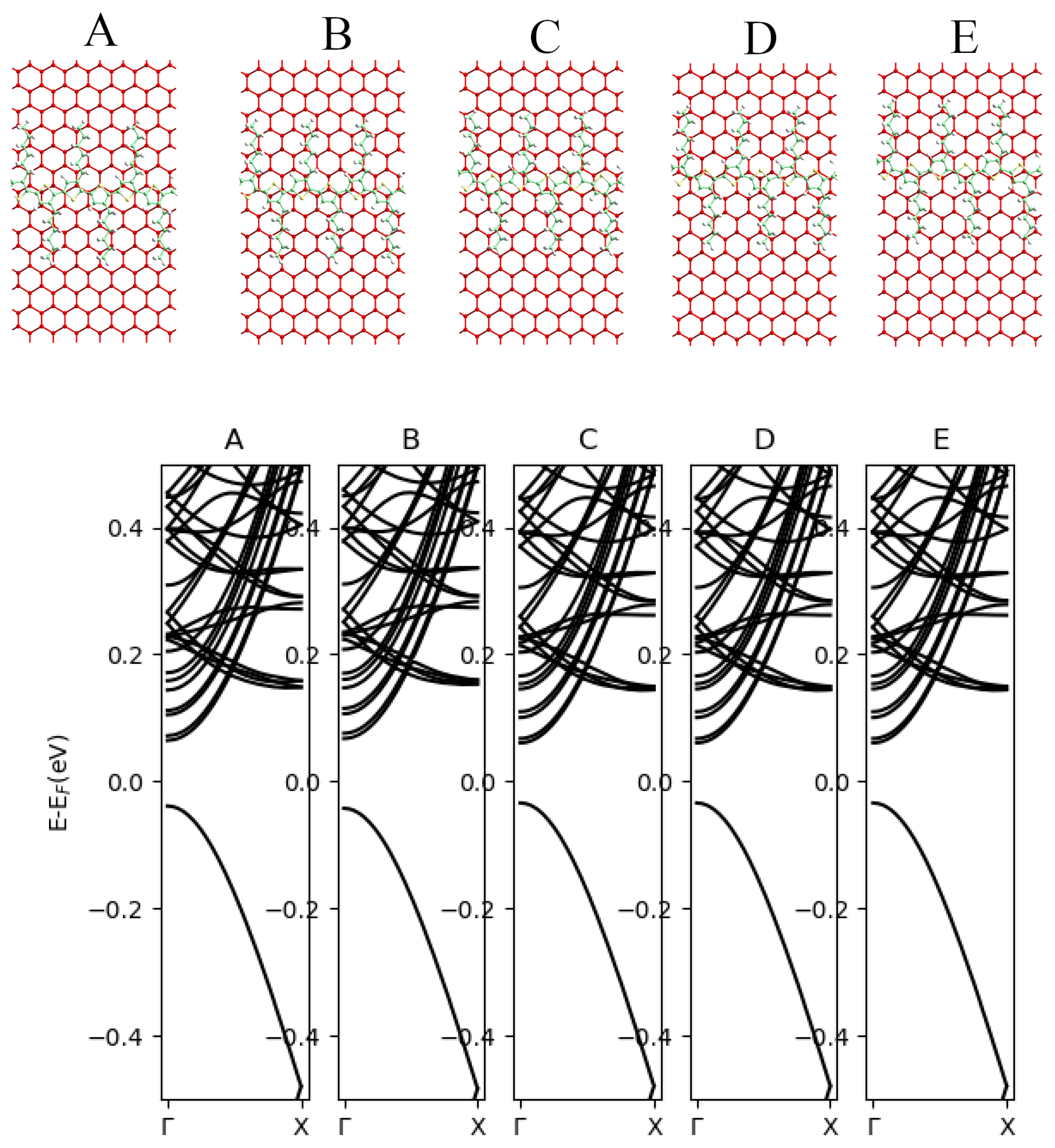
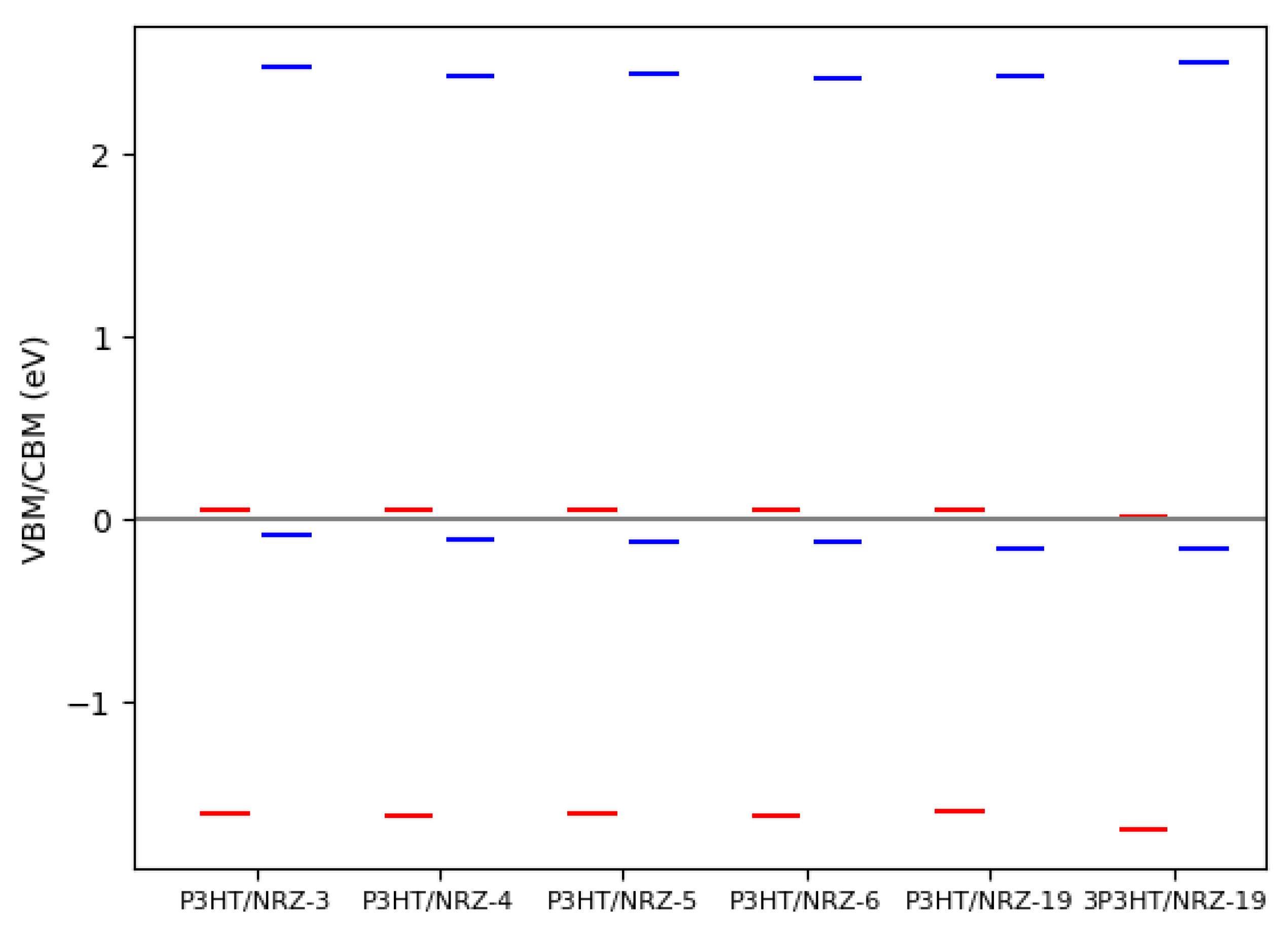
3.3. The Blue Phosphorene Nanoribbon plus P3HT Complex
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geim, A.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.; Jiang, D.; Schedin, F.; Booth, T.; Khotkevich, V.; Morozov, S.; Geim, A. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Grazianetti, C.; Molle, A. Introduction. In Xenes; Molle, A., Grazianetti, C., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Cambridge, UK, 2022; pp. xxi–xxx. [Google Scholar] [CrossRef]
- Grazianetti, C.; Martella, C. The Rise of the Xenes: From the Synthesis to the Integration Processes for Electronics and Photonics. Materials 2021, 14, 4170. [Google Scholar] [CrossRef] [PubMed]
- Kaur, S.; Kumar, A.; Srivastava, S.; Tankeshwar, K. Electronic structure engineering of various structural phases of phosphorene. Phys. Chem. Chem. Phys. 2016, 18, 18312–18322. [Google Scholar] [CrossRef]
- Zhu, Z.; Tománek, D. Semiconducting layered blue phosphorus: A computational study. Phys. Rev. Lett. 2014, 112, 176802. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, S.; Han, C.; Wang, Z.; Zhong, S.; Sun, S.; Guo, R.; Zhou, X.; Gu, C.; Yuan, K.; et al. Epitaxial growth of single layer blue phosphorus: A new phase of two-dimensional phosphorus. Nano Lett. 2016, 16, 4903–4908. [Google Scholar] [CrossRef]
- Han, N.; Gao, N.; Zhao, J. Initial Growth Mechanism of Blue Phosphorene on Au(111) Surface. J. Phys. Chem. C 2017, 121, 17893–17899. [Google Scholar] [CrossRef]
- Zhuang, J.; Liu, C.; Gao, Q.; Liu, Y.; Feng, H.; Xu, X.; Wang, J.; Zhao, J.; Dou, S.; Hu, Z.; et al. Bandgap Modulated by Electronic Superlattice in Blue Phosphorene. ACS Nano 2018, 12, 5059–5065. [Google Scholar] [CrossRef]
- Zhang, W.; Enriquez, H.; Mayne, A.J.; Bendounan, A.; Seitsonen, A.; Kara, A.; Dujardin, G.; Oughaddou, H. First steps of blue phosphorene growth on Au(111). Mater. Today Proc. 2021, 39, 1153–1156. [Google Scholar] [CrossRef]
- Shaikh, G.A.; Raval, D.; Babariya, B.; Gupta, S.; Gajjar, P. An ab-initio study of blue phosphorene monolayer: Electronic, vibrational and optical properties. Mater. Today Proc. 2021, 47, 576–579. [Google Scholar] [CrossRef]
- Tyagi, S.; Rout, P.; Schwingenschlogl, U. High-performance junction-free field-effect transistor based on blue phosphorene. npj 2D Mater. Appl. 2022, 6, 86. [Google Scholar] [CrossRef]
- He, C.; Xu, S.; Dong, X.; He, C.; Hu, X.; Liu, G.; Xu, H. Step-guided epitaxial growth of blue phosphorene on vicinal Ag(111). Phys. Rev. Mater. 2023, 7, 034003. [Google Scholar] [CrossRef]
- Xie, J.; Si, M.; Yang, D.; Zhang, Z.; Xue, D. A theoretical study of blue phosphorene nanoribbons based on first-principles calculations. J. Appl. Phys. 2014, 116, 073704. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Yang, X.; Hong, X.; Feng, J.; Si, M.; Wang, X. Spin caloritronics of blue phosphorene nanoribbons. Phys. Chem. Chem. Phys. 2015, 17, 10462–10467. [Google Scholar] [CrossRef] [PubMed]
- Ospina, D.; Duque, C.; Mora-Ramos, M.; Correa, J. Effects of external electric field on the optical and electronic properties of blue phosphorene nanoribbons: A DFT study. Comput. Mater. Sci. 2017, 135, 43–53. [Google Scholar] [CrossRef]
- Xiong, P.Y.; Chen, S.Z.; Zhou, W.X.; Chen, K.Q. Semiconductor-metal transition induced by giant Stark effect in blue phosphorene nanoribbons. Phys. Lett. A 2017, 381, 2016–2020. [Google Scholar] [CrossRef]
- Swaroop, R.; Ahluwalia, P.; Tankeshwar, K.; Kumar, A. Ultra-narrow blue phosphorene nanoribbons for tunable optoelectronics. RSC Adv. 2017, 7, 2992–3002. [Google Scholar] [CrossRef]
- An, Y.; Sun, Y.; Zhang, M.; Jiao, J.; Wu, D.; Wang, T.; Wang, K. Tuning the Electronic Structures and Transport Properties of Zigzag Blue Phosphorene Nanoribbons. IEEE Trans. Electron Devices 2018, 65, 4646–4651. [Google Scholar] [CrossRef]
- Dey, A.; Chakraborty, D. Engineering the Band Structures of Zigzag Blue Phosphorene and Arsenene Nanoribbons by Incorporating Edge Corrugations: A First Principles Exploration. J. Nanosci. Nanotechnol. 2021, 21, 5929–5936. [Google Scholar] [CrossRef]
- Saravanan, S.; Nagarajan, V.; Srivastava, A.; Chandiramouli, R. Blue phosphorene nanoribbon for detection of chloroform vapours—A first-principles study. Int. J. Environ. Anal. Chem. 2019, 101, 1697–1709. [Google Scholar] [CrossRef]
- Maibam, A.; Chakraborty, D.; Joshi, K.; Krishnamurty, S. Exploring edge functionalised blue phosphorene nanoribbons as novel photocatalysts for water splitting. New J. Chem. 2021, 45, 3570–3580. [Google Scholar] [CrossRef]
- Macdonald, T.; Clancy, A.; Xu, W.; Jiang, Z.; Lin, C.T.; Mohan, L.; Du, T.; Tune, D.; Lanzetta, L.; Min, G.; et al. Phosphorene Nanoribbon-Augmented Optoelectronics for Enhanced Hole Extraction. J. Am. Chem. Soc. 2021, 143, 21549–21559. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Tang, W.; Ren, Q.; Wang, S.; Yu, J.; Du, Y. A first-principles study of light non-metallic atom substituted blue phosphorene. Appl. Surf. Sci. 2015, 356, 110–114. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y. Structural, electronic, and magnetic properties of adatom adsorptions on black and blue phosphorene: A first-principles study. J. Phys. Chem. C 2015, 119, 10610–10622. [Google Scholar] [CrossRef]
- Sun, M.; Hao, Y.; Ren, Q.; Zhao, Y.; Du, Y.; Tang, W. Tuning electronic and magnetic properties of blue phosphorene by doping Al, Si, As and Sb atom: A DFT calculation. Sol. Stat. Commun. 2016, 242, 36–40. [Google Scholar] [CrossRef]
- Bai, R.; Chen, Z.; Gou, M.; Zhang, Y. A first-principles study of group IV and VI atoms doped blue phosphorene. Sol. Stat. Commun. 2018, 270, 76–81. [Google Scholar] [CrossRef]
- Arif Khalil, R.; Hussain, F.; Hussain, M.; Parveen, A.; Imran, M.; Murtaza, G.; Sattar, M.; Rana, A.; Kim, S. The investigation of optoelectronic, magnetic and dynamical properties of Ce and Ti doped 2D blue phosphorene: A dispersion corrected DFT study. J. Alloys Compd. 2020, 827, 154255. [Google Scholar] [CrossRef]
- Correa, J. First principles calculations of opto-electronic properties of doped blue phosphorene nanoribbons. Superlattices Microstruct. 2019, 130, 401–408. [Google Scholar] [CrossRef]
- Ihn, K.; Moulton, J.; Smith, P. Whiskers of poly(3-alkylthiophene)s. J. Polym. Sci. B Polym. Phys. 1993, 31, 735–742. [Google Scholar] [CrossRef]
- Jian, L.; Bao, X.; Uchida, Y.; Liu, J.; Kathuria, Y.; Furuhashi, H.; Uchida, Y. Blue spectral shift of P3HT organic film by KrF excimer laser ablation. In Proceedings of the 2009 International Conference on Optical Instruments and Technology: Optoelectronic Devices and Integration, Shanghai, China, 19–21 October 2009; Zhang, X., Bock, W., Lu, X., Ming, H., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7509, p. 75090F. [Google Scholar] [CrossRef]
- Moulé, A.J.; Neher, D.; Turner, S. P3HT-Based Solar Cells: Structural Properties and Photovoltaic Performance. In P3HT Revisited—From Molecular Scale to Solar Cell Devices; Ludwigs, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 181–232. [Google Scholar] [CrossRef]
- El Gemayel, M.; Narita, A.; Dössel, L.F.; Sundaram, R.S.; Kiersnowski, A.; Pisula, W.; Hansen, M.R.; Ferrari, A.C.; Orgiu, E.; Feng, X.; et al. Graphene nanoribbon blends with P3HT for organic electronics. Nanoscale 2014, 6, 6301–6314. [Google Scholar] [CrossRef]
- Tiwari, S.; Verma, R.; Alam, M.; Kumari, R.; Sinha, O.; Srivastava, R. Charge transport study of P3HT blended MoS2. Vacuum 2017, 146, 474–477. [Google Scholar] [CrossRef]
- Gutiérrez-González, I.; Molina-Brito, B.; Götz, A.W.; Castillo-Alvarado, F.; Rodríguez, J.I. Structural and electronic properties of the P3HT–PCBM dimer: A theoretical Study. Chem. Phys. Lett. 2014, 612, 234–239. [Google Scholar] [CrossRef]
- Roy, J.K.; Kar, S.; Leszczynski, J. Optoelectronic Properties of C60 and C70 Fullerene Derivatives: Designing and Evaluating Novel Candidates for Efficient P3HT Polymer Solar Cells. Materials 2019, 12, 2282. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.P.; Shim, J.H. Hybrid density functional study on the electronic structures and properties of P3HT-PbS and P3HT-CdS hybrid interface for photovoltaic applications. J. Comput. Chem. 2018, 39, 1990–1999. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Basabe, Y.; Orsi Gordo, V.; Daminelli, L.; Mendoza, C.D.; Vicentin, F.; Matusalem, F.; Rocha, A.; de Matos, C.; Larrudé, D. Interfacial electronic coupling and band alignment of P3HT and exfoliated black phosphorous van der Waals heterojunctions. Appl. Surf. Sci. 2021, 541, 148455. [Google Scholar] [CrossRef]
- Ferreira, L.; Marques, M.; Teles, L. Approximation to density functional theory for the calculation of band gaps of semiconductors. Phys. Rev. B 2008, 78, 125116. [Google Scholar] [CrossRef]
- Ferreira, L.; Marques, M.; Teles, L. Slater half-occupation technique revisited: The LDA-1/2 and GGA-1/2 approaches for atomic ionization energies and band gaps in semiconductors. AIP Adv. 2011, 1, 032119. [Google Scholar] [CrossRef]
- Slater, J.; Johnson, K. Self-Consistent-Field Xα Cluster Method for Polyatomic Molecules and Solids. Phys. Rev. B 1972, 5, 844–853. [Google Scholar] [CrossRef]
- Slater, J. Statistical Exchange-Correlation in the Self-Consistent Field. Adv. Quantum Chem. 1972, 6, 1–92. [Google Scholar] [CrossRef]
- Soler, J.; Artacho, E.; Gale, J.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Artacho, E.; Anglada, E.; Diéguez, O.; Gale, J.; García, A.; Junquera, J.; Martin, R.; Ordejón, P.; Pruneda, J.; Sánchez-Portal, D.; et al. The SIESTA method; developments and applicability. J. Phys. Condens. Matter 2008, 20, 064208. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Peralta, J.E.; Scuseria, G.E.; Martin, R.L. Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional. J. Chem. Phys. 2005, 123, 174101. [Google Scholar] [CrossRef] [PubMed]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 2006, 124, 219906. [Google Scholar] [CrossRef]
- Mortensen, J.J.; Hansen, L.B.; Jacobsen, K.W. Real-space grid implementation of the projector augmented wave method. Phys. Rev. B 2005, 71, 035109. [Google Scholar] [CrossRef]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dułak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V.; Hansen, H.A.; et al. Electronic structure calculations with GPAW: A real-space implementation of the projector augmented-wave method. J. Phys. Condens. Matter 2010, 22, 253202. [Google Scholar] [CrossRef]
- Marsman, M.; Paier, J.; Stroppa, A.; Kresse, G. Hybrid functionals applied to extended systems. J. Phys. Condens. Matter 2008, 20, 064201. [Google Scholar] [CrossRef]
- Ansari, M.A.; Mohiuddin, S.; Kandemirli, F.; Malik, M.I. Synthesis and characterization of poly(3-hexylthiophene): Improvement of regioregularity and energy band gap. RSC Adv. 2018, 8, 8319–8328. [Google Scholar] [CrossRef]
- Kucur, E.; Riegler, J.; Urban, G.A.; Nann, T. Charge transfer mechanism in hybrid bulk heterojunction composites. J. Chem. Phys. 2004, 120, 1500–1505. [Google Scholar] [CrossRef]
- Cook, S.; Katoh, R.; Furube, A. Ultrafast studies of charge generation in PCBM: P3HT blend films following excitation of the fullerene PCBM. J. Phys. Chem. C 2009, 113, 2547–2552. [Google Scholar] [CrossRef]
- Zhang, S.; Xie, M.; Li, F.; Yan, Z.; Li, Y.; Kan, E.; Liu, W.; Chen, Z.; Zeng, H. Semiconducting Group 15 Monolayers: A Broad Range of Band Gaps and High Carrier Mobilities. Angew. Chem. Int. Ed. 2016, 55, 1666–1669. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Guo, S.; Chen, Z.; Wang, Y.; Gao, H.; Gómez-Herrero, J.; Ares, P.; Zamora, F.; Zhu, Z.; Zeng, H. Recent progress in 2D group-VA semiconductors: From theory to experiment. Chem. Soc. Rev. 2018, 47, 982–1021. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turiján-Clara, B.; Correa, J.D.; Mora-Ramos, M.E.; Duque, C.A. Properties of Blue Phosphorene Nanoribbon-P3HT Polymer Heterostructures: DFT First Principles Calculations. Condens. Matter 2023, 8, 74. https://doi.org/10.3390/condmat8030074
Turiján-Clara B, Correa JD, Mora-Ramos ME, Duque CA. Properties of Blue Phosphorene Nanoribbon-P3HT Polymer Heterostructures: DFT First Principles Calculations. Condensed Matter. 2023; 8(3):74. https://doi.org/10.3390/condmat8030074
Chicago/Turabian StyleTuriján-Clara, Benita, Julián D. Correa, Miguel E. Mora-Ramos, and Carlos A. Duque. 2023. "Properties of Blue Phosphorene Nanoribbon-P3HT Polymer Heterostructures: DFT First Principles Calculations" Condensed Matter 8, no. 3: 74. https://doi.org/10.3390/condmat8030074
APA StyleTuriján-Clara, B., Correa, J. D., Mora-Ramos, M. E., & Duque, C. A. (2023). Properties of Blue Phosphorene Nanoribbon-P3HT Polymer Heterostructures: DFT First Principles Calculations. Condensed Matter, 8(3), 74. https://doi.org/10.3390/condmat8030074






