Simple Explanation of Cuprates Linear Magnetoresistance Enigma
Abstract
1. Introduction
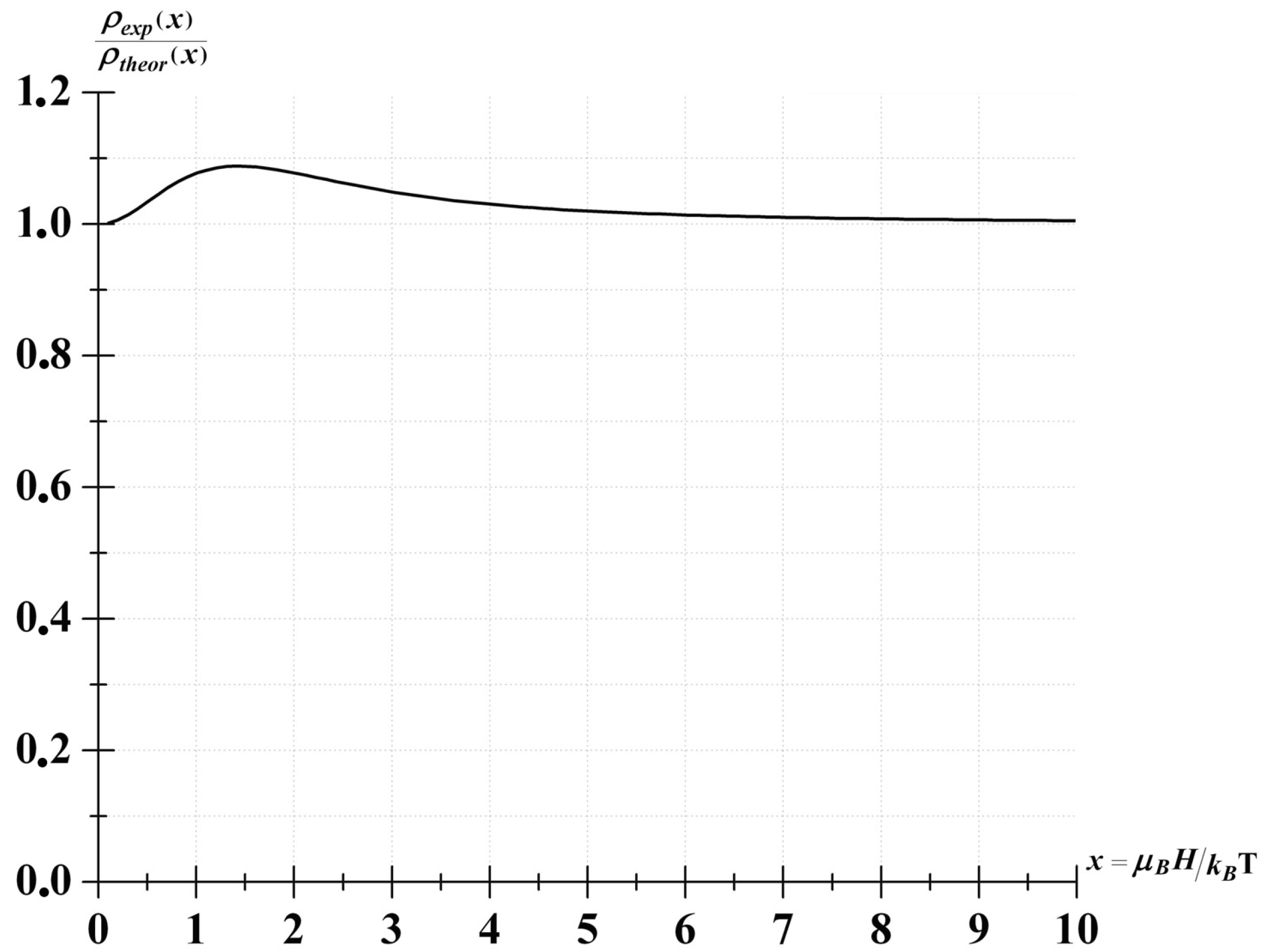
2. Results
3. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Hayes, I.M.; McDonald, R.D.; Breznay, N.P.; Helm, T.; Moll, P.J.W.; Wartenbe, M.; Shekhter, A.; Analytis, J.G. Scaling between magnetic field and temperature in the high-temperature superconductor BaFe2(As1-xPx)2. Nat. Phys. 2016, 12, 916–919. [Google Scholar] [CrossRef]
- Maksimovic, N.; Hayes, I.M.; Nagarajan, V.; Analytis, J.G.; Koshelev, A.E.; Singleton, J.; Lee, Y.; Schenkel, T. Magnetoresistance Scaling and the Origin of H-Linear Resistivity in BaFe2(As1-xPx)2. Phys. Rev. X 2020, 10, 041062. [Google Scholar] [CrossRef]
- Licciardello, S.; Maksimovic, N.; Ayres, J.; Buhot, J.; Čulo, M.; Bryant, B.; Kasahara, S.; Matsuda, Y.; Shibauchi, T.; Nagarajan, V.; et al. Coexistence of orbital and quantum critical magnetoresistance in FeSe1-xSx. Phys. Rev. Res. 2019, 1, 023011. [Google Scholar] [CrossRef]
- Yang, C.; Liu, H.; Liu, Y.; Wang, J.; Qiu, D.; Wang, S.; Wang, Y.; He, Q.; Li, X.; Li, P.; et al. Signatures of a strange metal in a bosonic system. Nature 2022, 601, 205–221. [Google Scholar] [CrossRef] [PubMed]
- Giraldo-Gallo, P.; Galvis, J.A.; Stegen, Z.; Modic, K.A.; Balakirev, F.F.; Betts, J.B.; Lian, X.; Moir, C.; Riggs, S.C.; Wu, J.; et al. Scale-invariant magnetoresistance in a cuprate superconductor. Science 2018, 361, 479–481. [Google Scholar] [CrossRef] [PubMed]
- Batlogg, B. Physical Properties of High-Tc Superconductors. Phys. Today 1991, 44, 44. [Google Scholar] [CrossRef]
- Iye, Y. Transport Properties of High-Tc Cuprates. In Physical Properties of High Temperature Superconductors III; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1992; pp. 285–361. [Google Scholar] [CrossRef]
- Greene, R.L.; Mandal, P.R.; Poniatowski, N.R.; Sarkar, T. The Strange Metal State of the Electron-Doped Cuprates. Annu. Rev. Condens. Matter. Phys. 2020, 11, 213. [Google Scholar] [CrossRef]
- Lakhno, V.D. High-Temperature Superconductivity: Bipolaron Mechanism; De Gruyter: Berlin, Germany; Boston, MA, USA, 2022. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translation-Invariant Bipolarons and Charge Density Waves in High-Temperature Superconductors. Front. Phys. 2021, 9, 662926. [Google Scholar] [CrossRef]
- Kubo, R. Statistical Mechanics. An Advanced Course with Problems and Solutions; North-Holland Publishing Company: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Pippard, A.B. Magnetoresistance in Metals; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Ayres, J.; Berben, M.; Čulo, M.; Hsu, Y.-T.; van Heumen, E.; Huang, Y.; Zaanen, J.; Kondo, T.; Takeuchi, T.; Cooper, J.R.; et al. Incoherent transport across the strange-metal regime of highly overdoped cuprates. Nature 2021, 595, 661–666. [Google Scholar] [CrossRef] [PubMed]
- Zaanen, J. Why the temperature is high. Nature 2004, 430, 512–513. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakhno, V.D. Simple Explanation of Cuprates Linear Magnetoresistance Enigma. Condens. Matter 2022, 7, 64. https://doi.org/10.3390/condmat7040064
Lakhno VD. Simple Explanation of Cuprates Linear Magnetoresistance Enigma. Condensed Matter. 2022; 7(4):64. https://doi.org/10.3390/condmat7040064
Chicago/Turabian StyleLakhno, Victor D. 2022. "Simple Explanation of Cuprates Linear Magnetoresistance Enigma" Condensed Matter 7, no. 4: 64. https://doi.org/10.3390/condmat7040064
APA StyleLakhno, V. D. (2022). Simple Explanation of Cuprates Linear Magnetoresistance Enigma. Condensed Matter, 7(4), 64. https://doi.org/10.3390/condmat7040064