Abstract
In functional materials such as thermoelectric materials and superconductors, the interplay between functionality, electronic structure, and phonon characteristics is one of the key factors to improve functionality and to understand the underlying mechanisms. In the first part of this article, we briefly review investigations on lattice anharmonicity in functional materials on the basis of the Grüneisen parameter (γG). We show that γG can be a good index for large lattice anharmonicity and for detecting a change in anharmonicity amplitude in functional materials. Then, we show original results on the estimation of γG for recently developed high-entropy alloy-type (HEA-type) functional materials with a layered structure and a NaCl-type structure. As a common trend for those two systems with two- and three-dimensional structures, we found that γG increased with a slight increase in the configurational entropy of mixing (ΔSmix) and then decreased with increasing ΔSmix in the high-entropy region.
1. Introduction
1.1. Thermoelectric Materials and Superconductors
In the last two decades, the development of effective energy-creating and energy-saving technologies has supplied interesting tools to solve the energy problem and to prevent climate change. One of the solutions is represented by thermoelectric (TE) materials and modules [1,2]. TE modules allow the direct conversion of unused thermal energy into useful electrical power, which can help to reduce carbon dioxide emissions and contribute to a more sustainable society. However, the performance of TE devices needs to be further improved for their practical application, and thus, the development of new TE materials that can allow us to fabricate high-performance TE devices is needed. To estimate the performance of TE materials, dimensionless figure-of-merit (ZT), which is calculated by the following Formula (1), is essential.
where S, σ, κ, and T are Seebeck coefficient, electrical conductivity, thermal conductivity, and absolute temperature, respectively. Generally, κ is considered as the sum of κel and κph, which are contributed by electron (mobile carrier) and phonon. Since κel can be controlled by the modification of the electronic transport properties, as described by the Wiedemann–Franz law [3], finding a material with essentially low κph with a large S2σ has been one of the strategies for developing high-ZT materials, typically with ZT ˃ 1 [1]. One of the key strategies for improving the TE properties is creating a layered structure. Several layered compounds, such as Bi2Te3, Co oxides, and CsBi4Te6, exhibit high thermoelectric performance [4,5,6,7]. In layered systems, low-dimensional electronic states, a structure composed of a stacking of sheets, and/or a large unit cell could be advantageous for producing high TE properties. In addition, nano-structuring and band convergence have been found to be effective to improve ZT in TE materials such as PbTe [2,8]. Another way to reduce κph is the use of lattice anharmonicity [9,10,11,12]. This strategy is relatively new, but various TE materials have been discovered to exhibit a high TE performance [13,14,15]. Recently, the introduction of high-entropy states in TE materials has been developed [2,16,17,18,19,20]. Due to the introduced disorder, κph is expected to be largely suppressed, and a high ZT~2 is observed in high-entropy alloy-type (HEA-type) chalcogenides [19]. However, a strategy to obtain a low κph by entropy control or the effect on anharmonicity has not been established. Therefore, in this article, we addressed this issue on HEA-type TE materials using the Grüneisen parameter (γG) [21], which will be reviewed in the next section.
Other functional materials important for solving the energy problem are the superconductors (SC). As it is well known, SCs exhibit zero-resistivity states at temperatures lower than their SC transition temperature (Tc). For most superconductors, SC states emerge through the formation of electron pairs called Cooper pairs, which is achieved via electron–phonon interactions [22]. Therefore, the mechanisms of superconductivity mediated by phonons for most superconductors are classified as being of the conventional type. Since 1986, high-Tc SCs were discovered in Cu-based [23] and Fe-based [24] SCs, and their SC mechanisms are believed to be unconventional, namely, not mediated by phonons. However, conventional mechanisms have been regarded as a promising way to achieve a high Tc due to the recent development of hydrogen-based SC materials under extremely high pressure [25,26]. In addition, lattice anharmonicity has been considered as a key factor for SC in hydrogen-based materials [27]. Therefore, the understanding of lattice anharmonicity in SCs is also an important issue. As in HEA-type TE materials, the effect of high entropy has recently been introduced in various SC [28,29,30,31,32,33,34,35,36,37]. In HEA-type SCs, the effect of disorder on electronic and phonon characteristics and the modification of anharmonicity have not been addressed yet. Therefore, knowledge about the relationship between high-entropy states and anharmonicity would be useful for further design of SCs with a high Tc.
Motivated by this background, we studied the anharmonicity of two-dimensional and three-dimensional systems with different configurational entropy of mixing, from zero entropy to HEA states. To investigate the evolution of anharmonicity with the increase in configurational entropy, we used γG in this study. As a conclusion, we propose that anharmonicity in both two- and three-dimensional structures can be modified by the increase in configurational entropy. The suppression of anharmonicity in HEA states would be a common feature in HEA-type materials with different structural dimensionalities.
1.2. Grüneisen Parameter (γG)
The γG of inorganic materials is calculated using the following formula; γG = βVBVmol/CV, where βV, B, Vmol, and CV are the volume thermal expansion coefficient, the bulk modulus, the molar volume, and the specific heat, respectively. The parameters needed for the estimation of γG are calculated as follows
In the formulas, dV/dT, ρ, vL, vs, vm, θD, h, kB, n, NA, and M denote the temperature gradient of the lattice volume, the density of the material, the longitudinal sound velocity, the shear sound velocity, the average sound velocity, the Debye temperature, the Plank’s constant, the Boltzmann’s constant, the number of atoms in the molecule (formula unit), the Avogadro’s constant, and the molecular weight (per formula unit). Although the absolute value of γG of functional materials depends on their crystal structure or constituent elements, at least, the value becomes a good index for discussing the evolution of lattice anharmonicity by doping, pressurizing, or element substitution in similar compounds.
For example, in the metal telluride system Pb1−xSnxTe, which is a TE material family [8] and a parent phase of SCs with topological electronic states [38,39], the solution of Sn and Pb results in an increase of γG: γG = 1.5, 2.5, 2.8, and 2.1 for x = 0, 0.25, 0.5, and 1 [40]. By the enhanced lattice anharmonicity in the alloy phase (x = 0.25 and 0.5), κph is clearly suppressed, and the effect was explained by the changes in γG [40]. In our previous study on LaOBiS2−xSex, which is a TE system [15] and parent phase of layered SCs [41], we revealed that the anharmonic lattice vibration is the origin of a low κph, using neutron inelastic scattering [12]. By partial Se substitution in LaOBiS2−xSex, phonon softening was observed, and κph decreased with the decrease of the low-energy phonon energy. This trend was reproduced by the Se concentration dependence of γG in LaOBiS2−xSex [42]. As described above, estimation of γG is a good way to investigate the evolution of lattice anharmonicity in functional materials. Therefore, in this article, we investigated γG for HEA-type compounds, because these materials, including TE and SC materials, have recently been drawing attention as electronic materials. Here, we estimated γG for the layered BiS2-based system REO0.7F0.3BiS2 with an HEA-type RE (rare-earth) site and for Mte with an HEA-type M (metal) site.
1.3. Motivation of the Study
In our previous work on RE(O,F)BiS2, we synthesized polycrystalline samples of REO0.5F0.5BiS2 with different configurational entropy of mixing (ΔSmix) at the RE site [28], according to a compositional guideline established for alloy-based HEAs [43,44], where the HEA composition is defined as one containing five or more elements with a composition range of 5–35%; ΔSmix is defined as ΔSmix = −R Σi ci ln ci, where ci and R are the compositional ratio and the gas constant, respectively [44]. Some of the alloy-based HEAs exhibit superconductivity, and the observed superconducting characteristics of HEAs were clearly different from those of pure or low-entropy alloys and amorphous [45,46,47,48,49,50,51,52,53,54,55,56]. Therefore, the investigation on the effects on local structure and superconducting properties by the introduction of high configurational entropy should be important for understanding superconductivity in HEA-type materials. In the layered compound RE(O,F)BiS2, by changing the number of element and composition at the RE site, samples with different ΔSmix were systematically synthesized [56]. Notably, the SC shielding fraction was improved via the suppression of in-plane Bi-S1 local disorder (local distortion) (see Figure 1e for crystal structure and the definition of the S1 site) by an increase in the ΔSmix in REO0.5F0.5BiS2 [56]. Since all the examined samples had similar lattice constants, we concluded that the increase in ΔSmix resulted in the modification of the local structure and of the SC properties of REO0.5F0.5BiS2 [56]. Therefore, the estimation of γG for RE(O,F)BiS2 would be useful to understand the effect explained above. In addition, we investigated the effect of ΔSmix on γG of metal telluride (Mte) to understand the generalizability of the effects.
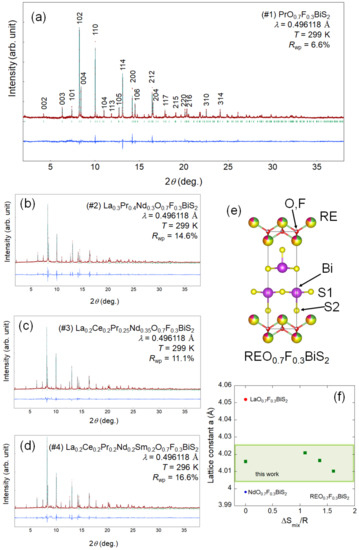
Figure 1.
SXRD patterns and Rietveld refinement results for (a) #1, (b) #2, (c) #3, and (d) #4. The numbers in Figure 1a are Miller’s indices. (e) Schematic image of the crystal structure of REO0.7F0.3BiS2. (f) ΔSmix dependence of the lattice constant a at T = 300 K for the examined samples and RE = La, Nd [41].
2. Results
In this study, we designed and synthesized polycrystalline samples of REO0.7F0.3BiS2 according to the material design concept described in [45]. We fixed F concentration to a uniform electron-doping level; the composition of REO0.7F0.3BiS2 was that typical of the superconducting phase of the BiS2-based family. Considering the in-plane chemical pressure, which was tuned by the a-axis in the BiS2-based system [41], we chose the RE site composition to prepare samples with similar constant a after trial and error. As shown in Figure 1f, the lattice constant a for all samples was similar. Information for the REO0.7F0.3BiS2 samples (sample #1–#4) is reported in Table 1. By changing the RE-site elements, ΔSmix was systematically tuned, and sample #4 could be regarded as an HEA-type compound because of ΔSmix > 1.5 R. The relative density and the values of vL were measured using high-pressure annealed samples. We found that vL slightly decreased with the increase of ΔSmix. To evaluate βV, the temperature dependence of the lattice volume was measured using synchrotron XRD (SXRD). Figure 1 shows the Rietveld refinement results of the SXRD patterns measured at temperatures near 300 K. Although small impurity peaks of RE2O2S and/or REF3 were found, the single-phase analysis appeared sufficient for the estimation of the lattice volume using the Rietveld refinement. The temperature dependence of the estimated lattice volume (V) was determined by refining all the SXRD patterns collected at different temperatures and plotted in Figure 2. V linearly increased with the increasing temperature. By linear fitting of the data and Formula (2), βV was estimated and is presented in Table 1.

Table 1.
Sample information, including nominal composition, ΔSmix/R, relative density, sound velocity (vL and vS), volume thermal expansion coefficient (βV), Debye temperature (θD), bulk modulus (B), and γG.
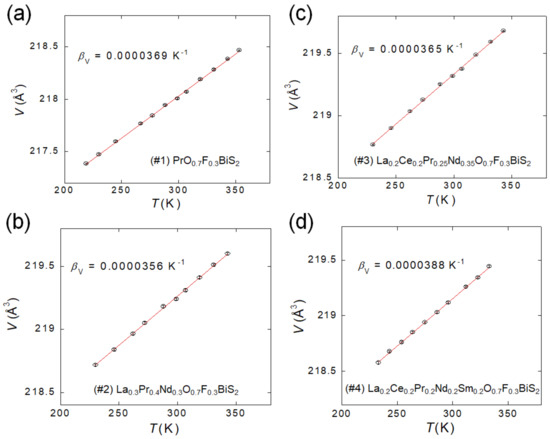
Figure 2.
Temperature (T) dependence of the lattice volume (V) for (a) #1, (b) #2, (c) #3, and (d) #4. The red lines show the linear fitting results; the estimated βV is displayed.
Figure 3 shows the results of specific heat (C) for samples #1–#4. The data were analyzed based on a model for the low-temperature region; C = γT + βT3, where γ and β are specific heat constants of electronic and phonon contributions, respectively. θD was calculated from β using the following formula
where CV was calculated using the Dulong–Petit law, which gave CV = 3R. Vmol was calculated using ideal density and molar mass estimated from the compositions. The parameters needed for calculating γG for REO0.7F0.3BiS2 are listed in Table 1. The estimated γG is plotted in Figure 4a. The γG of #2 was larger than that of #1. The trend of γG increasing with a small increase of ΔSmix is similar to the trend reported for Pb1−xSnxTe [40]. However, with a further increase of ΔSmix, γG decreased in the middle-to-high entropy region. These results would suggest that the anharmonicity in REO0.7F0.3BiS2 was enhanced in the low-entropy region and was suppressed in the middle- and HEA regions. To explore the commonality of this trend, we plotted the data presented in [40] in Figure 4b and added γG for HEA-type metal telluride (AgInSnPbBiTe5) in the plot.
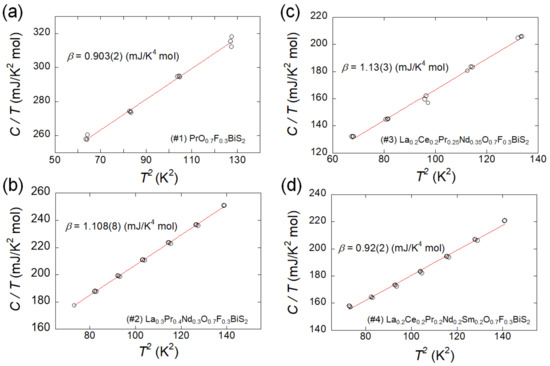
Figure 3.
T2 dependence of specific heat (C/T) for (a) #1, (b) #2, (c) #3, and (d) #4. The red lines show linear fitting results; the estimated phonon-contribution constant (β) is displayed.
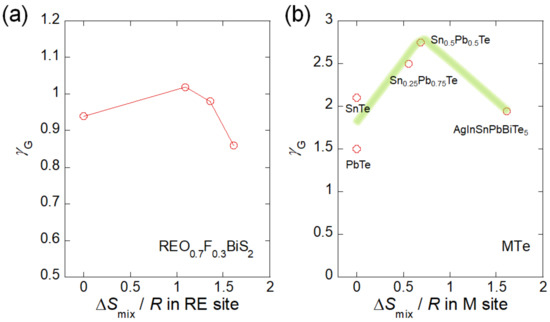
Figure 4.
Estimated γG for (a) REO0.7F0.3BiS2 and (b) MTe plotted as a function of ΔSmix/R. The data for Pb1−xSnxTe were taken from [39]. The green line is an eye guide.
The temperature dependence of SXRD and the low-temperature specific heat were measured for AgInSnPbBiTe5. Figure 5a,b shows the results of Rietveld refinement of the SXRD pattern and the temperature evolution of V. We estimated βV = 0.0000672 K−1. Figure 5c shows the low-temperature specific heat and the fitting result using the formula C = β1T3 + β2T5, which was used in previous work on MTe [57]. Using β1, θD was calculated as 136 K. The vL obtained at high density (relative density of ~100%) was 2740 m/s. The calculated B was 33.8 GPa, and the obtained γG was 1.94. The trend of γG calculated for MTe (Figure 4b) is quite interesting. As highlighted by the green line, γG of MTe decreased in the HEA region; this trend is similar to that shown in Figure 4a (REO0.7F0.3BiS2). We considered that this trend would be caused by entropy tuning and that this is possibly a universal feature for HEA-type functional materials. In the next section, we will briefly discuss the possible origin of the ΔSmix dependence of γG.
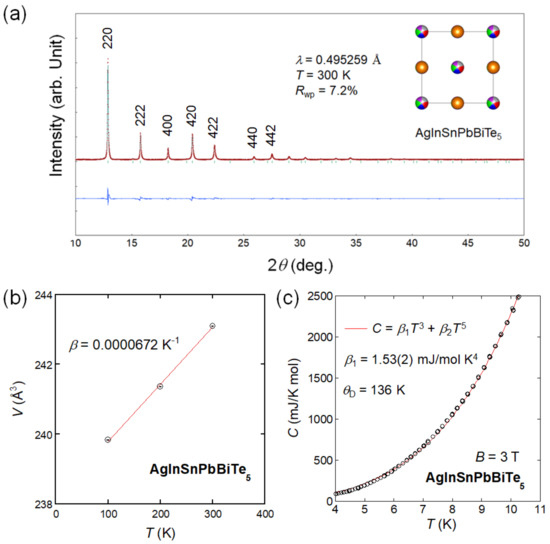
Figure 5.
(a) SXRD pattern and Rietveld refinement results for AgInSnPbBiTe5. The numbers in Figure 1a are Miller’s indices. The inset shows a schematic image of the crystal structure. (b) Temperature dependence of V for AgInSnPbBiTe5. (c) Specific heat data for AgInSnPbBiTe5 plotted as a function of T. The red line shows the fitting results.
3. Discussion
Entropy is a general concept related to various physical quantities. To discuss the phenomena observed in this work, we have to consider at least two different entropies, i.e., the above-mentioned configurational entropy of mixing and the vibrational entropy. In a field of glass transition, configurational and vibrational entropies have been separately considered and analyzed, and their interplay has been discussed [58,59,60]. On the basis of such a concept established for metallic glasses, we will discuss the origin of the results shown in Figure 4. In the low-to-middle-entropy region, the small disorder introduced by element substitution affected the average atomic positions, and weak displacements of the atoms and/or bonds were introduced. As revealed by the extended X-ray absorption fine structure of Pb1−xSnxTe [40], bond anharmonicity was enhanced in the alloyed region, resulting in a large γG. Basically, structural disorder should be enhanced by an increase in ΔSmix for both REO0.7F0.3BiS2 and MTe systems. Therefore, in the HEA region, the local structure (atomic positions and bonds) should approach glass-like states. In such a case, the total entropy in the system would be governed by the configurational entropy, resulting in the suppression of the vibrational entropy. Although the results in this study are not exhibiting direct evidence of the interplay between configurational and vibrational entropies, this concept would be useful to develop functional materials with lattice anharmonicity via entropy tuning. To establish this new concept, further investigation of γG and lattice anharmonicity of functional materials are necessary. Investigation on materials with harmonic lattice vibration is also needed.
4. Materials and Methods
The polycrystalline samples of REO0.7F0.3BiS2 (see Table 1 for the nominal composition of the examined four samples indicated as #1–#4) were synthesized by a solid-state reaction method. Powders of La2S3 (99.9%), Ce2S3 (99.9%), Pr2S3 (99.9%), Nd2S3 (99%), Sm2S3 (99.9%), Bi2O3 (99.999%), and BiF3 (99.9%) and grains of Bi (99.999%) and S (99.99%) were used. The Bi2S3 powders were synthesized by reacting Bi and S in an evacuated quartz tube. The mixture of starting materials with a nominal composition was obtained by mortar and pestle, pelletized, and sealed into an evacuated quartz tube. The samples were heated at 700 °C for 20 h for #1 and at 750 °C for 20 h for #2–#4. The obtained products were ground, pelletized, sealed into an evacuated quartz tube, and heated under the same heating conditions for homogenization. Since dense samples are needed for sound velocity measurements, the obtained REO0.7F0.3BiS2 powders were annealed at 400 °C for 15 min using a cubic–anvil-type high-pressure synthesis system under 1.5 GPa. The obtained samples had a relative density higher than 97%. For the AgInSnPbBiTe5 sample, a precursor powder was synthesized by reacting Ag (99.9%) powder and In (99.99%), Sn (99.999%), Pb (99.9%), Bi, and Te (99.999%) grains with a nominal composition at 800 °C in an evacuated quartz tube. The obtained precursor was annealed at 500 °C for 30 min under a high pressure of 3 GPa.
The synchrotron XRD (SXRD) was performed with the beamline BL02B02, SPring-8 (under proposals Nos.: 2020A0068 and 2021B1175). The wavelength of the X-ray was 0.496118(1) Å for the experiments with REO0.7F0.3BiS2 and 0.495259(1) Å for that with AgInSnPbBiTe5. The SXRD experiments were performed with a sample rotator system; the diffraction data were collected using a high-resolution one-dimensional semiconductor detector (multiple MYTHEN system [61]) with a step size of 2θ = 0.006°. The temperature of the samples was changed by a N2-gas temperature controller.
The crystal structure parameters were refined using the Rietveld method with the RIETAN-FP program [62]. The tetragonal P4/nmm (#129) model was used for the refinements for REO0.7F0.3BiS2. For AgInSnPbBiTe5, the NaCl-type (cubic Fm-3m; #225) model was used for the refinements. For the structural parameters, we reported them in earlier works [28,29,41]. The schematic images of the crystal structure were drawn using VESTA software [63].
The temperature dependence of specific heat was measured with a Physical Property Measurement System (PPMS, Quantum Design) by a relaxation method. The longitudinal sound velocity (vL) of the sample was measured on dense samples using an ultrasonic thickness detector (Satotech-2000C). The vL was corrected using the relative density of the polycrystalline sample [42], and the corrected vL was used for the calculation of γG.
5. Conclusions
In the introduction, the characteristics of TE and SC materials and the importance of lattice anharmonicity in those materials were reviewed. Motivated by recent works on the analysis of anharmonicity and γG, we investigated the structural and physical properties of REO0.7F0.3BiS2, which is a layered (two-dimensional) system, and of the NaCl-type (three-dimensional) metal telluride (MTe); for both systems, ΔSmix was controlled by changing the solution elements at the RE and M sites. By plotting the estimated ΔSmix, we found that an increase in ΔSmix in the low-to-middle-entropy region resulted in the enhancement of anharmonicity, but a further increase in ΔSmix in the middle-to-high-entropy region clearly suppressed anharmonicity. Since this trend was observed in both cases with two- and three-dimensional structures, we propose that this trend would be a universal feature of functional materials in which the configurational entropy of mixing is modified by alloying one or more sites. Further studies on γG for various functional materials are desired to confirm this concept and will open a new pathway for material development by entropy tuning.
Author Contributions
Conceptualization, A.Y. and Y.M.; methodology, F.I.A., Y.N., K.T., R.M., C.M. and Y.M.; validation, A.Y., Y.G. and Y.M.; formal analysis, F.I.A., Y.N., A.Y., M.R.K., M.Y., Y.G., A.M., K.T., R.M., Y.T., C.M. and Y.M.; investigation, F.I.A., Y.N., A.Y., M.R.K., M.Y., Y.G., A.M., K.T., R.M., Y.T., C.M. and Y.M.; resources, Y.G., K.T., R.M., Y.T., C.M. and Y.M.; data curation, F.I.A., A.Y., M.R.K., K.T., R.M., C.M. and Y.M.; writing—original draft preparation, F.I.A. and Y.M.; writing—review and editing, F.I.A., Y.N., A.Y., M.R.K., M.Y., Y.G., A.M., K.T., R.M., Y.T., C.M. and Y.M.; visualization, F.I.A. and Y.M.; supervision, A.Y., Y.G., Y.T. and Y.M.; project administration, Y.G., K.T., C.M. and Y.M.; funding acquisition, Y.G. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by Grant-in-Aid for Scientific Research (KAKENHI) (Nos. 18KK0076, 21K18834, 21H00151), JST-CREST (No. JPMJCR20Q4) and Tokyo Metropolitan Government Advanced Research (No. H31-1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data reported in this article can be provided by the corresponding author (Yoshikazu Mizuguchi) upon reasonable request.
Acknowledgments
The authors thank R. Kurita, M. Omprakash, and O. Miura for their supports in the experiments and for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Jia, N.; Tan, X.Y.; Xu, J.; Yan, Q.; Kanatzidis, M.G. Achieving Enhanced Thermoelectric Performance in Multiphase Materials. Acc. Mater. Res. 2022, 3, 237–246. [Google Scholar] [CrossRef]
- Franz, R.; Wiedemann, G. Ueber die Wärme-Leitungsfähigkeit der Metalle. Annalen Der Physik 1853, 165, 497–531. [Google Scholar]
- Goldsmid, H.J. The Electrical Conductivity and Thermoelectric Power of Bismuth Telluride. Proc. Phys. Soc. 1958, 71, 633. [Google Scholar] [CrossRef]
- Terasaki, I.; Sasago, Y.; Uchinokura, K. Large thermoelectric power in NaCo2O4 single crystals. Phys. Rev. B 1997, 56, 12685–12687. [Google Scholar] [CrossRef]
- Chung, D.Y.; Hogan, T.; Brazis, P.; Lane, M.R.; Kannewurf, C.; Bastea, M.; Uher, C.; Kanatzidis, M.G. CsBi4Te6: A High-Performance Thermoelectric Material for Low-Temperature Applications. Science 2000, 287, 1024–1027. [Google Scholar] [CrossRef] [Green Version]
- Romanenko, A.I.; Chebanova, G.E.; Chen, T.; Su, W.; Wang, H. Review of the thermoelectric properties of layered oxides and chalcogenides. J. Phys. D Appl. Phys. 2021, 55, 143001. [Google Scholar] [CrossRef]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, H.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef]
- Takabatake, T.; Suekuni, K.; Nakayama, T.; Kaneshita, E. Phonon-glass electron-crystal thermoelectric clathrates: Experiments and theory. Rev. Mod. Phys. 2014, 86, 669–716. [Google Scholar] [CrossRef] [Green Version]
- Suekuni, K.; Lee, C.H.; Tanaka, H.I.; Nishibori, E.; Nakamura, A.; Kasai, H.; Mori, H.; Usui, H.; Ochi, M.; Hasegawa, T.; et al. Retreat from Stress: Rattling in a Planar Coordination. Adv. Mater. 2018, 30, 1706230. [Google Scholar] [CrossRef]
- Li, C.; Hong, J.; May, A.F.; Bansal, D.; Chi, S.; Hong, T.; Ehlers, G.; Delaire, O. Orbitally driven giant phonon anharmonicity in SnSe. Nat. Phys. 2015, 11, 1063–1069. [Google Scholar] [CrossRef]
- Lee, C.H.; Nishida, A.; Hasegawa, T.; Nishiate, H.; Kunioka, H.; Ohira-Kawamura, S.; Nakamura, M.; Nakajima, K.; Mizuguchi, Y. Effect of rattling motion without cage structure on lattice thermal conductivity in LaOBiS2−xSex. Appl. Phys. Lett. 2018, 112, 023903. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Suekuni, K.; Tsuruta, K.; Ariga, T.; Koyano, M. Thermoelectric Properties of Mineral Tetrahedrites Cu10Tr2Sb4S13 with Low Thermal Conductivity. Appl. Phys. Express 2012, 5, 051201. [Google Scholar] [CrossRef]
- Nishida, A.; Miura, O.; Lee, C.H.; Mizuguchi, Y. High thermoelectric performance and low thermal conductivity of densified LaOBiSSe. Appl. Phys. Express 2015, 8, 111801. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Yu, Y.; Cui, J.; Liu, X.; Xie, L.; Liao, J.; Zhang, Q.; Huang, Y.; Ning, S.; Jia, B.; et al. High-entropy-stabilized chalcogenides with high thermoelectric performance. Science 2021, 371, 6531. [Google Scholar] [CrossRef]
- Yamashita, A.; Goto, Y.; Miura, A.; Moriyoshi, C.; Kuroiwa, Y.; Mizuguchi, Y. n-Type thermoelectric metal chalcogenide (Ag,Pb,Bi)(S,Se,Te) designed by multi-site-type high-entropy alloying. Mater. Res. Lett. 2021, 9, 366. [Google Scholar] [CrossRef]
- Luo, Y.; Hao, S.; Cai, S.; Slade, T.J.; Luo, Z.Z.; Dravid, V.P.; Wolverton, C.; Yan, Q.; Kanatzidis, M.G. High Thermoelectric Performance in the New Cubic Semiconductor AgSnSbSe3 by High-Entropy Engineering. J. Am. Chem. Soc. 2020, 142, 15187–15198. [Google Scholar] [CrossRef]
- Jiang, B.; Yu, Y.; Chen, H.; Cui, J.; Liu, X.; Xie, L.; He, J. Entropy engineering promotes thermoelectric performance in p-type chalcogenides. Nat. Commun. 2021, 12, 3234. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, R.; Bos, J.W.G.; Reece, M.J. Synthesis and thermoelectric properties of high-entropy half-Heusler MFe1−xCoxSb (M = equimolar Ti, Zr, Hf, V, Nb, Ta). J. Alloys Compd. 2022, 892, 162045. [Google Scholar] [CrossRef]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Annalen Der Physik 1912, 344, 257–306. [Google Scholar] [CrossRef] [Green Version]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef] [Green Version]
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba−La−Cu−O system. Z. Physik B-Condensed. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05−0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.; Eremets, M.; Troyan, I.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Gao, G.; Li, Y.; Ma, Y. Hydrogen-rich superconductors at high pressures. WIREs Comput. Mol. Sci. 2018, 8, e1330. [Google Scholar] [CrossRef]
- Setty, C.; Baggioli, M.; Zaccone, A. Anharmonic theory of superconductivity in the high-pressure materials. Phys. Rev. B 2021, 103, 094519. [Google Scholar] [CrossRef]
- Sogabe, R.; Goto, Y.; Mizuguchi, Y. Superconductivity in REO0.5F0.5BiS2 with high-entropy-alloy-type blocking layers. Appl. Phys. Express 2018, 11, 053102. [Google Scholar] [CrossRef]
- Mizuguchi, Y. Superconductivity in High-Entropy-Alloy Telluride AgInSnPbBiTe5. J. Phys. Soc. Jpn. 2019, 88, 124708. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, A.; Jha, R.; Goto, Y.; Matsuda, T.D.; Aoki, Y.; Mizuguchi, Y. An efficient way of increasing the total entropy of mixing in high-entropy-alloy compounds: A case of NaCl-type (Ag,In,Pb,Bi)Te1−xSex (x = 0.0, 0.25, 0.5) superconductors. Dalton Trans. 2020, 49, 9118–9122. [Google Scholar] [CrossRef]
- Kasem, M.R.; Hoshi, K.; Jha, R.; Katsuno, M.; Yamashita, A.; Goto, Y.; Matsuda, T.D.; Aoki, Y.; Mizuguchi, Y. Superconducting properties of high-entropy-alloy tellurides M-Te (M: Ag, In, Cd, Sn, Sb, Pb, Bi) with a NaCl-type structure. Appl. Phys. Express 2020, 13, 033001. [Google Scholar] [CrossRef]
- Mizuguchi, M.; Kasem, M.R.; Matsuda, T.D. Superconductivity in CuAl2-type Co0.2Ni0.1Cu0.1Rh0.3Ir0.3Zr2 with a high-entropy-alloy transition metal site. Mater. Res. Lett. 2021, 9, 141–147. [Google Scholar] [CrossRef]
- Kasem, M.R.; Yamashita, A.; Goto, Y.; Matsuda, T.D.; Mizuguchi, Y. Synthesis of high-entropy-alloy-type superconductors (Fe,Co,Ni,Rh,Ir)Zr2 with tunable transition temperature. J. Mater. Sci. 2021, 56, 9499–9505. [Google Scholar] [CrossRef]
- Yamashita, A.; Matsuda, T.D.; Mizuguchi, Y. Synthesis of new high-entropy alloy-type Nb3(Al, Sn, Ge, Ga, Si) superconductors. J. Alloys Compd. 2021, 868, 159233. [Google Scholar] [CrossRef]
- Shukunami, Y.; Yamashita, A.; Goto, Y.; Mizuguchi, Y. Synthesis of RE123 high-Tc superconductors with a high-entropy-alloy-type RE site. Physica C 2020, 572, 1353623. [Google Scholar] [CrossRef] [Green Version]
- Ying, T.; Yu, T.; Shiah, Y.S.; Li, C.; Li, J.; Qi, Y.; Hosono, H. High-Entropy van der Waals Materials Formed from Mixed Metal Dichalcogenides, Halides, and Phosphorus Trisulfides. J. Am. Chem. Soc. 2021, 143, 7042–7049. [Google Scholar] [CrossRef]
- Mizuguchi, Y.; Yamashita, A. Superconductivity in HEA-Type Compounds. In Advances in High-Entropy Alloys-Materials Research, Exotic Properties and Applications; Kitagawa, J., Ed.; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Bawden, L.; Cavendish, S.; Lees, M.R. Superconducting properties of the In-substituted topological crystalline insulator SnTe. Phys. Rev. B 2013, 87, 140507. [Google Scholar] [CrossRef] [Green Version]
- Mitobe, T.; Hoshi, K.; Kasem, M.R.; Kiyama, R.; Usui, H.; Yamashita, A.; Higashinaka, R.; Matsuda, T.D.; Aoki, Y.; Goto, Y.; et al. Superconductivity in In-doped AgSnBiTe3 with possible band inversion. Sci. Rep. 2021, 11, 22885. [Google Scholar] [CrossRef]
- Knura, R.; Parashchuk, T.; Yoshiasa, A.; Wojciechowski, K.T. Origins of low lattice thermal conductivity of Pb1−xSnxTe alloys for thermoelectric applications. Dalton Trans. 2021, 50, 4323–4334. [Google Scholar] [CrossRef]
- Mizuguchi, Y. Material Development and Physical Properties of BiS2-Based Layered Compounds. J. Phys. Soc. Jpn. 2019, 88, 041001. [Google Scholar] [CrossRef]
- Abbas, F.I.; Yamashita, A.; Hoshi, K.; Kiyama, R.; Kasem, M.R.; Goto, Y.; Mizuguchi, Y. Investigation of lattice anharmonicity in thermoelectric LaOBiS2−xSex through Gruneisen parameter. Appl. Phys. Express 2021, 14, 071002, Erratum in Appl. Phys. Express 2022, 15, 039302. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Tsai, M.H.; Yeh, J.W. High-Entropy Alloys: A Critical Review. Mater. Res. Lett. 2014, 2, 107–123. [Google Scholar] [CrossRef]
- Koželj, P.; Vrtnik, S.; Jelen, A.; Jazbec, S.; Jagličić, Z.; Maiti, S.; Feuerbacher, M.; Steurer, W.; Dolinšek, J. Discovery of a superconducting high-entropy alloy. Phys. Rev. Lett. 2014, 113, 107001. [Google Scholar] [CrossRef]
- Sun, L.; Cava, R.J. High-entropy alloy superconductors: Status, opportunities, and challenges. Phys. Rev. Mater. 2019, 3, 090301. [Google Scholar] [CrossRef] [Green Version]
- Kitagawa, J.; Hamamoto, S.; Ishizu, N. Cutting edge of high-entropy alloy superconductors from the perspective of materials research. Metals 2020, 10, 1078. [Google Scholar] [CrossRef]
- Marik, S.; Varghese, M.; Sajilesh, K.P.; Singh, D.; Breard, Y.; Boullay, P.; Singh, R.P. Superconductivity in a new hexagonal high-entropy alloy. Phys. Rev. Mater. 2019, 3, 060602. [Google Scholar] [CrossRef] [Green Version]
- Vrtnik, S.; Koželj, P.; Meden, A.; Maiti, S.; Steurer, W.; Feuerbacher, M.; Dolinsek, J. Superconductivity in thermally annealed Ta-Nb-Hf-Zr-Ti high-entropy alloys. J. Alloys Compd. 2017, 695, 3530–3540. [Google Scholar] [CrossRef]
- Stolze, K.; Cevallos, F.A.; Kong, T.; Cava, R.J. High-entropy alloy superconductors on an α-Mn lattice. J. Mater. Chem. C 2018, 6, 10441–10449. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, Y.; Luo, H.; Wang, Z.; Liang, X.; Yang, Z.; Wang, H.; Liu, X.; Lu, Z. Superconducting Ti15Zr15Nb35Ta35 high-entropy alloy with intermediate electron-phonon coupling. Front. Mater. 2018, 5, 72. [Google Scholar] [CrossRef] [Green Version]
- Ishizu, N.; Kitagawa, J. New high-entropy alloy superconductor Hf21Nb25Ti15V15Zr24. Results Phys. 2019, 13, 102275. [Google Scholar] [CrossRef]
- Von Rohr, F.O.; Cava, R.J. Isoelectronic substitutions and aluminium alloying in the Ta-Nb-Hf-Zr-Ti high-entropy alloy superconductor. Phys. Rev. Mater. 2018, 2, 034801. [Google Scholar] [CrossRef] [Green Version]
- Stolze, K.; Tao, J.; von Rohr, F.O.; Kong, T.; Cava, R.J. Sc–Zr–Nb–Rh–Pd and Sc–Zr–Nb–Ta–Rh–Pd high-entropy alloy superconductors on a CsCl-type lattice. Chem. Mater. 2018, 30, 906–914. [Google Scholar] [CrossRef]
- Guo, J.; Wang, H.; von Rohr, F.O.; Wang, Z.; Cai, S.; Zhou, Y.; Yang, K.; Li, A.; Jiang, S.; Wu, Q.; et al. Robust zero resistance in a superconducting high-entropy alloy at pressures up to 190 GPa. Proc. Natl. Acad. Sci. USA 2017, 114, 13144–13147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sogabe, R.; Goto, Y.; Abe, T.; Moriyoshi, C.; Kuroiwa, Y.; Miura, A.; Tadanaga, K.; Mizuguchi, Y. Improvement of superconducting properties by high mixing entropy at blocking layers in BiS2-based superconductor REO0.5F0.5BiS2. Solid State Commun. 2019, 295, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Katsuno, M.; Jha, R.; Hoshi, K.; Sogabe, R.; Goto, Y.; Mizuguchi, Y. High-Pressure Synthesis and Superconducting Properties of NaCl-Type In1−xPbxTe (x = 0–0.8). Condens. Matter 2020, 5, 14. [Google Scholar] [CrossRef] [Green Version]
- Smith, H.L.; Li, C.W.; Hoff, A.; Garrett, G.R.; Kim, D.S.; Yang, F.C.; Lucas, M.S.; Swan-Wood, T.; Lin, J.Y.Y.; Stone, M.B.; et al. Separating the configurational and vibrational entropy contributions in metallic glasses. Nat. Phys. 2017, 13, 900–905. [Google Scholar] [CrossRef]
- Gibbs, J.H.; DiMarzio, E.A. Nature of the glass transition and the glassy state. J. Chem. Phys. 1958, 28, 373–383. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Kawaguchi, S.; Takemoto, M.; Osaka, K.; Nishibori, E.; Moriyoshi, C.; Kubota, Y.; Kuroiwa, Y.; Sugimoto, K. High-throughput powder diffraction measurement system consisting of multiple MYTHEN detectors at beamline BL02B2 of SPring-8. Rev. Sci. Instrum. 2017, 88, 085111. [Google Scholar] [CrossRef]
- Izumi, F.; Momma, K. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 2007, 130, 15–20. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystalogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).