Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model
Abstract
:1. Introduction
2. Majorana BBH Model
3. Strip of Four Interacting Chains
3.1. Analytical Results
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Matrix Product Operator
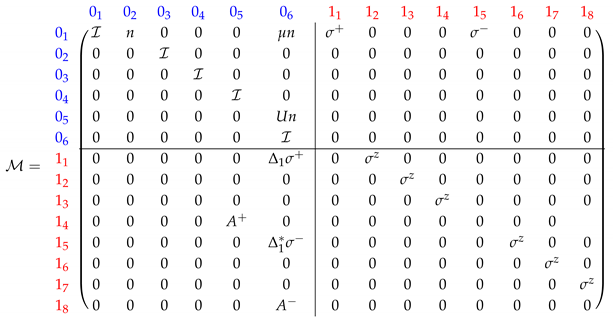
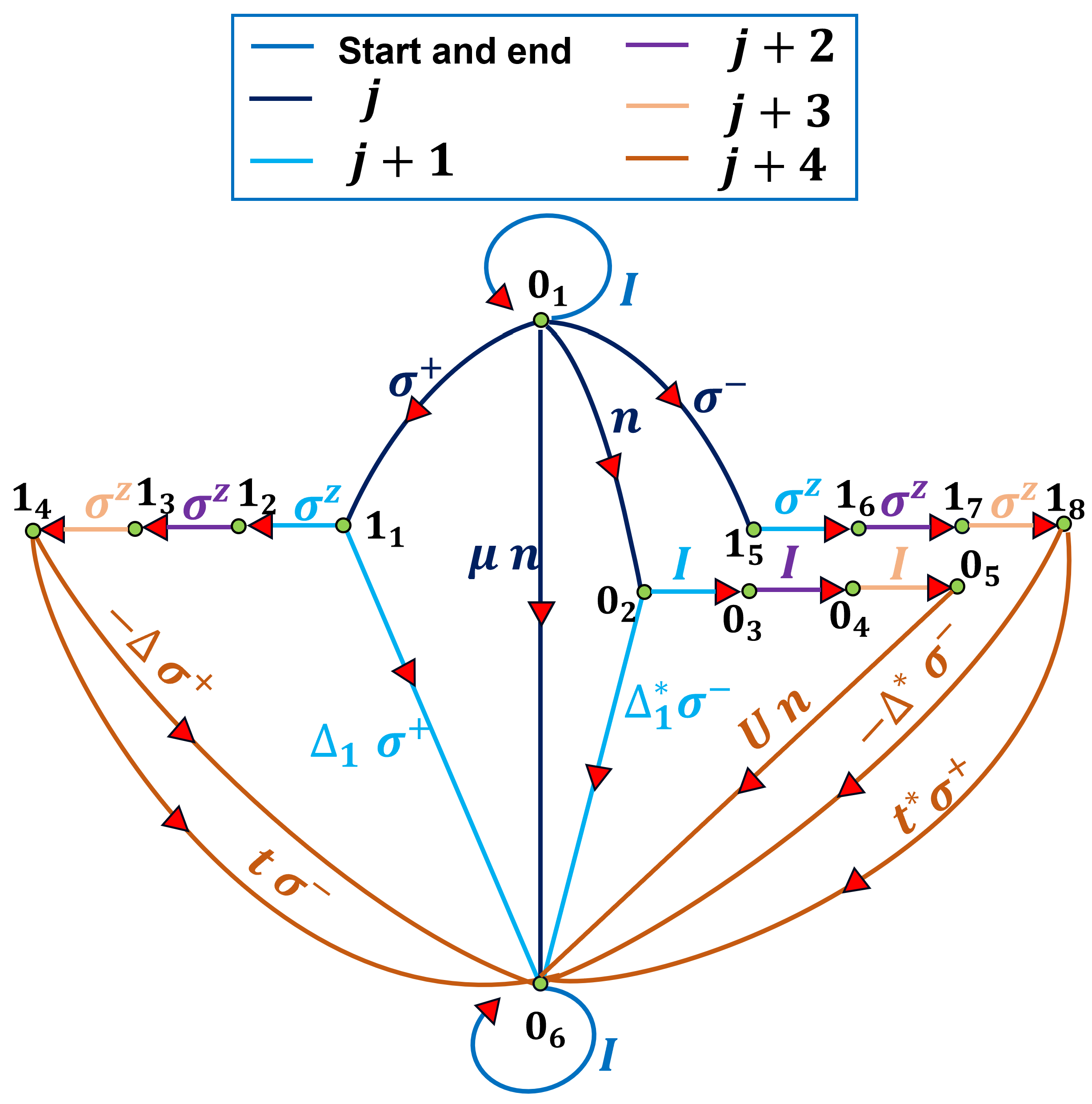
References
- Teo, J.C.Y.; Hughes, T.L. Existence of Majorana-Fermion Bound States on Disclinations and the Classification of Topological Crystalline Superconductors in Two Dimensions. Phys. Rev. Lett. 2013, 111, 047006. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Bi, R.; Wang, Z. Majorana Zero Modes Protected by a Hopf Invariant in Topologically Trivial Superconductors. Phys. Rev. Lett. 2017, 118, 147003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 2018, 97, 205136. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.H.; Stano, P.; Klinovaja, J.; Loss, D. Majorana Kramers Pairs in Higher-Order Topological Insulators. Phys. Rev. Lett. 2018, 121, 196801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- You, Y.; Litinski, D.; von Oppen, F. Higher-order topological superconductors as generators of quantum codes. Phys. Rev. B 2019, 100, 054513. [Google Scholar] [CrossRef] [Green Version]
- Pahomi, T.E.; Sigrist, M.; Soluyanov, A.A. Braiding Majorana corner modes in a second-order topological superconductor. Phys. Rev. Res. 2020, 2, 032068. [Google Scholar] [CrossRef]
- Zhang, S.B.; Rui, W.B.; Calzona, A.; Choi, S.J.; Schnyder, A.P.; Trauzettel, B. Topological and holonomic quantum computation based on second-order topological superconductors. Phys. Rev. Res. 2020, 2, 043025. [Google Scholar] [CrossRef]
- Zhang, S.B.; Calzona, A.; Trauzettel, B. All-electrically tunable networks of Majorana bound states. Phys. Rev. B 2020, 102, 100503. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [Green Version]
- Hyart, T.; van Heck, B.; Fulga, I.C.; Burrello, M.; Akhmerov, A.R.; Beenakker, C.W.J. Flux-controlled quantum computation with Majorana fermions. Phys. Rev. B 2013, 88, 035121. [Google Scholar] [CrossRef] [Green Version]
- Lian, B.; Sun, X.Q.; Vaezi, A.; Qi, X.L.; Zhang, S.C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl. Acad. Sci. USA 2018, 115, 10938–10942. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muthukrishnan, A.; Stroud, C.R. Multivalued logic gates for quantum computation. Phys. Rev. A 2000, 62, 052309. [Google Scholar] [CrossRef] [Green Version]
- Maiellaro, A.; Citro, R. Topological Edge States of a Majorana BBH Model. Condens. Matter 2021, 6, 15. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altland, A.; Zirnbauer, M.R. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 1997, 55, 1142–1161. [Google Scholar] [CrossRef] [Green Version]
- Trifunovic, L.; Brouwer, P.W. Higher-Order Topological Band Structures. Phys. Status Solidi (b) 2021, 258, 2000090. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Liu, F.; Wakabayashi, K. Novel Topological Phase with a Zero Berry Curvature. Phys. Rev. Lett. 2017, 118, 076803. [Google Scholar] [CrossRef] [Green Version]
- Jünemann, J.; Piga, A.; Ran, S.J.; Lewenstein, M.; Rizzi, M.; Bermudez, A. Exploring Interacting Topological Insulators with Ultracold Atoms: The Synthetic Creutz-Hubbard Model. Phys. Rev. X 2017, 7, 031057. [Google Scholar] [CrossRef]
- Stoudenmire, E.M.; Alicea, J.; Starykh, O.A.; Fisher, M.P. Interaction effects in topological superconducting wires supporting Majorana fermions. Phys. Rev. B 2011, 84, 014503. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, S.C. Simplified Topological Invariants for Interacting Insulators. Phys. Rev. X 2012, 2, 031008. [Google Scholar] [CrossRef]
- Kraus, C.V.; Dalmonte, M.; Baranov, M.A.; Läuchli, A.M.; Zoller, P. Majorana Edge States in Atomic Wires Coupled by Pair Hopping. Phys. Rev. Lett. 2013, 111, 173004. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Geier, M.; Ingham, J.; Scammell, H. Higher-order topological superconductivity from repulsive interactions in kagome and honeycomb systems. 2D Mater. 2021, 9, 015031. [Google Scholar] [CrossRef]
- Scammell, H.D.; Ingham, J.; Geier, M.; Li, T. Intrinsic first and higher-order topological superconductivity in a doped topological insulator. arXiv 2021, arXiv:2111.07252. [Google Scholar]
- Liu, H.; Franca, S.; Moghaddam, A.G.; Hassler, F.; Fulga, I.C. Network model for higher-order topological phases. Phys. Rev. B 2021, 103, 115428. [Google Scholar] [CrossRef]
- Pasek, M.; Chong, Y.D. Network models of photonic Floquet topological insulators. Phys. Rev. B 2014, 89, 075113. [Google Scholar] [CrossRef] [Green Version]
- De Beule, C.; Dominguez, F.; Recher, P. Aharonov-Bohm Oscillations in Minimally Twisted Bilayer Graphene. Phys. Rev. Lett. 2020, 125, 096402. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Zhou, L.; Pan, J.; Gong, J. Coupled-wire construction of static and Floquet second-order topological insulators. Phys. Rev. B 2019, 99, 045441. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Vega, M.; Kumar, A.; Seradjeh, B. Higher-order Floquet topological phases with corner and bulk bound states. Phys. Rev. B 2019, 100, 085138. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef] [Green Version]
- Liang, G.Q.; Chong, Y.D. Optical Resonator Analog of a Two-Dimensional Topological Insulator. Phys. Rev. Lett. 2013, 110, 203904. [Google Scholar] [CrossRef] [PubMed]
- Chalker, J.T.; Coddington, P.D. Percolation, quantum tunnelling and the integer Hall effect. J. Phys. C Solid State Phys. 1988, 21, 2665–2679. [Google Scholar] [CrossRef]
- Afzal, S.; Zimmerling, T.J.; Ren, Y.; Perron, D.; Van, V. Realization of Anomalous Floquet Insulators in Strongly Coupled Nanophotonic Lattices. Phys. Rev. Lett. 2020, 124, 253601. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Gao, Z.; Shi, X.; Yang, Z.; Lin, X.; Xu, H.; Joannopoulos, J.D.; Soljačić, M.; Chen, H.; Lu, L.; et al. Probing topological protection using a designer surface plasmon structure. Nat. Commun. 2016, 7, 11619. [Google Scholar] [CrossRef]
- Pillay, J.C.; McCulloch, I.P. Topological phase transition and the effect of Hubbard interactions on the one-dimensional topological Kondo insulator. Phys. Rev. B 2018, 97, 205133. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Moon, E.; Isobe, H.; Nagaosa, N. Quantum criticality of topological phase transitions in three-dimensional interacting electronic systems. Nat. Phys. 2014, 10, 774–778. [Google Scholar] [CrossRef] [Green Version]
- Xue, F.; Zhang, X.X. Instability and topological robustness of Weyl semimetals against Coulomb interaction. Phys. Rev. B 2017, 96, 195160. [Google Scholar] [CrossRef] [Green Version]
- Stoudenmire, E.; White, S.R. Studying Two-Dimensional Systems with the Density Matrix Renormalization Group. Annu. Rev. Condens. Matter Phys. 2012, 3, 111–128. [Google Scholar] [CrossRef] [Green Version]
- McCulloch, I.P. From density-matrix renormalization group to matrix product states. J. Stat. Mech. Theory Exp. 2007, 2007, P10014. [Google Scholar] [CrossRef] [Green Version]
- Orús, R. A practical introduction to tensor networks: Matrix product states and projected entangled pair states. Ann. Phys. 2014, 349, 117–158. [Google Scholar] [CrossRef] [Green Version]
- Silvi, P.; Tschirsich, F.; Gerster, M.; Jünemann, J.; Jaschke, D.; Rizzi, M.; Montangero, S. The Tensor Networks Anthology: Simulation techniques for many-body quantum lattice systems. SciPost Phys. Lect. Notes 2019. [Google Scholar] [CrossRef] [Green Version]
- Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. [Google Scholar] [CrossRef] [Green Version]
- Franchini, F. An Introduction to Integrable Techniques for One-Dimensional Quantum Systems. Lect. Notes Phys. 2017. [Google Scholar] [CrossRef] [Green Version]
- Maiellaro, A.; Marino, A.; Illuminati, F. Squashed entanglement: Order parameter for topological superconductors. arXiv 2022, arXiv:2201.12035. [Google Scholar]
- Maiellaro, A.; Romeo, F.; Citro, R. Topological phase diagram of a Kitaev ladder. Eur. Phys. J. Spec. Top. 2018, 227, 1397–1404. [Google Scholar] [CrossRef]
- Maiellaro, A.; Romeo, F.; Citro, R. Topological phases of a Kitaev tie. Eur. Phys. J. Spec. Top. 2020, 229, 637. [Google Scholar] [CrossRef]
- Paeckel, S.; Köhler, T.; Manmana, S.R. Automated construction of U(1)-invariant matrix-product operators from graph representations. SciPost Phys. 2017, 3, 035. [Google Scholar] [CrossRef] [Green Version]
- Pirvu, B.; Murg, V.; Cirac, J.I.; Verstraete, F. Matrix product operator representations. New J. Phys. 2010, 12, 025012. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiellaro, A.; Illuminati, F.; Citro, R. Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model. Condens. Matter 2022, 7, 26. https://doi.org/10.3390/condmat7010026
Maiellaro A, Illuminati F, Citro R. Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model. Condensed Matter. 2022; 7(1):26. https://doi.org/10.3390/condmat7010026
Chicago/Turabian StyleMaiellaro, Alfonso, Fabrizio Illuminati, and Roberta Citro. 2022. "Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model" Condensed Matter 7, no. 1: 26. https://doi.org/10.3390/condmat7010026
APA StyleMaiellaro, A., Illuminati, F., & Citro, R. (2022). Topological Phases of an Interacting Majorana Benalcazar–Bernevig–Hughes Model. Condensed Matter, 7(1), 26. https://doi.org/10.3390/condmat7010026






