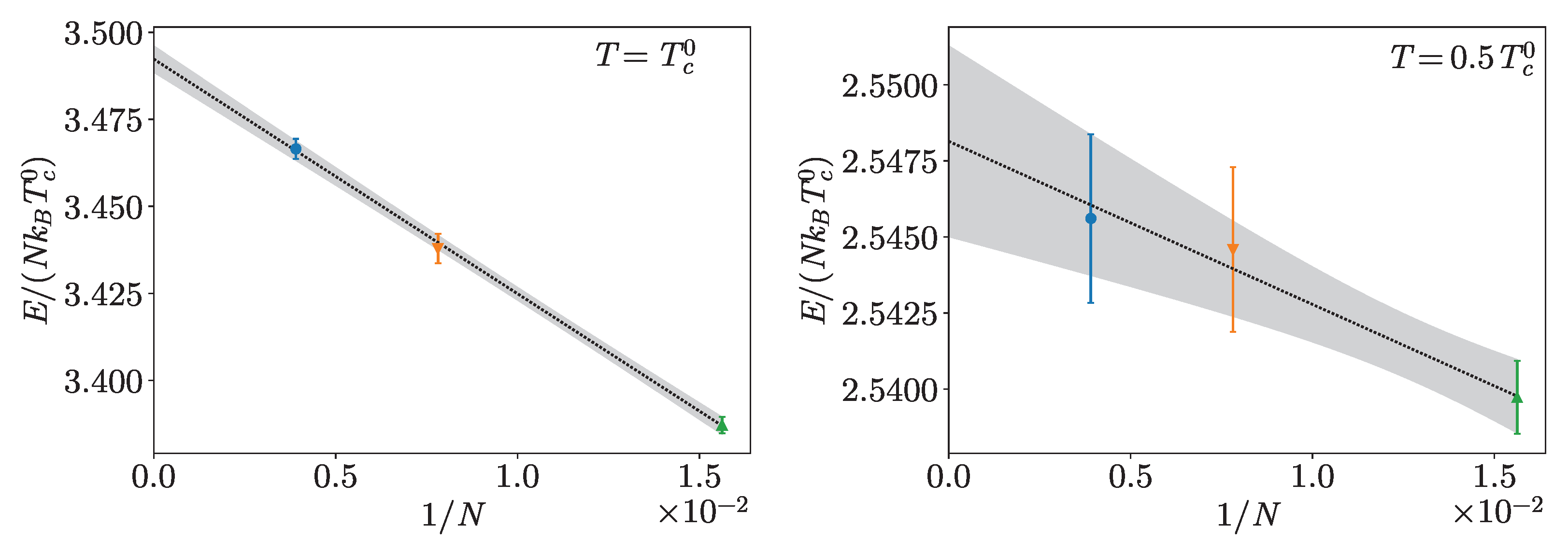Path-Integral Monte Carlo Worm Algorithm for Bose Systems with Periodic Boundary Conditions
Abstract
1. Introduction
2. Path Integral Monte Carlo
2.1. Path Integral for One Particle with Periodic Boundary Conditions
2.2. Path Integral for N Bosons with Periodic Boundary Conditions
2.3. Worm Algorithm
2.4. Monte Carlo Updates
2.4.1. Translate
2.4.2. Redraw
2.4.3. Open/Close
- Select the particle index from a uniform random distribution.
- Select a time slice from a uniform random distribution, with the positive integer a tunable parameter.
- Propose a new value for the position of the new head by displacing the point by a quantity uniformly sampled in the space , with an adjustable parameter.
- Redraw the portion of the polymer going from the bead to the bead by constructing a free particle path starting at and ending after steps at with the staging algorithm described above.
- Accept the update with probability
- Identify the particle indices and corresponding to the head and the tail of the worm, respectively.
- Select a time slice from a uniform random distribution.
- Find the periodic image of the first bead of the tail that is the nearest to the head bead and check whether their difference is within in every direction. If that is the case set , otherwise abort the update.
- Redraw the portion of the polymer going from the bead to the bead by constructing a free particle path starting at and ending after steps at with the staging algorithm.
- Accept the update with probability
2.4.4. Swap
2.4.5. Move Head
2.4.6. Move Tail
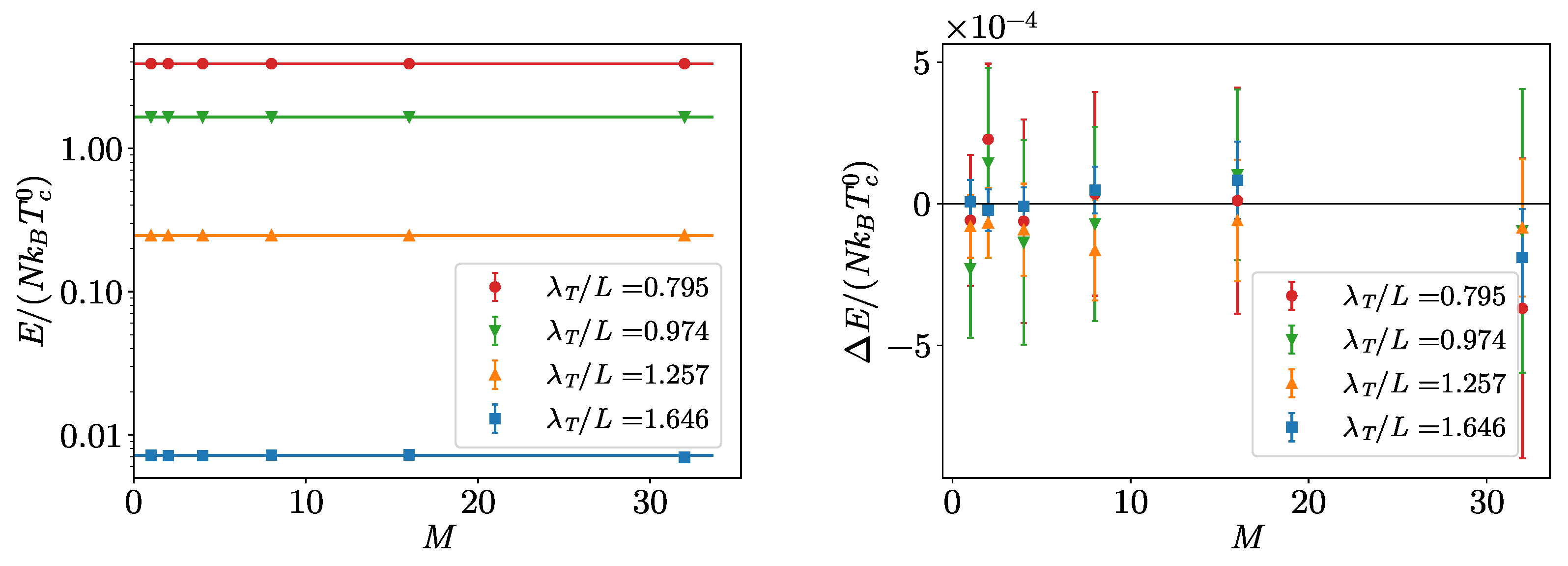
3. Non-Interacting Bose Gas
Benchmarks
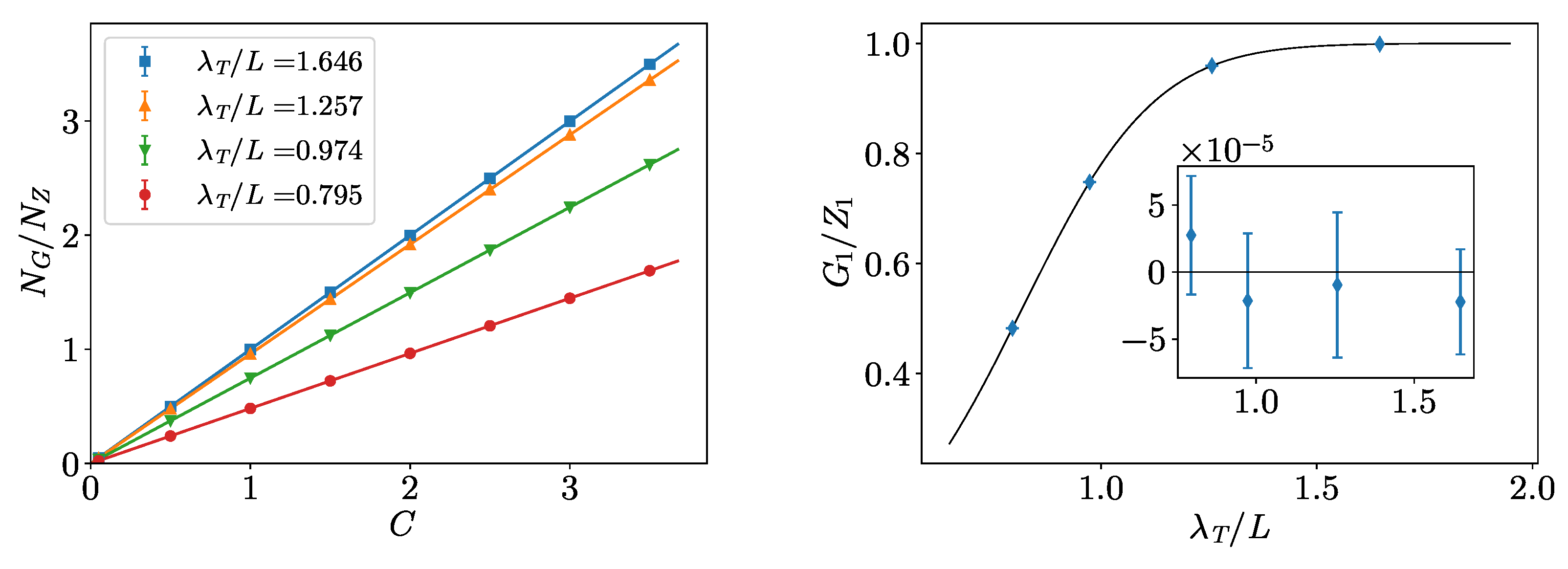
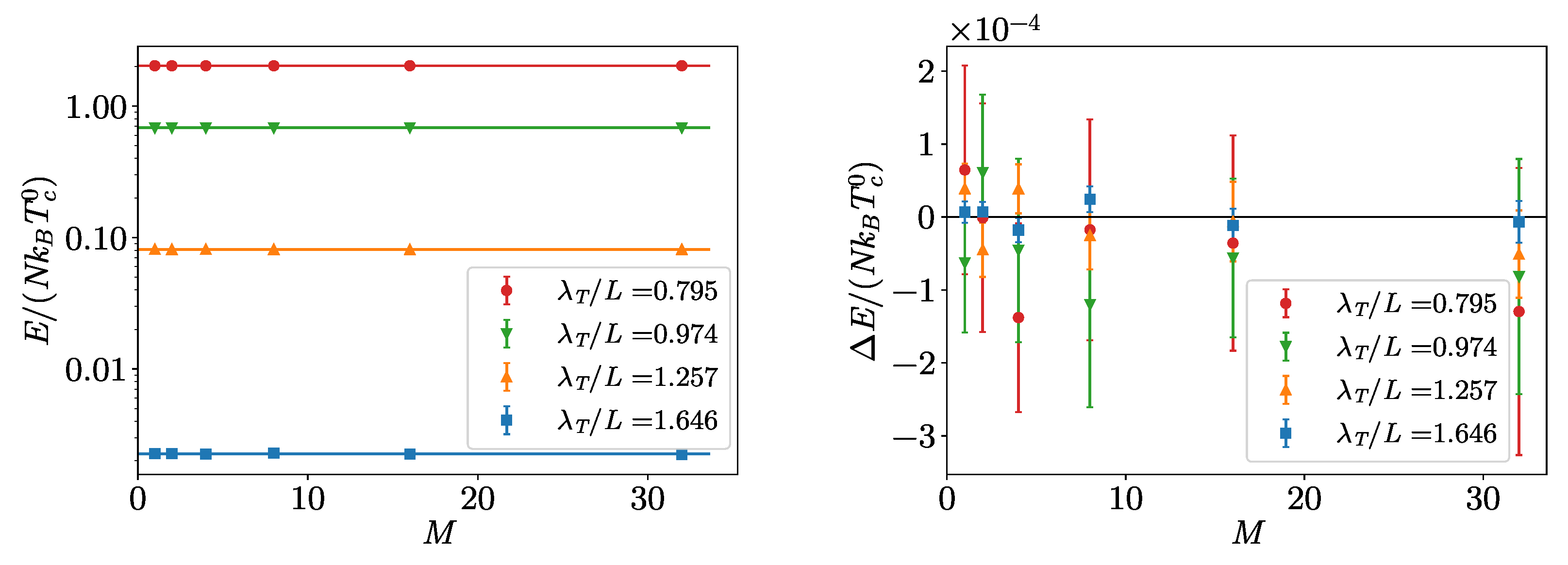
4. Hard-Spheres Bose Gas
Benchmarks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Energy
Appendix A.2. Pressure
References
- Pollock, E.L.; Ceperley, D.M. Simulation of quantum many-body systems by path-integral methods. Phys. Rev. B 1984, 30, 2555. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Pollock, E.L. Path-integral computation of the low-temperature properties of liquid 4He. Phys. Rev. Lett. 1986, 56, 351–354. [Google Scholar] [CrossRef]
- Ceperley, D.M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 1995, 67, 279–355. [Google Scholar] [CrossRef]
- Pollock, E.L.; Ceperley, D.M. Path-integral computation of superfluid densities. Phys. Rev. B 1987, 36, 8343–8352. [Google Scholar] [CrossRef] [PubMed]
- Boninsegni, M. Permutation Sampling in Path Integral Monte Carlo. J. Low Temp. Phys. 2005, 141, 27–46. [Google Scholar] [CrossRef]
- Prokof’ev, N.; Svistunov, B.; Tupitsyn, I.S. “Worm” algorithm in quantum Monte Carlo simulations. Phys. Lett. A 1998, 238, 253–257. [Google Scholar] [CrossRef]
- Prokof’ev, N.; Svistunov, B. Worm algorithms for classical statistical models. Phys. Rev. Lett. 2001, 87, 160601. [Google Scholar] [CrossRef]
- Boninsegni, M.; Prokof’ev, N.; Svistunov, B. Worm algorithm and diagrammatic Monte Carlo: A new approach to continuous-space path integral Monte Carlo simulations. Phys. Rev. E 2006, 74, 036701. [Google Scholar] [CrossRef]
- Boninsegni, M.; Prokof’ev, N.; Svistunov, B. Worm algorithm for continuous-space path integral Monte Carlo simulations. Phys. Rev. Lett. 2006, 96, 070601. [Google Scholar] [CrossRef]
- Cinti, F.; Cappellaro, A.; Salasnich, L.; Macrì, T. Superfluid Filaments of Dipolar Bosons in Free Space. Phys. Rev. Lett. 2017, 119, 215302. [Google Scholar] [CrossRef]
- Cinti, F.; Wang, D.-W.; Boninsegni, M. Phases of dipolar bosons in a bilayer geometry. Phys. Rev. A 2017, 95. [Google Scholar] [CrossRef]
- Bombín, R.; Mazzanti, F.; Boronat, J. Berezinskii-Kosterlitz-Thouless transition in two-dimensional dipolar stripes. Phys. Rev. A 2019, 100, 063614. [Google Scholar] [CrossRef]
- Cinti, F.; Jain, P.; Boninsegni, M.; Micheli, A.; Zoller, P.; Pupillo, G. Supersolid Droplet Crystal in a Dipole-Blockaded Gas. Phys. Rev. Lett. 2010, 105, 135301. [Google Scholar] [CrossRef] [PubMed]
- Saccani, S.; Moroni, S.; Boninsegni, M. Phase diagram of soft-core bosons in two dimensions. Phys. Rev. B 2011, 83, 092506. [Google Scholar] [CrossRef]
- Carleo, G.; Boéris, G.; Holzmann, M.; Sanchez-Palencia, L. Universal Superfluid Transition and Transport Properties of Two-Dimensional Dirty Bosons. Phys. Rev. Lett. 2013, 111, 050406. [Google Scholar] [CrossRef]
- Cinti, F.; Macrì, T.; Lechner, W.; Pupillo, G.; Pohl, T. Defect-induced supersolidity with soft-core bosons. Nat. Commun. 2014, 5, 3235. [Google Scholar] [CrossRef] [PubMed]
- Pascual, G.; Boronat, J. Quasiparticle Nature of the Bose Polaron at Finite Temperature. Phys. Rev. Lett. 2021, 127, 205301. [Google Scholar] [CrossRef]
- Boninsegni, M.; Prokof’ev, N.; Svistunov, B. Superglass Phase of 4He. Phys. Rev. Lett. 2006, 96, 105301. [Google Scholar] [CrossRef]
- Boninsegni, M.; Kuklov, A.B.; Pollet, L.; Prokof’ev, N.V.; Svistunov, B.V.; Troyer, M. Fate of Vacancy-Induced Supersolidity in 4He. Phys. Rev. Lett. 2006, 97, 080401. [Google Scholar] [CrossRef]
- Corboz, P.; Boninsegni, M.; Pollet, L.; Troyer, M. Phase diagram of 4He adsorbed on graphite. Phys. Rev. B 2008, 78, 245414. [Google Scholar] [CrossRef]
- Boninsegni, M. Quantum statistics and the momentum distribution of liquid parahydrogen. Phys. Rev. B 2009, 79, 174203. [Google Scholar] [CrossRef]
- Rota, R.; Boronat, J. Path Integral Monte Carlo Calculation of Momentum Distribution in Solid 4He. J. Low Temp. Phys. 2011, 162, 146–153. [Google Scholar] [CrossRef][Green Version]
- Osychenko, O.N.; Rota, R.; Boronat, J. Superfluidity of metastable glassy bulk para-hydrogen at low temperature. Phys. Rev. B 2012, 85, 224513. [Google Scholar] [CrossRef]
- Ferré, G.; Boronat, J. Dynamic structure factor of liquid 4He across the normal-superfluid transition. Phys. Rev. B 2016, 93, 104510. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Trotter, H.F. On the product of semi-groups of operators. Proc. Am. Math. Soc. 1959, 10, 545–551. [Google Scholar] [CrossRef]
- Sprik, M.; Klein, M.L.; Chandler, D. Staging: A sampling technique for the Monte Carlo evaluation of path integrals. Phys. Rev. B 1985, 31, 4234–4244. [Google Scholar] [CrossRef]
- Sakkos, K.; Casulleras, J.; Boronat, J. High order Chin actions in path integral Monte Carlo. J. Chem. Phys. 2009, 130, 204109. [Google Scholar] [CrossRef]
- Prokof’ev, N.V.; Svistunov, B.V.; Tupitsyn, I.S. Exact, complete, and universal continuous-time worldline Monte Carlo approach to the statistics of discrete quantum systems. J. Exp. Theor. Phys. 1998, 87, 310–321. [Google Scholar] [CrossRef]
- Lévy, P. Sur certains processus stochastiques homogènes. Compos. Math. 1940, 7, 283–339. [Google Scholar]
- Borrmann, P.; Franke, G. Recursion formulas for quantum statistical partition functions. J. Chem. Phys. 1993, 98, 2484–2485. [Google Scholar] [CrossRef]
- Krauth, W. Statistical Mechanics Algorithms and Computations; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover Books on Mathematics; Dover Publications: Mineola, NY, USA, 1965. [Google Scholar]
- Hansen, J.P.; Levesque, D.; Schiff, D. Fluid-Solid Phase Transition of a Hard-Sphere Bose System. Phys. Rev. A 1971, 3, 776–780. [Google Scholar] [CrossRef]
- Kalos, M.H.; Levesque, D.; Verlet, L. Helium at zero temperature with hard-sphere and other forces. Phys. Rev. A 1974, 9, 2178–2195. [Google Scholar] [CrossRef]
- Spada, G.; Pilati, S.; Giorgini, S. Thermodynamics of a dilute Bose gas: A path-integral Monte Carlo study. Phys. Rev. A 2022, 105, 013325. [Google Scholar] [CrossRef]
- Cao, J.; Berne, B.J. A new quantum propagator for hard sphere and cavity systems. J. Chem. Phys. 1992, 97, 2382–2385. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spada, G.; Giorgini, S.; Pilati, S. Path-Integral Monte Carlo Worm Algorithm for Bose Systems with Periodic Boundary Conditions. Condens. Matter 2022, 7, 30. https://doi.org/10.3390/condmat7020030
Spada G, Giorgini S, Pilati S. Path-Integral Monte Carlo Worm Algorithm for Bose Systems with Periodic Boundary Conditions. Condensed Matter. 2022; 7(2):30. https://doi.org/10.3390/condmat7020030
Chicago/Turabian StyleSpada, Gabriele, Stefano Giorgini, and Sebastiano Pilati. 2022. "Path-Integral Monte Carlo Worm Algorithm for Bose Systems with Periodic Boundary Conditions" Condensed Matter 7, no. 2: 30. https://doi.org/10.3390/condmat7020030
APA StyleSpada, G., Giorgini, S., & Pilati, S. (2022). Path-Integral Monte Carlo Worm Algorithm for Bose Systems with Periodic Boundary Conditions. Condensed Matter, 7(2), 30. https://doi.org/10.3390/condmat7020030